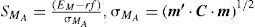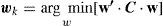¿Han sido el IBEX35 y el IPC definiciones financieramente eficientes del portafolio de mercado?

Resumen

En este trabajo se presenta un estudio inicial que cuestiona la eficiencia financiera de las aproximaciones del portafolio de mercado más empleadas en España y México (IBEX35 e IPC); se observa que podrían no considerarse como tales, con lo que se pone en duda su uso como “referencias neutrales”, según lo proponen Black y Litterman (1992), para la gestión de los mismos. Con el objeto de probar la eficiencia financiera en estos dos índices, se desarrollaron dos simulaciones de eventos discretos empleando el modelo Markowitz-Tobin-Sharpe-Lintner (Markowitz, 1987) con datos de frecuencia mensual —a partir de febrero de 2001 a diciembre de 2010— de sus acciones miembro en una ventana temporal. Los resultados fueron comparados a través del ratio de Sharpe (1966) y demostraron que, en el corto plazo, los supuestos de equilibrio no se mantienen y las aproximaciones del portafolio de mercado estudiadas resultan ineficientes en relación con otros portafolios óptimos derivados de manera simultánea.

Abstract

The present paper questions the financial efficiency of the most used market portfolio proxies in Spain and Mexico (IBEX35 and IPC) in order to determine if these can be considered a proper market portfolio proxy. The paper questions if they can be used as “neutrals”, according to Black & Litterman (1992) proposals in portfolio management. For this purpose, two discrete event simulations that use the Markowtiz-Tobin-Sharpe-Linter model (Markowitz, 1987, p.5) are performed with monthly data of the stock members of these indices in a February 2001 to December 2010 time window. The results are compared by using the Sharpe ratio (Sharpe, 1966) and show that the equilibrium assumptions in the market do not hold, leading to conclude that these market portfolio proxies are inefficient.

Introducción

De su propuesta en 1952, el modelo estándar de selección de portafolios de Harry Markowitz y la Teoría de la preferencia por la liquidez ante el riesgo, también conocida como el Teorema de la Separacion de James Tobin (1958), han sido el punto de referencia teórica del modelo Markowitz-Tobin-Sharpe-Lintner (MTSL) o de Portafolios Mixtos, así como de los supuestos de equilibrio propuestos de forma separada por Sharpe (1964) y Lintner (1965) para aproximar la elección racional de los inversionistas de manera agregada. Esto último llevó a la propuesta de Sharpe conocida como el Modelo de Valuación de Activos de Capital o CAPMSML,² por sus siglas en inglés, a sus formas no estándar como son el modelo de Beta Cero de Black (1972), el de liquidez de Amihud y Mendelson (1986), el de tiempo continuo de Merton (1992) y la versión para activos poco líquidos o no negociables de Heaton y Lucas (2000), por mencionar algunos modelos de CAPM no estándar.

Aunque algunos de estos supuestos de equilibrio parecen ser poco aplicables a la realidad, muchos teóricos y profesionales los han empleado para justificar la gestión pasiva de portafolios y la valuación de activos³ en este contexto; otros los han utilizado como puntos teóricos de partida o referencias neutrales para los métodos cuantitativos de administración activa de portafolios (Black y Litterman, 1992). Las primeras aproximaciones que buscaron resolver el problema de la optimización de portafolios empleando los supuestos de equilibrio⁴ son las realizadas por Treynor y Black (1973) y Elton, Gruber y Padberg (1976). Después de estas propuestas, las más recientes se deben a Black y Litterman (1992) y a Xu y Liu (2011); la segunda es un modelo enfocado a la resolución de un programa cuadrático paramétrico que atiende las llamadas restricciones de corte relacionadas con el nivel mínimo de inversión entre activos o el número de transacciones o activos permitido. El caso de interés de estas propuestas es la de Black y Litterman que emplea los supuestos de equilibrio de mercado no como parte de un contexto teó-rico para la administración de portafolios, la valuación de activos o la asignación de los mismos, sino como referencias neutrales o puntos de partida de la optimización, al utilizar, una transformación bayesiana de los insumos.

El empleo de las betas (β) de mercado como una medida de riesgo de activo y el desarrollo del CAPM para valuar con esta lógica son notoriamente criticados —al principio— por el propio Black, junto con Jensen y Scholes (1972) debido a la falta de significancia estadística (prueba t) de los coeficientes beta de los activos revisados en relación con el índice S&P500. A su vez, estos autores criticaron la poca consistencia empírica de los valores alpha (α) de las regresiones de cada activo financiero con respecto al portafolio de mercado en relación con su magnitud teóricamente esperada. Como una respuesta a esta observación y como una de las críticas más notables a las pruebas realizadas al CAPM, Roll (1977) observa que esta situación se produce porque el portafolio de mercado empleado para valuar el CAPM no es financieramente eficiente; es decir, se encuentra en un punto geométricamente ajeno a la frontera eficiente. Derivado de esto, propone que a pesar de la limitante que encuentra la forma más apropiada de aproximar la definición del portafolio de mercado sea a través de métodos de capitalización.

Por el hecho de que muchos de los supuestos propuestos por Sharpe y Lintner no son asequibles en los mercados de capitales de la vida real y debido a que α puede utilizarse como referencia neutral o punto de partida tanto del modelo propuesto por ellos como del proceso de administración activa de portafolios para definir el conjunto de posibilidades de inversión⁵, surge la principal motivación del presente trabajo emerge: determinar si la definición de M_A es financieramente eficiente en las plazas bursátiles española y mexicana y, por ende, si resulta ser un buen punto de referencia en la administración (pasiva o activa) de portafolios, así como en otro tipo de modelos de valuación propios de las finanzas corporativas.

Se han realizado análisis previos de este tipo pero, a pesar de su notoria oportunidad, éstos realizan comparaciones estáticas de la frontera eficiente contra M_A en periodos largos y fijos de tiempo. Es decir, sólo calculan la frontera eficiente en un periodo determinado de tiempo y no observan si esta falta de eficiencia sigue presente en diferentes lapsos de la misma longitud, aumentando con esto el error muestral y confirmando la potencial presencia de la ineficiencia en los mismos. Por ello surgen las siguientes preguntas que motivan, en buena medida, este primer estudio: ¿qué habría pasado para el mercado de las emisoras pertenecientes a los índices IBEX35 e IPC mexicano de febrero de 2001 a diciembre de 2010 en una evaluación periódica mensual de los resultados del modelo MTSL?, ¿pertenecen los portafolio del IBEX35 y el IPC al conjunto de portafolios eficientes?, y ¿son realmente las aproximaciones estadísticas estudiadas igual de eficientes que un portafolio óptima derivado con el modelo MTSL? La respuesta de estas preguntas permitirá determinar si las definiciones (o, propiamente dicho, aproximaciones) de portafolio de mercado son apropiadas para utilizar como referencia neutral en modelos de valuación y/o selección óptima de portafolios. El comparar los casos estudiados con otros potenciales índices e incluso sugerir una alternativa de las definiciones actuales es algo que se responderá en otro espacio una vez que se logren los objetivos que atañen al presente.

Revisión de literatura

La forma funcional del modelo CAPM-SLM que da fundamento a la administración pasiva de portafolios o a los puntos de partida neutrales en la activa requiere —dentro de los supuestos mencionados en Sharpe (1964) o en Lintner (1965)— que existan condiciones de expectativas homogéneas⁶ en los inversionistas o agentes en los mercados financieros y el empleo del mismo conjunto de información por parte de los mismos, lo que llevará a definir lo que se conoce como condiciones de equilibrio en los mercados financieros y si se emplea el modelo MTSL (Markowitz, 1987) de manera agregada se llega a la definición del denominado portafolio de mercado (M). La forma funcional del CAPM-SLM se da por un análisis de sección cruzada que parte de la siguiente regresión auxiliar o ecuación de la línea característica del activo i (Sharpe, 1963):

En r_i se representa el rendimiento observado en el activo i y en α_i la tasa que se lograría si β_i tuviera un valor de cero. Partiendo de las propuestas de Sharpe (1964) se observa que, conforme la cardinalidad del portafolio óptimo del inversionista se incrementa, se llega a la propiedad de que ε_i tiene una influencia baja en el nivel de riesgo del portafolio si el número de activos en el mismo es muy grande, dejando entonces, como medida de interés, la prima de riesgo que se obtendría con el portafolio de mercado M respecto a una tasa libre de riesgo, la cual se fija con la regresión que fundamenta el CAPM-SLM:

Si en (2) se emplea, como insumo, la diferencia del rendimiento observado en el activo i respecto a la tasa de interés libre de riesgo (r_f) se tiene que E_i = E(r_i − r_f). En el primer caso (r_i) con la existencia de condiciones de equilibrio se llega a γ ≈ r_f que y en el segundo (r_i − r_f) a γ ≈ 0. Las primeras pruebas realizadas al CAPMSLM como modelo para la valuación de activos, bajo el supuesto de la existencia un portafolio de mercado M_A previamente definida y correcta,⁷ se enfocaron a demostrar este último hecho (γ ≈ 0). Tal es el caso de la revisión de Black, Jensen y Scholes (1972) quienes encuentran que en términos de significancia estadística γ ≠ 0 observando que existe una variabilidad en su valor, situación que lleva a poner en duda la validez de la forma funcional CAPM-SLM. En un estudio similar, Fama y Macbeth (1973) realizan otro tipo de prueba al modelo al realizar estudios con una forma funcional dada por:

En la expresión anterior γ₀ = γ, γ₁ = (r_m −γ) y γ₂ representan la prima de riesgo atribuida a la presencia de no linealidades (es decir, establecería la relación entre riesgo y rendimiento como algo no lineal). En la misma ecuación, γ₃ se define como la prima de riesgo recibida dada S_εi que es la desviación estándar del error de la regresión auxiliar en (1). La hipótesis de Fama y Macbeth era establecer que γ₂ = 0 y γ₃ = 0 para demostrar que el CAPM-SLM tiene validez externa, situación que los llevó a rechazar dicha hipótesis.

Los resultados de las pruebas anteriores y dada la propuesta del modelo Beta-Cero de Black (1972) llevaron a Blume y Friend (1973) a realizar pruebas en donde se establece que —dada la supuesta ausencia de un rendimiento libre de riesgo r_f, y sustituyendo el mismo por el rendimiento r_z de un portafolio ortogonal M perteneciente al segmento con pendiente negativa del conjunto de portafolios eficientes— en condiciones de equilibrio lleva a establecer r_z = r_f, situación que les llevó a demostrar —junto con los resultados de Fama y Macbeth— que r_z > r_f, por lo que a la luz de sus resultados es más sugerente el empleo del modelo Beta-Cero de Black que el propio CAPM-SLM.

Las conclusiones de estos estudios previamente descritos condujeron a la búsqueda de modelos alternativos de valuación de activos como las formas funcionales propuestas por Amihud y Mendelson (1986), la cual relaja el supuesto de liquidez perfecta; el modelo propuesto por Merton (1992) para valuar activos en tiempo continuo y de manera intertemporal; o el que estudia la valuación de activos no negociables como capital humano o activos no negociados en mercados líquidos de Heaton y Lucas (2000); éstas son algunas de las múltiples propuestas que por situación de espacio y facilidad de exposición no se mencionaron y son conocidas como versiones no estándar del modelo CAPM.

Las revisiones teóricas realizadas al CAPM-SLM, como las previamente citadas, tienen relación con el presente estudio en el sentido de que sólo cuestionan si real-mente se observan las condiciones de equilibrio en los mercados financieros; dejan de lado la revisión del objeto de estudio de interés: la definición (o aproximación) del portafolio de mercado. Existen varias críticas a los estudios anteriores, como la de Roll (1977) quien observa (resaltando los trabajos de Black, Jensen y Scholes, Fama y French, así como Blume y Friend) que los estudios previos tratan de demostrar la presencia de equilibrio presuponiendo la validez, de manera conjunta, de dos hipótesis:

H1: El portafolio de mercado es eficiente de manera ex ante.

H2: El portafolio que hace tangencia con la frontera eficiente en el modelo MTSL de manera ex ante es el de mercado.

Las observaciones de Roll van en el sentido de cuestionar estas revisiones citadas porque:

• 1.

  No se conoce la verdadera conformación del portafolio de mercado M ∈ G⁸, en donde G es el conjunto de todos los activos financieros objeto de inversión existentes (sean o no objeto de inversión en la política de un agente determinado).

• 2.

  M se ubica geométricamente en el punto en donde hace tangencia una línea, conocida como línea de asignación de capital (LAC), con el conjunto de portafolios eficientes (Ξ) perteneciente aG. Esta recta parte de la tasa pagada por el activo considerado libre de riesgo (rf) permitiendo considerar, de manera agregada, a M como óptima en la lógica del modelo MTSL con el supuesto de expectativas homogéneas (Lintner, 1965). Esto lleva a W = M.

• 3.

  M se aproxima con portafolios tipo como son los índices bursátiles, por lo que se corre el riesgo de hacer un análisis de portafolios y una valuación de activos de un subconjunto A ⊂ G que no representa al conjunto total de posibles activos G, lo que lleva a derivar fronteras eficientes y portafolios de mercado tautológicas⁹ a la luz de la matemática de la teoría de portafolios, las cuales dado el método de selección empleado¹⁰ pueden ser ineficientes.

Esta última afirmación de Roll permite observar que M puede incluso no ser eficiente. Esto es, dado un conjunto de portafolios eficientes Ξ ⊂ G la eficiencia de M puede llevar a localizarle en un punto geométricamente inferior a los portafolios en Ξ, lo que podría dar validez parcial a los resultados de las críticas mencionadas. Sin embargo, dado que sólo se conoce A¹¹ y su conjunto de portafolios eficientes ξ, se llegará a la definición de un portafolio de mercado de dicho subconjunto M_A ∈ ξ ⊂ A, originando con esto alguno de los siguientes supuestos:

• 1.

  Se acepte la hipótesis de que M_A no sea eficiente cuando M sí lo es.

• 2.

  Que M_A sea eficiente cuando M no lo es.

• 3.

  Que ambos portafolios sean eficientes

• 4.

  Que ninguno de los portafolios sea eficiente.

Por lo tanto, la coloquialmente conocida como crítica de Roll se enfoca a observar el hecho de que γ ≠ 0 en (2) no implica que el modelo CAPM-MSL sea inválido, o aun mayor en las implicaciones a la luz del presente estudio, y que las aproximaciones de M dadas por M_A ∈ A sean útiles o adecuadas (léase eficientes) para los fines de valuación en el proceso de selección de portafolios óptimos.

Aunque hay propuestas como el modelo de optimización propuesto por Treynor y Black (1973) o el de Black y Litterman (1990) que buscan conciliar a través de la incorporación de las preferencias o expectativas individuales por medio de una o múltiples transformaciones bayesianas la potencial debilidad de los supuestos de equilibrio del modelo CAPM-SLM, éstas presentan una limitante teórica: si se parte de los parámetros Θ₁ = {e,C}¹² y de una distribución de probabilidad determinada considerada como distribución previa P(T | Θ₁) que modela la generación de los valores de T = [r_i,…,r_n] y, posteriormente, se realiza una transformación aplicando el teorema de Bayes dado por:

Se tiene que los nuevos parámetros Θ₂ logrados con dicha transformación pueden ser sesgados respecto a sus verdaderos valores teóricos. Esto se debe primordialmente a:

• 1.

  Provienen de la aplicación de (1) a una variable vectorial o conjunto de vectores de rendimientos enT que se forma de los precios del conjunto de activos de A ⊂ G llevando a que M_A ∈ A no sea el portafolio verdadero M ∈ G, independientemente de si éstas son o no eficientes (M_A ≺M | A ⊂ G).

• 2.

  Si M_A no es eficiente, la generación de Θ₁ partiendo de una definición de los rendimientos de equilibrio logrados con (2), como lo proponen Black y Litterman (1990)-, puede llevar a una definición ineficiente de Θ₂ y de la correspondiente selección del portafolio óptimo para el inversionista.

• 3.

  Aplicando la matemática de la teoría de portafolios, si ξ es ineficiente respecto a Ξ, se tendrá entonces como causal la definición de A ⊂ G que lleva a M_A ≺ M.

Como resultado de la observación anterior y partiendo de que el propio Roll (1977) sugiere como apropiado el método de capitalización para calcular la aproximación del portafolio de mercado, surge la principal motivación u objetivo del presente estudio: demostrar si realmente la aproximación de dicho portafolio (M_A) en las plazas bursátiles española y mexicana, dado su método de cálculo con el valor de capitalización de sus acciones miembro, pertenecen al subconjunto de portafolios eficientes ξ del subconjunto A ⊂ G formado por cada mercado, llevando a observar que no existen opciones con mayor eficiencia financiera. Esto sería:

La demostración de si M_A es financieramente eficiente respecto a M¹³ no se hará debido a que se desconoce el verdadero conjunto G y, por ende, se carece de una adecuada, y generalmente aceptada, definición de M para realizar el contraste. Esto es, no se tiene información de todo tipo de activos financieros objeto de inversión en el nivel mundial, los cuales según el CAPM-SLM deben conformar M. Para poder lograr esto debería tenerse un índice global de los diferentes tipos activos financieros (títulos mercado de deuda, acciones, instrumentos de inversión bienes raíces, mercancías, etc.) que sea generalmente aceptado y financieramente eficiente como definición de M.

Por lo que concierne a definir si el portafolio de mercado de un subconjunto A es una definición apropiada o no en las plazas bursátiles de interés se ha escrito poco. Más bien se han tenido revisiones respecto a la preferencia y fundamento de emplear las dos citadas (IBEX35 e IPC) respecto a índices similares. Para el caso del mercado bursátil español, se observa que existen múltiples estudios empíricos que buscan abordar de forma alguna este objetivo, en concreto sobre el índice IBEX35. Al hacer una revisión bibliográfica no exhaustiva, se cita a Ferruz y Sarto (1997), Acosta y González (1999) o Jara y Martínez (2000) quienes en sus trabajos¹⁴ analizan la conveniencia de considerar el IBEX35 como portafolio de mercado frente al IGBM (Índice General de la Bolsa de Madrid). En concreto, Lucas (1998) señala como causa de la elección del IBEX35 que “la eficacia y competitividad de los gestores se mide por el IBEX35 en lugar de por el Índice General de la Bolsa de Madrid”¹⁵, aspecto que se hace propio al presente trabajo al elegir este índice (IBEX35) como referencia y punto de partida dada la afirmación anterior.¹⁶ Ya en la primera década del siglo XXI, Gómez-Sala e Yzaguirre (2003) analizan la evolución de los precios de las acciones ante entradas y salidas del IBEX35; de igual manera, Miralles y Miralles (2005) estudian la relación entre ocho índices bursá-tiles europeos y sus efectos sobre la composición de los portafolios óptimos en el periodo 1995-2002; de manera complementaria, cabe destacar el trabajo realizado por Guijarro y Moya (2006) en el que presentan un algoritmo que permite abordar el problema del Index Tracking o réplica de índices bursátiles como estrategia de administración pasiva de portafolios en cinco índices europeos, entre los que se encuentra el IBEX 35 para el periodo de 2004 a 2006; otro trabajo de Miralles y Miralles (2009) se adentra en la composición del portafolio óptimo del IBEX 35 y de los índices IBEX Medium Cap e IBEX Small Cap, mostrando la importancia de las empresas de tamaño mediano en la composición de los mismos.

Para el mercado mexicano se tienen pocos, pero contundentes estudios relacionados que buscan contrastar y, en su defecto, determinar la utilidad del índice IPC como portafolio de mercado en diferentes formas funcionales del CAPM. Entre los más destacados se observan el de López Herrera (2000) quien sugiere la importancia de una definición adecuada de dicho portafolio y su eficiencia al contrastar el riesgo sistemático derivado con el Índice de Precios y Cotizaciones (IPC) y el Índice México (Inmex). En dicho estudio, López Herrera observa que el modelo se creó para valuar activos y no para aprovechar oportunidades de inversión, situación que podría contradecir los modelos de selección óptima como los de Treynor y Black o Black y Litterman. Esto último lo afirma dado que los valores de las betas podrían ser observablemente diferentes si se tienen diferentes índices con los cuales referenciarse, por lo que se corre el riesgo de estar sobre o subvaluando el riesgo sistemático y, por ende, al activo financiero. Por esto, desde su punto de vista —y en línea con lo expuesto por Frankfurter (1976) y lo establecido en Roll (1977)— será prudente delimitar si la aproximación del portafolio de mercado M_A es apropiada en términos de eficiencia financiera en el nivel del subconjunto de activos A ⊂ G, objetivo que se busca lograr con el presente trabajo; en otros términos, si M_A ∈ ξ y W = M_A. Otra investigación en el ámbito mexicano y que es consistente con lo observado por los proponentes de las versiones no estándar del CAPM es la realizada por Del Castillo (2006) quien empleó modelos econométricos no paramétricos (regresión kernel) para evitar problemas de distribución de probabilidad y sesgos atribuidos a una mala especificación del modelo en la versión condicional del CAPM en México. El autor demostró que, dada una determinada información sobre determinadas variables en la economía, el CAPM puede ser válido en dicho contexto al incorporar algunas variables de estado tanto monetarias como de la balanza comercial. Por último, se tienen las aportaciones realizadas por Sansores (2008) quien destaca que el CAPM tiene limitaciones en su aplicación en economías emergentes. Esto lo atribuye a que deben considerarse otras variables estadísticas, económicas o financieras en la valuación, lo que le lleva a sugerir el empleo de una versión multifactor del CAPM como es el modelo de Fama y Schwert (1977), situación que va en línea con lo expuesto en Fama y Macbeth (1973) y que da fundamento al empleo del CAPM con relaciones no lineales o incluso la presencia de otros factores explicativos adicionales a la aproximación del portafolio. Las conclusiones a las que llegan Del Castillo y Sansores se pueden atribuir a que la aproximación del portafolio de mercado M_A ∈ A ⊂ G no logra incorporar en su información la totalidad de la descripción de la covarianza conjunta de los activos en G y este efecto debe aproximarse con los coeficientes β de factores ajenos a dicho portafolio.

A diferencia de los estudios previamente citados, el presente busca repetir el análisis de contraste W_A = M_A y M_A ∈ ξ ⊂ A no en un periodo estático, sino en varios periodos mensuales de febrero de 2001 a diciembre de 2010 para determinar si, en términos estadísticos, la definición de M_A generalmente aceptada (IBEX35 o IPC) es apropiada para la selección óptima de portafolios en un contexto de administración pasiva o activa o en un escenario de valuación de activos, ya sea utilizando el CAPM-SLM o alguna de sus formas no estándar, situación que tiene implicación en diferentes aplicaciones que abarcan desde la operativa en mercados financieros hasta modelos y casos específicos de modelos de valuación en las finanzas corporativas.

Estudio estadístico por realizar

Para poder demostrar la eficiencia financiera de las aproximaciones del portafolio de mercado estudiado y retomando los supuestos de equilibrio propuestos por Sharpe (1964) y Lintner (1965), se utilizará el modelo MTSL en las acciones miembro de cada índice, el cual consiste en un problema de selección óptima compuesto de dos pasos. El primero de ellos consiste en —dado un vector de nx1 de niveles de inversion w — una matriz de covarianzas de los activos financieros objeto de inversión C de rango n, un vector de nx1 de rendimientos esperados por activo¹⁷r; con un vector de unos de nx1 y una tasa de interés pagada por un activo libre de riesgo rf, se debe resolver la siguiente definición de un activo o portafolio riesgoso w^*:

Sujeto a:

w ′ · 1 = 1

w ≥ 0

De acuerdo con los supuestos de equilibrio propuestos por Sharpe (1964) y Lintner (1965), si todos los inversionistas fuesen racionales utilizarían (6) para valuar y seleccionar el portafolio óptimo y tendrían expectativas de inversión homogéneas (Samuelson, 1973). Con esto, el portafolio w^* se convertiría en el óptimo para todos los agentes en el mercado, definiéndolo como el portafolio del mercado w* = W = M_A. Este caso hipotético debería tener todos los activos tranzados en el mercado estudiado por lo que su conformación debe ser la misma que la de una derivada con el modelo MTSL. Dado que la pendiente de la línea de asignación de capital es lo que se maximiza en (6) —y en el análisis del desempeño de un portafolio se conoce como ratio de Sharpe (Sharpe, 1966), denotado con S — se llega a la siguiente hipótesis de trabajo basada en (5):

Esto es, si el portafolio óptimo w* y la de mercado M_A fuesen los mismos, el ratio de Sharpe deberá ser igual en ambos casos, lo que llevaría a observar que la definición de M dada M_A por es eficiente. El problema dado en (6) no incorporará, en esta primera revisión teórica, el impacto de las restricciones de cardinalidad dado que se relaja el supuesto de expectativas homogéneas de los inversionistas a nivel monoagente, permitiendo que se presente el fenómeno de concentración de niveles de inversión en pocos activos dadas sus covarianzas y sus rendimientos esperados,¹⁸ lo cual puede, potencialmente, llevar a una selección ya sea de portafolios o activos más eficientes que M_A. Esto se origina porque si realmente la definición de M_A es la misma que w*, entonces la ausencia de restricciones de cardinalidad, propias del método de cálculo de un índice bursátil, tendría un efecto marginal; es decir, a pesar de la heterogeneidad de los parámetros y objetivos de riesgo y rendimiento, las preferencias de éstos se agregan de tal forma que el portafolio óptimo derivado con el modelo MTSL es el mismo que la aproximación (índice bursátil estudiado) utilizada.¹⁹

Para demostrar (7) se programó una simulación de eventos discretos y se emplearon datos históricos de los rendimientos mensuales de los precios de las acciones miembro de los índices bursátiles estudiados para el periodo de febrero de 2001 a diciembre de 2010. Los mismos fueron extraídos de la base de datos de Bloomberg (2010). Las series de tiempo de los rendimientos de los i-ésimos activos involucrados en cada periodo se calcularon directamente de sus precios de cierre empleando la fórmula de rendimientos aritméticos²⁰. Por cuestiones de exposición, se presenta una descripción general del algoritmo de simulación en el anexo II.

El ratio de Sharpe para W y M_A se calculó con datos de 30 meses, definiendo a m como el vector de niveles de inversión o ponderaciones de las emisoras miembro en M_A y utilizando las siguientes expresiones:

Para obtener S_w y SMA se utilizó la tasa de mercado secundario de las letras del tesoro español de tres meses en España y la tasa de CETES de 91 días en México como definiciones de tasa libre de riesgo (r_f). Estos valores (SwySMA) fueron comparados estadísticamente con un análisis de varianza unidireccional (ANOVA 1) para confirmar la igualdad o diferencia en ambas series de tiempo y para deter-minar el caso con el mayor nivel de eficiencia financiera. Dentro de las pruebas adicionales por realizar, se comparará, en un espacio geométrico tridimensional, la posición geométrica de M_A respecto a W y la frontera eficiente ξ cuyo método de derivación se presenta en el anexo I.

En la expresión anterior, la matriz de covarianzas se determinó con el método de cálculo de varianzas y covarianzas constantes [(ri,t−r¯i)·(rj,t−r¯j)]·n−1 que se logra partiendo de una variable vectorial de dimensión txn (t = tamaño de serie de tiempo) T = [r_i,…,r_n], un vector de unos de nx1 y una matriz identidad de rango n:

Una vez establecidos los parámetros generales de las simulaciones realizadas, se revisan los resultados que se obtuvieron con las mismas. Para una consulta más detallada del algoritmo del simulador empleado se puede consultar el anexo II.

Resultados observados

Para el caso del mercado español, en concreto el submercado o conjunto de activos del IBEX35 (cuadros grises de la figura 1), se observa que la aproximación del portafolio de mercado no es eficiente en el sentido de que su posición geométrica en el espacio tridimensional tiempo-riesgo-rentabilidad es inferior a la de los elementos del conjunto de portafolios en la superficie de fronteras eficientes a lo largo del periodo de simulación. Esto implica que el IBEX35 es inferior al portafolio óptimo (W) derivado con el modelo MTSL (triángulos obscuros sobre la superficie de fronteras eficientes). También, en algunos casos, la referencia estudiada tiene rentabilidades esperadas negativas (puntos con rentabilidad esperada de cero). Este conjunto de situaciones observadas a lo largo de la simulación sugieren que la definición de eficiencia financiera estricta del IBEX35 propuesta en (7) no se sostenga, sugiriendo el empleo de una administración activa en W respecto a una pasiva empleando la aproximación M_A.

Figura 1.

Fronteras eficientes con las emisoras miembro del IBEX35 en contraste al portafolio de mercado

Fuente: Elaboración de los autores con base en los resultados de las simulaciones.

Esta consideración preliminar se corrobora con la pendiente de la línea de asignación de capital que lleva a la cuantificación del ratio de Sharpe tanto de M_A como de W, situación que se aprecia en la figura 2 al exponer el comportamiento histó-rico de SMA y S_w.

Figura 2.

Índices de Sharpe históricos del portafolio óptimo (W) y del IBEX 35(M_A) observados en las simulaciones

Fuente: Elaboración de los autores con base en los resultados de las simulaciones.

En las dos exposiciones se puede apreciar que existen algunos comportamientos, los cuales pueden considerarse, a primera vista, como “atípicos” en el sentido de que no se aprecia un comportamiento uniforme en las series de tiempo. Esto último se aprecia en el caso de W. Para explicar la situación, se han revisado tanto el algoritmo empleado en la simulación como las conformaciones históricas de dicho portafolio, destacando dos causas potenciales.

La primera de ellas es la relativa a circunstancias propias al modelo MTSL, tal como lo señalan Black y Litterman (1992), en las que el programa cuadrático paramétrico descrito en el anexo I y expuesto en (8) lleva a conformaciones y niveles de inversión con altos niveles de concentración (niveles de inversión en pocos elementos del conjunto de activos financieros) cuando se establecen restricciones de no negatividad.

Esto se corrobora con el número promedio de 6.51 activos (de 35) que conforman W en cada periodo, así como el número mínimo de dos²¹ y de uno el 18 en noviembre de 2009 (Telefónica), lo que aparece como una excepción a los principios fundamentales de la teoría de portafolios (diversificación en dos o más activos). En el mismo tenor del comportamiento de los resultados, también puede atribuirse cambios en la estructura de las fronteras eficientes y a la falta de longitud en las series de tiempo de rendimientos empleadas (n<30) como es el caso en el año 2001 para Amadeus Global IT.

Entre los factores económicos que pueden explicar esta situación se resaltan tres periodos en los que existe una relativa homogeneidad en el comportamiento de los ratios de Sharpe (SMA,Sw): 2001 a 2004, 2004 a 2007 y 2007 a 2010, sugiriendo —en función de este comportamiento claramente segmentado de manera intertemporal— una separación de la prueba ANOVA unidireccional en esos mismos tres segmentos. La razón de esto obedece a situaciones sistémicas en el nivel global que influyeron en el comportamiento de la economía española, en los resultados del análisis de selección óptima con el modelo MTSL y en la derivación de M_A. A su vez, hicieron lo propio en el valor del estadístico F de la prueba ANOVA cuando se empleó la totalidad de datos de manera conjunta y no segmentada al generar una mayor variabilidad total. Por tanto, dado este observable cambio de ciclo de crecimiento en los mercados financieros y de una manera discrecional, es que se emplea esta segmentación en el análisis de varianza por realizar.

Los resultados del análisis de varianza unidireccional segmentado en estos tres periodos de tiempo se exponen en la figura 3. De las tablas ANOVA correspondientes, así como de los diagramas de caja, se confirma que en cada caso se rechaza la hipótesis nula de trabajo dada en (7) y se acepta la de preferencia de W sobre M_A confirmando una hipótesis alternativa dada por:

Figura 3.

Prueba ANOVA unidireccional de los ratios de Sharpe de los portafolios comparados en el IBEX35

Fuente: Elaboración de los autores con base en los resultados de las simulaciones.

En el mercado bursátil mexicano se observaron los mismos resultados que el caso español en el comparativo de fronteras eficientes dado en la figura 4, así como comportamientos irregulares en la superficie de fronteras eficientes y los índices de Sharpe de la figura 5. Esto se debe, en buena parte, tanto a los parámetros empleados en el modelo²² como a los eventos económicos mencionados líneas atrás (a excepción de la implementación del euro y los ataques de marzo de 2003 en España).

Figura 4.

Fronteras eficientes para el mercado de los miembros del IPC en contraste al portafolio de mercado

Fuente: Elaboración de los autores con base en los resultados de las simulaciones.

Figura 5.

Ratios de Sharpe históricos observados en toda la simulación para el IPC

Fuente: Elaboración de los autores con base en los resultados de las simulaciones.

Para el caso mexicano, se agregan a la explicación de esta situación cuestiones corporativas al producirse, a lo largo de la simulación, una serie de fusiones, escisiones y adquisiciones de empresas con influencia considerable en el mercado bursátil y el índice²³, situación que redundó en que el número de miembros no fuese siempre de 35 (como es el caso de la referencia española), lo que impactó en la generación de irregularidades en los parámetros de riesgo y rendimiento (léase elementos en el vector de rendimientos esperados e, el de pesos o niveles de inversión w y la matriz de varianzas y covarianzas C), los que llevaron a niveles de concentración de activos en varios periodos dada la propiedad del programa cuadrático ante la ausencia de restricciones de cardinalidad y la restricción a las ventas en corto.

Entre los factores económicos que pueden explicar esta situación se resaltan tres periodos en los que existe una relativa homogeneidad en el comportamiento de los ratios de Sharpe (SMA,Sw): 2001 a 2004, 2004 a 2007 y 2007 a 2010, sugiriendo en función de este comportamiento claramente segmentado de manera intertemporal una separación de la prueba ANOVA unidireccional en esos mismos tres segmentos. La razón de esto obedece a situaciones sistémicas en el nivel global que influyeron en el comportamiento de la economía española, en los resultados del análisis de selección óptima con el modelo MTSL y en la derivación de M_A. A su vez, hicieron lo propio en el valor del estadístico F de la prueba ANOVA cuando se empleó la totalidad de datos de manera conjunta y no segmentada al generar una mayor variabilidad total. Por tanto, dado este observable cambio de ciclo de crecimiento en los mercados financieros y de una manera discrecional, es que se emplea esta segmentación en el análisis de varianza por realizar.

Los resultados del análisis de varianza unidireccional segmentado en estos tres periodos se exponen en la figura 3. De las tablas ANOVA correspondientes, así como de los diagramas de caja, se confirma que en cada caso se rechaza la hipótesis nula de trabajo dada en (7) y se acepta la de preferencia de W sobre M_A confirmando una hipótesis alternativa dada por:

Todo esto influyó en el comportamiento de los ratios de Sharpe de la figura 5, así como en la derivación de las fronteras eficientes sugiriendo que también se empleara la separación de la prueba ANOVA undireccional en los mismos tres segmentos empleados en el estudio del mercado español, llevando a los resultados de la figura 6. Con esto se observa que en los dos índices o aproximaciones del portafolio de mercado se rechaza la hipótesis nula de trabajo dada en (7) y se acepta la alternativa Ha:W≠MA|SW>SMA dada en (11).

Figura 6.

Prueba ANOVA unidireccional de los ratios de Sharpe de los portafolios comparados en el IPC

Fuente: Elaboración de los autores con base en los resultados de las simulaciones.

Conclusiones

A pesar de que las aproximaciones del portafolio de mercado estudiados pertenecen a diferentes plazas bursátiles, se observó que éstas, al realizar un backtest con simulaciones de eventos discretos y dados los supuestos empleados, no cumplen con la validez de los supuestos de equilibrio, expectativas homogéneas y de evaluación y elección racional de un portafolio empleando el modelo MTSL, sugeridos por Sharpe y Lintner. Esto lleva a observar que las mismas no son aproximaciones financieramente eficientes del portafolio de mercado y que su uso en la administración de portafolios debe sujetarse a revisión.

La situación anterior puede fundamentarse dado el hecho de que la conformación y cálculo de las referencias estudiadas son resultado de metodologías estadísticas específicas ajenas a la selección racional²⁴ de portafolios realizada en el modelo MTSL y que sólo presuponen que las ponderaciones se dan como óptimas a nivel agregado, situación que se refuta con los resultados observados.

Dentro de las limitantes observadas resalta que, dada la naturaleza del programa cuadrático con que se derivó la frontera eficiente al eliminar la posibilidad de realizar ventas en corto y en virtud de que no se emplearon restricciones de cardinalidad para determinar el portafolio óptimo en el modelo MTSL, se tuvieron casos con alta concentración de activos, lo cual no contraviene del todo a la teoría de portafolios salvo los casos en que se eligió un solo activo, situación que se hubiera prevenido con las restricciones utilizadas al determinar el IBEX35 o IPC, pero que no se tomó en consideración al ser éstas, para los casos de los índices bursátiles estudiados, parámetros de cardinalidad propios de criterios estadísticos y no resultado de un comportamiento y selección racional.

A pesar de la falta de eficiencia, los portafolios de mercado deben utilizarse como un punto de partida o referencia neutral para los modelos de administración activa de portafolios. Sin embargo, es necesario observar que los resultados logrados partirían de una definición financieramente ineficiente en sus proporciones de inversión de equilibrio, lo cual podría llevar a costos de oportunidad observables en la definición de los niveles de inversión w^* óptimos para cada inversionista.

Anexo I:

Derivación del portafolio óptimo en el modelo MTSL

La forma en que se determinó el portafolio óptimo W en el contexto del modelo MTSL y en la forma en que operó en el simulador programado parte de dos pasos fundamentales. El primero de ellos es la derivación del conjunto de portafolios que conforma geométricamente a la frontera eficiente (ξ), el cual tendrá una cardinalidad de 100. El segundo de ellos consiste, partiendo de una tasa de interés que paga un activo libre de riesgo rf, determinar cuál de los 100 miembros de ξ es el que maximiza la pendiente de la línea de asignación de capital o ratio de Sharpe. El primer paso se resuelve utilizando programación cuadrática empleando un algoritmo sugerido por Martin (1955), el cual utiliza métodos de optimización restringida con multiplicadores de Lagrange que permite satisfacer tanto las restricciones de no negatividad (exclusión de ventas en corto) como la restricción presupuestal que hace que w_k sea un vector de norma unidad.

Para lograr esto se resuelve la minimización de la función de varianza del portafolio, w_k dado el nivel de rendimiento esperado Ek*∈[min(r),max(r)] dado por Ek*=e′·wk.. Esto es:

Este problema de optimización se presenta como sigue:

Sujeto a:

El mismo lleva al planteamiento de la siguiente ecuación lagrangeana:

Dadas las condiciones de primer orden de (14), se llega al siguiente planteamiento matricial:

Dado que el vector a se forma del vector de multiplicadores de Lagrange y del vector de pesos w_k (a = [w_k, λ₁, λ₂]′), se resuelve (15) y se observa cuáles elementos de w_k violan la restricción de no negatividad. Posteriormente, se eliminan de, D, a y b en (15) las filas y columnas correspondientes al i-ésimo activo que incurre en dicha violación, se le asigna un valor de w_i = 0 en el resultado final a ese activo y se resuelve el nuevo sistema planteado para (15) hasta lograr que todas las entradas del vector w_k cumplan con las restricciones dadas, lo que implica que algunos activos financieros tengan niveles de inversión de cero y se llegue incluso a colocar todo el balance de inversión en uno solo, situación que al no incorporar restricciones de cardinalidad en w_k deriva en un problema de concentración de activos observable en los resultados del presente estudio. Con la derivación de (15) para 100 valores de Ek*∈[min(e),max(e)], se deriva ξ. Los pasos anteriormente expuestos se realizaron en un algoritmo informático programado en MATLAB:

Algoritmo 1 para derivar W con el modelo MTSL:

Inicio

• •

  Definir:

  t= fecha de derivación o análisis,T = [r_i,t,…,r_n,t],e = [E(r_i,t),…E(r_n,t)]′,

  

  D=C−11'0 con 1 y -1 de dimensión (2x1) y 0 de rango 2.

• •

  Hacer para 100 diferentes valores de : Ek*∈[min(e),max(e)]

  • •

    Definir:

    
    • •

      Determinarw_k ∈a empleando (14):a = C^–1· b

    • •

      Siw_k < 0, hacer mientras queencontrado=falso

      ∀w_i ∈w_k,w_i = 0 ⇔ w_i < 0

      Eliminar i-ésimas columna y fila deC, a yb que verifican w_i < 0.

      Resolverw_k ∈a empleando de nuevo (15):a = C^–1 ·b

      Siw_k ≥ 0 ⇒encontrado=verdadero

      Se establece:w_k∈ ξ_t

• •

  Determinar la definición deW_t por observación directa de los valores de S_ξ con (6):

  

• •

  Determinar el ratio de Sharpe dado para Wt:SW,t=(EW−rft)·σξ−1

Fin

Anexo II:

Lógica general del algoritmo empleado en el simulador programado.

El algoritmo que se utilizó para realizar las simulaciones de eventos discretos se programó, al igual que el previamente expuesto, en MATLAB y la lógica general y pasos realizados se exponen a continuación.

Algoritmo 2 para realizar la simulaciones de eventos discretos Inicio

• •

  Definir:t = 01 de febrero de 2001.

• •

  Hacer mientras Condición de paro de Loop=falso:

  • ∘

    Definir ξ_t,W_t y S_W,t al realizar el Algoritmo 1 para derivar W con el modelo MTSL.

  • ∘

    Determinar vector niveles de inversiónm por activo en definición de portafolio de mercado M_A.

  • ∘

    Calcular el ratio de Sharpe de M_A con (9):

    

  • ∘

    Si t = 31 de diciembre de 2010 ⇒ Condición de paro de Loop = verdadero.

  • •

    Si _t ∈ [01 de febrero de 2001, 31de diciembre de 2010]⇒Condición de paro de Loop = falso

  • •

    Definir t = fecha mensual y laborable siguiente a la actual.

• •

  Contrastar gráficamente el conjunto de fronteras eficientes Ξ = {ξ_t} y valores de E_W,t, σ_W,t,E_M,t, σ_M,t.

• •

  Realizar prueba ANOVA unidireccional para contrastar SMA y S_W,t.

• •

  Graficar los valores históricos de SMA y S_W,t.

  • ∘

    Si existen comportamientos o fluctuaciones atípicas enS_W,t⇒ Segmentar las observaciones de SMA y S_W,t en periodos homogéneos atendiendo algún criterio preferentemente relacionado a los ciclos económicos.

  • •

    Realizar de cuenta nueva la prueba ANOVA unidireccional para contrastar SMA y S_W,t en cada segmento temporal creado.

Fin