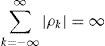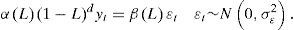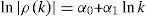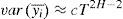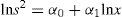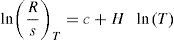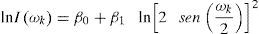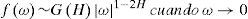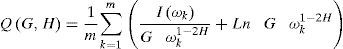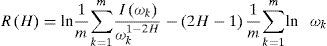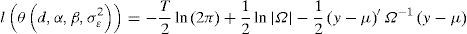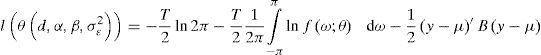En este trabajo se examina la dinámica del tipo de cambio con respecto del dólar americano para varias economías, desarrolladas y en vías de desarrollo, con el fin de encontrar evidencia de memoria larga durante el periodo 1971-2012. Para ello se aplican las siguientes pruebas: coeficiente de Hurst, correlograma, gráfico de la varianza, Geweke y Porter-Hudak, así como estimador local de Whittle de Robinson. Al respecto, Chile, China, Islandia, Israel, México y Turquía presentaron evidencia de memoria larga de acuerdo con pruebas consistentes y, en consecuencia, se estimó para ellos un modelo Autorregresivo Fraccionalmente Integrado con Medias Móviles en los dominios del tiempo y la frecuencia. En el dominio del tiempo se empleó el método de máxima verosimilitud (Sowell, 1992), y en el dominio de la frecuencia se utilizó la técnica de Fox y Taqqu (1986). Los resultados del modelo Autorregresivo Fraccionalmente Integrado con Medias Móviles muestran que Chile, China, Islandia y México presentan evidencia de memoria larga en el tipo de cambio; el método de estimación que presenta el mejor ajuste a la curva original es el método de máxima verosimilitud exacta de acuerdo con el criterio de información de Akaike.
This paper examines the dynamics of the exchange rate against the American dollar for several economies, developed and developing, in order to find evidence of long memory in the period 1971-2012. To do this, we apply the tests: Hurst coefficient, correlogram, variance graphic, Geweke and Porter-Hudak and the local Whittle estimator of Robinson. In this regard, Chile, China, Iceland, Israel, Mexico and Turkey presented evidence of long memory based on robust tests and, therefore, it was estimated for them an autoregressive integrated moving average model in the domains of time and frequency. In the time domain, we used the maximum likelihood method (Sowell, 1992), and in the frequency domain we apply the technique from Fox and Taqqu (1986). The results from the autoregressive integrated moving average model show that Chile, China, Iceland and Mexico have evidence of long memory in the exchange rate; the estimation method that presented the best fit to the original curve was the exact maximum likelihood method according to criteria Akaike information.
La identificación de memoria larga en el tipo de cambio es un tema de actualidad, ya que muchos países que han adoptado un tipo de cambio variable han estado sujetos, en diversos periodos, a variaciones severas que no han podido ser explicadas por modelos económicos tradicionales. Las variaciones en el tipo de cambio pueden representar o una oportunidad, o, por el contrario, una crisis económica y/o financiera, dependiendo de las ventajas comparativas que un país tenga con respecto a otros. Asimismo, los bancos centrales pueden tomar mejores decisiones de política económica si pueden prever movimientos en el tipo de cambio que puedan afectar los instrumentos u objetivos de política monetaria. Por otro lado, los inversionistas, privados e institucionales, que participan en los mercados de divisas pueden anticipar el comportamiento del tipo de cambio y cubrirse contra el riesgo de mercado por medio de productos derivados y/o diversificar eficientemente sus portafolios de inversión con varias divisas.
En el trabajo pionero de McLeod y Hippel (1978) se caracteriza y define, por primera vez, cuándo una serie tiene memoria corta o larga con base en la tendencia de la autocorrelación teórica de una serie. Por otro lado, Granger y Joyeux (1980) y Hosking (1981) desarrollaron de manera simultánea un modelo que captura este fenómeno, conocido como modelo Autorregresivo Fraccionalmente Integrado con Medias Móviles (ARFIMA), con lo cual, se añade el supuesto de que las condiciones iniciales influyen en el futuro, y no solamente en el pasado, cuando se quiere explicar el comportamiento de una serie. Asimismo, se han desarrollado diferentes tipos de pruebas para el fenómeno de memoria larga, como la del correlograma, la gráfica de la varianza, la prueba de Geweke y Porter-Hudak (1983) o GPH, y el estimador local de Whittle, propuesto por Robinson (1995), entre otras.
En este trabajo se revisa la evidencia empírica internacional sobre los efectos de memoria larga del tipo de cambio durante el periodo 1971-2012, así como para verificar si las condiciones iniciales tienen un efecto sobre el comportamiento futuro del tipo de cambio y, por ende, en el horizonte del pronóstico.
En general, los estudios sobre la dinámica del tipo de cambio que se han realizado para buscar evidencia de memoria larga son para economías desarrolladas. En este artículo se abordan economías en vías de desarrollo y desarrolladas. Las economías desarrolladas bajo estudio son Australia, Canadá, Dinamarca, Japón, Nueva Zelanda, Noruega, Reino Unido, Suecia y Suiza, mientras que las economías en desarrollo están representadas por Chile, China, Corea del Sur, Islandia, India, Indonesia, Israel, México, Sudáfrica y Turquía.
Este texto está organizado de la siguiente manera: después de esta introducción, se realiza una breve revisión de la literatura sobre el concepto de memoria larga; en seguida, se presenta la definición de memoria larga y los modelos propuestos por Granger y Joyeux (1980) y Hosking (1981), así como las pruebas de memoria larga, entre ellas, la del correlograma, el gráfico de la varianza, el rango reescalado, la prueba de Geweke y Porter-Hudak (1983) y el estimador local de Whittle propuesto por Robinson (1995); así mismo se presentan los métodos de estimación en los dominios temporal y de frecuencias. Posteriormente, se lleva a cabo el análisis estadístico-gráfico de los tipos de cambio, la aplicación de las pruebas de memoria larga y los métodos de estimación; finalmente, se ofrecen las conclusiones derivadas de este estudio.
Breve revisión de la literatura de memoria larga del tipo de cambioLas aplicaciones de la metodología ARFIMA han sido numerosas1. Al respecto, Baillie (1996) llevó a cabo un resumen de los trabajos realizados hasta 1995 que buscaban evidencia de memoria larga en variables relevantes en economía y finanzas. Entre las investigaciones más recientes sobre el tipo de cambio se encuentran las de Cheung y Lai (2001), que estudiaron el tipo de cambio real con respecto del dólar en Francia, Holanda, Italia, Japón, Reino Unido, Suecia y Suiza, durante 1973-1997, mediante simulación de Monte Carlo y con la aplicación de pruebas de raíz unitaria; Hwang (2001) busca el mejor modelo para pronosticar el tipo de cambio de Canadá durante 1973-1998 y de la Comunidad Europea durante 1978-1998, para lo cual utilizó los modelos GARCH, FIGARCH, FIEGARCH, FITGARCH, FINGARCH y FIFGARCH; Henry y Olekalns (2002) analizan el tipo de cambio real de Australia con respecto del dólar durante 1973-1999, aplicando la metodología ARFIMA y pruebas de memoria larga como la de GPH (1983) y Robinson (1995), sin encontrar evidencia de memoria larga; Gil-Alana (2002) estudia el tipo de cambio spot y futuro de 1986-1998 por medio de la prueba de Robinson (1995) y bajo la hipótesis nula de raíz unitaria, encontrando que el tipo de cambio spot sigue un proceso I(1) y el tipo de cambio futuro tiene memoria larga; Kirman y Teyssiere (2002) estudiaron la volatilidad del tipo de cambio de Alemania, Francia, Japón e Inglaterra con respecto al dólar durante 1986-1997, utilizando la metodología del modelo FIGARCH, simulación de Monte Carlo y aplicando pruebas de memoria larga paramétricas y no paramétricas; Morana y Beltratti (2004) examinaron al tipo de cambio de Alemania y Japón con respecto del dólar en 1986-1996, empleando varias pruebas como el estimador local de Whittle y la prueba GPH (1983), entre otras, y comparando pronósticos realizados por medio de modelos ARFIMA, encontrando cambios estructurales y memoria larga en la varianza; Pong, Shackleton, Taylor y Xu (2004) revisaron el tipo de cambio de Inglaterra, Alemania y Japón durante 1987-1998; Dufrénot, Lardic, Mathieu, Mignon y Péguin-Feissolle (2008) comparan 4 modelos para pronosticar la volatilidad del tipo de cambio de Alemania, Francia, Inglaterra, Holanda y Portugal de 1979 a 1999, específicamente utilizaron los modelos ARIMA, GARCH, ARFIMA y de volatilidad implícita; Aloy, Boutahar, Gente y Péguin-Feissolle (2011) estudiaron la paridad del poder de compra por medio de la tasa real de cambio de 78 países de 1970-2006, la cual se esperaría que tuviera reversión a la media, aplicando pruebas de memoria larga como KPSS, el estimador local de Whittle de Robinson (1995), el estimador local de Whittle exacto de Shimotsu (2010) y la prueba de Perron y Qu (2010) basada en el logaritmo del periodograma, obteniendo resultados mixtos; Wang, Yu y Suo (2012) analizaron los efectos en política del tipo de cambio de China con respecto del dólar americano antes y después de la crisis de 2008, obteniendo un coeficiente de Hurst significativo durante la crisis financiera.
Las aplicaciones que buscan memoria larga en el tipo de cambio se han enfocado a estudiar los efectos después de la caída del sistema Bretton Woods en 1973, ya que el tipo de cambio flexible puede ser volátil. Muchos de estos estudios encuentran memoria corta con reversión a la media y algunos de ellos examinan la volatilidad con la familia de modelos GARCH.
Modelación y pruebas de memoria largaMcLeod y Hippel (1978) definen un proceso estacionario con memoria corta y larga si la suma de la autocorrelación tiende a ser finita o infinita, respectivamente. Específicamente, sea yt una serie de tiempo cualquiera, se dice que tiene memoria larga si:
donde ρk es la función de autocorrelación de yt. Otras definiciones alternativas se pueden encontrar en Beran (1992), Taqqu, Teverovsky y Willinger (1995), Granger y Hyung (2004). Por ejemplo, considere las definiciones: vary¯t≈ct−α cuando t→∞, ρk≈ck−α cuando k→∞ y fλ≈cλ−β cuando λ→0, donde c es una constante positiva y en cada caso α, β satisfacen con 0<α<1 y 0<β<1. La primera definición se refiere a la varianza, la segunda, a las correlaciones, y la tercera, a la densidad espectral.Otro modelo que puede capturar este tipo de fenómeno fue propuesto por Granger y Joyeux (1980) y Hosking (1981). Por su parte, Hosking estableció el modelo bajo 2 condiciones de comportamiento, la primera trata con un modelo ARIMA (0, d, 0), y la segunda, con p≠0 y q≠0. Actualmente se le conoce como modelo ARFIMA o FARIMA y es representado por la siguiente ecuación:
donde αL=1−α1L−⋯−αpLp, βL=1−β1L−⋯−βqLq y L es el operador rezago, 1−Ld es el operador rezago fraccional2 y ¿t es un proceso ruido blanco con media 0 y varianza constante. El parámetro d es un número real que puede tomar valores en el intervalo cerrado −0.5,0.5. Si d<0.5, entonces yt es estacionaria y todas las raíces de AR (p) están fuera del círculo unitario. Si d>−.05, entonces yt es invertible y todas las raíces MA (q) están fuera del círculo unitario. Si −0.5<d<0.5, entonces yt es estacionaria e invertible, de tal manera que la función de autocorrelación existe y ρk es finita cuando k→∞ lim k1−2dρk existecuandok→∞. Si d>0.5, entonces la varianza de yt es infinita y no es estacionaria.En algunas ocasiones puede presentarse el caso de que el orden de integración es superior a la unidad d>1, lo cual evidencia que la variable original tiene que ser transformada por medio de diferenciación, esto es yt−yt−1, con el fin de obtener una solución estacionaria3. El parámetro d dentro del modelo es el que captura la memoria larga, y los parámetros ARp y MAq, la memoria corta.
Pruebas de memoria largaExisten diversos métodos para detectar si una serie de tiempo yt tiene memoria larga. Por un lado, se tienen los métodos informales, los cuales son utilizados como herramientas de diagnóstico; no son concluyentes, pero sí ofrecen una idea del comportamiento de la serie. Beran (1994) y Palma (2007) mencionan que los métodos más utilizados son el correlograma, el gráfico de la varianza, el rango reescalado de Hurst (1951) y la prueba de Geweke y Porter-Hudak (1983). Por otro lado, se encuentra el método de estimación semiparamétrica de Robinson (1995) o estimador local de Whittle.
En el correlograma se pueden examinar la autocorrelación y la autocorrelación parcial4. Existen 2 maneras de trabajar con la función de autocorrelación y autocorrelación parcial, la primera se hace al graficar lnρk contra lnk, donde k es el número de rezagos; además, en esta curva se observa una pendiente negativa que está dada por 2H−2. Cuando se trabaja con la autocorrelación parcial se supone lo anterior con la diferencia de que se tiene una caída hiperbólica igual a k−H−1/2. En la segunda se realiza una regresión de la siguiente ecuación para obtener la pendiente α1:
la cual es utilizada para obtener el coeficiente de Hurst como H=α1/2+1.
La gráfica de la varianza es otra forma de observar la memoria larga en una serie y esta se relaciona con la anterior, ya que cuando se observa una caída lenta en la autocorrelación, se incrementa la varianza de la media muestral (Beran, 1994). Si yt tiene un proceso estacionario con memoria larga, entonces la siguiente ecuación define su movimiento:
donde c>0. La metodología para calcular el parámetro H utiliza diferentes cortes de los datos yt y obtiene sus varianzas s2. El número de varianzas obtenidas es x (es igual al número de cortes). La variable x es un número entero que satisface la condición 2≤x≤T/2, donde T es el tamaño de la muestra. Posteriormente se realiza una regresión de acuerdo con la siguiente ecuación:donde s2 es el valor de la varianza de cada corte y x es el número de cortes. La pendiente de la regresión, la cual es negativa, es α1=2H−2; al despejar H se obtiene el coeficiente de Hurst (1951)5. El coeficiente de Hurst se obtiene por medio de la estimación de la siguiente ecuación a través del método de máxima verosimilitud:
donde R/sT es la notación utilizada para el estadístico de rango reescalado, RT es el rango ajustado, sT es la desviación estándar, c es la constante de proporcionalidad, T es el número de datos por intervalo y H es el coeficiente de Hurst.El coeficiente de Hurst puede tomar valores en 0≤H≤1, de manera que se pueden presentar los siguientes casos. Si 0<H<0.5, se le conoce como ruido rosa e indica memoria corta, además, la serie es antipersistente; a menudo se le conoce como un modelo en donde la media regresa a su condición inicial. Si 0.5<H<1, se le conoce como ruido negro y la serie es persistente; este tipo de serie posee memoria larga y se espera que nunca regrese a su condición inicial. Si H=0.5 es una caminata aleatoria, donde los eventos presentes no influyen en el futuro.
La prueba de Geweke y Porter-Hudak (1983) también es conocida como método del periodograma. Considere la ecuación:
donde Iω=12πT∑k=1TXkeîkω2 es el periodograma, ωk=2πkT son las frecuencias con su respectiva transformación con ωk=−π,π, β0 es la parte autónoma y β1 es la pendiente. La estimación de la ecuación (7) se realiza por el método de máxima verosimilitud, el cual proporciona el orden de integración −d=β1 e indirectamente el coeficiente de Hurst H=1−β1/2 de la serie yt6.El estimador local de Whittle propuesto por Robinson (1995) es un método semiparamétrico que se basa en el periodograma y que solo especifica la densidad espectral en su forma paramétrica cuando ω→0, es decir, se trata con frecuencias cercanas a 0.
La función discreta del estimador local de Whittle está dada por:
donde m es un número entero menor a T/2 y satisface las siguientes condiciones: T→∞, 1/m +m/T→0, Iω=12πT∑k=1TXkeîkω2 es el periodograma, la frecuencia está dada por ωk=2πkT con ωk=−π,π. En este caso se remplaza G por su estimador, el cual se define como Gˆ=1m∑k=1mIωkωk1−2H y se obtiene finalmente:
Estimación de un modelo Autorregresivo Fraccionalmente Integrado con Medias MóvilesExisten 2 métodos para estimar los modelos ARFIMA: en los dominios del tiempo y la frecuencia. En el primero se utiliza el método de máxima verosimilitud exacta de Sowell (1992) y de cuasi máxima verosimilitud de Bollerslev y Wooldridge, 1992. En el segundo se emplea el estimador de Whittle y métodos semiparamétricos.
La estimación en el dominio del tiempo, a través del método máxima verosimilitud exacto, se basa en que y se distribuye normal con media y varianza constante y∼Nμ,Ω entonces la función de verosimilitud está dada por:
donde Ω es la matriz de varianza-covarianza de y−μ, y μ=Xβ es la media. Para obtener los parámetros del modelo se debe maximizar con respecto al vector θd,α,β,σε2, como lo indican Sowell (1992), Beran (1994) y Doornik y Ooms (2003).La estimación en el dominio de la frecuencia, propuesta por Fox y Taqqu (1986), es un método que se aproxima al resultado de la maximización de la función de verosimilitud por medio del reemplazo de la matriz de varianza-covarianza en la función, y se escribe en términos de la densidad espectral, como indica la siguiente ecuación:
donde lnΩ≈T2π∫−ππlnfω;θ dω, Ω−1≈2π−2∫−ππfω;θ−1eikωdω y μ=Xβ es la media.Para obtener los parámetros del modelo se tiene que minimizar con respecto del vector θd,α,β,σε2, como lo indican Beran (1994) y Feldman y Valdez-Flores (2010).
Análisis empíricoLos datos utilizados en este estudio son observaciones mensuales del tipo de cambio nominal de diferentes países con respecto al dólar americano en el periodo comprendido entre el 1-02-1971 y el 1-08-2012. Se cuenta con un total de 499 datos para cada serie de dólar australiano, dólar canadiense, peso chileno, yuan chino, won coreano, corona danesa, corona islandesa, rupia india, rupia indonesia, shekel israelí, yen japonés, peso mexicano, dólar neozelandés, corona noruega, libra esterlina, corona sueca, franco suizo, rand sudafricano y lira turca. Los datos fueron obtenidos del Banco de la Reserva Federal de San Luis y fueron transformados por medio de la aplicación de logaritmos naturales.
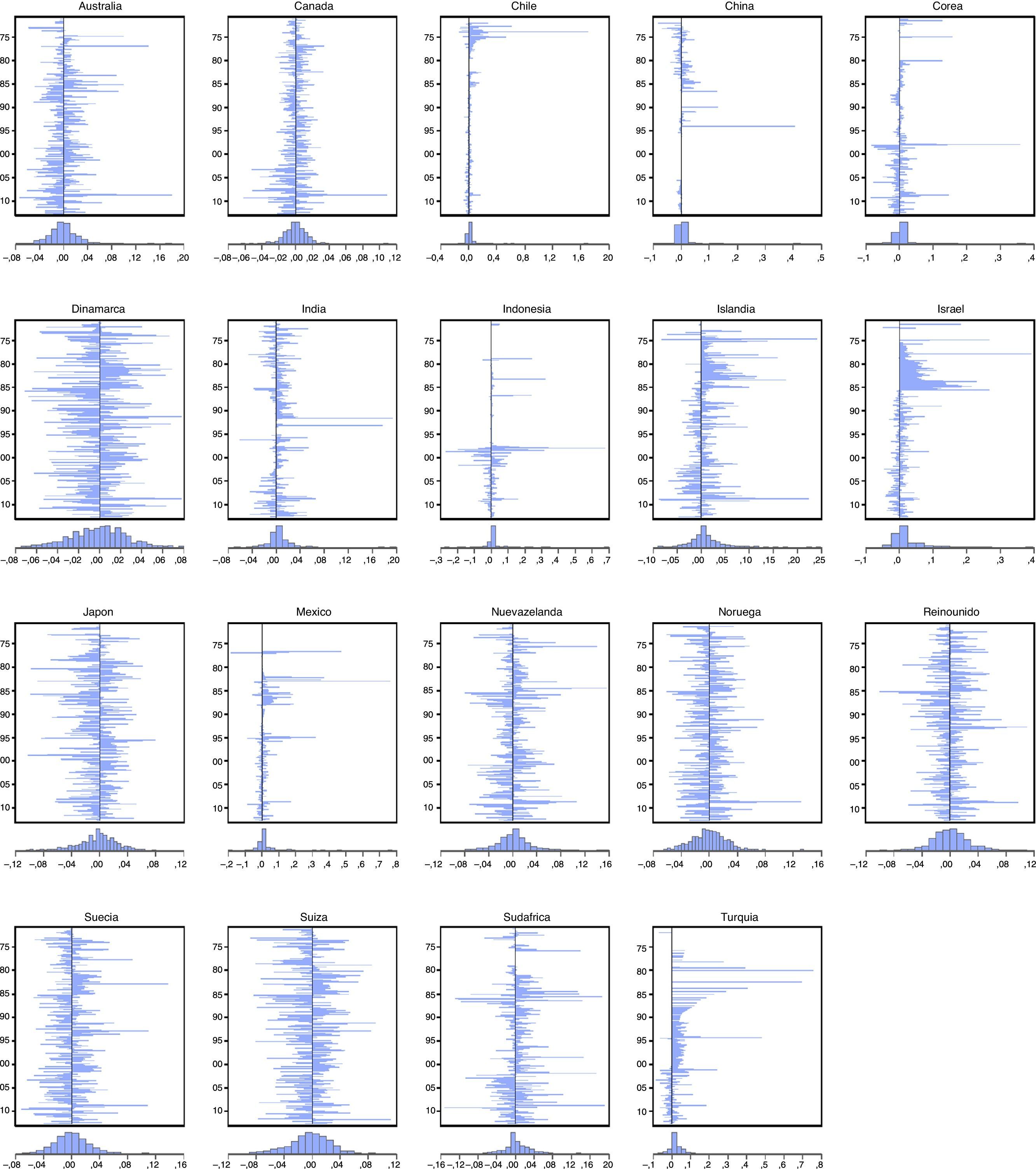
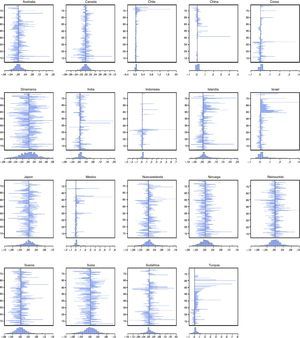
La figura 1 muestra que el tipo de cambio puede presentar colas pesadas en países como Chile, China, Corea del Sur, India, Indonesia, Israel, México, Sudáfrica y Turquía. Por otro lado, Dinamarca, Noruega, Reino Unido y Suiza no muestran saltos abruptos.
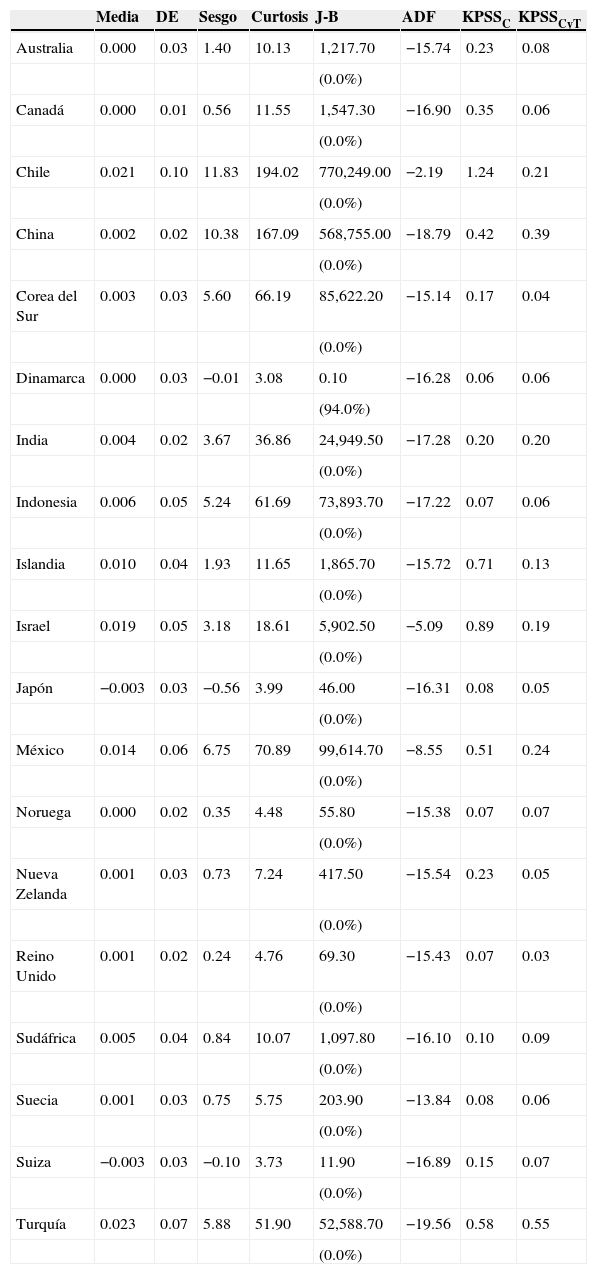
En la tabla 1 se muestran los estadísticos básicos de cada uno de los tipos de cambio estudiados; la media en la mayoría de las variables es positiva y cercana a 0, lo cual es evidencia de que los valores medios se concentran en una sola región; esto confirma que la forma de la distribución empírica es diferente a una normal. Por otro lado, los valores positivos indican que el tipo de cambio tuvo más aumentos en su cotización que disminuciones; en otras palabras, el tipo de cambio tuvo más depreciaciones que apreciaciones (teniendo en cuenta que varios países tuvieron un tipo de cambio fijo), exceptuando a Japón y Suiza. Los países que presentaron una mayor volatilidad fueron Chile y México. El coeficiente de sesgo confirma que la mayoría de los países tuvieron aumentos en la cotización del tipo de cambio. El país con más depreciaciones fue Chile, seguido por China, México, Turquía, Corea del Sur e Indonesia. Por su parte, el valor de coeficiente de curtosis confirma que el tipo de cambio presenta una distribución leptocúrtica, con excepción de Dinamarca. La prueba Jarque-Bera confirma lo anterior, dado que Dinamarca es el único país que presenta una distribución normal. Por otro lado, y de acuerdo con las pruebas de existencia de raíz unitaria de Dickey y Fuller (1981), no existe una raíz unitaria, es decir, la serie es estacionaria al 95% de confianza, con excepción de Chile. Los resultados de la prueba de estacionariedad de Kwiatkowski, Phillips, Schmidt y Shin (1992) muestran que Chile e Israel tienen problemas de no estacionariedad cuando se toma en cuenta la constante. Cuando la prueba KPSS se realiza con una tendencia, China, México y Turquía no presentan estacionariedad; el resto de los tipos de cambio son estacionarios al 95% de confianza en ambas pruebas. Lee y Schmidt (1996) proponen que la prueba KPSS (1992) también se considere como prueba para memoria corta y larga; en este caso, la hipótesis nula de estacionariedad se confronta con la alternativa de integración fraccional. De acuerdo con lo anterior, los países que rechazan la hipótesis nula son Chile, China, Israel, México y Turquía, ya que posiblemente tengan algún tipo de integración fraccional.
Estadísticos principales del tipo de cambio
| Media | DE | Sesgo | Curtosis | J-B | ADF | KPSSC | KPSSCyT | |
|---|---|---|---|---|---|---|---|---|
| Australia | 0.000 | 0.03 | 1.40 | 10.13 | 1,217.70 | −15.74 | 0.23 | 0.08 |
| (0.0%) | ||||||||
| Canadá | 0.000 | 0.01 | 0.56 | 11.55 | 1,547.30 | −16.90 | 0.35 | 0.06 |
| (0.0%) | ||||||||
| Chile | 0.021 | 0.10 | 11.83 | 194.02 | 770,249.00 | −2.19 | 1.24 | 0.21 |
| (0.0%) | ||||||||
| China | 0.002 | 0.02 | 10.38 | 167.09 | 568,755.00 | −18.79 | 0.42 | 0.39 |
| (0.0%) | ||||||||
| Corea del Sur | 0.003 | 0.03 | 5.60 | 66.19 | 85,622.20 | −15.14 | 0.17 | 0.04 |
| (0.0%) | ||||||||
| Dinamarca | 0.000 | 0.03 | −0.01 | 3.08 | 0.10 | −16.28 | 0.06 | 0.06 |
| (94.0%) | ||||||||
| India | 0.004 | 0.02 | 3.67 | 36.86 | 24,949.50 | −17.28 | 0.20 | 0.20 |
| (0.0%) | ||||||||
| Indonesia | 0.006 | 0.05 | 5.24 | 61.69 | 73,893.70 | −17.22 | 0.07 | 0.06 |
| (0.0%) | ||||||||
| Islandia | 0.010 | 0.04 | 1.93 | 11.65 | 1,865.70 | −15.72 | 0.71 | 0.13 |
| (0.0%) | ||||||||
| Israel | 0.019 | 0.05 | 3.18 | 18.61 | 5,902.50 | −5.09 | 0.89 | 0.19 |
| (0.0%) | ||||||||
| Japón | −0.003 | 0.03 | −0.56 | 3.99 | 46.00 | −16.31 | 0.08 | 0.05 |
| (0.0%) | ||||||||
| México | 0.014 | 0.06 | 6.75 | 70.89 | 99,614.70 | −8.55 | 0.51 | 0.24 |
| (0.0%) | ||||||||
| Noruega | 0.000 | 0.02 | 0.35 | 4.48 | 55.80 | −15.38 | 0.07 | 0.07 |
| (0.0%) | ||||||||
| Nueva Zelanda | 0.001 | 0.03 | 0.73 | 7.24 | 417.50 | −15.54 | 0.23 | 0.05 |
| (0.0%) | ||||||||
| Reino Unido | 0.001 | 0.02 | 0.24 | 4.76 | 69.30 | −15.43 | 0.07 | 0.03 |
| (0.0%) | ||||||||
| Sudáfrica | 0.005 | 0.04 | 0.84 | 10.07 | 1,097.80 | −16.10 | 0.10 | 0.09 |
| (0.0%) | ||||||||
| Suecia | 0.001 | 0.03 | 0.75 | 5.75 | 203.90 | −13.84 | 0.08 | 0.06 |
| (0.0%) | ||||||||
| Suiza | −0.003 | 0.03 | −0.10 | 3.73 | 11.90 | −16.89 | 0.15 | 0.07 |
| (0.0%) | ||||||||
| Turquía | 0.023 | 0.07 | 5.88 | 51.90 | 52,588.70 | −19.56 | 0.58 | 0.55 |
| (0.0%) |
DE: desviación estándar.
ADF al 1, 5 y 10%; −3.44, −2.87 y −2.57, respectivamente.
KPSS al 1, 5 y 10%; 0.739, 0.463 y 0.347.
Fuente: Elaboración propia con datos del Banco de la Reserva Federal de San Luis.
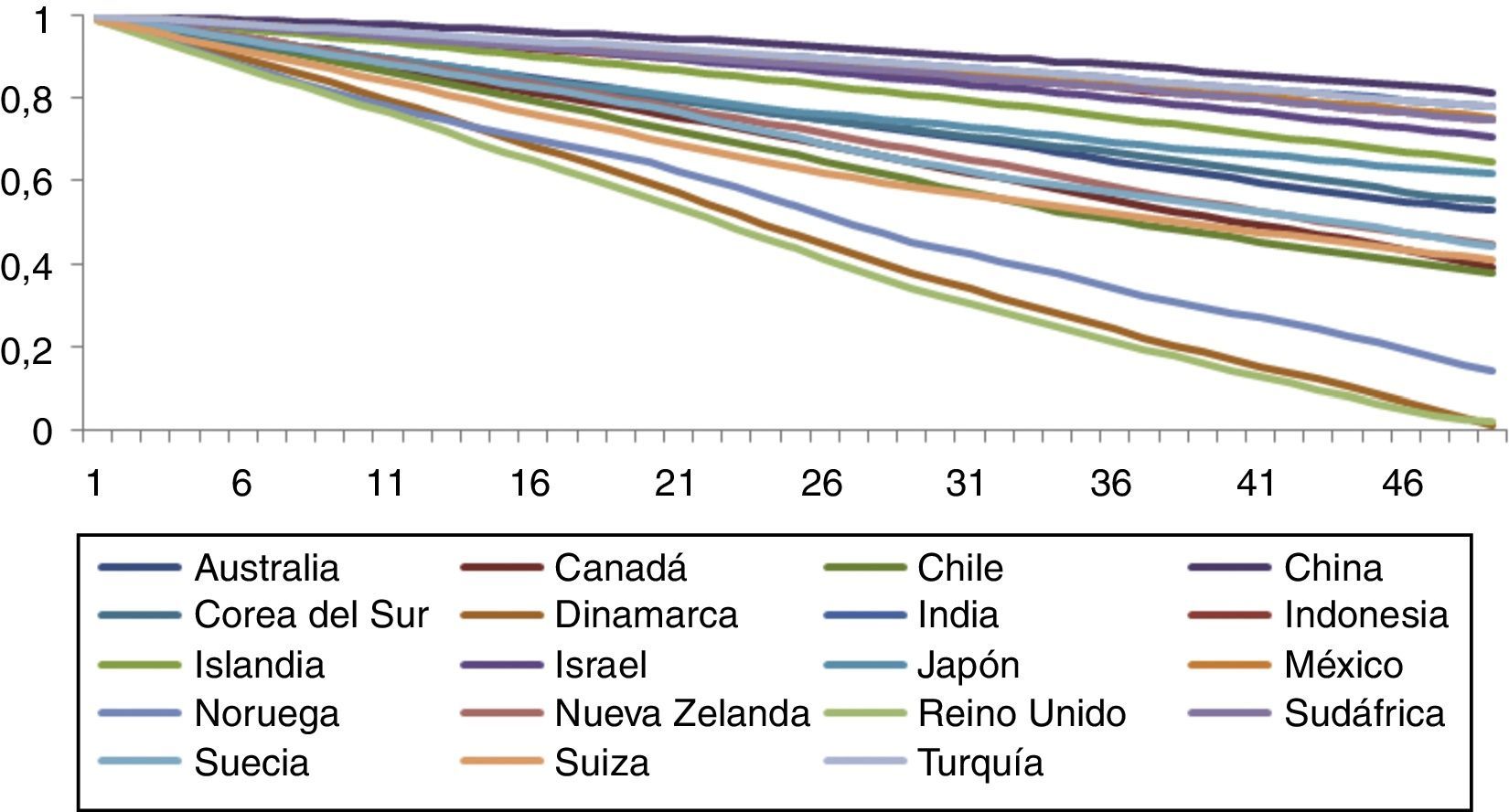
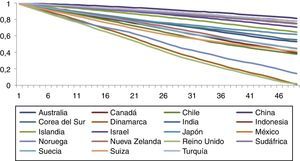
La figura 2 muestra la prueba de correlograma de los tipos de cambio de los países ln ρkcontraln k. Asimismo, la gráfica muestra que el correlograma de los países tiene pendiente negativa, como se esperaba.
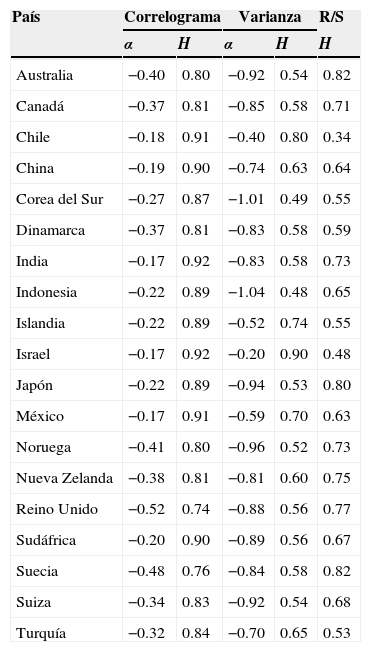
Por otro lado, se estimó la pendiente del método de las correlaciones en la tabla 2, con k igual a 150. Los valores del coeficiente de Hurst del tipo de cambio se encuentran en el rango 0.74,0.92. Esta prueba dice que si H>0.5, entonces el tipo de cambio de un país tiene memoria larga de tipo persistente. La persistencia que presentan las series hace que los valores medios crezcan de un momento a otro y que ni en el corto ni el largo plazo regresen a ellos. El coeficiente de Hurst fue calculado por medio de α=2H−2 o H=1+α/2, donde α es el valor de la pendiente.
Coeficiente de Hurst obtenido por medio del correlograma α=2H−2
| País | Correlograma | Varianza | R/S | ||
|---|---|---|---|---|---|
| α | H | α | H | H | |
| Australia | −0.40 | 0.80 | −0.92 | 0.54 | 0.82 |
| Canadá | −0.37 | 0.81 | −0.85 | 0.58 | 0.71 |
| Chile | −0.18 | 0.91 | −0.40 | 0.80 | 0.34 |
| China | −0.19 | 0.90 | −0.74 | 0.63 | 0.64 |
| Corea del Sur | −0.27 | 0.87 | −1.01 | 0.49 | 0.55 |
| Dinamarca | −0.37 | 0.81 | −0.83 | 0.58 | 0.59 |
| India | −0.17 | 0.92 | −0.83 | 0.58 | 0.73 |
| Indonesia | −0.22 | 0.89 | −1.04 | 0.48 | 0.65 |
| Islandia | −0.22 | 0.89 | −0.52 | 0.74 | 0.55 |
| Israel | −0.17 | 0.92 | −0.20 | 0.90 | 0.48 |
| Japón | −0.22 | 0.89 | −0.94 | 0.53 | 0.80 |
| México | −0.17 | 0.91 | −0.59 | 0.70 | 0.63 |
| Noruega | −0.41 | 0.80 | −0.96 | 0.52 | 0.73 |
| Nueva Zelanda | −0.38 | 0.81 | −0.81 | 0.60 | 0.75 |
| Reino Unido | −0.52 | 0.74 | −0.88 | 0.56 | 0.77 |
| Sudáfrica | −0.20 | 0.90 | −0.89 | 0.56 | 0.67 |
| Suecia | −0.48 | 0.76 | −0.84 | 0.58 | 0.82 |
| Suiza | −0.34 | 0.83 | −0.92 | 0.54 | 0.68 |
| Turquía | −0.32 | 0.84 | −0.70 | 0.65 | 0.53 |
Los valores fueron obtenidos por medio de las ecuaciones (3), (4) y (6), con el software Gretl y datos del Banco de la Reserva Federal de San Luis.
El método de gráfica de la varianza de la ecuación (8), para cada país, se presenta en la tabla 2. Los resultados muestran que Corea del Sur e Indonesia presentan memoria corta de tipo antipersistente, ya que el valor del coeficiente de Hurst se encuentra en [0, 0.5]. El fenómeno de antipersistencia resalta el hecho de que los tipos de cambio de estos países tienen variaciones a la alza y a la baja en el corto plazo, pero que en el largo plazo regresan a sus valores medios.
El método del rango reescalado para calcular el coeficiente H se obtuvo por medio de la ecuación (10), los resultados son presentados en la tabla 2 con R/S. El valor del coeficiente de Hurst del tipo de cambio de Chile es de 0.34, indicio de que la serie es del tipo antipersistente y que sus variaciones a la alza y a la baja son compensadas en el largo plazo. El resto de los países presentan persistencia, dado que el valor del coeficiente H es superior a 0.5.
Por otro lado, los valores de los coeficientes H cercanos a la unidad son evidencia de problemas de volatilidad, más que de memoria larga, pues son estacionarios en la media por los resultados mostrados en la tabla 2. Se observa que la mayor parte de los países se concentran en la prueba del gráfico de la varianza, y que Corea del Sur, Israel y Turquía tienen soporte en el método del rango reescalado.
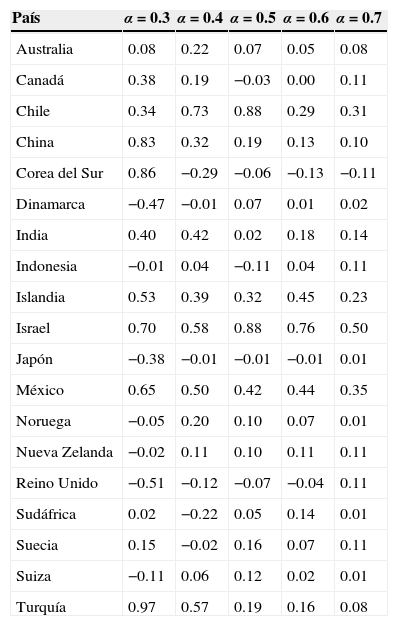
En la tabla 3 se muestran los cálculos obtenidos de la pendiente d, nótese que se pueden obtener a partir de H=d+(1/2), de acuerdo con la ecuación (7). La tabla 3 muestra un análisis de sensibilidad para diferentes valores de α, es decir, la prueba se realizó con diferentes cantidades de bloques de datos, por ejemplo, si α=0.5, se tiene T=499 de acuerdo con Tα=m. Los resultados muestran que dependiendo del valor de α que se utilice en la regresión se puede pasar de una serie antipersistente donde d está en [−.05, 0] a una persistente donde d se encuentra [0, 0.5] o viceversa. También se muestra que Chile, Islandia, Israel, México y Turquía son consistentes con la definición de memoria larga, ya que a pesar de los cambios en el valor de α, el parámetro de integración d sigue siendo consistente.
Prueba del periodograma de Geweke y Porter-Hudak (Tα=m)
| País | α=0.3 | α=0.4 | α=0.5 | α=0.6 | α=0.7 |
|---|---|---|---|---|---|
| Australia | 0.08 | 0.22 | 0.07 | 0.05 | 0.08 |
| Canadá | 0.38 | 0.19 | −0.03 | 0.00 | 0.11 |
| Chile | 0.34 | 0.73 | 0.88 | 0.29 | 0.31 |
| China | 0.83 | 0.32 | 0.19 | 0.13 | 0.10 |
| Corea del Sur | 0.86 | −0.29 | −0.06 | −0.13 | −0.11 |
| Dinamarca | −0.47 | −0.01 | 0.07 | 0.01 | 0.02 |
| India | 0.40 | 0.42 | 0.02 | 0.18 | 0.14 |
| Indonesia | −0.01 | 0.04 | −0.11 | 0.04 | 0.11 |
| Islandia | 0.53 | 0.39 | 0.32 | 0.45 | 0.23 |
| Israel | 0.70 | 0.58 | 0.88 | 0.76 | 0.50 |
| Japón | −0.38 | −0.01 | −0.01 | −0.01 | 0.01 |
| México | 0.65 | 0.50 | 0.42 | 0.44 | 0.35 |
| Noruega | −0.05 | 0.20 | 0.10 | 0.07 | 0.01 |
| Nueva Zelanda | −0.02 | 0.11 | 0.10 | 0.11 | 0.11 |
| Reino Unido | −0.51 | −0.12 | −0.07 | −0.04 | 0.11 |
| Sudáfrica | 0.02 | −0.22 | 0.05 | 0.14 | 0.01 |
| Suecia | 0.15 | −0.02 | 0.16 | 0.07 | 0.11 |
| Suiza | −0.11 | 0.06 | 0.12 | 0.02 | 0.01 |
| Turquía | 0.97 | 0.57 | 0.19 | 0.16 | 0.08 |
Fuente: Elaboración propia con el software Gretl y datos del Banco de la Reserva Federal de San Luis.
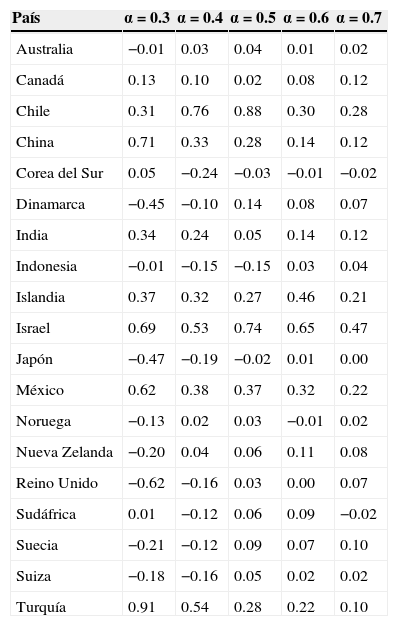
En la tabla 4 se muestran los resultados obtenidos del estimador local de Whittle proveniente de la ecuación (10). Esta tabla muestra valores similares a los obtenidos en la prueba anterior, dado que ambas se basan en el periodograma; es decir, se notan cambios de memoria corta d=[−0.5, 0] a memoria larga d=[0, 0.5] dependiendo de los valores que tome el coeficiente de α. Algunos países muestran consistencia con el fenómeno de memoria larga, como son Chile, Islandia, Israel, México y Turquía, con resultados similares al método anterior. Obsérvese que China, con esta prueba, también es consistente con el fenómeno de memoria larga.
Estimador local de Whittle de Robinson (Tα=m)
| País | α=0.3 | α=0.4 | α=0.5 | α=0.6 | α=0.7 |
|---|---|---|---|---|---|
| Australia | −0.01 | 0.03 | 0.04 | 0.01 | 0.02 |
| Canadá | 0.13 | 0.10 | 0.02 | 0.08 | 0.12 |
| Chile | 0.31 | 0.76 | 0.88 | 0.30 | 0.28 |
| China | 0.71 | 0.33 | 0.28 | 0.14 | 0.12 |
| Corea del Sur | 0.05 | −0.24 | −0.03 | −0.01 | −0.02 |
| Dinamarca | −0.45 | −0.10 | 0.14 | 0.08 | 0.07 |
| India | 0.34 | 0.24 | 0.05 | 0.14 | 0.12 |
| Indonesia | −0.01 | −0.15 | −0.15 | 0.03 | 0.04 |
| Islandia | 0.37 | 0.32 | 0.27 | 0.46 | 0.21 |
| Israel | 0.69 | 0.53 | 0.74 | 0.65 | 0.47 |
| Japón | −0.47 | −0.19 | −0.02 | 0.01 | 0.00 |
| México | 0.62 | 0.38 | 0.37 | 0.32 | 0.22 |
| Noruega | −0.13 | 0.02 | 0.03 | −0.01 | 0.02 |
| Nueva Zelanda | −0.20 | 0.04 | 0.06 | 0.11 | 0.08 |
| Reino Unido | −0.62 | −0.16 | 0.03 | 0.00 | 0.07 |
| Sudáfrica | 0.01 | −0.12 | 0.06 | 0.09 | −0.02 |
| Suecia | −0.21 | −0.12 | 0.09 | 0.07 | 0.10 |
| Suiza | −0.18 | −0.16 | 0.05 | 0.02 | 0.02 |
| Turquía | 0.91 | 0.54 | 0.28 | 0.22 | 0.10 |
Fuente: Elaboración propia con el software Gretl y con datos del Banco de la Reserva Federal de San Luis.
La mayor parte de las series de tipo de cambio muestran variaciones drásticas que tal vez estén más asociadas con fenómenos de volatilidad que con el de memoria larga. Por ejemplo, se presentan colas pesadas que dan origen a distribuciones de tipo leptocúrtica, sesgos mayores a 0, positivos y negativos, que indican acumulación de datos en zonas específicas de la distribución y que son verificadas por las pruebas que rechazan la normalidad, como la de Jarque-Bera. En consecuencia, el problema está en la varianza, no en la media, ya que las pruebas de raíz unitaria y de estacionariedad (ADF y KPSS) aceptan la hipótesis de estacionariedad. Este tipo de series pueden ser analizadas con modelos que capturen la volatilidad, como el ARCH, de Engle (1982), o el GARCH, de Bollerslev (1986).
Estimación del modelo de los modelos Autorregresivo Fraccionalmente Integrado con Medias MóvilesLa metodología para estimar los parámetros α, β y d que se aplicó a los tipos de cambio de Chile, China, Islandia, Israel, México y Turquía, demostraron memoria larga de acuerdo con las pruebas del estimador local de Whittle de Robinson (1995) y de Geweke y Porter-Hudak (1983).
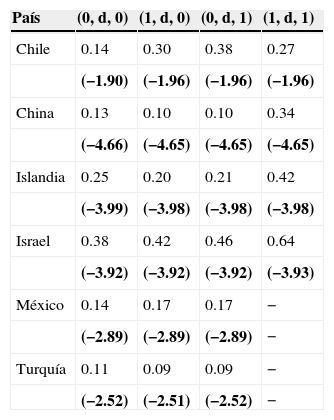
La tabla 5 muestra los resultados de la estimación por medio del método de máxima verosimilitud exacta y teniendo en cuenta la discriminación por medio del criterio de información de Akaike. Para Chile, el mejor modelo de comportamiento es el parámetro de integración 0.139, teniendo en cuenta que posee problemas en la parte residual, de allí que con 0.378 el criterio marca un buen ajuste a la curva original. Para China es mínimo el orden de integración, que es de 0.097. Con Chile también se observan problemas con los residuos. Para Islandia se observa un orden de integración considerable de memoria larga, el cual es de 0.204, y, por lo tanto, posee memoria larga. Israel no tiene memoria larga, ya que su orden de integración es cercano a 0.5, esto es evidencia de problemas en la varianza. El tipo de cambio de México sí posee memoria larga y su orden de integración es de 0.165, y, por último, Turquía no posee memoria larga debido a que su orden de integración es muy bajo, concretamente, de 0.094.
Estimación del parámetro d por el método exacto de máxima verosimilitud en el dominio del tiempo
| País | (0, d, 0) | (1, d, 0) | (0, d, 1) | (1, d, 1) |
|---|---|---|---|---|
| Chile | 0.14 | 0.30 | 0.38 | 0.27 |
| (−1.90) | (−1.96) | (−1.96) | (−1.96) | |
| China | 0.13 | 0.10 | 0.10 | 0.34 |
| (−4.66) | (−4.65) | (−4.65) | (−4.65) | |
| Islandia | 0.25 | 0.20 | 0.21 | 0.42 |
| (−3.99) | (−3.98) | (−3.98) | (−3.98) | |
| Israel | 0.38 | 0.42 | 0.46 | 0.64 |
| (−3.92) | (−3.92) | (−3.92) | (−3.93) | |
| México | 0.14 | 0.17 | 0.17 | − |
| (−2.89) | (−2.89) | (−2.89) | − | |
| Turquía | 0.11 | 0.09 | 0.09 | − |
| (−2.52) | (−2.51) | (−2.52) | − |
Entre paréntesis, el criterio de información de Akaike.
Fuente: Elaboración propia con el software Matrixer y datos del Banco de la Reserva Federal de San Luis.
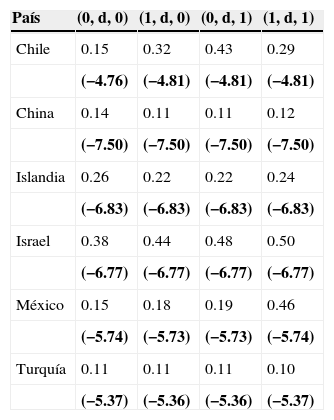
En la tabla 6 se muestran los resultados de la estimación de los parámetros por medio del método de máxima verosimilitud en el dominio de la frecuencia, y los resultados son muy similares a los obtenidos en el dominio del tiempo. Hay una diferencia importante en el grado de ajuste a la curva original, es decir, la estimación a través del dominio del tiempo es superior a la frecuencia, tomando en cuenta al criterio de información de Akaike. En ambos métodos de estimación, Chile, Islandia y México tienen memoria larga, con un orden de integración superior a 0.1.
Estimación del parámetro d por máximo verosimilitud en el dominio de la frecuencia
| País | (0, d, 0) | (1, d, 0) | (0, d, 1) | (1, d, 1) |
|---|---|---|---|---|
| Chile | 0.15 | 0.32 | 0.43 | 0.29 |
| (−4.76) | (−4.81) | (−4.81) | (−4.81) | |
| China | 0.14 | 0.11 | 0.11 | 0.12 |
| (−7.50) | (−7.50) | (−7.50) | (−7.50) | |
| Islandia | 0.26 | 0.22 | 0.22 | 0.24 |
| (−6.83) | (−6.83) | (−6.83) | (−6.83) | |
| Israel | 0.38 | 0.44 | 0.48 | 0.50 |
| (−6.77) | (−6.77) | (−6.77) | (−6.77) | |
| México | 0.15 | 0.18 | 0.19 | 0.46 |
| (−5.74) | (−5.73) | (−5.73) | (−5.74) | |
| Turquía | 0.11 | 0.11 | 0.11 | 0.10 |
| (−5.37) | (−5.36) | (−5.36) | (−5.37) |
Entre paréntesis, el criterio de información de Akaike.
Fuente: Elaboración propia con el software R y datos del Banco de la Reserva Federal de San Luis.
Este trabajo analizó el tipo de cambio nominal de países desarrollados y en vías de desarrollo. Para encontrar evidencia de memoria larga en el tipo de cambio nominal se utilizaron, primero, 3 diferentes métodos y pruebas de detección de memoria larga como son la prueba del correlograma, el gráfico de varianza y el coeficiente de Hurst. Estas 3 pruebas indicaron una prevalencia de memoria larga en el tipo de cambio de cada país; la excepción se dio en el método de gráfico de la varianza en Corea del Sur e Indonesia, mientras que con el coeficiente de Hurst se dio en Chile e Israel, que muestran antipersistencia o memoria corta. Por otro lado, las pruebas de Geweke y Porter-Hudak (1983) y el estimador local de Whittle propuesto por Robinson (1995) son pruebas que dependen del tamaño de la muestra y, por lo tanto, el coeficiente de Hurst cambiaba de memoria corta a larga, lo cual es indicio de problemas en la varianza. El tipo de cambio de los países de Chile, China, Islandia, Israel, México y Turquía fue el que mostró consistencia en todas las pruebas de memoria larga. Las series que mostraron el fenómeno de memoria larga fueron estimadas en los dominios del tiempo y de la frecuencia. En el primer caso se utilizó el método de máxima verosimilitud exacta de Sowell (1992), y en el segundo, el método de aproximación de Whittle, propuesto por Fox y Taqqu (1986). El resultado de ambos métodos fue similar en lo que se refiere al parámetro de integración; sin embargo, con respecto al ajuste, el primer método fue superior dado que presentó el criterio de información de Akaike más cercano a cero.
Estudios de memoria larga para variables macroeconómicas se encuentran en Crate y Rothman (1996); Barkoulas y Baum (1997); Dueker y Startz (1998); Tsay (2000); Baillie, Han y Kwon (2002); Doornik y Ooms (2004); Barkoulas y Baum (2006). Estudios de memoria larga para los mercados de valores se hallan en Lux (1996); Wright (1999); Barkoulas, Baum y Travlos (2000); Sadique y Silvapulle (2001); Henry (2002); Tolvi (2003); Granger y Hyung (2004); Sibbertsen (2004); Bilel y Nadhem (2009); López-Herrera, Venegas-Martínez y Sánchez-Daza (2009); Baillie y Bollerslev (1994).
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.
Véase Hamilton (1994) para observar el desarrollo matemático del operador rezago fraccional por medio de derivadas.
Por ejemplo, si d=1.4, entonces el orden de integración en realidad es de 0.4 debido a la aplicación de la primera diferencia a la variable original.
Es importante destacar que si en la autocorrelación se observa una caída lenta que tiende a cero, por ejemplo, una caída hiperbólica igual a k2H−2(con 1/2<H<1, siendo H el coeficiente de Hurst), si además se obtiene un orden de integración d→0, es difícil saber si la serie tiene memoria larga o no, ya que la serie yt se confundiría con una serie estacionaria con un orden de integración cero, esto es, un modelo ARMA (p,q).
El desarrollo de la metodología para obtener el coeficiente de Hurst puede consultarse en Peters (1994) y Beran (1994).
De acuerdo con Shimotsu y Phillips (2002), en la ecuación (7) se reemplaza 2 senωk/2 por 2 ln ωk para la estimación.