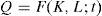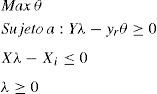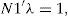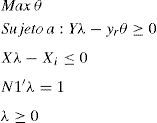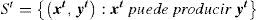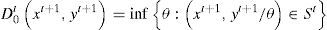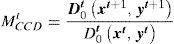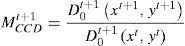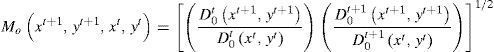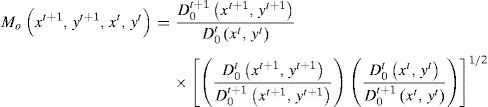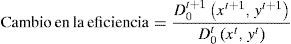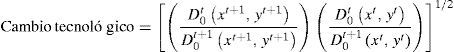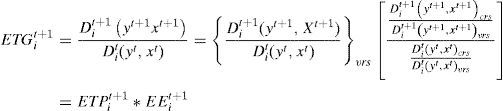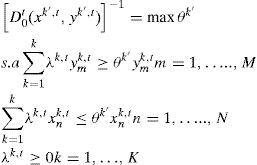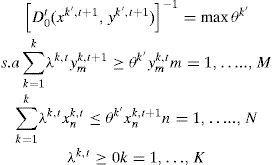En este trabajo se presenta un análisis del cambio en la productividad total de los factores (PTF) de las terminales de contenedores de los principales puertos de México en el periodo 1982-2010. Para ello se propone la elaboración del índice Malmquist, el cual descompone el cambio de la productividad en 2 factores: cambio en eficiencia (catch-up effect) y cambio tecnológico (frontier shift). Los resultados muestran que en general hubo un aumento en la productividad durante el periodo analizado, el cual es explicado por el cambio tecnológico; Manzanillo fue el puerto que tuvo un mayor crecimiento en la productividad, y del lado opuesto, Tuxpan fue el que tuvo la mayor reducción, en este último caso debido principalmente a la tendencia negativa en el tráfico de contenedores movilizados en el periodo. Estos resultados muestran la necesidad de formular políticas públicas portuarias para que los puertos puedan operar en su máxima capacidad.
This paper presents an analysis of change in the Total Factor Productivity (TFP) of container terminals in major ports in Mexico in the period 1982-2010. For this, we propose Malmquist Index, which decomposing the change in productivity in two factors: Change in efficiency (catch-up effect) and technological change (shift frontier). The results show that in general there was an increase in productivity over the period analyzed, which is explained by technological change; Manzanillo was the port that had higher growth in productivity, and opposite Tuxpan was the one who had the greatest reduction, it was due mainly for the negative trend in traffic mobilized during containers. These results show the need to develop public policies for ports to operate at maximum capacity.
En los últimos años, los puertos mexicanos han destacado por su elevada presencia en los volúmenes de mercancías manejadas, por la diversificación de sus actividades y como áreas de oportunidad para nuevas inversiones y generación de empleos en terminales, instalaciones y negocios portuarios (CGPMM, 2010).
La infraestructura portuaria existente ha sido el resultado de la inversión por parte del sector público y del privado. Los cambios tecnológicos incorporados a las unidades navieras (mayores dimensiones y velocidad) y equipos portuarios (grúas más sofisticadas), así como el crecimiento del comercio mundial, han permitido a los puertos incorporar nuevas actividades (centros de distribución, desempaque, empaque, etc.), generando el concepto de puerto logístico.
Las características de la infraestructura portuaria tienen efectos significativos sobre la inversión: el riesgo que debe asumir una empresa para desarrollar un proyecto portuario es elevado. Si la demanda por el producto portuario resulta inferior a su capacidad de oferta, puede llevar a una situación financiera peligrosa para los inversionistas (Rus, Campos y Nombela, 2003).
En el caso específico de las terminales de contenedores, el mercado de los servicios de maniobras a contenedores comprende la carga, descarga, alijo1, almacenaje, estiba y acarreo que se realiza en cada puerto. Estos servicios son maniobras que se efectúan para trasladar un contenedor entre la embarcación y otro modo de transporte terrestre. Las maniobras a contenedores ofrecidas en los puertos mexicanos se realizan a través de equipos móviles y fijos con distintos niveles de productividad, que permiten identificar 2 modalidades de servicio: especializados y no especializados de maniobras a contenedores (Chang, 1978). Adicionalmente, tanto las navieras como los usuarios demandan servicios con alta productividad, de tal modo que en la medida que esta sea mayor, el tiempo de estadía de la embarcación será menor, así como los costos por el uso de la infraestructura portuaria (Kim y Sachis, 1986; Paredes, 2007).
Es por eso que medir el desempeño de las actividades portuarias es una tarea fundamental por parte de las autoridades. En este sentido, algunos investigadores han realizado estudios de productividad parcial para medir actividades específicas, y para efectuarlo de una manera global han propuesto usar el concepto de «productividad total de los factores» (PTF) en la industria portuaria.
La PTF se obtiene al relacionar la totalidad de los productos con la totalidad de los insumos empleados durante el proceso de producción. La aplicación de esta medida al sector portuario es reciente, y la técnica más empleada ha sido el índice de Malmquist, que permite medir el cambio que se produjo en la PTF durante distintos periodos. Asimismo, este índice permite conocer los cambios en cada uno de los componentes de la productividad total: la eficiencia técnica, el cambio tecnológico y la eficiencia en la escala de producción (Färe, Grosskopf, Norris y Zhang, 1994).
González y Trujillo (2006) mencionan que los puertos buscan maximizar la transferencia de carga, y que la capacidad de manipulación de la mercancía de un puerto depende de su productividad. Es por ello que las mejoras en la productividad portuaria pueden originarse de una mezcla de factores, incluyendo las mejores medidas o políticas que adopte una autoridad de gobierno portuaria, aduanera o directamente del operador de una terminal sobre la mano de obra, infraestructura, sistemas, equipos, etc. También puede deberse a factores externos tales como las demandas de las compañías navieras por nuevos itinerarios o por aspectos relativos al transporte, infraestructura y logística en la cadena de distribución asociada al puerto (Doerr y Sánchez, 2006).
Conocer el comportamiento de la productividad de un puerto es importante para adoptar las medidas que permitan corregir las ineficiencias detectadas y mejorar las fortalezas del puerto (Kim y Sachis, 1986). En este sentido, la hipótesis que se plantea en este trabajo es la siguiente: la PTF en los puertos marítimos mexicanos está determinada por el progreso tecnológico.
Sistema portuario mexicanoUn sistema portuario es un conjunto de elementos interrelacionados cuyos objetivos son participar en el desarrollo y aprovechamiento del litoral de una región, apoyando a la industria, o servir como vínculo entre los transportes marítimos o terrestres (López, 1999).
La estructura de este sistema portuario ha sufrido grandes cambios en las últimas 2 décadas, ya que a partir del ingreso de nuestro país al GATT, y posteriormente en el marco de la firma del TLCAN, se realizaron una serie de reformas hacendarias, fiscales, políticas y económicas, cambiando el modelo tradicional de desarrollo de sustitución de importaciones a una economía abierta. Empiezan entonces diversas actividades para modernizar y reorganizar económicamente el país, como fue el de la privatización y venta de paraestatales. Tal fue el caso del sistema portuario, por lo que en el año 1993 se reformó la ley de puertos para dar lugar a que la iniciativa privada administrara, operara y explotara los puertos, y en el año 1994 se creó la figura de la Administración Portuaria Integral como una sociedad mercantil; todo esto con la finalidad de que se cumpliera con el rol necesario para el nuevo modelo de desarrollo (Pérez, 1995).
En la actualidad, la organización portuaria está integrada por 3 organismos: el gobierno federal, las Administraciones Portuarias Integrales y el sector privado. Esta integración permite realizar diversas funciones en materia de regulación política, administrativa, de inversión, de mantenimiento, planeación y fomento de la competencia. La estructura de los puertos se divide en puertos de altura y puertos de cabotaje, teniendo 114 puertos y terminales habilitadas: 56 en el Pacífico y 58 en el Golfo de México y Caribe (SCT, 2008). De acuerdo al tipo de mercancía que se maneja, se tiene la siguiente división: industrial, comercial, pesquero y turístico.
Con esta estructura portuaria, en el año 2013 los puertos mexicanos manejaron 287,912,404 toneladas de productos diversos, y en el caso de los contenedores se manejaron 4,892,881 TEUS2 en ambas costas: Pacífico y Atlántico (SCT, 2014).
Marco teóricoEn los puertos, los indicadores de productividad juegan un rol importante en el desarrollo de sus actividades. Estos indicadores se construyen según los intereses o las perspectivas de quienes lo utilizan. Algunos estudios sobre indicadores portuarios presentan propuestas que permiten medir y comparar la productividad intra e interpuerto, además de comparar los rendimientos reales de un puerto con sus rendimientos máximos posibles. Con el objetivo de adaptar a la medición de la productividad, el efecto combinado de todos los factores de producción se define el concepto de PTF.
Productividad total de los factoresLa productividad se define como la razón entre la cantidad producida y los insumos utilizados, y la PTF es la razón de la producción neta con la suma asociada con los factores de insumos de mano de obra y capital (Sumanth, 1994). Fue Solow quien contribuyó a establecer el factor total de la productividad como un concepto operacional, a partir de la función de producción. En su artículo «Technical change and the aggregate production function», publicado en 1957, describe una forma de separar las variaciones en el producto per cápita debida al cambio técnico y la disponibilidad de capital per cápita.
Solow (1957) define la función de producción agregada como:
donde Q=producción, K=insumo de capital, L=insumo de mano de obra; K y L representan los insumos de capital y mano de obra en unidades físicas, y t representa el tiempo y aparece en F para considerar el cambio técnico.Por su parte, Kendrick (1961), en diferentes trabajos, ha medido la productividad de los sectores agrícola, manufacturero, comercial, financiero, de transporte y de servicios públicos en Estados Unidos tomando como punto de partida una función de producción del tipo Q=f (X1,…Xn), donde Q es igual al valor agregado y (X1,…Xn) es igual a «n» factores tangibles que se utilizan en la producción. Este autor construyó un índice de la PTF con el que cuantificó la productividad de la industria manufacturera de Estados Unidos para el periodo 1889-1957. Para Kendrick, la PTF es una relación entre el producto real y los insumos:
En donde insumo de mano de obra=horas-hombre ajustadas según los cambios en la calidad de la mano de obra; insumo de capital=inventario neto de estructuras+equipo en las plantas+inventarios+capital de trabajo+terrenos.
El estudio de la PTF en la teoría económica se basa en la idea de una función de producción como una representación de la tecnología actual en un periodo de tiempo dado, el cual indica la salida máxima que puede ser factible obtener a partir de un conjunto dado de factores y el estado tecnológico. Este concepto se interpreta generalmente como una frontera que limita el potencial productivo de la empresa. En este sentido, se puede asociar a un cambio técnico con un cambio en esta frontera, mientras que una mejora en la eficiencia puede ser entendida como una reducción en la distancia de esta frontera por la combinación de una firma de factores y productos. El progreso técnico se asocia generalmente con una serie de innovaciones y cambios en las técnicas de producción o de gestión, mientras que la eficiencia técnica es la capacidad de la empresa para gestionar sus recursos y para adaptarse al medio ambiente y las condiciones en las que opera la empresa. Por lo tanto, las mejoras en la productividad pueden ser desglosadas en los cambios en la eficiencia y el progreso técnico (Coelli, Prasada Rao y Battese, 1998).
La eficiencia técnicaLas técnicas de análisis de eficiencia mediante la «función frontera» son consideras las alternativas más adecuadas para medir la eficiencia portuaria, ya que para su aplicación se utilizan indicadores de inputs y outputs calculables para este tipo de estudios (González y Trujillo, 2007).
Farrell (1957) fue el primer autor en introducir una aproximación cuantitativa de la eficiencia, proponiendo una medición donde cada unidad de decisión puede ser evaluada en relación a otras unidades homogéneas, de forma tal que la eficiencia se convierte en un concepto relativo y no absoluto, donde el valor tomado por la eficiencia para cada entidad indica la desviación observada respecto a aquellas consideradas como eficientes.
El modelo de análisis de la envolvente de datos (DEA) es una técnica no paramétrica que facilita la construcción de una superficie envolvente o frontera eficiente a partir de los datos disponibles del conjunto de entidades objeto de estudio conocidas como Decision Making Unit (DMU) (Charnes, Cooper y Rhodes, 1978), donde cada una de estas DMU obtiene un peso o valor de los inputs y outputs que maximizan el valor de eficiencia de su producción. De esta manera las unidades ineficientes quedan fuera de la frontera, permitiendo evaluar la eficiencia relativa de cada una de las unidades.
La literatura sobre la eficiencia técnica tiene su origen en los primeros años de la década de los cincuenta. La primera definición formal de la eficiencia técnica se debe a Koopmans (1951:460): «es aquella en donde un incremento en cualquiera de los outputs exige una reducción en al menos de uno de los restantes o el incremento de alguno de los inputs», y la primera medida de la eficiencia técnica es propuesta por Debreu (1951) y Shephard (1953), aunque con diferente orientación (output e input, respectivamente).
Los modelos DEA pueden clasificarse en función de:
- •
El tipo de medida de eficiencia que proporcionan: modelos radiales y no radiales.
- •
La orientación del modelo: input orientado, output orientado o input-output orientado.
- •
La tipología de los rendimientos a escala que caracteriza la tecnología de producción, entendida esta como la forma en que los factores productivos pueden caracterizarse por la existencia de rendimientos a escala: constantes o variables a escala.
El estudio de Farrell se complementa con los trabajos de Charnes et al. (1978), que partían de rendimientos a escala constantes (CRS), de forma tal que un cambio en los niveles de inputs conlleva a un cambio proporcional en el nivel del output, el cual requiere tantas optimizaciones como unidades de decisión (DMU). Tiene 2 orientaciones: input (la comparación entre el nivel mínimo de inputs necesario, para un nivel dado de outputs, y el realmente empleado) y la orientación output (la comparación entre el output máximo alcanzable, para un nivel dado de inputs, y el realmente alcanzado). Puede escribirse en términos generales en 3 formas: fraccional, multiplicativa y envolvente.
Se muestra el modelo de programación lineal con orientación output en su forma envolvente:
donde θ indica la distancia en outputs a la envolvente de datos, es decir, la medida de eficiencia; X es la matriz de inputs de orden (mxn); Y es la matriz de outputs de orden (sxn); λ es el ventor (nx1) de pesos o intensidades, y xi, yr representan vectores de inputs y outputs, respectivamente.Posteriormente, Banker, Charnes y Cooper (1984) extendieron el modelo original para incluir rendimientos a escala variables (VRS). Considerando que diversas circunstancias como la competencia imperfecta, las restricciones en el acceso a fuentes de financiación, etc., pueden provocar que las unidades no operen a escala óptima, y modificando el programa lineal de manera que introduzca una restricción:
esta restricción permite que una unidad ineficiente solo sea comparada con unidades productivas de su mismo tamaño. Sin esta restricción, las unidades evaluadas pueden ser comparadas con otras unidades mayores o menores.
Para diferenciarlo del anterior, se le llama modelo de rendimientos variables a escala (VRS), siendo el modelo con orientación output el siguiente:
Esta modificación permitió descomponer la eficiencia técnica global en eficiencia técnica pura y eficiencia de escala. Para poder realizarlo se deben calcular los 2 modelos (CRS y VRS) con los mismos datos. Si existe una diferencia para las 2 mediciones para una DMU en particular, entonces significa que esa DMU posee ineficiencia de escala y que el valor de ineficiencia es la diferencia entre la medición CRS y VRS (Coll y Blasco, 2006).
Revisión de la literaturaSe han realizado diversos estudios sobre la PTF en los puertos a través del índice Malmquist. A continuación se muestra la evidencia empírica más reciente.
Halkos y Tzeremes (2012) calculan la PTF de los puertos en Grecia durante el período 2006-2010, a través del índice Malmquist, descomponiéndolo en el cambio de la eficiencia de escala, cambio en la eficiencia técnica pura, cambio en la eficiencia técnica global y cambio tecnológico; aplican además la técnica bootstrap para darle mayor confiabilidad al índice. En una segunda etapa, los autores utilizan el modelo de regresión lineal Kernel con la finalidad de medir el efecto del tamaño de los puertos con respecto a la productividad. Los resultados muestran que la longitud de los puertos tiene un efecto negativo en la productividad; sin embargo, el número de terminales de los puertos influye positivamente. En general se muestra un estancamiento en el progreso tecnológico.
Por otro lado, Dan, Luan y Pian (2013) evalúan la eficiencia dinámica y los cambios en la productividad de las terminales de contenedores de los principales puertos de China aplicando la técnica de análisis de la envolvente (DEA) y el índice Malmquist durante el periodo 2007-2010. El resultado da cuenta de que el cambio tecnológico fue mejorando a lo largo del periodo; sin embargo, el cambio en la eficiencia técnica disminuyó y la mayoría de los puertos presentaron ineficiencia de escala. En esta misma línea, Lan-binga, Junb y Chun-huib (2011) realizan una medición de la eficiencia dinámica y de la PTF a través del índice Malmquist de los principales puertos de China continental, Hong Kong y Taiwán. Los resultados obtenidos muestran que el rendimiento general de los puertos era muy bajo y empeoró durante la crisis financiera. Este estudio también mostró ineficiencia de escala en la mayoría de los puertos debido en gran medida a la dispersión de los recursos. China continental fue quien presentó mayor puntuación en el índice Malmquist, mientras que Hong Kong solo creció al inicio del periodo y Taiwán tuvo los niveles más bajos.
Guner y Coskun (2013) evalúan la PTF y el cambio técnico y tecnológico de los 4 puertos de Turquía durante el período de 2003 a 2010 utilizando el índice Malmquist. En los resultados las puntuaciones de eficiencia no siguieron una tendencia estable, presentando fluctuaciones. Fue, por lo tanto, el cambio tecnológico quien tuvo mayor representatividad en el índice Malmquist. En esa misma dirección, Song y Cui (2013) y Bo-xin Fu et al. (2009) presentan resultados similares donde el cambio en la tecnología tuvo mayor influencia en la productividad; en ambos trabajos se efectúa un estudio sobre las operaciones portuarias de China, utilizando el índice Malmquist para determinar y analizar los cambios de la productividad; sin embargo, los primeros autores lo realizan durante el periodo 2006-2011 y los resultados muestran que hubo un crecimiento en el cambio de la productividad del 4.6%, siendo la terminal portuaria de Yangtze Delta la más productiva. Los segundos autores analizaron el cambio en la eficiencia operativa de los 10 principales puertos de China en el periodo del 2001 al 2006, en los que se obtiene un alto nivel de eficiencia de escala.
Salem, Tajudin y Khader (2009), Lozano (2009) y Guerrero y Rivera (2009) miden la PTF a través del índice Malmquist. Los primeros autores evalúan la eficiencia de las terminales de contenedores en la región de África Oriental y el Oriente Medio; el segundo estima el crecimiento de la productividad de los puertos españoles, y los últimos autores calculan la PTF de los puertos más importantes de México. En todos los casos se calcula el cambio de eficiencia técnica pura, cambio en la eficiencia de escala y cambio tecnológico. Los resultados obtenidos, a diferencia de los que se observan en el párrafo anterior, muestran que es la eficiencia técnica la que determina la productividad.
Bichou (2011) analiza los impactos de los requerimientos de las normas de seguridad portuaria con respecto a la eficiencia operativa de las terminales de contenedores del mundo. Utiliza el índice Malmquist para realizar un seguimiento de los cambios de productividad de 420 unidades de toma de decisiones de contenedores en el periodo 2002-2008. Los resultados muestran que la eficiencia operativa varía bastante dependiendo del tipo de regulación y de la terminal; sin embargo, existe evidencia de que en general la productividad va aumentado a lo largo del periodo.
Por último, Cheon, Dowall y Song (2010) realizan un estudio donde se evalúa la influencia de las reformas institucionales portuarias con respecto a la eficiencia de las ganancias entre 1991 y 2004. Construyeron un panel de datos para la propiedad portuaria, la estructura corporativa y las entradas y salidas para los 98 principales puertos del mundo utilizando el índice de productividad de Malmquist. En los resultados se observa que la reestructuración de la propiedad contribuyó al aumento de la PTF. La reestructuración logra la optimización de las terminales de contenedores, especialmente para los grandes puertos, ya que permite a las entidades privadas especializadas concentrarse en la operación de terminales y servicios de carga.
La revisión de la literatura permitió conocer el estado del arte de las investigaciones donde utilizaron la técnica Malmquist, por lo que la aportación que se tiene con este análisis viene dada en varios sentidos: 1)se identificaron los inputs y outputs que se utilizaron en los diversos trabajos, con lo cual se tuvieron elementos que coadyuvaron en la construcción de la hipótesis en esta investigación, vinculándola con las características del sistema portuario mexicano; 2)se analiza el desarrollo de la metodología para calcular el índice Malmquist y su viabilidad para obtener la PTF, y 3)se contrastan los resultados obtenidos en el presente trabajo con los de otros autores revisados.
El índice Malmquist mide la productividad a partir de funciones de distancia que pueden estimarse de forma no paramétrica, empleando técnicas de programación matemática. El índice que se desarrolla en este trabajo permite descomponer la productividad en cambio de eficiencia de escala, cambio de eficiencia técnica pura, cambio de eficiencia técnica global y cambio tecnológico.
Desarrollo metodológicoUna manera de medir la PTF es a través de la elaboración de índices donde destacan: el índice de Fisher (1922), el índice de Törnqvist (1936) y el índice de Malmquist (1953). En el presente trabajo se utiliza el índice Malmquist, el cual permite la descomposición en el cambio productivo en mejoras de eficiencia técnica y en cambios en la tecnología; además permite describir una tecnología multiinsumo y multiproducto sin la necesidad de especificar un objetivo de comportamiento, tal como la minimización de costos o la maximización de beneficios (Coelli et al., 1998).
El índice MalmquistMalmquist (1953) introdujo este concepto en relación con el nivel de utilidad del consumidor entre 2 periodos de tiempo, y Moorsteen (1961) fue el primero en utilizarlo en la teoría de la producción. También considera la presencia de ineficiencias desde el punto de vista del output, interpretando las diferencias en productividad (entre empresas o de una misma empresa en momentos diferentes del tiempo) como aquellas capacidades distintas para incrementar el output sin consumo adicional de recursos, dadas unas restricciones impuestas en la tecnología.
La aproximación del cambio productivo mediante la elaboración del índice de Malmquist fue aplicada por Caves, Christensen y Diewert (1982). Estos autores desarrollaron el índice aplicándolo desde la óptica de los inputs y de los outputs. En el índice que elaboran Caves y colaboradores se excluía la posibilidad de que las empresas pudieran mostrar comportamientos ineficientes. Sin embargo, el desarrollo posterior de Fare, Grosskopf, Lindgren y Roos (1989) y Färe et al. (1994) plantea la posibilidad de descomponer los avances en productividad a través del índice Malmquist relacionándolo con las medidas de eficiencia de Farrell.
Este índice de productividad se puede elaborar a partir del cálculo de funciones distancia, en concreto, midiendo la distancia de una unidad productiva en 2 periodos determinados; se asume que cada periodo de tiempo t=1,…,T, la producción tecnológica St modela la transformación de inputsxtεℝ+N y en outputsytεℝ+N.
Basándose en la tecnología del periodo inicial t, el índice Malmquist de productividad lo muestra la siguiente expresión (Färe et al., 1994):
Se asume que St satisface ciertos axiomas que bastan para definir funciones de distancia de salida significativas; la distancia de la función output es definida en t como:(2)D0txt,yt=infθ:xt,yt/θ∈St=(supθ:xt,θyt∈St)−1
Esta función se define como el recíproco de la máxima expansión proporcional del vector output yt dados los inputs xt. Esto caracteriza completamente a la tecnología. En particular se observa que D0txt,yt ≤1 si y solo si xt,yt∈St. En adición, D0txt,yt =1 si y solo si xt,yt está en la frontera de la tecnología. De acuerdo con Farrell (1957), esto ocurre cuando la producción es técnicamente eficiente.
Para definir el índice Malmquist se necesita definir la distancia de las funciones con respecto a 2 diferentes periodos de tiempo, tales como:
Esta distancia de la función mide el máximo cambio proporcional que se requiere de outputs para hacer xt+1,yt+1 factible en relación con la tecnología en t. En este sentido se puede definir la distancia de la función que mide el máximo cambio proporcional en un output requerido para hacer xt, yt en relación con la tecnología de t+1, el cuál lo nombran D0t+1xt,yt.
Caves et al. (1982) definen el índice de productividad Malmquist con la siguiente expresión:
En esta fórmula, la tecnología en un periodo t es la referencia tecnológica. Alternativamente, el índice Malmquist de productividad puede obtenerse basándose en la tecnología existente en el periodo posterior t+1, como se observa en la siguiente expresión:
Con la finalidad de evitar la elección de un punto de referencia arbitrario, se especifica el índice Malmquist para el cambio en la productividad basada en resultados como la media geométrica de los 2 índices de productividad de Malmquist de tipo Caves, Christensen y Diewert:
El índice propuesto por Färe et al. resulta más adecuado para estudiar largos periodos de tiempo y permite abordar el cambio tecnológico. En consecuencia, con su propuesta consiguen que la tecnología de referencia cambie con el tiempo.
donde la relación fuera de los corchetes mide el cambio en la eficiencia relativa entre los años t y t+1. La media geométrica de las 2 relaciones dentro de los corchetes captura el cambio en la tecnología entre los 2 periodos evaluados xty xt+1, como se observa a continuación:El primer elemento se relaciona con el cambio en la posición relativa respecto a la frontera tecnológica que resulta de la gestión del propio proceso productivo, y concretamente de la capacidad para incorporar el progreso tecnológico en su función de producción. Por su parte, la segunda fuente de productividad considera la existencia de progreso técnico y hace referencia a un conjunto de innovaciones y cambios en las técnicas que desplazan la frontera de producción obteniéndose, así, un output mayor sin variar la cantidad de inputs utilizados o el mismo nivel de producción con un consumo más reducido de factores.
El cambio de la eficiencia técnica, medida como cociente entre las eficiencias entre los períodos que se consideran, si el cociente es >1 revela una mejora en la eficiencia en el periodo t a t+1, si es <1 la eficiencia ha empeorado y si es =1 la eficiencia se ha mantenido.
Por su parte, el cambio tecnológico, si este adopta un valor >1 indica que ha habido progreso tecnológico, si es <1, que hay regresión tecnológica, y si es =1, la tecnología se ha mantenido. Este componente indica cómo varía el cambio técnico, y por tanto se está generando una innovación en las terminales de contenedores.
Así, la multiplicación entre estos 2 cocientes da como resultado el índice Malmquist. Un resultado superior a la unidad indica que se ha producido un incremento en la productividad entre 2 periodos (t y t+1) debido a mejoras en la eficiencia o mejoras en la tecnología. Por el contrario, resultados menores a la unidad, significan que hay una reducción en la productividad entra ambos periodos, y un resultado =1 significa que la productividad se ha mantenido.
Para calcular el índice Malmquist, Färe et al. (1994) utilizan los rendimientos de escala constante (CRS), pero además proponen el cambio en la eficiencia técnica global (ETG), la cual se puede descomponer en el cambio de la eficiencia técnica pura (ETP), que se corresponde con la gestión exclusivamente técnica de la empresa independientemente de su tamaño; y el cambio de la eficiencia de escala (EE), derivada del tamaño de la unidad productiva en relación con la escala óptima. Esta distinción permite contemplar aquellas situaciones en que una unidad productiva pueda ser técnicamente eficiente, pero no se sitúa en la escala óptima de producción. Esta descomposición se obtiene incorporando el supuesto de una tecnología con rendimientos de escala variables, es decir:
En los periodos de tiempo t y t+1, bajo el supuesto que los puertos como unidades de producción generan un producto yt=contenedores.Para estimar las medidas de distancia del índice Malmquist se debe seleccionar una orientación. a)Hacia los inputs (reducción de las cantidades de insumos aplicados mientas se mantienen constantes los niveles de producción). b)Con orientación output (aumento de niveles de producción mientras los niveles de insumos permanecen constantes).
La estimación del índice Malmquist requiere del cálculo de las funciones de distancia correspondientes, para la cual existen varias maneras de abordarlo (Färe, Grosskopf y Roos, 1998). Una manera de realizar este cálculo es a través de programación matemática DEA, donde la función de distancia de un puerto k¿ en el periodo t y t+1, requiere resolver 4 problemas de programación lineal: D0tyt,xt,D0t+1yt,xt,D0tyt+1,xt+1 y D0t+1yt+1,xt+1. Para ello, se toma en cuenta que la función de distancia del output es recíproca a la medida de eficiencia técnica de Farrell orientada al ouput:
Donde x e y representan los insumos y productos, respectivamente, del proceso productivo de las terminales de contenedores de cada puerto k¿ y k=1,…k, que en este caso se describe de la siguiente manera:x=(inputs) longitud de muelle total más número de trabajadores totales,
y=(output) número de TEUS movidos anualmente en todos los puertos.
Por lo que, en la fórmula, k¿ representa 1,2,…,k puertos, utilizando n=1, 2,…, N inputs (longitud de muelle y número de trabajadores) xnk,t, en cada periodo de tiempo t=1,2,…,T. Esos inputs se usan para producir m=1,…, M outputs (TEUS) ymk,t.
Para calcular la función de distancia con respecto del periodo t+1, se utiliza una expresión matemática similar, para lo cual se sustituye el superíndice t por t+1 en las ecuaciones anteriores presentadas. Con respecto a la función distancia D0txt+1,yt+1, se estima con la sustitución del superíndice t por t+1. Así mismo, la estimación de la función D0t+1(xt,yt) se concreta reemplazando el superíndice t por t+1, quedando de la siguiente manera:
Las distancias respecto a la tecnología con rendimientos variables a escala se obtienen imponiendo la restricción adicional de que la suma de los elementos del vector de intensidades debe ser igual a la unidad (Banker et al., 1984).
El índice Malmquist, al estar basado en el método DEA, presenta ventajas y desventajas: Entre las principales ventajas encontramos (Schuschny, 2007): a)permite trabajar con múltiples inputs y outputs, medidos en diferentes sistemas de unidades; b)a diferencia de los métodos econométricos que emplean una aproximación a la frontera de producción estocástica, la estimación del índice Malmquist no impone el uso de formas funcionales explícitas para la tecnología; c)los puertos son comparados con el puerto ideal, construido a partir del desempeño de puertos «pares» reales, que son productivamente más eficientes, y d)el índice Malmquist se puede descomponer en cambio técnico y cambio en eficiencia, y por lo tanto aporta información sobre los efectos relativos de estos factores.
Entre las desventajas o limitaciones se destacan (Schuschny, 2007): a)es sensible a errores de medición, los outliers representados por puertos altamente productivos pueden sesgar los resultados al determinar la frontera de referencia; por el contrario, los puertos muy poco productivos no afectan los resultados; b)la exclusión de variables relevantes puede dar lugar a la identificación de ineficiencias (espurias); c)se estiman muy bien las eficiencias o ineficiencias relativas, pero no absolutas, y d)otra de las debilidades que tiene es que no distingue entre el «ruido» y la ineficiencia técnica, como ocurre en las estimaciones de frontera estocástica; así, cualquier desviación de la frontera sería considerado en este caso como «ineficiente».
Especificaciones del modeloCon el propósito de analizar la evolución de la productividad en el sistema portuario mexicano, en este trabajo se propone la elaboración del índice Malmquist, que permite valorar sus mejoras productivas.
Para ello se construye una función de producción no paramétrica a través del análisis de la envolvente de datos (DEA), con la cual se calcula la eficiencia técnica global, donde se trabajan los modelos de rendimientos de escala constantes (CRS) y de rendimientos de escala variables (VRS) con orientación output, debido a que se pretende analizar la posibilidad de maximizar la cantidad de TEUS con los insumos que se tienen.
Posteriormente se calcula el índice de productividad Malmquist, donde se muestra el cambio en eficiencia (catch-up effect) y el cambio tecnológico (frontier shift). A su vez, el cambio en la eficiencia se desagrega en cambio en la eficiencia técnica pura y cambio en la eficiencia de escala. De esta manera se medirá la variación de la productividad en el periodo 1982-2010 que han tenido las unidades de toma de decisión (DMU).
La muestra que se utilizó fueron los puertos que manejaron contenedores en el periodo de estudio, y se eliminaron aquellos que en algún año no movieron ningún contenedor, quedando finalmente los siguientes puertos: Mazatlán, Manzanillo, Lázaro Cárdenas, Altamira, Tuxpan, Veracruz, Progreso y Salina Cruz.
Identificación de inputs y outputsEn este apartado se identifican los inputs y outputs con el objeto de determinar los supuestos sobre los que se basa el modelo. En primer lugar se hizo una revisión literaria de aquellos autores que han realizado estudios de investigación de productividad portuaria, y en un segundo lugar se utilizó el programa SPSS para realizar una matriz de correlaciones bivariadas de Pearson.
Para seleccionar los inputs se tomaron en cuenta los 3 insumos básicos que se emplean en la función de producción tierra, trabajo y capital (Guerrero y Rivera (2009). Los datos de infraestructura del puerto representan muy bien a los insumos tierra y capital, y de acuerdo con la revisión literaria, los inputs seleccionados en una primera etapa para el insumo capital fueron: longitud de muelle y superficie de área. En cuanto al insumo trabajo, se considera la cantidad de trabajadores de la terminal de contenedores de cada puerto, así como también las grúas pórtico y las grúas de patio. En el caso del output, se consideró el número de TEUS manejados anualmente en cada puerto, debido a que en los últimas 2 décadas la carga contenedorizada ha sido el flujo más dinámico movilizado en los puertos mexicanos.
Una vez realizada la revisión literaria, se sometió al análisis estadístico de correlación y se observó que longitud de muelle y superficie de área están estadísticamente muy correlacionadas, por lo que resulta redundante incluir a ambas, y se optó por dejar el input que estadísticamente está más relacionado con el output que fue el caso de la longitud de muelle. Por otro lado, se observó que tanto las grúas de patios como las grúas pórtico están muy correlacionadas con el número de trabajadores, por lo que se optó por dejar a los trabajadores debido a que mostraron un nivel alto de correlación con los TEUS (tabla 1).
Matriz de correlación de Pearson
| Long. muelle | Trabajadores | TEUS | |
|---|---|---|---|
| Long. muelle | |||
| Correlación de Pearson | 1 | 0.483 | 0.945** |
| Sig. (bilateral) | 0.225 | 0.000 | |
| Trabajadores | |||
| Correlación de Pearson | 0.483 | 1 | 0.591 |
| Sig. (bilateral) | 0.225 | 0.123 | |
| TEUS | |||
| Correlación de Pearson | 0.945** | 0.591 | 1 |
| Sig. (bilateral) | 0.000 | 0.123 | |
Fuente: elaboración propia con base en resultados obtenidos del programa SPSS.
Inputs:
- 1.
Longitud de muelle (medido en metros): este insumo contempla únicamente la longitud de mulle de la terminal de contenedores de cada puerto.
- 2.
Trabajadores: este insumo contempla el total de trabajadores que operan en la terminal de contenedores de cada puerto.
Outputs: número de TEUS movilizados anualmente.
Para obtener los datos que modelizan la función de producción se recurrió a las siguientes fuentes:
- a)
Anuario estadístico de la CGPMM, 2005.
- b)
Anuario estadístico de la CGPMM, 2008.
- c)
Anuario estadístico de la CGPMM, 2010.
- d)
Anuario estadístico de la CGPMM, 2012.
- e)
Planes de desarrollo portuarios de cada puerto de los periodos seleccionados.
En este apartado se presentan los resultados del cálculo de la eficiencia técnica de las terminales de contenedores de los principales puertos utilizando el modelo DEA con orientación output; asimismo, se exponen los resultados del cálculo del índice Malmquist.
Se empieza con la presentación de las estadísticas descriptivas, como se observa en las tablas 2 y 3, donde existe una evolución en la media de las variables longitud de muelle y TEUS entre 1982 y 2010. Esto da cuenta del crecimiento considerado en el manejo de contenedores a lo largo del periodo. Del lado opuesto se encuentra el número de trabajadores; la media de esta variable disminuyó durante el periodo debido a que la mano de obra fue disminuyendo con el aumento de la maquinaria empleada.
Estadísticas descriptivas 1982
| Variable | Media | Suma | Desviación estándar | Varianza | Mínimo | Máximo | Rango |
|---|---|---|---|---|---|---|---|
| Longitud de muelle | 274.94 | 2,199.5 | 187.92 | 35,314.75 | 100 | 550 | 450 |
| Trabajadores | 90.12 | 721 | 63.6 | 4,045.55 | 20 | 202 | 182 |
| TEUS | 10,773 | 86,184 | 11,365.11 | 129,165,815.4 | 82 | 33,575 | 33,493 |
Fuente: elaboración propia con base a los resultados del estadístico SPSS.
Estadísticas descriptivas 2010
| Variable | Media | Suma | Desviación estándar | Varianza | Mínimo | Máximo | Rango |
|---|---|---|---|---|---|---|---|
| Longitud de muelle | 980.31 | 7,842.5 | 1,168.01 | 1,364,258.07 | 125.5 | 3,635 | 3,509.5 |
| Trabajadores | 76.88 | 615 | 54.44 | 2,963.55 | 21 | 186 | 165 |
| TEUS | 443,093.25 | 3,544,746 | 538,129.58 | 289,583,445,107.93 | 18 | 1,511,378 | 1,511,360 |
Fuente: elaboración propia con base a los resultados del estadístico SPSS.
La desviación estándar muestra que los valores están muy dispersos de la media, lo que indica la heterogeneidad de los datos entre los diferentes puertos, sobre todo en el número de TEUS, ya que en el año 2010 hubo puertos (Tuxpan) que manejaron menos de 100 contenedores anuales, en contraste con otros, como Manzanillo, que manejaron más de un millón de TEUS anuales.
EficienciaLos resultados obtenidos muestran que, en general, se tiene una baja eficiencia técnica en el sector portuario en México durante el período objeto de estudio. No obstante, sobresale el puerto de Manzanillo, ya que es eficiente para el lapso 2000-2010, mientras que los puertos de Lázaro Cárdenas y Veracruz, si bien son eficientes para algunos años, no se distinguen por tener continuidad en este indicador. En el caso particular de Lázaro Cárdenas para el 2000, fue mínimo el movimiento de contenedores que tuvo respecto a otros años, lo que llevó a que se tuviera el nivel de eficiencia más bajo en las cifras obtenidas para este puerto. Tuxpan, Salina Cruz y Mazatlán se encuentran en una situación delicada en términos de su eficiencia técnica global, no solo por su pronunciada tendencia descendente sino por sus valores mínimos en las mediciones de eficiencia (tabla 4).
Eficiencia técnica global en los puertos de méxico 1982-2010
| 1982 | 1990 | 1995 | 2000 | 2005 | 2010 | |
|---|---|---|---|---|---|---|
| Mazatlán | 0.2946 | 0.1649 | 0.1856 | 0.1081 | 0.0635 | 0.1394 |
| Manzanillo | 0.3142 | 0.4633 | 0.5259 | 1 | 1 | 1 |
| Lázaro Cárdenas | 0.5982 | 1 | 1 | 0.0087 | 0.3451 | 1 |
| Altamira | 0.733 | 0.7784 | 0.623 | 0.4449 | 0.4031 | 0.505 |
| Tuxpan | 1 | 0.0432 | 0.0079 | 0.0012 | 0.0001 | 0.0002 |
| Veracruz | 1 | 0.876 | 1 | 1 | 0.647 | 0.5892 |
| Progreso | 0.0247 | 0.1147 | 0.2095 | 0.5304 | 0.3291 | 0.349 |
| Salina Cruz | 0.7373 | 0.4304 | 0.2751 | 0.0534 | 0.0044 | 0.0236 |
| Promedio | 0.58775 | 0.4838625 | 0.478375 | 0.3933375 | 0.3490375 | 0.4508 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
En relación con la PTF, se observa que durante el periodo estudiado en general la mayoría de los puertos tuvieron un aumento en la productividad, sobresaliendo Manzanillo y Veracruz; en el lado opuesto se encuentra el puerto de Tuxpan, el cual tuvo una tendencia negativa en casi todos los años. El periodo 1985-1990 fue donde se dio un mayor aumento en la productividad, y el periodo 1982-1985 se caracterizó por tener una reducción en la productividad en todos los puertos (tabla 5).
Índice Malmquist de los puertos de México 1982-2010
| DMU | 1982-1985 | 1985-1990 | 1990-1995 | 1995-2000 | 2000-2005 | 2005-2010 | 1982-2010 |
|---|---|---|---|---|---|---|---|
| Mazatlán | 0.58 | 1.5 | 0.75 | 0.7 | 1.67 | 0.63 | 0.94 |
| Manzanillo | 0.09 | 1.95 | 0.78 | 1.72 | 1.43 | 1 | 2.44 |
| Lázaro Cárdenas | 0.12 | 1.04 | 0.77 | 1 | 1.32 | 0.76 | 1.51 |
| Altamira | 0.29 | 1.46 | 1.37 | 1.69 | 1.96 | 0.8 | 1.94 |
| Tuxpan | 0.3 | 0.21 | 1 | 0.52 | 0.38 | 1 | 0 |
| Veracruz | 0.51 | 1.81 | 1.37 | 1.26 | 1.51 | 0.85 | 2.11 |
| Progreso | 0.15 | 1.08 | 1.33 | 0.68 | 1.13 | 0.79 | 1.3 |
| Salina Cruz | 0.2 | 1.55 | 0.93 | 1.03 | 0.08 | 0.45 | 0.55 |
| Promedio | 0.28 | 1.325 | 1.0375 | 1.075 | 1.185 | 0.785 | 1.34875 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
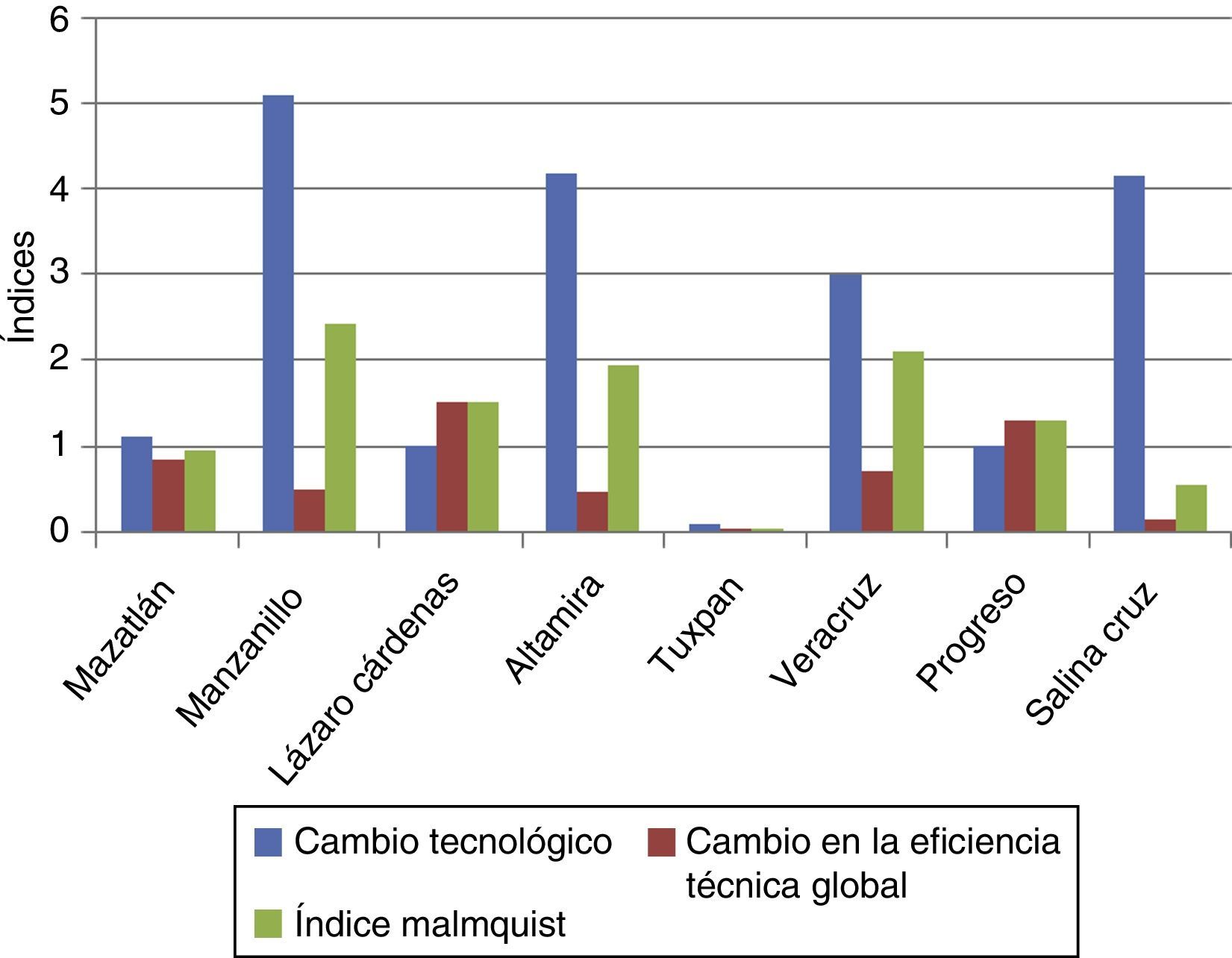
En el periodo 1982-2010, la tasa de crecimiento media anual de la productividad fue del 34%; este avance fue resultado del progreso tecnológico que tuvieron en general los puertos, específicamente Mazatlán, Manzanillo, Altamira, Veracruz y Salina Cruz, ya que realizaron innovaciones y cambios en las técnicas asociados a la actividad en las terminales de contenedores. Por el otro lado, en los puertos de Lázaro Cárdenas y Progreso el cambio en la productividad lo determinó la eficiencia técnica debido a la capacidad de incorporar el proceso tecnológico en sus actividades productivas, así como también la manera en que optimizan los insumos utilizados (tabla 6).
Productividad portuaria 1982-2010
| DMU | Cambio eficiencia de escala | Cambio eficiencia técnica pura | Cambio eficiencia técnica global | Cambio tecnológico | Índice Malmquist |
|---|---|---|---|---|---|
| Mazatlán | 1.05 | 0.81 | 0.85 | 1.11 | 0.94 |
| Manzanillo | 0.48 | 1 | 0.48 | 5.08 | 2.44 |
| Lázaro Cárdenas | 1.51 | 1 | 1.51 | 1 | 1.51 |
| Altamira | 1.08 | 0.43 | 0.46 | 4.18 | 1.94 |
| Tuxpan | 0.02 | 1 | 0.02 | 0.09 | 0 |
| Veracruz | 0.95 | 0.74 | 0.7 | 3 | 2.11 |
| Progreso | 1.3 | 0.99 | 1.29 | 1.01 | 1.3 |
| Salina Cruz | 0.37 | 0.36 | 0.13 | 4.15 | 0.55 |
| Promedio | 0.845 | 0.79125 | 0.68 | 2.4525 | 1.34875 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
Desagregando el cambio en la eficiencia técnica global en sus componentes (eficiencia de escala y eficiencia técnica pura) se observa que los puertos de Mazatlán, Lázaro Cárdenas, Altamira y Progreso obtuvieron una mayor puntuación en la eficiencia de escala, debido a que aumentaron la movilización de contenedores en todo el periodo a una escala adecuada. En cuanto a la eficiencia técnica pura, los puertos que sobresalieron fueron Manzanillo, Lázaro Cárdenas y Tuxpan, debido a que optimizan mejor sus recursos.
En el caso de Salina Cruz, si bien mostró una reducción en la eficiencia técnica pura durante el periodo analizado, también fue uno de los puertos que tuvo mayor progreso tecnológico. Esto quiere decir que aunque el puerto recibió una inversión considerable adquiriendo equipo y realizando innovaciones en los procesos, no fue eficiente en la optimización de sus recursos, y el aumento en la movilización de los contenedores no se realizó en la misma proporción en que aumentó la infraestructura en la terminal.
En la figura 1 se observa como el cambio tecnológico y el cambio en la eficiencia técnica global tuvieron un comportamiento opuesto, ya que la eficiencia técnica tuvo una tendencia decreciente en casi todo el periodo, mientras que el 75% de los puertos presentaron progreso tecnológico, sobresaliendo Manzanillo, Altamira y Salina Cruz. El puerto de Tuxpan fue el que tuvo el mayor descenso tecnológico, debido a su mínima innovación, así como también una reducción en la eficiencia lo que se expresó en la tendencia negativa en la movilización de contenedores.
Eficiencia y productividad por períodosEl estudio sobre eficiencia y productividad portuaria se ha convertido en una prioridad tanto para el sector público como el privado, debido a la necesidad de contar con puertos más competitivos que den respuesta a las necesidades de mercados cuyo crecimiento y complejidad son cada vez mayores.
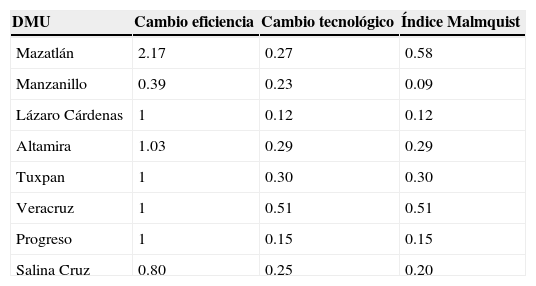
Si bien los resultados obtenidos en esta investigación dan cuenta de que los puertos en general tienen un aumento en la productividad en el periodo 1982-2010, el cambio en la productividad muestra diferentes comportamientos en cada uno de los periodos analizados. En el periodo 1982-1985 no se dieron incrementos en la productividad debido a una disminución del índice tecnológico en casi todos los puertos, ya que la inversión pública fue prácticamente nula. También se tuvo una eficiencia técnica baja debido a que no se utilizaron adecuadamente los insumos, y hubo en consecuencia un reducido tráfico de contenedores (véase tabla 7).
Productividad portuaria 1982-1985
| DMU | Cambio eficiencia | Cambio tecnológico | Índice Malmquist |
|---|---|---|---|
| Mazatlán | 2.17 | 0.27 | 0.58 |
| Manzanillo | 0.39 | 0.23 | 0.09 |
| Lázaro Cárdenas | 1 | 0.12 | 0.12 |
| Altamira | 1.03 | 0.29 | 0.29 |
| Tuxpan | 1 | 0.30 | 0.30 |
| Veracruz | 1 | 0.51 | 0.51 |
| Progreso | 1 | 0.15 | 0.15 |
| Salina Cruz | 0.80 | 0.25 | 0.20 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
En el periodo 1985-1990 se hizo una mayor inversión por parte del gobierno en infraestructura en la mayoría de los puertos para poder incrementar su productividad debido a la apertura comercial que se estaba preparando, ya que las políticas macroeconómicas iban orientadas a fomentar la exportación, y en esa etapa se estaba dejando de ver a los puertos como terminales de transferencias para convertirse en centros comerciales. Los puertos tuvieron en promedio una tasa de crecimiento media anual de la productividad del 32.5%, la más elevada de todos los periodos revisados; sobresaliendo Manzanillo y Veracruz, el primer puerto debido principalmente al aumento en la eficiencia durante el periodo y el segundo debido a su progreso tecnológico (véase tabla 8).
Productividad portuaria 1985-1990
| DMU | Cambio en la eficiencia | Cambio tecnológico | Índice Malmquist |
|---|---|---|---|
| Mazatlán | 1.06 | 1.41 | 1.50 |
| Manzanillo | 1.52 | 1.29 | 1.95 |
| Lázaro Cárdenas | 1 | 1.04 | 1.04 |
| Altamira | 0.73 | 1.99 | 1.46 |
| Tuxpan | 1 | 0.21 | 0.21 |
| Veracruz | 1 | 1.81 | 1.81 |
| Progreso | 8.60 | 0.13 | 1.08 |
| Salina Cruz | 1.89 | 0.82 | 1.55 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
En el siguiente periodo 1990-1995 es cuando se da la transición del antiguo modelo portuario, ya que se crea una administración descentralizada en cada puerto que promueve la participación de la inversión privada. Esta situación se vio reflejada en el progreso tecnológico, ya que se inician una serie de innovaciones y cambios en los procesos, mejorando la operatividad portuaria con excepción del puerto de Progreso, que tenía una saturación en la terminal de contenedores. Si bien el aumento en la productividad no se dio al mismo nivel que en el periodo anterior, se muestra un crecimiento medio anual del 3% (véase tabla 9).
Productividad portuaria 1990-1995
| DMU | Cambio en la eficiencia | Cambio tecnológico | Índice Malmquist |
|---|---|---|---|
| Mazatlán | 0.31 | 2.45 | 0.75 |
| Manzanillo | 0.20 | 4.01 | 0.78 |
| Lázaro Cárdenas | 0.60 | 1.30 | 0.77 |
| Altamira | 1 | 1.37 | 1.37 |
| Tuxpan | 1 | 1 | 1 |
| Veracruz | 1 | 1.37 | 1.37 |
| Progreso | 1.77 | 0.75 | 1.33 |
| Salina Cruz | 0.22 | 4.17 | 0.93 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
En el período 1995-2000 se registró una tasa de crecimiento de la productividad en promedio del 7.3% en los puertos de México, debido principalmente al aumento en la eficiencia, sobresaliendo Manzanillo y Altamira. Se observa también que el progreso tecnológico fue menor que en los periodos anteriores, lo que se debió a que, después de haber realizado fuertes inversiones para aumentar su infraestructura y equipamiento al inicio de la etapa de privatización, los puertos ya no continuaron con el mismo dinamismo en los siguientes años. Concretamente Tuxpan fue el puerto que tuvo menor puntuación debido a la baja movilización de contenedores que presentó en esos años (véase tabla 10).
Productividad portuaria 1995-2000
| DMU | Cambio en la eficiencia | Cambio tecnológico | Índice Malmquist |
|---|---|---|---|
| Mazatlán | 2.56 | 0.27 | 0.70 |
| Manzanillo | 0.84 | 2.03 | 1.72 |
| Lázaro Cárdenas | 1 | 1 | 1 |
| Altamira | 2.20 | 0.77 | 1.69 |
| Tuxpan | 1 | 0.52 | 0.52 |
| Veracruz | 1 | 1.26 | 1.26 |
| Progreso | 0.21 | 3.25 | 0.68 |
| Salina Cruz | 2.75 | 0.38 | 1.03 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
En el siguiente periodo 2000-2005 la tasa de crecimiento en la productividad fue del 18.5%, originado por el trabajo en conjunto tanto del sector público como privado en la inversión portuaria, sobresaliendo el puerto de Altamira, que empieza a tener un crecimiento considerable debido a la saturación del puerto de Tampico, el cual prácticamente se quedó como un puerto petrolero y todo el tráfico de carga general se pasó al puerto de Altamira. En el caso de Lázaro Cárdenas, si bien venía presentando un progreso tecnológico en los años anteriores, tuvo una regresión debido a su baja operatividad al inicio del periodo, sin recibir prácticamente ninguna inversión para su desarrollo (véase tabla 11).
Productividad portuaria 2000-2005
| DMU | Cambio en la eficiencia | Cambio tecnológico | Índice Malmquist |
|---|---|---|---|
| Mazatlán | 1.60 | 1.04 | 1.67 |
| Manzanillo | 1 | 1.43 | 1.43 |
| Lázaro Cárdenas | 2.02 | 0.66 | 1.32 |
| Altamira | 1.10 | 1.78 | 1.96 |
| Tuxpan | 1 | 0.38 | 0.38 |
| Veracruz | 1.41 | 1.07 | 1.51 |
| Progreso | 1 | 1.13 | 1.13 |
| Salina Cruz | 0.19 | 0.41 | 0.08 |
Fuente: elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
En el último periodo 2005-2010 se registró una tasa de crecimiento de la productividad negativa del 22%. Una de las principales razones se encuentra en la contracción económica que hubo en el año 2008, donde se vio afectado el volumen del comercio mundial de mercancías, y específicamente el comercio vía marítima se contrajo un 4,5%. En nuestro país el sector gubernamental intervino para fortalecer a la industria portuaria, quien realizó la mayor aportación de inversión en los años 2009 y 2010 (véase tabla 12.).
Productividad portuaria 2005-2010
| DMU | Cambio en la eficiencia | Cambio tecnológico | Índice Malmquist |
|---|---|---|---|
| Mazatlán | 0.43 | 1.47 | 0.63 |
| Manzanillo | 1 | 1 | 1 |
| Lázaro Cárdenas | 0.50 | 1.53 | 0.76 |
| Altamira | 0.74 | 1.07 | 0.80 |
| Tuxpan | 1 | 1 | 1 |
| Veracruz | 0.96 | 0.89 | 0.85 |
| Progreso | 1.01 | 0.78 | 0.79 |
| Salina Cruz | 3.62 | 0.12 | 0.45 |
Fuente: Elaboración propia con base en los cálculos realizados a partir de la metodología DEA.
En general, en el periodo 1982-2010 se puede decir que se tuvo un aumento en la productividad debido al progreso tecnológico, sobresaliendo Manzanillo, que fue el puerto en el que se dio el mayor progreso tecnológico. Mientras que en el lado opuesto se encuentra Tuxpan, en el que se dio una reducción en la productividad por su mínima innovación, lo que se vio reflejado en su baja movilización de contenedores.
ConclusionesEn el trabajo se presentó la medición de la productividad total de los factores (PTF) de los puertos mexicanos en el periodo 1982-2010, utilizando el índice Malmquist, el cual descompone el cambio de la productividad en 2 factores: cambio en eficiencia (catch-up effect) y cambio tecnológico (frontier shift).
Para calcular la eficiencia se desarrolló un modelo de rendimientos constantes a escala y rendimientos variables a escala con orientación output. Se hizo el cálculo del índice Malmquist con las terminales de contenedores de los puertos de Mazatlán, Manzanillo, Lázaro Cárdenas, Altamira, Tuxpan, Veracruz, Progreso y Salina Cruz, utilizando como inputs la longitud de muelle y el número de trabajadores, y como output el número de contenedores movilizados anualmente.
En los resultados obtenidos sobre la eficiencia en el periodo 1982-2010 se observa que, al inicio del periodo, los puertos más eficientes fueron Tuxpan y Veracruz, y el más ineficiente, Progreso. Al final del periodo los puertos más eficientes fueron Manzanillo y Lázaro Cárdenas, y el más ineficiente fue el puerto de Tuxpan.
En cuanto al índice Malmquist, 5 de los 8 puertos tuvieron un incremento en la PTF. El puerto con un mayor aumento en la PTF fue Manzanillo, lo que se debió en gran medida a las inversiones que se hicieron en infraestructura y logística, que reflejan un mayor movimiento de contenedores manejados anualmente (el 47.8% de los TEUS a nivel nacional). En el lado opuesto, el puerto que tuvo una reducción en su productividad y sus resultados se ubicaron por debajo de la unidad fue Tuxpan; se da esta tendencia negativa en la movilización de los contenedores, ya que al inicio del periodo manejó 18,066 TEUS, y para el año 2010, únicamente 18 TEUS.
El periodo que tuvo los niveles más altos en el cambio en la eficiencia técnica fue de 1985-1990; en estos años, la mayoría de los puertos optimizaron mejor sus recursos. En contraste, el periodo donde hubo menor crecimiento fue de 1990-1995: fue la etapa donde se inició la transición a la apertura hacia una mayor participación de la inversión privada. Durante todo el periodo, un mayor número de puertos tuvieron mejores eficiencias de escala en relación con la eficiencia técnica pura, es decir, movilizaron sus contenedores a una escala óptima.
En el caso del cambio tecnológico, fue 1990-1995 el periodo donde los puertos tuvieron un mejor desempeño tecnológico. Es precisamente en 1993 cuando se crea la figura de Administración Portuaria Integral para dar entrada a la inversión privada, teniendo un crecimiento tecnológico en casi todos los puertos, a diferencia del periodo 1982-1985, donde no se registró ningún cambio, ya que los puertos contaban solo con la inversión pública para todo el desarrollo operativo portuario.
El índice Malmquist durante el período 1982-2010 fue en promedio de 1.34, esto es, se tuvo un valor superior a la unidad, lo que indica que se registró una tasa de crecimiento promedio anual del 34% en el periodo. Asimismo, los resultados de esta investigación dan cuenta que es el cambio tecnológico el que explica las variaciones en la PTF. En la generalidad de los puertos los valores del cambio tecnológico fueron superiores a 1, mientras que los cambios en la eficiencia técnica pura, en la eficiencia de escala y en la eficiencia técnica global se ubicaron por debajo de la unidad. Más aún, en promedio el valor del cambio en la eficiencia técnica global fue del orden del 0.68, en tanto que el cambio tecnológico se situó en 2.45. En este sentido, la hipótesis planteada en el trabajo se confirma, según la cual la PTF —expresada a través del índice Malmquist— en los puertos marítimos mexicanos se encuentra determinada por el progreso tecnológico.
Si bien la PTF se incrementó durante el período 1982-2010 en los puertos mexicanos, no fue el resultado de una evolución positiva de todos sus componentes. Ciertamente el cambio tecnológico es quien determina este crecimiento; sin embargo, la eficiencia técnica pura y la eficiencia de escala no avanzan en la misma dirección, y sus reducciones inciden de manera negativa en la productividad de este sector. En materia de política económica se hace necesario, en consecuencia, diseñar estrategias que afecten de manera directa la inversión en infraestructura y fortalezcan el capital humano; de igual manera deberán instrumentarse políticas dirigidas a optimizar la utilización de los insumos.
En resumen, la política económica portuaria en México debe ir enfocada a fomentar el crecimiento económico a través de los planes maestros de desarrollo portuario, promoviendo el desarrollo de actividades que den valor agregado a las operaciones en las terminales de contenedores con la participación activa del gobierno federal y de la inversión privada, para que de esta manera se genere una dinámica donde se incremente la infraestructura portuaria, especialmente para ampliar la capacidad de manejo de contenedores, y se desarrollen puertos como parte de un sistema integrado de transporte multimodal.
La metodología a través de la cual se calcula la PTF, como es el índice Malmquist, ofrece un diagnóstico de lo que sucede en este campo en las terminales de contenedores de los puertos mexicanos. Más aún, los niveles de desagregación que se pueden alcanzar con este índice permiten atender en el futuro deficiencias específicas; en este caso concreto, de la productividad y sus componentes en uno de los rubros fundamentales de la economía mexicana como es el sector portuario.
Finalmente, con respecto a los diferentes estudios que se han efectuado en las mediciones de la productividad portuaria, dentro de las fortalezas que presenta este trabajo sobresalen: a)la amplitud del periodo de estudio considerado; aquí el análisis de la productividad se da antes y después de la privatización de los puertos en México; b)el nivel de desagregación del índice Malmquist en eficiencia de escala, eficiencia técnica pura, eficiencia técnica global y cambio tecnológico, estudio que no realizan la mayoría de las investigaciones y que se alejan en este sentido de la propuesta original del modelo de Färe et al. (1994); c)los inputs y los outputs utilizados en este artículo no son contemplados por otros trabajos debido a la dificultad que se tiene para encontrar la información correspondiente, además de las propias diferencias que se encuentran en las correlaciones de los inputs y outputs seleccionados, y d)los puertos objeto de estudio no son los mismos y, por consiguiente, los resultados expresan sus propias particularidades que los hacen diferentes.
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.
Según el código marítimo, significa «acción de aligerar o aliviar la carga de una embarcación, o bien desembarcarla en su totalidad».
Twenty-foot Equivalent Unit, que significa «unidad equivalente a veinte pies»; representa una unidad de medida de capacidad inexacta del transporte marítimo (buques portacontenedores y terminales portuarios para contenedores) expresada en contenedores. Un TEU es la capacidad de carga de un contenedor normalizado de 20pies (6,1m), una caja metálica de tamaño estandarizado que puede ser transferida fácilmente entre diferentes formas de transporte tales como buques, trenes y camiones.