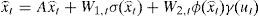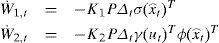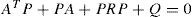En este trabajo se utiliza una red neuronal diferencial (RND) para describir las series de valores de cierre diarios de los índices accionarios DAX de Alemania y S&P 500 de Estados Unidos entre el periodo del 3 de julio de 2000 y el 13 de enero de 2012. Con la RND se lleva a cabo el pronóstico de los valores de cierre diarios de esos índices durante un periodo de cuatro semanas (del 16 de enero al 10 de febrero de 2012). Los resultados obtenidos confirman el hecho de que las redes neuronales diferenciales pueden constituirse en una de las herramientas más poderosas y precisas para poder pronosticar valores futuros de activos financieros.
This paper uses a differential neural network (DNN) to describe the behavior of daily closing values of German DAX and USA S&P 500 stock indices between July 3, 2000 and January 13, 2012. Then, by the use of DNN a four-week forecast is performed of the daily closing values of these indices, from January 16 to February 10, 2012. The results obtained confirm that the differential neural networks can become one of the most powerful and accurate tools to predict future values of financial assets.
Como es sabido, uno de los problemas más importantes para la toma de decisiones en general es la anticipación de los resultados futuros posibles, particularmente cuando el contexto en el cual se requiere el pronóstico se caracteriza por un alto grado de incertidumbre respecto al estado que pueden alcanzar las variables de interés. De manera particular, pronosticar las variables financieras es una de las tareas más difíciles, pues dichas variables han resultado por demás elusivas. Obviamente, la cantidad de los esfuerzos que se han hecho y se siguen haciendo para pronosticar los valores de las variables financieras tienen su justificación no sólo por el interés en torno al desarrollo de mejores métodos y técnicas predictivas en beneficio de la curiosidad académica (motivo que tal vez podría ser suficiente por sí mismo), sino de manera destacada por la utilidad que esos pronósticos pueden tener para quienes deben tomar decisiones de inversión financiera y para la administración de los riesgos de tales inversiones.
El repertorio de las técnicas y enfoques con que se ha abordado la problemática de los pronósticos de series financieras, como los índices bursátiles, ha abarcado una gama amplia que incluye el uso de indicadores construidos con algunos datos sobre la actividad en los mercados financieros (volumen e historial de precios esencialmente), así como técnicas para pronosticar la tendencia entre las cuales se encuentran, por un lado, el análisis de regresión y los modelos convencionales de series de tiempo (como los promedios móviles, por ejemplo) y, por otro, el enfoque contemporáneo de series de tiempo (como los modelos ARIMA y otros que se han derivado de éstos).
En épocas más recientes, el crecimiento de las ciencias de la computación ha proporcionado un gran impulso al uso de métodos y técnicas más sofisticadas para el desarrollo de sistemas expertos para el procesamiento que requieren los datos que se usan para auxiliar a la toma de decisiones. Entre esos desarrollos destacan los métodos de lo que ha dado en llamarse inteligencia artificial, como es el diseño, programación y aplicación de los modelos de redes neuronales artificiales. La investigación de este tipo de modelos como auxiliares para la toma de decisiones en problemas financieros se ha vuelto un área de creciente actividad, lo cual de ninguna manera excluye su aplicación a otros problemas de análisis y toma de decisiones que enfrentan los directivos de empresas y otros tipos de organizaciones.
En este artículo se presentan los resultados del diseño y programación de una red neuronal diferencial, la cual se aplica, en primer lugar, a la identificación del comportamiento del índice del mercado bursátil alemán Deutscher Aktienindex (DAX) y el indicador estadounidense Standard and Poor’s 500 (S&P 500). Posteriormente, dicha red se utiliza para efectuar pronósticos de los valores de ambos indicadores bursátiles para un horizonte temporal de cuatro semanas de operación posteriores a la etapa de identificación de la red.
Además de la evaluación de la capacidad predictiva de dicha red neuronal, este estudio contribuye también a la literatura del análisis bursátil porque extiende la aplicación de las redes neuronales diferenciales al caso de los pronósticos de los valores de los índices de mercados bursátiles desarrollados o maduros en los cuales, de acuerdo con la hipótesis de los mercados eficientes, se debe esperar que muestren un mayor grado de eficiencia que otros mercados menos desarrollados (como los llamados emergentes) y, por lo tanto, también cabe esperar que su comportamiento resulte más difícil de pronosticar.
La estructura que sigue este trabajo se describe en seguida. En la siguiente sección se enuncia a grandes rasgos la evolución de las redes neuronales y sus principales aplicaciones, enfatizando aquellas relacionadas con problemas financieros; después se dedica una sección a la presentación de la metodología utilizada en el diseño, programación y evaluación de la red empleada en el análisis y pronóstico de los índices bursátiles estudiados; posteriormente, se muestran los resultados obtenidos; finalmente se presentan las conclusiones de este estudio.
Las redes neuronales y sus aplicacionesDesde el periodo final de la Segunda Guerra Mundial se empezaron a desarrollar modelos computacionales que intentaban simular el funcionamiento del cerebro humano; ello dio lugar al surgimiento y evolución de una nueva disciplina la cual ha llegado a conocerse en el transcurso del tiempo como inteligencia artificial. Entre esos modelos destacan las llamadas redes neuronales artificiales (RNA), que modelan los procesos de aprendizaje y procesamiento inspirándose en el funcionamiento del sistema nervioso. Uno de los primeros trabajos formales en este campo de la inteligencia artificial se debe a los neurólogos McCulloch y Pitts (1943).
Desde el punto de vista del diseño y programación de una red, el objetivo básico es en primera instancia representar el problema por tratar mediante modelos mate-máticos para, posteriormente, formular una solución a dicho problema valiéndose de un algoritmo cuyas propiedades le permitan resolverlo mediante su implementación en un sistema de cómputo.
El elemento fundamental de los modelos de redes neuronales artificiales es una estructura en forma de red, formada por nodos (neuronas) interconectados entre sí; esos nodos representan, mediante modelos matemáticos, procesos del funcionamiento cerebral que van incorporando a través de su interacción a lo largo del tiempo los distintos estados (resultados) de otros nodos, de acuerdo con una estructura y un orden establecido por las reglas de interacción de la red. Las RNA dependen de la estructura de aprendizaje o leyes de aprendizaje para alcanzar el objetivo de identificar la evolución temporal de las variables de interés; esto lo realizan a partir del algoritmo de back propagation, un algoritmo de cambio discreto basado en el gradiente negativo de la variación del error cuadrático establecido en las señales medidas y las identificadas por la red.
El uso de las RNA como una herramienta útil para llevar a cabo procesos de mode-lado, simulación y descripción de sistemas dinámicos no lineales se ha ido consolidando en un tiempo relativamente corto como una técnica eficaz y rápida gracias a los siguientes aspectos:
- •
La relativa simplicidad de su uso e implementación.
- •
El crecimiento acelerado en la capacidad y rapidez de los sistemas computacionales.
- •
Desde el punto de vista matemático, por la gran capacidad que esta técnica tiene para poder llevar a cabo el proceso de seguir y describir con gran aproximación el comportamiento de cualquier función matemática o de cualquier serie de datos aun sin aparente coherencia o patrón de comportamiento.
- •
La capacidad que tienen para identificar patrones de comportamiento a partir de datos de entrada complejos e imprecisos, los cuales serían muy difíciles de identificar mediante otras técnicas computacionales o econométricas.
El uso de las redes neuronales artificiales como herramienta de seguimiento y análisis del comportamiento de sistemas dinámicos no lineales se ha venido presentando con resultados muy favorables desde principios de la década de 1940 con el trabajo de McCulloch y Pitts (1943) ya mencionado, sobre todo en aplicaciones de ingeniería y biotecnología. Sin embargo, su aplicación para la descripción de procesos de naturaleza económica y financiera tuvo que esperar casi medio siglo. Desde principios de los años noventa del siglo pasado, la aplicación de las redes neuronales para analizar problemas de naturaleza económica o financiera ha tenido un gran éxito como técnica de estimación y pronóstico de funciones no lineales que se encuentran frecuentemente en las finanzas.
A continuación presentamos una lista, meramente enunciativa, con algunos ejemplos de aplicaciones de las redes neuronales artificiales como técnica de descripción y pronóstico a problemas de naturaleza financiera, que involucran sistemas dinámicos no lineales.
- •
Calificación de la calidad crediticia de bonos empresariales, Dutta y Shekkar (1988), Surkan y Singleton (1990), así como Albanis y Batchelor (1999).
- •
Predicción de quiebras empresariales, Odom y Sharda (1990), Coleman et al. (1991), Tam y Kiang (1992), Tyree y Long (1996), Yang (1999).
- •
Método de estimación de precios de productos derivados, Hutchinson (1994), Saxena (2008), así como Gradojevic et al. (2009).
- •
Cálculo de la eficiencia de pagos en tarjetas de crédito, Jagielska (1996).
- •
Diseño de un portafolio de inversiones, Hung (1996), Naïm et al. (2000).
- •
Identificación del comportamiento de series de tiempo financieras, Chen (2001) y Refenes (2001).
- •
Descripción de diversos fenómenos y comportamientos financieros, McNelis (2005).
- •
Pronóstico de precios de acciones financieras, Haykin (1999), Hanias et al. (2007), Mehrara et al. (2010).
- •
Construcción de reglas de clasificación para la evaluación de solicitudes de tarjetas de crédito y de créditos en general, Albanis (2003).
- •
Descripción y pronóstico de paridades cambiarias, Kamruzzaman y Sarker (2003), Dunis et al. (2010), Hu y Zhang (1997), Yu et al. (2007).
- •
Descripción y pronóstico de índices de precios y cotizaciones de mercados bursátiles, Sing y Kumar (2010), Kishore y Prasad (2011).
Todos los ejemplos anteriores fueron desarrollados utilizando redes neuronales artificiales de tipo discreto; estas redes neuronales ciertamente han mostrado un excelente desempeño en las aplicaciones de naturaleza financiera en las que se han usado. Sin embargo, es conveniente destacar que, a pesar del éxito relativo de las redes neuronales de tipo discreto, se ha encontrado evidencia de que los resultados obtenidos con ellas pueden mejorarse tanto en precisión como en el requerimiento de la cantidad de datos históricos necesarios para llevar a cabo el proceso de aprendizaje o entrenamiento de la red. En varios trabajos se ha demostrado que esta mejora se ha podido obtener mediante el uso de una nueva clase de modelos: las redes neuronales diferenciales o dinámicas en tiempo continuo (RND), que empezaron a diseñarse a mediados de la década de 1990.
Las dos diferencias fundamentales entre las redes discretas y las redes en tiempo continuo son las siguientes: primero, realizan el análisis de las series de tiempo en tiempo continuo; segundo, la estructura de convergencia se fundamenta en la teoría de estabilidad planteada por Lyapunov, la cual contiene criterios de convergencia más robustos que permiten obtener convergencia más acelerada (véase Poznyak et al., 2001). Las primeras aplicaciones de las RND se presentaron primordialmente en la resolución de problemas de control óptimo en biotecnología, en procesos químicos e incluso en sistemas de dosificación de medicamentos. A continuación presentamos una lista en la que se enuncian algunos de los trabajos que muestran las aplicaciones de las RND que se han hecho en varios campos de la biotecnología, control automático y medicina.
- •
Biotecnología, en la estimación del valor algunas variables no medibles de manera directa en procesos de fermentación, Cabrera et al. (2002).
- •
Medicina, en la estimación de la dosis de medicamentos para atacar el cáncer, Aguilar y Chairez (2006).
- •
Control automático, en el desarrollo de sistemas de seguimiento adaptativo no lineal, Pozniak et al. (1999); desarrollo de sistemas de observación indirecta a través de un sensor virtual, Cabrera y Ramírez (2007).
- •
En un sistema de pronóstico de dosificación de insulina en pacientes diabéticos, Fonseca et al. (2003).
Por otro lado, aunque todavía en un número bastante limitado, ya se tienen algunos trabajos de aplicaciones de las redes neuronales diferenciales en problemas financieros, por ejemplo:
- •
En el modelado del tipo de cambio entre el peso y el dólar norteamericano, Ortiz et al. (2012a)
- •
En la elaboración del pronóstico del rendimiento intradía del índice de Precios y Cotizaciones de la Bolsa Mexicana de Valores, Cabrera y Ortiz (2012); pronósticos del rendimiento de las bolsas de valores de Madrid y de México, Ortiz et al. (2012b)
La metodología empleada para llevar a cabo este análisis de seguimiento y pronóstico de valores de ambas series financieras consta fundamentalmente de las tres fases que se describen a continuación.
Primera fase- •
Mediante el uso de una RND se logró identificar el comportamiento de las series de los valores diarios de cierre de los índices accionarios DAX de Alemania, así como del S&P 500 de los Estados Unidos de América, a lo largo del periodo comprendido entre el 3 de julio de 2000 y el 13 de enero de 2012.
- •
Se consideró un periodo de entrenamiento o aprendizaje de la red neuronal de seis meses: del 3 de enero de 2000 al 30 de junio de 2000. éste es un punto importante por tomar en cuenta, pues las redes neuronales artificiales de tipo discreto requieren de al menos 500 datos para usarlos en el periodo de entrenamiento; es decir, alrededor de dos años de información.
- •
Para llevar a cabo los procesos de seguimiento y de pronóstico de los valores de las series financieras citadas se utilizó el si:
con x0 conocida y con dominio xt ∈ Rn, yt ∈ Rp, t≥0,ut ∈ Rm; C ∈ Rp×n, ξ1,t ∈ Rn×1 y ξ2,t ∈ Rp×1. La función f (xt, ut, t) representa la dinámica de las variables analizadas, pero debido a que no se tiene una forma explícita se toma como una función arbitraria y no lineal; para nuestro caso representa la serie de tiempo que evoluciona en el periodo de tiempo que se estudia. Por otra parte, la evolución de la variable analizada, yt, se observa en la evolución dinámica de las variables xt o variables de estado; asimismo, se describe el rango de validez de este modelo a partir de los superíndices de la representación de los espacios vectoriales en los que consideramos evolucionan las variables, por lo que los términos n, p, m, etc., representan el número de estados, el número de salidas y finalmente el número de entradas de excitación que permiten hacer evolucionar el sistema.
La red neuronal diferencial dada por
donde x⌢t representa los estados estimados de la red; W1,t y W2,t representan las matrices de cambio de ponderación que ajustan a la red en la evolución de los estados y de la acción de la excitación al sistema respectivamente, mediante el sistema de ecuaciones diferenciales no lineal acoplado descritas por
y describen la ley de aprendizaje. Estas ecuaciones son obtenidas al aplicar el teorema de Lyapunov de estabilidad a la función propuesta
esta expresión es llamada la función de Lyapunov.
La evolución de la red es activada mediante las funciones
junto con la condición de que la matriz P de la ley de aprendizaje, sea una matriz definida positiva y sea solución a la ecuación de Ricatti:
- •
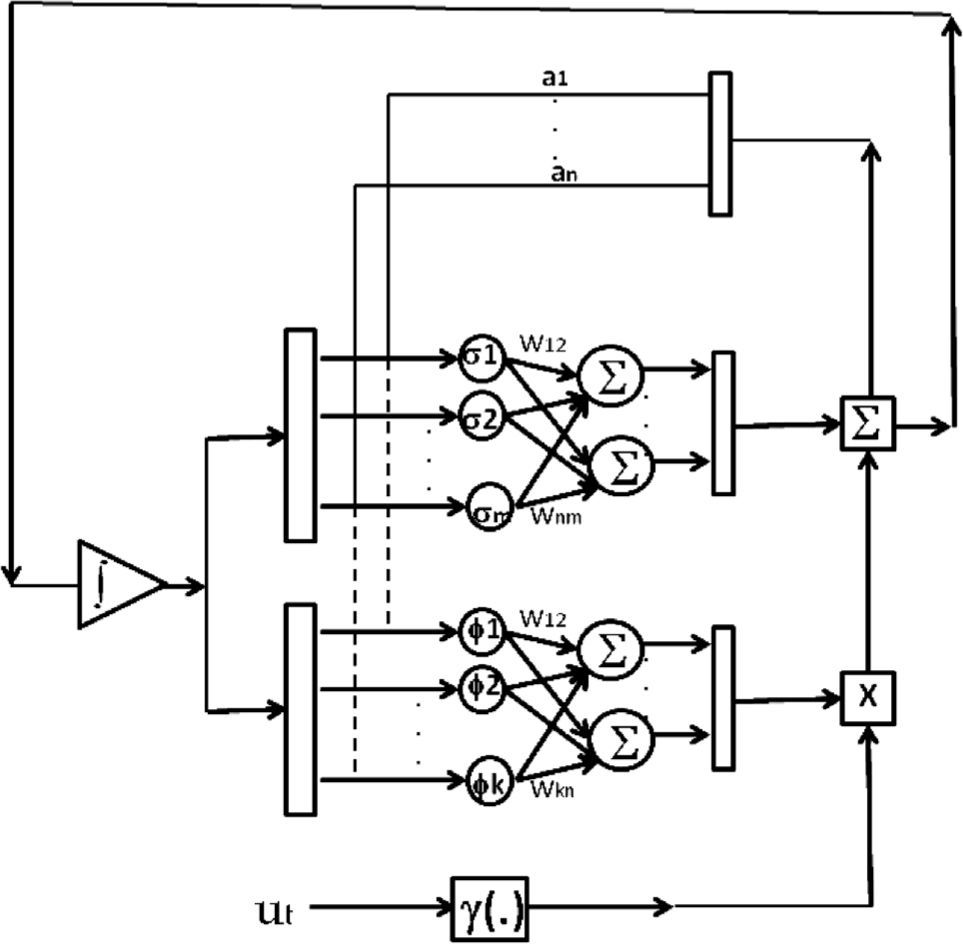
Con base en lo anterior, el sistema de ecuaciones diferenciales no lineales, así como el conjunto de restricciones se programaron en la plataforma de Matlab-Simulink. La figura 1 muestra en forma esquemática la red neuronal diferencial utilizada en este estudio.
- •
La red neuronal diferencial empleada para la estimación de los estados sobre el sistema dinámico no lineal fue del tipo Hopfield, éstos se basan en el análisis de la estabilidad propuesto por Lyapunov. La ventaja del uso de la teoría de estabilidad de Lyapunov es que garantiza el proceso de convergencia de los valores obtenidos por la red a los valores reales de las series.
- •
Se reanuda el programa de cómputo de la RND para llevar a cabo el proceso de seguimiento de los valores de ambas series durante el periodo del 3 de julio de 2000 al 13 de enero de 2012.
- •
Se lleva a cabo el análisis de la precisión de los cálculos del seguimiento, observándose que se obtuvieron resultados sumamente aproximados a los datos reales, lo cual se muestra a través de las gráficas comparativas (1 a 10), donde se comparan los valores calculados con la RND y los valores reales de las series.
- •
Nuevamente se reinicia el programa de cómputo de la RND en Matlab y ahora se lleva a cabo el proceso de pronóstico de los valores de cierre diario de los índices DAX y S&P 500 en cuatro grupos, cada uno con cinco días y que comprende el periodo de cuatro semanas que van del 16 de enero al 10 de febrero de 2012.
Esta sección se divide en dos partes: en la primera se muestran los resultados del proceso de seguimiento o descripción del comportamiento de los índices DAX y S&P 500 bajo estudio; en la segunda se muestran los resultados de los pronósticos y su evaluación. Para la etapa del proceso de descripción de las series se utilizan los valores de cierre diario de esos índices durante el periodo que va del 3 de julio de 2000 al 13 de enero de 2012. El periodo para los pronósticos de ambos indicadores bursátiles, con su correspondiente evaluación, va del 16 de enero al 10 de febrero de 2012.
Seguimiento o descripción de las seriesComo veremos a continuación, los valores obtenidos con la RND son sumamente aproximados a los valores de las series, tanto en la parte de seguimiento —en la cual se describe el comportamiento de los índices bursátiles— como en la parte de pronóstico de sus valores futuros.
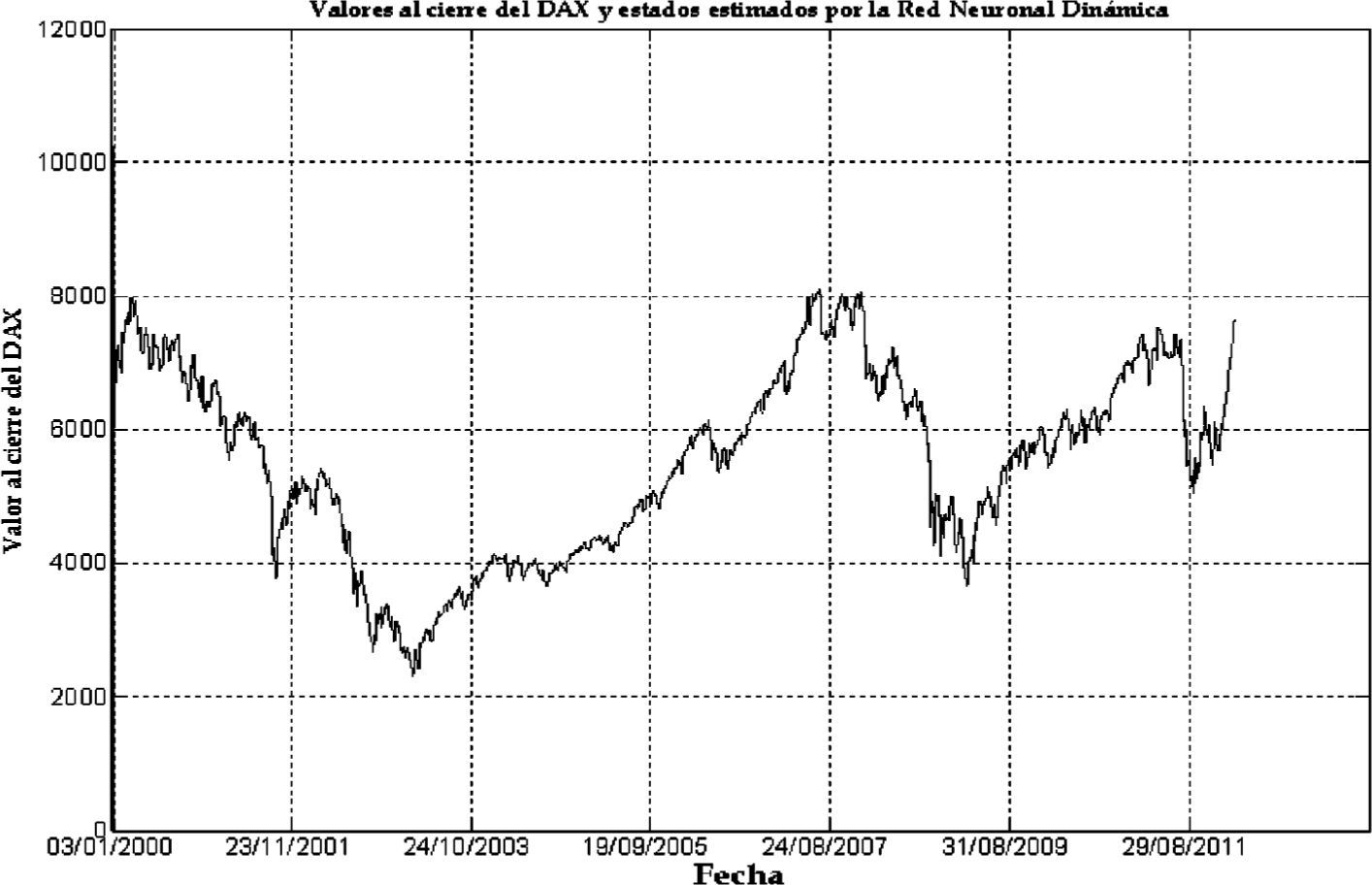
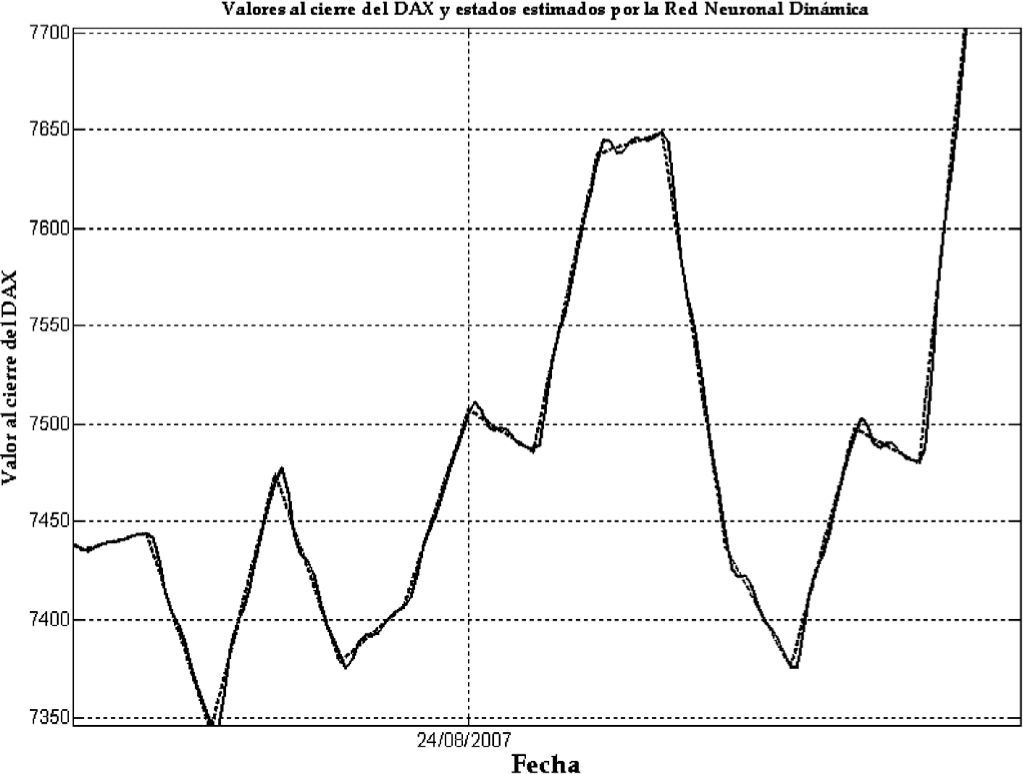
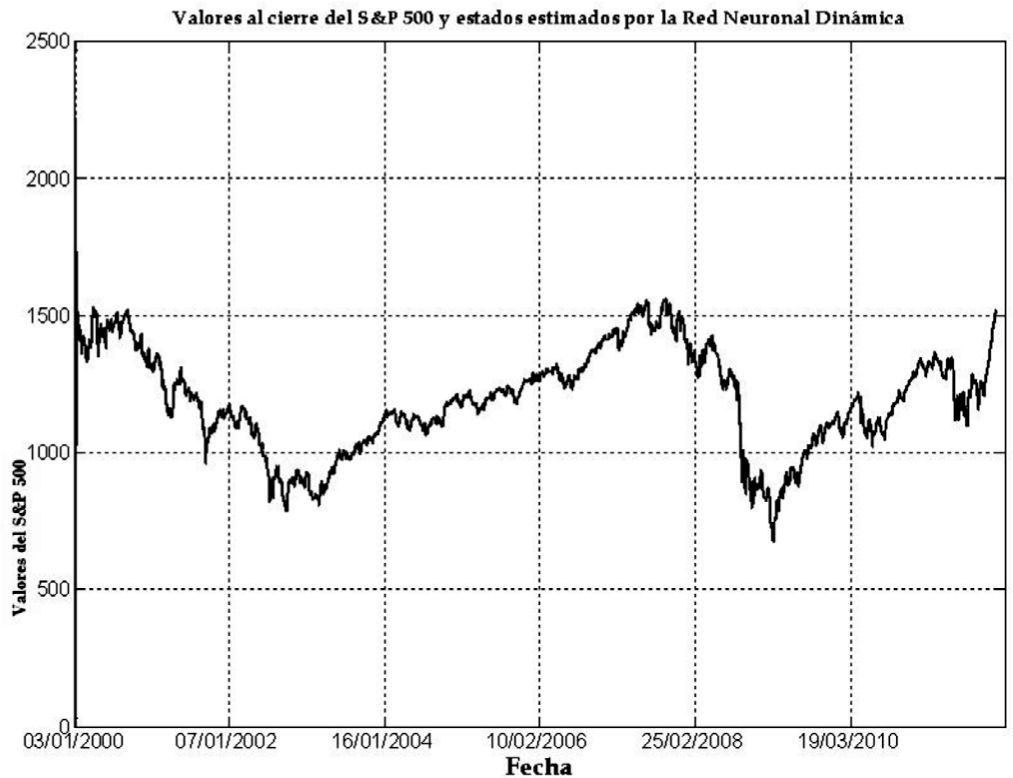
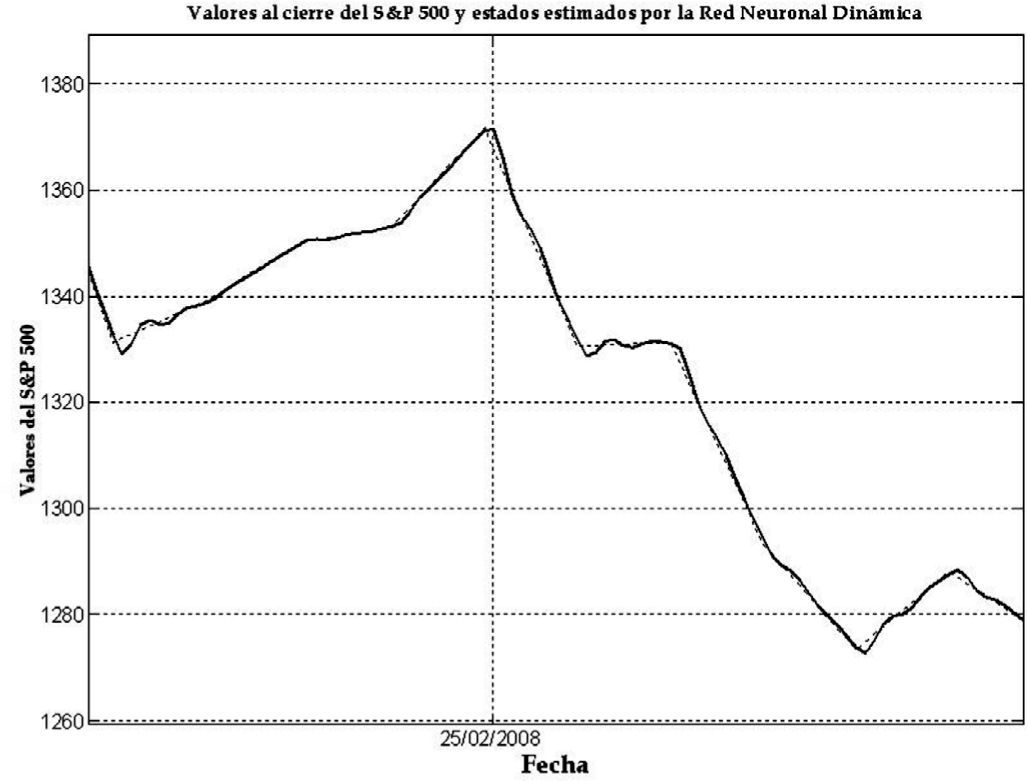
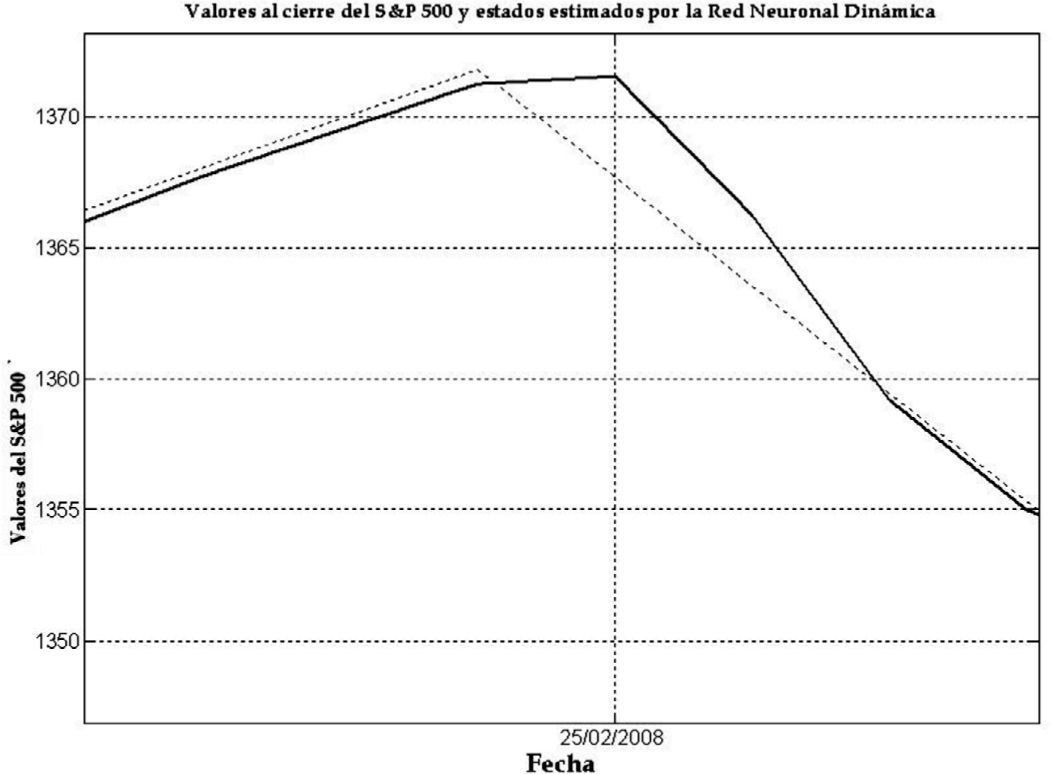
En las gráficas 1 a 6 se presenta la evolución de los valores reales y de los valores generados con la red tanto para el índice DAX como para el índice S&P 500 durante el periodo de seguimiento o descripción del 3 de julio de 2000 al 13 de enero de 2012.
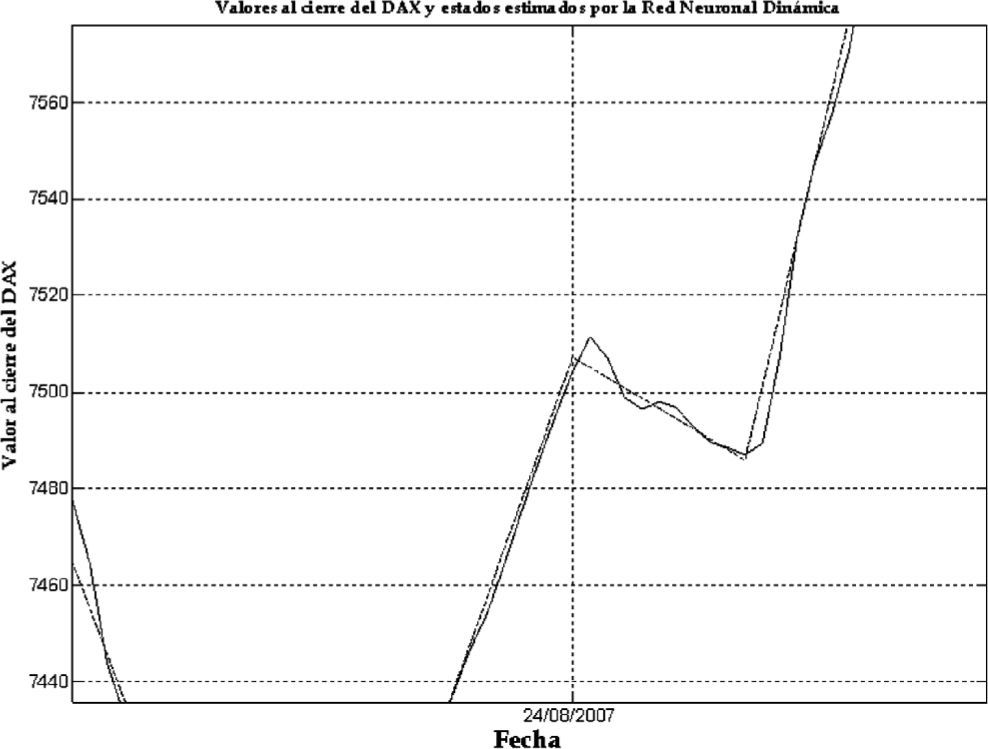
Como puede apreciarse, el grado de aproximación que tienen los valores generados con la RND (línea punteada) es muy alta; de hecho las pequeñas discrepancias se logran apreciar hasta el segundo acercamiento que se hace de las gráficas, inclusive en periodos de alta variación de precios en un corto intervalo de tiempo como se muestra en la gráfica 3, que se enfoca en el 24 de agosto de 2007. En dicha gráfica podemos apreciar como la red “sigue” de manera instantánea las variaciones del índice DAX en un corto intervalo de tiempo; una situación similar se presenta en el caso del índice S&P 500, como lo muestra la gráfica 6, la cual se enfoca en el 25 de febrero de 2008, donde también un cambio abrupto en el valor del índice y la red se ajusta de manera inmediata al valor de mercado del índice S&P 500.
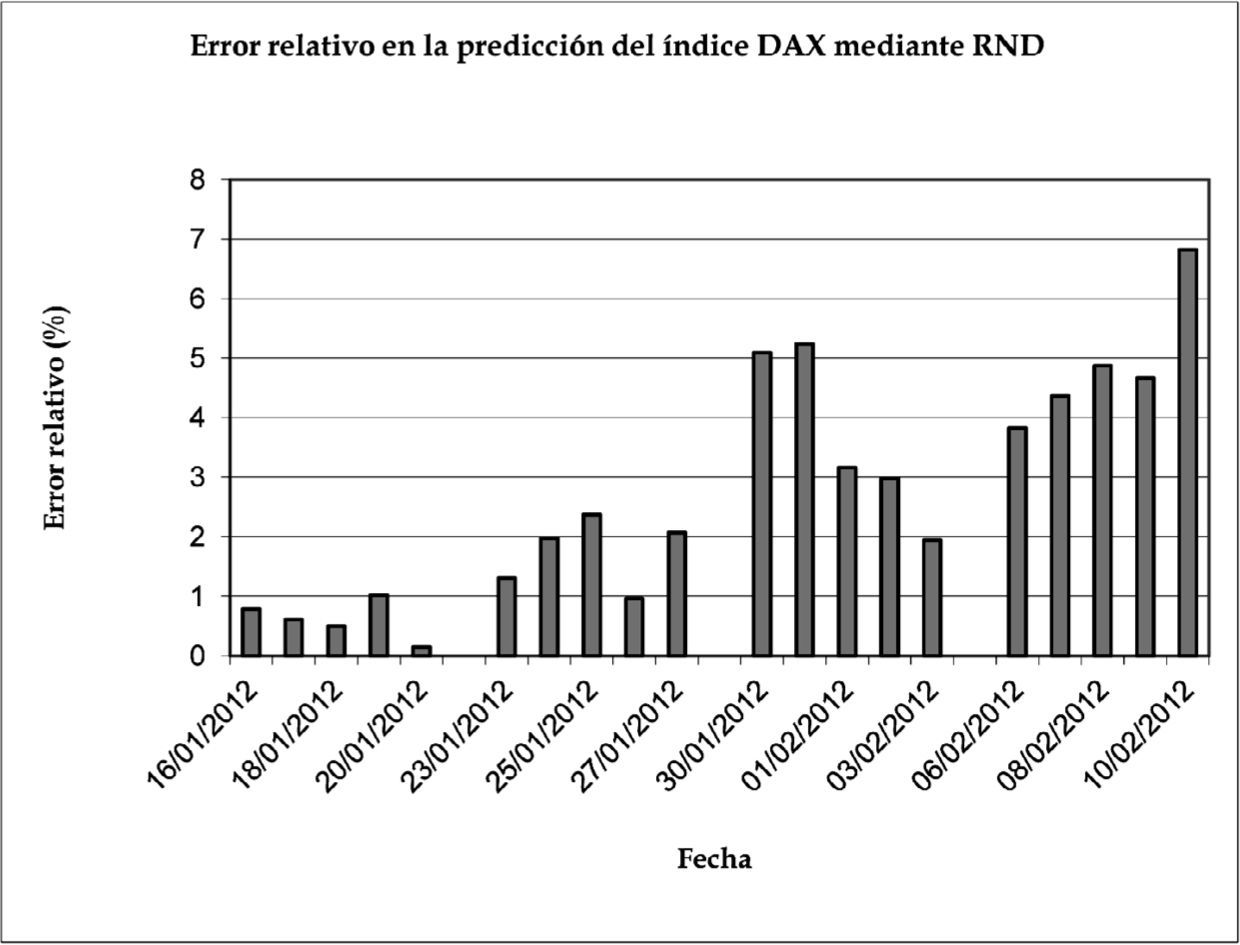
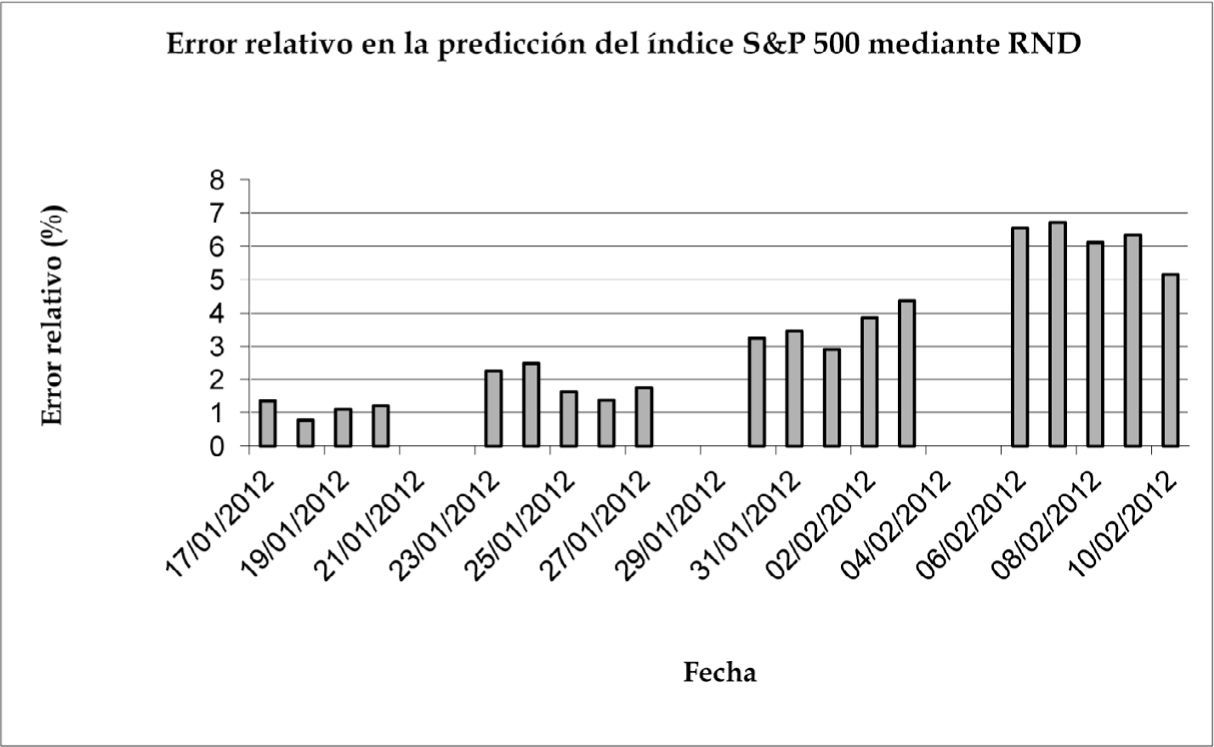
Esta parte del trabajo es la más interesante, pues es la relativa al proceso de predicción de valores de cierre diario de los índices DAX y S&P 500 durante un periodo de cuatro semanas. Si se toma en cuenta que los errores porcentuales oscilan durante las dos primeras semanas de 0.15% al 2.37% para el pronóstico de los valores de cierre del DAX y de 0.77% a 2.48 % para el caso del S&P 500, se puede decir que los resultados de los pronósticos son altamente satisfactorios.
Los resultados alcanzados son bastante cercanos a los valores realmente observados en los índices bursátiles estudiados, sobre todo si se comparan con trabajos de este tipo que fueron realizados con redes neuronales artificiales discretas. Por ejemplo, los trabajos de Hanias et al. (2007) para el pronóstico del índice de precios del mercado de valores de Grecia, o el de Mehrara et al. (2010) para el pronóstico de valores del índice de precios del mercado de valores de Irán, o el de Kishore y Prasad (2011) que lleva a cabo la predicción de valores de índices accionarios de varios países, pero con menor nivel de aproximación que la obtenida en este trabajo.
Las gráficas 7 y 8 nos muestran los niveles del error relativo entre los valores reales y los pronosticados con la RND por día durante las cuatro semanas de predicción, tanto para la serie de valores del DAX como del S&P 500, respectivamente.
Para complementar el análisis, presentamos los cuadros 1y2, en los cuales se muestran los rangos de error relativo por semana. En ambos cuadros podemos apreciar que las predicciones de la RND durante las dos primeras semanas son sumamente aproximadas a los datos reales y que empiezan a divergir a partir de la tercera semana. Es decir, el uso de las redes neuronales diferenciales como método para pronosticar los valores futuros de los índices accionarios analizados ofrece valores pronosticados de esas series con un alto grado de precisión cuando se utiliza para una ventana de predicción de dos semanas de operación del mercado.
En este trabajo se han presentado los resultados del análisis del desempeño de una red neuronal diferencial para identificar el comportamiento de índices bursátiles de dos mercados accionarios desarrollados: el alemán y el estadounidense.
De acuerdo con los resultados obtenidos mediante la RND en el proceso de descripción o seguimiento del comportamiento de los valores de los índices DAX y S&P 500, podemos afirmar que las RND son una excelente herramienta para describir el comportamiento de los valores de estos índices bursátiles.
Además, con base en los valores de los errores relativos entre los valores reales de las series analizadas y los valores pronosticados, podemos concluir que el sistema de pronóstico de los valores de estos índices accionarios basado en redes neuronales diferenciales muestra un desempeño altamente satisfactorio, sobre todo tomando en consideración las primeras dos semanas de pronóstico.
Esto es particularmente relevante si se toma en cuenta que en este estudio se alcanzó una mayor nivel de aproximación que la que se muestra en los resultados de otros trabajos previos, cuyos autores llevan a cabo pronósticos de índices de mercados accionarios por medio de redes neuronales de tipo discreto.
El potencial del poder predictivo de la red neuronal diferencial utilizada en este estudio es todavía de mayor importancia, dado que los índices analizados corresponden a mercados accionarios maduros cuyo comportamiento debe ser más difícil de pronosticar si se toma en cuenta que son mercados que operan con un mayor grado de eficiencia.
Los resultados de este estudio indican que las redes neuronales diferenciales son muy buenas herramientas para la descripción del comportamiento detallado de una variable financiera —en este caso los índices de mercados financieros maduros—, pues constituyen una herramienta robusta, precisa y confiable para llevar a cabo esta labor. Por lo anterior, estas redes se pueden considerar como candidatos adecuados para analizar problemáticas complejas de carácter financiero y económico, tales como el comportamiento de las tasas de interés, paridades cambiarias, precios de acciones, rendimientos accionarios e incluso volatilidades de éstas variables. Es decir, las redes neuronales diferenciales pueden ser herramientas de gran utilidad para problemas concretos de toma de decisiones relacionados con la administración de portafolios y de riesgos económico-financieros.
Finalmente, se puede plantear que la utilización de redes neuronales diferenciales para el análisis, descripción y pronóstico de series de tiempo puede ser de interés no sólo para las decisiones de problemas financieros, sino que su uso también puede extenderse a otros tipos de problemas que pueden enfrentar los tomadores de decisiones en otras áreas de la administración de empresas y de otros tipos de organizaciones. Por lo tanto, es necesario continuar avanzando en la investigación respectiva.