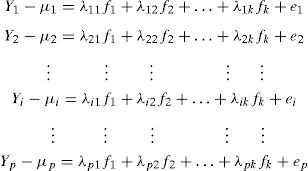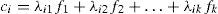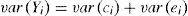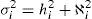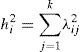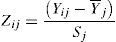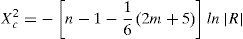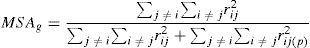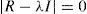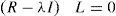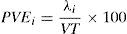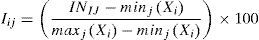En este artículo se presenta una propuesta de modelo para medir la competitividad de los tres niveles geográficos simultáneamente: país, estados y municipios, utilizando para ello un método multivariado de análisis factorial que ayuda a identificar a cinco factores, siete subfactores y treinta variables, con los que se miden y presentan los resultados de un estudio empírico sobre once entidades: el país, el Estado de Sonora y nueve municipios que representan el 80% de la población y el 80% de su PBT. Los resultados indican que el municipio de Hermosillo fue el más competitivo en 2010.
This article presents a proposal of a model to measure competitiveness at the three geographical levels simultaneously: country, states, and municipalities by using a multivariate factor analysis resulting in the identification of five factors, seven subfactors and thirty variables used to measure and to present the results of an empirical study of several entities: the country, the state of Sonora and nine municipalities that represent 80% of the population and 80% of its Total Gross Production (PBT). The results show that the municipality of Hermosillo was the most competitive in 2010.
Desde la antigüedad, la productividad ha sido un tema relevante en el desarrollo económico y en el bienestar social de los países, y ha sido estudiada desde las teorías clásicas de la ventaja absoluta, la ventaja comparativa y la ventaja competitiva de las naciones, hasta los modelos extendidos que solventan algunas de las deficiencias de estas teorías.
En esta investigación se presenta una propuesta de un modelo conceptual, el cual fue probado empíricamente para medir la competitividad simultáneamente en los tres niveles geográficos que son el objeto de estudio: municipal, estatal y nacional. Con este trabajo se pretende contribuir con un paso más en el camino hacia la competitividad en las regiones.
Marco analítico de la competitividadConcepto de competitividad y sus factores determinantes. Los orígenes del concepto de competitividad se remontan a los siglosxv-xvii, con la teoría económica llamada mercantilismo. En esta teoría, la forma de crear riqueza para el país era por medio del comercio exterior, en donde se aplicaba la siguiente regla: el valor de lo que se vende a los extranjeros anualmente debe ser siempre mayor a nuestro consumo de sus productos. Así, el mercantilismo miraba el comercio exterior como un juego de suma cero, en donde la riqueza de un país se da por el déficit comercial del otro país (Hidalgo Capitán, 1998). Sin embargo, la teoría clásica de Adam Smith de 1776, en el título «Investigación sobre la naturaleza y causa de la riqueza de las naciones», critica el punto de vista mercantilista que concebía al comercio como un juego de suma cero (Smith, 1937). En su lugar, Adam Smith entendía el comercio como un juego de suma-suma en donde todos los socios comerciales se pueden beneficiar con los menores costos unitarios, es decir, con base en la ventaja absoluta. Por su parte, David Ricardo (1817) aplica la siguiente regla: «el país superior debería especializarse en la producción de aquel bien donde se tiene la mayor ventaja absoluta y el país inferior debería especializarse en el bien donde se tenga la menor desventaja absoluta» (Ricardo, 1971). Esta regla fue conocida como «la ventaja comparativa» (Cho y Moon, 2013; Ramos Ramos, 2001). Aun cuando el modelo de Ricardo explica el comercio con base en los niveles de productividad entre las naciones, este no explica por qué existen dichas diferencias.
Teoría neoclásica. Eli Heckscher (1919) y Bertil Ohlin (1933) crearon la teoría de la dotación de los factores (Heckscher, 1949). Ellos desarrollaron el modelo atendiendo la idea de que todas las naciones cuentan con una tecnología similar, pero que dichas naciones difieren en sus dotaciones en tres determinantes (o factores) de producción, que son: capital, fuerza laboral y recursos naturales (Jones, 2011). Esto significa que, en el marco del modelo HO, un país o una región tenderá a ser exportadora neta de los productos y/o servicios factoriales «relativamente abundantes» en su geografía e importadora neta de aquellos bienes y/o servicios factoriales «relativamente escasos» (Artal, Castillo y Requena, 2006; Artal-Tur, Llano-Verduras y Requena-Silvente, 2009; Nyahoho, 2010; Juozapaviciene y Eizentas, 2010). La teoría moderna basada en los principios clásicos se asocia inicialmente a Paul Krugman (1979), y de acuerdo con sus proponentes la ventaja comparativa se mide por la productividad, la cual a su vez se define no solo por la dotación de los tres factores antes señalados, sino también por factores como inversión en capacidades laborales, infraestructura especializada, redes de proveedores y vigilancia tecnológica, entre otros factores determinantes (Travkina y Tvaronaviciené, 2010).
La teoría de la competitividad es representada por Michael Porter (1990), quien en su libro The Competitive Advantage of Nations creó sus bases y la conceptualizó: «La prosperidad de una nación depende de su competitividad, la cual se basa en la productividad con la cual esta produce bienes y servicios. Políticas macroeconómicas e instituciones legales sólidas y políticas estables son condiciones necesarias pero no suficientes para asegurar una economía próspera. La competitividad está fundamentada en las bases microeconómicas de una nación: la sofisticación de las operaciones y estrategias de una compañía y la calidad del ambiente microeconómico de los negocios en la cual las compañías compiten. Entender los fundamentos microeconómicos de la competitividad es vital para la política económica nacional» (Hergnyan, Gabrielyan y Makaryan, 2008, p. 13). En este contexto, la productividad se basa en dos factores: la calidad del ambiente microeconómico en el que los negocios compiten, referente a los factores físicos del modelo de diamante (en donde dentro de la condición de los factores se identifican, entre otros, los tres factores determinantes de la ventaja comparativa), y la sofisticación de la empresa referente a la capacidad tecnológica de absorción, de mejora y de creación de innovación.
Nivel geográfico de análisis del concepto de competitividad. De la teoría de Porter (1990) se desprende un debate, encabezado por Paul Krugman (1994), sobre el concepto de competitividad de las naciones. Primeramente argumenta que a nivel de empresa, industria o corporación el concepto de competitividad es claro, pero no lo es a nivel nacional.
Finalmente, para Krugman, el cambio en el estándar de vida de los ciudadanos es determinado por factores domésticos relacionados con la productividad (factores microeconómicos), pero no por la productividad relacionada con otros países competidores, sino simplemente por la productividad doméstica. Por lo que entiende el término «competitividad» como una forma poética de decir productividad, pero esto no implica que en competencia internacional este término tenga utilidad. En otras palabras, el término «competitividad de las naciones» es incorrecto (Krugman, 1994).
Lombana y Rozas Gutiérrez (2009) abordan la definición del concepto de competitividad atendiendo tres niveles de análisis: en el nivel micro y meso encontraron coincidencias; sin embargo, a nivel macro hacen referencia al economista Paul Krugman, quien critica el uso del concepto de competitividad a nivel nacional. Para superar este debate, los autores proponen que en lugar de hacer referencia a la «competitividad de las naciones» (se refiere entre las naciones) sería más conveniente utilizar el término «ambiente competitivo de la nación» (interno a la nación). Por lo tanto, para estos autores aún no hay consenso en el concepto de competitividad; sin embargo, argumentan que se podría unificar en un concepto único que abarque las dos teorías: clásica y moderna; como una definición vinculante de la competitividad. En ese sentido, los autores exponen que «uno no debe escoger entre una de las dos teorías, pues no son ni mutuamente excluyentes ni explícitamente separables». Por tanto, se puede sostener que es inapropiado presentar a la ventaja competitiva como una alternativa (sustituta) de la ventaja comparativa. Las dos teorías tienen que ser debidamente vistas como complementos más que como competidores en la formulación de políticas comerciales e industriales (Lombana y Rozas Gutiérrez, 2009).
Romo Murillo y Musik (2005) también abordan el concepto de competitividad atendiendo tres niveles de análisis: el micro (o local), donde la unidad de análisis son las empresas; el meso (regional o estatal), en el que la unidad de análisis son las industrias, los clúster y los sectores, y el macro (nacional e internacional), en el que la unidad de análisis es el país o la región de un grupo de países (competitividad intrapaíses). Ellos encontraron que existe consenso en la definición del término «competitividad» aplicada a las naciones en prácticamente todos los autores, sin importar si son economistas clásicos, neoclásicos o de escuelas de negocios, cuando se relaciona con la tasa de crecimiento de la productividad del país (pero no con la tasa de crecimiento de la productividad con relación a otros países, que lleven a presentar la competitividad como un juego de suma cero) (Romo Murillo y Musik, 2005).
Michael Porter (1990), que es el pionero de la teoría de la competitividad, sugiere que la competitividad se mida primeramente por la productividad al declarar que «la prosperidad de una nación depende de su competitividad, la cual se basa en la productividad». En este contexto, la mejor aproximación teórica sobre competitividad es productividad, o bien, tal como afirma el profesor Paul Krugman (1994), competitividad es un sinónimo de productividad.
Una de las críticas fuertes al modelo de Porter (1990) fue hecha por Rugman (1991), Rugman y D’Cruz (1993), Moon, Rugman y Verbeke (1998) y Dunning (2003) debido a su enfoque centrado únicamente en el país de origen, es decir, que no se había considerado, por una parte, el alcance geográfico de las empresas multinacionales y globales y, por otra parte, el papel del gobierno como factor endógeno en su modelo. Y debido a dichas omisiones los países pequeños con una gran actividad exportadora no podían ser explicados con su modelo. Para solventar dichas críticas se desarrolla el «doble diamante generalizado», que explica la competitividad de una nación mediante el análisis de dos diamantes: uno relacionado con el ambiente micro o local, y el otro, con el ambiente internacional macro, en donde se incluyen las empresas multinacionales y las empresas globales, así como al gobierno. Por otra parte, Cho (1994) y Cho y Moon (2013) identificaron la falta de dos factores de la competitividad nacional en el modelo de Porter (1990), que son: factores físicos y factores humanos. Dentro de los factores físicos, se incluyen los cuatro factores endógenos del modelo de Porter (1990), y dentro del factor humano, este se desglosa en cuatro subfactores: trabajadores, profesionales, empresarios y políticos y burócratas. Finalmente se incluye al azar como factor exógeno; así se desarrolló el «modelo de los nueve factores». Cho, Moon y Kim (2009) consecuentemente agregaron dos categorías para el alcance del nivel geográfico: el contexto doméstico y el contexto internacional; con esta adecuación al modelo se cubren los faltantes de los tres modelos: el modelo de Porter, el modelo de los nueve factores y el doble diamante generalizado, generando así una propuesta de modelo llamado del «doble diamante dual», que integra a los anteriores (Castro-Gonzáles, Peña-Vinces, Ruiz-Torres y Sosa, 2013; Cho, Moon y Kim, 2009).
De la teoría económica clásica y moderna se han derivado otras definiciones y modelos aplicables a nivel internacional, nacional, estatal y municipal. A nivel global, los más reconocidos son el Global Competitiveness Report, que genera el World Economic Forum; el World Competitiveness Yearbook, que genera el International Institute for Management Development (WEF, 2014-2015; IMD, 2014; Ramos Ramos, 2001; Cho y Moon, 2013; Cho y Moon, 2005; Lall, 2001), y el modelo del doble diamante dual, que se genera en Seúl (Corea). A nivel país y de las entidades mexicanas, los dos modelos más importantes son los que genera el Instituto Mexicano para la Competitividad A.C. (IMCO-Estatal) y el generado por la Escuela de Graduados en Administración Pública y Política Pública (EGAP) (Benzaquen, del Carpio, Zegarra y Valdivia, 2010; IMCO, 2014; EGAP, 2010). A nivel de desagregación de los municipios de los estados mexicanos se cuenta con el modelo del IMCO-Urbano (IMCO, 2007) (CONAPO, 2010), el trabajo de Bracamonte Sierra (2011) y el trabajo de Quijano Vega (Quijano Vega, 2007; IMCO, 2007; CONAPO, 2010; Bracamonte Sierra, 2011).
El presente estudio se desprende principalmente del enfoque conceptual realizado por Cho y Moon (2013) y la metodología de medición de OECD & JRC (2008); además se apoya en WEF (2014-2015), EGAP (2010) e IMCO (2014) para la determinación de las variables de la competitividad a nivel geográfico del país, del estado y de los municipios. Finalmente, puesto que algunos de estos modelos fueron adaptados para generar indicadores compuestos de la competitividad o relacionados con esta a escala geográfica estatal (o municipal), se trabaja a partir de las metodologías que originalmente fueron diseñadas para analizar países. Sin embargo, las metodologías antes mencionadas, aplicadas tanto al contexto nacional como al estatal, presentan la deficiencia de no contemplar en un mismo modelo a los tres niveles geográficos (municipio, estado y país). En este sentido, se contribuye por un lado en cubrir parte del vacío existente en las investigaciones en competitividad que relacionan los ámbitos geográficos nacional, estatal y municipal, y por otro lado en medir la competitividad mediante la técnica multivariante del análisis factorial.
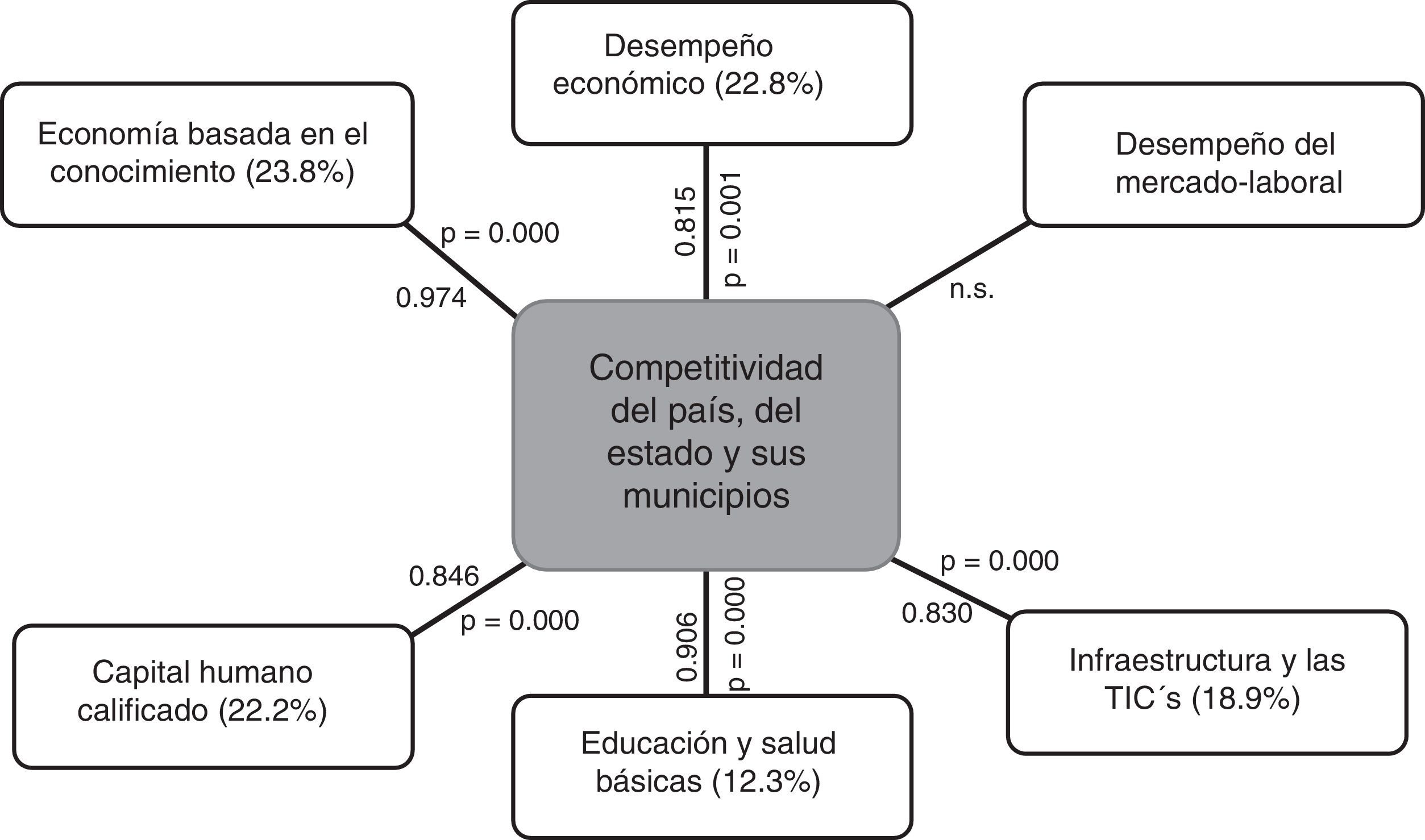
Teniendo en cuenta el anterior marco contextual, en el presente trabajo se define y se mide la competitividad como el conjunto de tres grandes categorías relacionadas con los aspectos económicos, humanos y físicos en el ambiente micro, meso y macro que determinan el nivel de productividad sostenida en el ámbito de las regiones geográficas (o entidades). Una vez definido el concepto de competitividad que guía el punto de inicio de esta investigación, se establece como objetivo central la propuesta de un modelo de competitividad en los tres niveles (MC3N), mediante la desagregación de estas tres categorías en sus factores determinantes; entre estos, el factor económico contiene el desempeño económico; el factor humano contiene la fuerza laboral saludable que se forma con la educación básica, el capital humano que se forma en las universidades, posgrados y que participa como profesionista en los sistemas productivos, las personas que generan riqueza a partir del conocimiento que son especialistas e investigadores, las personas que participan como políticos y burócratas en las instituciones; y el factor físico contiene el desempeño del mercado, las infraestructuras y las tecnologías de información y comunicación (TIC). Con base a lo anterior, se planteó la siguiente hipótesis de trabajo: Probar que la competitividad en los tres niveles geográficos (país, estado y municipios) está influenciada por los factores determinantes de la competitividad (desempeño económico, desempeño del mercado laboral, infraestructura y TIC, educación y salud básicas, capital humano calificado y economía del conocimiento), debido a que estos factores determinantes concentran las principales variables identificadas. Y que con esta interrelación estructural es posible construir un indicador de competitividad compuesto que mida a dichas entidades.
Diseño de la investigación. El tipo de estudio fue de diseño cuasiexperimental de clasificación transeccional, y dada la naturaleza de la relación entre las variables interdependientes con la variable de respuesta obtenida, se consideró a su vez como un diseño de investigación correlacional-causal compleja (Hernández Sampieri, Fernández Collado y Baptista Lucio, 2010, pp. 71-75).
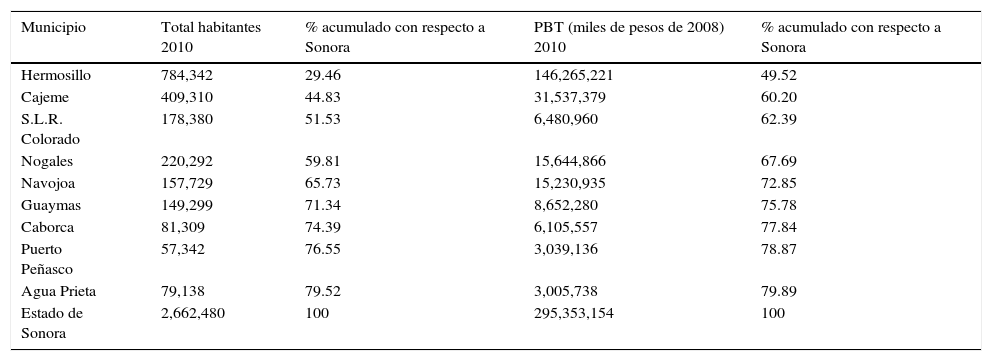
Objeto de estudio y selección de la muestra. Las entidades objeto de investigación corresponden a nueve municipios, los cuales forman parte del Estado de Sonora, con quien además se contrastan, y estos a su vez son contrastados con los de nivel país. La muestra es tomada de estos nueve municipios que representan al estado de un total de 72 de ellos, y que se seleccionaron en base a dos criterios (Garza, 2010; IMCO, 2007): 1) que concentren el 80% de la población del estado, y 2) que concentren el 80% de la producción bruta total (PBT) del estado. La tabla 1 contiene la información señalada.
Selección de los municipios representativos del Estado de Sonora
| Municipio | Total habitantes 2010 | % acumulado con respecto a Sonora | PBT (miles de pesos de 2008) 2010 | % acumulado con respecto a Sonora |
|---|---|---|---|---|
| Hermosillo | 784,342 | 29.46 | 146,265,221 | 49.52 |
| Cajeme | 409,310 | 44.83 | 31,537,379 | 60.20 |
| S.L.R. Colorado | 178,380 | 51.53 | 6,480,960 | 62.39 |
| Nogales | 220,292 | 59.81 | 15,644,866 | 67.69 |
| Navojoa | 157,729 | 65.73 | 15,230,935 | 72.85 |
| Guaymas | 149,299 | 71.34 | 8,652,280 | 75.78 |
| Caborca | 81,309 | 74.39 | 6,105,557 | 77.84 |
| Puerto Peñasco | 57,342 | 76.55 | 3,039,136 | 78.87 |
| Agua Prieta | 79,138 | 79.52 | 3,005,738 | 79.89 |
| Estado de Sonora | 2,662,480 | 100 | 295,353,154 | 100 |
Fuente: elaboración propia con base al Anuario estadístico y geográfico de Sonora (INEGI, 2013).
Datos: instrumento, fuentes de información secundaria y variables de estudio. Se diseñó un modelo conceptual de competitividad para caracterizar las entidades objeto de estudio (fig. 1, de la sección de resultados) a partir de la revisión de la literatura y atendiendo la consistencia con la definición y el marco conceptual. Los principales problemas con los que se enfrentan al construir un modelo es la falta de información desagregada disponible a nivel municipal, que esté de acuerdo con el marco teórico, la credibilidad de la información y la disponibilidad de esta al público. Considerando los desafíos anteriores, la construcción del MC3N se nutre de fuentes de información de los bancos de datos de INEGI y de otras fuentes oficiales. La matriz de datos, formada por 6 factores, 8 subfactores y 35 criterios, utilizados para valorar las 11 entidades para el periodo de análisis del 2010, se muestra en el anexo, en las tablas A1-A3.
Modelo. El modelo de análisis factorial, que describe las covarianzas o correlaciones de un conjunto de variables observables y1, y2, ..., yp en términos de un reducido número de factores comunes que son latentes no observadas, se presenta en su forma desarrollada como un sistema de ecuaciones lineales en 1 (OECD & JRC, 2008; Timm, 2002; Peña, 2002).
Donde: Yi representa a las variables observadas obtenidas de las bases de datos. Pero al estandarizarlos tendrán media cero y varianza unitaria para toda i=1,2,…,p; las λ11, λ12, ..., λk son los coeficientes de regresión, y en esta técnica son conocidos como los pesos o las cargas de los factores; las f1, f2, ..., fk son los factores comunes latentes o variables latentes no observadas que se investigan, cada uno con media cero y varianza unitaria; finalmente, los residuales ei son las perturbaciones no observadas de los factores únicos o específicos. El modelo está limitado a trabajar con variables de razón o de intervalo y cuidar que las variables tengan la misma dirección o sentido.Así, cada observación o dato con respecto a la media se representa como dos partes, la parte común y la parte específica, representadas por ci e ei, respectivamente. El modelo de análisis factorial (1) es usado para investigar las partes comunes que no son observables de los datos Yi, expresando para el i-ésima variable observada o dato con la ecuación 2.
Donde: Ci son los efectos ahora observados que resultan de la relación entre los coeficientes λi1, λi2, …, λik y los k factores comunes latentes.En términos de la varianza de los datos del modelo (1), puede ser descompuesta en factores comunes y en factores únicos, como se puede observar en la ecuación 3:
Donde: var(Yi) es la varianza de las observaciones aleatorias Yi; la varianza de ci se refiere a la varianza común o comunalidad que se investiga, y la varianza de ei es la varianza única o especifica. La ecuación anterior también se puede representar como:Donde: el primer término es la suma de los efectos de los factores y el segundo el efecto de la perturbación. Llamando a la suma de los efectos de los factores como:Donde: hi2 es la varianza común o comunalidad.Metodología del análisis factorial confirmatorio. Existen varias alternativas para tratar el modelo dado en (1). Sin embargo, el más común es el relacionado con el método de extracción por componentes principales para la construcción de indicadores compuestos a partir de modelos conceptuales (OECD & JRC, 2008). La metodología general para el análisis se presenta a continuación:
1. Estandarizar o normalizar las variables originales. Formalmente esto se logra con una transformación de la distribución normal estándar con media cero y varianza uno mediante la ecuación 6, debido a que estas vienen expresadas en distintas unidades de medición (OECD & JRC, 2008; Espejo Benítez e Hidalgo Pérez, 2011; Gutiérrez Pulido y Gama Hernández, 2010).
Donde: Zij es la variable j estandarizada con media cero y varianza uno de la entidad de observación i; Yij representa a cada variable j de la entidad de observación i; YJ¯ representa la media aritmética de los valores de la variable j; Sj representa la desviación estándar de la variable j.2. Obtener las varianzas de las variables originales estandarizadas (Yij) con media cero y varianza uno. La nueva variable obtenida de esta transformación se simboliza por (Zij), a la cual se la conoce como la matriz de correlación estandarizada1 (De la Garza García, Morales Serrano y González Cavazos, 2013).
3. Mediante la prueba de contraste de esfericidad de Bartlett y la medida de adecuación muestral de Kaiser-Meyer-Olkin se determina el grado de correlación general, la correlación parcial entre las variables y la conveniencia del análisis factorial para el análisis que se propone. Con la ecuación 7 se obtienen los valores de la ji cuadrado de Bartlett y con la ecuación 8 se obtiene la medida de suficiencia de muestreo general (MSAg), el cual puede extenderse a las variables individuales (MSAj), usando la ecuación 9 para excluir aquellas que sean inaceptables (también se identifican por valores menores a 0.5 en la diagonal principal de la matriz de correlación antiimagen) (Hair, Anderson, Tatham y Black, 1999; De la Garza García et al., 2013).
Donde: Xc2 es la ji cuadrada calculada; n es el número de datos; m es el número de variables; R es la determinante de la matriz de correlación, la cual oscila entre 0 y 1, es decir 0≤R≤∼1, el valor de 1 indica que es una matriz identidad2.Donde: el índice MSAg es la medida de suficiencia o adecuación de muestreo general acotada entre: 0 a 1, lo aceptable es que MSAg ≥0.5; rijp2 es el coeficiente de correlación parcial entre (zi, zj) eliminando la influencia del resto de las variables.Donde: el índice MSAj es la medida de suficiencia o adecuación individual la cual se acota desde 0 a 1, lo aceptable es que MSAj ≥0.5; rij(p)2 es el coeficiente de correlación parcial entre (zi, zj) eliminando la influencia del resto de las variables.4. Se calculan los valores y vectores propios mediante la ecuación 10 y 11. La ecuación 11 da origen a la matriz ortogonal para la transformación, renombrada L⌢ (Pla, 1986; De la Garza García et al., 2013; Peña, 2002; Timm, 2002).En donde: R es la matriz de correlación estandarizada de dimensión (p x p); λ es un escalar cuyos valores de lambda son encontrados y se les denominan valores propios (eigenvalores); I es la matriz identidad; L es un vector de dimensión (px1), no nulo, que se le llama vector propio (eigenvector).
5. Determinar el número óptimo de factores, atendiendo los siguientes tres criterios: a)scree test, que es un gráfico de sedimentación entre el número de factores y los eigenvalores que se obtiene de la ecuación (10). Una variante u opción a este criterio es el uso del valor propio o eigenvalor ≥1; b)porcentaje de correlación lineal múltiple de cada variable con los factores o comunalidad ≥60%, de acuerdo con Hair et al. (1999, p. 93); c)porcentaje de la varianza explicada acumulada (PVEA) ≥60%, mediante la ecuación 12 (Timm, 2002; De la Garza García et al., 2013; Espejo Benítez e Hidalgo Pérez, 2011; OECD & JRC, 2008; Hair et al., 1999).
En donde: PVEi es el porcentaje de la variación explicada individual del factor i ésimo; λi es el eigenvalor de la observación i ésima; VT es la variación total (o número de variables).
6. Probar el modelo conceptual planteado.
7. Llevar a cabo una rotación ortogonal de la matriz factorial siguiendo el método de rotación varimax3 que simplifique la identificación visual de grupos de variables, mediante las cargas de los factores óptimos determinados (Hair et al., 1999; De la Garza García et al., 2013).
8. Construcción de un traductor de competitividad o codificación para el MC3N. A partir de las cargas del eigenvector del modelo conceptual ya probado, es decir, con la interpretación de las dos primeras componentes que asegure al menos un 60% de varianza explicada de acuerdo con el tercer criterio de los mencionados en el apartado sobre la selección óptima de los factores, se hace una interpretación conjunta de las dos primeras componentes, y así se escogen las cargas de los factores (eigenvector) que multiplican a cada una de las variables estandarizadas con la ecuación (6) de cada entidad (OECD & JRC, 2008).
Para la construcción tanto del ranking individual de los factores determinantes comunes como para el ranking global, se hace como ya se señaló en este paso. Sin embargo, con la finalidad de permitir una fácil interpretación de estos índices, se utiliza la ecuación 13 para ordenar los datos codificados en una escala de cero a cien (OECD & JRC, 2008).
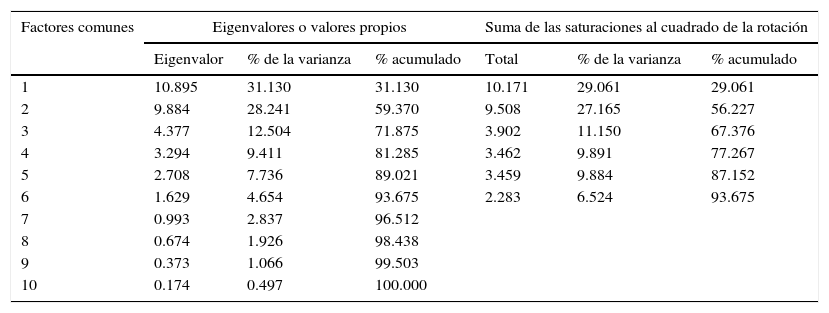
Dónde: Iij es el valor del indicador i en escala de 0 a 100 para le entidad j; INij es el valor del indicador i para la entidad j; minjXi representa al indicador más bajo desde la entidad j, y maxjXi representa al indicador más grande desde la entidad j.ResultadosComo anteriormente se comentó, con base en la evidencia empírica de investigaciones relacionadas y con el apoyo del programa estadístico SPSS 17.0 y Minitab 17.0, se logró identificar la reducción de las 35 variables iniciales en 6 factores comunes que proporcionan un 93.675% de la varianza total explicada, utilizando en dicho análisis el criterio de eigenvalor4 ≥1 en sus variables estandarizadas, tal como se muestra en la tabla 2, que presenta tanto la matriz de componentes sin rotar como la matriz de componentes rotada. Los seis factores comunes antes mencionados fueron usados también como apoyo para elaborar las tablas A1-A3 (anexo).
Varianza total explicada y determinación de la dimensión de los factores comunes
| Factores comunes | Eigenvalores o valores propios | Suma de las saturaciones al cuadrado de la rotación | ||||
|---|---|---|---|---|---|---|
| Eigenvalor | % de la varianza | % acumulado | Total | % de la varianza | % acumulado | |
| 1 | 10.895 | 31.130 | 31.130 | 10.171 | 29.061 | 29.061 |
| 2 | 9.884 | 28.241 | 59.370 | 9.508 | 27.165 | 56.227 |
| 3 | 4.377 | 12.504 | 71.875 | 3.902 | 11.150 | 67.376 |
| 4 | 3.294 | 9.411 | 81.285 | 3.462 | 9.891 | 77.267 |
| 5 | 2.708 | 7.736 | 89.021 | 3.459 | 9.884 | 87.152 |
| 6 | 1.629 | 4.654 | 93.675 | 2.283 | 6.524 | 93.675 |
| 7 | 0.993 | 2.837 | 96.512 | |||
| 8 | 0.674 | 1.926 | 98.438 | |||
| 9 | 0.373 | 1.066 | 99.503 | |||
| 10 | 0.174 | 0.497 | 100.000 | |||
Método de extracción: análisis de componentes principales.
Fuente: elaboración propia.
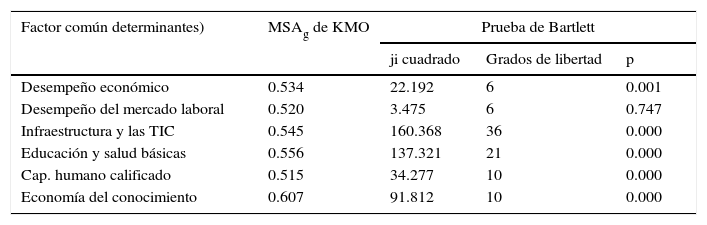
Para explicar la relación existente entre las variables de los factores determinantes y la competitividad de las entidades, es decir, la existencia del grado de interrelación entre los grupos de variables, el requisito es probar el grado de correlación de las variables deslindadas con cada factor común. El test de esfericidad de Bartlett y la medida de adecuación de la muestra de Kaiser-Meyer-Olkin nos dicen el grado de adecuación del análisis factorial. En la tabla 3 se presentan los resultados, en donde se demuestra que ambas pruebas determinan que el análisis factorial es adecuado para estudiar las interrelaciones entre las variables de cada factor común, con excepción del determinante denominado desempeño del mercado laboral, debido a que su nivel de significancia es muy bajo (0.747); esto se debe a que se comprueba la ausencia de correlaciones significativas entre las variables precisadas en este factor, es decir, se prueba la hipótesis nula de que la determinante de la matriz de correlaciones se ajusta a la matriz identidad, por lo que no debe utilizarse el determinante desempeño del mercado laboral en el análisis factorial. Por otra parte, el determinante de economía basado en el conocimiento fue aceptado con 10 grados de libertad, debido a que se eliminó una de las variables (candidatos) por tener un valor de MSAj<0.5, es decir, por presentar un índice de correlación parcial muy bajo con respecto del grupo de variables en dicho determinante.
Kaiser-Meyer-Olkin y prueba de Bartlett
| Factor común determinantes) | MSAg de KMO | Prueba de Bartlett | ||
|---|---|---|---|---|
| ji cuadrado | Grados de libertad | p | ||
| Desempeño económico | 0.534 | 22.192 | 6 | 0.001 |
| Desempeño del mercado laboral | 0.520 | 3.475 | 6 | 0.747 |
| Infraestructura y las TIC | 0.545 | 160.368 | 36 | 0.000 |
| Educación y salud básicas | 0.556 | 137.321 | 21 | 0.000 |
| Cap. humano calificado | 0.515 | 34.277 | 10 | 0.000 |
| Economía del conocimiento | 0.607 | 91.812 | 10 | 0.000 |
Fuente: elaboración propia.
Del sistema de ecuaciones (1) y las ecuaciones (10) y (11) finalmente se obtienen los eigenvectores correspondientes a los pesos de las variables originales estandarizadas usados para estimar a cada variable latente individual (o indicador individual), y con el conjunto de estas variables latentes se obtienen los eigenvectores para estimar la variable latente global. Los resultados resumidos se muestran en la tabla A4 del anexo para el conjunto de dichas variables.
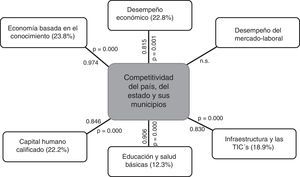
Los resultados anteriores demuestran la hipótesis planteada en este trabajo relacionado con el sustento del diseño del modelo MC3N a partir de la revisión de la literatura, la validez y la confiabilidad estadística, que están resumidas en las tablas 2, 3 y en el anexo (tabla A4). Así mismo, en la figura 1 se muestra el modelo MC3N, que presenta las interrelaciones entre las variables de los factores determinantes y la competitividad de las entidades. Los datos entre paréntesis se refieren a la variación total explicada acumulada del primer factor común para cada determinante calculado con la ecuación (12) desde la tabla A4 del anexo; los otros se refieren al dato referente al coeficiente de correlación lineal múltiple de cada determinante en el conjunto de los dos factores, quienes explican un 87.4% de la variación total acumulada, calculada con la ecuación (5); el otro dato se refiere al valor p en test de Bartlett, presentado en la tabla 3.
Aun cuando el determinante desempeño del mercado no fue considerado en el análisis, debido a que no se encontró correlación significativa entre las variables consideradas en el estudio, sin embargo esto no significa que dicho determinante no sea importante, pues existen otras variables que se pueden considerar, tales como: exportaciones totales, importaciones totales, inversión extranjera directa (IED) entrante, IED saliente, participación porcentual en las llegadas de IED mundial, que son las variables más citadas por los principales autores, como Porter (2008), entre otros. Sin embargo, los datos de estas variables no están disponibles a nivel de desagregación de los municipios y, por ende, no fue posible evaluar su impacto en el modelo conceptual.
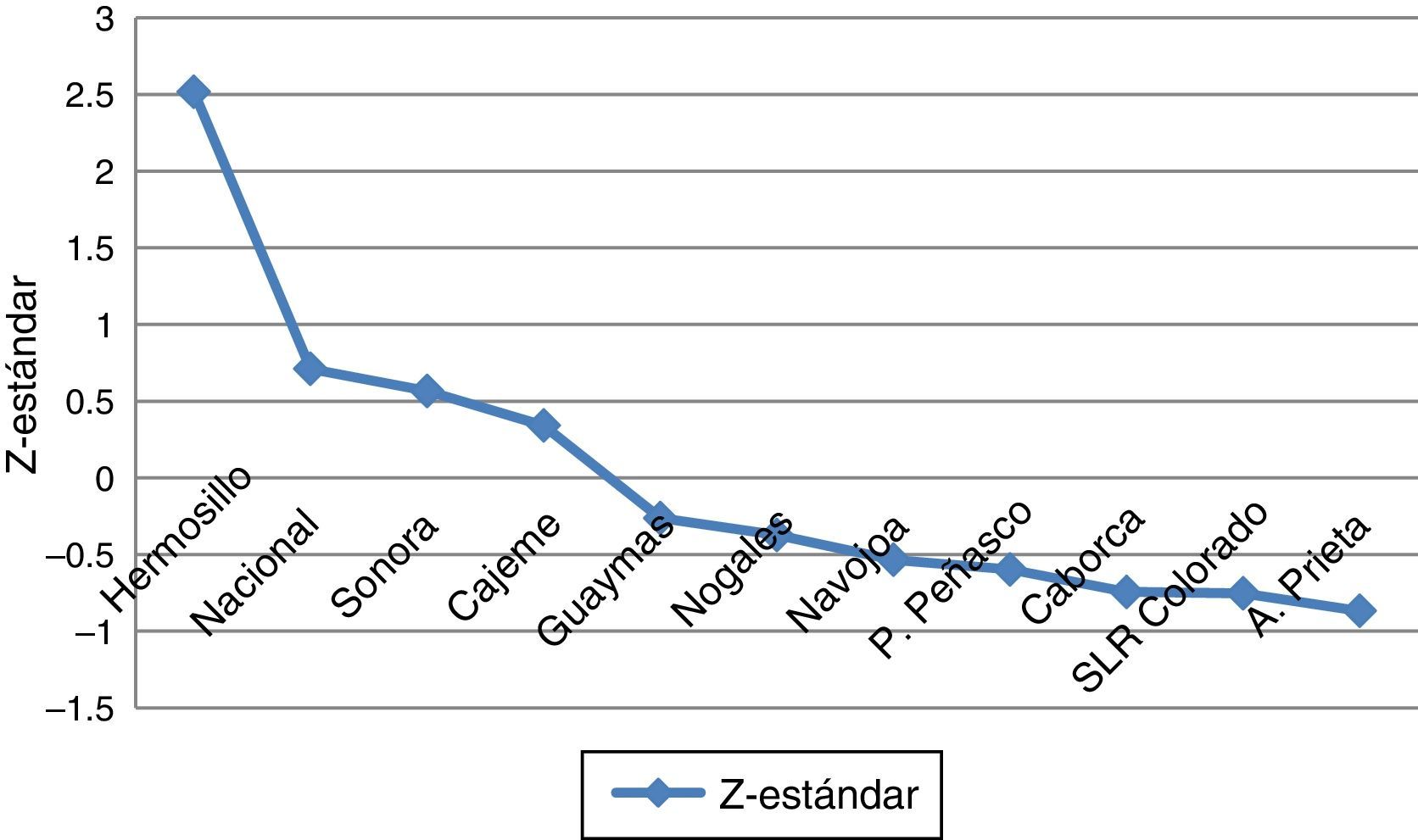
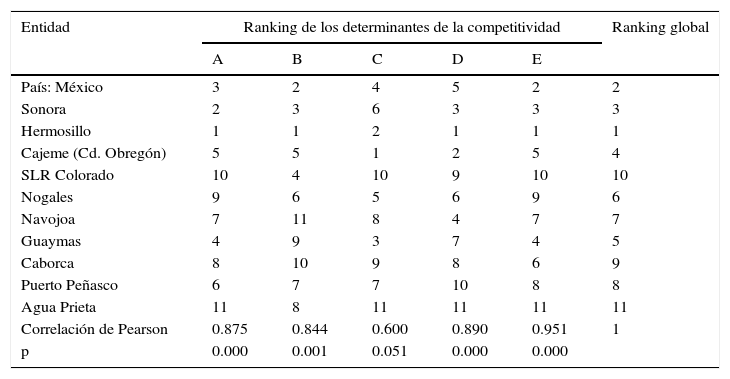
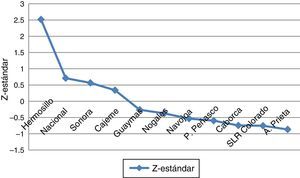
Para caracterizar la competitividad de las entidades se procedió a lo descrito en el paso8 de la metodología. Así, tanto en la tabla 4 como en la figura 2 se muestra el ranking traducido al lugar de la posición que le corresponde a cada una de las once entidades.
Indicadores de competitividad, año 2010
| Entidad | Ranking de los determinantes de la competitividad | Ranking global | ||||
|---|---|---|---|---|---|---|
| A | B | C | D | E | ||
| País: México | 3 | 2 | 4 | 5 | 2 | 2 |
| Sonora | 2 | 3 | 6 | 3 | 3 | 3 |
| Hermosillo | 1 | 1 | 2 | 1 | 1 | 1 |
| Cajeme (Cd. Obregón) | 5 | 5 | 1 | 2 | 5 | 4 |
| SLR Colorado | 10 | 4 | 10 | 9 | 10 | 10 |
| Nogales | 9 | 6 | 5 | 6 | 9 | 6 |
| Navojoa | 7 | 11 | 8 | 4 | 7 | 7 |
| Guaymas | 4 | 9 | 3 | 7 | 4 | 5 |
| Caborca | 8 | 10 | 9 | 8 | 6 | 9 |
| Puerto Peñasco | 6 | 7 | 7 | 10 | 8 | 8 |
| Agua Prieta | 11 | 8 | 11 | 11 | 11 | 11 |
| Correlación de Pearson | 0.875 | 0.844 | 0.600 | 0.890 | 0.951 | 1 |
| p | 0.000 | 0.001 | 0.051 | 0.000 | 0.000 | |
A: desempeño económico; B: infraestructura y TIC; C: educación y salud básicas; D: capital humano calificado; E: economía basada en el conocimiento.
Fuente: elaboración propia.
Es de notarse, tal como apunta Garza (2010), que se llega a una jerarquización muy similar de competitividad de las entidades si solo se considera el determinante desempeño económico. Esto es debido a que dicho determinante presenta una alta correlación lineal múltiple compuesta (o global) o correlación de Pearson. Sin embargo, en nuestro caso del presente estudio la interpretación del ranking global es más completa, ya que contiene la información del conjunto de los factores determinantes de la competitividad.
ConclusionesAun cuando el concepto de competitividad es muy complejo, existe consenso en dicho término cuando es usado en los niveles micro y meso. Sin embargo, en un nivel macro, el concepto se presta para el debate al referirse a la «competitividad de las naciones». No obstante, como ya se señaló, hay consenso entre las escuelas de los clásicos y la de negocios cuando se relaciona el concepto con el de productividad interna al país, pero no con relación a otros países. De este modo se ha desarrollado, entre otros métodos, el presente modelo MC3N como una herramienta para los hacedores de políticas de Estado, tomadores de decisiones del sector empresarial, académicos e investigadores interesados en medir, conocer o explicar la competitividad geográfica del país, del estado o de sus municipios e identificar por un lado qué factores deben mejorarse y por otro lado las variables de los factores determinantes que más han contribuido al éxito de su competitividad.
El modelo conceptual MC3N fue desarrollado estableciendo causalidad mediante justificación teórica en otros modelos, y apoyándose en datos empíricos se identificaron seis determinantes de la competitividad, a los que se denominó factores: 1)desempeño económico; 2)desempeño del mercado; 3)infraestructura y las TIC; 4)educación y salud básicas; 5)capital humanos calificado, y 6)economía basada en el conocimiento. Además, para cada uno de los factores se identificaron los subfactores y sus variables, que miden finalmente los seis factores determinantes de la competitividad. Los subfactores constituyen un segundo nivel y las variables un tercer nivel de desagregación, tanto para los insumos de información como para su análisis.
La aplicación empírica del modelo MC3N muestra que al verificarse se logró comprobar la hipótesis para 5 factores determinantes que inciden en la competitividad de las entidades; estos son: desempeño económico, infraestructura y las TIC, educación y salud básicas, capital humano calificado y economía basada en el conocimiento. En cuanto a la determinante desempeño del mercado laboral, se encontró que no fue significativa debido a que las variables no estaban suficientemente correlacionadas, lo que significa que dichas variables han tenido una relación plausible, o bien que desde un análisis de este tipo, donde no se distingue la perspectiva del tiempo (más de un año), con dichas variables no se puede demostrar la causalidad. Lo anterior no significa que este factor debe ser eliminado del modelo conceptual, sino que se debe probar esta dimensión utilizando otras variables desagregadas a nivel municipal e incluir la perspectiva del tiempo.
Los resultados del modelo empírico MC3N que se muestran en la figura 2 muestran que el municipio de Hermosillo es el más competitivo tanto del país como del Estado de Sonora y del resto de los municipios. Por otro lado, se encontró que el municipio de Cajeme, el Estado de Sonora y el país se encuentran en la misma etapa media de desarrollo competitivo, mientras que los municipios de Guaymas, Nogales, Navojoa, Puerto Peñasco, Caborca, San Luis Río Colorado y Agua Prieta se encuentran en un nivel de competitividad baja. Los hallazgos coinciden con los resultados reportados por el IMCO en 2010, en el sentido de identificar primero a Hermosillo con competitividad más alta (en la clasificación de adecuada); sin embargo, los resultados divergen al identificar después a Cd. Obregón (o Cajeme) y Guaymas en la misma etapa de desarrollo localizada por encima de la media de competitividad; el resto de los municipios no son tomados en consideración en su análisis.
Finalmente, como resultado concluyente de este primer trabajo, se deriva una segunda fase de esta investigación que corresponde a la identificación de la competitividad en los 72 municipios del Estado de Sonora, y que además esta sea comparable en el tiempo.
Agradecemos al editor, al subcomité del comité editorial y a dos árbitros anónimos. Un agradecimiento especial al Dr. Miguel Ángel Vázquez Ruiz, al Dr. Juan Enrique Huerta Wong, y al M.I. Carlos Anaya Heredia por sus valiosos comentarios en la primera versión de este artículo.
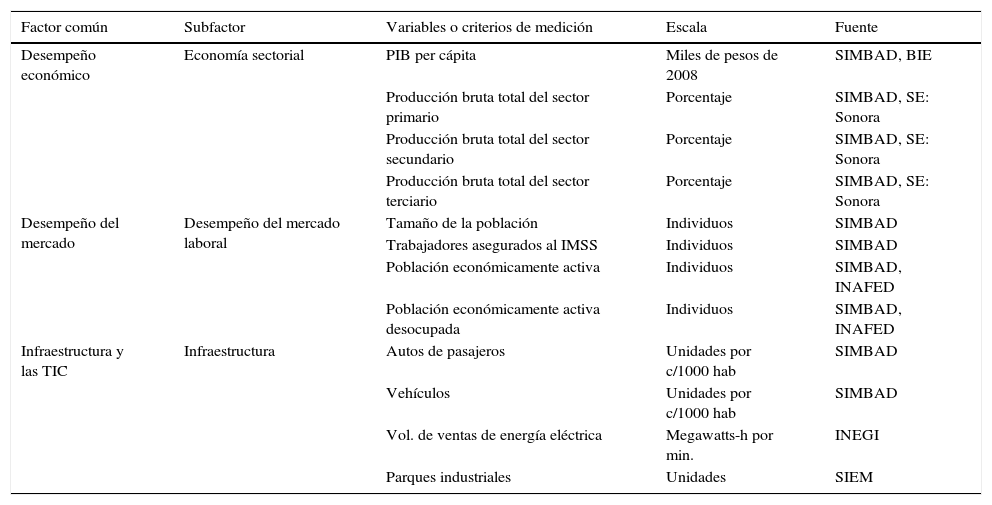
Factores determinantes y variables de la competitividad municipal. Parte 1
| Factor común | Subfactor | Variables o criterios de medición | Escala | Fuente |
|---|---|---|---|---|
| Desempeño económico | Economía sectorial | PIB per cápita | Miles de pesos de 2008 | SIMBAD, BIE |
| Producción bruta total del sector primario | Porcentaje | SIMBAD, SE: Sonora | ||
| Producción bruta total del sector secundario | Porcentaje | SIMBAD, SE: Sonora | ||
| Producción bruta total del sector terciario | Porcentaje | SIMBAD, SE: Sonora | ||
| Desempeño del mercado | Desempeño del mercado laboral | Tamaño de la población | Individuos | SIMBAD |
| Trabajadores asegurados al IMSS | Individuos | SIMBAD | ||
| Población económicamente activa | Individuos | SIMBAD, INAFED | ||
| Población económicamente activa desocupada | Individuos | SIMBAD, INAFED | ||
| Infraestructura y las TIC | Infraestructura | Autos de pasajeros | Unidades por c/1000 hab | SIMBAD |
| Vehículos | Unidades por c/1000 hab | SIMBAD | ||
| Vol. de ventas de energía eléctrica | Megawatts-h por min. | INEGI | ||
| Parques industriales | Unidades | SIEM |
Fuente: Elaboración propia, tomada de las bases de datos.
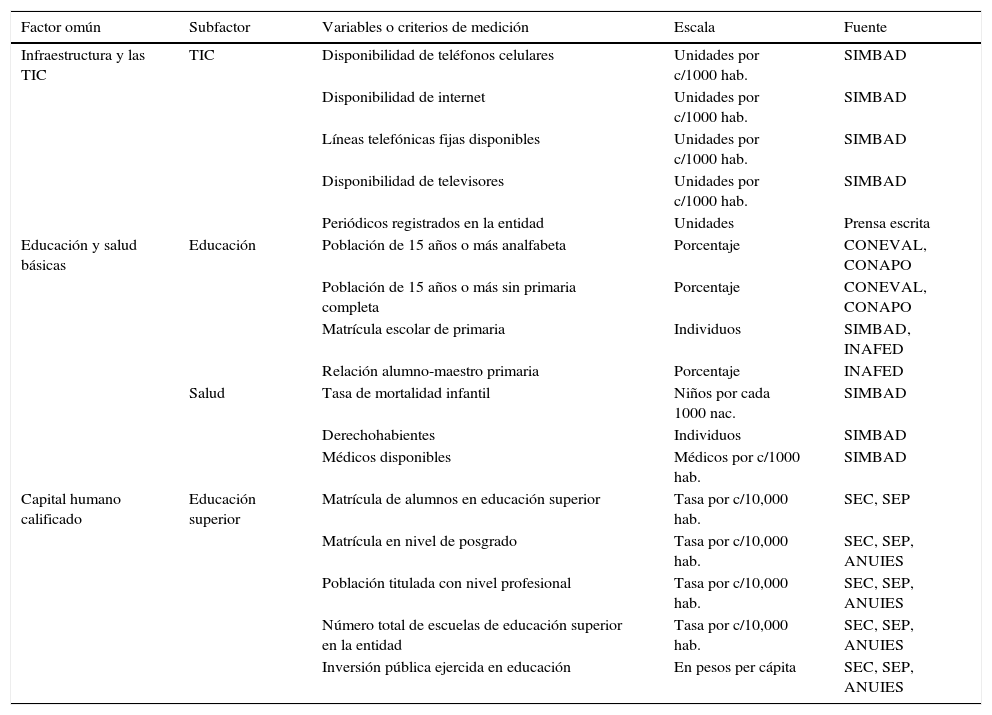
Factores determinantes y variables de la competitividad municipal. Parte 2
| Factor omún | Subfactor | Variables o criterios de medición | Escala | Fuente |
|---|---|---|---|---|
| Infraestructura y las TIC | TIC | Disponibilidad de teléfonos celulares | Unidades por c/1000 hab. | SIMBAD |
| Disponibilidad de internet | Unidades por c/1000 hab. | SIMBAD | ||
| Líneas telefónicas fijas disponibles | Unidades por c/1000 hab. | SIMBAD | ||
| Disponibilidad de televisores | Unidades por c/1000 hab. | SIMBAD | ||
| Periódicos registrados en la entidad | Unidades | Prensa escrita | ||
| Educación y salud básicas | Educación | Población de 15 años o más analfabeta | Porcentaje | CONEVAL, CONAPO |
| Población de 15 años o más sin primaria completa | Porcentaje | CONEVAL, CONAPO | ||
| Matrícula escolar de primaria | Individuos | SIMBAD, INAFED | ||
| Relación alumno-maestro primaria | Porcentaje | INAFED | ||
| Salud | Tasa de mortalidad infantil | Niños por cada 1000 nac. | SIMBAD | |
| Derechohabientes | Individuos | SIMBAD | ||
| Médicos disponibles | Médicos por c/1000 hab. | SIMBAD | ||
| Capital humano calificado | Educación superior | Matrícula de alumnos en educación superior | Tasa por c/10,000 hab. | SEC, SEP |
| Matrícula en nivel de posgrado | Tasa por c/10,000 hab. | SEC, SEP, ANUIES | ||
| Población titulada con nivel profesional | Tasa por c/10,000 hab. | SEC, SEP, ANUIES | ||
| Número total de escuelas de educación superior en la entidad | Tasa por c/10,000 hab. | SEC, SEP, ANUIES | ||
| Inversión pública ejercida en educación | En pesos per cápita | SEC, SEP, ANUIES |
Fuente: Elaboración propia, tomada de las bases de datos.
Factores determinantes y variables de la competitividad municipal. Parte 3
| Factor omún | Subfactor | Variables o criterios de medición | Escala | Fuente |
|---|---|---|---|---|
| Economía basada en el conocimiento | Innovación | Miembros del sistema nacional de investigadores (SIN) | Individuos por c/100,000 hab. | CONACYT, UNISON |
| Investigadores de nivel 3 | Individuos por c/100,000 hab. | CONACYT | ||
| Investigadores de nivel 2 | Individuos por c/100,000 hab. | CONACYT | ||
| Investigadores de nivel 1 | Individuos por c/100,000 hab. | CONACYT | ||
| Investigadores de nivel candidato | Individuos por c/100,000 hab. | CONACYT | ||
| Patentes nacionales registradas ante el IMPI | Unidades por c/100,000 hab. | IMPI |
Fuente: Elaboración propia, tomada de las bases de datos.
Pesos o cargas desde las variables latentes, para estimar la variable latente global
| Factor común | Eigenvector | Factor común | Eigenvector | Comunalidad | ||
|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 2 | |||
| D. del mercado | No cumplió con la prueba de Bartlett | A | 0.903 | 0.015 | 0.815 | |
| B | 0.823 | 0.390 | 0.830 | |||
| C | 0.662 | −0.684 | 0.906 | |||
| D | 0.890 | −0.231 | 0.846 | |||
| E | 0.922 | 0.351 | 0.974 | |||
| Eigenv. | 3.574 | 0.797 | 4.371 | |||
| % var. | 0.715 | 0.159 | 0.874 | |||
A: desempeño económico; B: infraestructura y TIC; C: educación y salud básicas; D: capital humano calificado; E: economía basada en el conocimiento.
Método de extracción: análisis de componentes principales.
Fuente: elaboración propia.
Una matriz de correlación estandarizada está formada en su diagonal principal por números unos y será simétrica (Pla, 1986; De la Garza García et al., 2013).
La revisión por pares es responsabilidad de la Universidad Nacional Autónoma de México.
Una matriz identidad contiene en su diagonal principal unos y fuera de ella ceros, lo que indica que no existe correlación entre las variables, por lo que el análisis no debe llevarse a cabo (Timm, 2002; De la Garza García et al., 2013).
Para aplicar el método de rotación varimax se debe calcular una matriz B = AL, donde: A es la matriz factorial y L es la matriz ortogonal a ser calculada; donde Lˆ*LˆT=I (Becerril Torres, Alvarez Ayuso, del Moral Barrera y Vergara González, 2009).
El término eigenvalor se refiere a la cantidad de información que cada uno de los factores logra captar del conjunto de variables, es decir, es la varianza total explicada por cada factor común (De la Garza García et al., 2013).