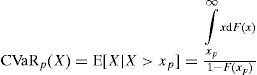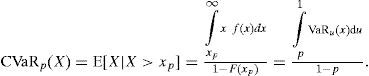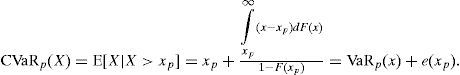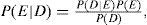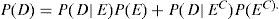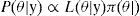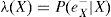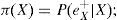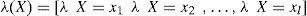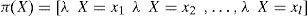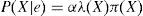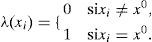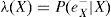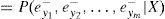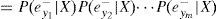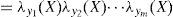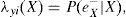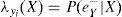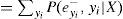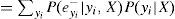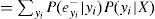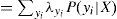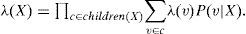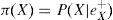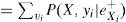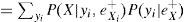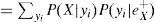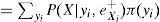Riesgo operacional en el proceso de pago del Procampo Un enfoque bayesiano

Resumen

Este trabajo identifica y cuantifica, a través de un modelo de red bayesiana (RB), los diversos factores de riesgo operacional (RO) asociados al proceso de pago del Programa de Apoyos Directos al Campo (Procampo). El modelo de RB es calibrado con datos de eventos que se presentaron durante el periodo 2008-2011. A diferencia de los métodos clásicos, la calibración del modelo de RB incluye fuentes de información tanto objetivas como subjetivas, lo cual permite capturar de manera más adecuada la interrelación (causa-efecto) entre los diferentes factores de riesgo operativo.

Abstract

This paper identifies and quantifies through a Bayesian Network model (BN) the various factors of Operational Risk (OR) associated with the payment process PROCAMPO. The BN model is calibrated with data from events that occurred during the period 2008-2011. Unlike classical methods, the BN model calibration sources include both objective and subjective ones, allowing to more adequately capture the relationship (cause and effect) between the several elements of operational risk.

Introducción

El enfoque bayesiano es una alternativa viable para el análisis de riesgos en condiciones de incertidumbre. Por construcción, los modelos bayesianos incorporan información inicial a través de una distribución de probabilidad a priori, mediante la cual se puede incluir información subjetiva en la toma de decisiones como la opinión de expertos, el juicio de analistas o las creencias de especialistas. Este trabajo utiliza un modelo de red bayesiana (RB) para examinar la interrelación entre factores de riesgo operacional¹ (RO) en el proceso de pago del Programa de Apoyos Directos al Campo (Procampo). El modelo RB que se propone se calibra con datos observados en eventos que se presentaron durante el proceso de bancarización² y con información que se obtuvo de los expertos³ o externa; el periodo de análisis es el comprendido desde 2008 hasta 2011.

A pesar de la existencia de trabajos —como los de Reimer y Neu (2002, 2003), Kartik y Reimer (2003), Leippold (2003), Aquaro et al. (2009), Neil, Márquez y Fenton (2004) y Alexander (2002)— que abordan de manera general la aplicación de las RB en la administración del RO, no existe una guía completa sobre cómo clasificar los eventos de RO, cómo identificarlos, cómo cuantificarlos y cómo calcular el capital económico de manera consistente. ⁴ Este trabajo pretende cerrar estas brechas de la siguiente forma: primero, establecer estructuras de información sobre eventos de RO de manera que sea posible identificar, cuantificar y medir el RO; posteriormente, cambiar el supuesto de independencia de eventos para mode-lar de manera realista el comportamiento causal de los eventos de RO.

La posibilidad de utilizar funciones de distribución condicionales, discretas o continuas, calibrar el modelo con fuentes de información, tanto objetivas como subjetivas, y establecer una relación causal entre los factores de riesgo, son los rasgos que precisamente distinguen esta investigación en comparación con los modelos estadísticos clásicos.

Este trabajo se organiza de la siguiente forma. En primer lugar, se presenta la terminología que se empleará para el cálculo de RO de acuerdo con los procesos y sistemas de pago relacionados con el Procampo. Después, se analiza el marco teó-rico para el desarrollo del trabajo, enfatizando sobre las características y bondades de las RB. Posteriormente, se describe la problemática que se pretende resolver, así como el alcance de la aplicación de la metodología propuesta. En seguida, se construyen dos redes: una para la frecuencia y otra para la severidad; para cuantificar cada nodo de las redes y obtener las probabilidades a priori se “ajustan” distribuciones de probabilidad para los casos donde existe información histórica; en caso contrario se recurre a la opinión o juicio de los expertos para obtener las probabilidades correspondientes; una vez que se cuenta con las probabilidades a priori de las dos redes, se procede a calcular las probabilidades a posteriori a través de algoritmos de inferencia bayesiana, en específico se utiliza el algoritmo junction tree.5 A continuación, se calcula el riesgo operacional condicional a través de simulación Monte Carlo con las distribuciones a posteriori calculadas para la frecuencia y la severidad; asimismo, se calcula la máxima pérdida esperada con el modelo clásico y se comparan ambos resultados. Por último, se presentan las principales conclusiones de este trabajo.

Sistema de pagos

Antecedentes

El sistema de pagos de Procampo fue desarrollado gradualmente por Apoyos y Servicios a la Comercialización Agropecuaria (Aserca) a partir de 1993 para hacer llegar directamente a los productores los recursos federales derivados de la operación de Procampo, operado por Aserca. ⁶ Al integrar el padrón de beneficiarios del citado Programa con más de 2.7 millones de productores y con una superficie apoyada de, aproximadamente, 14 millones de hectáreas cultivables —distribuida en 4.2 millones de predios— se creó la base de datos más completa del sector. Así, pues, Procampo y el sistema de pagos que lo acompaña tienen el mismo origen temporal y la misma explicación causal; pero, en forma adicional y progresiva, este sistema y su amplia base de datos fueron aprovechados para la emisión y distribución de apoyos de otros programas de la Secretaría como Programa de Estímulos a la Productividad Ganadera (Progan), apoyos al café, comercialización, rastros TIF (Tipo Inspección Federal), energéticos agropecuarios, entre otros.

Estructura del sistema de pagos

El sistema de pagos es el instrumento que tiene la Secretaría de Agricultura, Ganadería, Desarrollo Rural, Pesca y Alimentación (Sagarpa) para administrar el pago de subsidios de los diferentes programas; actualmente operado por Aserca, está estructurado en tres subsistemas: gobernabilidad, procesos sustantivos y tecnología informática.

Desde el punto de vista de la gobernabilidad, el pago de subsidios se apoya en el sistema de pagos para el cumplimiento de los objetivos y líneas de acción establecidos en el Programa Sectorial de Desarrollo Agropecuario y Pesquero, dentro de las cuales se destaca:

• I.

  Poner en marcha los nuevos esquemas de Procampo y Progan (Programa de Producción Pecuaria Sustentable y Ordenamiento Ganadero y Apícola) con nuevas reglas de operación.

• II.

  Establecer un sistema bancarizado.

Respecto al proceso sustantivo del sistema de pagos, éste involucra cuatro subprocesos a través de los cuales recibe, procesa, calcula y emite, anualmente, alrededor de 5.8 millones de solicitudes de pago de apoyos. El 84% corresponde a Procampo; el 1.57%, a comercialización; el 8.91%, a energéticos; y el 5.5%, a otros programas (fomento café, pro-oleaginosas, cítricos).

En cuanto a la tecnología informática del sistema de pagos, actualmente está conformada por una infraestructura con los siguientes componentes:

• I.

  Desarrollo de aplicaciones (lenguajes de programación y equipos)

• II.

  Administración de bases de datos (bases de datos y servidores)

• III.

  Mesa de ayuda y explotación de información (sistema de control de incidencias)

• IV.

  Soporte técnico (red de voz y datos, equipos y periféricos, correo electrónico y directorio activo)

• V.

  Servicios informáticos (telecomunicaciones, alojamiento, mantenimiento y licenciamiento de bases de datos y servidores de cómputo)

• VI.

  Interfaces con el sistema bancario y financier

Bancarización

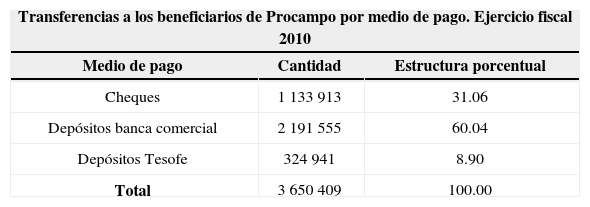
En los últimos tres años se ha logrado un avance muy significativo en sustituir los cheques, como medio de pago, por transferencias electrónicas a las cuentas de los beneficiarios que se han abierto para tal efecto a través de convenios con las instituciones financieras participantes; este proceso se conoce como bancarización. En el ejercicio fiscal de 2010, el 31% de las transferencias a los beneficiarios de Procampo se realizó a través de cheques y el 60% a través de transferencias o depósitos a las cuentas de los beneficiarios. Para 2011 la participación de las transferencias será mucho mayor, toda vez que al cierre de 2010 se habían abierto cuentas a 2 168 000 beneficiarios, de los cuales sólo a 1 552 706 se les pagó el apoyo con depósito en ese año.

Cuadro 1.

Distribución de pagos por medio de pago

Transferencias a los beneficiarios de Procampo por medio de pago. Ejercicio fiscal 2010
Medio de pago	Cantidad	Estructura porcentual
Cheques	1 133 913	31.06
Depósitos banca comercial	2 191 555	60.04
Depósitos Tesofe	324 941	8.90
Total	3 650 409	100.00

Fuente: Aserca

Ventajas de la bancarización

La bancarización erradica prácticas no deseables que se han detectado en el proceso de entrega de los cheques a los beneficiarios; muchas veces aquéllos son endosados por el beneficiario a una tercera persona —ya sea por su voluntad o mediante engaños— que paga en efectivo al beneficiario una cantidad menor al importe nominal del cheque. En ciertos casos esta práctica se puede considerar un servicio que se brinda al beneficiario al darle liquidez a partir de los cheques. Estos instrumentos son líquidos si y sólo si existe una infraestructura bancaria adecuada dentro de un rango de distancia razonable. En otros casos, las prácticas de cambio de cheques por dinero en efectivo son abusos hacia los beneficiarios por parte de los prestadores de distintos servicios (tenderos, restauranteros, etc.); agentes diversos de la sociedad rural (iglesias, autoridades ejidales, organizaciones económicas, etc.); o bien, son prácticas de corrupción cuando involucran a funcionarios públicos. Estas prácticas reflejan muchas veces la existencia de factores de poder en la sociedad rural. Algunas de ellas podrían replicarse bajo el nuevo esquema de pagos mediante transferencias, a través de exacciones, chantajes y presiones a los beneficiarios.

Con la bancarización los beneficiarios pueden acceder a sus recursos en efectivo sin recurrir a ningún tipo de intermediarios al acudir a los cajeros automáticos o sucursales bancarias. Sólo en casos extremos en los que los beneficiarios no pueden hacer sus retiros por cuestiones de edad, educación, o rechazo cultural, recurren a un familiar o amigo para que les auxilie en el retiro del dinero.

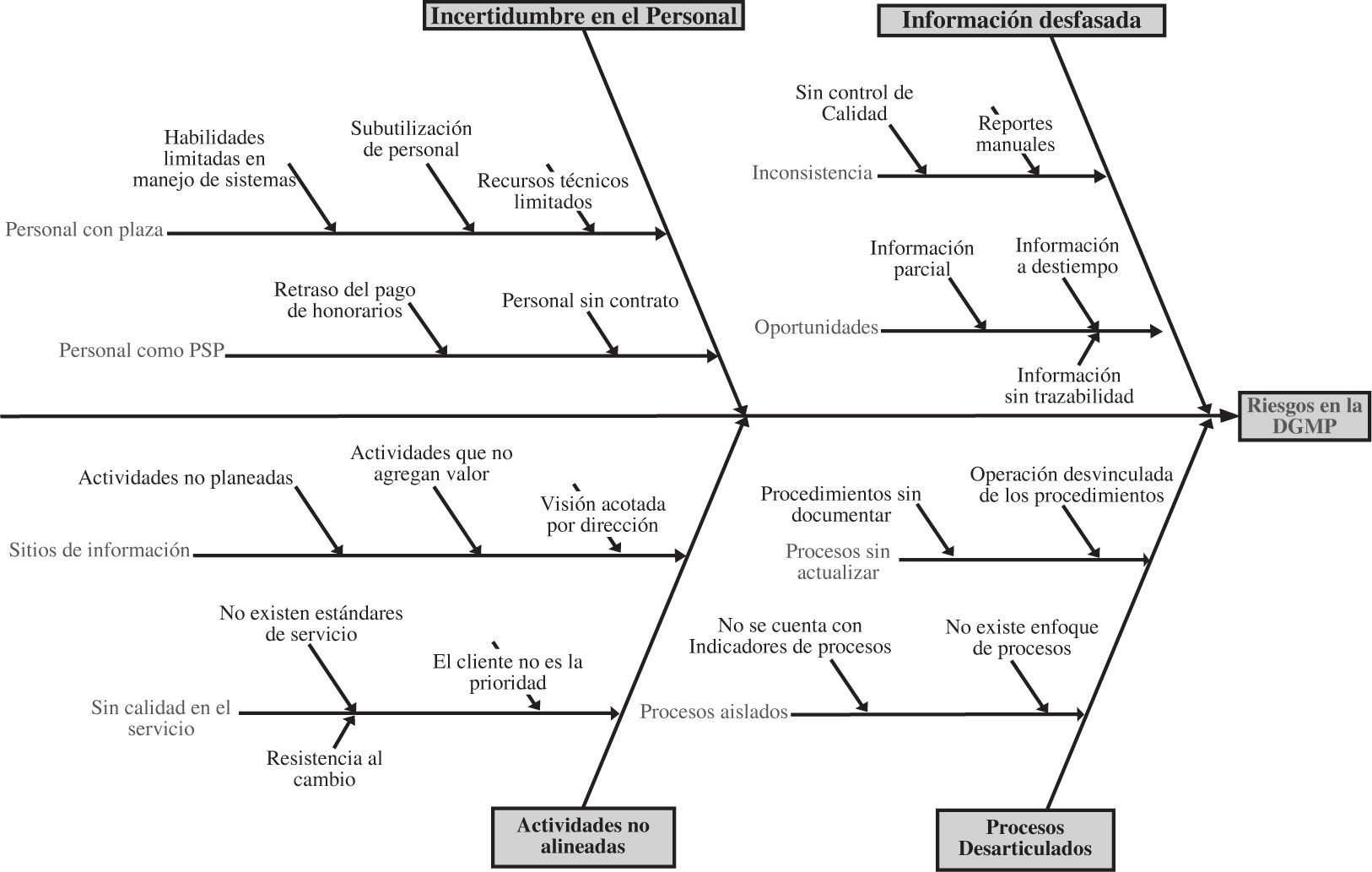
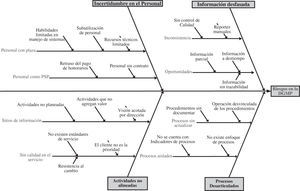
Identificación de riesgos en la bancarización

Para identificar los factores de riesgo asociados a la bancarización se utilizó la técnica denominada análisis causa-efecto (Ishikawa, 1943). Al analizar los riesgos y sus factores, estaremos identificando fallas en los procesos, duplicidad de actividades, actividades que no agregan valor, fallas en los servicios de terceros, entre otros.

Con base en el análisis anterior se identificaron los nodos (variables aleatorias) que formarán parte de la RB, las cuales se describen y analizan estadísticamente más adelante.

Medición del riesgo operacional

La naturaleza de los métodos para la cuantificación y medición del riesgo opera-cional varía desde lo más simple hasta métodos de gran complejidad y entre mode-los que consideran un solo indicador y modelos estadísticos muy sofisticados.

Métodos para medir el riesgo operacional

A continuación se describen los métodos existentes en la literatura para medir el RO (véanse, por ejemplo, Heinrich, 2006, y Basilea II, 2001).

El desarrollo de técnicas para la medición y administración de riesgo operacional es muy dinámico. Hay, sin embargo, algunas prácticas comunes surgidas entre algunos bancos. La naturaleza dinámica de las técnicas implicadas se pueden dar por dos razones: el hecho de que el acuerdo de Basilea permite un grado sustancial de flexibilidad (en el contexto de unos criterios estrictos de clasificación) en el método utilizado para evaluar los requisitos de capital, especialmente en el método de medición avanzada (AMA, por sus siglas en inglés). La medición y administración de riesgo operacional hace frente a muchos desafíos, entre los cuales están el relativo corto periodo de tiempo de datos históricos de pérdidas, el rol del ambiente de control interno —el cual naturalmente cambia y hace que la pérdida de los datos históricos sea irrelevante—, el importante papel de los eventos de poca frecuencia, pero con pérdidas muy grandes. Estos desafíos son manejados con varios enfoques en la práctica. El estudio de los métodos de riesgo operacional trata de separar modelos que se utilizan para cuantificar el riesgo operacional y el capital económico de aquellos que se utilizan solamente para la administración del riesgo. Esta separación, sin embargo, es muy difícil de efectuar, pues el modelo usado para cuantificar el riesgo operacional puede también ser usado por su administración. Lo que en la práctica se hace es separar los modelos que son usados por la administración de riesgos operacionales internamente de los que son usados para el cálculo del capital económico para propósitos regulatorios. Llamamos al primer grupo modelos de administración de riesgo operacional; al segundo grupo se le denomina modelos para cuantificación y asignación de capital. Hay básicamente tres diferentes modelos para la cuantificación y asignación de capital dentro del método de medición avanzada: enfoque de distribución de pérdidas, enfoque de control y enfoque de escenario-básico.

Las principales diferencias entre estos enfoques es el énfasis de los elementos comunes. El enfoque de distribución de pérdidas enfatiza el uso de pérdida de datos internos, el enfoque de control enfatiza la evaluación del entorno empresarial y el sistema de control interno, mientras que el enfoque de escenario-básico usa varios escenarios para evaluar el riesgo de la organización. A pesar de las diferencias en el énfasis, en la práctica la mayoría de los bancos está tratando de usar los elementos de estos tres enfoques.

El enfoque de distribución de pérdidas (LDA, por sus siglas en inglés) comienza con la recopilación de datos sobre pérdidas que es el indicador más objetivo de riesgos actualmente disponible. Con estos datos se estima la distribución de pérdidas; sin embargo, éstos proporcionan solamente una retrospectiva y, por lo tanto, no refleja necesariamente los cambios en el riesgo actual, ambiente de control y la pérdida de datos; en segundo lugar, no siempre está disponible en cantidades suficientes en cualquier institución financiera para permitir una evaluación razonable de exposición.

El LDA se ocupa de estas deficiencias mediante la integración de otros elementos de la AMA como datos externos, análisis de escenarios y factores que reflejen el entorno empresarial y el sistema de control interno; usa técnicas actuariales para modelar el comportamiento de las pérdidas operacionales de una empresa a través de la estimación de la frecuencia y severidad para producir una estimación objetiva de las pérdidas esperadas e inesperadas. Se inicia con la recolección de los datos de pérdidas para modelar la frecuencia y la severidad de éstas por separado; después, se agregan estas distribuciones a través de simulación Monte Carlo o técnicas estadísticas para obtener una distribución de las pérdidas totales de cada tipo de pérdida. Algunas distribuciones estadísticas de uso común son la de Poisson, distribución binomial negativa, Weibull y Gumbel para la frecuencia; y Lognormal, Gamma y la distribución logarítmica normal gamma para la severidad. El último paso consiste en ajustar una curva a la distribución de pérdidas totales obtenidos; para comprobar la bondad de ajuste se emplean técnicas estadísticas estándar como el de Pearson, Chi-cuadrado y el test de Kolmogorov-Smirnov.

Con el nuevo acuerdo de Basilea II, los bancos están obligados a calcular el capital económico; esto es cierto para los tres enfoques en la AMA. La diferencia entre el valor de la pérdida correspondiente al percentil en la cola y la media de la distribución de la pérdida total es el capital económico de los percentiles elegidos. La media se llama la pérdida esperada y la diferencia pérdida inesperada, de la que los bancos están obligados a protegerse.

En resumen:

• 1)

  Los métodostop-down de indicador simple. Este método fue elegido por el comité de Basilea como una primera aproximación al cálculo del riesgo operacional. Un solo indicador como el ingreso total de la institución, o la volatilidad del ingreso o los gastos totales se pueden considerar como el cargo total a cubrir por este riesgo.

• 2)

  Los métodosbottom-up que incluyen el juicio de un experto. La base para el análisis de un experto es un conjunto de escenarios. Los expertos identifican los riesgos y sus probabilidades de ocurrencia.

• 3)

  Medición interna. El Comité de Basilea propone el método de medición interna como un procedimiento más avanzado para calcular el costo de capital regulatorio.

• 4)

  Enfoque estadístico clásico. Análogamente a lo que se ha utilizado en los métodos de cuantificación para el riesgo de mercado y, más recientemente, el riesgo de crédito, también se ha avanzado en la investigación relativa a los métodos de cálculo para el riesgo operacional. Sin embargo, contrario a lo que sucede con el riesgo de mercado, es muy difícil encontrar un método estadístico ampliamente aceptado.

• 5)

  Modelos causales. Como alternativa a la estadística clásica surgen los modelos causales, que suponen dependencia entre eventos de riesgo; en otras palabras, cada evento representa una variable aleatoria (discreta o continua) con función de distribución condicional. Los eventos que no cuenten con registros históricos o bien que la calidad de los mismos no sea la requerida, se recurre a la opinión o juicio de los expertos para determinar las probabilidades condicionales de ocurrencia. La herramienta para modelar esta causalidad son las RB, las cuales se fundamentan en el teorema de Bayes y la topología de redes; esta herramienta es la que se desarrolla y aplica en este trabajo.

Marco teórico

En esta sección se presenta la teoría que soporta el desarrollo del trabajo. Se inicia con una discusión sobre el VaR condicional como medida de riesgo coherente en el sentido de Artzner et al. (1998). Después se utiliza el enfoque bayesiano para la construcción de RB, destacando sus ventajas con respecto del enfoque clásico en el estudio del RO.

Valor en Riesgo Condicional (CVaR)

De acuerdo con Panjer (2006), el CVaR (del término en inglés Conditional Value at Risk) o Expected Shortfall (ES, por sus siglas en inglés) es una medida alter-nativa al VaR que cuantifica las pérdidas que se pueden encontrar en las colas de las distribuciones. Se define como la pérdida esperada para los casos en donde la pérdida de valor del portafolio exceda el valor del VaR.

Si X denota la variable aleatoria de pérdida, el CVaR de X a un nivel de confianza del (1 − p) × 100%, denotado por CVaRp(X), es la pérdida esperada dado que las pérdidas totales exceden el cuantil 100p de la distribución de X. Para distribuciones arbitrarias se puede escribir CVaRp(X) como:

donde F(x) es la función de distribución acumulada de X. Además, para distribuciones continuas se puede usar la función de densidad para escribir lo anterior como:

Así, el CVaR se puede ver como el promedio de todos los valores VaR sobre el nivel de confianza p. Además CVaR puede escribirse como:

donde e(x_p) es la media de excesos de la función de pérdidas. ⁷

El paradigma bayesiano

En el análisis estadístico existen dos paradigmas: el frecuentista y el bayesiano. La diferencia fundamental se relaciona con la definición de probabilidad. Los frecuentistas señalan que la probabilidad de un evento es el límite de su frecuencia relativa en el largo plazo, mientras que los bayesianos sostienen que la probabilidad es subjetiva, un nivel de creencias que se actualiza con la incorporación de nueva información; la probabilidad subjetiva (creencias) fundamentadas en una base de conocimientos constituye la probabilidad a priori; la probabilidad a posteriori representa la actualización de las creencias.

Un tomador de decisiones bayesiano aprende y revisa sus creencias con base en la nueva información que tenga disponible. Desde este punto de vista, las probabilidades son interpretadas como niveles de creencias. Por lo tanto, el proceso de aprendizaje bayesiano consiste en estar revisando y actualizando probabilidades. El teorema de Bayes es el medio formal para poner en práctica lo anterior. ⁸

Teorema de Bayes

El teorema de Bayes es una regla que puede ser utilizada para actualizar creencias con base en nueva información (por ejemplo, datos observados). Si se denota por E como la evidencia y se supone que un experto cree que se puede asociar con una probabilidad P(E), el teorema de Bayes (TB) dice que después de observar los datos, D, las creencias sobre E son ajustadas de acuerdo con la siguiente expresión:

donde

• 1)

  P (D |E) es la probabilidad condicional de los datos, dado que la evidenciaa priori,D, es cierta.

• 2)

  P (D) es la probabilidad incondicional de los datos,P(D) > 0; también se puede expresar como:

  

La probabilidad de E, antes de tener los datos P(E), es llamada probabilidad a priori, una vez actualizada P(E|D) es denominada probabilidad a posteriori.

Se reescribe la forma continua del TB de la siguiente manera:

donde θ es un parámetro desconocido por estimar, y es un vector de observaciones, registradas, π (θ) es una distribución a priori que depende de uno o más parámetros, denominados hiper-parámetros, L(θ | y) es la función de verosimilitud para θ y P(θ | y)es la distribución a posteriori de θ (actualización de la a priori). Dos preguntas surgen de lo anterior: ¿cómo traducir la información a priori en su forma analítica π (θ) ?, ¿qué tan sensible es la inferencia a posteriori, a la selección de la a priori? Cabe destacar que estas preguntas han sido un amplio tema de interés en la literatura bayesiana⁹.

Inferencia bayesiana

La distribución a posteriori —una combinación de datos y de la distribución a priori— del parámetro o vector de parámetros θ, dada la información y, denotada por P(θ | y), es obtenida a través de la aplicación del teorema de Bayes y contiene la información relevante sobre el parámetro desconocido.

Redes bayesianas

Una red bayesiana (RB) es una gráfica que representa el dominio de las variables de decisión, las relaciones cuantitativas y cualitativas de éstas y sus medidas de probabilidad; asimismo, puede incluir funciones de utilidad que representan las preferencias del tomador de decisiones.

Una importante característica de las RB es su forma gráfica, lo cual permite representar en una forma visual complicados razonamientos probabilísticos. Otro aspecto por destacar es su parte cuantitativa porque permiten incorporar elementos subjetivos como lo son la opinión de expertos, así como probabilidades basadas en datos estadísticos. Tal vez la característica más importante es que son una representación directa del mundo real y no un proceso de razonamiento.

Las redes bayesianas son gráficas dirigidas acíclicas (GDA). Una gráfica es definida como un conjunto de nodos unidos por arcos. Si entre cada par de nodos hay una relación de precedencia representada por arcos, entonces la gráfica es dirigida. Un ciclo es una trayectoria que inicia y termina en el mismo nodo. Una trayectoria es una serie de nodos contiguos conectados por arcos dirigidos. Cada nodo en una RB se asocia con un conjunto de tablas de probabilidades. Los nodos representan las variables de interés, las cuales pueden ser discretas o continuas. Una red causal, de acuerdo con Pearl (2000), es una RB con la propiedad adicional de que los nodos padres son las causas dirigidas. ¹⁰

Algoritmos para cálculo de inferencia en redes bayesianas

Una red bayesiana es empleada básicamente para inferencia a través del cálculo de las probabilidades condicionales dada la información disponible hasta el momento para cada nodo (creencias). Existen dos clases de algoritmos para el proceso de inferencia: el primero genera una solución exacta y el segundo produce una solución aproximada con alta probabilidad. Entre los algoritmos de inferencia exacta se tienen, por ejemplo, polytree, clique tree, junction tree, algorithms of variable elimination y method of Pear.

El uso de soluciones aproximadas es motivado por el crecimiento exponencial de tiempo de procesamiento requerido para soluciones exactas, de acuerdo con Guo y Hsu (2002) este tipo de algoritmos puede agruparse en stochastic simulation, model simplification methods, search based methods y loopy propagation methods; el más conocido es el de simulación estocástica que se divide en importance sampling algorithms y Markov Chain Monte Carlo (MCMC) methods.

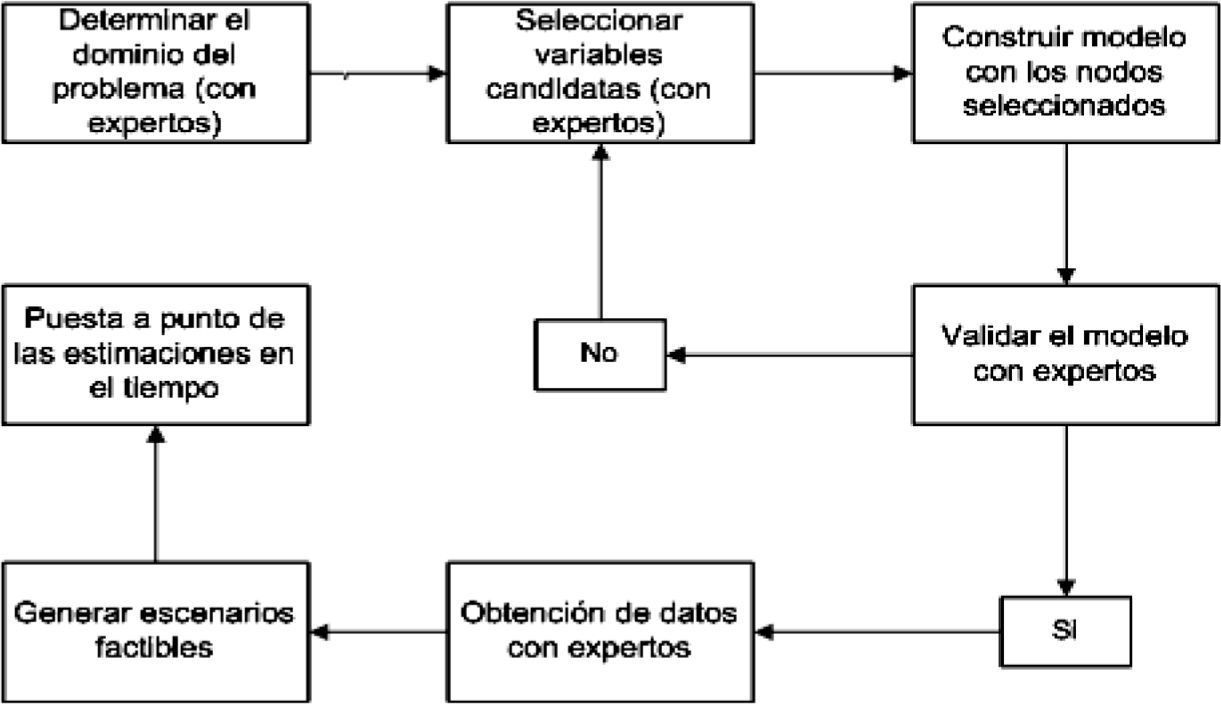
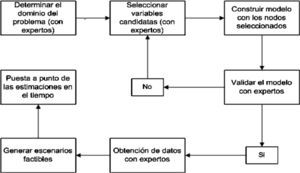
Construcción de una red bayesiana para el proceso de bancarización de Procampo

En la gráfica 1 se muestra un flujograma simple para construir una RB. El primer paso es definir el dominio del problema donde se especifique el propósito de la RB. Posteriormente se identifican las variables o nodos importantes en el dominio del problema. Después se representa en forma gráfica la interrelación entre nodos o variables. El modelo resultante debe ser validado por los expertos en el tema. En caso de haber desacuerdo entre ellos se regresa a uno de los pasos anteriores hasta alcanzar el consenso. Los últimos tres pasos son incorporar la opinión de los expertos (referida como la cuantificación de la red), crear escenarios factibles con la red (aplicaciones de redes) y poner a punto las estimaciones en el tiempo (mantenimiento de la red).

Gráfica 1.

Diagrama de causa-efecto

Problemática

Los principales problemas a que se enfrenta un administrador de riesgo que emplea RB son ¿cómo implementar una red bayesiana?, ¿cómo modelar su estructura?, ¿cómo cuantificarla?, ¿cómo utilizar datos subjetivos (de expertos) u objetivos (estadísticos) o ambos?, ¿qué instrumentos se deben utilizar para obtener mejores resultados?, ¿cómo validar el modelo? Las respuestas a estos cuestionamientos, en su momento, se abordarán en la aplicación del modelo bayesiano.

El objetivo principal de la aplicación consiste en elaborar una guía para implementar una RB para medir el riesgo operacional en el proceso de bancarización de Procampo. Asimismo, se pretende generar una medida consistente del capital económico necesario para hacer frente a pérdidas derivadas de eventos de riesgo operacional.

Alcances de la aplicación

El caso de estudio se enfoca en el análisis de los eventos de riesgo operacional que se presentaron durante la dispersión de recursos para el pago de apoyos de Procampo por parte de los bancos contratados para este servicio. Una vez identificados los factores de riesgo asociados a cada fase del proceso, se definen los nodos que formaran parte de la red bayesiana y que son variables aleatorias que pueden ser discretas o continuas, las cuales tienen asociadas distribuciones de probabilidad.

Para el caso de que se tengan datos históricos relacionados con los nodos (variables aleatorias) se les ajusta una función de distribución; en caso contrario, se recurre a los expertos o fuentes externas para determinar las probabilidades de ocurrencia o el parámetro de alguna función de probabilidad conocida. Los datos disponibles son quincenales y abarcan el periodo de 2008 a 2011; se calcula la máxima pérdida esperada quincenal derivada de fallas en el proceso de pagos de Procampo por trasferencia electrónica.

Construcción y cuantificación del modelo

Los nodos seleccionados son conectados con arcos dirigidos (con flechas) para formar una estructura que muestra la dependencia o relación causal entre éstos. La RB se divide en dos redes: una para modelar la frecuencia y la otra para la severidad. Lo anterior facilita su análisis, pues una vez obtenidos los resultados por separado se agregan a través del método de simulación Monte Carlo para obtener la pérdida esperada.

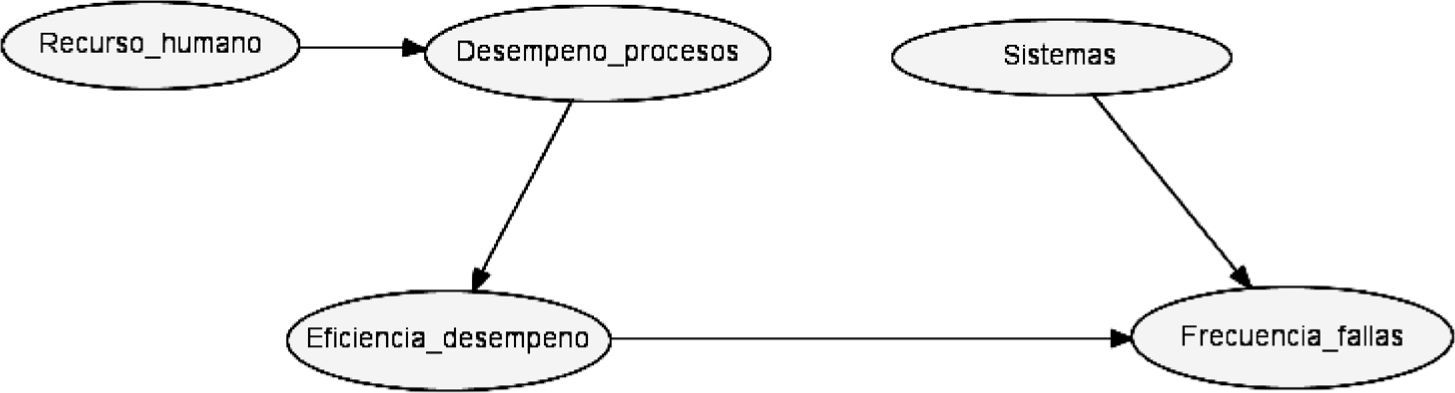
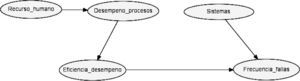
Frecuencia

La red completa de la frecuencia se muestra en la gráfica 3, que se genera a partir del análisis de factores de riesgo vinculados con la bancarización. Estos factores se presentan durante el proceso de dispersión de recursos (transferencias electrónicas a las cuentas de beneficiarios) que se opera a través del sector bancario. Los riesgos se clasificaron de la siguiente manera:

• a)

  Sistemas

  • I.

    Cancelación del servicio

  • II.

    Causa indefinida

  • III.

    Cuenta bloqueada

• b)

  Recursos humanos

  • I.

    Insuficiencia de fondos

  • II.

    Cuenta inexistente

  • III.

    Cuenta no pertenece al banco receptor

• c)

  Procesos

  • I.

    Cuenta cancelada

  • II.

    Cuenta en otra divisa

  • III.

    Cuenta inexistente

Gráfica 3.

Red para frecuencia de fallas

Severidad

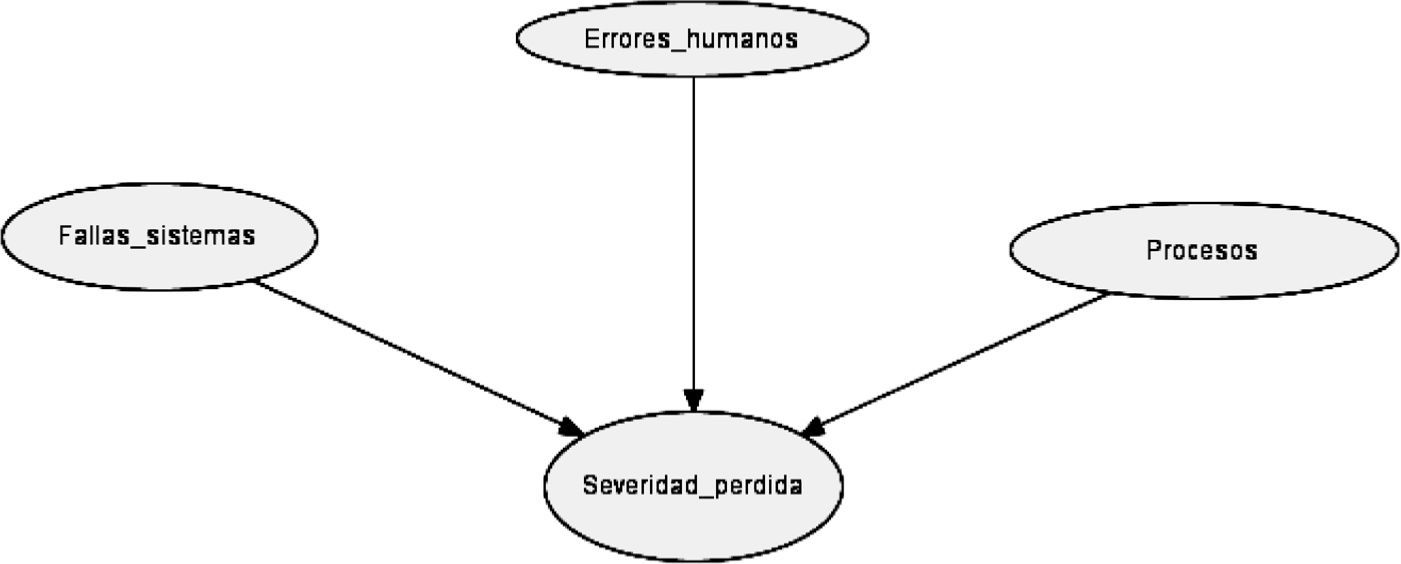
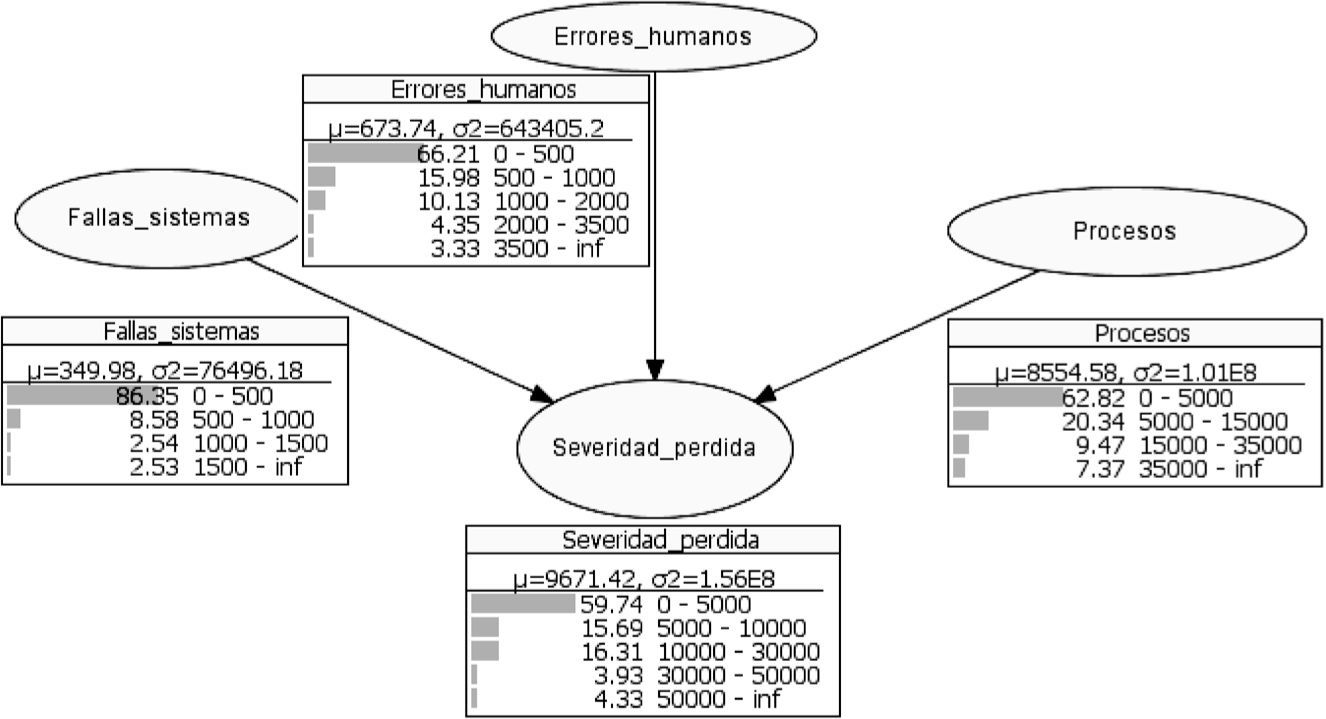
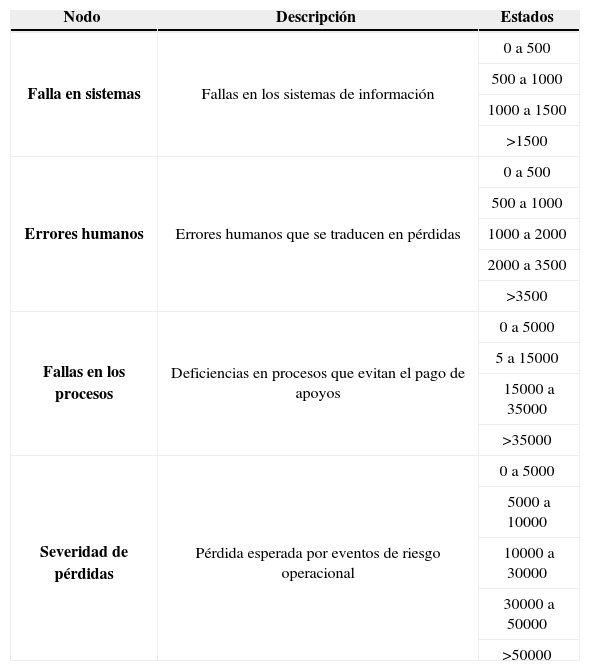
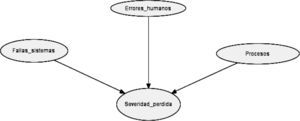
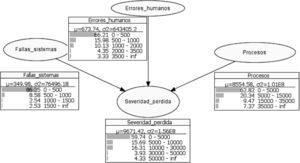
La red de la severidad se muestra en la gráfica 4, que se integra por cuatro nodos, aunque requiere una cantidad importante de probabilidades. El nodo etiquetado como severidad de pérdida es el costo adicional que se incurre por no realizar las trasferencias de manera exitosa, lo que obliga a pagar a través de cheques; los otros nodos se consideran variables informativas.

Gráfica 4.

Red para severidad de fallas

A continuación se describen las características y estados de cada nodo de las redes de severidad y frecuencia respectivamente.

Cuadro 2.

Nodos de la red de severidad

Nodo	Descripción	Estados
Falla en sistemas	Fallas en los sistemas de información	0 a 500
		500 a 1000
		1000 a 1500
		>1500
Errores humanos	Errores humanos que se traducen en pérdidas	0 a 500
		500 a 1000
		1000 a 2000
		2000 a 3500
		>3500
Fallas en los procesos	Deficiencias en procesos que evitan el pago de apoyos	0 a 5000
		5 a 15000
		15000 a 35000
		>35000
Severidad de pérdidas	Pérdida esperada por eventos de riesgo operacional	0 a 5000
		5000 a 10000
		10000 a 30000
		30000 a 50000
		>50000

Cuadro 3.

Nodos de la red de frecuencia

Nombre nodo	Descripción del nodo	Estados
Recurso humano	Errores humanos que se traducen en no pagos	Insuficiencia de recursos en cuenta
		Cuenta no pertenece al banco receptor
		Orden de no pagar al emisor
Desempeño de procesos	Fallas de procesos de pago	Cancelación de cuenta
		Cuenta en otra divisa
		Cuenta inexistente
Eficiencia en desempeño	Eficiencia del desempeño de personas y procesos	Excelente
		Promedio
		Mal
Fallas en sistemas	Fallas en los sistemas que procesan las órdenes de pago	Cancelación del servicio
		Causa indefinida
		Bloqueo de cuentas
Frecuencia de fallas	Número de fallas en un periodo de tiempo.Retrasos, pagos incorrectos, pagos mal direccionados, sin pago, pagos duplicados	0 a 500
		500 a 1000
		1000 a 2000
		2000 a 3000
		Más de 3000

Cuantificación de la red bayesiana

Para cuantificar las redes bayesianas identificadas en la sección anterior, se utilizaron tanto datos objetivos como subjetivos. A continuación se describen las herramientas o técnicas que se emplearon para obtener, codificar y cuantificar los tipos de datos.

• •

  Análisis estadístico de la red de frecuencia

En este apartado se analiza cada nodo de la red de frecuencia; para el caso de nodos con información histórica disponible, se ajusta¹¹ la distribución de probabilidades correspondiente y se calculan las probabilidades requeridas. Cuando no se cuenta con datos suficientes se obtiene la información de los expertos o de fuentes externas. Los errores ocasionados por el personal interno en el desempeño de sus funciones denotado por el nodo Recurso humano tiene la siguiente distribución de probabilidades:

Cuadro 4.

Probabilidades Recurso humano

Probabilidades
Insuficiencia de recursos	0.85
Cuenta no pertenece al emisor	0.1
Orden de no pagar al emisor	0.05

Fuente: Elaboración propia con información de expertos o externa.

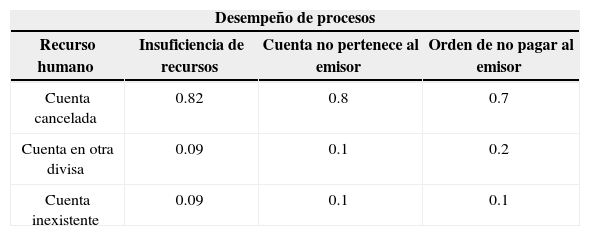
El buen funcionamiento de las instituciones bancarias depende del desempeño de sus procesos; la madurez de éstos se asocia a sistemas de gestión de la calidad en el nivel proceso y producto. Las probabilidades condicionales del nodo etiquetado como Desempeño de procesos son las siguientes:

Cuadro 5.

Probabilidades Desempeño de procesos

Desempeño de procesos
Recurso humano	Insuficiencia de recursos	Cuenta no pertenece al emisor	Orden de no pagar al emisor
Cuenta cancelada	0.82	0.8	0.7
Cuenta en otra divisa	0.09	0.1	0.2
Cuenta inexistente	0.09	0.1	0.1

Fuente: Elaboración propia con información de expertos o externa.

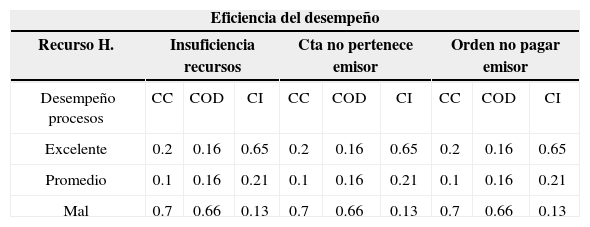
Con respecto a las probabilidades del nodo etiquetado como Eficiencia del desempeño son condicionadas a las probabilidades de los nodos Desempeño de procesos y Recurso humano, con lo cual se obtiene la siguiente tabla de probabilidades condicionales:

Cuadro 6.

Probabilidades condicionales Eficiencia del desempeño

Eficiencia del desempeño
Recurso H.	Insuficiencia recursos			Cta no pertenece emisor			Orden no pagar emisor
Desempeño procesos	CC	COD	CI	CC	COD	CI	CC	COD	CI
Excelente	0.2	0.16	0.65	0.2	0.16	0.65	0.2	0.16	0.65
Promedio	0.1	0.16	0.21	0.1	0.16	0.21	0.1	0.16	0.21
Mal	0.7	0.66	0.13	0.7	0.66	0.13	0.7	0.66	0.13

Fuente: Elaboración propia con información de expertos y externa.

Existe una probabilidad condicional del 20% —dado que por error del recurso humano no se tengan recursos presupuestales suficientes y que por proceso se cancelé la cuenta— de que el desempeño sea excelente. Las otras probabilidades condicionales se leen de manera similar.

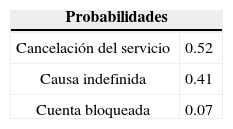
Con respecto al nodo etiquetado como Sistemas, son errores generados por los sistemas de información del banco que tienen la siguiente distribución de probabilidades que se calcularon con información cualitativa proporcionada por los expertos en los sistemas de pago de Aserca.

Cuadro 7.

Probabilidades Sistemas

Probabilidades
Cancelación del servicio	0.52
Causa indefinida	0.41
Cuenta bloqueada	0.07

Fuente: Elaboración propia con información de expertos o externa.

Finalmente, para el nodo objetivo Frecuencia de fallas, se supone una función de distribución binomial negativa con probabilidad de éxito p=0.51 y límite de éxitos igual a 1.000; este supuesto es consistente con la práctica financiera y estudios del riesgo operacional que muestran que el número de fallas usualmente siguen una distribución de Poisson o una binomial negativa. Para estimar el valor de los parámetros se recurrió a los expertos y se complementó con resultados del análisis de los otros nodos de la red de frecuencia.

• •

  Análisis estadístico de la red de severidad

En este apartado se analiza cada nodo de la red de severidad. Para el caso de nodos con información histórica disponible se ajusta la distribución de probabilidad correspondiente y se calculan las posibilidades requeridas. Cuando no se cuenta con datos suficientes se obtiene la información de los expertos o externa.

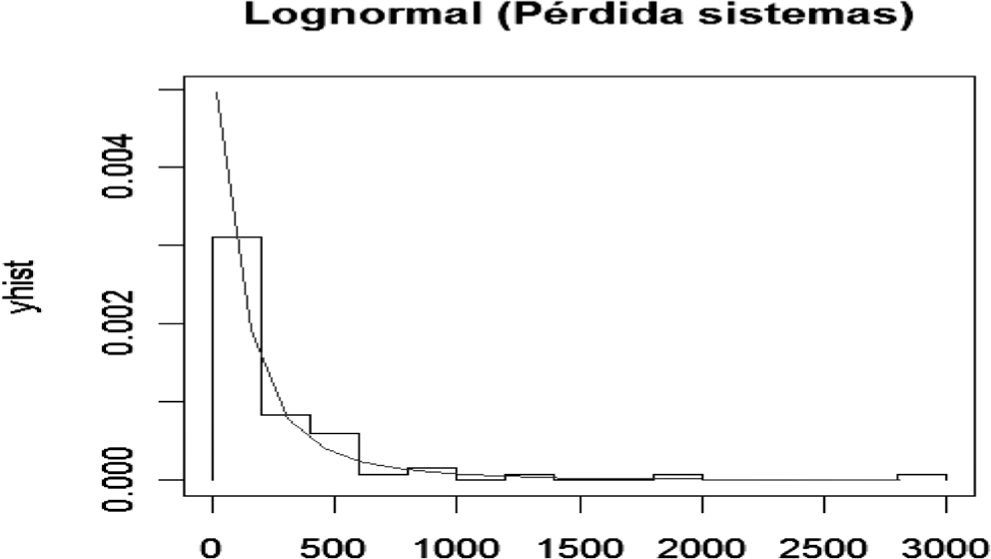
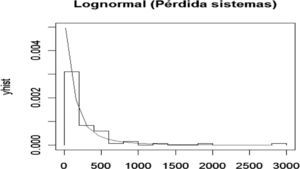
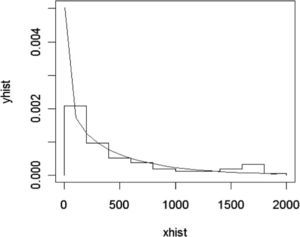
El nodo Falla en sistemas presenta la siguiente distribución de frecuencias y densidad exponencial ajustada para las pérdidas ocasionadas por fallas en los sistemas.

Para determinar la bondad del ajuste se realizó la prueba de Kolmogorov-Smirnov con los siguientes valores: D = 0.0811, p-value = 0.77. En otras palabras se acepta la hipótesis nula de que la muestra proviene de una Lognormal. Por lo tanto, se calcula la tabla de probabilidad para este nodo de la red de severidad misma que constituye las probabilidades a priori.

Cuadro 8.

Probabilidades Falla en sistema

Falla en sistema
0 a 500	0.86
500 a 1000	0.09
1000 a 1500	0.025
>1500	0.025

A partir del cuadro se ve que existe una probabilidad del 86% de que se pierdan hasta 500 pesos por fallas en los sistemas, 9% de probabilidad de que se pierdan entre 500 y 1 000 pesos, 2.5% de la pérdida está entre 1 000 y 1 500 pesos, y 2.5% de probabilidad de que la pérdida sea mayor a 1 500 pesos en un periodo de 15 días.

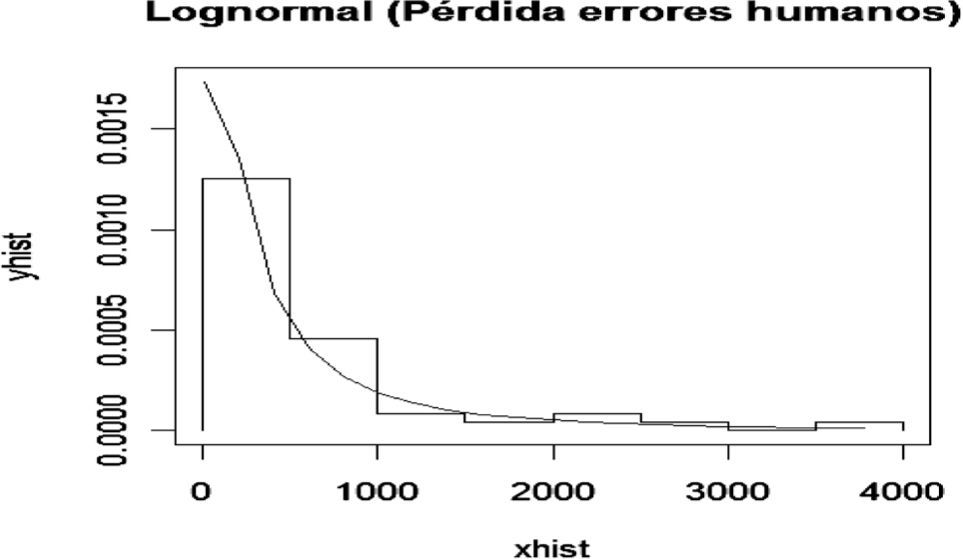
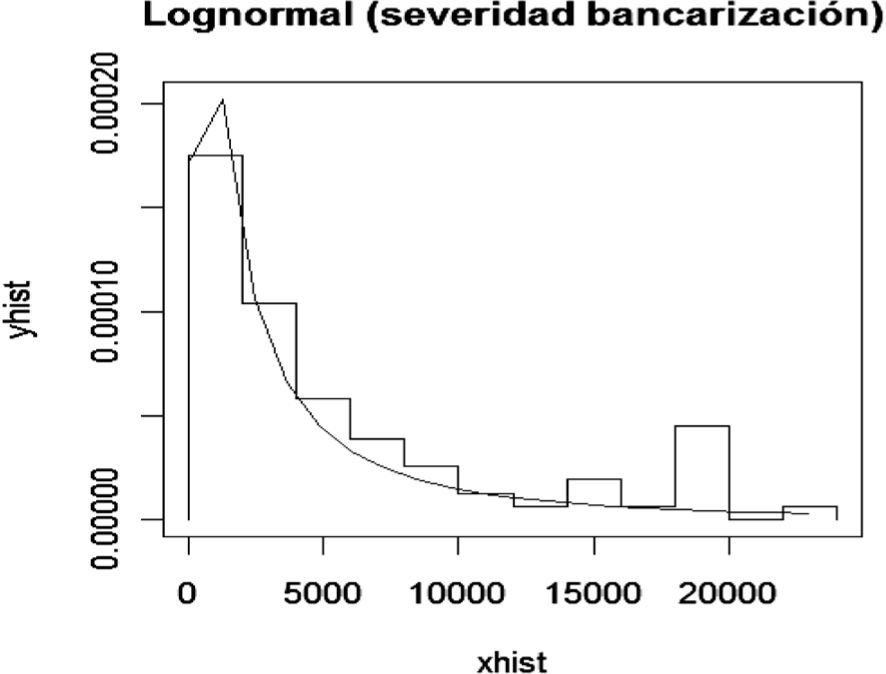
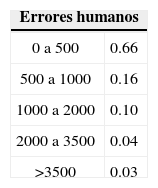
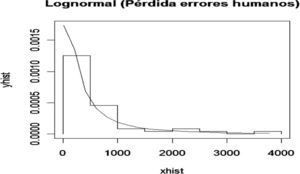
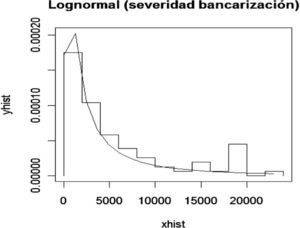
A continuación se analiza el nodo Errores humanos, el cual presenta la siguiente distribución de frecuencia y densidad Lognormal ajustada para pérdidas ocasionadas por errores humanos.

Para determinar la bondad del ajuste se realizó la prueba K-S con los siguientes resultados: D = 0.1064 y p-value = 0.6486. De esta manera se acepta la hipótesis nula de que la muestra proviene de una Lognormal. Por lo tanto, se calculan las probabilidades para este nodo de la red de severidad, las cuales constituyen las probabilidades a priori.

Cuadro 9.

Probabilidades Errores humanos

Errores humanos
0 a 500	0.66
500 a 1000	0.16
1000 a 2000	0.10
2000 a 3500	0.04
>3500	0.03

A partir del cuadro se observa que existe una probabilidad del 66% de que se pier-dan menos de 500 pesos por fallas en errores humanos, 16% de probabilidad de que se pierdan entre 500 y 1 000 pesos, 10% de que la pérdida esté entre 1 000 y 2 000 pesos, 4% de que la pérdida esté entre 2 000 y 3 500 pesos, y 3% de probabilidad de que la pérdida sea mayor a 3 500 pesos quincenales.

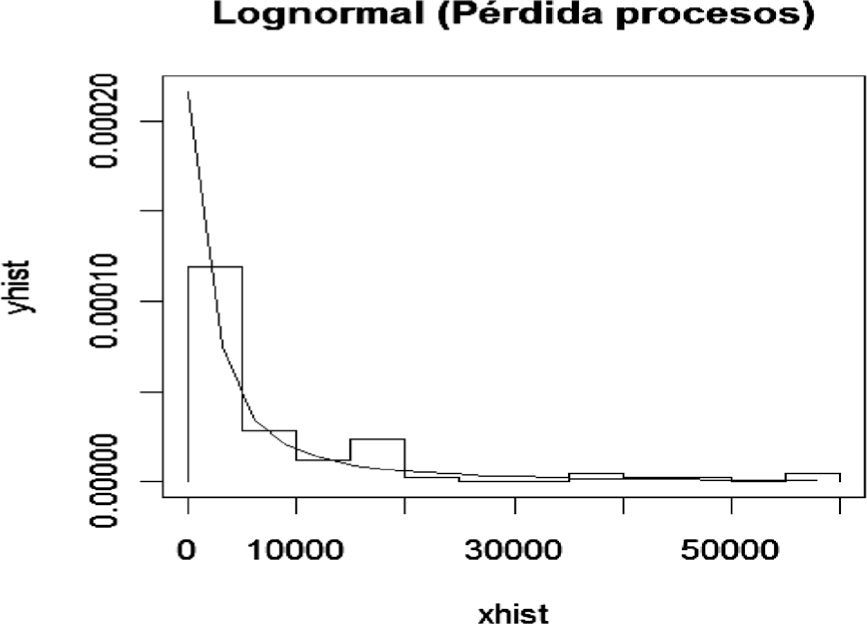
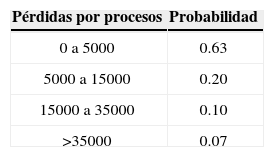
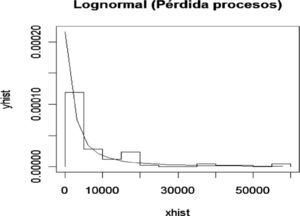
Para el nodo Procesos se presenta la siguiente distribución de frecuencias y densidad Lognormal ajustada para las pérdidas ocasionadas por fallas en los procesos o procedimientos, entre otros.

Para determinar la bondad del ajuste se realizó la prueba K-S que produce los siguientes valores: D = 0.0799, p-value = 0.6575. En otras palabras se acepta la hipótesis nula de que la muestra proviene de una Lognormal; por lo tanto, se calcula la probabilidad para este nodo de la red de severidad que constituye las probabilidades a priori.

Cuadro 10.

Procesos

Pérdidas por procesos	Probabilidad
0 a 5000	0.63
5000 a 15000	0.20
15000 a 35000	0.10
>35000	0.07

Fuente: Elaboración propia con información de los expertos.

De acuerdo con los datos generados existe una probabilidad del 63% de que se pierdan menos de 5 000 pesos por eventos derivados en fallas en procesos, 20% de probabilidad de que se pierdan entre 5 000 y 15 000 pesos, 10% de que se pierdan entre 15 000 y 35 000 pesos, y 7% de probabilidad de que la pérdida sea mayor a 35 000 pesos en una quincena.

Por último, el nodo objetivo Severidad de la pérdida representa las pérdidas asociadas con los nodos Fallas en sistemas, Errores humanos y Eventos en procesos. Para el cálculo de la tabla de probabilidades condicional se utilizó una función de distribución Lognormal con parámetros media de log(x)=8.13 y desviación estándar de 1.57. A continuación se generan las probabilidades a posteriori para lo cual se utilizan técnicas de inferencia bayesiana.

Probabilidades a posteriori

Una vez analizados cada uno de los nodos (variables aleatorias continuas o discretas) de las redes tanto de frecuencia como de severidad y asignadas las correspondientes funciones de distribución de probabilidades, se generan las probabilidades a posteriori; para ello se utilizan técnicas de inferencia para redes bayesianas, en particular el algoritmo denominado junction tree. ¹² Las probabilidades a posteriori para los nodos de la red de frecuencia que tienen al menos un padre¹³ son las siguientes.

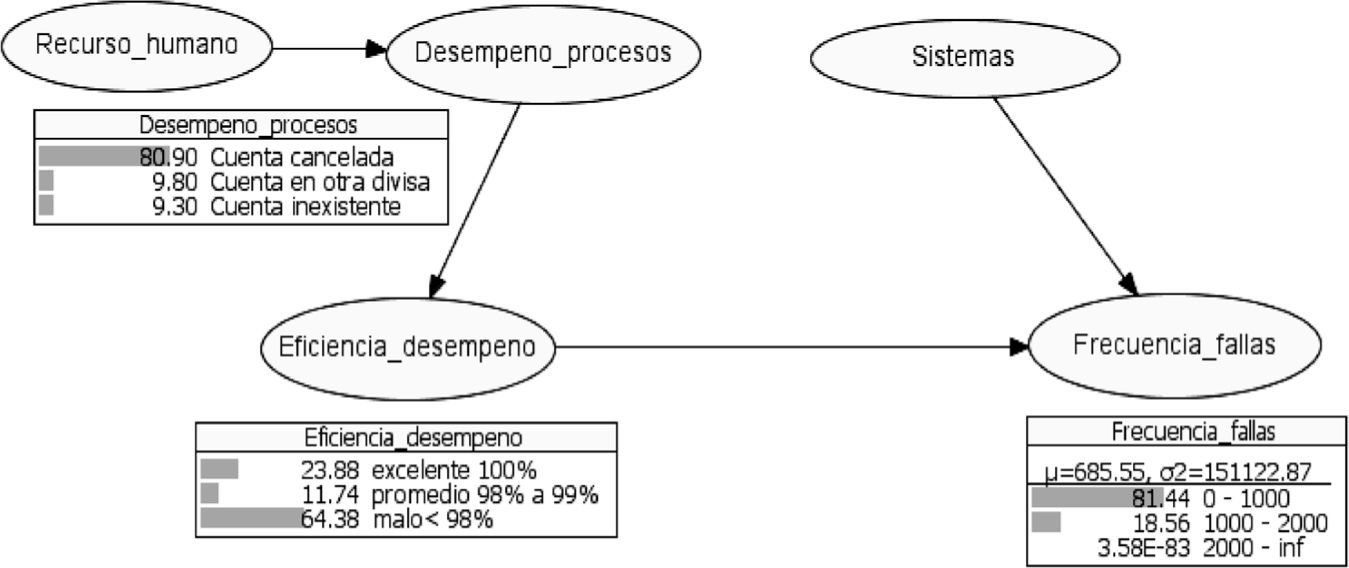
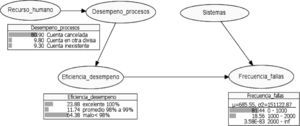
Los resultados del nodo Eficiencia del desempeño muestran que existe una probabilidad del 24% de tener un desempeño excelente. Asimismo, una probabilidad del 12% de que se presenten problemas menores con un desempeño medio y una probabilidad del 64% de que el desempeño sea deficiente. Las probabilidades calculadas están condicionadas por el desempeño de los procesos.

En cuanto al nodo Desempeño de procesos, la probabilidad de que existan cuentas canceladas es del 81%, de que la cuenta esté en otra divisa es del 10% y de que la cuenta no exista es del 9%; todo esto condicionado a que existan fallas en el recurso humano.

Por último, la distribución de probabilidades del nodo de interés Frecuencia de fallas muestra una probabilidad del 81% de que se presenten menos de 1 000 fallas, una probabilidad del 19% de que tengan entre 1 000 y 2 000 fallas, y una probabilidad nula de que se presenten más de 2 000 fallas; dichas probabilidades están condicionadas a los equívocos de sistemas y de la eficiencia de los procesos y confiabilidad de las personas.

Para el cálculo de las probabilidades del nodo de interés se utilizó una binomial negativa con parámetros número de éxitos=1000 y probabilidad de éxito p = 0.51, lo cual es consistente con la evidencia empírica de que la frecuencia de eventos de riesgo operacional tienen un ajuste adecuado bajo esta distribución. ¹⁴ Para el caso de la red de severidad se tiene las siguientes probabilidades a posteriori.

Las pérdidas originadas por errores humanos en promedio son de 673 pesos quincenales; por lo que respecta a las pérdidas por eventos en los procesos son de 8 554 pesos quincenales en promedio. En cuanto a fallas en los sistemas en promedio se tiene una pérdida quincenal de 350 pesos. La distribución de probabilidades del nodo de interés Severidad de pérdida muestra una probabilidad del 59.7% de que la pérdida esté entre 0 y 5 000 pesos, una probabilidad del 15.69% de que esté entre 5 000 y 10 000 pesos, una probabilidad del 16.31% de que esté entre 10 000 y 30 000 pesos, una probabilidad del 3.93% de que esté entre 30 000 y 50 000 pesos, y una probabilidad del 4.33% de que la pérdida sea mayor a 50 000 pesos quincenales.

Cálculo del Valor en Riesgo Operacional (OpVaR)

Una vez realizada la inferencia bayesiana para obtener las distribuciones de probabilidad a posteriori de la frecuencia y severidad de pérdidas, se integran ambas distribuciones para generar la distribución de pérdidas potenciales (se utilizó una binomial negativa para la frecuencia y una Lognormal para la severidad) a través de un proceso de simulación Monte Carlo. ¹⁵

Para el cálculo del OpVar se ordenan los valores obtenidos para las pérdidas esperadas en orden descendente y se calculan los percentiles correspondientes:

Cuadro 11.

Percentiles para modelo bayesiano

Posición	Pérdida(pesos)	Porcentaje
5	14 747.69	100.00%
21	14 733.59	97.90%
25	14 691.29	95.80%
24	14 493.90	89.50%
40	14 493.90	89.50%
45	14 493.90	89.50%
35	14 465.70	87.50%
4	14 451.60	85.40%
44	14 282.41	83.30%
17	14 197.82	81.20%
37	14 155.52	79.10%
10	14 028.63	77.00%
18	13 972.23	72.90%
22	13 972.23	72.90%
12	13 958.13	70.80%
9	13 873.54	68.70%
6	13 788.94	66.60%
27	13 760.75	64.50%
49	13 746.65	62.50%
47	13 732.55	60.40%
38	13 718.45	58.30%
2	13 633.85	52.00%
14	13 633.85	52.00%
30	13 633.85	52.00%
19	13 577.46	50.00%
26	13 549.26	47.90%
36	13 535.16	45.80%
3	13 506.96	43.70%
31	13 492.86	41.60%
34	13 464.66	39.50%
15	13 394.17	35.40%
39	13 394.17	35.40%
41	13 365.97	33.30%
13	13 337.77	31.20%
46	13 210.88	29.10%
11	13 196.78	27.00%
1	13 041.69	25.00%
7	12 999.39	20.80%
16	12 999.39	20.80%
48	12 971.20	18.70%
20	12 943.00	14.50%
33	12 943.00	14.50%
43	12 886.60	12.50%
23	12 858.40	10.40%
29	12 816.10	8.30%
32	12 703.31	6.20%
8	12 238.04	4.10%
42	12 012.45	2.00%
28	11 941.96	0.00%

En consecuencia, si se considera calcular el OpVaR con un nivel de confianza del 96%, se tiene una máxima pérdida esperada de 14 691.29 pesos quincenales por riesgo operacional, relacionados con el proceso de bancarización de Procampo.

Validación del modelo bayesiano

Para validar los resultados del modelo bayesiano, se estiman con modelos clásicos la distribución de probabilidades para la frecuencia y la severidad. Posteriormente, a través de simulación Monte Carlo, se integran ambas distribuciones para obtener la distribución de pérdidas esperadas. Por último, se calcula el riesgo operacional con la distribución de pérdidas estimada en forma clásica y se comparan los resultados con los obtenidos con el modelo bayesiano.

Gráfica 8.

Probabilidades a posteriori para la red de frecuencia

Gráfica 9.

Probabilidades a posteriori para la red de severidad

Análisis clásico de frecuencia

Se considera el número de fallas que quincenalmente se presentan en la dispersión de los apoyos que se realizan a través de los principales bancos en México y se le ajusta una distribución binomial negativa con parámetro μ=477, según se muestra en la siguiente gráfica.

La prueba Kolmogorov-Smirnov tuvo los siguientes resultados: D = 0.058, p-value = 0.95, lo que implica aceptar la hipótesis nula de que la muestra proviene de una distribución binomial negativa.

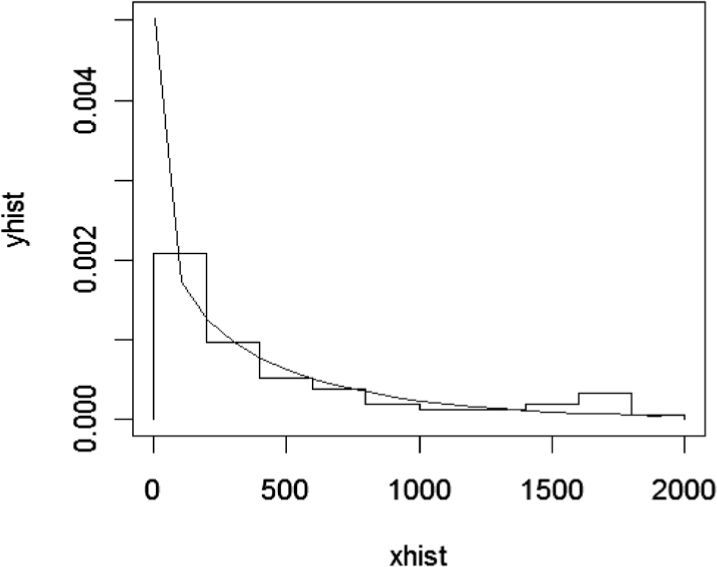
Análisis clásico de severidad

Como pérdidas se considera el monto quincenal que se paga por reexpedición del cheque debido a que no se realizó la trasferencia electrónica a la cuenta del beneficiario y se le ajusta una distribución Lognormal con parámetro media=7.58 y desviación estándar=1.53, según se muestra en la siguiente gráfica.

Se realizó la prueba K-S con los siguientes resultados: D = 0.098, p-value = 0.44. El p-value es mayor al 5%; por tanto, se acepta que la muestra proviene de una Lognormal.

Cálculo del valor en riesgo operacional con el modelo clásico

A través de Monte Carlo se integran las distribuciones clásicas de frecuencia y severidad para generar la distribución de pérdidas potenciales (se utilizó una binomial negativa para la frecuencia y una Lognormal). Para el cálculo del OpVar se ordenan los valores obtenidos para las pérdidas esperadas en orden descendente y se calculan los percentiles correspondientes; a continuación se muestran los resultados con niveles de confianza mayor a 96.

Cuadro 14.

Percentiles para modelo clásico

Posición	Pérdida(pesos)	Porcentaje
5	5 672.37	100.00%
21	5 666.95	97.90%
25	5 650.68	95.80%
24	5 574.76	89.50%
40	5 574.76	89.50%
45	5 574.76	89.50%
35	5 563.91	87.50%
4	5 558.49	85.40%
44	5 493.41	83.30%
17	5 460.88	81.20%
37	5 444.61	79.10%
10	5 395.80	77.00%
18	5 374.11	72.90%
22	5 374.11	72.90%
12	5 368.69	70.80%
9	5 336.15	68.70%
6	5 303.61	66.60%
27	5 292.77	64.50%
49	5 287.34	62.50%
47	5 281.92	60.40%
38	5 276.50	58.30%
2	5 243.96	52.00%
14	5 243.96	52.00%
30	5 243.96	52.00%
19	5 222.27	50.00%
26	5 211.42	47.90%
36	5 206.00	45.80%
3	5 195.15	43.70%
31	5 189.73	41.60%
34	5 178.89	39.50%
15	5 151.77	35.40%
39	5 151.77	35.40%
41	5 140.93	33.30%
13	5 130.08	31.20%
46	5 081.27	29.10%
11	5 075.85	27.00%
1	5 016.20	25.00%
7	4 999.93	20.80%
16	4 999.93	20.80%
48	4 989.08	18.70%
20	4 978.24	14.50%
33	4 978.24	14.50%
43	4 956.55	12.50%
23	4 945.70	10.40%
29	4 929.43	8.30%
32	4 886.05	6.20%
8	4 707.09	4.10%
42	4 620.33	2.00%
28	4 593.21	0.00%

Si se calcula el OpVaR con un nivel de confianza del 96%, se tiene una máxima pérdida esperada de 5 650 pesos quincenales por riesgo operacional con el modelo clásico. Los resultados anteriores muestran que el OpVaR calculado con el modelo bayesiano es mayor al calculado con el modelo clásico, lo cual se explica por la causalidad entre los distintos factores de riesgo, la cual no está considerada en el modelo clásico. Con base en los parámetros (media) de las funciones de distribución calculadas con el modelo bayesiano y el modelo clásico tenemos los siguientes resultados.

Modelo	Frecuencia promedio (F)	Severidad promedio (S)	Pérdida promedio por evento (S/F)
Bayesiano	685	9671	14.11
Clásico	477	Exp(7.58)=1958	4.1

La pérdida promedio por evento obtenida con el modelo bayesiano es de 14 pesos, lo que se aproxima más al costo de reexpedición de un cheque cuando no se puede realizar la trasferencia electrónica de recursos a los beneficiarios; en este sentido, el resultado es consistente.

Los factores de riesgo relacionados con los procesos cuenta cancelada, cuenta en otra divisa y cuenta inexistente se traducen en un mal desempeño del proceso con probabilidad del 64% (ver gráfica 8), lo que genera pérdidas quincenales del orden de 8 554 pesos quincenales (ver gráfica 9); para mitigar estos riesgos se proponen las siguientes acciones:

• •

  Mantener actualizado el padrón de beneficiarios.

• •

  Evitar en la medida de lo posible pagos con ambos medios (cheque y depósito).

• •

  Evitar la cancelación de cuentas de manera sistemática.

• •

  Sólo trabajar con cuentas abiertas por Sagarpa.

• •

  Incorporar la orden de pago como otro medio alternativo.

• •

  Concluir con el proceso de bancarización.

Conclusiones

El cambio de pago por cheque a transferencia electrónica en Procampo incrementó de manera considerable la transparencia y oportunidad de la entrega de los apoyos a los beneficiarios del programa, además de reducir los costos administrativos y operativos. Sin embargo, como quedó demostrado en el desarrollo de este trabajo, existen factores de riesgo asociados al proceso de dispersión de recursos que impiden la entrega de éstos a través del depósito en la cuenta de los beneficiarios, lo que obliga a realizar el pago a través de cheques, generándose un costo adicional por cada transacción no exitosa. Los factores de riesgo que más impactan están relacionados con actividades internas para el pago de apoyos, los cuales se pueden mitigar con mejoras a los procesos de dispersión y actualización del padrón, además de continuar con la política de bancarización.

En congruencia con lo anterior, este trabajo proporciona los elementos teóricos necesarios, así como una guía práctica para identificar, medir, cuantificar y administrar el RO en el proceso de dispersión de recursos (transferencia electrónica) con un enfoque bayesiano que mostró utilizar elementos más apegados a la realidad como probabilidades obtenidas de los expertos o externos cuando no existe información histórica, distribuciones de probabilidad específicas para cada factor de riesgo que pueden ser discretas o continuas, actualización de datos que se incorporan al modelo y la interrelación (causalidad) de los factores de riesgo a través de modelos de redes. Asimismo, se mostró que las redes bayesianas son una opción viable para administrar el riesgo operacional en un ambiente de incertidumbre y de información escasa o de calidad cuestionable. El capital requerido en riesgo operacional calculado se basa en el supuesto de interrelación (causa-efecto) entre factores de riesgo, lo cual es consistente con la realidad.

Las redes bayesianas están basadas en algoritmos eficientes de propagación de evidencias, que actualizan dinámicamente el modelo con datos actuales. Para el caso del objeto de estudio de este trabajo fue posible construir la RB y calcular el capital requerido para administrar el riesgo operacional combinando datos estadísticos, así como opiniones o juicios de los expertos o información externa.

El VaR calculado con el enfoque bayesiano es consistente en el sentido de Artzner (1998), pero también resume las complejas relaciones causales entre los diferentes factores de riesgo que derivan en un evento de riesgo operacional. En resumen, debido a que la realidad es mucho más compleja que eventos independientes idénticamente distribuidos, el enfoque bayesiano es una alternativa para modelar una realidad compleja y dinámica.