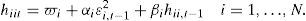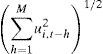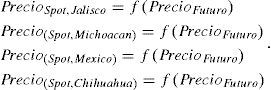Transmisión de precios futuros de maíz del Chicago Board of Trade al mercado spot mexicano

Resumen

En México, el uso del programa de coberturas de la Agencia de Servicios a la Comercialización y Desarrollo de Mercados Agropecuarios (ASERCA) es un instrumento que ha sido utilizado por los productores de maíz (principalmente blanco) para la adquisición de productos derivados en el Chicago Board of Trade (CBOT), cuyo subyacente es el maíz amarillo calidad US#2. En un entorno de alta volatilidad en los precios del maíz, los precios del CBOT deberían ajustarse con los precios spot domésticos para incentivar a los productores mexicanos a participar en el programa, sin embargo, mediante un análisis de volatilidad estocástica multivariante durante el periodo de 2007 a 2012, se mostró que el precio de mercado de futuros de maíz no se encuentra fuertemente relacionado con los precios registrados en algunos estados del país, por lo que se puede inferir que la cobertura mediante el programa ASERCA no cumple adecuadamente con su propósito de proteger a los agricultores nacionales que siembran maíz blanco, a pesar de que su uso se ha incrementado.

Abstract

In Mexico, the use of currency hedging program from the Agency Services for Marketing and Agricultural Market Development (ASERCA) is an instrument that has been used by producers of corn (mostly white), for the acquisition of derivatives in the Chicago Board of Trade (CBOT), whose underlying is yellow corn quality US#2. In an environment of high volatility in corn prices, CBOT prices should be adjusted with domestic spot prices to encourage Mexican producers to participate in the program, but through an analysis of multivariate stochastic volatility during the period 2007 to 2012, it showed that the market price of corn futures is not closely related to those recorded prices in some country states, so we can infer that the coverage by ASERCA program does not adequately serves the purpose of protecting domestic farmers growing white corn, although their use has increased.

Introducción

Una forma de identificar las interrelaciones entre diferentes mercados es mediante el estudio de transmisión de volatilidades. En el presente trabajo se estudió la integración existente en el precio spot de maíz blanco doméstico mexicano y el futuro de maíz amarillo #2 negociado en el Chicago Board of Trade (CBOT), bajo el contexto del programa «Apoyos y Servicios a la Comercialización Agropecuaria» (ASERCA) ofrecido por la Secretaría de Agricultura, Ganadería, Desarrollo Rural, Pesca y Alimentación (SAGARPA).

Es a través del programa ASERCA que los productores mexicanos de maíz tienen acceso a las coberturas de precio ofrecidas en el CBOT. El esquema de cobertura de precios surgió en 1993 ante la drástica caída en los precios del algodón y, por ende, la necesidad de garantizar un precio justo al productor, y es a partir de 1997 que las coberturas en el precio de maíz se hicieron a través de posiciones de opciones put y call.

Resulta interesante conocer la relación que existe entre los precios del maíz en el mercado spot mexicano y el de futuros de Chicago, considerando que los precios domésticos no son competitivos, de acuerdo con el SIAP¹ (2012), debido a que el maíz blanco producido en el país es aproximadamente un 35% más caro que el maíz amarillo; adicionalmente, la política agrícola que aplica Estados Unidos (principal país productor de maíz) se caracteriza por mantener altos subsidios a sus productores y bajos precios de exportación.

Como se mencionó antes, una manera de conocer las interrelaciones entre diferentes mercados es estudiar la transmisión de volatilidades entre ellos, para lo cual se pueden utilizar los modelos Generalised Autorregresive Conditionally Heterocedastic (GARCH) y GARCH multivariados (MGARCH). Los autores que proponen este tipo de modelación son Bollerslev (1990), Longin y Solnik (1995), Karoyi y Stulz (1996), Engle (2002), entre otros. Bawens, Hafner y Pierret (2013) utilizan un modelo GJR-GARCH para modelar la volatilidad dinámica y la correlación en la estructura de los futuros del European Energy Exchange index. Una revisión muy completa de la literatura sobre este tipo de modelos la ofrecen Bawens, Laurent y Rombouts (2006); desde el punto de vista de la econometría, un estudio similar desarrollan Asai, McAleer y Yu (2006) para modelos estocásticos; Bawens, Hafner y Laurent (2012) presentan un análisis y aplicaciones detalladas tanto de modelos GARCH multivariados como de modelos de volatilidad estocástica.

Respecto a la integración entre los mercados spot y futuro algunos estudios que ofrecen evidencia mediante modelos MGARCH pueden encontrarse en Ledebur y Schmitz (2009), Shawky, Marathe y Barrett (2003), Hernández e Ibarra (2011), Bekiros y Diks (2008).

El estudio de la relación precios spot y futuros de maíz blanco y amarillo, respectivamente, ha sido poco profundizado; un primer avance mediante la estimación de vectores autorregresivos lo ofrece Godínez (2006); posteriormente, con un modelo MGARCH lo hace Rapsomanikis (2011). La presente investigación presenta avances significativos empleando un modelo de volatilidad estocástica multivariante mediante el cual se logra medir la dinámica del programa ASERCA. El presente trabajo se desarrolla de la siguiente manera: en la primera sección se plantea la política de cobertura en el precio del maíz en México, también se describen las bases de operación del programa ASERCA, como medio de cobertura a los precios del maíz. En la segunda sección se establece brevemente el marco de referencia sobre los modelos de volatilidad estocástica, dando un mayor énfasis a los multivariantes. En la tercera sección se presentan los datos empleados para el estudio realizado. En la cuarta sección se plantea el desarrollo del análisis econométrico, empleando los modelos de volatilidad estocástica multivariante descritos en la segunda sección. Finalmente se presentan las conclusiones de este trabajo.

Política de cobertura en el precio del maíz en México

La naturaleza cíclica de la agricultura, su dependencia financiera y el comportamiento del clima propician que la producción de granos en México se desarrolle en un ambiente de incertidumbre, lo cual se ve reflejado en la tendencia de los precios de los granos y en los ingresos de los productores.

Al estar México dentro de un contexto de apertura comercial a partir de la década de los noventa, los productores de maíz mexicanos vieron afectados sus ingresos por la saturación del mercado en épocas de cosecha, pues provenían de una economía protegida, un régimen de precios establecido por el Estado y subsidios importantes a la producción que los alejaron del contexto internacional (Ochoa, 2011a).

Para aminorar estos efectos negativos, en 1991 el Gobierno Federal creó el programa ASERCA, teniendo como una de sus funciones principales el proteger los ingresos de los productores de movimientos adversos en los precios, a través de coberturas con instrumentos de mercados de futuros. Sin embargo, fue hasta 1996, cuando la Compañía Nacional de Subsistencias Populares (CONASUPO) dejó de regular los precios del maíz, que el programa empezó a ser utilizado por los productores (en su mayoría de maíz blanco) para la adquisición de instrumentos bursátiles en el CBOT, los cuales tienen como subyacente el maíz amarillo calidad US#2.

Las coberturas que operan ASERCA involucran una posición en el mercado de futuros opuesta a la que tiene el participante en el mercado spot doméstico; entonces, cualquier pérdida en el mercado spot es compensada con la cobertura en el mercado de futuros (Ochoa, 2011b).

Durante el periodo 1997-2011 se cubrieron 705,672 contratos de maíz, lo que indica que este tipo de herramienta ha tenido un importante impulso gubernamental y respuesta por parte de los productores (Ochoa, 2011b). En la figura 1 puede observarse claramente la forma en que se ha incrementado a lo largo del tiempo el uso de los contratos de coberturas para el precio de diversos productos agrícolas a través del programa ASERCA.

Figura 1.

Contratos de coberturas colocadas de 1997 a 2011.

Fuente: elaboración propia con base en Ochoa (2011b).

Los productos sujetos a cobertura durante el periodo 1997-2007 han sido: maíz, trigo, sorgo, café, algodón, ganado porcino, ganado bovino, soya, cártamo y jugo de naranja. Es el maíz, con 50.15% del total de contratos, el producto con mayores coberturas contratadas. Sinaloa es el mayor Estado productor de maíz en el país y el que ha tenido el mayor número de colocaciones con 26.9% (Ochoa, 2011b) (fig. 1).

Por otra parte, el 24 de octubre de 2012, a través del Mercado Mexicano de Derivados (MexDer), la SAGARPA presentó el primer contrato de futuros de maíz amarillo en México, señalando como beneficiarios a los productores, comercializadores, industriales e inversionistas financieros del sector agropecuario (SAGARPA, 2012).

ASERCA (2012) indicó que México se encuentra lejos de tener una bolsa agropecuaria, ya que no existen precios conocidos, mecanismos de regulación, arbitraje, resolución de conflictos y certificados de calidad de físicos. De esta forma, un primer avance fue listar contratos de futuros de maíz del CME Group², fungiendo el Fideicomisos Instituidos en Relación con la Agricultura (FIRA) como agente financiero del Gobierno para desempeñar las funciones de ASERCA. Con la participación de los intermediarios bancarios y no bancarios que operan con FIRA, se subsidiaría la compra de coberturas con recursos de la SAGARPA.

La experiencia internacional, de acuerdo con CEDDRSSA (2007), es que antes de contar con un mercado de futuros es necesario contar con una bolsa de físico. Sin embargo, en México se comenzó listando contratos de futuros de maíz amarillo, producto que es más barato que el maíz blanco, y considerando que de acuerdo al SIAP (2012) la producción nacional de maíz fue 94% de maíz blanco, por lo cual el precio al productor se ve castigado cuando participa en las coberturas.

Ante la dificultad de contar con una bolsa de futuros agropecuarios en México, resulta de gran interés conocer la relación entre el precio futuro de maíz amarillo calidad US#2 comercializado en el CME Group con los precios spot de maíz blanco mexicano, ya que este producto es el que ha tenido mayor subsidio de ASERCA y el maíz amarillo empleado para la cobertura es de menor calidad y precio.

Modelos de volatilidad estocástica

La volatilidad puede ser modelada mediante el cálculo de la varianza o la desviación estándar de los rendimientos de una serie financiera en un periodo de tiempo determinado, lo cual permite realizar el pronóstico de volatilidad para periodos futuros. Sin embargo, existe evidencia que sugiere que predecir la volatilidad de una forma más sofisticada conduce a valuaciones más exactas de la serie financiera (Brooks, 2008).

Debido a que la volatilidad no puede observarse directamente, se debe recurrir a aprovechar algunas características que pueden ser observadas en una serie de tiempo (Tsay, 2005):

• •

  Se puede agrupar, es decir, puede ser alta en ciertos periodos de tiempo y en otros puede ser más baja (volatility cluster).

• •

  Involucra al tiempo de forma continua, esto es, que los saltos en la volatilidad son poco comunes.

• •

  La volatilidad no tiende a infinito, varía dentro de un rango fijo. Estadísticamente, significa que la volatilidad algunas veces es estacionaria.

• •

  La volatilidad reacciona diferente a un aumento grande en el precio que a una caída grande en el mismo, esto se conoce como el efecto de apalancamiento (leverage).

Dos características adicionales son que las series presentan leptocurtosis y tienen colas más gruesas que la distribución normal, así como distribuciones simétricas (Nieto, Oribe y Zarraga, 2011). Ruiz y Veiga (2008) afirman que desde el punto de vista de la econometría, la eficiencia de los estimadores y la construcción de intervalos de predicción obedecen en parte a que la heterocedasticidad (evolución temporal de la volatilidad) se encuentre modelada adecuadamente.

Por otra parte, Broto y Ruiz (2004) declaran que el incremento en el interés por los modelos de volatilidad estocástica se debe a que son frecuentemente empleados en la teoría financiera para modelar el comportamiento de los precios financieros. Comparados con los modelos más populares conocidos como GARCH, los primeros capturan más eficientemente las principales propiedades de los rendimientos observados en series financieras.

De acuerdo a Soriano y Climent (2006), las metodologías más empleadas para el análisis de la transmisión de volatilidad se pueden agrupar en 3 categorías: modelos GARCH, modelos de cambio de régimen y modelos de volatilidad estocástica. En esta sección se plantea una breve descripción de los modelos GARCH y de volatilidad estocástica, haciendo un mayor énfasis en los modelos multivariantes. Iniciaremos con los modelos GARCH, los cuales permiten modelar la varianza a partir de la dependencia de sus propios rezagos (Tsay, 2010); en el caso multivariado MGARCH, es posible estimar las interacciones entre las volatilidades (varianza-covarianza) de diferentes series en todas las direcciones (Soriano, 2004; Ruíz y Veiga, 2008; Philipov y Glickman, 2006; Asai et al., 2006). El modelo general es descrito en Bawens et al. (2006, 2012).

Dado que existen diferentes representaciones de los modelos MGARCH que se estiman por el método de máxima verosimilitud, se consideró adecuado presentar de manera breve las representaciones más utilizadas, las cuales se muestran en la tabla 1.

Tabla 1.

Clasificación de los principales modelos MGARCH

Fuente: elaboración propia con base en Bawens et al. (2006) y Tsay (2010).

En el caso de los modelos econométricos, como es el caso de los constant correlation model (CCC) y dynamic correlation model (DCC), estos se han vuelto populares debido a que las restricciones impuestas son simples de modelar. Un modelo similar es el varying conditional correlation (VCC). Estos son los modelos utilizados para cumplir con el objetivo del presente trabajo.

Las especificaciones de los modelos MGARCH se mencionan a continuación y son descritas a detalle en Bawens et al. (2006).

Constant correlation model (CCC)

En esta especificación de los modelos MGARCH las correlaciones condicionales son constantes y, en consecuencia, las covarianzas son proporcionales al producto de las desviaciones estándar condicionales correspondientes. Esta restricción reduce el número de parámetros desconocidos y simplifica la estimación. El modelo CCC se define como:

donde:

h11t1/2 es cualquier modelo GARCH univariante. Y R=ρij es una matriz simétrica definida positiva con ρ_ii = 1, ∀ i

R es la matriz que contiene las correlaciones condicionales constantes ρ_ij. El modelo original tenía un GARCH (1,1) como especificación para cada varianza condicional en D_t:

La matriz H_t es definida positiva si, y solo si, las varianzas condicionales son positivas y R también es definida positiva.

El supuesto de que las correlaciones condicionales son constantes puede parecer no realista, aun así este modelo ayuda a conocer el grado de interdependencia entre mercados.

Dynamic correlation model (DCC)

Este modelo es una generalización del modelo anterior. Este permite a la matriz de correlación condicional variar en el tiempo, la cual debe ser definida positiva a través del tiempo. Las especificaciones originales del modelo son:

D_t es nuevamente:

Y h_iit puede ser definido como cualquier modelo GARCH univariante.

θ₁ y θ₂ on parámetros no negativos que satisfacen la condición: θ₁ + θ₂ < 1, R es una matriz simétrica de parámetros definida positiva con ρ_ii = 1 ψ_t−1 es una matriz de correlaciones de orden NXN de ε_τ para τ = t − M, t − M + 1, …, t − 1. Sus elementos i, j ésimos están dados por:

donde,

y la matriz ψ_t−1 es posible definirla como:

Y B_t−1 es una matriz diagonal de orden NXN como i-ésimos elementos diagonales dados por:

Y Lt−1=ut−1,…,ut−M es una matriz NXM que contiene a ut=u1tu2t…uNt′

Una condición necesaria para garantizar que ψ_t−1 y R_t sean positivos es que M ≥ N.

Varying conditional correlation model (VCC)

Finalmente, Tsay y Tsui (2001) retoman el modelo anterior y, asumiendo rendimientos normales, la función logarítmica de verosimilitud lt de la observación yt es:

Donde el número total de parámetros a estimar es 3K +K(K +1)/2 +2.

Información

A partir del segundo semestre del 2006, los precios mundiales de los principales alimentos comenzaron a incrementarse. Para el primer semestre de 2008 se registraron los niveles más altos de los últimos 30 años. A pesar de que al siguiente año disminuyeron, los precios en la actualidad son superiores a los niveles observados antes de 2006 (FAO, 2009).

Con el objetivo de no incorporar los incrementos de precios de 2006 y que estos afecten a los resultados de las estimaciones, el periodo de análisis comprende desde la primera semana de 2007 hasta la última de 2012, por lo que se cuenta con 313 observaciones.

Los precios de los contratos de futuros del maíz amarillo #2 del CBOT se obtuvieron en el Sistema Nacional de Información de Mercados (SNIIM) de la Secretaría de Economía (SE); se usa el futuro con vencimiento a marzo, fundamentado lo anterior en las «Bases teóricas de maíz» del MexDer, y la unidad de medida es dólar por kilogramo.

A continuación se muestran los principales Estados productores de maíz en modalidad de riego y temporal. Los datos fueron obtenidos en época de cosecha para el año 2012 (tabla 2)

Tabla 2.

Porcentaje de producción de maíz en México por entidad federativa, 2007-2012

Estado	Porcentaje de producción obtenida						Total
	2007	2008	2009	2010	2011	2012
Aguascalientes	0.26	0.45	0.02	0.28	0.37	0.31	0.28
Baja California	0.11	0.15	0.07	0.07	0.14	0.18	0.12
Campeche	0.22	0.44	0.31	1.65	1.76	0.92	0.85
Coahuila	0.13	0.12	0.10	0.20	0.05	0.07	0.12
Colima	0.23	0.21	0.17	0.12	0.23	0.19	0.19
Chiapas	3.52	2.73	3.17	2.98	4.66	3.66	3.40
Chihuahua	4.56	4.36	5.47	5.37	5.97	6.17	5.28
Distrito Federal	0.04	0.04	0.05	0.04	0.03	0.03	0.04
Durango	0.62	1.11	1.08	1.31	0.81	0.64	0.93
Guanajuato	6.84	5.68	4.73	5.31	6.60	5.93	5.83
Guerrero	5.58	6.05	6.50	5.24	7.72	5.56	6.04
Hidalgo	3.22	3.30	3.01	3.12	3.25	3.89	3.30
Jalisco	10.47	10.63	10.42	11.54	11.39	12.23	11.10
México	6.46	7.27	5.96	5.83	3.71	7.47	6.22
Michoacán	6.94	7.05	6.07	5.44	7.80	7.33	6.73
Morelos	0.49	0.37	0.42	0.42	0.49	0.27	0.41
Nayarit	0.21	0.54	0.76	0.56	1.01	0.71	0.61
Nuevo León	0.30	0.14	0.20	0.28	0.14	0.35	0.24
Oaxaca	3.24	2.73	2.89	2.51	4.07	3.51	3.12
Puebla	4.80	4.74	3.45	4.74	3.19	4.59	4.31
Queretaro	1.21	0.98	0.95	1.26	0.88	0.94	1.05
Quintana Roo	0.08	0.02	0.10	0.21	0.38	0.13	0.14
San Luis Potosí	0.93	1.09	0.65	0.81	0.62	0.54	0.78
Sinaloa	27.47	27.70	30.77	28.33	20.46	20.36	26.04
Sonora	0.77	0.94	0.60	1.29	0.57	0.89	0.86
Tabasco	0.46	0.65	0.67	0.55	0.92	0.92	0.68
Tamaulipas	3.31	2.84	2.44	2.69	3.32	2.85	2.90
Tlaxcala	1.33	1.32	1.23	1.46	0.89	1.49	1.31
Veracruz	4.08	4.03	5.59	4.55	6.40	5.98	5.04
Yucatán	0.24	0.07	0.11	0.40	0.66	0.39	0.30
Zacatecas	1.86	2.26	2.05	1.43	1.48	1.49	1.78
Total	100	100	100	100	100	100	100
Total (toneladas)	18,315,683	18,997,413	16,951,453	18,507,924	14,006,294	17,971,564	104,750,331

Fuente: SIAP (2012).

De la misma manera, para obtener los precios spot de México, en el SNIIM se seleccionaron 4 Estados con altos niveles de producción de maíz³, y se verificó que durante el periodo de análisis ASERCA brindara apoyos directos a coberturas de precios para maíz en los Estados de Jalisco, México, Michoacán y Chihuahua. Los precios del SNIIM se obtuvieron de las principales centrales de abasto de cada Estado, por lo que se encuentran cotizados al mayoreo por kilogramo comercializado en bulto de 50 kg, y son los más frecuentes; estadísticamente se utilizó la moda; para convertir los precios spot a dólares se obtuvo el tipo de cambio fix del Banco de México.⁴

Para realizar las estimaciones del modelo econométrico se empleó el programa estadístico Stata (MR) versión 12.

Análisis de resultados

Para poder estudiar de manera adecuada las series de precios tratadas es necesario que estas sean estacionarias. Para comprobar la presencia de estacionariedad se utilizó la prueba de raíz unitaria de Dickey-Fuller aumentada, que sustenta las siguientes hipótesis:

Al realizar la prueba de raíz unitaria a nivel en todas las series, se encontró que no existe evidencia estadística suficiente para no rechazar la hipótesis nula de raíz unitaria, es decir, la serie no es estacionaria. Dado que no se puede aplicar la teoría de series de tiempo a series no estacionarias, fue necesario aplicar la prueba sobre primeras diferencias, de la cual se obtuvo que todas las series eran estacionarias. Los resultados se muestran en la tabla 3.

Tabla 3.

Prueba Dickey-Fuller aumentada

Variable (precio)	Estadístico t	Valores críticos
		1%	5%	10%
Jalisco	–1.750	–3.455	–2.878	–2.570
México	–0.755	–3.455	–2.878	–2.570
Michoacán	–3.002	–3.455	–2.878	–2.570
Chihuahua	–1.446	–3.455	–2.878	–2.570
Futuro	–1.644	–3.455	–2.878	–2.570
Δ Jalisco	–25.146	–3.455	–2.878	–2.570
Δ México	–18.175	–3.455	–2.878	–2.570
Δ Michoacán	–20.088	–3.455	–2.878	–2.570
Δ Chihuahua	–19.844	–3.455	–2.878	–2.570
Δ Futuro	–16.662	–3.455	–2.878	–2.570

Fuente: elaboración propia con datos obtenidos del SNIIM.

Por otro lado, empleando la prueba de Engle-Granger, la cual consiste en realizar una prueba de hipótesis Dickey-Fuller aumentada sobre los residuos estimados a partir de la regresión de las variables ya estacionarias, de acuerdo a los resultados obtenidos se confirma que las variables de estudio están cointegradas (tabla 4).

Tabla 4.

Prueba de cointegración Engle-Granger

Variable	Estadístico t	Valores críticos
		1%	5%	10%
Residuo	–5.900	–3.456	–2.878	–2.570

Fuente: elaboración propia con datos obtenidos del SNIIM.

Analizando los correlogramas de cada serie, se identificaron los procesos AR y MA, ninguna serie presentó estacionalidad. Los estadísticos t para las cinco series muestran, con un nivel de confianza del 95%, que los componentes autorregresivos de medias móviles y estacionales son significativamente diferentes de cero, y las raíces características son invertibles. Los correlogramas y el estadístico Durbin-Watson, por su parte, indican que los coeficientes estimados no están correlacionados entre sí, por lo que son estables.

Si existe verdadera simultaneidad entre un conjunto de variables que representan a los precios del maíz, todas deben ser tratadas con igualdad y no debe existir distinción a priori, como en los modelos de ecuaciones simultáneas. El término autorregresivo se refiere a la aparición del valor rezagado de la variable dependiente del lado derecho.

En el caso bivariado, suponiendo una causalidad entre 2 variables y que cada ecuación contiene k valores rezagados, se puede estimar cada ecuación por mínimos cuadrados ordinarios de la siguiente forma:

Donde las u_it son los términos de error, conocidos como impulsos, innovaciones o shocks.

Los criterios para seleccionar el orden óptimo de rezagos fueron:

• 1)

  Criterio de información de Akaike.

• 2)

  Criterio de información bayesiano de Schwarz.

• 3)

  Criterio de información de Hannan-Quinn.

Con base en esto se estimaron modelos bivariados de acuerdo a las siguientes consideraciones:

En este caso, utilizando los rezagos sugeridos por los criterios de información, se observa a un nivel de confianza del 95% que ante un shock los precios del mercado de futuros tienen poca influencia sobre los precios spot de cada Estado. Asimismo, se comprobó que los valores propios caen dentro del círculo unitario y, por lo tanto, se puede afirmar que los modelos son estacionarios.

En la tabla 5 se presentan las gráficas de las funciones de impulso-respuesta de la descomposición estructural de los residuos del VAR. Estas gráficas representan el efecto temporal de una perturbación cuya magnitud equivale a una desviación estándar sobre el nivel medio de cada variable. Con base en estos es posible interpretar la naturaleza de los impulsos o shocks de acuerdo a sus signos. Para los cuatro casos analizados en la tabla 5a-d), que corresponden respectivamente al efecto del shock debido a los precios futuros de maíz amarillo del CBOT sobre los precios spot domésticos del maíz blanco en los Estados de Jalisco, México, Michoacán y Chihuahua, los resultados obtenidos nos muestran que es posible concluir que un shock originado en el CBOT no afecta considerablemente a los precios spot domésticos del maíz, por lo que no existe interrelación entre la variable futuro de maíz amarillo con los precios de maíz blanco nacionales en el largo plazo. Las innovaciones provenientes del CBOT tampoco muestran persistencia, el proceso de ajuste es muy rápido. Particularmente, para la relación de precios futuros y spot, la descomposición de varianza indica que las variaciones en los precios futuros provenientes del CBOT no afectan a las variaciones en los precios spot de las variables nacionales.

Tabla 5.

Funciones de impulso-respuesta de VAR

Fuente: elaboración propia con datos obtenidos del SNIIM.

Posteriormente, fue necesario comprobar la presencia de efectos ARCH sobre las series, por lo que se aplicó el contraste de heterocedasticidad LM-ARCH a los residuos de las estimaciones ARMA, el cual tiene como hipótesis:

Los resultados obtenidos se muestran en la tabla 6.

Tabla 6.

LM-test para heterocedasticidad condicional autorregresiva

Rezago	Prob > χ^2
	Jalisco	México	Michoacán	Chihuahua	Futuro
1	0.4036	0.0000	0.3942	0.9454	0.1123
2	0.3212	0.0000	0.6716	0.0000	0.0461
3	0.4870	0.0000	0.8416	0.0000	0.0878
4	0.6365	0.0000	0.9334	0.0000	0.0125
5	0.7509	0.0001	0.0210	0.0000	0.0244
6	0.8401	0.0003	0.0345	0.0000	0.0361
7	0.8925	0.0006	0.0565	0.0000	0.0609
8	0.9354	0.0012	0.0908	0.0000	0.0293
9	0.9653	0.0021	0.1319	0.0000	0.0407
10	0.9778	0.0030	0.1518	0.0001	0.0398
11	0.9856	0.0035	0.2097	0.0001	0.0618
12	0.9916	0.0062	0.2647	0.0000	0.0819
13	0.9943	0.0088	0.0542	0.0000	0.1034
14	0.9968	0.0091	0.0775	0.0000	0.1443
15	0.9983	0.0144	0.1080	0.1292	0.0852

Fuente: elaboración propia con datos obtenidos del SNIIM.

De los coeficientes obtenidos en las estimaciones, es posible resaltar que en Michoacán existe persistencia de volatilidad ante un shock de volatilidad.

A partir de las estimaciones realizadas de los modelos ARCH y GARCH para las series de los Estados de México, Michoacán, Chihuahua y Futuro se obtuvieron los resultados que se muestran en la tabla 7.

Tabla 7.

Resultados de los modelos ARCH y GARCH

México	Coeficiente	p	Futuro	Coeficiente	p
AR	–0.1235	0.077	ARCH	0.0828	0.002
ARCH	0.2451	0.002	GARCH	0.8731	0.000

Chihuahua	Coeficiente	p	Michoacán	Coeficiente	p
AR	0.1730	0.033	AR	0.2827	0.000
ARCH	0.1310	0.000	ARCH	2.5684	0.000
GARCH	0.7932	0.000	GARCH	0.1881	0.000

Fuente: elaboración propia con datos obtenidos del SNIIM.

Como se muestra en los resultados anteriores, existe evidencia de la presencia de heterocedasticidad condicional en los residuos de cada variable de precios, por lo que los modelos GARCH son candidatos convenientes para modelar las variables de estudio, dada su naturaleza heterocedástica. Debido a que la volatilidad en diferentes mercados se mueve en el tiempo conjuntamente, tiene sentido realizar un análisis multivariado. Esto nos permitió estimar de manera eficiente los derrames de volatilidad y el impacto de las noticias en la determinación de precios spot domésticos.

El nivel de interdependencia entre los precios se captura mediante el modelo CCC, el cual muestra que para los Estados de Michoacán y Chihuahua no existen correlaciones entre el precio de maíz amarillo futuro y los precios de maíz blanco. Esta relación solo es válida para el Estado de México, sin embargo, la correlación —aunque es estadísticamente significativa— es muy pequeña, es decir, por cada variación positiva en el precio de maíz amarillo futuro, el precio spot de Michoacán registra una variación positiva de 0.1360 (tabla 8).

Tabla 8.

Resultados del modelo MGARCH-CCC

Variable	Coeficiente	z	p > z
ARCH Futuro	0.0001	12.49	0.0001
ARCH Michoacán	0.0003	12.49	0.0002
ARCH México	0.0002	12.49	0.0001
ARCH Chihuahua	0.0001	12.49	0.0001

Correlación Futuro	Coeficiente	z	p > z
Michoacán	0.0971	1.73	0.083
México	0.1360	2.45	0.014
Chihuahua	0.2860	0.51	0.613

Fuente: elaboración propia con datos obtenidos del SNIIM.

La volatilidad en este tipo de modelos es entendida como la varianza condicional de las series, es decir, oscilaciones a corto plazo. Analizando las variables de precios futuro y spot como un sistema en el que las variaciones de los precios de las demás influyen en la variación de precios de cada una, es posible apreciar, mediante los parámetros ARCH estimados, que sí existe transmisión de volatilidad de las demás variables a cada una; sin embargo, el derrame de volatilidad es muy pequeño.

Como se mencionó en la sección anterior, el modelo DCC es una generalización del modelo CCC y permite a las correlaciones condicionales variar en el tiempo. Los parámetros θ₁ y θ₂ son parámetros de noticias y decadencia, por lo que muestran el efecto de las innovaciones en las correlaciones condicionales conforme varía el tiempo y su persistencia en el mercado, dado que el parámetro de noticias tiene un valor de 0.0271, mientras que el parámetro de decadencia muestra que existe persistencia en la transmisión de volatilidad con un valor de 0.9265; por lo cual ambos parámetros son estadísticamente significativos, lo cual puede apreciarse en la tabla 9.

Tabla 9.

Resultados del modelo MGARCH-DCC

Variable	Coeficiente	z	p > z
ARCH Futuro	0.0001	12.45	0.0000
ARCH Michoacán	0.0003	12.18	0.0002
ARCH México	0.0001	11.64	0.0001
ARCH Chihuahua	0.0001	11.97	0.0001
theta 1	0.0271	3.62	0.0000
theta 2	0.9265	80.74	0.0000

Correlación Futuro	Coeficiente	z	p > z
Michoacán	0.1501	1.72	–0.0204
México	0.0870	0.78	–0.1311
Chihuahua	0.0832	0.75	–0.1347

Fuente: elaboración propia con datos obtenidos del SNIIM.

En los resultados de este modelo, las variables Estado de México y Chihuahua no presentan correlación con los precios futuros del CBOT. El coeficiente de correlación de Michoacán muestra que ante una variación positiva en el precio de maíz amarillo futuro el precio spot registra una variación positiva de 0.1501.

En el caso de los estadísticos ARCH se observa un derrame de volatilidad de todos los precios, por lo cual al analizarlos como un sistema se obtuvieron los resultados que se muestran en la tabla 9.

Dado que un modelo similar al DCC es el VCC, se utilizó también este para comparar resultados, los cuales se muestran en la tabla 10.

Tabla 10.

Resultados del modelo MGARCH-VCC

Variable	Coeficiente	z	p > z
ARCH Futuro	0.0001	12.39	0.0001
ARCH Michoacán	0.0003	12.27	0.0002
ARCH México	0.0001	11.64	0.0001
ARCH Chihuahua	0.0001	12.31	0.0001
theta 1	0.1486	3.55	0.0000
theta 2	0.6188	5.06	0.0000

Correlación Futuro	Coeficiente	z	P > z
Michoacán	0.0911	1.09	0.277
México	0.0840	0.97	0.332
Chihuahua	0.0603	0.67	0.504

Fuente: elaboración propia con datos obtenidos del SNIIM.

En este caso, es posible apreciar la consistencia con los resultados del modelo DCC. Los parámetros θ₁ y θ₂ muestran también el efecto de las innovaciones en las correlaciones condicionales conforme varía el tiempo y su persistencia en el mercado. Ambos parámetros son estadísticamente significativos, e indican nuevamente que existe persistencia en la transmisión de la volatilidad y en la decadencia con valores respectivos de 0.1486 y 0.6188.

Respecto a las correlaciones entre los precios futuro de maíz amarillo y spot domésticos, los resultados no son estadísticamente significativos, por lo que sugieren que no existe relación entre las variables de precios nacionales con el precio futuro del CBOT.

Finalmente, y en concordancia con los resultados de los modelos CCC y DCC, analizando todas las variables en conjunto se puede apreciar que sí existen efectos en la transmisión de volatilidad de todas las variables a cada una de ellas; sin embargo, el derrame de volatilidad es casi nulo.

Conclusiones

En esta investigación se examinó la dinámica de la volatilidad entre el precio empleado como cobertura por los productores de maíz blanco mexicanos y el realmente registrado en el país. Es así que se analizan 4 precios spot de maíz blanco provenientes de los Estados de Jalisco, México, Michoacán y Chihuahua, y un precio originario del CBOT el cual es, para maíz amarillo, calidad US#2.

Ante la imposibilidad de contar con un mercado de futuros en México, con base en lo discutido en la primera sección, las coberturas del precio de maíz deben ser competitivas y brindarle seguridad al productor en su ingreso.

De acuerdo al análisis de correlación cruzada, es posible que existiera una relación entre los precios spot domésticos y el precio futuro; sin embargo, en una primera etapa, se pudo apreciar mediante la estimación de vectores autorregresivos que un shock originado en el CBOT no afecta significativamente a los precios spot domésticos, por lo que no existe interrelación entre la variable futuro de maíz amarillo con los precios de maíz blanco nacionales. Las innovaciones provenientes del CBOT tampoco muestran persistencia, el proceso de ajuste es muy rápido.

Aunque los precios spot del mercado mexicano se encuentran integrados a los precios futuros del CBOT (de acuerdo a la prueba de cointegración de Engle-Granger), analizando todas las variables en conjunto, los resultados de los modelos CCC, DCC y VCC indican que sí existe transmisión de volatilidad en los precios, sin embargo, el derrame de volatilidad es muy pequeño.

Cuando se estudió el grado de interdependencia entre las volatilidades de precios de los mercados a través del análisis de volatilidad estocástica multivariante mediante los modelos CCC, DCC y VCC, los resultados de las estimaciones mostraron que la volatilidad del precio de mercado de futuros agrícolas no se encuentra relacionada con la volatilidad de los precios registrados en los Estados de México y Michoacán, y con el único Estado que muestra una pequeña correlación negativa es Chihuahua.

Los coeficientes individuales de las ecuaciones ARCH de los 3 modelos estimados son estadísticamente significativos e indican que la varianza de las variables de estudio no depende solamente de su información pasada, sino también de los shocks de los demás precios considerados en esta investigación.

Derivado de los resultados de la investigación es posible aceptar la hipótesis planteada, es decir, que mediante el cálculo del grado de interdependencia entre las volatilidades de los precios estudiados fue posible inferir que la cobertura de precios de maíz blanco ofrecida por el programa ASERCA no es eficiente ante la volatilidad de los precios futuros de maíz amarillo.

En un contexto internacional, el precio del maíz puede negociarse en mercados financieros, donde los precios del producto varían constantemente, sin embargo, conforme a los resultados es posible apreciar que el precio nacional no incorpora inmediatamente tales variaciones.

Para que la cobertura de precios propuesta por ASERCA represente un beneficio real para los productores mexicanos, es necesario que los precios spot incorporen rápidamente los movimientos en los precios provenientes del CBOT.

Si los precios del mercado de futuros no guían a los precios nacionales, la cobertura mediante el esquema de ASERCA no es la adecuada, por lo que en una investigación futura se podría analizar, en primer lugar, el motivo por el cual el programa ha aumentado de forma considerable el número de contratos cubiertos, ya que la cobertura de precios opera en paralelo con otros programas ofrecidos por ASERCA; y, por otra parte, si la cobertura de precios presenta una desventaja al no proveer de manera correcta los precios, investigar el motivo por el cual los productores de maíz blanco mexicano la demandan.