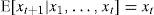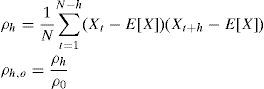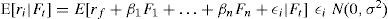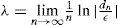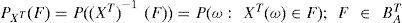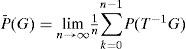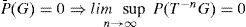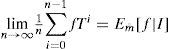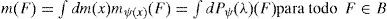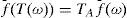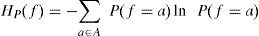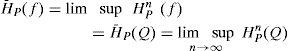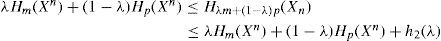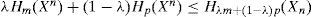Una medida de eficiencia de mercado. Un enfoque de teoría de la información

Resumen

En este trabajo, con base en el concepto de entropía de Shannon, se propone una medida de eficiencia de mercado que utiliza la función de densidad empírica de los rendimientos como alfabeto para calcular la entropía del sistema y proveer con ello una medida de eficiencia de mercado. Se demuestra que bajo ciertas condiciones de ergodicidad y de estacionariedad la entropía muestral converge a la entropía del estado dominante, lo que valida el uso de la entropía muestral como medida de eficiencia del sistema. Asimismo, se demuestra que la medida propuesta es consistente con algunos de los axiomas de Artzner et al. (1999) acerca de una medida coherente de riesgo. Por último, con fines ilustrativos, se llevan a cabo varias aplicaciones de la medida de eficiencia propuesta a distintos mercados de capitales: DJIA, S&P500, FTSE100 e IPC.

Abstract

In this paper, based on the concept of Shannon entropy, we propose a measure of market efficiency by using the empirical density function of returns. Under certain conditions of ergodicity and stationarity, it is shown that the sample entropy converges to the entropy of the dominant state. It is also shown that the proposed measure is consistent with some of the axioms from Artzner et al. (1999) of a coherent risk measure. Bounds on the behavior of entropy as a measure of efficiency on the basis of extreme cases are also established; going from deterministic processes to pure white noise stochastic processes. Finally, for illustrative purposes, we carry out several applications of the proposed efficiency measure of capital to different markets: DJIA, S&P500, FTSE100 and IPC.

Introducción

A través del tiempo se ha construido un complejo aparato de conocimientos al que llamamos ciencia. Para su desarrollo, ésta requiere de supuestos que usualmente van cambiando con el tiempo. Un ejemplo de la transformación de los supuestos sobre los cuales se fundamenta el corpus teórico de alguna ciencia está dado por el concepto de eficiencia de los mercados en las finanzas modernas.

El concepto de eficiencia de mercado nace con el trabajo de Fama (1970), el cual modeló la teoría financiera en las siguientes décadas. Aunque los vaivenes en el comportamiento de los mercados y las subsecuentes investigaciones empíricas que buscaron explicarlos —v.g. Taleb (2008), Lo y MacKinlay (2002) y Clare y Thomas (1995) o Mandelbrot (1963, 1966, 1967 y 1971), por citar algunos— han erosionado y, por ende, relajado el concepto, éste sigue siendo un referente en la industria y academia.

A pesar de que este concepto es fundamental en la teoría de portafolios, aún se carece de una métrica ampliamente aceptada para dicha teoría. Esto favorece la formación de burbujas especulativas, dadas las rachas irracionales no identificadas, y con ello los movimientos súbitos de ajuste que merman la confianza pública en los mercados e impide la correcta transferencia de riesgos y recursos entre agentes económicos.

La métrica propuesta en este trabajo se basa en la variabilidad de la información provista por los rendimientos de mercado, es decir, sobre la capacidad de innovación (sorpresa) del proceso estocástico que conduce estos rendimientos; su lógica es bastante simple, pues tiene como extremos la eficiencia fuerte de mercado (entropía máxima) y la completa predictibilidad del sistema (entropía cero). La gran ventaja de la medida propuesta sobre el resto de las existentes es su no linealidad y su independencia respecto a supuestos teóricos restrictivos, v.g. distribuciones de probabilidad específicas o dependencia de algún momento muestral.

Así, el objetivo de este trabajo es proponer una medida de eficiencia que capture toda la estructura de dependencia que las medidas lineales son incapaces de incorporar. En la siguiente sección se hace un breve resumen de algunos trabajos que han estudiado y medido, desde diversas perspectivas y con distintos enfoques, la eficiencia de los mercados financieros. Posteriormente, se define la entropía de Shannon, se propone como medida de eficiencia de mercado y se verifica su pertinencia teórica en el análisis del problema; también se establecen las cotas superior e inferior para la medida y la lógica detrás del uso de distribuciones empíricas para el cálculo de la entropía. Más adelante se aplica la propuesta metodológica a series de volumen y rendimientos de algunos índices bursátiles representativos: DJIA, S&P500, FTSE100 e IPC; asimismo, se demuestra que los periodos de crisis aguda y las consecuentes caídas en el valor de capitalización de estos índices están relacionados con fuertes caídas en la entropía, es decir, se demuestra la existencia de corridas bursátiles que eliminan la sorpresa del mercado, haciéndolo temporalmente predecible. Por último, se establecen las conclusiones y las posibles líneas de investigación futuras.

¿Cómo se ha intentado probar la eficiencia de mercado?

En su artículo clásico, Fama (1970) define como eficiencia débil de mercado a la imposibilidad de obtener, en el largo plazo, rendimientos más allá de los esperados a través del análisis de los precios del activo financiero, dejando como única posibilidad para obtenerlos el uso del análisis fundamental o de información privilegiada, esto es,

donde x_t es el precio del activo en el tiempo t. Esta definición plantea la ausencia de patrones en los precios de los activos, no necesariamente como un equilibrio.

Tradicionalmente, esta definición de eficiencia ha sido analizada mediante diversas pruebas de covarianza y estacionariedad,¹v.g.Granger y Morgenstern (1963), Lehman (1990) y Pincus and Kalman (2004), quienes investigaron si los rendimientos provienen de una martingala.

Analizando el mismo problema desde otra perspectiva, Mandelbrot (1971) demuestra que la presencia de valores extremos en los rendimientos de mercado no viola el supuesto de martingala (sólo el de proceso markoviano), pero que hacen prácticamente imposible el arbitraje en los mercados por la gran cantidad de capital necesario para hacerlo.

En los trabajos donde se supone normalidad² en los rendimientos de los activos, suele realizarse un correlograma para verificar la correlación del proceso³ con respecto a sus rezagos, ρ_h,0; esto es, hay que verificar la correlación a h periodos, ρ_h, con la varianza de los rendimientos, ρ₀ = σ². Es decir:

Este problema ya ha sido examinado en varios trabajos como el de Oponga et al. (1999) y el de Yeh y Liao (2001). En estas investigaciones se ha aportado evidencia empírica (usualmente a través de pruebas BDS⁴) que rechaza la independencia entre los rendimientos de diversos mercados, por lo que también se rechaza la hipótesis de martingala.

Este mismo punto también ha sido discutido por Mandelbrot (1963). Este autor analiza la distribución de los rendimientos de algunos activos commodities y sugiere que sus rendimientos siguen una distribución de Pareto, además de presentar dependencia de largo plazo (efecto José). Por tanto, cualquier inferencia basada en el teorema del límite central dejará de lado los efectos de las colas pesadas y la recurrencia de largo plazo, i.e. rechaza la independencia de las variables aleatorias del proceso estocástico.

El siguiente nivel de eficiencia de mercado señalado por Fama es la eficiencia semifuerte; en ésta se supone que ni los precios de los activos ni el análisis fundamental son suficientes para obtener, de forma sistemática, rendimientos por encima del mercado. Esta forma de eficiencia es, usualmente, formalizada mediante el uso de esperanzas condicionales y conjuntos crecientes de información de mercado que son conceptualizados a través de una filtración,⁵ F, o una filtración aumentada {Ft}t≥0∪N.⁶ En el desarrollo de pruebas para esta forma de eficiencia es necesario hacer algunos supuestos sobre la distribución de los rendimientos de mercado o sobre su interacción con todo el conjunto de información. Esto significa hacer supuestos sobre la distribución de las perturbaciones del modelo; ejemplos tradicionales de este enfoque son las pruebas indirectas que hacen uso de modelos como el CAPM, esto es

donde se supone que los rendimientos de un activo se determinan por su sensibilidad al premio al riesgo de mercado, β, y por la tasa de interés libre de riesgo de crédito, r_f; se da por sentado que cualquier desviación sobre esta línea de mercado será producto de una perturbación, la cual se supone que proviene de una variable aleatoria normal con media cero y varianza constante. Sobre esta línea de investigación también se pueden encontrar modelos como el APT, el cual pretende ortogonalizar factores de riesgo, F_i, que afectan a los rendimientos de mercado. Al igual que el CAPM, se supone que cualquier desviación respecto al modelo es causada por una variable aleatoria normal, esto es

Existen trabajos —como los de Roll y Ross (1980) y Fama y French (1992)— que exploran esta posibilidad y muestran que la hipótesis de mercados eficientes no necesariamente está ligada al cumplimiento del CAPM o del APT. De hecho, Fama y French encuentran que la β es un predictor pobre de los rendimientos en presencia de otros regresores asociados a las variables fundamentales de la empresa, v.g. cantidad de activos, razón precio-ingresos, apalancamiento o la razón del valor en libros y el valor de mercado. Otras críticas a esta forma de contrastar la hipótesis de eficiencia semifuerte de mercado están basadas en el trabajo de Roll (1977), el cual establece que al probar CAPM no se está probando la eficiencia de todo el mercado, sino únicamente de un índice; esto es, el problema de la hipótesis conjunta.

La última forma de eficiencia introducida por Fama es la eficiencia fuerte, la cual implica que ningún agente económico es capaz de obtener ganancias extraordinarias de manera sistemática aun usando información privilegiada. Tradicionalmente, esta forma de eficiencia es probada mediante el estudio de ventanas de tiempo alrededor del evento corporativo (análisis de eventos). La idea básica de esta técnica es que antes del anuncio formal del evento algunos agentes tendrán información privilegiada de primera mano que pretenderán usar en el mercado con el fin de obtener ganancias extraordinarias; con ello mueven tanto el volumen comerciado como el precio.

Autores como Darell y Bacon (2010) y Pichardo y Bacon (2009) hacen uso de esta técnica para analizar las perturbaciones en los rendimientos o volúmenes de mercado en eventos como la quiebra de Lehman Brothers. En ambos casos, se encontraron evidencias débiles de operaciones con información privilegiada, aunque ellas desaparecen con la inclusión de otros factores de riesgo; asimismo, la evidencia empírica no es concluyente sobre los efectos del uso de información privilegiada en el mercado dado el pequeño tamaño relativo de las operaciones analizadas con respecto al resto del mercado.

En cualquier caso, la entropía de Shannon es capaz de captar esta clase de eventos, pues se reflejan, irremediablemente, en el precio de mercado que se usa para el cálculo de la distribución empírica porque forman parte del alfabeto generado por el mercado bajo esas circunstancias específicas, por lo que la medida aquí propuesta es capaz, incluso, de detectar formas de dependencia no lineal, ya que hace uso de toda la función de distribución.

Los enfoques basados en el supuesto de linealidad para probar la eficiencia de mercado en cualquiera de sus formas han sido los dominantes a partir del artículo seminal de Fama; sin embargo, no han sido los únicos. A partir del desarrollo de los modelos de volatilidad condicional de Engle (1982) y Bollerslev (1986), una gran cantidad de pruebas de dependencia de segundo orden han sido implementadas para probar dicha eficiencia, aunque los resultados de estos trabajos han sido mixtos; véanse, por ejemplo, Brock, Hsieh y LeBaron (1991), Lux (2000), Hsieh (1991), Chen, Lux y Marchesi (2001), así como Hong y Lee (2003), quienes han dejado un importante cúmulo de ideas sobre la elusiva naturaleza del problema y algunas técnicas para probar la no linealidad que subyace.

Tal vez la más conocida de estas pruebas es la desarrollada por Brock, Dechert y Scheinkman (1991), la cual está basada en el concepto de dimensión de correlación. La idea básica de esta prueba es establecer si una serie es independiente e idénticamente distribuida (iid) al examinar la estructura de probabilidad implícita en la serie, lo que en el fondo constituye una búsqueda de dependencia no lineal dentro de la distribución empírica de los datos. Lamentablemente, esta prueba arroja un resultado dicotómico sobre la eficiencia de mercado, por lo que no puede ser usada como una medida de su eficiencia.

Aunque estos modelos han tenido un gran éxito encontrando estructuras de dependencia lineal dentro de las series, aún permanecen sin explicar algunos fenómenos como las colas pesadas y la persistencia en las series de alta frecuencia. Tal vez sea en este punto donde radica la principal bondad de la entropía de Shannon como medida de eficiencia de mercado, pues capta ambos fenómenos al incluir mediciones consecutivas de entropía inducida por la distribución empírica de los rendimientos de mercado. Este punto se tratará con más detalle posteriormente.

Otra técnica que pudiera ser usada en la medida de la eficiencia de mercado es el cálculo del exponente de Lyapunov, λ. Éste mide la tasa de divergencia después de n pasos, d_n, a la que dos trayectorias se separan una de otra para cada par de puntos, x₀ y x₀+ε, dentro de la serie. Esto es, d_n = e^{nλ (x₀)}ε, lo que implica que el exponente de Lyapunov, λ, está dado por

Básicamente, el exponente de Lyapunov provee de un indicador de la sensibilidad de la trayectoria a las condiciones iniciales. Es importante notar que esta herramienta puede ser usada en series de tiempo, aun cuando estén “contaminadas”, por una variable aleatoria, aun cuando ocasione mayor tasa de errores del tipo β.⁷

Este problema es tratado por Tanaka, Aihara y Taki (1998) y Nychka, Ellner, McCaffrey y Gallant (1992). En sus trabajos, estos autores concluyen que la medida puede ser imprecisa cuando el proceso estocástico que contamina la serie no es iid o presenta colas pesadas a intervalos irregulares, tal como lo hacen las series financieras.

La evidencia empírica presentada en todos estos trabajos sugiere que para medir la eficiencia de mercado es necesaria una métrica independiente del proceso gaussiano que además sea capaz de captar los cambios abruptos (efectos de cola) de los rendimientos de mercado; incluso se sugiere que la métrica debería de ser capaz de captar los efectos de dependencia de largo plazo que exhiben estos fenómenos. A lo largo de las siguientes secciones se mostrará que todas estas cualidades deseables son exhibidas por la media aquí presentada.

La pregunta natural que surge de esta profunda revisión bibliográfica es ¿qué tan lejos se encuentra un mercado en particular de la eficiencia fuerte de mercado?, o expresado de otro modo: ¿qué tan eficiente es un mercado? Con la intención de dar una respuesta a esta interrogante se propone el uso del concepto entropía de Shannon (1948) para medir la eficiencia de un mercado. En efecto, si un mercado es perfectamente eficiente, cada variación en el precio aportará nueva información útil para la descripción del sistema, mientras que un mercado menos eficiente podrá ser descrito con menores cantidades de información.

La entropía en el análisis de los mercados

La teoría de la información nace con el artículo de Shannon (1948), donde se establece que la entropía puede ser entendida como una medida de incertidumbre asociada a una variable aleatoria. Aunque en la literatura especializada existen varios trabajos que buscan asociar el concepto de entropía con algún aspecto del mercado, ésta no ha sido plenamente explotada como medida de eficiencia del mismo. Algunos ejemplos de estos trabajos son el de Pincus (1991) y el de Gabjin, Seunghwan y Cheoljun (2007), los cuales hacen uso de la entropía aproximada para medir la aleatoriedad de una serie de tiempo y, de forma indirecta, su eficiencia.

En otros trabajos, como los de Chen (2006) y Risso (2008), se hace uso de la entropía de Shannon para determinar el valor de la información según el número de personas que la conocen, mientras que autores como Zunino, Zanin, Tabak, Pérez y Rosso (2009) usan las permutaciones de la entropía y que puede ser vista de forma heurística como el número de trayectorias no asequibles para los rendimientos de mercado, dada la información conocida, para tratar de medir su eficiencia.

La idea central de este trabajo es ver al mercado como una fuente de información, i.e. como un fenómeno que produce una sucesión de resultados aleatorios que son agrupados en un alfabeto, A, el cual está constituido por todos los posibles resultados del experimento, lo que equivale a un espacio muestral, Ω.

Del mismo modo, es posible establecer una σ-álgebra de Borel, B, basada en el espacio muestral del alfabeto, lo que genera un espacio medible, (Ω, B). Para introducir un proceso estocástico es necesario dotar una función de probabilidad para generar un espacio de medida⁸, (Ω, B, P), y más tarde un sistema dinámico de la forma (Ω, B, P, T)⁹ sobre el cual se define un proceso estocástico que da lugar a una serie de alfabetos, A_i, correspondientes a cada una de las variables aleatorias x_t que representan los rendimientos del mercado;¹⁰ para más detalles véase Halmos (1956). Lo anterior significa que cada rendimiento es una letra del alfabeto de mercado que proporciona información sobre este (sin importar como fue producida esta información), por lo que capta toda su estructura de dependencia).

El proceso estocástico anteriormente descrito determina un nuevo vector aleatorio, X^j={x_n;n∈J}J⊂T, T = Z⁺, que está soportado en un espacio de probabilidad de la forma,(AT, BAT, PXT) donde la medida de probabilidad inducida está dada por:

Es importante notar que ambos espacios de probabilidad son equivalentes dado que su estructura estocástica es la misma. El primer modelo definido para un espacio de probabilidad desconocido y el segundo para las realizaciones observa bles (transformaciones); éste último es conocido como modelo de Kolmogorov para procesos estocásticos. Esta transformación también genera su propio sistema dinámico, (AT, BAT, PXT, T) el cual puede ser combinado con una función de muestreo definida incluso para el tiempo cero, Π₀, 0∈T de tal forma que es posible definir una función de muestreo, Y_n (x) = Π₀ (Tⁿx), x = x^T ∈ A^T equivalente al modelo de Kolmogorov y que está relacionada con las muestras obtenidas a partir del alfabeto, A^T, dado por los rendimientos de mercado.

Ésta no es una cuestión intrascendente, pues implica que se puede establecer un alfabeto para el proceso estocástico que genera los precios (o rendimientos) del mercado, aun cuando esté formado por una serie de elementos ocultos para el observador (microestructura del mercado). Incluso esto implica que el alfabeto generado a través de la distribución empírica es una transformación del alfabeto original.

Con el fin de obtener medidas confiables de la entropía del mercado es necesario establecer su estacionariedad asintótica en media (AMS)¹¹, i.e., se requiere que el sistema dinámico, (Ω, B, P, T), generado por el mercado cumpla con

donde todos los subconjuntos G pertenecen a la σ-álgebra de Borel, G ∈ B, lo que dota al sistema dinámico de propiedades asintóticas que permiten establecer la equivalencia entre los diferentes espacios de medida mencionados anteriormente; para más detalles véase Gray (1988). Estas propiedades de estacionariedad asintótica en media (AMS) del sistema incluyen:

• a)

  La equivalencia en probabilidad, P(G)=P¯(G) si el evento G es invariante, T⁻¹(G) = G

• b)

  Equivalencia en media, EP[g]=EP¯[g], si la variable g es invariante a.s, P(g(T(x))) = g(x)) = 1.

• c)

  La media asintótica de la medida P¯ domina asintóticamente a la medida P, i.e., si

Estas tres características garantizan la convergencia de los promedios muestrales y caracterizan los límites de las inferencias sobre las fuentes dando lugar al teorema de descomposición ergódica para sistemas dinámicos, (Ω, B,m, T), con media finita, m¯, i.e.,

donde la función f pertenece al espacio de las funciones integrables, f∈ L1(m¯) e I es una σ-álgebra de eventos invariantes.

La idea central de este teorema de descomposición ergódica es que cualquier fuente estacionaria, aun siendo no ergódica¹², puede ser representada mediante una mezcla de subfuentes estacionarias y ergódicas.

Esto no es una cuestión menor, pues aun suponiendo que el mercado no sigue la propiedad Markoviana de un paso¹³ podría presentar efectos de memoria larga como los sugeridos por Mandelbrot, los cuales son susceptibles de ser medidos en algunos intervalos de tiempo.¹⁴ Este teorema provee las bases para proponer a la entropía (y transformaciones de ella) como una medida de eficiencia que puede ser aplicada a una amplia gama de procesos estocásticos, entre ellos a los rendimientos de mercado; para más detalles al respecto véase Gray (2009). En pocas palabras, este teorema permite usar sucesiones en el tiempo de distribuciones empíricas de los rendimientos de mercado como el alfabeto generado por éste.

Por lo anterior es necesario definir un espacio de medida (Ω, B) y una transformación T: Ω → Ω sobre la cual es posible establecer otro espacio medible, (Λ, L), con una familia de medidas ergódicas, {m_λ;λ ∈ Λ}, sobre el primer espacio (Ω, B) y un mapeo medible, ψ :Ω → Λ tal que la transformación sea invariante, ψ(T(x)) = ψ(x), para toda x. Del mismo modo, si se establece una medida estacionaria, m, sobre el espacio medible, (Ω, B), y P_ψ es la distribución inducida, P_ψ(G) = m(ψ⁻¹(G)) para G ∈ Λ, entonces

Además, si se define una función sobre el espacio de las funciones m-integrables, f∈L¹(m), sobre la medida de probabilidad original, también lo será sobre la medida de probabilidad inducida, ∫ dP_ψ(λ)m_λ (F) para toda F∈B. Esta última propiedad garantiza la existencia de la entropía tanto para el proceso original (los rendimientos de mercado) como para cualquier transformación que se haga de ella, v.g. una transformación logarítmica, como la usada en la construcción de la entropía.

Todos estos resultados, propios de los procesos estocásticos y comúnmente utilizados por econometristas y financieros, implican la posibilidad de medir la eficiencia del mercado, al menos durante algunos periodos donde la independencia del proceso y su estacionariedad sean demostrables a través de transformaciones logarítmicas sobre la medida de probabilidad empírica; es decir, a través de la entropía del alfabeto generado por el mercado.

En efecto, la variedad de los posibles resultados y la distribución de los rendimientos observados en el mercado determinan el grado de “sorpresa” generado por el proceso estocástico asociado a la distribución de los rendimientos, por lo que se puede esperar que un mercado con poca variación en los rendimientos tenga una menor entropía que un mercado donde las sorpresas son comunes. Esta cualidad convierte a la entropía en un candidato para medir la eficiencia del mercado y hacerla comparable con otros periodos, pues en teoría el proceso estocástico que genera el alfabeto es el mismo.¹⁵

Una vez revisados los conceptos de procesos estocásticos necesarios para establecer a la entropía como medida de eficiencia, dado que mide la cantidad de información nueva (sorpresa) generada por los nuevos precios o rendimientos, es necesario explicar, a grandes rasgos, la naturaleza de esta medida y algunos de los alcances de su uso como medida de eficiencia.

Entropía de Shannon

Sea (Ω, B, P, T) un sistema dinámico y f una función sobre el alfabeto definido en sobre el cual está definido un proceso estocástico, f_n = f Tⁿ, que puede ser visto como una función “codificadora” del espacio original, i.e., de los estados de la naturaleza a los rendimientos, y que puede ser transformado en un modelo de Kolmogorov que genera, a su vez, un alfabeto finito, i.e., las frecuencias de la función de distribución empírica. Estas dos funciones generan una sucesión estacionaria o de códigos invariantes¹⁶ que son equivalentes bajo ambas transformaciones, esto es:

lo cual puede ser interpretado como la transformación de los estados de la naturaleza (reportes de ganancias, escándalos corporativos, cambios tecnológicos, etc.) en rendimientos de activos que pueden ser medidos y clasificados en una función de distribución empírica sobre con la cual se calcule la entropía del sistema.

Estas transformaciones pueden ser usadas para generar un espacio de probabilidad de la forma (Ω, B, P) sobre el cual se calcule la entropía, entendida como el supremo de todas las tasas de entropía del sistema, la cual está dada por

donde es necesario definir al producto de 0[ln(0)] como 0 con el fin de mantener el orden de la ecuación anterior.¹⁷

Esta entropía máxima también es llamada la entropía invariante Kolmogorov-Sinai del sistema, por lo que la tasa de entropía media del sistema está dada por

Para el análisis de la eficiencia de mercado, la entropía será encontrada de manera computacional; así, se calcula una función de distribución empírica —histograma con 100 particiones— para cada año de actividades. Este histograma es construido de la manera tradicional: primero se encuentra el valor de la distancia entre el máximo y el mínimo de la muestra; después se separa por el número de particiones deseadas (100); posteriormente se realiza un conteo de los valores que quedan dentro de cada una de las 100 clases (letras del alfabeto) de cada histograma.

Una vez obtenido, se calcula la entropía de Shannon siguiendo (9). Este mismo proceso se realiza para todos los años de la muestra, por lo que se genera una serie de tiempo correspondiente a la entropía de cada año. Esto equivale a hacer una serie de tiempo con el promedio ponderado (por la distribución empírica) de la información nueva provista por cada parte del alfabeto (clase) de cada año.

Este proceso meramente numérico es válido dado que se cumple con todas las hipótesis señaladas en párrafos anteriores, a saber: se trata de un proceso ergódico con una función de distribución equivalente a la del mercado para cada parte de la discretización del proceso estocástico que genera los precios de mercado o sus transformaciones (rendimientos).

Esta forma de construcción de la entropía está basada en el trabajo de Billingsley (1965), quien propone que dado un alfabeto finito¹⁸ {x_n} con una distribución m es posible establecer un vector de variables aleatorias Xkn=(Xk, Xk+1,…, Xk+n+1) de dimensión n que proporcionen un bloque de la muestra. Por lo tanto, las variables aleatorias n⁻¹ ln m(Xkn) son uniformemente integrables.

Este importante hecho permite establecer a una función empírica como la base del cálculo de la entropía del alfabeto generado por el mercado y representado por sus rendimientos. Ahora sólo resta establecer la afinidad¹⁹ entre el alfabeto generado por el proceso estocástico generado por el mercado y la entropía calculada mediante las distribuciones empíricas de los rendimientos.

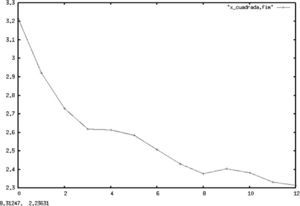
En su trabajo, Gray (2009) demuestra que si un alfabeto discreto de un proceso estocástico, {x_n}, tiene dos medidas de probabilidad, m, q, entonces para cualquier mezcla entre ellas dada por λ∈(0,1) la entropía del alfabeto está acotada por la inducida por la distribución dominante. Esto es,

donde h₂ (λ) es una función positiva de λ. La igualdad se alcanza en el caso particular de encontrar un proceso estacionario, esto es

Por lo tanto, la expresión (11) representa un argumento para suponer que, aun bajo procesos estocásticos que presentan un cambio de régimen,²⁰ la combinación lineal de las distribuciones de los procesos y, por ende, de sus entropías convergerán a la entropía del estado dominante.

Esto no es una cuestión menor, pues la aplicación de la medida de Kolmogorov-Sinai, expresada en (10), y la demostración de dominancia de una entropía en la propuesta de Gray, establecida en (11), permiten suponer que las entropías inducidas por las distribuciones empíricas del proceso convergerán a la entropía del estado dominante y, por lo tanto, el proceso de maximización de entropía puede ser sustituido por un algoritmo numérico que aproxime estas condiciones, como se hace en este trabajo.

Tal y como se puede observar, se detalló la forma en que se calcula la entropía de Shannon para cada año de la muestra y la validez del procedimiento numérico anteriormente explicado. Es decir, se aporta el aparato formal que valida la métrica aquí propuesta.

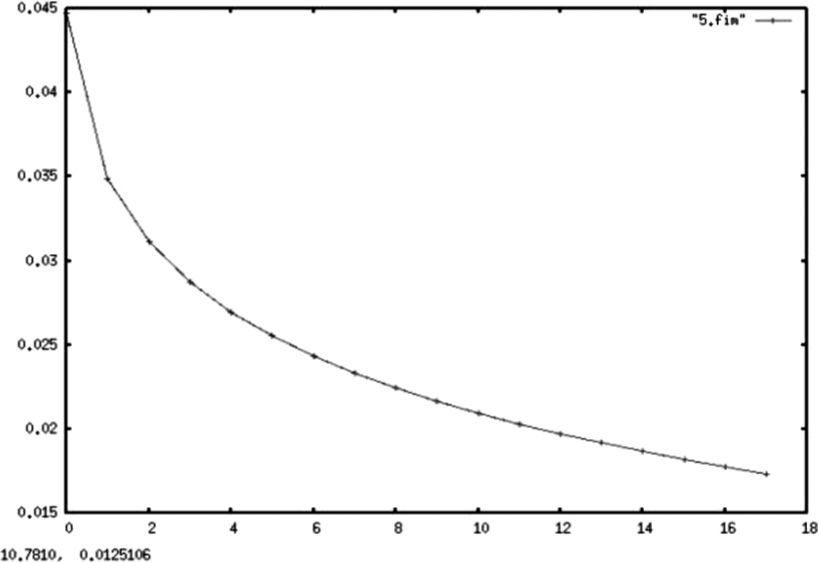
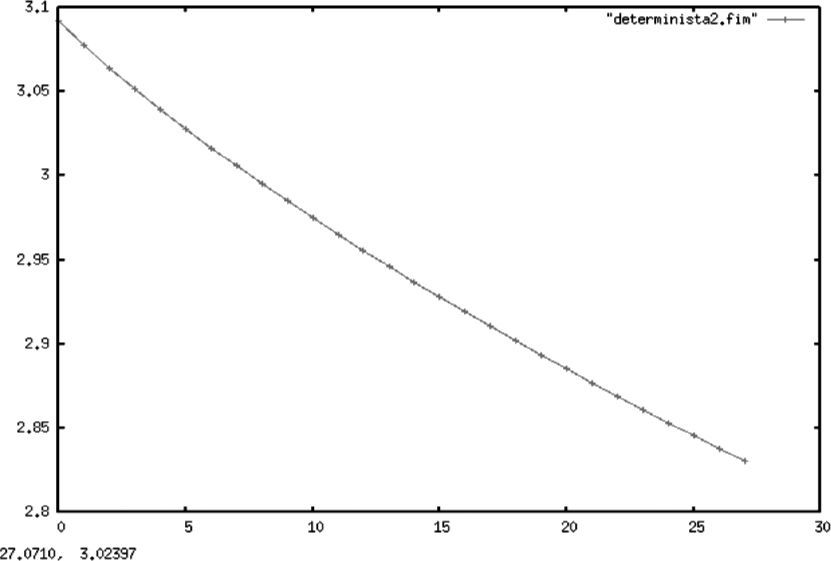
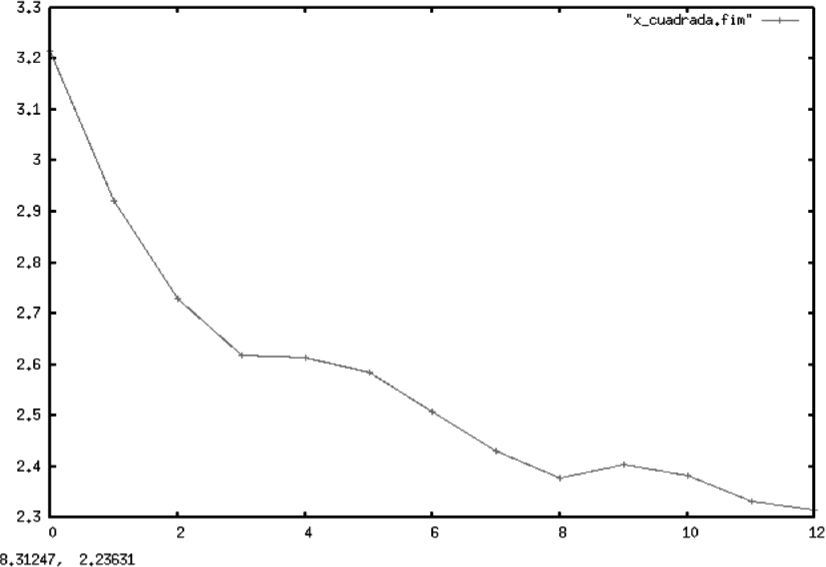
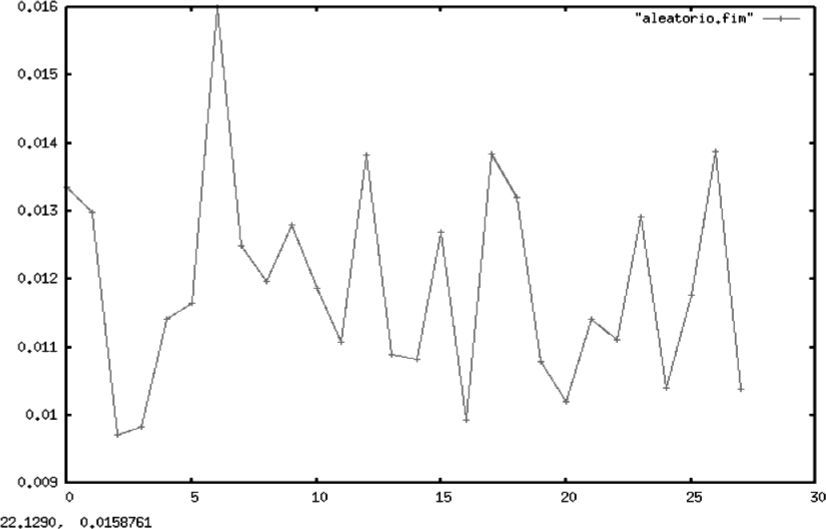
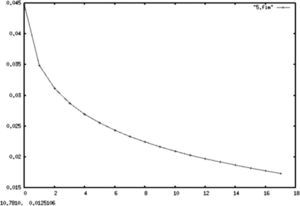
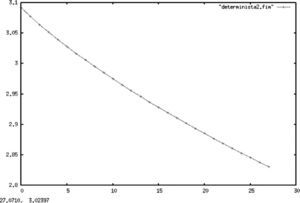
Cotas de comportamiento para la entropía como medida de eficiencia

A continuación se determinan las cotas sobre el comportamiento de la entropía como medida de eficiencia de mercado. Dichas cotas se establecen considerando los casos extremos, es decir, yendo de procesos deterministas puros a procesos estocásticos definidos únicamente por ruido blanco. De esta manera, en un punto intermedio se encontrarían los procesos deterministas contaminados por alguna clase de ruido, tal y como podría esperarse en los procesos estocásticos propios de las finanzas.

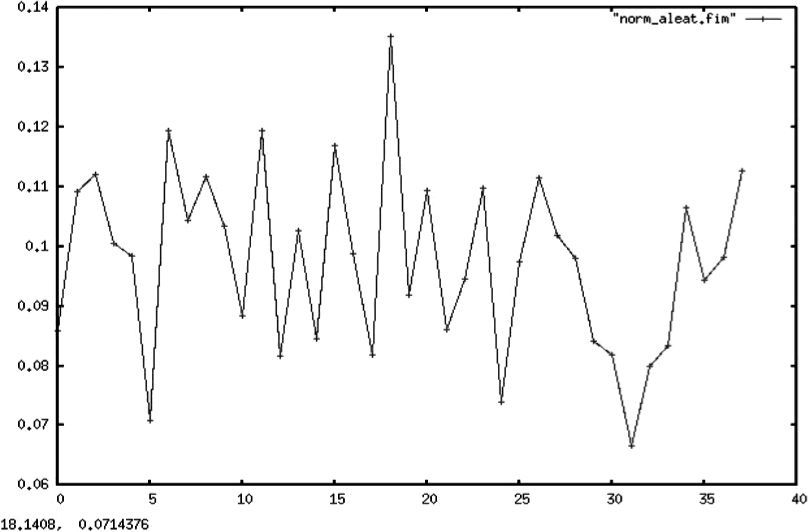
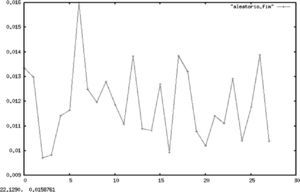
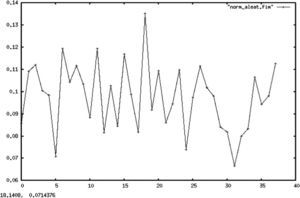
En las gráficas 1, 2 y 3 se muestran, respectivamente, los cálculos para la entropía de una constante, una recta y una parábola. En todos los casos, se hizo una serie de tiempo (determinista) siguiendo una función que arrojó 500 valores²¹ (para cada una de las funciones) que fueron agrupados en un histograma para aplicar después el algoritmo descrito anteriormente.

Gráfica 1.

Entropía para una constante

Gráfica 2.

Entropía para una recta

Gráfica 3.

Entropía para una parábola

Resulta importante aclarar que en todos los casos el alfabeto usado para el cálculo de la entropía del proceso es el generado por las distribuciones empíricas de la muestra, lo que resulta válido dada la convergencia de la entropía muestral a la del proceso original demostrada en secciones anteriores. Esto es válido aun en casos degenerados como los de procesos deterministas, los cuales sufren de un rápido decaimiento de la tasa de información dada proporcionada por el proceso.

Todos los gráficos mostrados a continuación mantienen en el eje Y el valor de la entropía de Shannon, mientras que en el eje X se muestra el número de particiones muestrales asociadas a cada entropía.

En contraste con el caso determinista, las gráficas 4 y 5 muestran la entropía de ruido blanco y de un proceso estocástico de variables uniformes iid. En ambos casos, la entropía permanece en un patrón oscilante dado que cada nueva realización aporta nueva información sobre el proceso.

Gráfica 4.

Entropía para un proceso estocástico uniforme

Gráfica 5.

Entropía para un ruido blanco

Es importante aclarar al lector que esta sección no pretende otra cosa sino mostrar de forma empírica las cotas teóricas que Shannon dio en su trabajo seminal para el comportamiento de la entropía. En él se establece que una constante tendrá una entropía de cero y se demuestra que la distribución de probabilidad con mayor entropía es la uniforme, pues corresponde a la distribución de mayor sorpresa en la información, lo que coincide con el criterio bayesiano de menor información a priori.

Entropía como medida de eficiencia para series de tiempo de diversos índices bursátiles

En el transcurso de esta sección se lleva a cabo el cálculo de la entropía, siguiendo (6), de diversos índices bursátiles con un algoritmo (mostrado en un apéndice) que divide la muestra por años calendario. Específicamente, para cada año se toma una partición (alfabeto muestral), comenzando con 10 intervalos y llegando hasta 500, para calcular la distribución empírica de los rendimientos de cada mercado (visto como serie de tiempo), lo que permite captar cambios estructurales o rompimientos abruptos propios de periodos de gran estrés financiero; todo ello está basado en la idea de dominancia de un alfabeto (partición) específica tal y como lo explicó Grey (2009) y se resume en (11).

Sobre estas particiones se toma el valor más grande de la entropía del sistema y se repite el procedimiento un número grande de veces tomando como partición aquella que lleve a la entropía a su máximo valor, esto se hace para toda la muestra de tal manera que se alcance la entropía máxima del sistema, lo cual fue formalmente detallado en (10).

Todos estos cálculos parten del supuesto de que el alfabeto generado por los precios o sus transformaciones (rendimientos) representa el alfabeto generado por el mercado, lo cual se fue formalizando al establecer medidas equivalentes entre el mercado y sus precios (5) para después fundamentar la validez de este cálculo en series de tiempo ergódicas (6) y, finalmente, proveer de una base teórica para el uso de probabilidades empíricas como probabilidades inducidas del proceso (7).

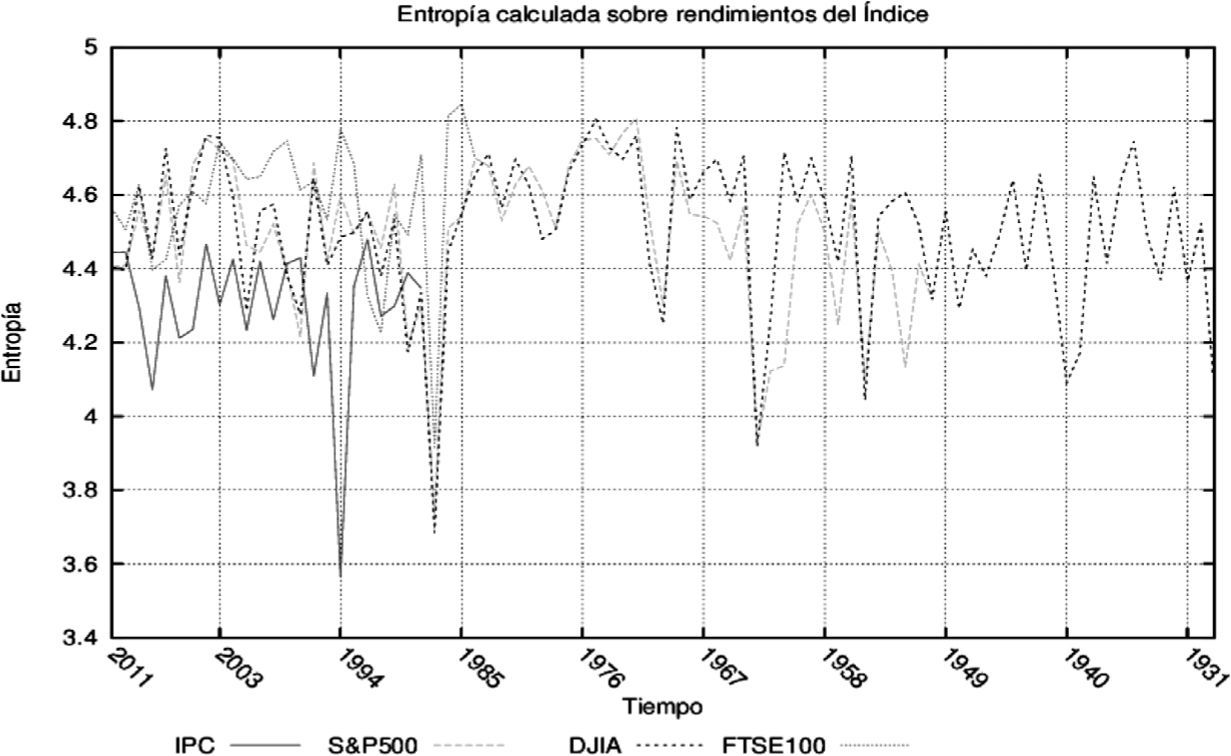
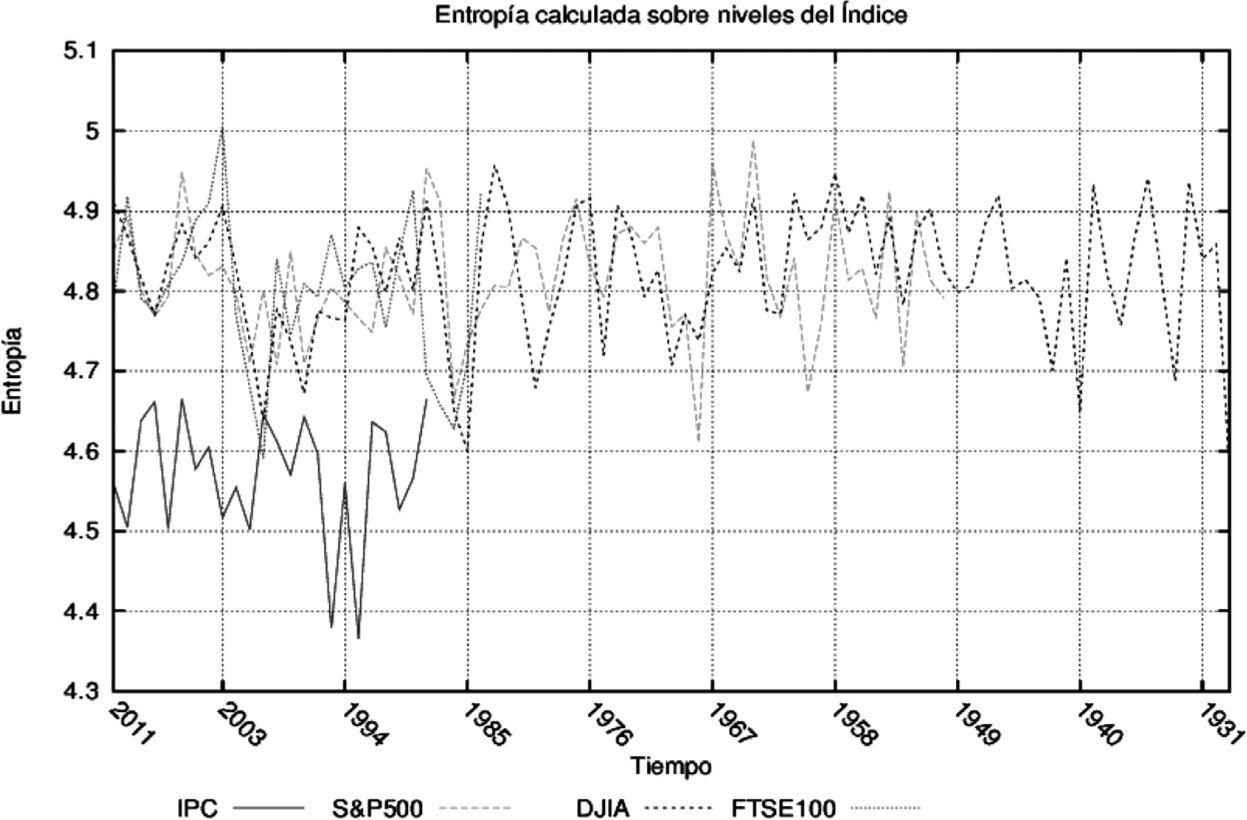
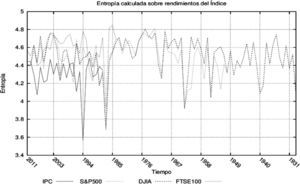
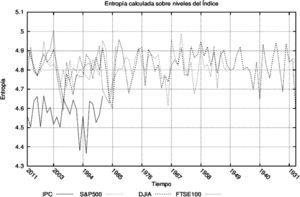
Con el fin de mostrar que la medida propuesta es adecuada, se calculó la entropía anual para el S&P500²², FTSE100²³, DJIA²⁴ e IPC²⁵. En todos ellos se observó una caída simultánea en la entropía de precios y rendimientos en las épocas de pánico financiero que estuvieron caracterizados por corridas en los mercados.

En las gráficas 6 y 7 se muestra la capacidad de esta medida de detectar periodos de pánico en los mercados durante periodos específicos de crisis y claramente identificables,v.g. el desplome de las bolsas norteamericanas en 1987 causado por los algoritmos de compra y venta, la caída de las bolsas de 1998, el asesinato de John F. Kennedy en 1963, el final de la guerra de Corea en 1953, la crisis de 1929, la reciente crisis subprime (2007 -2008) y otros momentos caracterizados por el pánico financiero en los que los agentes se deshacían de sus activos a cualquier costo.

Gráfica 6.

Entropía anual para los rendimientos de diversos índices de mercado

Gráfica 7.

Cambio porcentual en la entropía de diversos índices de mercado

Las gráficas anteriores sugieren una aparente sincronización en tiempos de pánico financiero que crece con la integración de los mercados (excepto la crisis de 1994 en México que no se contagió al resto del mundo), además de una adecuada respuesta de la entropía ante pánicos de mercado y la formación de la burbuja previa. En este sentido, es posible observar que la entropía de los niveles de los índices se mantiene debajo de los promedios anteriores en los dos o tres años previos al estallido de las burbujas especulativas de 2007, 2000 y 1987.²⁶

También de las gráficas anteriores se puede inferir que las entropías calculadas a partir de transformaciones hechas sobre los indicadores de mercado también siguen los cambios de la medida en niveles. Ello sugiere el cumplimiento de los supuestos hechos en la parte teórica del trabajo sobre las transformaciones y dominancia del alfabeto generado por la fuente (mercado).

Aunque limitada por la enorme cantidad de datos necesarios para la medición (un año de datos diarios arroja un único punto en las observaciones), la entropía se muestra como una buena medida de eficiencia de mercado. Posiblemente ejercicios con datos de mayor frecuencia o con muestras móviles de n observaciones (a cada paso salen las n observaciones más antiguas y se remplazan con n nuevas) resulten más adecuados para el control de formaciones de burbujas especulativos o como indicador de la construcción de rachas de mercado.

Conclusiones

A lo largo de este trabajo se ha mostrado que la entropía, traída de la teoría de la información, resultó ser una medida apropiada de eficiencia de mercado. A partir de la construcción teórica de un sistema dinámico que genera el alfabeto propio de los mercados, hasta el cálculo de la tasa de entropía inducida por la función de distribución empírica de los rendimientos de índices bursátiles de diferentes mercados, la entropía captura la estructura de dependencia del mercado y con ello la información que los índices proporcionan sobre el comportamiento colectivo del mismo. Muestra de ello es la capacidad mostrada para detectar, a posteriori, la pérdida de eficiencia de mercado en los años de fuertes caídas en los mercados cuando las ventas se realizaban en un ambiente de pánico.

También se hizo patente que lo importante en el cálculo de la eficiencia de mercado no es el valor tomado por la entropía, sino sus cambios con respecto de otros periodos (años). Esto se mostró al usar diferentes particiones para la misma muestra, teniendo como resultado caídas en la entropía (aún con valores diferentes) en los mismos años de irracionalidad (pánico) en los mercados. Con respecto a este punto es importante aclarar que la elección de la base del logaritmo sobre el cual se realiza la medición es irrelevante dada la posibilidad de cambiarla.

Del mismo modo, el análisis de eficiencia basado en entropía sugiere que la irracionalidad en los mercados es mayor en épocas de caídas drásticas que en épocas de auge, i.e., los operadores (traders) son más proclives a sobre-reaccionar a las malas noticias.²⁷ Esta cualidad de la entropía la vuelve una candidata natural para convertirse en una medida de detección de burbujas especulativas o de corridas de mercado; su uso queda como posible línea de investigación futura, así como también el uso de la entropía “intra-día” como medida de eficacia de los “formadores de mercado”. Otra posible línea de investigación surgida a partir de este trabajo es la posible sincronización de los mercados mundiales, la cual implicaría la disminución de los beneficios obtenidos por la diversificación internacional en los portafolios de inversión.