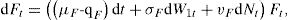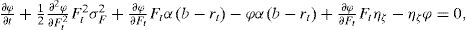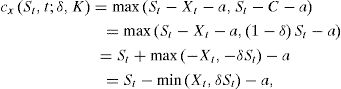Valuación con opciones reales de proyectos con flujos correlacionados con fundamentales económicos y con saltos extremos Viabilidad del caso COMERCI UCB

Resumen

Este trabajo extiende el método de flujos de efectivo descontados para valuar proyectos de inversión a través de la incorporación de opciones reales. Se supone que los flujos de efectivo generados por la empresa están correlacionados con fundamentales macroeconómicos, particularmente con la tasa de interés; asimismo, se supone que presentan saltos cuyo tamaño está dado por una distribución de valores extremos. Estos flujos son vistos como un portafolio de opciones reales, que surgen de un proceso de optimización dinámica estocástica donde el inversionista (el empresario) busca maximizar su utilidad total descontada, sujeto a la riqueza que posee. Esta riqueza incluye el proyecto de inversión, un bono libre de riesgo de incumplimiento y un conjunto de opciones reales asociadas al proyecto.

Abstract

This paper extends the method of discounted cash flows to value investment projects through incorporating real options. It is assumed the cash flows generated by the firm are correlated with macroeconomic fundamentals, particularly with the interest rate. It is also assumed that the cash flows have jumps whose size is given by an extreme value distribution. The flows are viewed as a portfolio of real options. The options arise from a stochastic dynamic optimization process where the investor (the entrepreneur) seeks to maximize his/her total profit discounted, subject to the wealth he/she possesses. This wealth includes the investment project, a risk-free bond, and a set of real options associated with the project.

Introducción

A pesar de los grandes avances en la valuación de activos financieros, en la creación de derivados cada vez más sofisticados y en las mejoras continuas en herramientas para el control de riesgos, existen todavía muchas empresas que —sin considerar todos estos avances— siguen valuando sus proyectos de inversión con métodos estáticos. Es difícil justificar que existan todavía grandes corporaciones que recurren a metodologías estáticas de valuación de proyectos que no toman en cuenta el dinamismo de los fundamentales macroeconómicos ni la flexibilidad en las decisiones futuras de inversión; del mismo modo, es fácil apreciar que las variaciones observadas en los flujos de efectivo distan mucho de lo que la simple aplicación del VPN (Valor Presente Neto) tradicional o el método de Gordon (1959) pueden explicar; también resulta natural pensar que la dinámica del entorno macroeconómico, los movimientos en la tasa de interés de referencia y los cambios esperados en el crecimiento de la empresa afectan el valor de la misma. Por ello, una propuesta metodológica completa para la valuación de proyectos deberá incorporar todos estos aspectos.

Este trabajo pretende incorporar una estructura de plazos sobre el factor de descuento en el proyecto y la posibilidad de saltos extremos en los flujos de efectivo, así como permitir la correlación de los flujos con la tasa de interés libre de riesgo y dar un valor a la flexibilidad de las decisiones futuras del negocio, v.g. cerrar, posponer o expandir un proyecto. Todo ello con el fin de modelar las posibles causas de las variaciones en los precios de mercado que escapan del VPN tradicional y que son captadas parcialmente por el Capital Asset Pricing Model (CAPM) o el Arbitrage Pricing Theory (APT).

El método propuesto en esta investigación difiere sustancialmente de la valuación de activos que utiliza la aproximación de Markov switching desarrollado por Lux (2008) o del análisis de volatilidad del tipo GARCH, v.g.Klaassen (2002), o de otros trabajos similares, ya que incorpora la posibilidad de saltos de tamaño extremo para los flujos del proyecto. Aunque algunos modelos de valuación basados en técnicas como el FIGARCH, véanse por ejemplo Baillie et al. (2007) o Kasman y Torun (2007), incluyen efectos de colas pesadas en el análisis, éstos no incorporan una correlación con el entorno económico (reflejado por la tasa de interés) o la incorporación de la flexibilidad corporativa en decisiones futuras de inversión, la cual es un elemento idiosincrático de la empresa y, por lo tanto, tomado frecuentemente como un error en el modelado.

Por otra parte, modelos como el de Chepakovich (2000) incorporan una tasa de interés variable y modelan el cambio de la estructura de capital de la firma hacia el promedio industrial; dicho modelo también incorpora el efecto de los warrants sobre ésta, a la vez que proyecta una política de crecimiento de activos en función del cambio de los ingresos operativos, aunque en el fondo es una extensión semiestocástica del VPN. A diferencia del modelo propuesto, el de Chepakovich no captura el efecto de reversión a la media de la tasa de interés, ni la correlaciona con los flujos de efectivo; además, no considera el efecto de la flexibilidad estratégica en la valuación. Por las razones señaladas, el modelo de Chepakovich no resulta adecuado para empresas dentro de industrias maduras o en consolidación.

Sobre la misma línea de investigación existen modelos del tipo de “información económica aplicada”, los cuales no son otra cosa sino el uso intensivo de métodos Monte Carlo que, junto con el juicio de expertos en la materia, buscan valuar la empresa a partir de datos contables y algunos otros datos del entorno económico y del ambiente de negocio; para más detalles véanse Hubbard (2010) o Fischhoff, Phillips y Lichenstein (1982). Este método tampoco vincula los resultados de la empresa con el desempeño actual y de largo plazo de la misma.

Por otra parte, existe una gran cantidad de modelos de valuación de activos que no toman en cuenta aspectos intrínsecos o macroeconómicos que rodean a la empresa, dejando todo el peso de la valuación en su comportamiento contable y de mercado de corto plazo en función de algunas razones tales como los ingresos por acción, utilidades por acción u otras eminentemente contables; para más detalles véanse White, Agee y Case (1981), Graham (2004) y Villalón (1991).

Como se ha podido ver, existen algunos trabajos que profundizan el estudio de la relación de los flujos de efectivo con la tasa de interés, v.g.Hirshleifer (1961), o bien que basan sus pronósticos en métodos semiparamétricos que tienen que ser calibrados con el fin de ser usados adecuadamente. A diferencia del modelo propuesto, éstos no toman en cuenta, de manera simultánea, la dependencia de los negocios con respecto del ciclo o con las principales variables financieras, la posibilidad de incluir valores extremos en los flujos de efectivo, o menos aún el uso de opciones reales, las cuales no son otra cosa sino el uso de la tecnología de opciones financieras aplicadas a la valuación financiera de proyectos, v.g.Henderson y Hobson (2002), como una forma de valuar la flexibilidad corporativa en un entorno de riesgo e incertidumbre; para más detalles sobre opciones reales véanse Dixit y Pindyck (1994, 1995, 2000), Schwartz y Trigeorgis (2001), Abel (1983) y Trigeorgis (1996).

Durante el desarrollo del presente trabajo, se llevará a cabo un experimento de simulación Monte Carlo donde se construyen, en cada periodo (trimestral), estimaciones de los flujos de efectivo a través de un modelo ARIMA, los cuales serán descontados usando la WACC del periodo hasta, por ejemplo, el trimestre veinte, después del cual se supone una perpetuidad. Una vez valuados los flujos de efectivo del proyecto, éstos son usados para calcular las primas asociadas a las opciones reales con el fin de valuar un proyecto de inversión de manera más realista.

Una vez establecida las características distintivas de este trabajo con respecto de la literatura existente, se mostrará a continuación que esta valuación corresponde al óptimo de un problema de optimización dinámica estocástica en las condiciones antes planteadas. Posteriormente, se valuarán —con el modelo propuesto— las acciones COMERCI UCB en el periodo 2000:1–2010:4. Más adelante se efectuará la descripción de las opciones reales asociadas al proyecto.

La elección de esta empresa obedece, en particular, a las peculiares circunstancias asociadas con el incumplimiento crediticio asociado al mal manejo de posiciones cortas en opciones de venta de dólar estadounidense que estuvo a punto de quebrar la empresa a finales de 2008 y que condujo a una interesante negociación con los acreedores que desembocó en una reestructuración de la deuda.¹

A casi dos años de la reestructuración de la empresa, ha trascendido el hecho que los acreedores estuvieron de acuerdo en renegociar la deuda debido a la alta posibilidad de supervivencia de la empresa si se le daba a ésta la opción de permanecer en el mercado, pues sus aceptables resultados operativos hacían plausible el pago, en el largo plazo, del pasivo recién adquirido. También trascendió que durante la negociación se plantearon las posibilidades de contraer o cerrar la empresa en función a los resultados de los siguientes trimestres. Es este hecho, y su imprevisibilidad, el que da lugar al ejercicio de valuación de opciones americanas mostrado en la sección Valor de la flexibilidad de permanencia o abandono de Comercial Mexicana. Para finalizar este trabajo, se establecen las conclusiones y posibles líneas de investigación futuras. Básicamente, se demuestra que la inclusión de opciones reales, así como la modelación de los saltos de valores extremos en los flujos de efectivo y la correlación de la tasa de interés, proveen de una mejor valuación del activo, incorporando el valor pecuniario de la flexibilidad en la decisión corporativa.

Solución teórica del problema de optimización dinámica estocástica (PODE)

Con el fin de cumplir con los objetivos establecidos en el trabajo, se considerará una versión modificada del VPN donde se supondrá un proyecto de inversión con duración de n años, un desembolso inicial I₀, flujos de efectivo del proyecto η_t, t = 1,2.…,n, y una tasa de descuento representada por la tasa WACC (Weighted Average Cost of Capital). Si los flujos de efectivo son aleatorios, el VPN aumentado (VPNA) por las primas de las opciones puede ser expresado mediante:

donde E[η_t| F] representa el beneficio neto esperado del flujo de efectivo en el periodo, t, el cual no necesariamente es positivo; ϕ_i, i = 1,2,…,j, representan las primas de las opciones reales al alcance de la firma. En esta ecuación podría considerarse que todos sus elementos, a excepción del desembolso inicial I₀, son aleatorios, aunque relacionados a la tasa de interés libre de riesgo crédito, la cual será modelada mediante el modelo de tasa corta de Vasicek (1977).

El problema de optimización dinámica estocástica, en tiempo continuo, que enfrenta un productor bajo las condiciones especificadas por este trabajo, puede ser descrito mediante la esperanza del valor presente de los beneficios del inversionista, condicionado al conjunto de información representado por la sigma-álgebra², F_t, en tiempo t, esto es

donde λ es la tasa de descuento aplicada según el sector y grado de apalancamiento del proyecto (en este caso la WACC) y F_t representa una sigma-álgebra al tiempo t (información relevante al tiempo t). Observe que (2) es la versión en tiempo continuo del segundo término del lado derecho de (1). Las opciones reales, en el tercer término del lado derecho, se introducirán posteriormente. Por último, sin pérdida de generalidad, se supondrá que I₀ ≡ 0.

Surge ahora la necesidad de estimar el valor pecuniario de la flexibilidad de decisión corporativa como un derivado, pues a solicitud de los diversos agentes interesados en el desarrollo de la empresa, los accionistas deberán tomar decisiones futuras que se verán reflejadas en las opciones reales, ϕ_i, i = 1,2,…, j, relacionadas con el desarrollo de la firma. Observe que a estas opciones les falta especificar el plazo de vencimiento y la forma de ejercicio, i.e., las condiciones de frontera; ambas características determinan el tipo de opción real analizada. Para mayores detalles, véanse Damodaran (2001) o Venegas-Martínez (2008).

En el caso de los tiempos de ejercicio del portafolio de opciones, la naturaleza casi impredecible del mismo hace necesaria la modelación a través de opciones americanas —para más detalles véase Barone-Adesi y Whaley (1987)—, lo que vuelve imprescindible el uso de métodos numéricos en la valuación³. Por tanto, es posible suponer que el portafolio del inversionista está conformado por posiciones largas en un bono, B_t, que paga una tasa libre de riesgo y en el activo riesgoso, F_t, además de un portafolio de opciones, ϕ_t sobre dicho activo; esto es:

donde ω_i representa la proporción de riqueza que el inversionista asigna a cada activo en su portafolio. En el caso de la tasa pagada por bono libre de riesgo, B_t, se supondrá que sus cambios marginales, dB_t, siguen un proceso de difusión, con reversión a la media, como el establecido en Vasicek (1977); esto es:

donde α es la velocidad de ajuste de la tasa corta, r_t, hacia su valor de largo plazo, b, por unidad de tiempo. Esta tendencia es alterada por la volatilidad, σ_B, que amplifica o contrae al movimiento browniano bW_Bt, mientras que la diferencial del activo riesgoso sigue una ecuación de difusión con saltos de la forma

donde µ_F representa la tendencia del rendimiento del activo riesgoso, q_F la tasa de dividendos pagada por la empresa, σ_F la volatilidad instantánea y ν_F el tamaño medio del salto en los rendimientos. La ocurrencia de saltos está dada por un proceso de Poisson, dN_t, que presenta un salto por unidad de tiempo con probabilidad ζdt. El parámetro de intensidad ζ mide el número promedio de saltos por unidad de tiempo. En general, el salto es inesperado y sus efectos pueden ser, dada la periodicidad trimestral, englobados en un solo evento, lo cual es consistente con el modelado a través de saltos de Poisson.

En esta investigación se obtendrá el tamaño promedio del salto como el promedio de los excesos de los rendimientos, i.e. rendimientos por encima de dos desviaciones estándar,⁴ lo cual coincide con lo que tradicionalmente se considera en la literatura un exceso de valores extremos; para más detalles véase Reiss y Thomas (2007).

Dado que en este trabajo se aborda el problema de las opciones reales (americanas) desde la perspectiva planteada por Barone-Adesi y Whaley (1987), es necesarioplantear la opción americana, ϑ_t, como una combinación lineal entre el valor de su contraparte europea, ε_t, y el valor del premio por ejercicio anticipado, ϕ_t. Es decir, ϑ_t = ε_t + ϕ_t

La inclusión del enfoque planteado por Barone-Adesi y Whaley no afecta sustancialmente el desarrollo de la ecuación diferencial estocástica (EDE) que sigue el derivado. En efecto, en su artículo estos autores demuestran que la inclusión de un término adicional que representa el premio por ejercicio anticipado, ϕ_t, redunda en una ecuación diferencial parcial de segundo orden cuya solución puede ser incorporada al problema global al ser función del mismo subyacente, F_t. Este premio por ejercicio anticipado puede ser expresado mediante ϕ_t = ϑ_t –ε_t, el cual sigue una ecuación diferencial estocástica similar a la de cualquier otro derivado;⁵ para más detalles véase Mikosh (1998).

La presencia de un proceso de difusión con saltos para los rendimientos del activo riesgoso conlleva a que cualquier derivado siga una ecuación diferencial estocástica con saltos de la forma

donde

y

Es importante hacer notar que la inclusión de los términos de saltos en el activo únicamente afecta al segundo término de la ecuación (6), el cual se transmitirá a lo largo de todo el ejercicio a través de la ecuación diferencial estocástica del premio por ejercicio anticipado. Aunque no afecta la solución propuesta en el trabajo original, pues ésta es absorbida en el premio por ejercicio anticipado, por lo que el uso de su metodología no se ve afectado.

Una vez obtenidas las ecuaciones diferenciales que modelan los rendimientos de los tres tipos de activos a los que tiene acceso el inversionista, es posible modelar la ecuación dinámica estocástica del rendimiento de su riqueza, a_t, de tal forma que:

Para determinar la solución del problema de maximizar (2) sujeto a (7) es necesario establecer las tenencias óptimas de cada uno de los activos a los que tiene acceso el agente, así como el beneficio esperado óptimo.⁶ Para ello se tiene que plantear el problema de maximización del valor esperado de los beneficios descontados⁷ del inversionista por la tasa apropiada, λ, sujeto a la restricción presupuestal de su riqueza; esto es:

donde F_t representa toda la información relevante disponible hasta el tiempo t. Para resolver este problema —véase, por ejemplo, Chiang (1992)— se recurre a una función de valor de la forma

a partir de la cual se obtiene la ecuación recursiva:

La ecuación anterior incluye al proceso de Poisson (salto) en la ecuación diferencial que rige los rendimientos de la opción real a través de la cual se modela el riesgo de la empresa. En general, esta opción carece de valor (se encuentra profundamente fuera del dinero), excepto en los momentos que un rumor creíble sobre un choque endógeno o exógeno de la economía detona el componente de salto, dN_t, y la lleva a niveles donde su existencia afecta el valor del portafolio implícito⁸ de los accionistas, lo cual se realiza a través del componente de ejercicio anticipado de la opción americana establecido en (6).

Al plantear las ecuaciones diferenciales estocásticas que rigen los rendimientos del activo riesgoso y del derivado, sus tendencias y volatilidades se harán notorias hasta obtener la diferencial de la funcional, J(a_t,t). De esta manera se incluye la restricción que considera la opción “activa” que modela el valor pecuniario de la flexibilidad de decisión corporativa en la búsqueda del óptimo. Para resolver el problema en cuestión, se tiene que la siguiente ecuación de Hamilton-Jacobi-Bellman:

Esta ecuación refleja también la dependencia de los flujos de efectivo con respecto a la tasa de interés libre de riesgo, aunque no es un tema nuevo en la literatura, lo cual puede verse en Jiang (1998) o en Ingersoll (1987). Es importante destacar que ésta no es explícitamente reconocida como un elemento en la valuación de empresas mediante el VPN.

Para establecer la trayectoria estocástica de la riqueza, es necesario tomar la esperanza de la expresión (10) y tomar su límite cuando el intervalo (infinitesimal) analizado tiende a cero, de lo que se obtiene:

Observe que esta expresión difiere de otros problemas de optimización diferencial estocástica cuando la restricción está dada por un proceso de difusión, v.g. Venegas-Martínez (2008). En el valor promedio del número de saltos por unidad de tiempo, ζ(ω_2t + ω_1t), el cual es agregado a la esperanza de la derivada parcial con respecto de la riqueza de la funcional, J_a (a_t,t), afecta la riqueza promedio del inversionista en J_aa_tζ (ω_2t + ω_1t) unidades, no así su varianza, modificando con ello su restricción presupuestal y, por tanto, su conjunto alcanzable de beneficios. Para encontrar la solución del PODE anterior, se propone como candidato de solución a:

Después de hacer las sustituciones necesarias, se obtiene el siguiente hamiltoniano (o ecuación de Hamilton-Jacobi-Bellman):

Al tomar las derivadas parciales del hamiltoniano con respecto de cada una de las variables de control, se obtiene el siguiente sistema de ecuaciones (condiciones necesarias):

Se puede observar que la trayectoria óptima esperada del reparto de dividendos, dada por la primera derivada parcial, permanece sin cambio, a saber, Π, = β¹/(γ−1)a_t, lo que corrobora débilmente el teorema de separación de Fisher (1930).

Observe que la inclusión de un salto de Poisson correlacionado con los rendimientos del activo afecta las proporciones óptimas de las opciones y del subyacente, ω₁.y ω₂, que el inversionista debe mantener en su portafolio, no así sus beneficios. Esta solución redunda en que, ante un momento de incertidumbre provocada por el anuncio de una posible decisión corporativa, el inversionista cambia la razón de cobertura delta del activo riesgoso. El monto y dirección de este cambio será resultado de la percepción del mercado sobre la decisión corporativa, es decir, sobre el tamaño medio del salto, ν_F, o el número promedio de saltos por unidad de tiempo, ζ.

Ahora sólo resta encontrar la ecuación diferencial parcial de segundo orden que rige el precio del derivado necesario para cubrir el riesgo por decisión corporativa. A partir de las derivadas parciales del hamiltoniano con respecto a las proporciones óptimas, ω_1t y ω_2t, se tiene que:

Lo anterior implica que los premios al riesgo de las opciones reales⁹ y del subyacente son iguales. En este caso, el premio al riesgo es afectado tanto por las vola tilidades de los activos incluidos en el portafolio como por la correlación, ρ, de la tasa corta con el riesgo de decisión corporativa asociado al subyacente. Después de igualar las ecuaciones anteriores y sustituir µ_ϕ y σ_ϕ, se obtiene una ecuación diferencial parcial de segundo orden cuando el subyacente está correlacionado con la tasa libre de riesgo crédito y la tasa de interés sigue un proceso de difusión con reversión a la media; esto es:

donde

Como puede constatarse en la expresión anterior, la nueva EDP (ecuación diferencial parcial) incorpora el número promedio de saltos por unidad de tiempo, ζ, manteniendo la forma tradicional de las EDP seguidas por los derivados. Es importante hacer destacar que en esta expresión se incluye el valor de la opción americana y que su solución será obtenida a través de métodos de aproximación numérica que cumplen con una ecuación diferencial similar.

En la solución a esta ecuación la tasa de interés no es otra cosa sino un cambio de numeralia para la función de pagos; para más detalles véase Girsanov (1960) o Lamberton y Lapeyre (1996). En efecto, la ecuación (15) demuestra que la inclusión del portafolio de opciones reales en la valuación de los beneficios del inversionista toma en cuenta una parte de su riqueza que era omitida en el VPN tradicional.

También es importante notar que la EDP producto del ejercicio de optimización anterior es no lineal y su solución queda fuera del alcance de la propuesta de Black y Scholes. Del mismo modo, su solución queda fuera del alcance de los métodos tradicionalmente usados en la valuación de opciones reales, pues la presencia de saltos imposibilita el uso de árboles recombinantes. Es importante hacer notar que hasta el momento, sólo se ha hablado del valor promedio del tamaño medio del salto, ν_F, sin mencionar todavía la distribución de éste, la cual se supondrá de valores extremos (tipo Gumbell), posteriormente se detallará su estimación e inclusión en la solución.¹⁰

El caso de Comercial Mexicana, parametrización del modelo

Antes de iniciar con el desarrollo de esta sección, tal vez resulte conveniente familiarizar al lector con el caso de Comercial Mexicana. Esta empresa es una cadena de tiendas de autoservicio y restaurantes con presencia en toda la República Mexicana; en 2008 saltó a los titulares de los diarios financieros mexicanos después de un fuerte quebranto sufrido en posiciones cortas de opciones de venta de dólares norteamericanos (sus ingresos son en pesos) por un monto cercano a los cinco mmdd.¹¹

Antes de este incidente, la empresa mostraba un fuerte crecimiento en sus ventas, un adecuado posicionamiento de marca y buenas perspectivas de crecimiento a pesar de la recesión global, lo que la convertía en una empresa atractiva para la inversión. Después del incidente con los derivados, la empresa se encontró con una gran cantidad de pasivos de corto plazo (cinco mmdd) que la hacían financieramente inviable, aun a pesar de sus buenos resultados operativos.

Resumiendo, el caso planteado se trata de una empresa financieramente inviable, con buenos resultados operativos en medio de una recesión global, i.e. es el clásico caso de una empresa que debería cerrar según el VAN clásico, pero que resulta viable de incorporar la versatilidad en la valuación que introduce la valuación estocástica con opciones reales.

Durante el desarrollo de esta sección se utiliza la técnica de simulación Monte Carlo en el análisis de inversión bajo condiciones de riesgo, en la cual se incorporan las estructuras de dependencia entre los diversos factores de riesgo que afectan a la empresa, v.g. tasa de interés estocástica, la dependencia de los flujos de efectivo a ésta y la dependencia del premio al riesgo de mercado.

En el cuadro 1 se presenta la parametrización¹² que requiere la simulación Monte Carlo. Las trayectorias fueron construidas a partir de la modelación de los flujos de efectivo de COMERCI UBC de 2000:1 a 2010:2.

Cuadro 1.

Parametrización de la EDE de los flujos de efectivo

Parametrización de los flujos de efectivo
µF	0.01809663	F0	736159.00
σF	0.995491	ρ	-.14430825
ζF	2.26

Estimación de la tasa de descuento del modelo de valuación estocástico

Una dificultad para determinar el valor actual de una inversión es que pequeñas variaciones en la tasa de descuento pueden ocasionar grandes variaciones en el valor actual. En la aproximación clásica, la tasa de actualización representa la rentabilidad que el inversor exige a su proyecto. Una posibilidad es considerar que esta rentabilidad viene determinada por el costo del capital, en cuyo caso, para obtener el valor efectivo de la inversión, la tasa de descuento que debe emplear el inversionista es el costo medio ponderado de capital que tendrá, el cual es un indicador de la rentabilidad mínima que exigirá.

Si se usa como tasa de descuento el costo de capital, se estará empleando entonces la rentabilidad mínima que exigirá el inversionista. Ahora bien, otra alternativa es considerar que la rentabilidad exigida debe ser superior al costo del capital, por lo que la tasa que se debe emplear será, a su vez, más elevada. En este caso hay dos posibilidades para su determinación: la primera es suponer que la tasa debe ser la rentabilidad de las inversiones alternativas; la segunda consiste en obtener las tasas de actualización como la suma de una tasa base (entre las distintas alternativas, la más adecuada es considerar la tasa de interés de las operaciones a largo plazo sin riesgo) más una prima de riesgo y corregir el nivel de inflación; para más detalles véase Stanton (1997). En tal caso la tasa de actualización WACC_t aleatoria vendría dada por

donde

En este caso, el cambio en la tasa de interés libre de riesgo crédito sigue el modelo propuesto por Vasicek y el costo de capital sigue el modelo CAPM. Para fines prácticos, la dinámica del modelo de Vasicek puede plantearse en términos discretos como una ecuación estocástica en diferencias (Venegas-Martínez, 2008). Si se escribe β₀ = ab y β₁ = l–a, una versión discreta de r_t está dada por

donde ε_t es una variable aleatoria independiente y normalmente distribuida con media cero y varianza σ². Por lo tanto, realizando un modelo de regresión lineal simple sobre CETES¹³ a 91 días entre el 31 de marzo de 2000 y el 30 de septiembre de 2010 se sigue que la regresión está dada de la siguiente manera:

Cuadro 2.

Regresión lineal para la parametrización del modelo de Vasicek 2000:01–2010:09, para la variable CETES 2010 (129 observaciones válidas)

Desv. típica.	β0	β1	última tasa CETE
3.278505	6.51361	0.147016	4.61

Lo que redunda en los parámetros de modelado expresado en el cuadro 3.

Cuadro 3.

Parametrización para la tasa de interés libre de riesgo

Parametrización para el modelado de la tasa de interés libre de riesgo
a	0.00852984	¿r	0.0327850519038652
b	0.07636322	r0	0.0461

Aplicación del modelo de Vasicek para el cálculo de los rendimientos de mercado

En esta sección se utiliza el modelo de Vasicek para calcular los rendimientos de mercado. Asimismo, se muestra, en el cuadro 4, cómo los parámetros pueden ser estimados utilizando un proceso autorregresivo de orden uno con tendencia.

Cuadro 4.

Regresión para parametrizar los rendimientos de mercado

Desv. típica.	β0	β1	Rendimiento del mercado	Correlación rendimientos de mercado - rt
0.0621481	0.0133625	0.207885	0.05210	−0.16675632

Estadísticas principales, usando las observaciones 2000:03–2010:09 para la variable rendimiento de mercado (127 observaciones válidas).

Finalmente, se obtienen las tasas de rendimiento (tipo Vasicek) que alimentarán el algoritmo que calcula el VPN_t estocástico. En el cuadro 5 se muestran los parámetros de la ecuación de la tasa corta para los rendimientos de mercado, obtenidos a partir del IPyC.¹⁴

Cuadro 5.

Parametrización para los rendimientos de mercado

Parametrización de los rendimientos de mercado
a	0.792115	r0	0.0521
b	0.016869	ρ	-0.166756319878824
σr	0.062148

Caracterización de los saltos en los rendimientos (Distribución Gumbell)

Con el objeto de parametrizar el tamaño medio de los saltos a los que están sujetos los rendimientos de la empresa, se supondrá que los excesos sobre el umbral experimentados por éstos son un proceso estocástico independiente e idénticamente distribuido. Esto a fin de poder realizar estimaciones a través del método de Máxima Verosimilitud¹⁵.

En este caso, se supone que los excesos después del umbral siguen una distribución de valores extremos, la cual resulta del teorema de atracción del máximo (Fisher-Tippet); para mayores referencias véase Reiss y Thomas (2007). La naturaleza de los saltos en los rendimientos de una empresa requiere de una función de densidad de probabilidad que sea capaz de permitir saltos extremos en ambas direcciones, para este trabajo se optó por una distribución Gumbell, la cual está dada por:

Con el fin de modelar mediante valores extremos los flujos de efectivo del proyecto, se muestran, en el gráfico 1, los excesos sobre el umbral de los rendimientos de la empresa Comercial Mexicana, los cuales están asociados primordialmente a la revelación de información relacionada con el problema de los derivados.

Gráfica 1.

Excesos sobre el umbral para los flujos de efectivo de Comercial Mexicana (Controladora Comerci)

En la gráfica anterior se pueden observar los efectos que las operaciones con derivados tuvieron sobre la capacidad generadora de efectivo de la empresa, así como la inyección de recursos de la que fue objeto después de la renegociación con los acreedores. Evidentemente, la existencia de outliers requiere cambiar por completo la estimación de los flujos de efectivo y, por ende, la valuación de la empresa. Después de la estimación, mediante el método de máxima verosimilitud,¹⁶ usando el paquete estadístico R, se obtuvieron los siguientes parámetros para la media, µ_g, y desviación estándar, σ_g, de la distribución Gumbell:

Cuadro 6.

Parámetros para la simulación de los excesos sobre el umbral de dos desviaciones estándar

Parametrización de los saltos de los flujos de efectivo
Umbral^17	.95121951	µg	−0.14912915	σg	2.69819659

A continuación se hará una breve descripción sobre las opciones reales por considerar en el portafolio de la empresa, así como sus funciones de pago y la forma en que serán incorporadas a la valuación.

Opciones reales para la valuación financiera de proyectos de inversión

En esta sección se establece la importancia del uso de opciones reales en la toma de decisiones al interior de los consejos de administración de las empresas, pues esta técnica facilita la toma de decisiones sobre proyectos de inversión o estrategias de negocios cuando existe la flexibilidad (opcionalidad) de tomar en el futuro nuevas decisiones relacionadas con dichos proyectos o estrategias como pueden ser extender, contraer, posponer o abandonar un proyecto. En conclusión, la metodología de opciones reales, en términos generales, es la aplicación de las técnicas de valuación de opciones financieras a la valuación de proyectos de inversión y estrategias de negocios cuando existe la flexibilidad de tomar, en el futuro, nuevas decisiones relacionadas con dichos proyectos y estrategias.

Para iniciar es necesario recordar que el criterio del VPN sugiere que un nuevo proyecto o estrategia se acepta si el VPN ≥ 0; en caso contrario se rechaza. Es decir, el VPN es una regla dicotómica de decisión sobre proyectos de inversión. Una vez que un proyecto es aceptado con este criterio, rígido y pasivo, los planes de inversión no se modifican, o sea, la inversión es irreversible.

El VPN estocástico con tasa de interés variable, propuesto en este trabajo, extiende esta metodología. Sin embargo, para consolidar las decisiones sobre proyectos de inversión o estrategias de negocios se le sumarán las opciones reales como parte del método de valuación estocástico propuesto, aumentando con ello la posibilidad de que si el ambiente económico y/o el entorno de negocios son favorables dentro de un cierto periodo de tiempo, el proyecto o estrategia se expanda; hoy no se sabe si en el futuro se tendrán o no condiciones favorables para tomar esta nueva decisión. Por lo anterior, en la metodología de opciones reales un proyecto o estrategia con VPN<0 podría incluso ser aceptado si existe la flexibilidad de extenderlo, posponerlo, enmendarlo, etcétera.

A continuación se ilustra el concepto de opción real y se discute cómo la flexibilidad en las decisiones de inversión consolida el criterio del VPN estocástico. Asimismo, se introduce el VPN modificado (o aumentado) asociado a una opción real; para mayores detalles sobre el uso y tratamiento de las opciones reales véase, por ejemplo, Dixit y Pindyck (1994, 1995, 2000), Schwartz y Trigeorgis (2001), Abel (1983), Trigeorgis (1996), Venegas-Martínez (2008), Hull (2008), entre otros.

Opción real de expansión

Una empresa podría aumentar el valor presente de los flujos esperados de un proyecto en una proporción α si realiza una inversión, K', en alguna clase de activos, v.g. mediante el incremento en el nivel de ventas futuras, en la capacidad de la producción o en la base de clientes, en el tiempo T. Esta posibilidad estratégica tiene una opción asociada con el proyecto subyacente existente; si (1 + α) S_T – K' es el valor presente neto aumentado en la proporción α menos el costo de la inversión adicional K' al tiempo T, el valor intrínseco de esta opción está dado por

donde K =K'/ α y c (S_T, T; K) es el valor intrínseco de una opción europea de compra. Es importante destacar que los flujos de efectivo esperados no son un activo que se compre o venda en el mercado, lo que genera una situación de mercados incompletos. Por lo tanto, los resultados que arroja la valuación de la opción americana mediante el algoritmo de Barone-Adesi y Whaley (1987) deberán ser tomados con reserva, además de reinterpretados adecuadamente.

En el siguiente cuadro se presentan los parámetros exógenos faltantes¹⁸ para la valuación de la opción de expansión. En general, estos valores son únicamente del conocimiento de la dirección de la empresa o estimables cuando alguna información es filtrada respecto al proyecto en cuestión. Dada esta fuerte restricción, se supondrá en todos los casos que las opciones tendrán un tiempo a expiración arbitrario, T-t, de 3 años¹⁹ a partir del segundo trimestre de 2010 (tiempo de la valuación).

Cuadro 7.

Valores exógenos, arbitrarios, para la opción real de expansión

Opción de expansión
Inversión (Ke)^20	1,000,000
Incremento (α)^21	.0324

Opción real de contracción

La naturaleza estocástica de los flujos de efectivo de una empresa, y sobre todo su volatilidad, exponen a la firma a caídas que pueden poner en peligro su supervivencia. En tal situación, la solución más viable parece ser el reducir el tamaño de la firma hasta un punto en el que dicho tamaño y sus costos estén acordes con sus ingresos.

Un ejemplo particularmente frecuente de esta situación es el lanzamiento de un producto que después de un periodo inicial no presenta la aceptación esperada. En ese caso, la empresa puede ejercer la opción real de contraer la producción a través del recorte de inversiones futuras.

Con el objeto de plantear el problema anterior como una opción real, se propone nombrar como M al costo de la inversión inicial en t, con una inversión en el segundo por una cantidad más pequeña N, N < M, lo que traerá como consecuencia una contracción, en producciónβ, del valor presente de los flujos de efectivo esperados del proyecto subyacente. El valor intrínseco de esta opción de contracción satisface

donde K = e^r(T-t) es el valor presente de la inversión final, i.e. se invierte K o se invierte N; esto último trae como consecuencia una contracción de los flujos esperados. A continuación se establecen los parámetros que determinan la opción planteada a la empresa.

Cuadro 8.

Valores exógenos para la opción real de contracción

Parámetros de la opción real de contracción^22
Inversión en 2^a etapa (N)^23	2,000,000
Inversión en 1^a etapa (M)^24	1,000,000
Proporción de caída (β)^25	.06301396

Opción real de cierre temporal

En este caso se supone que el costo variable anual de la empresa, X_T, puede ser pensado como el precio de ejercicio de una opción real de cierre temporal en T. También se supone que el costo de cierre temporal de la empresa es C, el cual es una proporción fija, δ, del valor presente de los flujos de efectivo esperados del proyecto subyacente, S_T. Esto significa que C=δS_T. Asimismo, suponga que esta opción expira en T. Si los flujos de efectivo previstos son menores que los costos variables, entonces las operaciones se suspenden, lo cual genera un ahorro en los costos variables. En este caso, el valor intrínseco de la opción está dado por

donde a representa los costos fijos de la firma, con lo que de nuevo sólo resta especificar algunas constantes para determinar el valor de la opción real anteriormente descrita.

Cuadro 9.

Valores exógenos para la opción real de cierre temporal

Parámetros de la opción de cierre temporal
Costo variable^26 (Xt)	51,599,823
Porcentaje de cierre^27 (δ)	.8
Costo fijo^28 (a)	1,075,108

Opción real de abandono

Dado que el principal objetivo que persigue cualquier productor es maximizar la esperanza de sus beneficios a lo largo del tiempo, resulta poco creíble que este agente mantenga dentro de su portafolio un activo del cual no se espera que produzca flujos de efectivo, por lo cual tiene fuertes incentivos para abandonar el proyecto; esto es, tomar la decisión de cierre total si el valor presente de los flujos de efectivo esperados, S_t, es menor que cierto valor de recuperación, V_t. En consecuencia, el valor intrínseco de esta opción real está dado por

Si V_t > S_t, la opción se ejerce. Si V_t es constante, por ejemplo, V_t = K, entonces

En este caso,

donde c_BA (S_t,t) es la valuación propuesta por Barone-Adesi y Whaley para valuar una opción americana de compra. Una vez determinados los valores respectivos mediante el uso de la teoría descrita, éstos se registran en el siguiente cuadro.

Cuadro 10.

Valores exógenos para la opción real de cierre temporal

Parámetros para la opción real de abandono
Valor ofrecido^29 (K)	0

Valor de la flexibilidad de permanencia o abandono de Comercial Mexicana

En esta sección se calculan a través de regresiones para el caso de β y de los estados financieros de la empresa Comercial Mexicana los parámetros que complementan las estimaciones necesarias para la valuación del proyecto o estrategia de inversión de la citada empresa. Posteriormente, a través de la metodología Monte Carlo se valuará la flexibilidad de permanencia o abandono en el mercado de dicho proyecto.

Estimación del parámetro β

El premio al riesgo se determina en el cuadro 11 mediante la estimación del parámetro β en una regresión lineal, el cual está relacionado con premio al riesgo de mercado (prm).

Cuadro 11.

Construcción de la beta

EQ01_CAPM_5A: MCO, usando las observaciones 2005:4–2010:3 (T = 20) Variable dependiente: rcm (beta)
	Coeficiente	Desv. Típica	Estadístico t
prm (beta)	1.64824	0.525428	5.137

(rcm: rendimiento comercial mexicana)

Las variables contables y de modelado que se requieren en este ejercicio para valuar la empresa Comercial Mexicana mediante la metodología ya establecida y apoyándose en la simulación de Monte Carlo se establecen en el cuadro 12.

Cuadro 12.

Valores contables y de modelado para la valuación dinámica (estocástica) de Comercial Mexicana

Variables Contables		Variables de simulación
% Deuda (D)	.71507334	Trayectorias	10,000
% Capital (E)	.28492666	Particiones	360
Beta (β)	1.64824	Tiempo	3 años
Spread	.1	Periodo por partición	4

A lo largo de esta sección se obtendrán todos los elementos faltantes para el análisis de los flujos de efectivo aleatorios y la determinación de la tasa de descuento (WACC) con dos componentes aleatorios: tasa de interés libre de riesgo y rendimiento esperado para la empresa. Para calcularlos, se modelarán los rendimientos de mercado, los cuales estarán correlacionados con la tasa libre de riesgo y presentarán saltos cuyo tamaño medio, ν_F, estará determinado por una distribución Gumbell; además, se introducirán las opciones reales asociadas a los proyectos correspondientes a cada escenario de decisión.

Con todo ello se alcanza entonces el objetivo de este trabajo que consiste en desarrollar un nuevo modelo de valuación: el VPN estocástico modificado con opciones reales, donde existe correlación entre las variables de mercado y el proyecto, además de saltos en los rendimientos de dicho proyecto. Sólo resta especificar el algoritmo que será usado con los datos obtenidos, el cual permitirá tomar en cuenta la posibilidad de que el entorno de negocios y el ambiente económico sean favorables o no dentro de los próximos tres años para la empresa Comercial Mexicana. Una vez establecidos los periodos (trimestrales) junto con todos los parámetros necesarios, se llevará a cabo el ejercicio de simulación.

Algoritmo de valuación VPN estocástico asociado a opciones reales

Con la finalidad de ilustrar el uso de la metodología propuesta en la valuación de un proyecto de inversión, se presenta a continuación un caso práctico basado en información pública de Comercial Mexicana. El algoritmo consiste en una simulación Monte Carlo, en la cual se generan cien mil trayectorias de los posibles valores de la empresa, la tasa de interés libre de riesgo y los rendimientos de mercado.

Una vez realizadas las simulaciones, respetando la estructura de dependencia existente entre las variables relevantes³⁰ (valores de la empresa, la tasa de interés libre de riesgo y los rendimientos del mercado), se realizó la estimación de los rendimientos trimestrales de cada variable para después obtener el VPN estocástico y posteriormente valuar el portafolio de las opciones reales asociadas al proyecto, las cuales reflejan el valor pecuniario de la flexibilidad en la toma de decisiones. Conocer el valor de esta flexibilidad resulta particularmente útil cuando el proyecto es altamente volátil o dependiente del ciclo económico y financiero. En efecto, el VPN estocástico propuesto en este trabajo simula las condiciones macroeconómicas determinantes para la valuación del proyecto y la interacción esperada de éstas con la empresa.

Esta simulación abandona el paradigma de la distribución normal —tradicionalmente usado en finanzas— al permitir la existencia de outliers asociados con movimientos bruscos e inesperados del mercado o de las acciones sorpresivas de la empresa. Su calibración constituye uno de los principales desafíos del proyecto, pues supone calibrar la heterogeneidad de la economía y su interacción con la empresa; asimismo, se incorpora en el modelado la distribución de valores extremos que conducirá a los saltos.

A continuación se muestran los resultados de la simulación Monte Carlo, incluyendo el cálculo de las opciones reales americanas aproximadas mediante el algoritmo de Barone-Adesi y Whaley. Es importante destacar que los signos (+,−) presentados en las opciones implican un incremento/decremento sobre el VAN estocástico mostrado al inicio del cuadro, dependiendo de la decisión tomada por los accionistas.

Tal y como puede intuir el lector, estas decisiones son excluyentes entre sí, pues no es razonable expandir y cerrar un negocio al mismo tiempo. En todos los casos, se presenta el valor de la opción americana suponiendo que todos los parámetros de valuación permanecen constantes hasta el momento de la valuación (segundo trimestre de 2010).

Resulta relevante especificar al lector que estos resultados fueron obtenidos después de 100 000 simulaciones practicadas en un algoritmo de elaboración propia sobre un ordenador con procesador Intel Core I3. Este algoritmo tarda en converger dada la volatilidad de los flujos de efectivo y la presencia de saltos extremos.

Cuadro 13.

Convergencia del Monte Carlo para la valuación del proyecto y las opciones reales asociadas

Valor esperado del proyecto bajo valuación estocástica
3,606,067.20
Valor de la opción de expansión
+152,418.52
Valor de la opción de contracción
−534187.836125005
Valor de la opción de cierre temporal
−718,730.77
Abandono^31
+3,606,067.20

El resultado VPN estocástico con opciones reales representa el valor presente de la empresa incluyendo la flexibilidad del manejo corporativo en un entorno cambiante y correlacionado con variables económicas fundamentales, tal y como ocurre en la realidad. En particular, el resultado obtenido indica que la Comercial Mexicana es un proyecto viable aun con los niveles de deuda actuales,³² por lo que la conversión de los pasivos de corto plazo asociados a las pérdidas en los mercados de derivados en pasivos de mediano y largo plazo representa una decisión racional para los acreedores. Como puede inferirse a partir de los últimos estados financieros,³³ la conversión de los pasivos asociados a derivados en capital resulta una alternativa menos atractiva para los inversionistas, pues gran parte del valor de la empresa proviene de la perpetuidad asociada y de las opciones reales, lo que implica un mayor tiempo de tenencia.

Conclusiones

El análisis de proyectos constituye una técnica financiera a través de la cual se determinan los beneficios o pérdidas en las que se puede incurrir al pretender realizar un proyecto o una estrategia de inversión; uno de sus objetivos es obtener resultados que apoyen la toma de decisiones.

A lo largo de esta investigación se ha mostrado que aun cuando se supone una tasa de interés no plana, proveniente del modelo Vasicek, y saltos con una distribución de valores extremos en la dinámica de los rendimientos del subyacente (los flujos de efectivo), la opción que debe satisfacer la ecuación diferencial parcial parabólica lineal de los derivados y, por lo tanto, sus soluciones están asociadas a un proceso de optimización dinámica estocástica de un empresario sujeto a una restricción presupuestal que incluye una opción americana.

Asimismo, se mostró que el valor de los títulos de capital de empresas que están bajo amenaza de cierre o abandono del proyecto puede ser modelado mediante la técnica de VPN asociado a opciones reales y que su implementación no está restringida a los supuestos estándar de Black y Scholes (1973). Para ilustrar la propuesta metodológica se ha valuado a la empresa Comercial Mexicana después de su anuncio de posibilidad de quiebra. A lo largo del desarrollo de la valuación se ha puesto de manifiesto que la inclusión de la aleatoriedad en las tasas de interés, rendimientos y de mercado, añade realismo a las estimaciones de los flujos de efectivo, aunque incrementa la volatilidad de los mismos y hace más lenta la convergencia del algoritmo.

Es importante destacar que en momentos de incertidumbre, como la del periodo analizado, la volatilidad de ambos procesos tiene un fuerte impacto en la valuación del activo. Por último, queda pendiente extender el modelo propuesto cuando la tasa de interés sigue un proceso distinto al de Vasicek.