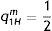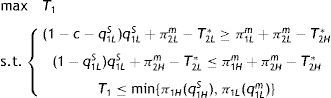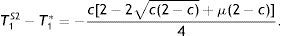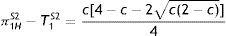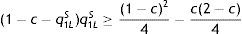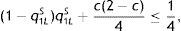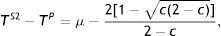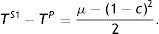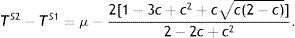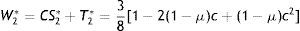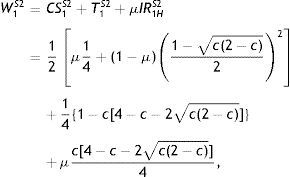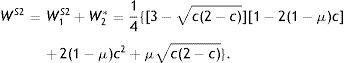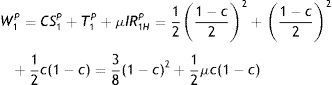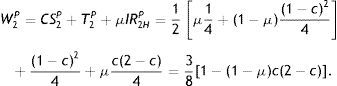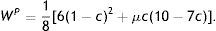Using a two-period tax-signalling model, a study is performed on the behaviour of a revenue-raising government in setting profit-based corporate taxes for a company with private information on its potential profitability. In a separating equilibrium in which both the high- and low-profit company produce a positive amount in period 1 (separating equilibrium S2), the tax set for that period is lower than that of the symmetric information, resulting in informational rent to the high-profit company in that period, but not in period 2. As result, taxes increase with time. In a separating equilibrium in which only the high-profit company produces (separating equilibrium S1 or shut-down equilibrium), no informational rent goes to the high-profit company in either period, but at the cost that the low-profit firm exits the market. Finally, in a pooling equilibrium, taxes are time-invariant and charged in such a way that period-1 informational rent to the high-profit company is lower than in S2, but persists in period 2. Consequently, the government can maximize tax revenue by not forcing information disclosure. The impact of government behaviour on welfare is also examined.
Este artículo examina, a través de un modelo de señalización de dos períodos, el comportamiento de un gobierno recaudatorio a la hora de fijar el impuesto de sociedades a una empresa con información privada sobre su potencial de rentabilidad. En un equilibrio separador en el que tanto la empresa muy rentable como la poco rentable producen una cantidad positiva en el periodo 1 (equilibrio separador S2), el impuesto fijado para dicho período es inferior al de información simétrica, lo que resulta en rentas informacionales a la empresa rentable, aunque estas rentas desaparecen en el periodo 2. Como resultado, el impuesto crece con el tiempo. En un equilibrio separador en el que solo la empresa rentable produce (equilibrio separador S1), el gobierno ahorra cualquier renta informacional a esta empresa en ambos periodos, pero a costa de que la empresa poco rentable salga del mercado. Por último, en un equilibrio agrupador, el impuesto es invariante en el tiempo y fijado de forma que la renta informacional de la empresa rentable en el período 1 es menor que en S2, pero persiste en el periodo 2. En consecuencia, el gobierno puede maximizar los ingresos fiscales no forzando la divulgación de información. También se examina el impacto que la citada conducta del gobierno tiene en el bienestar.
In most economies, tax revenues provide a substantial portion of funds aimed at financing public services or enabling governments to redistribute resources. Firms contribute to tax revenues through input, output and profit taxes. In fact, the direct taxation of businesses is a widespread practice worldwide. Since firms are legal entities separate from their owners, the justification for this corporate tax remains rather unclear, as the government could just as easily directly tax owners by means of an income tax. The literature on public finance describes three potential justifications for taxing corporate gains. First, a corporate tax as a tax on pure profits causes less distortion. Second, since corporate status provides protection in bankruptcy situations it seems reasonable to pay for this privilege that is not available to individuals. Finally, myopic owners who do not perceive themselves as paying the corporate tax will more readily accept this tax than an income tax; therefore, if the government wants to maximize votes, it will tend to set a corporate tax (Bachetta and Caminal, 1991).
The fact remains that governments tax businesses. Taken together, personal and corporate income taxes are the most important sources of revenues for public spending in almost half of all OECD countries (OECD, 2012), and even though personal income taxes typically represent the largest portion of total tax revenues, corporate taxes are also an important source. According to OECD data, in 2010 the corporate share of tax revenues was around 10% on average, although with wide variations across countries, from a low of 3% in Iceland and Hungary to a high of 24% in Norway, with rates for Germany, France, the UK, the USA and Australia applied at 4.2%, 6%, 8.8%, 10.8% and 19%, respectively. (See also Devereux et al. [2002] and Devereux [2012], among others.)
Apart from other factors, a government's ability to obtain more or less corporate tax revenues relies on firms’ behaviour regarding correct reporting of earnings. In a context of perfect information, the government is obviously in the best position to optimally calibrate corporate taxes according to a firm's profits. However, it is more logical to assume that the government has—at least in some periods—less information on the firm's profits or entrepreneurial ability than firms themselves, and, consequently, on tax-paying capacity. Therefore, a government dilemma is determining whether information disclosure by firms is preferable to non-disclosure.
As Klinger and McFate (2013) argue corporate tax disclosure has grown increasingly opaque. A decade ago, the SEC imposed uniform disclosure standards for executive compensation. As result, all public companies report the same CEO pay data in a common format, making comparisons of one firm to another both easy and straightforward. In contrast, corporate tax disclosure has no uniformity. Corporations present rudimentary information on the taxes they expect to pay in a given year, but many are quick to complain that these are not the “real numbers” when they are cited in the media. Corporations should disclose how much they pay in income taxes and to whom those taxes are paid.
Put differently, improved tax disclosure would help policymakers and tax collectors to see which corporations are reporting billions of dollars of profits in small tax haven countries where they have no sales, employees, or physical assets. The magnitude of offshore tax abuse would be plain to see and create the political will to address the problem (Klinger and McFate, 2013, p. 18).
This paper develops a simple model of asymmetric information with adverse selection that considers a revenue-raising government and a single firm that can be either high-profit or low-profit. The government wants to set a tax on profits in two periods in such a way as to maximize its revenue. The firm has private information concerning its profit potential (high or low), whereas the government can only make a prior probability assessment. A two-period model is developed in which the firm's period-1 output may transmit (or not) information to the government concerning firm profitability.
Entrepreneurial ability is an unobservable input that cannot be directly taxed (Moresi, 1998). Output, however, is publicly observable and enables the government to infer (or not) the firm's profits. In this context, the high-profit firm would like to hide its private information and convince the government that it is a low-profit firm and so pay lower taxes. For reported output to be a credible signal of low profit there must be a cost associated with output under-reporting. The model developed below addresses the following issues: How should the government tax firms to maximize tax revenues? Does the government prefer to induce the taxed firm to disclose its information? How does optimal taxation affect social welfare? Under what conditions is government's behaviour socially optimal? Real-life taxation situations seem quite similar to the simple framework described here.
The main contribution of this paper is to show that the government faces a trade-off when setting corporate taxes under asymmetric information. On one hand, by observing the firm's output in period 1 (in a perfect Bayesian separating equilibrium), it can elicit information on the firm's tax-paying potential.1 In this case, it needs to offer an incentive to the taxed firm to fully disclose its private information, resulting in the high-profit firm obtaining an informational rent in period 1. On the other hand, the government need not grant any informational rent in period 2 because complete information is restored for this period. The high-profit firm will want to reduce the informational content of its output report to increase the probability that it is perceived as a low-profit firm. Conversely, a low-profit firm will want to enhance the informational content of its output report to ensure that the payable tax coincides more closely with the tax corresponding to complete information. Derived thus is the separating equilibrium (S2) for the two-period tax-signalling game in which both firm types are producing, with the result that the low-profit firm must distort its period-1 output below the complete-information profit-maximizing level to convince the government that it is genuinely low-profit. The optimal period-1 tax for the government is consequently lower in the presence than in the absence of signalling, and such tax is time-increasing.
Alternatively the government can opt to elicit the firm's information by observing its period-1 output and, further, by preventing the high-profit firm from obtaining informational rent in either period. This is separating equilibrium S1 or shut-down equilibrium, in which the cost to the government of not granting informational rent to the high-profit firm is that the low-profit firm does not produce at all.
Yet another alternative is for the government to refuse to update its firm-type information and allow both firm types to produce. This is a pooling equilibrium, in which both firm types produce the same output in period 1. The informational rent that the government grants to the high-profit firm in this period is lower than in S2, but unlike in S2, this rent persists in period 2.
In S2 equilibrium of the game, the government sets period-1 tax for the high-profit firm in such a way that informational rent is sufficiently large for this firm not to misrepresent itself. This rent is, however, restricted to period 1, that is, informational rent no longer holds in period 2. In S1 equilibrium, the government also identifies the firm type but provides no informational rent to the high-profit firm, although at the cost of the low-profit firm exiting the market. In pooling equilibrium, the government gives less informational rent in period 1 to the high-profit firm than in S2, but, unlike in S2, this rent persists in period 2.
In general, the government prefers firms to disclose their ability to make (more or less) profits, because disclosure results in higher tax revenue than non-disclosure. In particular, if the ratio of high-profit firms is small enough, the pooling equilibrium outcome is the best option for the government, even though the high-profit firm obtains an informational rent in both periods (higher in period 2 than in period 1). If the ratio of high-profit firms is moderate, given the level of efficiency of low-profit firms, the government prefers to impose S2, with the result that informational rent to the high-profit firm is higher than in pooling equilibrium, but is only granted in period 1. Finally, if the ratio of high-profit firms is high enough, informational rent to the high-profit firm would be so large (both in pooling equilibrium and S2) that the government would prefer to impose separation by ensuring that only the high-profit firm produces and that it obtains no informational rent in either period.
The intuition behind this result is as follows. In a symmetric information context, this (lump-sum) tax does not distort the firm's behaviour (Atkinson and Stiglitz, 1980). However, in an asymmetric information context even a lump-sum tax as corporation tax can be distorting. And the aim of the government wishing to maximize revenues is to reduce distortion as much as possible. Thus, when there is a small ratio of high-profit firms, the government prefers not to distort the period-1 output of the low-profit firm but to distort that of the high-profit firm, because, in this way, it reduces the informational rent granted to the latter. In fact, the ratio of high-profit firms is so small as to result in a small informational rent in expected terms. However, when there is a moderate ratio of high-profit firms, the government prefers disclosure to hold even if this results in some distortion for the low-profit firm in period 1. Consequently, period-1 informational rent for the high-profit firm is increased relative to the pooling equilibrium situation and, in return, neither firm obtains informational rent in period 2. Finally, when there is a very high ratio of high-profit firms, the optimal behaviour for the government is to assume that the firm has a high tax-paying potential. In this case, it renounces revenues if the firm is, in fact, low-profit (a rather unlikely scenario), but instead fully eliminates the informational rent to the high-profit firm.
From a social standpoint, the incentives of a government that sets corporate taxes to maximize tax revenue are not generally aligned with social incentives. Inducing disclosure generally maximizes social welfare: aggregate welfare is only maximized when the government opts for pooling equilibrium and in a small region where S2 holds. Otherwise government incentives are not aligned with social incentives. From a social perspective, for example, when the government imposes S2, pooling equilibrium is socially optimal, and when the government imposes S1, S2 is socially optimal.
For an environment in which entrepreneurs chose between risky projects (higher potential profits) and safe projects (lower potential profits), Becker and Fuest (2007) examined the relationship between limited liability and corporate taxation, showing that a corporate tax on all entrepreneurs with limited liability is optimal when entrepreneurs can offset potential losses in a situation of asymmetric information concerning project qualities. For a similar context, Miglo (2007) confirmed that entrepreneurs’ ability to offset losses and the presence of asymmetric information may affect tax policy, although the optimal taxation policy differed from that suggested by Becker and Fuest (2007).
The remainder of the paper is organized into five sections. Section 2 outlines the model. Section 3 derives, as a benchmark, taxation on profits under symmetric information. Section 4 analyses the optimal taxation strategy under asymmetric information and discusses the corresponding distortions in government and firm behaviours. Section 5 examines the welfare implications of government behaviour. Finally, Section 6 concludes the paper.
2The modelAn economy with a revenue-raising government that charges corporate tax to a firm over two periods is considered. Firm activity is restricted to this single country,2 and corporate tax amounts to 100% of capital gains. Assumptions are as described as follows.Assumption 1 The taxed firm faces linear market demand pt(qt)=1−qt in each period t, t=1, 2, for qt<1 and pt(qt)=0 for qt≥1, where pt denotes unit price in period t when qt units of the good are sold. (1 denotes the market parameter.)
Asymmetric information is characterized by the following assumption:Assumption 2 The distribution for the firm's profit is common knowledge, but only the firm knows its potential profit.
That is, the firm privately knows whether its potential profitability is high or low (i.e., whether its potential to pay taxes is high or low) because, better than the government, it knows the demand level and its own efficiency level. Two possible profitability values derive from the following assumption:Assumption 3 The intercept term for the demand described in Assumption 1, net of costs, can take one of two values, 1 and 1−c, with 0
The high-profit firm and low-profit firm are labelled H and L, respectively. Profit levels over two periods are the same.Assumption 4 The prior probability assessment of a high-profit firm is μ, 0<μ<1.
The only information available to the government at the beginning of the game is the probability of a firm being high profit or low profit. However, the firm's potential to pay taxes may be then inferred by the government (in a perfect Bayesian separating equilibrium) or not (in a perfect Bayesian pooling equilibrium) after observing the output produced by the firm in period 1.
Finally, the discount factor between periods is assumed to be 1, all players are assumed to be risk-neutral3 and the government is assumed to seek to maximize tax revenue throughout both periods of the tax game.
3Symmetric informationIn a symmetric information scenario, all players are assumed to know the firm's potential to pay taxes, in which case the tax game proceeds as follows.Period 1 At the beginning of period 1, Nature chooses the firm's ability to make profits and this ability is publicly observable. For this period, the firm pays (lump-sum) corporate tax T1k*4 as a function of type k, k∈{H,L} and produces output level q1k*. Corporate tax and output in period 2 are the same as for period 1, namely T2k*=T1k* and q2k*=q1k*.
In this context, the following result is achieved.Lemma 1 Under incomplete but symmetric information, in each period t, t=1, 2, the government sets corporate tax TtH*=1/4 for the high-profit firm and TtL*=(1−c)2/4 for the low-profit firm.
In expected terms, the tax paid by the firm in each period t amounts to Tt*=[1−(1−μ)(2−c)c]/4, t=1, 2, and decreases as the probability of the firm being high-profit type increases and/or as the disparity between profits for both types of firm increases. The firm's equilibrium output in each period amounts to 1/2 when the firm is H and to (1−c)/2 if it is L. Governmental revenues over both periods are 1/2 for the firm if it is H, and (1−c)2/2 if it is L. The government's expected revenue over both periods thus amounts to R*=2Tt*, i.e., the government obtains the firm's whole per-period profit. Needless to say, the presence of (lump-sum) taxes does not in any way distort the firm's behaviour under symmetric information. However, this situation no longer holds when information is asymmetric. In this case, taxes will distort firm behaviour, despite of the fact that such taxes are lump-sum.
4Asymmetric informationWe now return to the original context, where information is asymmetric. A firm that is better informed than the government concerning its tax-paying potential will try to benefit from this advantage by representing itself as a firm with low tax-paying potential. This incentive derives from the fact that the corporate tax set by the government for period 2—when it believes the firm is low-profit—is lower than the tax set when the government believes that the firm is high-profit. In a separating Bayesian equilibrium—where the government infers type from observing period-1 output—the government will try to mitigate opportunism by setting a period-1 tax for that induces the firm to disclose the kind of private information that would enable better calibration of period-2 tax. Conversely, in a pooling Bayesian equilibrium the government would be unable to update its prior probability assessment concerning firm type from period-1 output; hence, tax in period 2 would be the same as in period 1.
4.1Perfect Bayesian separating equilibriumThe tax game when separating equilibrium holds unfolds as follows.Period 1 At the beginning of period 1, the government announces and commits to period-1 corporate tax T1S (superscript S denotes separation) for the firm, given some prior probability assessment that the firm is high-profit. At this stage, the firm knows its tax-paying potential, whereas the government only has imprecise information. However, the distribution of firm type is common knowledge. The firm chooses, in period 1, an output level according to its type and the impact of its output on updated beliefs. Given the prior probability assessment that the firm is high-profit and that tax is T1S, the firm chooses period 1 output to maximize profit. At the end of this period, the government observes period-1 output and uses this information to update its probability assessment regarding the firm's tax-paying potential. At the beginning of period 2 (when complete information has been restored), given its updated probability assessment, the government announces and commits to period-2 corporate tax T2k*, this time different for each firm type and equal to that set in conditions of symmetric information. Given this tax and the government's updated probability assessment, the firm chooses period-2 output to maximize profits, and the game ends.
Sought as a solution for this tax game is the separating pure-strategy perfect Bayesian-Nash equilibrium. Comparing the period-2 net profits of each firm type in the equilibrium and off-equilibrium paths, the firm is found to be interested in being perceived as low-profit by the government.
In period 1 the government cannot distinguish one firm type from another, so the tax charged in this period must be the same for both. However, separating equilibrium implies that the output for each firm type in this period will be different. Thus, the government will update its prior probability assessment after it observes period-1 output and detects the true firm type. In these circumstances, the best the high-profit firm can do in period 1 is to produce the output level of a myopic profit-maximizing monopolist, i.e.,
(the m superscript stands for myopic monopolistic behaviour), who makes the corresponding gross profits π1Hm=1/4. Together with period-1 output level q1LS for the low-profit firm, the period-1 output given in Eq. (1) forms part of the separating equilibrium if the corresponding incentive-compatibility conditions are satisfied. In sum, in period 1 the government solves the following problem:where, by virtue of Lemma 1, T2L*=π2Lm and T2H*=π2Hm. The first restriction in Eq. (2) is a self-selection constraint, which states that a low-profit firm, in period 1, would prefer to produce output q1LS (a level that may differ from the profit-maximizing amount) and to be perceived by the government as a low-profit firm rather than as a high-profit firm by producing an amount other than q1LS. The second restriction in Eq. (2) is the incentive-compatibility constraint for a high-profit firm, which states that, in period 1, a high-profit firm would prefer to produce q1Hm and to be perceived by the government as a high-profit firm rather than as a low-profit firm and be forced to produce q1LS. Finally, the third restriction in Eq. (2) summarizes the participation condition of both firm types.In the abovementioned separating equilibrium, both types of firm produce in period 1 (and also in period 2). For this reason, we call this situation S2. However, another way for the government to induce disclosure is to set a tax in period 1 (and also in period 2) that is only acceptable to the high-profit firm. In this case, the period-1 output for the low-profit firm will be zero, q1LS=0. Once the government observes a positive period-1 output, it infers that the firm is of high-profit type. We call this situation S1.
The solution for problem (2) and the possibility of identifying firm type by forcing the low-profit firm out of the market is as follows, where the superscript 2 (resp., 1) indicates that both firm types (resp., only the high-profit firm) produce a positive output.Proposition 1 (Separating equilibrium S2) In the least-cost separating equilibrium in which both types of firm produce, the government charges, in period 1, the corporate tax T1S2={1−c[4−c−2c(2−c)]}/4 to both firm types. The firm thus produces q1HS2=1/2 if it is high-profit and q1LS2=[1−c(2−c)]/2 if it is low-profit. The government's posterior beliefs are μ(q1HS2)=1 and μ(q1LS2)=0. Hence, in period 2, both taxes and outputs are as in Lemma 1. (Separating equilibrium S1) In the separating equilibrium in which only the high-profit firm produces output, the government charges, in period 1, the corporate tax T1S1=1/4. The firm thus produces q1LS1=q2L=1/2 if it is high-profit (and q1LS1=0 if it is low-profit). The government's updated beliefs are μ(q1=1/2)=μ and μ(q1≠1/2)=1. Hence, in period 2, q2HS1=1/2 and q2LS1=0.
See Appendix.
Separation of types when both produce is costly because the high-profit firm finds it optimal to apply a low-profit firm's reporting policy under asymmetric information. Thus, to prevent the high-profit firm from projecting itself as a low-profit firm, in period 1 the low-profit firm needs to produce an output below the symmetric-information profit-maximizing level. This reduces its gross profits5 and, consequently, the corporate tax acceptable to both firm's types decreases relative to the situation where no high-profit firm exists. In fact, when comparing taxes in both information contexts, it follows that T1S2
The presence of a low-profit firm benefits the high-profit firm because the latter obtains net profits as follows:
This represents its informational rent in period 1 (informational rent at the top). The low-profit firm, on the other hand, obtains no informational rent, i.e., π1LS2−T1S2=0 (no informational rent at the bottom). In sum, the government faces a trade-off. For the low-profit firm to accept paying the proposed period-1 tax, the government needs to provide an informational rent to the high-profit firm in period 1; in contrast, the government appropriates all profits for period 2, irrespective of firm type. In separating equilibrium, in sum, time-increasing taxation would be observed as information evolved from asymmetric to symmetric.
Also costly is the situation in which the government sets corporate tax as T1S1=1/4 in period 1 and identifies the high-profit firm as accepting this tax and consequently producing. In fact, the government does not have to grant informational rent to the high-profit firm in either period 1 or 2, but at the cost of the low-profit firm not producing in either period.
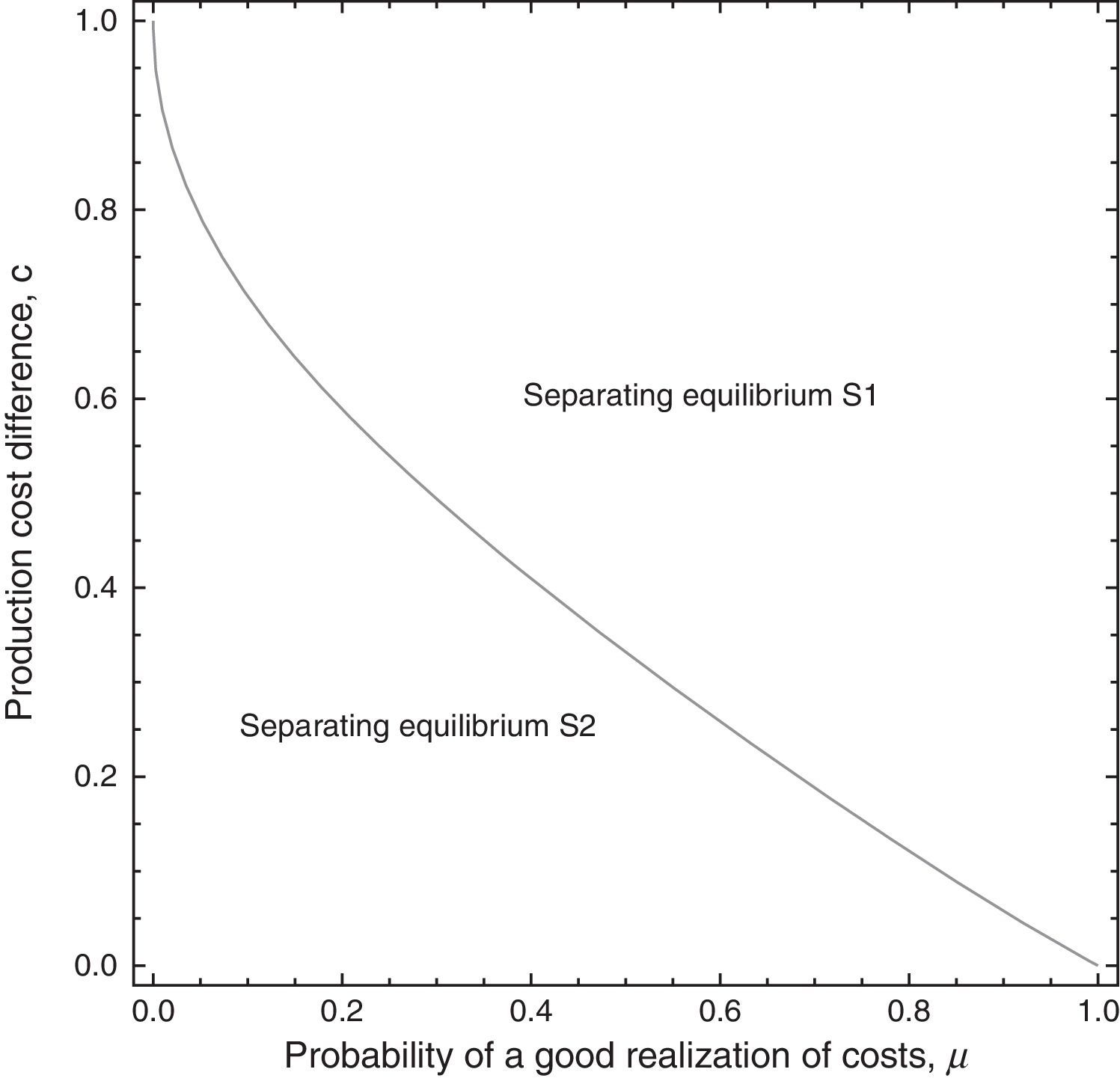
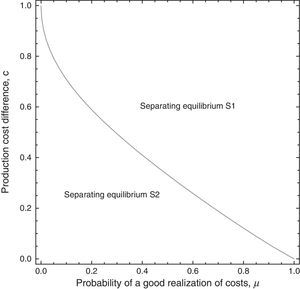
Depending on the government's prior probability assessment concerning firm type, will choose the corporate tax that maximizes tax revenue. This is formally described as follows.Proposition 2 Given the value of parameter c, let us define μ2=2[1−3c+c2+cc(2−c)]/(2−2c+c2), where 0<μ2<1 for all c. Then: If μ∈(0,μ2), the government prefers to identify the type of the firm by making both produce different outputs in period 1 (S2). If μ∈(μ2,1), the government prefers to identify the type of the firm by making both produce different outputs in period 1 and, particularly, by forcing the low-profit type dropping out of the market (S1).
The result of Proposition 2 is very intuitive. Given the value of parameter c, when the probability of the firm being high-profit is sufficiently low, the government opts to maintain both types of firm producing. Otherwise, it prefers not to grant informational rent to the high-profit firm, but at the cost of forcing the low-profit firm to exit the market. This result is illustrated in Fig. 1.
4.2Perfect Bayesian pooling equilibriumWhen both types of firm produce the same output in period 1, the tax-signalling game proceeds as follows.Period 1 After Nature has chosen the firm's type, the government sets the same corporate tax T1P (the P superscript denotes pooling) for both types. In period 1, both firm types produce the same output level, q1H=q1L=q1P, from which no additional information concerning tax-paying potential can be inferred. The government continues to use μ as its probability assessment that the firm is high-profit. Thus, the government continues to announce and commit to the same corporate tax for both firm types, which equals the tax previously applied in period 1, namely, T2P=T1P.
Only one corporate tax level can form part of the pooling equilibrium in period 1, namely, T1P=(1−c)2/4, charged in period 1 (and also in period 2). Both firm types accept the tax and produce q1P=(1−c)/2 in period 1. This equilibrium is supported by the government's beliefs μ(q1=q1P)=μ and μ(q1≠q1P)=1, in which case T2P=1/4. This is formally described as follows.Proposition 3 In the pooling equilibrium, the government charges corporate tax TtP=(1−c)2/4 to both firm types in each period t. Both firm types produce q1LP=q1HP=q1P=(1−c)/2 in period 1. The government's updated beliefs are μ(q1P)=μ and μ(q1≠q1P)=1. Hence, in period 2 the firm's output is q2HP=1/2 if it is high-profit and q2LP=(1−c)/2 if it is low-profit.
However, the disadvantage of this equilibrium to the government is that the high-profit firm obtains informational rent in each period, amounting to c(1−c)/2 in period 1 and c(2−c)/4 in period 2.6
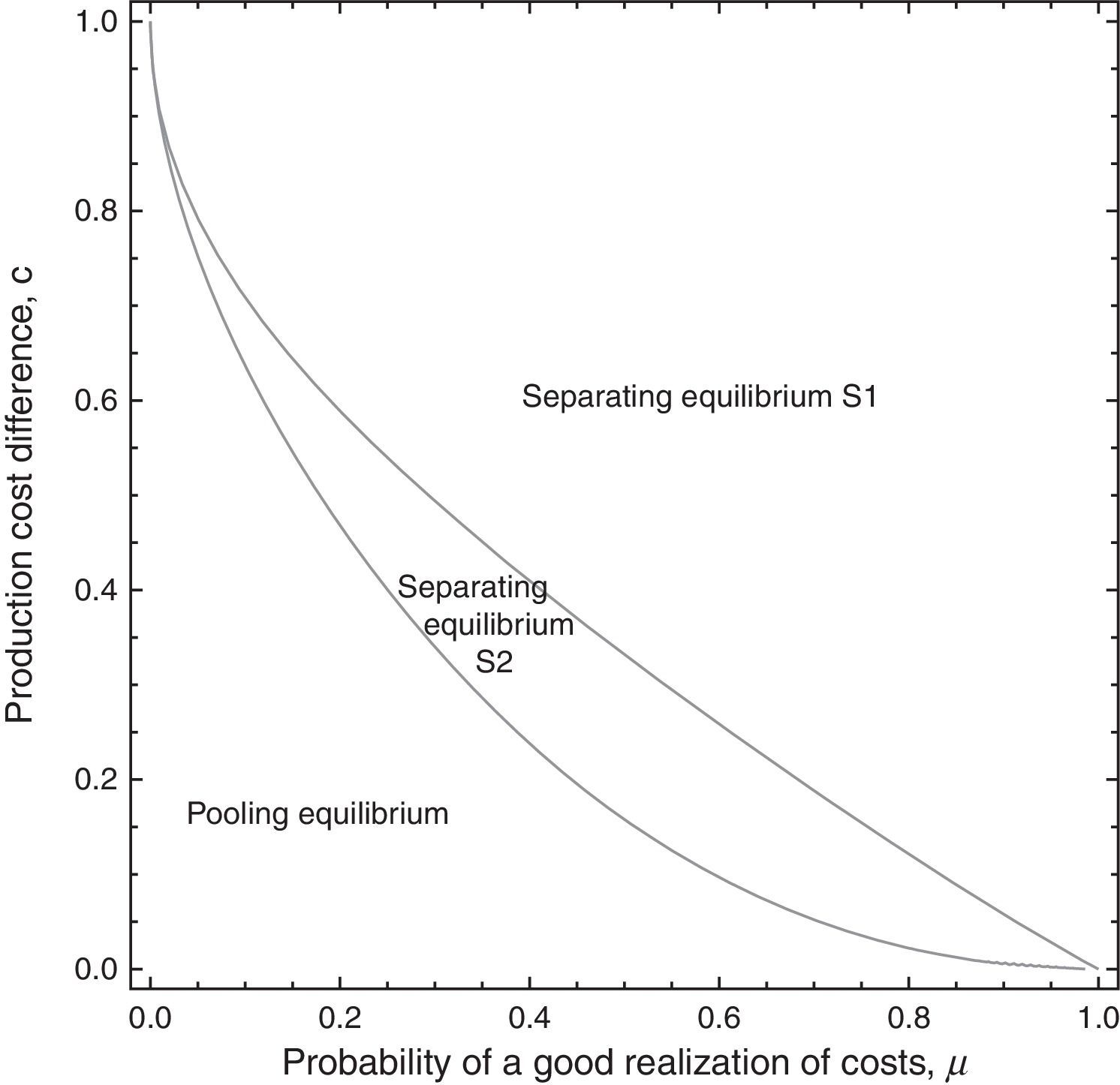
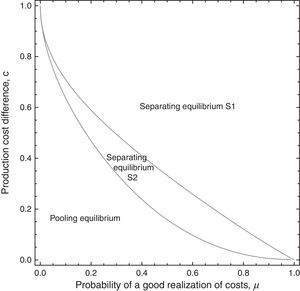
4.3To induce or not to induce information disclosure?Regarding period 2, the government always prefers the taxed firm to disclose information because the government's revenue is such that T2S2=T2*>T2P. This is due to the fact that no informational rent in this period is granted to the high-profit firm—as happens when asymmetric information prevails in the pooling equilibrium. In contrast, when the firm is induced to disclose rather than withhold information, period-1 tax is lower, i.e., T1S2 For a given value of parameter c, let us define μ1=2[1−c(2−c)]/(2−c), and μ2=2[1−3c+c2+cc(2−c)]/(2−2c+c2), where 0<μ1<1, 0<μ2<1, and μ1<μ2 for all c. The government's behaviour under asymmetric information depending on its prior probability assessment μ is as follows: If μ∈(0,μ1), the corporate tax T1P is charged to both types of firms in period 1 (and also in period 2) and the private information is not disclosed. The high-profit firm thus obtains an informational rent in both periods. If μ∈(μ1,μ2), the corporate tax T1S2 is charged to both types of firm in period 1 and induces the firm to disclose its information. The high-profit firm thus obtains an informational rent in period 1, but not in period 2. If μ∈(μ2,1), the corporate tax T1S1 is charged to both types of firms in period 1 (and also in period 2). Information is disclosed because the low-profit firm does not produce. The high-profit firm does not obtain informational rent in either period 1 or in period 2.
See Appendix.
Proposition 4 (i) states that, given the earnings of the low-profit firm, if there is a small enough ratio of high-profit firms the government prefers to renounce identifying firm type because separation would imply granting too much informational rent to the high-profit firm. Instead, the government reduces corporate tax in each period compared to the tax set under a symmetric information scenario, TtP−Tt*=−μc(2−c)/4<0, t=1, 2. Hence, both firm types can produce and the high-profit firm receives, as informational rent, c(1−c)/2 in period 1 and c(2−c)/4 in period 2. In contrast, Proposition 4 (ii) states that if the ratio of highly profitable firms is moderate, the government imposes S2, whereby the high-profit firm obtains an informational rent in period 1 but not in period 2. Finally, Proposition 4 (iii) states that when the ratio of high-profit firms is high enough, the government charges such a high tax in each period that it is only acceptable to the high-profit firm (the low-profit firm refuses to pay). This high tax means that the high-profit firm receives no informational rent. This is the S1 situation, where per-period corporate tax is well above that expectedly set under symmetric information, TtS1−Tt*=(1−μ)c(2−c)/4>0, t=1, 2. This is because per-period output diminishes relative to per-period output as expected under symmetric information, qtS1−qt*=−(1−μ)(1−c)/2<0; hence, the price of the good to consumers increases.
This result is illustrated in Fig. 2.
Meanwhile, the taxed firm would prefer the government to choose pooling equilibrium rather than S1 or S2, because its informational rents over both periods, IRP=c(4−3c)/4, IRS2=c[4−c−2c(2−c)]/4 and IRS1=0, are such that IRP>IRS2. Finally, the government obtains less revenue under asymmetric information than under symmetric information, regardless of whether or not it induces the taxed firm to disclose its private information, namely, TS2 The analysis so far has examined the government's incentives to induce or not information disclosure. Welfare implications of such behaviour are now examined in order to ascertain whether or not the incentives of a revenue-raising government are aligned with social interests. To this end, (expected) welfare is defined as the un-weighted sum of consumer surplus, the firm's informational rents and government-collected tax revenue. Consumers are assumed to have the same prior probability assessment as the government regarding the firm's potential to make profit and pay taxes.Proposition 5 If a revenue-raising government induces the taxed firm to disclose its information, then WS2 If the government chooses not to induce the taxed firm to disclose its information, social welfare is such that WP See Appendix.
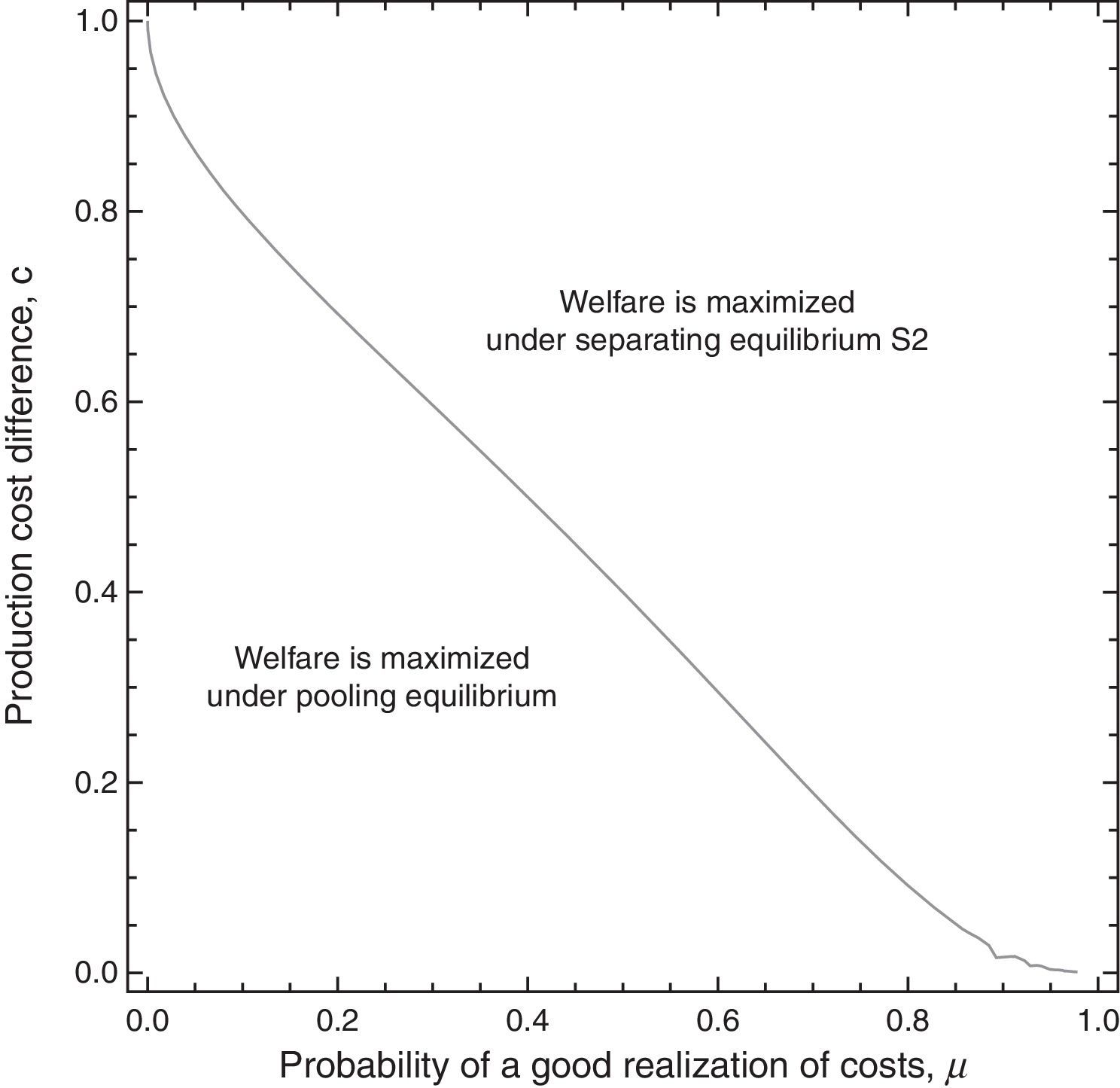
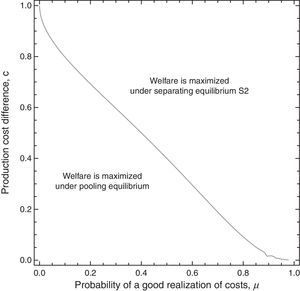
When the firm discloses information, its period-1 output is lower than that prevailing in a symmetric-information scenario. Thus, consumers pay more for the good in this period (lump-sum corporate taxes cause inflation when information is asymmetric as opposed to symmetric) and the consumer surplus decreases. In addition, expected profits (some going to the government as tax revenue and some retained by the high-profit firm as informational rent) also decrease relative to what happens in a symmetric-information context. Taking into account the welfare level in period 2 and that welfare distribution between the government, the firm and consumers is as under symmetric information, the result WS2 If pooling equilibrium prevails, in period 1 the firm's output decreases relative to that expected under symmetric information, resulting in a lower welfare level. In period 2 the firm produces the same output as expected under symmetric information, so welfare remains the same. However, welfare distribution among players shifts relative to the distribution in the symmetric information scenario. In sum, although government tax set in both symmetric and asymmetric information contexts is a lump-sum tax, the fact that the good's expected price is higher in the latter context leads to lower social welfare in the former context, regardless of whether or not the information is disclosed. Welfare outcome under asymmetric information is now compared as a function of the government's behaviour in maximizing its revenue, rendering the following proposition.Proposition 6 For each value of parameter c a prior probability assessment μ3 exists, μ3=[2c2+(2−4c)c(2−c)]/[2c+3c2+(2−4c)c(2−c)], where 0<μ3<1, for all c, for which the following hold: If μ∈(μ3,1), social welfare is maximized when the firm discloses its information (in S2). If μ∈(0,μ3), social welfare is maximized when the firm does not disclose its information. See Appendix.
Proof
The content of Proposition 6 may be illustrated in Fig. 3.
The tax-inducing S1 is not socially desirable, since it is dominated by the tax that induces S2. In fact, the low-profit firm produces no output in S1, so the distortion caused by that firm in period 1 is greater than in S2, where this distortion also emerges. Thus, in each period the price paid by consumers is higher in S1 than in S2, and social welfare is consequently lower in S1.
Likewise, when comparing S2 and pooling equilibrium, inducing separation is only socially efficient when—given the earnings of the low-profit firm—there is a sufficiently high ratio of high-profit firms. The socially optimal outcome in period 2 is that there is separation, because complete information is restored. On the other hand, the output distortion in period 1 that leads to separation, and hence reduces welfare, is more pronounced in separating than in pooling equilibrium. Overall, the welfare increase in period 2 caused by S2 relative to pooling equilibrium outweighs the welfare reduction in period 1.
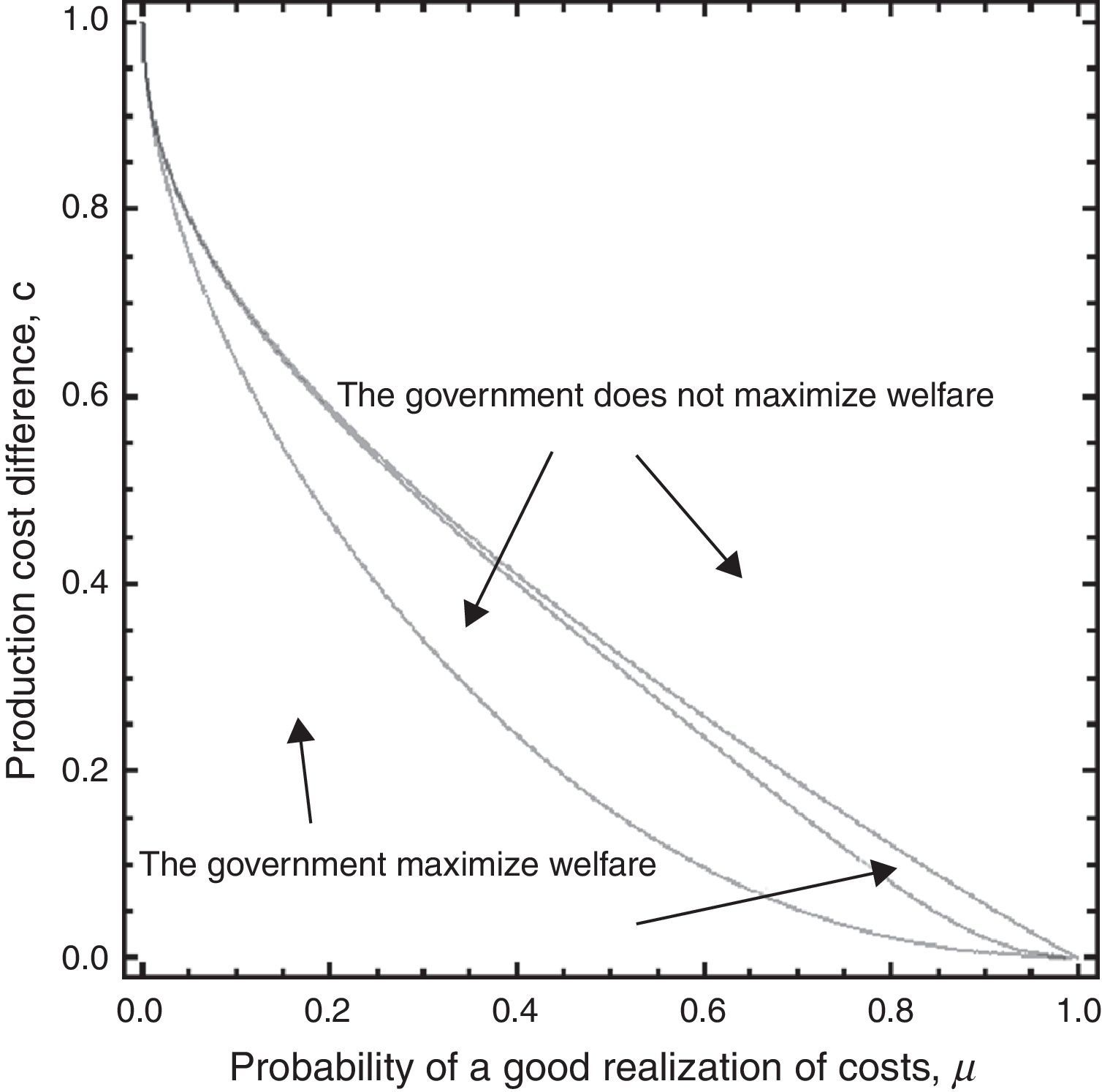
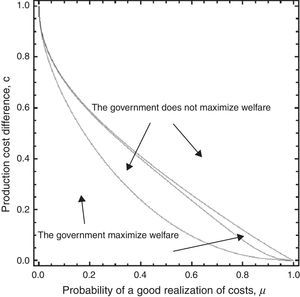
Bearing in mind the ratio of high-profit firms, if the profits of the low-profit firm are not very small, a large period-1 output reduction is required to separate the latter from the former. The government thus sets a very small tax in period 1 so that it is acceptable to the low-profit firm, but this makes informational rent very large for the high-profit firm. In this case, no separation is socially preferable. The opposite holds when the number of low-profit firms is small (Fig. 4)
Thus, a revenue-maximizing government that leads the taxed firm not to induce disclosure in also maximizes social welfare in all the region of the pooling equilibrium. The government's behaviour also maximizes aggregate welfare when it encourages, trough separating equilibrium S2, the firm to reveal its information. However, in this case the government and social objectives are only coupled in a very small separating equilibrium region. Finally, a tax-maximizing government that chooses to induce firm's types separation does not maximize social welfare in the entire S1 separating equilibrium region as well as in most of the S2 separating equilibrium region.
6ConclusionsThis paper examines the behaviour of a revenue-raising government when charging corporate taxes to a firm better informed than the government concerning its profitability and, hence, its tax-paying potential. In a two-period signalling model in which the government interacts with a single firm, the government's tax policy of inducing the firm to disclose its information is found to be generally desirable in order to maximize revenue.
In particular, when the prior probability assessment of the government about having a high-profit firm is high enough, the government prefers the firm to disclose its private information, although the cost is that the low-profit firm does not produce at all and no taxes from this firm are collected. In this case, the government saves the informational rent to the high-profit firm in period 2 as well as in period 1. The disclosure approach is also the best policy for the government when, given the earnings of the low-profit firm, the government's prior probability assessment that the firm has a high tax-paying potential is moderate. In this case, the government reduces period-1 tax relative to that which would expectedly be paid under symmetric information. The government is thus obliged to grant an informational rent to the high-profit firm in period 1; however, the restoration of complete information means that, in period 2, tax revenue is increased to the point that informational rent is reduced to zero. Finally, if the government's prior probability assessment is low enough, the government prefers not to identify the firm type but prefers instead to set a period-1 corporate tax that reduces this period's informational rent to the high-profit firm relative to separation, although the informational rent persists in period 2 (and even increases with respect to period 1).
From a social viewpoint, the strategy of a revenue-raising government in this signalling context is generally not aligned with social interests, especially when the government induces separation, as this leads to the low-profit firm exiting the market. Yet it is socially desirable to have separation with both firm types producing, as consumer prices would be lower in both periods. Likewise, when government-induced separation results in positive output in period 1 for both firm types, a region of parameters exists in which non-disclosure of information is socially desirable, given that, in welfare terms, disclosure is too costly relative to non-disclosure.
As Klinger and McFate (2013) pointed out “companies (in the U.S.) can make profits, pay taxes on those profits, and create jobs. Ensuring that all corporations pay taxes on their profits will provide the national government with the revenue needed to invest in modernizing the transportation, information, communications, and energy infrastructure the economy needs to grow. Demanding that corporate actors that benefit from operating in America help pay for the public systems that enable their success will ensure future generations of Americans are able to compete in the global economy and thrive” (p. 19). And the role of obtaining the necessary information is crucial to that end.
Conflict of interestThe author declares no conflict of interest.