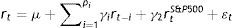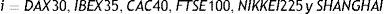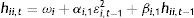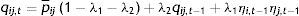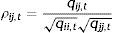El contagio se define generalmente como la correlación entre los mercados por encima de lo que ya está implícito en los propios fundamentos de los activos subyacentes; sin embargo, existe un desacuerdo considerable sobre las definiciones de los fundamentos y los mecanismos que vinculan dichos rendimientos de los activos. La presente investigación pretende capturar y detectar el contagio entre los principales índices bursátiles a nivel de los mercados de Estados Unidos, Europa y Asia.
Contagion is generally defined as the correlation between markets above what is already implicit in the fundamentals of the underlying assets. However, there is considerable disagreement on definitions of the foundations and the mechanisms that link these asset returns. The present study aims to capture and detect the spread between the main stock indices in the United States, Europe and Asia markets.
El creciente proceso de globalización económica acaecido durante las 2 últimas décadas ha coadyuvado a la integración de los mercados financieros, propiciando de este modo un alto grado de dependencia entre ellos. Consecuentemente, ha despertado gran interés por parte de los inversores, académicos y entidades reguladoras concitando, por una parte, la creciente volatilidad observada entre los mercados financieros, y de otra, el desarrollo de modelos econométricos que sean capaces de estudiar de mejor forma la evolución de las variables financieras y así poder comprender los factores asociados a sus fluctuaciones.
La crisis financiera iniciada en 2008 ha comportado enseñanzas notables en el mundo financiero. Sin duda, la caída de Lehman Brothers marcó un punto de inflexión en la crisis y propició una repercusión a nivel global en el sistema financiero. El efecto contagio que hubo en los mercados provocó un replanteamiento de la teoría del riesgo sistemático1 del propio mercado. Así, diversos estudios concluyen que la mayoría de los mercados de capitales internacionales han incrementado su integración y, por ende, un mayor riesgo sistemático. Concretamente, en la medida que los mercados se vuelven más integrados, los efectos en el largo plazo comparten tendencias comunes (Kasa, 1992).
El entorno de globalización, las plataformas High-Frequency Trading (HFT), la existencia de mecanismos y vehículos de transmisión cada vez más grandes, así como la intensificación de las relaciones económicas y financieras entre los países, hacen más probable que los mercados se influyan entre sí. Es más, es vital observar las correlaciones existentes con los diferentes activos subyacentes, tales como la renta fija, las divisas o los commodities, pues sirven de guía para detectar futuros contagios y así detectar los niveles de estrés en los segmentos de mercados considerados.
Durante los últimos años, entes privados, supervisores financieros e instituciones internacionales como el FMI y el Banco Mundial se han focalizado en el análisis de la identificación, la gestión y la mitigación del riesgo sistemático. A nivel europeo, la Junta Europea de Riesgo Sistemático (European Systemic Risk Board) ha desarrollado y agregado varias interconexiones existentes entre los mercados. En general, los principales indicadores de riesgo van asociados a las primas de riesgo, a las volatilidades, a las condiciones de liquidez o a las caídas sustanciales de precios de los activos financieros.
Dada la dinámica de los mercados financieros, los autores evidencian que la transmisión del comportamiento de los rendimientos y la volatilidad del mercado estadounidense ejercen una influencia significativa en los rendimientos y volatilidades en el resto de mercados. Ciertamente esta influencia puede detectarse observando el peso relativo de los índices estadounidenses en los índices bursátiles, hecho que refleja su mayor grado de madurez.
La línea de investigación del presente trabajo pretende capturar y detectar el contagio entre los principales índices bursátiles a nivel estadounidense, europeo y asiático. Para ello, se ha estructurado en 3 grandes partes; en la primera de ellas se ha desarrollado el modelo de DCC GARCH, a través del cual se pretende evidenciar la existencia de correlación entre los diferentes índices bursátiles considerados. En segundo lugar se estudia el efecto causal (correlación no implica causalidad) entre los índices a través de la prueba de Granger. Finalmente, con el objetivo de asegurar la consistencia de los resultados, se realiza la prueba de Johansen para poder aceptar la hipótesis nula de que las variables incluidas en los modelos no están cointegradas.
2Literatura existenteLa naturaleza y dinámica heterocedástica que caracteriza a los mercados financieros es ampliamente aceptada, por lo que un modelo autorregresivo de heterocedasticidad condicional (Autoregressive Conditional Heteroskedasticity [ARCH]) es un candidato natural para su modelación, siendo reconocido y estudiado por numerosos autores, entre ellos Baillie y Bollerslev (1989, 1991), Hsieh (1988, 1989a, 1989b), Diebold y Nerlove (1989), Milhøj (1987), Engle et al. (1990) y Vlaar y Palm (1993), entre otros.
Por otra parte y debido al hecho de que la volatilidad asociada a los mercados financieros se mueve conjuntamente en el tiempo a través de diferentes activos y entre distintos mercados, los análisis de volatilidades tienen sentido si se realizan en un contexto multivariado. Una estructura multivariada permite contrastar la existencia simultánea de efectos de contagio de la volatilidad entre los diferentes mercados, el impacto de los llamados shocks, innovaciones o noticias, así como de todas las relaciones que pueden acontecer y ocurrir entre los diferentes mercados financieros (Baillie y Bollerslev, 1991).
En este sentido, y tal como lo describen Bera y Kim (2002), los modelos de volatilidad multivariada permiten estimar de manera eficiente las correlaciones dinámicas cruzadas que pueden existir entre los retornos de un conjunto de activos, lo cual es un factor crucial para definir el mejor modelo de diversificación de un portafolio internacional.
A partir de las investigaciones y trabajos de Robert Engle (Engle, 1982) relativos al desarrollo de un modelo ARCH, la modelación y pronóstico de la volatilidad asociada a una serie de tiempo ha ido evolucionando de manera constante. La relevancia del modelo ARCH surge de la directa asociación que existe entre la varianza y el riesgo, pero también del trade-off existente entre el retorno de un activo y su riesgo asociado. Es de conocimiento común en el mundo financiero el hecho de que una inversión de mayor riesgo puede producir mayores retornos que una inversión libre de riesgo.
La gran ventaja asociada al uso de los modelos ARCH reside en que estos capturan muchas de las regularidades empíricas vinculadas a la volatilidad de los retornos de los activos financieros, como por ejemplo varianzas tiempo-variantes, distribuciones leptocúrticas, volatilidad por conglomerado o clúster, persistencia, asimetría en la volatilidad, fluctuaciones en los precios y efectos de apalancamiento o leverage, entre otras.
De acuerdo a Kasa (1992), en la medida en que los mercados se vuelven más integrados, los efectos de los eventos en uno de ellos se transmiten a los otros, estableciéndose relaciones a largo plazo entre los mercados, producto de la existencia de tendencias comunes. En términos econométricos y según Kasa (1992), el número de relaciones cointegrantes existentes entre los mercados proporciona una idea del grado de integración entre ellos, es decir, si hay integración plena entre m mercados se esperaría encontrar n-m relaciones cointegrantes, un menor número a n-m en el caso de integración parcial y ninguna si los mercados analizados están totalmente fragmentados o parcelados.
Una forma de analizar la interrelación de las volatilidades de los mercados financieros es mediante el uso de modelos generalizados de heterocedasticidad condicional autorregresiva (MGARCH), los cuales necesariamente requieren que la matriz de varianzas-covarianzas sea positiva. Engle y Kroner (1995) proponen el modelo BEKK4, un modelo alternativo que mediante restricciones reduce el número de parámetros a estimar y garantiza la positividad de la matriz de varianzas-covarianzas. No obstante, debido a la pérdida de información y, consecuentemente, de las correlaciones entre los mercados, estas restricciones pueden dificultar la interpretación de los parámetros estimados y la detección de los posibles mecanismos de transmisión y de contagio de la volatilidad entre los mercados. Para el caso de este estudio y debido al número de observaciones diarias de las que se dispone (5.924 retornos diarios), el modelo generalizado MGARCH y de correlaciones dinámicas condicionadas (Dynamic Conditional Correlation [DCC]) propuesto por Engle (2002) permite que la matriz de correlaciones varíe ampliamente en el tiempo, permitiendo detectar la posible interrelación existente entre los mercados (Engle y Sheppard, 2001).
De esta manera, las correlaciones dinámicas condicionadas (DCC) de los mercados de acciones son un síntoma de contagio, especialmente cuando estas se presentan en un período en el que algún mercado se ve afectado por un shock. Es importante destacar que el análisis del aumento en la correlación de los retornos de los mercados de valores, como un indicador de contagio de eventos de crisis, es según Forbes y Rigobon (2002) una teoría con alto consenso en la literatura y en el mundo académico. No obstante, la heterocedasticidad presente en estos modelos puede llevar a resultados erróneos. En efecto, Longin y Solnik (2001) demuestran empíricamente que la correlación no solo se incrementa por el aumento de la volatilidad, sino también por la tendencia que tenga el mercado en ese momento. Específicamente, los autores muestran que los aumentos se dan cuando los mercados están a la baja. Además, es importante destacar que el análisis de correlación debe recaer, en la medida de lo posible, sobre las correlaciones cambiantes en el tiempo, ya que en estudios como el de Longin y Solnik (1995), realizado para países desarrollados, se evidencia que las matrices de covarianzas y de correlaciones de los retornos son inestables en el tiempo, lo que puede ser capturado de manera eficiente adoptando un esquema de correlación dinámica. Asimismo, Longin y Solnik (1995) señalan que la correlación muestra aumentos en los períodos de alta volatilidad.
Mediante el análisis de correlaciones de los mercados de valores para Japón y los llamados tigres asiáticos, Yang (2005) detecta aumentos significativos de la correlación en los períodos de mayor volatilidad. Bajo el mismo esquema, Chen et al. (2002) explican la existencia de una relación a largo plazo de los mercados de capitales de Argentina, Brasil, Chile, Colombia, México y Venezuela, encontrando que existe un vector cointegrante que puede explicar la dependencia de precios para estos mercados, resultante de la alta interdependencia entre estos, lo que implica que un shock negativo se propaga por todos los mercados de esos países.
Chiang et al. (2007), haciendo uso de la metodología DCC MGARCH multivariado e incluyendo retornos de 9 países, confirman un efecto contagio en la crisis asiática. Los autores señalan que este enfoque analítico permite abordar el problema de la heterocedasticidad sin necesidad de dividir la muestra de forma arbitraria como se señala en Forbes y Rigobon (2002). En esta misma línea, Syllignakis y Kouretas (2011) analizan las correlaciones condicionadas dinámicas para Europa Central y del Este, encontrando que la correlación aumenta de forma significativa durante los episodios de crisis, lo que refleja la exposición de estos países a shocks externos.
Durante la presente década, Horvath y Poldauf (2012) detectan que la correlación de los mercados de valores de varios países con respecto a Estados Unidos aumentó durante la crisis. Por otra parte, el trabajo de Kotkatvuori-Örnberg et al. (2013) determina que el impacto más significativo en términos de propagación de la crisis fue la quiebra de Lehman Brothers ocurrida el 15 de septiembre de 2008.
3Metodología y datosEl presente estudio tiene por objeto capturar la evidencia de contagio financiero e interdependencia entre las diferentes series financieras utilizando el índice Standard & Poor's 500 [S&P 500] como eje central de análisis. Diversos autores han hecho uso de la representación DCC desarrollada por Robert Engle en 2002 para abordar el tema de contagio financiero, entre los que se encuentran Syllignakis y Kouretas (2011), Chiang y Doong (2001), Syllignakis y Kouretas (2010) y Chiang et al. (2007).
Las representaciones matemáticas de la metodología propuesta incluyen las siguientes ecuaciones:
Ecuación de la media:
Ecuación de la varianza:
Ecuación de correlaciones dinámicas condicionadas (DCC):
donde λ1 y λ2 son los parámetros que gobiernan la dinámica de las quasicorrelaciones condicionales. Además, λ1 y λ2 son parámetros positivos y satisfacen la condición de estacionariedad 0≤λ1+λ2<1.
En el caso que λ1=λ2=0, el modelo se reduce a uno del tipo DCC MGARCH de correlaciones condicionales, que para este estudio resulta ser un modelo extremadamente restrictivo debido a las posibles implicaciones y efectos de contagio que podrían subyacer entre los distintos índices bursátiles. Finalmente, es muy importante corroborar que para cada uno de los modelos se cumplan simultáneamente las condiciones λ1=λ2≠0 y 0≤λ1+λ2<1. En esta investigación se utiliza la prueba de Wald junto con el estadístico chi-cuadrado (χ2) para corroborar que ambas condiciones se cumplen para cada modelo.
En general, los modelos MGARCH estimados permiten estudiar diversos patrones de comportamiento dinámico de las series bursátiles para los periodos de tiempo especificado, en este caso del periodo comprendido entre el 2 de enero de 1995 y el 16 abril de 2016. Cada modelo es construido mediante una matriz de varianza-covarianza condicionada, una especificación y una distribución de densidad multivariada. Las matrices varianza-covarianza condicionada son aquellas de los modelos VECH, BEKK y DCC. Esta última (DCC) es la matriz de varianza-covarianza condicionada que se utiliza en el presente estudio. Las especificaciones corresponden a las ya previamente definidas ARCH y GARCH. Respecto de las distribuciones multivariadas, están las muy conocidas distribución normal y t de Student. Así, en esta investigación se construyen 4 modelos multivariados y de estimación econométrica distintos, para determinar los efectos que el índice S&P 500 tiene sobre otros activos bursátiles, renta fija y commodities, siendo las estructuras dinámicas de los modelos MGARCH los sistemas de ecuaciones desarrollados y definidos más arriba.
Finalmente, y como todo modelo de estimación econométrica, el análisis comparativo y de evaluación de los modelos DCC MGARCH se sustenta en estimadores de bondad de ajuste. Específicamente, los estimadores usados aquí son el logaritmo de verosimilitud (Log Likelihood) y los ampliamente utilizados criterios de información de Akaike (AIC) y bayesiano (BIC). La relevancia de usar estos estimadores es que proporcionan criterios alternativos para elegir al mejor modelo descriptivo de las series, siempre teniendo presente que las matrices de varianza-covarianza son semidefinidas positivas. Adicionalmente, existe otro aspecto relevante respecto del uso de estos criterios, ya que además proveen elementos que permiten sugerir la existencia de algunos patrones de comportamiento dinámico conjunto de las series bursátiles bajo análisis, que para el presente estudio corresponde a las series americana, europea y asiática.
En síntesis, los modelos MGARCH son del tipo multivariado dinámico, donde las varianzas y covarianzas condicionales de los errores siguen una estructura de promedio móvil autorregresivo. De esta forma, los modelos del tipo DCC MGARCH hacen uso de combinaciones no-lineales de GARCH univariados con los pesos o ponderaciones de las ecuaciones cruzadas de variación temporal, con el objeto de modelar la matriz condicional de covarianza de los errores.
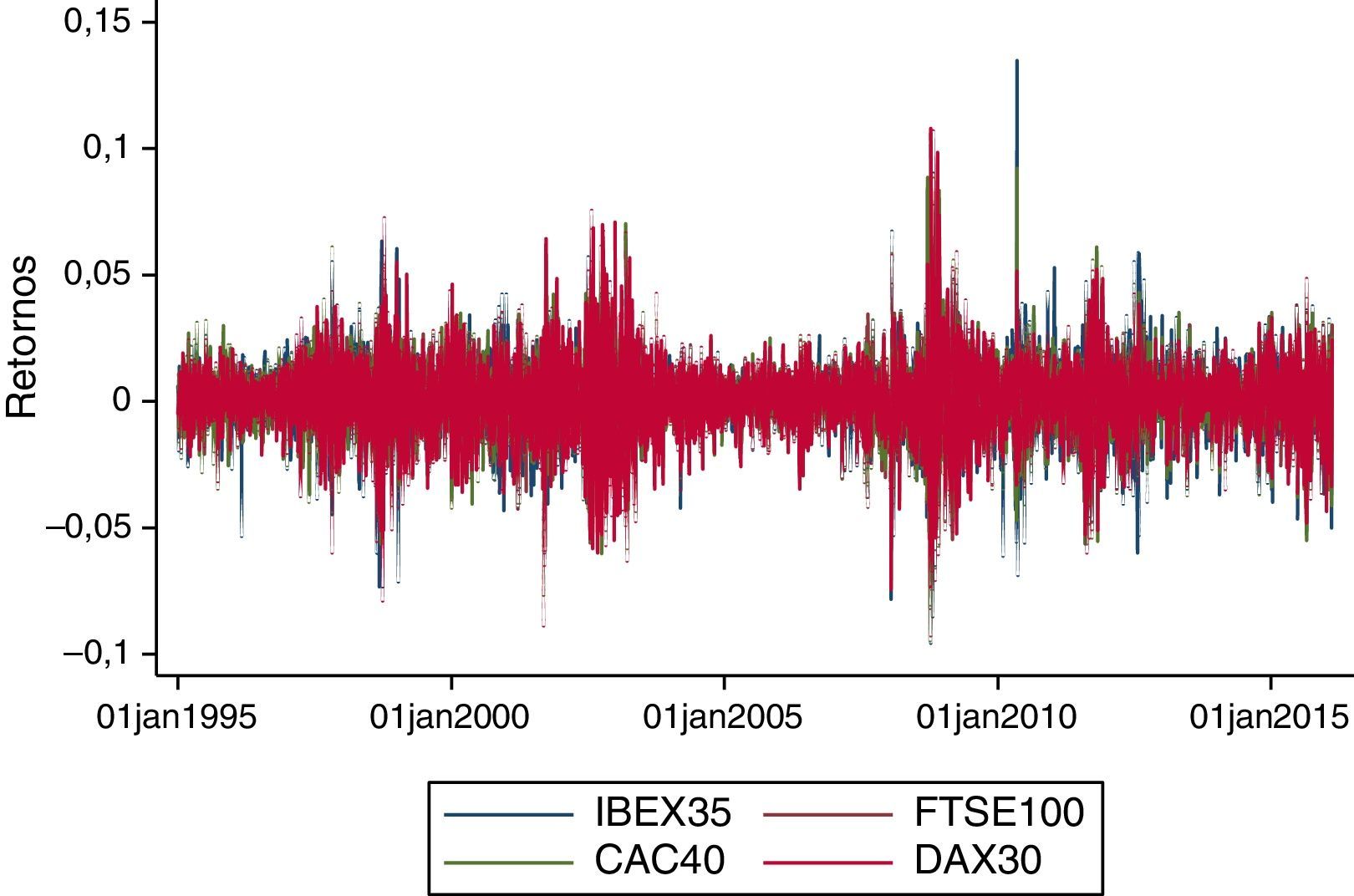
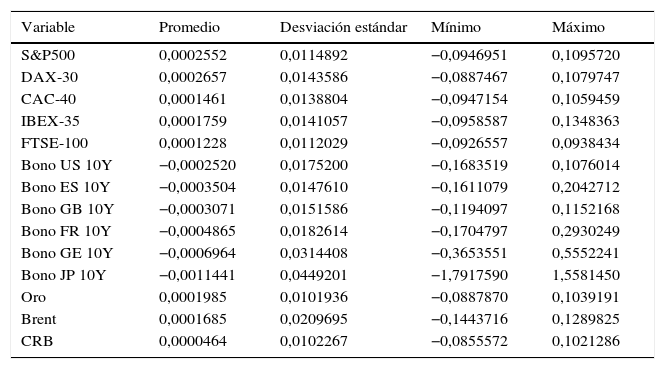
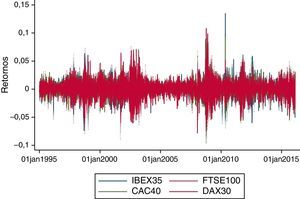
Respecto a los datos, para este estudio se utilizan datos diarios del índice S&P 500 para evaluar su relevancia y los posibles efectos sobre otros índices bursátiles como los de Europa (DAX-30, FTSE-100, IBEX-35 y CAC-40), Asia (Nikkei-225 y Shanghai Composite), instrumentos de renta fija de las principales economías (Bonos Soberanos a 10 años de EE.UU., Gran Bretaña, Alemania, España, Francia y Japón) y 3 de los principales índices de commodities (oro, petróleo Brent y CRB)2. El periodo de análisis es bastante extenso, contemplando valores entre el 2 de enero de 1995 y el 16 de abril de 2016 con un total de 5.924 observaciones. La tabla 1 resume las estadísticas descriptivas de los retornos diarios de las series especificadas.
Estadísticas descriptivas de los retornos diarios de las series
| Variable | Promedio | Desviación estándar | Mínimo | Máximo |
|---|---|---|---|---|
| S&P500 | 0,0002552 | 0,0114892 | −0,0946951 | 0,1095720 |
| DAX-30 | 0,0002657 | 0,0143586 | −0,0887467 | 0,1079747 |
| CAC-40 | 0,0001461 | 0,0138804 | −0,0947154 | 0,1059459 |
| IBEX-35 | 0,0001759 | 0,0141057 | −0,0958587 | 0,1348363 |
| FTSE-100 | 0,0001228 | 0,0112029 | −0,0926557 | 0,0938434 |
| Bono US 10Y | −0,0002520 | 0,0175200 | −0,1683519 | 0,1076014 |
| Bono ES 10Y | −0,0003504 | 0,0147610 | −0,1611079 | 0,2042712 |
| Bono GB 10Y | −0,0003071 | 0,0151586 | −0,1194097 | 0,1152168 |
| Bono FR 10Y | −0,0004865 | 0,0182614 | −0,1704797 | 0,2930249 |
| Bono GE 10Y | −0,0006964 | 0,0314408 | −0,3653551 | 0,5552241 |
| Bono JP 10Y | −0,0011441 | 0,0449201 | −1,7917590 | 1,5581450 |
| Oro | 0,0001985 | 0,0101936 | −0,0887870 | 0,1039191 |
| Brent | 0,0001685 | 0,0209695 | −0,1443716 | 0,1289825 |
| CRB | 0,0000464 | 0,0102267 | −0,0855572 | 0,1021286 |
Todas las series de datos fueron sometidas a pruebas de normalidad usando 4 distintas pruebas (Shapiro-Wilk, Shapiro-Francia, Jarque-Bera y Skewness-Kurtosis KS Test). En todas ellas, la hipótesis nula de normalidad fue rechazada al nivel del 1%. Adicionalmente, y como estos datos representan series de tiempo, todos ellos fueron sometidos a 3 pruebas de raíces unitarias (Augmented Dickey-Fuller, Phillips-Perron y KPSS [Kwiatkowski, Phillips, Schmidt and Shin], 1992), no encontrándose raíces unitarias en ninguno de ellos salvo para el caso del oro, razón por la cual esta variable está introducida en los modelos en forma de primeras diferencias.
Es importante enfatizar que los datos están expresados en retornos utilizando las primeras diferencias del logaritmo natural y, por lo tanto, la presencia de raíces unitarias es más bien dudosa, a excepción de la variable oro, razón por la cual se introduce en el modelo en primeras diferencias.
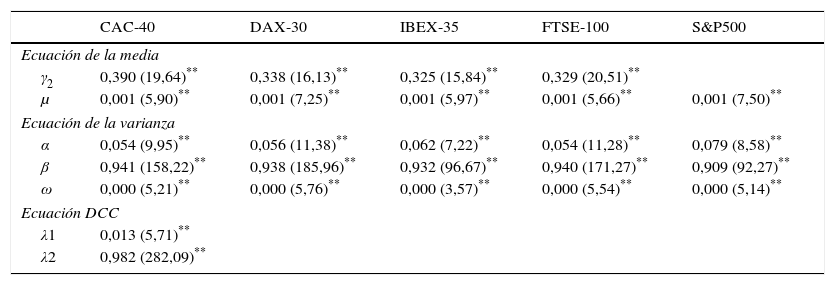
4ResultadosEn la tabla 2 se muestran los resultados de la estimación del modelo DCC MGARCH multivariado. El parámetro γ2 de la ecuación de la media es altamente significativo y representa la gran influencia y el efecto que tiene el S&P 500 sobre los retornos de los principales índices bursátiles de Europa. Respecto al orden de los rezagos, hay múltiples criterios de información, entre estos LL, LR, FPE, AIC, HQIC y SBIC, que confirman la inclusión de 1 a 2 rezagos como máximo para la ecuación de la media. Los coeficientes ARCH y GARCH de la ecuación de la varianza también son altamente significativos, lo que corrobora la especificación del modelo en el cual la varianza de cada error sigue un proceso del tipo GARCH (1,1). Esta última ecuación arroja los coeficientes α y β, que, sumados, muestran que la persistencia de la volatilidad es en promedio 0,99 para cada una de las especificaciones.
Modelo DCC MGARCH S&P 500-Europa
| CAC-40 | DAX-30 | IBEX-35 | FTSE-100 | S&P500 | |
|---|---|---|---|---|---|
| Ecuación de la media | |||||
| γ2 | 0,390 (19,64)** | 0,338 (16,13)** | 0,325 (15,84)** | 0,329 (20,51)** | |
| μ | 0,001 (5,90)** | 0,001 (7,25)** | 0,001 (5,97)** | 0,001 (5,66)** | 0,001 (7,50)** |
| Ecuación de la varianza | |||||
| α | 0,054 (9,95)** | 0,056 (11,38)** | 0,062 (7,22)** | 0,054 (11,28)** | 0,079 (8,58)** |
| β | 0,941 (158,22)** | 0,938 (185,96)** | 0,932 (96,67)** | 0,940 (171,27)** | 0,909 (92,27)** |
| ω | 0,000 (5,21)** | 0,000 (5,76)** | 0,000 (3,57)** | 0,000 (5,54)** | 0,000 (5,14)** |
| Ecuación DCC | |||||
| λ1 | 0,013 (5,71)** | ||||
| λ2 | 0,982 (282,09)** | ||||
En cuanto a la ecuación de correlaciones dinámicas condicionales DCC, ambos coeficientes λ1 y λ2 son estadísticamente significativos, por lo que se concluye que el comovimiento de los retornos es cambiante en el tiempo. De hecho, estos coeficientes muestran que son distintos de cero, pero su suma es menor a la unidad, lo que descarta la presencia de raíces unitarias, exhibiendo una alta persistencia en las correlaciones con valores para la suma de los coeficientes que oscilan entre 0,995 y 0,998.
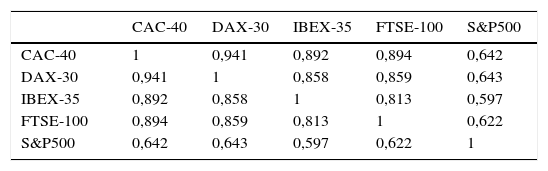
La tabla 3 resume las quasicorrelaciones condicionales entre los residuos estandarizados del índice S&P 500 y los índices de Europa, observándose una alta correlación entre estos con valores iguales o superiores a 0,60, como se observa para el S&P 500 con el DAX-30 de Alemania.
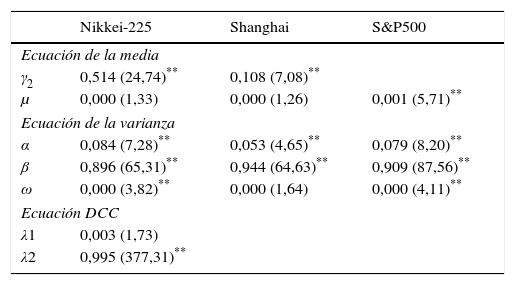
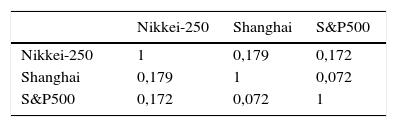
Siguiendo la misma metodología antes descrita, los resultados que arroja el modelo DCC MGARCH para el S&P 500 y las 2 principales bolsas de Asia (Nikkei-225 y Shanghai) se resumen en la tabla 4. Los resultados del modelo general son muy similares a los obtenidos para Europa, con valores significativos del parámetro γ2, así como de los parámetros de la ecuación de varianza y la alta persistencia. Sin embargo, al analizar las quasicorrelaciones condicionales entre los residuos estandarizados del índice S&P 500 y los índices de Asia se observa una menor correlación entre ellos, pudiendo deducirse que el grado de influencia del S&P 500 en estas bolsas es menor a lo observado en Europa (tabla 5).
Modelo DCC MGARCH S&P 500-Asia
| Nikkei-225 | Shanghai | S&P500 | |
|---|---|---|---|
| Ecuación de la media | |||
| γ2 | 0,514 (24,74)** | 0,108 (7,08)** | |
| μ | 0,000 (1,33) | 0,000 (1,26) | 0,001 (5,71)** |
| Ecuación de la varianza | |||
| α | 0,084 (7,28)** | 0,053 (4,65)** | 0,079 (8,20)** |
| β | 0,896 (65,31)** | 0,944 (64,63)** | 0,909 (87,56)** |
| ω | 0,000 (3,82)** | 0,000 (1,64) | 0,000 (4,11)** |
| Ecuación DCC | |||
| λ1 | 0,003 (1,73) | ||
| λ2 | 0,995 (377,31)** | ||
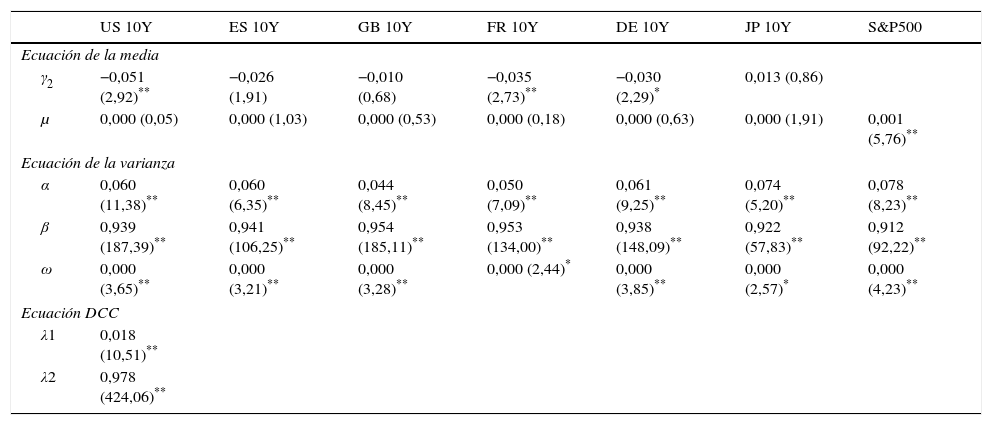
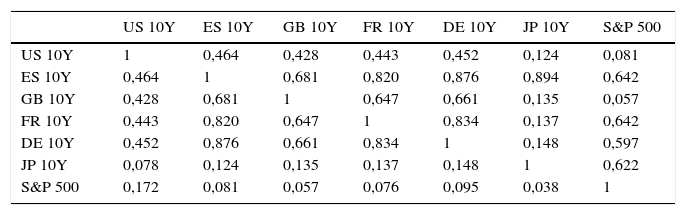
Para el caso del S&P 500 y los instrumentos de renta fija (Bonos Soberanos), el parámetro γ2 es significativo para los bonos a 10años de Estados Unidos, Alemania y Japón pero no significativo para los bonos de España, Francia y Gran Bretaña (tabla 6). También se observa que las quasicorrelaciones condicionales entre los residuos estandarizados del índice S&P 500 y los instrumentos de renta fija son más bien discretas comparadas con las quasicorrelaciones que se observan entre los bonos de distintos países (tabla 7).
Modelo DCC MGARCH S&P 500-Bonos Soberanos
| US 10Y | ES 10Y | GB 10Y | FR 10Y | DE 10Y | JP 10Y | S&P500 | |
|---|---|---|---|---|---|---|---|
| Ecuación de la media | |||||||
| γ2 | −0,051 (2,92)** | −0,026 (1,91) | −0,010 (0,68) | −0,035 (2,73)** | −0,030 (2,29)* | 0,013 (0,86) | |
| μ | 0,000 (0,05) | 0,000 (1,03) | 0,000 (0,53) | 0,000 (0,18) | 0,000 (0,63) | 0,000 (1,91) | 0,001 (5,76)** |
| Ecuación de la varianza | |||||||
| α | 0,060 (11,38)** | 0,060 (6,35)** | 0,044 (8,45)** | 0,050 (7,09)** | 0,061 (9,25)** | 0,074 (5,20)** | 0,078 (8,23)** |
| β | 0,939 (187,39)** | 0,941 (106,25)** | 0,954 (185,11)** | 0,953 (134,00)** | 0,938 (148,09)** | 0,922 (57,83)** | 0,912 (92,22)** |
| ω | 0,000 (3,65)** | 0,000 (3,21)** | 0,000 (3,28)** | 0,000 (2,44)* | 0,000 (3,85)** | 0,000 (2,57)* | 0,000 (4,23)** |
| Ecuación DCC | |||||||
| λ1 | 0,018 (10,51)** | ||||||
| λ2 | 0,978 (424,06)** | ||||||
Correlaciones S&P 500-Bonos Soberanos
| US 10Y | ES 10Y | GB 10Y | FR 10Y | DE 10Y | JP 10Y | S&P 500 | |
|---|---|---|---|---|---|---|---|
| US 10Y | 1 | 0,464 | 0,428 | 0,443 | 0,452 | 0,124 | 0,081 |
| ES 10Y | 0,464 | 1 | 0,681 | 0,820 | 0,876 | 0,894 | 0,642 |
| GB 10Y | 0,428 | 0,681 | 1 | 0,647 | 0,661 | 0,135 | 0,057 |
| FR 10Y | 0,443 | 0,820 | 0,647 | 1 | 0,834 | 0,137 | 0,642 |
| DE 10Y | 0,452 | 0,876 | 0,661 | 0,834 | 1 | 0,148 | 0,597 |
| JP 10Y | 0,078 | 0,124 | 0,135 | 0,137 | 0,148 | 1 | 0,622 |
| S&P 500 | 0,172 | 0,081 | 0,057 | 0,076 | 0,095 | 0,038 | 1 |
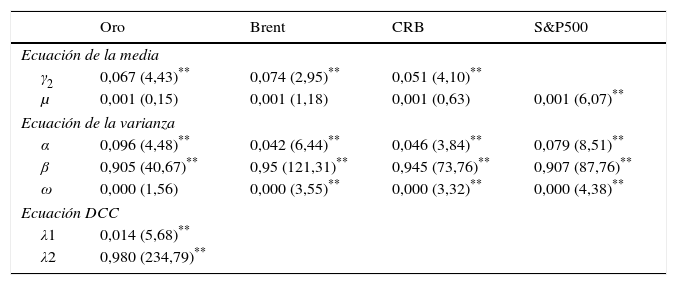
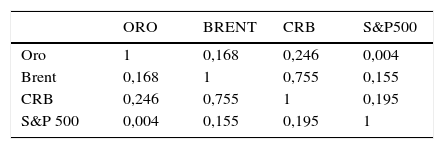
Finalmente, para el caso del S&P 500 y los 3 commodities incluidos en este estudio (oro, petróleo Brent y CRB), los parámetros para la ecuación de la media y de la varianza son altamente significativos, con una persistencia similar a la de los instrumentos analizados anteriormente (tabla 8). La gran diferencia se aprecia en la tabla 9, la cual presenta valores visiblemente menores para el caso de las quasicorrelaciones, lo que permite inferir que el índice no tendría gran impacto en el comportamiento de los commodities. Como se puede apreciar, las quasicorrelaciones no exceden a valores cercanos a 0,2 para el petróleo Brent y el índice de commodities CRB. En el caso del oro, la correlación de este con el S&P 500 es prácticamente cero, lo que reafirma el hecho de que ante turbulencias bursátiles, el oro es tal vez uno de los commodities más requerido y demandado como valor refugio y estrategia de diversificación.
Modelo DCC MGARCH S&P 500-Commodities
| Oro | Brent | CRB | S&P500 | |
|---|---|---|---|---|
| Ecuación de la media | ||||
| γ2 | 0,067 (4,43)** | 0,074 (2,95)** | 0,051 (4,10)** | |
| μ | 0,001 (0,15) | 0,001 (1,18) | 0,001 (0,63) | 0,001 (6,07)** |
| Ecuación de la varianza | ||||
| α | 0,096 (4,48)** | 0,042 (6,44)** | 0,046 (3,84)** | 0,079 (8,51)** |
| β | 0,905 (40,67)** | 0,95 (121,31)** | 0,945 (73,76)** | 0,907 (87,76)** |
| ω | 0,000 (1,56) | 0,000 (3,55)** | 0,000 (3,32)** | 0,000 (4,38)** |
| Ecuación DCC | ||||
| λ1 | 0,014 (5,68)** | |||
| λ2 | 0,980 (234,79)** | |||
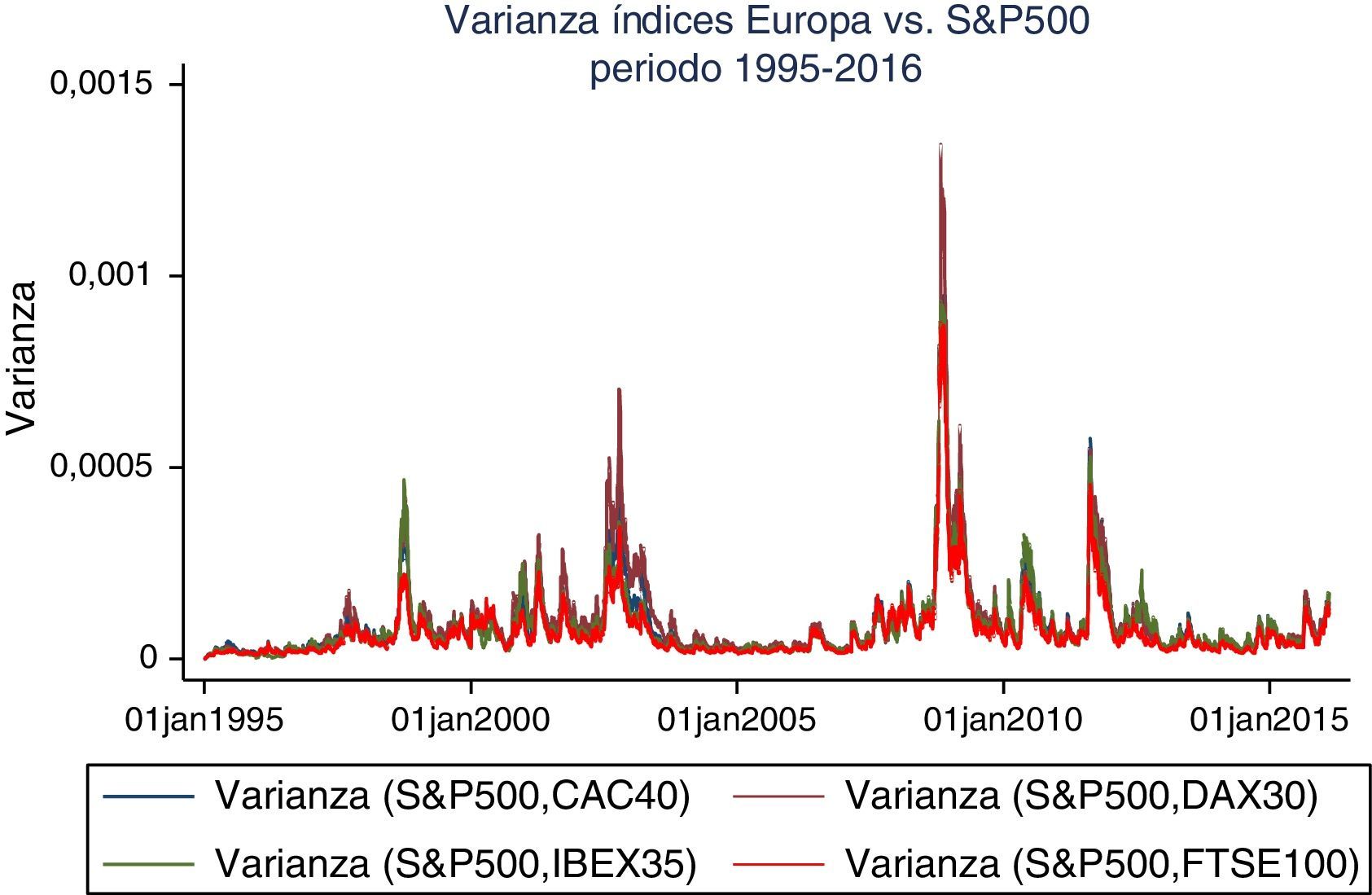
Aplicando la metodología DCC MGARCH, se estimaron las correlaciones cruzadas entre los retornos diarios del índice S&P 500 y los retornos de activos financieros de los mercados de valores de Europa y Asia. Con ello se observa que para el periodo 1995-2016 existen tendencias comunes entre los diferentes activos financieros. Sin lugar a dudas, la globalización ha provocado una mayor integración en los diferentes mercados financieros, y esta mayor integración en los mercados de capitales erosiona los beneficios de la diversificación entre los diferentes activos.
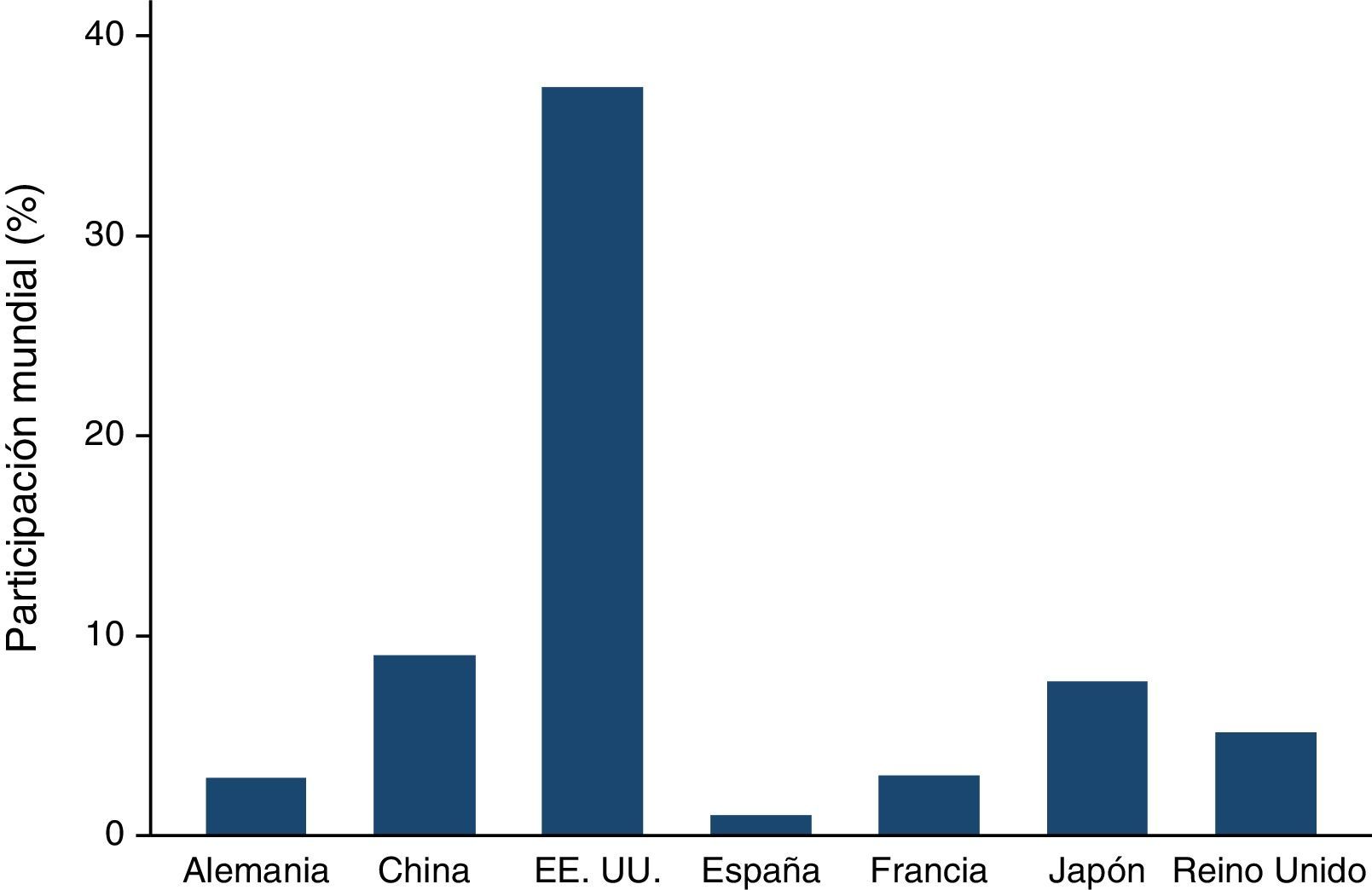
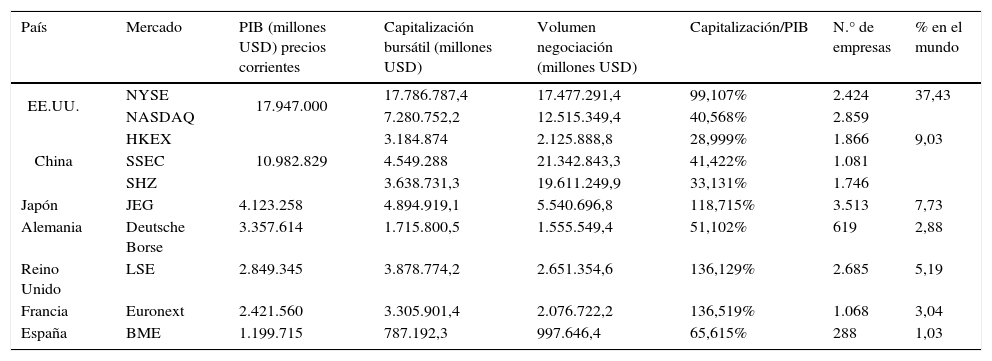
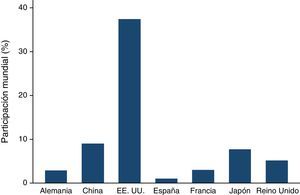
A nivel global, Estados Unidos es la referencia del mercado dado sus volúmenes y peso en términos de capitalización bursátil, con una representación del 37,43% **(véase la tabla 10 y la fig. A.1 en el Anexo). Con todo, Estados Unidos ejerce una influencia muy significativa sobre los otros mercados tanto a nivel de rendimientos como de volatilidad. En consecuencia, la volatilidad de Estados Unidos influye en mayor medida en la volatilidad de mercados más pequeños debido a su importancia relativa. Asimismo, la madurez del mercado estadounidense hace que ante caídas en Wall Street, el resto de los mercados amplifique los posibles descensos del mercado estadounidense, independientemente de si estos son más o menos pronunciados. Por otra parte, y a pesar de que China exhibe unos altos volúmenes de contratación, aún no se evidencia una correlación directa con los otros mercados financieros, aunque parece lógico pensar que su efecto sobre los activos de otras latitudes será cada vez más creciente, a medida que su importancia relativa se incremente.
Como corolario general, la mayor integración entre los diferentes mercados financieros y activos subyacentes provoca un mayor riesgo sistemático en el propio mercado. La presencia importante de flujos de capital entre Estados Unidos y Europa, así como el hecho de tener un horario semicompartido, conlleva que el alto grado de integración sea mayor que en el resto de los mercados financieros.
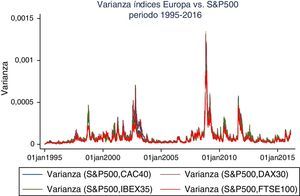
El modelo DCC MGARCH también deja en evidencia que los movimientos del S&P 500 están positivamente correlacionados con los índices europeos. Las correlaciones entre los diferentes activos de renta variable son altas, del orden de 0,6 o superiores, así como significativas al nivel del 1%. Ampliamente documentado ha sido el hecho de que los mercados de valores de todo el mundo están altamente correlacionados, y más aún en periodos de crisis, en que los procesos de contagio son mayores (Forbes y Rigobon, 2002).
Los movimientos del S&P 500 también están positivamente correlacionados de manera significativa con el Nikkei 225 y el índice Shanghai Composite, aun cuando los índices de correlación son menores a los resultados obtenidos entre el S&P 500 y Europa. Por otra parte, los resultados para el S&P 500 y el Shanghai Composite no muestran un grado de significación suficiente para determinar la existencia de correlación entre ambos índices. En Asia, es posible que la no coincidencia horaria, conjuntamente con el mayor peso de la información local, evidencien dicha descorrelación (Bekaert et al., 2003).
Respecto a las correlaciones entre el S&P 500 y los activos de renta fija, el índice se correlaciona positivamente con el bono a 10años, aunque con una significancia menor. El S&P 500 se correlaciona en mayor medida con el bono norteamericano a 10años y en menor medida con el resto de bonos europeos y asiáticos. Una explicación de la existencia de esta correlación podría ser el alto grado de globalización financiera que se ha traducido en un ciclo económico más homogéneo, una volatilidad más uniforme en los mercados financieros, así como una política monetaria por parte de los grandes bancos centrales que podría romper la heterogeneidad de los propios mercados financieros. Asimismo, el mayor grado de contagio debe abordar una futura arquitectura monetaria y financiera más coordinada entre los diferentes bancos centrales, es decir, los bancos centrales deben alinearse y mostrar un diagnóstico más compartido entre ambos para así poder tener una actuación más rápida y eficiente.
En este sentido, la gran liquidez que han aportado los bancos centrales al sistema ha provocado también una distorsión a la aversión al riesgo bursátil, ya que esta gran liquidez ha generado que tanto la renta fija como la renta variable se encuentren en máximos históricos en aquellos activos de calidad.
De esta forma, los resultados obtenidos al estudiar la correlación existente entre los diferentes bonos de los distintos Estados muestran que las políticas monetarias ultraexpansivas de los diferentes países han propiciado una interrelación entre los diversos bonos. La globalización financiera implica que una parte del dinero creado por los bancos centrales nacionales acabe fuera de sus propias fronteras económicas. Esta mayor integración requiere que se realicen más investigaciones sobre las interrelaciones entre los mercados a fin de identificar plenamente sus implicaciones. Adicionalmente, tanto las autoridades nacionales como internacionales deben acotar una mayor regulación preventiva con futuros riesgos bursátiles.
El tamaño del mercado financiero sigue incrementándose de una manera sustancial en comparación al crecimiento de la economía real que crece, pero a un menor ritmo. Tanto el tamaño del mercado de la renta variable como el tamaño de la renta fija, en términos generales, siguen mostrando un ensanchamiento que debe hacer reflexionar sobre la viabilidad del sistema actual3. En este sentido, los autores de este estudio creemos que el hecho de que el tamaño de los activos financieros permanezca tan alejado en relación con la economía real puede ser un factor contraproducente para paliar los futuros riesgos bursátiles.
Respecto a posibles relaciones de causalidad y mediante el uso de modelos de vectores autorregresivos (VAR) y la aplicación de la prueba de Granger, se determinó la existencia de relaciones de causalidad entre los movimientos del S&P 500 y los bonos. En efecto, un alza (baja) del S&P 500 implica un efecto positivo (negativo) con el resto de bonos. En este sentido, una baja del S&P 500 provoca una caída de la rentabilidad en la renta fija. En consecuencia, los fondos de inversión e inversionistas entran en mayor medida a la renta fija como valor refugio.
Los resultados obtenidos confirman la existencia de relación de causalidad entre los movimientos del S&P 500 y los bonos norteamericano, británico y alemán. Coincidencia o no, los 3 bonos obtienen la calificación de «investment grade» con un alto grado de valor refugio. En las siguientes líneas de investigación se deberá estudiar si las políticas monetarias ultraexpansivas han provocado que los bajos rendimientos de los bonos (incluso negativos para el Bund alemán en junio 2016) pierdan su carácter de valor refugio y conjeturen una percepción del riesgo inadecuada.
En relación con los commodities, se observa que hay una fuerte correlación significativa entre ellos, pero a la hora de ver la correlación existente entre el S&P 500 y el resto de commodities, hay una correlación significativa con el Brent y el CRB, mientras no se puede deducir estadísticamente que exista esta correlación con el oro. Dicha correlación entre las diferentes commodities es significativa en gran parte debido a que las materias primas comercializadas internacionalmente están cotizadas en dólares estadounidenses, por lo que un incremento del valor del dólar incrementa el valor de la misma cantidad de toneladas y/o barriles. No obstante, no se puede determinar que los grados de sensibilidad sean iguales para todas las materias primas.
No está de más agregar que antes de la implementación y utilización de modelos VAR en este estudio, se realizó para todos los modelos la prueba de Johansen en niveles, con el objeto de descartar la posible presencia de cointegración entre los diferentes activos financieros. Los resultados descartan la presencia de cointegración entre los activos utilizados en este análisis, excepto para el caso de los bonos, razón por la cual se estimaron las 2 ecuaciones de vectores de corrección del error (VEC) que arrojó la prueba de cointegración de Johansen. Tan solo después de esta corrección se pudo implementar la prueba de Granger para establecer posibles relaciones de causalidad entre el S&P 500 y los instrumentos de renta fija (bonos).
Agradecer la colaboración de los miembros, Andrea Gómez y Alejandro Ramon, del servicio de estudios de la Bolsa de Barcelona.BME por sus aportaciones en el trabajo de investigación.
Importancia absoluta y relativa de los mercados bursátiles
| País | Mercado | PIB (millones USD) precios corrientes | Capitalización bursátil (millones USD) | Volumen negociación (millones USD) | Capitalización/PIB | N.° de empresas | % en el mundo |
|---|---|---|---|---|---|---|---|
| EE.UU. | NYSE | 17.947.000 | 17.786.787,4 | 17.477.291,4 | 99,107% | 2.424 | 37,43 |
| NASDAQ | 7.280.752,2 | 12.515.349,4 | 40,568% | 2.859 | |||
| China | HKEX | 10.982.829 | 3.184.874 | 2.125.888,8 | 28,999% | 1.866 | 9,03 |
| SSEC | 4.549.288 | 21.342.843,3 | 41,422% | 1.081 | |||
| SHZ | 3.638.731,3 | 19.611.249,9 | 33,131% | 1.746 | |||
| Japón | JEG | 4.123.258 | 4.894.919,1 | 5.540.696,8 | 118,715% | 3.513 | 7,73 |
| Alemania | Deutsche Borse | 3.357.614 | 1.715.800,5 | 1.555.549,4 | 51,102% | 619 | 2,88 |
| Reino Unido | LSE | 2.849.345 | 3.878.774,2 | 2.651.354,6 | 136,129% | 2.685 | 5,19 |
| Francia | Euronext | 2.421.560 | 3.305.901,4 | 2.076.722,2 | 136,519% | 1.068 | 3,04 |
| España | BME | 1.199.715 | 787.192,3 | 997.646,4 | 65,615% | 288 | 1,03 |
Fuente: elaboración propia. Datos extraídos de WFE y FMI.
Riesgo sistemático se considera cuando se origina un problema financiero y este acaba teniendo una repercusión negativa en la actividad económica.
Creado en 1957, el índice se compone de los precios futuros de 19 commodities, cada una con su peso relativo, tales como aluminio, cacao, café, petróleo, oro, trigo, gasolina, gas natural, plata, maíz y algodón, entre otras.
Veáse Structural causes of the global financial crisis: a critical assessment of the «new financial architecture».