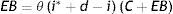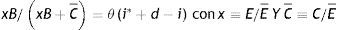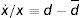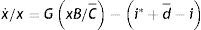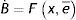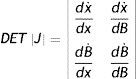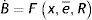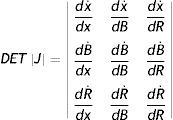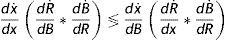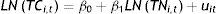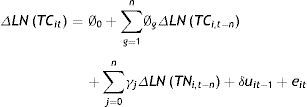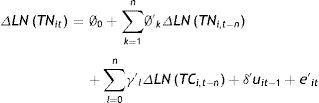La reciente implementación de restricciones cambiarias en Argentina y Venezuela nos invita a revisar la historia del control de cambios en América Latina. El presente trabajo tiene como objetivo analizar la efectividad de los controles a la hora de evitar bruscas devaluaciones del tipo de cambio oficial. Nuestro análisis extiende un sencillo modelo de portafolio y propone un test econométrico cuyo fin es indagar sobre la dinámica del tipo de cambio oficial y del tipo de cambio negro a partir de métodos de cointegración en paneles de datos. Encontramos que el tipo de cambio oficial y el tipo de cambio negro mantienen una relación estable de largo plazo y que principalmente el tipo de cambio oficial ajusta en presencia de desequilibrios. Esto sugiere que en América Latina los controles cambiarios no fueron una herramienta efectiva para evitar una brusca devaluación.
The recent implementation of foreign exchange restrictions in Argentina and Venezuela leads us to reconsider the history of foreign exchange controls in Latin-America. The aim of this paper is to analyse the effectiveness of these controls in preventing sudden devaluations in the official rate. The analysis uses a simple portfolio model and an econometric test is proposed that uses panel cointegration techniques to explore the relationship between official and black market rates. It was found that the official and the black market rates are cointegrated, and that mainly the official exchange rate is usually adjusted when there is a disequilibrium. This suggests that foreign exchange controls in Latin-America were not an effective tool to avoid large and abrupt devaluations.
Durante el período 1930-1990, la mayor parte de los países del mundo implementaron en alguna ocasión regulaciones que limitaron la compra y venta de divisas, restringiendo tantos los montos como los rubros sobre los que se podía operar. La circunstancia que solía motivar la implementación de medidas de este tipo era la existencia de fuertes presiones devaluatorias. En contextos muy complicados, como por ejemplo el que se impuso con el colapso del patrón oro a comienzos de los años 1930, las regulaciones se generalizaban para dar cuerpo a un sistema de control de cambios.
En esencia, un sistema de control de cambios busca enfrentar una situación de escasez de divisas, impidiendo, retrasando o eventualmente acompañando una devaluación, para preservar en la medida de lo posible la estabilidad macroeconómica. Al menos en una etapa inicial, las autoridades implementaban los controles con la idea de enfrentar desequilibrios considerados transitorios, de modo tal que una vez que los problemas desaparecieran, las regulaciones podrían ser eliminadas. Sin embargo, en la práctica los controles se transformaban en un elemento permanente de la política económica.
Los controles de cambio dan origen a un mercado negro donde es posible adquirir ilegalmente divisas, usualmente a un precio mayor que al tipo de cambio oficial (el tipo de cambio «negro»). En el pasado, brechas muy elevadas entre el tipo de cambio oficial y el tipo de cambio negro1 representaron un desafío para la administración de las políticas macroeconómicas. Cuando la brecha era muy elevada, la oferta de divisas en el mercado oficial tendía a desplazarse hacia el mercado negro, donde era posible conseguir un precio mayor, mientras que la demanda al tipo de cambio oficial tendía a incrementarse, ya que los agentes buscaban anticipar las compras de bienes transables cuyo precio (al tipo de cambio oficial) seguramente aumentaría en el futuro. Esto generaba un «efecto goteo» que presionaba reduciendo paulatinamente el stock de reservas internacionales, hasta que finalmente se producía la devaluación del tipo de cambio oficial (Dornbusch, 1986).
En la actualidad, si bien el número de países que aplican amplios sistemas de control de cambios es reducido, en América Latina Argentina (2011-2015) y Venezuela (desde 2003) implementaron un conjunto de restricciones al acceso a la moneda extranjera, y ante la demanda de divisas insatisfecha (al tipo de cambio oficial) emergió un mercado negro y apareció una brecha cambiaria de magnitud significativa.
Por otra parte, las regulaciones a los movimientos de capitales no han desaparecido por completo2. Si bien esquemas regulatorios demasiado duros como los de Argentina y Venezuela parecen ser la excepción y no la norma, analizar el funcionamiento de diversos sistemas de control puede aportar elementos para una valiosa discusión sobre cómo implementar con éxito esquemas de control en el futuro.
El presente trabajo tiene como objetivo analizar la efectividad de los controles cambiarios a la hora de evitar buscas modificaciones en la cotización del tipo de cambio oficial. Una de las lecciones principales es que cuando existen brechas cambiarias demasiado elevadas, la sostenibilidad de un esquema de control se encuentra en peligro. Nuestro análisis desarrolla tal idea presentando un modelo de portafolio simple que nos permite analizar la dinámica del tipo «goteo», para luego testear empíricamente la causalidad entre tipo de cambio oficial y negro. Más precisamente, proponemos un ejercicio econométrico que tiene el fin de indagar sobre la dinámica del tipo de cambio oficial y del tipo de cambio negro a partir de métodos de cointegración en paneles de datos. La muestra utilizada abarca el período comprendido entre enero de 1946 y junio de 1998 para América Latina y se basa en las series de tipos de cambios oficiales y negros de Reinhart y Rogoff (2004). Dichos autores han compilado la información a partir del Manual de Restricciones Cambiarias y el Anuario Pick, ambos del Fondo Monetario Internacional3.
La estructura del trabajo es la siguiente. Luego de esta primera sección introductoria, la segunda sección reseña la literatura sobre el control de cambios. La tercera sección discute un modelo de portafolio simple para analizar los determinantes de la brecha y discutir la dinámica que puede conducir a una brusca devaluación del tipo de cambio oficial. La cuarta sección desarrolla un modelo econométrico que busca analizar la relación de causalidad entre el tipo de cambio oficial y el tipo de cambio negro en América Latina. Finalmente, la quinta sección concluye.
2Reseña de la literaturaLa literatura sobre el control de cambios es amplia y ha abordado diversos tópicos. Una cuestión central es cómo clasificar las distintas experiencias. Al respecto, Bhagwati (1979) propuso distinguir entre regímenes basados en «regulaciones por precio» y regímenes basados en «restricciones cuantitativas». Por su parte Kiguel y O’Connell (1995) distinguieron entre esquemas de control en los cuales las transacciones menos importantes deben cursarse a un tipo de cambio libre, y esquemas en donde se hallan prohibidas, por lo que se deben cursar forzosamente por el mercado negro.
Otro segmento de la literatura indagó sobre los determinantes de la brecha y sus efectos sobre la macroeconomía. A nivel teórico, la mayor parte de los trabajos sobre los determinantes se basaron en el enfoque de portafolio, el cual se popularizó a partir de los años 1970 como consecuencia del auge de los flujos internacionales de capitales. En contraposición al enfoque basado en «flujos» que caracterizó la literatura anterior sobre los determinantes del tipo de cambio, este enfoque otorga un rol protagónico a los diferenciales de retornos y las expectativas de precio futuras a la hora de promover ajustes en los stocks. Pero a diferencia de los enfoques que asumen perfecta sustituibilidad entre activos domésticos y externos, en los modelos de portafolio las ofertas relativas de activos juegan un papel importante en la determinación de sus precios4.
Los modelos de portafolio no ignoran los flujos, pero les otorgan un papel relevante principalmente en el mediano plazo. En lo inmediato, la oferta de moneda extranjera se considera fija y el tipo de cambio es la variable que ajusta para equilibrar los portafolios en función de los retornos esperados. Finalmente, los flujos determinan la evolución de los stocks a lo largo del tiempo en función del nivel que toma el tipo de cambio (ver, por ejemplo, el modelo propuesto por Dornbusch y Fisher, 1980).
Este marco básico puede ser extendido para analizar la dinámica del tipo de cambio negro. Uno de los modelos más populares y más representativos que ha avanzado en tal dirección es el propuesto por Dornbusch et al. (1983). Dicho modelo considera a la oferta de dólares en el mercado negro como una variable predeterminada, por lo que la brecha cambiaria ajusta para equilibrar la demanda con la oferta preexistente de dólares. El nivel de la brecha determina el ritmo al cual varía el stock de activos externos a lo largo del tiempo.
La estructura del modelo es simple, pero permite incluir múltiples determinantes de la brecha, como las políticas cambiarias, monetarias y fiscales, por poner algunos ejemplos. Dicho modelo también ha sido expandido y utilizado para analizar programas de estabilización, dinámica inflacionaria y determinación del tipo de cambio real (ver, por ejemplo, Kamin, 1993). También ha servido de sustento teórico a muchos trabajos empíricos. Por ejemplo, Diamandis et al. (2005) analizaron el rol de las expectativas sobre la evolución del tipo de cambio oficial en la formación del tipo de cambio negro, con el fin de testear el modelo de portafolio sugerido por Dornbusch et al. (1983).
Para testear el impacto de shocks anticipados y no anticipados, los autores emplean la metodología propuesta por Barro (1977) y modificada luego por Hoffman et al. (1984). En una primera etapa, los autores construyeron una ecuación para predecir los movimientos del tipo de cambio oficial y negro. Las predicciones obtenidas constituyen los choques «anticipados», mientras que los residuos constituyen los choques «no anticipados». En la segunda etapa, se estimó una regresión para explicar la brecha cambiaria a partir de los valores presentes y rezagados de ambos tipos de choques. La significatividad conjunta e individual de los parámetros de la regresión se evalúa utilizando un test del tipoF. El principal resultado que surgió de aplicar dicha metodología para Grecia es que los modelos de portafolio resultan apropiados para entender la dinámica del tipo de cambio negro en dicho país.
A la hora de analizar los aspectos empíricos del funcionamiento de un esquema de control de cambios, la literatura indaga sobre los efectos y los determinantes de la brecha. Los trabajos que tratan sobre los efectos de la brecha sobre la economía utilizan principalmente regresiones de crecimiento «al estilo Barro» (Barro, 1991), en las cuales la brecha se introduce como variable explicativa en regresiones en donde el promedio de 5años de la tasa de crecimiento es la variable dependiente.
Este tipo de estimación ha sido utilizada en diversas ocasiones por Easterly. Dicho autor empleó regresiones del tipo corte transversal para 51 países entre 1970 y 1985 (Easterly, 1993), luego estimó un panel para 16 países de América Latina entre 1960 y 1993 (Easterly, 2001), y finalmente presentó un panel para 82 países entre 1960 y 2000 (Easterly, 2004). Por su parte, Ghura y Grennes (1993) estimaron una regresión de corte transversal para 33 países de África subsahariana entre 1972 y 1987. Los resultados obtenidos en la mayor parte de estos estudios sugieren que la brecha tiene un efecto negativo y significativo sobre el crecimiento (a niveles habituales), aunque de reducida magnitud.
Otra serie de estudios basados principalmente en la metodología de series de tiempo analizaron diversos determinantes de la brecha. La mayor parte de los trabajos utilizaron estimaciones basadas en mínimos cuadrados clásicos, incluyendo como variables explicativas de la brecha a la brecha rezagada un período, al tipo de cambio oficial, al diferencial entre la tasa de interés doméstica y la tasa de interés internacional más la devaluación esperada, a las reservas internacionales, a algunos agregados monetarios amplios (como M2) y a variables indicativas por mes o trimestre (Malone y ter Horst, 2010, Fishelson, 1988, Phylaktis, 1992, Shachmurove, 1999). Estos trabajos arrojan como resultado principal (dada su robustez) la presencia de una alta correlación entre la brecha y sus valores rezagados. El resto de las variables resultan estadística y económicamente significativas en algunos trabajos, pero no en otros.
Un problema de los trabajos que utilizan la metodología de mínimos cuadrados clásicos es que ignoran la potencial presencia de raíces unitarias en los datos. Esto implica la posibilidad de identificar relaciones espurias entre variables no estacionarias. Dada la correlación que suele existir entre la brecha y la brecha rezagada, se trata de un problema potencialmente importante. Por otra parte, estos trabajos desperdician valiosa información, pues la existencia de raíces unitarias en contextos en donde existe una relación de cointegración nos permitiría estimar la velocidad de convergencia al equilibrio (que en este caso nos puede indicar la duración promedio de los esquemas de control de cambios) o analizar si existe causalidad (en sentido de Granger) entre el tipo de cambio oficial y el tipo de cambio negro a partir de las ecuaciones que describen dinámica del ajuste.
Otros trabajos han implementado metodologías más sofisticadas, reconociendo el problema de la no estacionariedad de las variables. En particular, Agenor y Taylor (1993) estudiaron la causalidad entre el tipo de cambio oficial y el tipo de cambio negro utilizando técnicas de cointegración y causalidad en sentido Granger. Su análisis incluyó datos mensuales para 13 países no desarrollados y su principal hallazgo es que no existe un patrón único y claro que se aplique a la totalidad de su muestra.
Phylaktis y Kassimatis (1994) analizaron si la brecha predice adecuadamente la magnitud de la devaluación futura para 7 países de la Cuenca del Pacífico. Los autores encontraron que existe una relación estable entre el tipo de cambio oficial y el tipo de cambio negro, lo cual implica que no se alejan demasiado el uno del otro en el largo plazo. Adicionalmente, estos estudios verifican que el tipo de cambio negro ajusta en presencia de desequilibrios. Por último, la velocidad de ajuste varía de país a país. Moore y Phylaktis (2000) presentaron hallazgos similares.
Bahmani-Oskooee (1993), Baghestani (1997) y Sundar et al. (1997) discutieron la relevancia del tipo de cambio negro a la hora de testear la validez de la teoría de la paridad del poder adquisitivo (para los casos de Irán, India y 6 países de Asia, respectivamente). Estos trabajos encontraron que existe una relación estable y de largo plazo entre el tipo de cambio oficial y el tipo de cambio negro. Usando el tipo de cambio vigente en el mercado negro, estos trabajos encontraron evidencia en favor de la paridad del poder de compra, mientras que usando el tipo de cambio vigente en el mercado oficial rechazaron tal teoría. Esto parece sugerir que en determinados contextos el tipo de cambio negro es un mejor indicador de los precios relativos de bienes y activos financieros que el tipo de cambio oficial.
Finalmente, Caporale y Cerrato (2006) encontraron que el tipo de cambio oficial y el tipo de cambio negro están cointegrados (para una muestra compuesta por Irán, India, Indonesia, Corea del Sur, Pakistán y Tailandia). No obstante, Caporale y Cerrato también sugirieron que la velocidad de ajuste hacia el equilibrio de largo plazo es lenta, lo cual implica que existe un amplio espacio para hacer políticas como consecuencia de los controles.
A los fines del presente trabajo, es conveniente resumir los resultados de la literatura que se basan en técnicas de cointegración. Sintetizando, parece existir un consenso sobre la presencia de cointegración entre el tipo de cambio oficial y el tipo de cambio negro, más no sobre la dinámica del ajuste. Desconocemos la existencia de trabajos que hayan aplicado la metodología de cointegración para países de América Latina. Las dos secciones siguientes presentan un marco teórico y empírico para entender la dinámica del ajuste, con especial énfasis en la experiencia de dicha región.
3Un modelo simple de crisisConsiderando que la evidencia empírica recogida por la literatura sugiere que el tipo de cambio oficial y el tipo de cambio negro no se apartan demasiado entre sí en el largo plazo, es natural preguntarse por el proceso de ajuste ante desequilibrios. En general los modelos existentes en la literatura se concentran en analizar el proceso de determinación de la brecha cambiaria, pero no suelen dar cuenta del proceso de unificación cambiaria5. En muchos casos, los modelos propuestos sugieren que ante desequilibrios, la brecha converge a un determinado valor de equilibrio.
Este resultado es consistente con algunas experiencias en donde la brecha se estabiliza (ver, por ejemplo, Diamandis et al. (2005), pero no parece razonable para algunos casos de América Latina, donde, como veremos en la sección cuarta, todo parece indicar que brechas muy elevadas derivaron eventualmente en fuertes devaluaciones del tipo de cambio oficial.
Esta sección presenta un modelo de portafolio basado en Dornbusch et al. (1983) y discute una sencilla extensión que incorpora un mecanismo que puede generar endógenamente una crisis. El objetivo principal es ofrecer un marco estilizado simple que permita capturar la diversidad de experiencias sugerida por los distintos estudios teóricos existentes. Con tal fin, partimos del marco conceptual que mejor se adecua al problema del control de cambios, que es el enfoque de portafolio, y le incorporamos una sencilla función de reacción de las autoridades que captura la intensidad del marco regulatorio.
La especificación refleja uno de los principales hechos estilizados de la experiencia de América Latina (y posiblemente de otros países en desarrollo), como el endurecimiento de las regulaciones en presencia del fenómeno conocido como «goteo» (es decir, la pérdida paulatina de reservas). Mostraremos que la propia dinámica de las regulaciones puede desestabilizar el sistema (dependiendo de los parámetros del modelo), provocando una brusca devaluación del tipo de cambio oficial y un colapso del sistema de control de cambios. Primero presentamos el marco básico siguiendo a Dornbusch et al. (1983), para luego incorporar una función de reacción que estipula cómo las autoridades administran el control de cambios.
Un sencillo modelo de portafolio que contempla la presencia de controles cambiarios está estructurado de la siguiente forma. La primera ecuación representa la demanda de dólares B multiplicada por el tipo de cambio nominal en el mercado negro E, definido como el número de unidades de moneda doméstica que hay que entregar para adquirir un dólar:
Donde θ representa la fracción de la riqueza total medida en moneda doméstica (C+EB) que los agentes desean mantener bajo la forma de dólares. Dicha fracción es una función positiva del diferencial de retornos entre activos externos y domésticos, definido por (i*+d−i). Estas tres variables representan la tasa de interés doméstica, la devaluación esperada (que dado que las expectativas se forman racionalmente se asume igual a la tasa observada) y la tasa de interés internacional, respectivamente. Finalmente, la variable C representa el stock de activos domésticos.
Notemos que (1) no afirma que θ multiplica el término entre paréntesis (i*+d−i), ya que el diferencial de retornos es el argumento de la función que explica la demanda de activos externos, pero sí multiplica a la riqueza total (C+EB), pues θ representa una fracción del total de la riqueza del sector privado. La ecuación (1) nos dice que la demanda de dólares (evaluada al tipo de cambio negro) es una fracción de la riqueza total, por lo que se deduce que (1−θ) representa la fracción de la riqueza que se demanda bajo la forma del activo doméstico. Dado que la riqueza está dada en un instante del tiempo, (1) contiene suficiente información para determinar la demanda de los dos tipos de activos, una vez que conocemos el valor de la expresión (i*+d−i).
La dependencia funcional entre el valor del portafolio evaluado a la cotización del tipo de cambio negro es como sigue. A mayor retorno esperado, mayor es la fracción de portafolio que los agentes desean mantener bajo la forma de activo. A mayor riqueza, la demanda de todos los activos aumenta.
Dividiendo ambos lados de la ecuación (1) por la riqueza total (C+EB) y multiplicando y dividiendo el lado izquierdo por el tipo de cambio oficial E¯, se obtiene:
La nueva variable C¯ queda definida exógenamente y es susceptible de ser modificada por la política económica. Por su parte, la variable x es el ratio entre el tipo de cambio negro y el tipo de cambio oficial. Utilizando la notación a˙ para denotar la derivada de la variable genérica a con respecto al tiempo, la tasa de crecimiento de la prima cambiaria se define como la diferencia entre la tasa de devaluación en el mercado negro y la tasa de devaluación vigente en el mercado oficial6:
Como se asume que la fracción del portafolio en forma de dólares es una función continua y siempre creciente del diferencial de retornos, podemos despejar d en (3), sustituir en (2) y expresar la tasa de crecimiento de la prima cambiaria como función del nivel de la prima cambiaria y la oferta relativa de activos financieros de forma implícita7. Notemos que al definir la función inversa de θ como G()=θ−1, de (2) se desprende que G11+C¯xB=i*+d−i. De aquí se sigue la siguiente ecuación (4):
La ecuación (4) es la condición de equilibrio de stocks. Es la primera ecuación dinámica del sistema y nos dice que un aumento en la fracción del portafolio bajo la forma de dólares (evaluados a la cotización del mercado negro), sea por un aumento en x o un aumento en B, tiende a incrementar la tasa de crecimiento de la prima cambiaria. A la inversa, un mayor rendimiento de los activos externos reduce dicha tasa de crecimiento.
La razón de este poco intuitivo resultado es que ante un aumento en el stock de dólares se requiere un mayor premio para que los agentes deseen mantener dicho stock en su portafolio. Por lo tanto, la prima cambiaria tiene que crecer para que los agentes deseen mantener una mayor proporción de activos externos en su portafolio8.
En un punto del tiempo el stock de dólares es una variable predeterminada y, por ende, el stock existente de dólares es equivalente a la demanda de los agentes. La prima cambiaria es precisamente la variable que permite alcanzar tal equilibrio momentáneo. Pero a lo largo del tiempo el nivel de la prima afecta los flujos y, por ende, la oferta de dólares. El modelo se completa entonces definiendo la evolución de los flujos de dólares hacia el mercado negro. La restante ecuación del modelo especifica que la variación del stock de dólares depende positivamente de la prima cambiaria (a mayor prima, mayor es el incentivo a vender dólares en el mercado negro, y viceversa)9 y negativamente del tipo de cambio real e¯, el cual se considera determinado por fuera del sistema.
Con la antedicha dependencia funcional con respecto a los argumentos. La aproximación lineal del sistema compuesto por (4) y (5) en torno al punto de equilibrio define una matriz cuyo determinante jacobiano tiene la siguiente estructura:
Con las siguientes derivadas parciales dx˙dx>0, dx˙dB>0, dB˙dx>0 y dB˙dB=0. En consecuencia, la traza del sistema es positiva (TRJ=dx˙dx>0) y el determinante es negativo (DETJ=−dB˙dx*dx˙dB<0), con lo cual el sistema tiene un equilibrio del tipo «punto silla»10. Es decir, que fuera del equilibrio existe una única trayectoria que devuelve a la economía al equilibrio.
Un sistema con un equilibrio del tipo «punto silla» requiere un igual número de variables que puedan saltar como de raíces positivas para que la solución convergente sea única y pueda ser determinada a partir de las condiciones iniciales. Si el número de variables que pueden saltar es menor, tenemos un sistema inestable, mientras que si es mayor, tenemos un sistema sobredeterminado, con infinitas trayectorias que convergen al equilibrio11. Como en este caso el valor de la prima cambiaria puede «saltar» (es decir, es libre de tomar cualquier valor en un punto del tiempo), a priori es posible escoger un único valor que situé al sistema sobre el brazo estable. Esta práctica es habitual en la literatura que utiliza modelos con expectativas racionales (ver Blanchard y Khan, 1980).
Este tipo de soluciones excluyen las «burbujas» representadas por las trayectorias que divergen y que reducen la prima cambiaria a cero o la llevan al infinito en un período de tiempo finito. Excluyendo burbujas se puede mostrar que el sistema converge a un estado estacionario en donde la oferta de divisas en el mercado negro es constante e igual a la demanda. En dicho estado la prima cambiaria se estabiliza y queda definida como una función de los parámetros y las variables exógenas del modelo. Es decir, si denotamos el valor de equilibro de la brecha utilizando x*, nos queda una expresión del tipo x*=x*i,i*,e¯,C¯,d¯.
Si bien podríamos explicar los procesos de unificación a partir de burbujas que divergen del equilibrio, creemos que es más razonable introducir como determinante adicional una función de reacción de las autoridades. Dicho elemento nos permite dar cuenta de la dinámica del control de cambios en América Latina.
¿Qué elementos nos permiten caracterizar dicha función de reacción? Por ejemplo, es razonable argumentar que en general si el tipo de cambio se aleja demasiado de lo que las autoridades consideran su nivel de adecuado, estas intervendrán para evitar que la burbuja desestabilice por completo la economía. En los mercados oficiales es común observar un cierto «temor a flotar», pero incluso en los mercados negros, aun cuando se trate de mercados ilegales, existen mecanismos indirectos a través de los cuales las autoridades pueden intervenir indirectamente, estimulando determinadas decisiones de portafolio, o incluso incrementando o reduciendo la oferta de divisas (por ejemplo, endureciendo o flexibilizando las restricciones).
El mayor problema que enfrentan estas intervenciones es que los controles de cambio y los mercados negros suelen coexistir con niveles reducidos en el stock de reservas internacionales. Es posible que ante una caída en las reservas las autoridades endurezcan las restricciones, con el efecto de reducir el abastecimiento de dólares en el mercado negro. Pero esto puede tener el efecto indeseado de incrementar la prima cambiaria, reduciendo aún más las reservas del banco central.
Podemos capturar dinámicas inestables en el mercado negro incorporando factores que determinan la magnitud de la prima cambiaria en el largo plazo (es decir, la posición de la curva definida por B˙=0) en función de la intensidad de las regulaciones cambiarias. Proponemos modificar el modelo original y ampliar la ecuación (5) del siguiente modo:
Donde la variable R mide la intensidad de las regulaciones. A mayor intensidad de las regulaciones, menor es la oferta flujo de dólares hacia el mercado negro. Una forma intuitiva de concebir R es la de una multa a quien opere en el mercado negro, proporcional al valor de las transacciones ilegales realizadas. Las restantes variables tienen los mismos efectos sobre B˙ que en la especificación original.
Por otra parte, los hacedores de política ajustan las políticas de regulación en función de la prima cambiaria y del stock de dólares en el mercado negro. Presumiblemente, a mayor prima cambiaria las autoridades intensificarán las regulaciones, mientras que a mayor stock de dólares en negro supondremos que menor es el stock de reservas en poder del banco central y, por ende, las regulaciones tenderán a endurecerse. Tenemos pues:
Nos queda configurado un sistema dinámico de 3×3, cuyo determinante jacobiano está dado por:
Con dx˙dx>0, dx˙dB>0, dx˙dR=0, dB˙dx>0, dB˙dB=0, dB˙dR<0, dR˙dx>0, dR˙dB>0 y dR˙dR=0 en virtud de la dependencia funcional previamente comentada. Las condiciones necesarias y suficientes de estabilidad de Routh-Hurwitz no se cumplen12, pero podemos extraer algunas lecciones sobre la estabilidad a partir de la traza y del determinante, las que equivalen respectivamente a la suma y al producto de las raíces del sistema dinámico (ver Chiang y Wainwright, 2006, cap. 19).
Nuestra matriz de 3×3 tiene una traza positiva, que al igual que el sistema anterior está dada por TRJ=dx˙dx (porque los restantes términos son iguales a cero). La expresión del determinante es DETJ=−dx˙dxdR˙dB*dB˙dR+dx˙dBdR˙dx*dB˙dR, que es negativo o positivo, dependiendo del tamaño de cada término.
¿Cuáles son las condiciones bajo las cuales tenemos DETJ>0 y cuáles las que garantizan que DETJ<0? La condición crítica está dada por:
Notemos que dx˙dx=dx˙dB (dado que la condición de equilibrio de stocks, la ecuación 4, es una hipérbola equilátera en el espacio formado por x y B) y en consecuencia la condición se reduce a comparar dR˙dB con dR˙dx; es decir, cómo se ajustan las regulaciones ante una pérdida de reservas y cómo lo hacen ante un cambio en la prima cambiaria. Cuando las autoridades reaccionan más rápidamente ante la pérdida de reservas, el lado izquierdo de (7) es mayor al lado derecho, por lo que el determinante es negativo. Por el contrario, cuando las autoridades reaccionan más rápidamente ante un cambio en la prima cambiaria, el determinante es positivo. Notemos que el primer caso se verifica si las autoridades ignoran por completo el nivel de la brecha a la hora de ajustar las regulaciones, es decir, si dR˙dx=0.
Tenemos pues dos casos. En el primer caso, la traza es positiva y el determinante es negativo, lo cual implica que la suma de la parte real de las raíces del sistema es mayor a cero, pero su producto es negativo. Esto es posible únicamente con una raíz con parte real negativa. Pero nuestro sistema tiene una sola variable con la capacidad de saltar para situarse en el sendero estable, ya que B es una variable predeterminada y R no lo es (pues no es una variable que pueda situarse libremente sobre la trayectoria estable del sistema). Este caso es claramente inestable, ya que cuando existe una única raíz con parte real negativa, existen dos con parte real positiva, pero tenemos una sola variable con la capacidad de saltar para ubicar al sistema en el brazo estable (es decir, x).
En el segundo caso, la traza y el determinante son positivos. Por ende, tenemos dos o ninguna raíz con parte real negativa. El primer caso es similar al modelo propuesto originalmente por Dornbusch et al. (1983), mientras que el segundo es claramente inestable, por lo que no existe ninguna trayectoria que converja al equilibrio. En consecuencia, nuestro sistema de 3×3 o bien posee equilibrios que se pueden alcanzar a partir de trayectorias únicas, o bien es totalmente inestable.
La inestabilidad que puede exhibir nuestro modelo no es necesariamente una debilidad. De hecho, para ilustrar la situación típica en América Latina es lógico utilizar dinámicas de este tipo: ante la escasez de reservas las restricciones cambiarias se endurecen, y debido a que el tipo de cambio negro se incrementa más rápidamente que el tipo de cambio oficial, el proceso se refuerza y las reservas internacionales van declinando con el paso del tiempo. Esto lleva a un mayor endurecimiento de las regulaciones, lo cual refuerza las presiones devaluatorias. La razón es que cuando la prima crece, el incentivo a canalizar operaciones oficiales al mercado negro y a demandar divisas al tipo de cambio oficial se incrementa, con lo cual las reservas tienden a caer, hasta que finalmente las autoridades no tienen más remedio que devaluar el tipo de cambio oficial.
Recapitulando, la presente sección ha mostrado que una simple modificación a un modelo de portafolio estándar permite acomodar dinámicas inestables asociadas al fenómeno del «goteo» en presencia de controles de cambio. La lógica de este proceso es que si las autoridades endurecen los controles para intentar contener la pérdida de reservas, esto puede elevar la prima cambiaria y estimular conductas que reduzcan aún más el abastecimiento de divisas.
Para que nuestro modelo produzca dicho resultado es necesario que las autoridades reaccionen con mayor intensidad ante pérdidas de reservas que ante subas en la prima cambiaria. Por ejemplo, si las autoridades ignoran por completo la brecha pero se preocupan por la pérdida de reservas, este caso se verifica automáticamente.
En la siguiente sección brindaremos apoyo empírico a dicha idea para América Latina, mostrando que la dinámica del tipo de cambio oficial suele verse influida por la dinámica del tipo de cambio negro. Esto sugiere que en la experiencia regional las autoridades eventualmente se vieron forzadas a devaluar el tipo de cambio oficial.
4Un análisis econométricoUn resultado común de la literatura empírica reseñada en la sección número 2 es la existencia de cointegración entre el tipo de cambio oficial y el tipo de cambio negro, así como la falta de consenso sobre la naturaleza del proceso de ajuste. En la sección anterior presentamos un marco estilizado para entender la relación entre el tipo de cambio oficial y el tipo de cambio negro. Al añadir la dinámica de las regulaciones cambiarias mostramos que es posible generar trayectorias que divergen del equilibrio, por lo que la prima cambiaria tiende a cero o a infinito. Estos casos corresponderían a una «unificación exitosa» (dada una tasa de devaluación oficial, el tipo de cambio negro converge al oficial) o a una «crisis cambiaria» (dada la tasa de devaluación oficial, el tipo de cambio negro tiende a crecer sin límites hasta que las autoridades se ven forzadas a aplicar un programa de estabilización, usualmente eliminando las regulaciones), dependiendo de las condiciones iniciales.
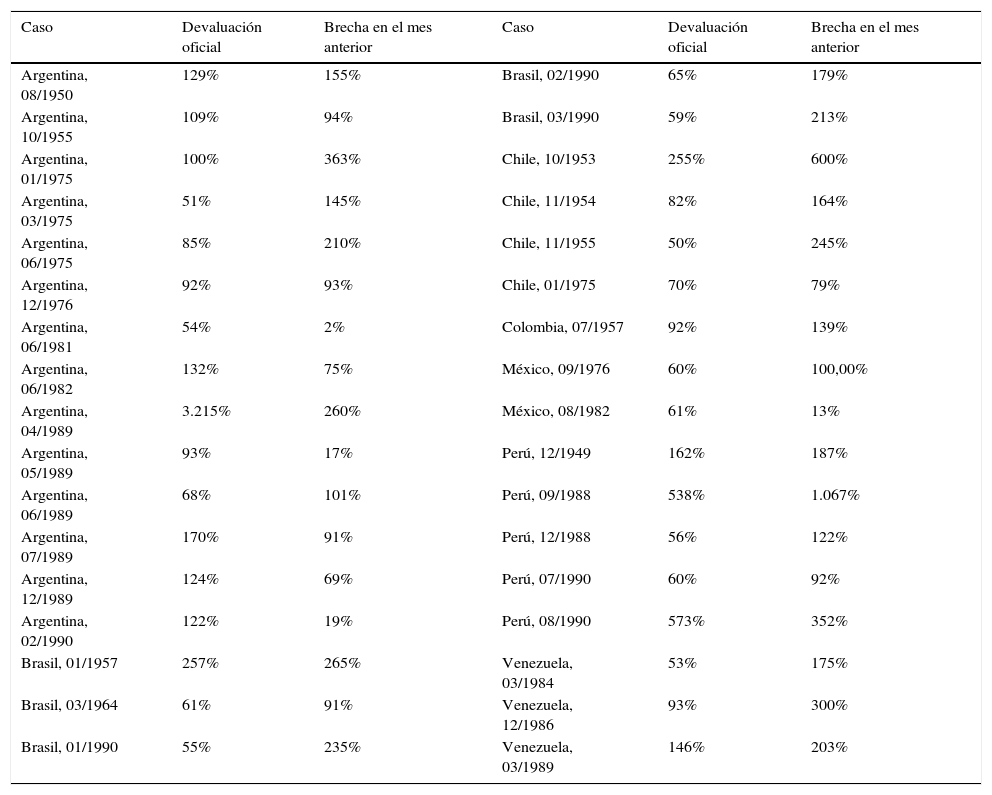
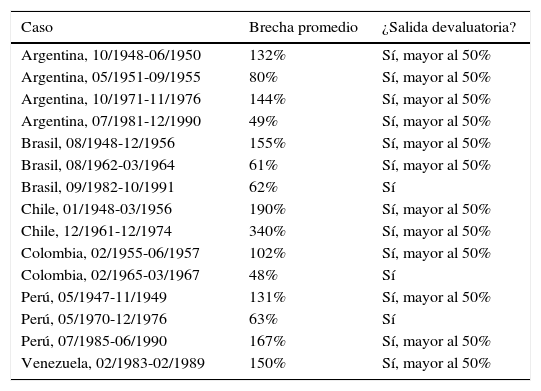
¿Cuál es la dinámica más plausible para describir el funcionamiento del control de cambios en América Latina? En la experiencia de la región, las grandes brechas derivaron frecuentemente en grandes devaluaciones del tipo de cambio oficial. Las tablas 1-2 reproducen las devaluaciones mayores al 50% en los siete países más importantes de América Latina (Argentina, Brasil, Chile, Colombia, México, Perú y Venezuela) para los episodios de unificación cambiaria durante 1950-2000. Los datos muestran que casi todas las grandes devaluaciones estuvieron acompañadas por una brecha elevada (tabla 2) y que una buena parte de los episodios de unificación cambiaria requirieron una devaluación importante del tipo de cambio oficial (mayor al 50% en la mayor parte de los casos, ver tabla 1). Esto significa que hasta la fecha en América Latina las grandes brechas nunca se eliminaron sin una gran devaluación13.
Grandes devaluaciones, 7 países (1950-2000)
| Caso | Devaluación oficial | Brecha en el mes anterior | Caso | Devaluación oficial | Brecha en el mes anterior |
|---|---|---|---|---|---|
| Argentina, 08/1950 | 129% | 155% | Brasil, 02/1990 | 65% | 179% |
| Argentina, 10/1955 | 109% | 94% | Brasil, 03/1990 | 59% | 213% |
| Argentina, 01/1975 | 100% | 363% | Chile, 10/1953 | 255% | 600% |
| Argentina, 03/1975 | 51% | 145% | Chile, 11/1954 | 82% | 164% |
| Argentina, 06/1975 | 85% | 210% | Chile, 11/1955 | 50% | 245% |
| Argentina, 12/1976 | 92% | 93% | Chile, 01/1975 | 70% | 79% |
| Argentina, 06/1981 | 54% | 2% | Colombia, 07/1957 | 92% | 139% |
| Argentina, 06/1982 | 132% | 75% | México, 09/1976 | 60% | 100,00% |
| Argentina, 04/1989 | 3.215% | 260% | México, 08/1982 | 61% | 13% |
| Argentina, 05/1989 | 93% | 17% | Perú, 12/1949 | 162% | 187% |
| Argentina, 06/1989 | 68% | 101% | Perú, 09/1988 | 538% | 1.067% |
| Argentina, 07/1989 | 170% | 91% | Perú, 12/1988 | 56% | 122% |
| Argentina, 12/1989 | 124% | 69% | Perú, 07/1990 | 60% | 92% |
| Argentina, 02/1990 | 122% | 19% | Perú, 08/1990 | 573% | 352% |
| Brasil, 01/1957 | 257% | 265% | Venezuela, 03/1984 | 53% | 175% |
| Brasil, 03/1964 | 61% | 91% | Venezuela, 12/1986 | 93% | 300% |
| Brasil, 01/1990 | 55% | 235% | Venezuela, 03/1989 | 146% | 203% |
Fuente: elaboración propia en base a Reinhart y Rogoff (2004).
Grandes brechas, 7 países (1950-2000)
| Caso | Brecha promedio | ¿Salida devaluatoria? |
|---|---|---|
| Argentina, 10/1948-06/1950 | 132% | Sí, mayor al 50% |
| Argentina, 05/1951-09/1955 | 80% | Sí, mayor al 50% |
| Argentina, 10/1971-11/1976 | 144% | Sí, mayor al 50% |
| Argentina, 07/1981-12/1990 | 49% | Sí, mayor al 50% |
| Brasil, 08/1948-12/1956 | 155% | Sí, mayor al 50% |
| Brasil, 08/1962-03/1964 | 61% | Sí, mayor al 50% |
| Brasil, 09/1982-10/1991 | 62% | Sí |
| Chile, 01/1948-03/1956 | 190% | Sí, mayor al 50% |
| Chile, 12/1961-12/1974 | 340% | Sí, mayor al 50% |
| Colombia, 02/1955-06/1957 | 102% | Sí, mayor al 50% |
| Colombia, 02/1965-03/1967 | 48% | Sí |
| Perú, 05/1947-11/1949 | 131% | Sí, mayor al 50% |
| Perú, 05/1970-12/1976 | 63% | Sí |
| Perú, 07/1985-06/1990 | 167% | Sí, mayor al 50% |
| Venezuela, 02/1983-02/1989 | 150% | Sí, mayor al 50% |
Fuente: elaboración propia en base a Reinhart y Rogoff (2004).
A continuación proponemos un test algo más formal sobre la relación entre el tipo de cambio oficial y el tipo de cambio negro utilizando cointegración en paneles de datos. Para analizar la relación entre el tipo de cambio oficial y el tipo de cambio negro, utilizamos los datos mensuales para un panel de 18 países de América Latina, cubriendo un periodo de 52 años (1946-1998). La lista de países y periodos es la siguiente: 1)Argentina (01:1946-07:1998); 2)Bolivia (01:1948-07:1998); 3)Brasil (01:1946-07:1998); 4)Chile (01:1948-07:1998); 5)Colombia (01:1952-07:1998); 6)Costa Rica (01:1948-07:1998); 7)Ecuador (01:1947-07:1998); 8)El Salvador (01:1961-07:1998); 9)Guatemala (01:1985-07:1998); 10)Haití (01:1985-07:1998); 11)Honduras (01:1985-07:1998); 12)Jamaica (01:1974-07:1998); 13)México (01:1947-07:1998); 14)Nicaragua (01:1947-07:1998); 15)Paraguay (03:1953-07:1998); 16)Perú (01:1946-07:1998); 17)Uruguay (01:1946-07:1998), y 18)Venezuela (11:1960-07:1998).
Buscamos corroborar si existe una relación de cointegración utilizando la metodología de Engle y Granger (ver Enders, 2010, cap. 6, para una descripción detallada). Las técnicas de cointegración en paneles presentan ventajas sobre el análisis basado en series de tiempo; por ejemplo, una mayor potencia de los test de raíz unitaria y una velocidad de convergencia de los estimadores hacia el verdadero valor de los parámetros (conforme aumenta el número de observaciones) más veloz14.
Sean los logaritmos naturales del tipo de cambio oficial y del tipo de cambio negro, LNTC y LNTN, dos variables no estacionarias. Estamos interesados en testear si existe una relación de cointegración del tipo:
Donde uit representa el término de error y los subíndices «i» y «t» representan el país y el período15. Si tal relación de cointegración existe, los residuos de la estimación de (8) son estacionarios, y existe un vector de corrección de errores que puede ser estimado introduciendo un cierto número de rezagos (n) de las primeras diferencias de LNTC y LNTN, así como los residuos de la estimación de (8) rezagados un período (uit−1):
En las ecuaciones (9) y (10) los términos eit y e'it son los errores (con las propiedades habituales), mientras que los términos δ y δ' capturan la dirección y la velocidad del ajuste hacia el equilibrio. En al menos una de las ecuaciones debe cumplirse que δ<0 o δ′<0, ya que de lo contrario no existe relación de cointegración.
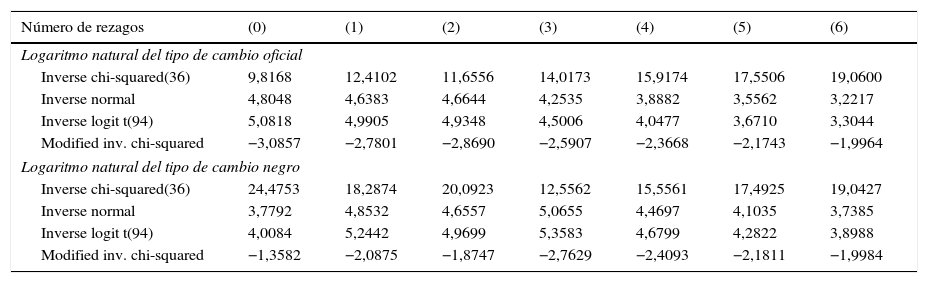
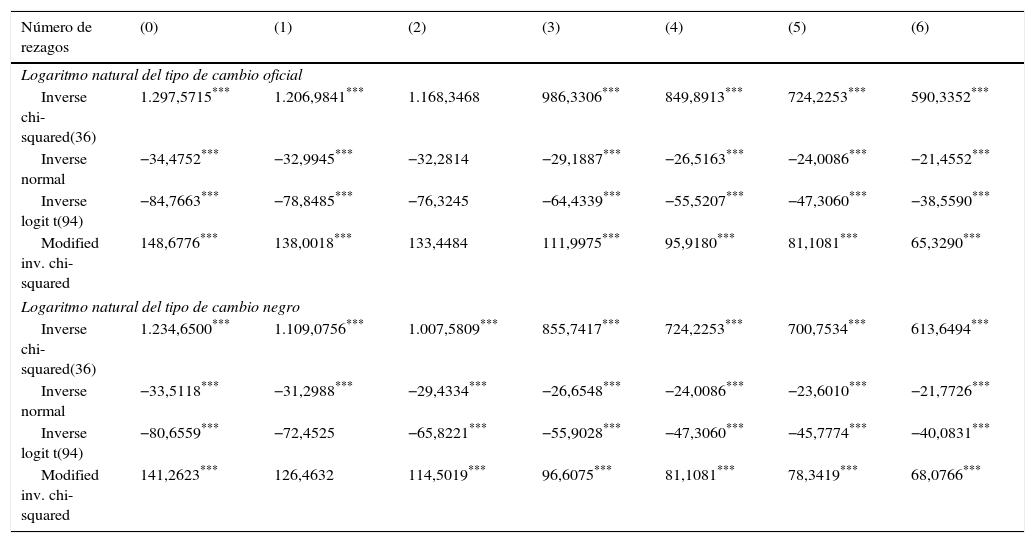
Para determinar el número óptimo de rezagos se cotejó el valor de los criterios de información de Akaike y Bayes, los cuales indicaron que es conveniente utilizar 5 rezagos (resultados disponibles para quien los solicite), por lo que optamos por presentar resultados incluyendo hasta 6 rezagos. Las tablas 3-4 reportan los resultados de los test de raíz unitaria de Fisher, aplicados sobre el logaritmo natural del tipo de cambio oficial y el tipo de cambio negro, tanto en niveles como en primeras diferencias.
Test de Fisher de raíz unitaria para los logaritmos naturales del tipo de cambio oficial y negro
| Número de rezagos | (0) | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|---|
| Logaritmo natural del tipo de cambio oficial | |||||||
| Inverse chi-squared(36) | 9,8168 | 12,4102 | 11,6556 | 14,0173 | 15,9174 | 17,5506 | 19,0600 |
| Inverse normal | 4,8048 | 4,6383 | 4,6644 | 4,2535 | 3,8882 | 3,5562 | 3,2217 |
| Inverse logit t(94) | 5,0818 | 4,9905 | 4,9348 | 4,5006 | 4,0477 | 3,6710 | 3,3044 |
| Modified inv. chi-squared | −3,0857 | −2,7801 | −2,8690 | −2,5907 | −2,3668 | −2,1743 | −1,9964 |
| Logaritmo natural del tipo de cambio negro | |||||||
| Inverse chi-squared(36) | 24,4753 | 18,2874 | 20,0923 | 12,5562 | 15,5561 | 17,4925 | 19,0427 |
| Inverse normal | 3,7792 | 4,8532 | 4,6557 | 5,0655 | 4,4697 | 4,1035 | 3,7385 |
| Inverse logit t(94) | 4,0084 | 5,2442 | 4,9699 | 5,3583 | 4,6799 | 4,2822 | 3,8988 |
| Modified inv. chi-squared | −1,3582 | −2,0875 | −1,8747 | −2,7629 | −2,4093 | −2,1811 | −1,9984 |
Se reportan únicamente los valores de cada estadístico.
Test de Fisher de raíz unitaria para las primeras diferencias de los logaritmos naturales del tipo de cambio oficial y negro
| Número de rezagos | (0) | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|---|
| Logaritmo natural del tipo de cambio oficial | |||||||
| Inverse chi-squared(36) | 1.297,5715*** | 1.206,9841*** | 1.168,3468 | 986,3306*** | 849,8913*** | 724,2253*** | 590,3352*** |
| Inverse normal | −34,4752*** | −32,9945*** | −32,2814 | −29,1887*** | −26,5163*** | −24,0086*** | −21,4552*** |
| Inverse logit t(94) | −84,7663*** | −78,8485*** | −76,3245 | −64,4339*** | −55,5207*** | −47,3060*** | −38,5590*** |
| Modified inv. chi-squared | 148,6776*** | 138,0018*** | 133,4484 | 111,9975*** | 95,9180*** | 81,1081*** | 65,3290*** |
| Logaritmo natural del tipo de cambio negro | |||||||
| Inverse chi-squared(36) | 1.234,6500*** | 1.109,0756*** | 1.007,5809*** | 855,7417*** | 724,2253*** | 700,7534*** | 613,6494*** |
| Inverse normal | −33,5118*** | −31,2988*** | −29,4334*** | −26,6548*** | −24,0086*** | −23,6010*** | −21,7726*** |
| Inverse logit t(94) | −80,6559*** | −72,4525 | −65,8221*** | −55,9028*** | −47,3060*** | −45,7774*** | −40,0831*** |
| Modified inv. chi-squared | 141,2623*** | 126,4632 | 114,5019*** | 96,6075*** | 81,1081*** | 78,3419*** | 68,0766*** |
Se reportan únicamente los valores de cada estadístico
Una de las principales ventajas de dicho test es que se puede implementar en paneles no balanceados como el nuestro. La hipótesis nula es que todos los paneles contienen raíz unitaria. Su rechazo puede deberse a que alguna de las series de los individuos del panel no posee raíz unitaria. Se implementó dicho test usando entre cero y seis rezagos, y en todos los casos se rechazó la hipótesis nula de estacionariedad para las variables en niveles. Al repetir el ejercicio usando las primeras diferencias, se rechazó la hipótesis nula de que existen raíces unitarias. Es decir, las series serían estacionarias en primeras diferencias.
El segundo paso consiste en testear la presencia de una relación de cointegración entre el tipo de cambio oficial y el tipo de cambio negro. Utilizamos con tal fin la batería de cuatro test propuestos por Westerlund (2007). La principal idea de la metodología propuesta por Westerlund es testear la hipótesis nula según la cual no existe cointegración, analizando si las series tienden a corregir los desvíos del equilibrio.
Consideremos el modelo de corrección de errores especificado por nuestras ecuaciones (9) y (10). Los test de Westerlund testean la hipótesis nula según la cual los términos δ o δ' son igual a cero. Más concretamente, los estadísticos «Ga» y «Gt» ponen a prueba la hipótesis nula δ=0 (y δ'=0) para todos los individuos del panel, versus una hipótesis alternativa según la cual δ<0 (o δ′<0), para al menos uno de los individuos. Estos estadísticos se construyen a partir de un promedio ponderado de cada uno de los términos de corrección de error de cada individuo del panel. Los estadísticos «Pa» y «Pt» se basan en un pool que incluye los datos de todos los individuos del panel, y ponen a prueba la hipótesis nula para todos los individuos del panel, contra una hipótesis alternativa según la cual alguno de los términos de corrección de error es negativo, también para todos los individuos del panel.
Nótese que un rechazo de la hipótesis nula en base a los estimadores «Ga» y «Gt» sugiere que existe una relación de cointegración para al menos alguno de los individuos, mientras que un rechazo en base a los estimadores «Pa» y «Pt» sugiere que existe una relación de cointegración para la totalidad del panel.
Los resultados de la implementación de los test de Westerlund se reflejan en la tabla 5. Podemos observar que se rechaza la hipótesis nula para los cuatro estimadores utilizando entre cero y seis rezagos.
Tests de cointegración de Westerlund (2007)
| Número de rezagos | (0) | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|---|
| Estadístico | |||||||
| Gt | −20,787*** | −14,224*** | −13,417*** | −12,729*** | −11,186*** | −10,429*** | −10,009*** |
| Ga | −40,100*** | −26,909*** | −25,784*** | −24,513*** | −22,355*** | −20,432*** | −19,945*** |
| Pt | −24,246*** | −15,893*** | −14,162*** | −12,823*** | −11,285*** | −10,086*** | −9,050*** |
| Pa | −59,870*** | −41,676*** | −36,978*** | −33,178*** | −29,807*** | −26,438*** | −23,700*** |
Se reportan únicamente los valores «z» de cada estimador.
Interpretamos estos resultados como un fuerte apoyo a la hipótesis de que el logaritmo natural del tipo de cambio oficial y el logaritmo natural del tipo de cambio negro están cointegrados, por lo que procedimos a estimar la relación de cointegración. Estimar la relación de cointegración usando mínimos cuadrados ordinarios produce resultados consistentes, pero levemente sesgados en muestras no muy grandes. Para corregir este sesgo, seguimos la metodología propuesta por Saikkonen (1991), conocida como mínimos cuadrados ordinarios dinámicos, que consiste en complementar una estimación por mínimos cuadrados ordinarios con adelantos y rezagos de la primera diferencia de la variable explicativa (el logaritmo natural del tipo de cambio negro, en nuestro caso).
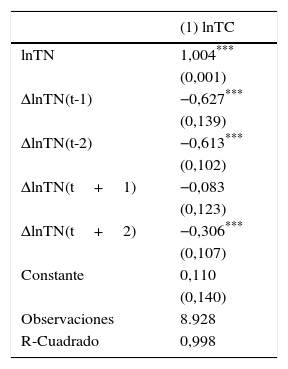
La tabla 6 muestra los resultados. Notemos que la elasticidad entre el tipo de cambio oficial y el tipo de cambio negro es aproximadamente 1, lo cual tiene sentido. El coeficiente asociado es estadísticamente significativo al 1%.
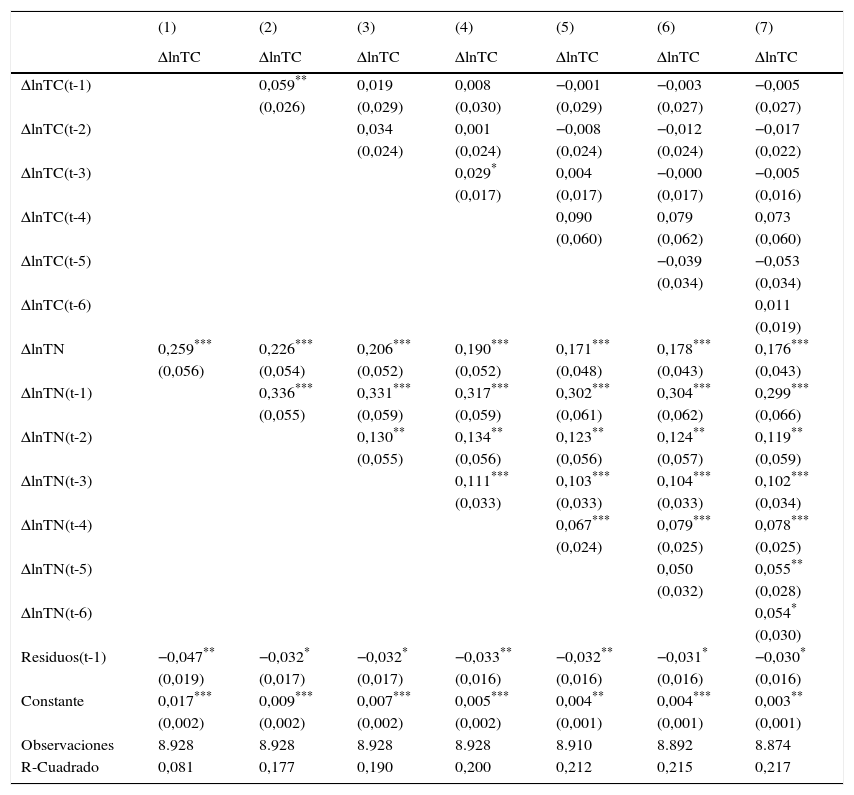
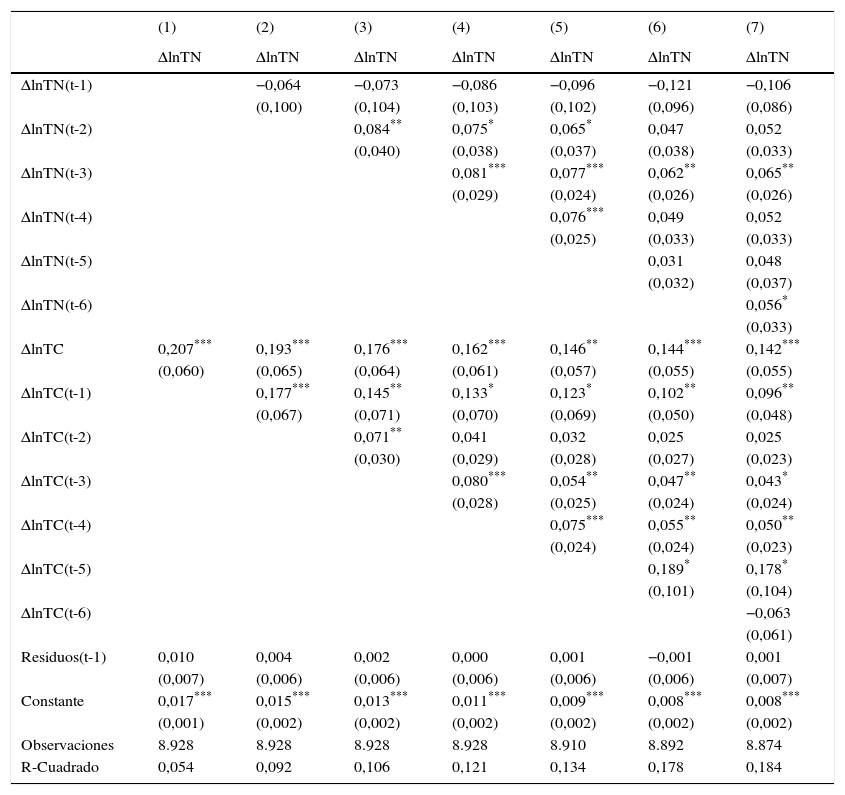
Finalmente, estimamos el modelo de corrección de errores descripto por las ecuaciones (9) y (10). Los resultados sugieren que cuando la brecha se desvía de su valor de equilibrio, el ajuste se produce por cambios en la cotización oficial y no por cambios en el tipo de cambio negro. El resultado se encuentra en las tablas 7-8. Mientras que el residuo rezagado es no significativo y cercano a cero para las ecuaciones que describen la dinámica del tipo de cambio negro, el residuo rezagado es significativo entre el 5 y el 10% para las ecuaciones que describen la dinámica del tipo de cambio oficial. En este último caso, el valor de los coeficientes que acompañan a los residuos rezagados un período oscila entre −0,030 y −0,047. Dichos valores implican una «vida media» de los desequilibrios de entre 15 y 23 meses, aproximadamente.
Modelo de corrección de errores (variable dependiente tipo de cambio oficial)
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
| ΔlnTC | ΔlnTC | ΔlnTC | ΔlnTC | ΔlnTC | ΔlnTC | ΔlnTC | |
| ΔlnTC(t-1) | 0,059** | 0,019 | 0,008 | −0,001 | −0,003 | −0,005 | |
| (0,026) | (0,029) | (0,030) | (0,029) | (0,027) | (0,027) | ||
| ΔlnTC(t-2) | 0,034 | 0,001 | −0,008 | −0,012 | −0,017 | ||
| (0,024) | (0,024) | (0,024) | (0,024) | (0,022) | |||
| ΔlnTC(t-3) | 0,029* | 0,004 | −0,000 | −0,005 | |||
| (0,017) | (0,017) | (0,017) | (0,016) | ||||
| ΔlnTC(t-4) | 0,090 | 0,079 | 0,073 | ||||
| (0,060) | (0,062) | (0,060) | |||||
| ΔlnTC(t-5) | −0,039 | −0,053 | |||||
| (0,034) | (0,034) | ||||||
| ΔlnTC(t-6) | 0,011 | ||||||
| (0,019) | |||||||
| ΔlnTN | 0,259*** | 0,226*** | 0,206*** | 0,190*** | 0,171*** | 0,178*** | 0,176*** |
| (0,056) | (0,054) | (0,052) | (0,052) | (0,048) | (0,043) | (0,043) | |
| ΔlnTN(t-1) | 0,336*** | 0,331*** | 0,317*** | 0,302*** | 0,304*** | 0,299*** | |
| (0,055) | (0,059) | (0,059) | (0,061) | (0,062) | (0,066) | ||
| ΔlnTN(t-2) | 0,130** | 0,134** | 0,123** | 0,124** | 0,119** | ||
| (0,055) | (0,056) | (0,056) | (0,057) | (0,059) | |||
| ΔlnTN(t-3) | 0,111*** | 0,103*** | 0,104*** | 0,102*** | |||
| (0,033) | (0,033) | (0,033) | (0,034) | ||||
| ΔlnTN(t-4) | 0,067*** | 0,079*** | 0,078*** | ||||
| (0,024) | (0,025) | (0,025) | |||||
| ΔlnTN(t-5) | 0,050 | 0,055** | |||||
| (0,032) | (0,028) | ||||||
| ΔlnTN(t-6) | 0,054* | ||||||
| (0,030) | |||||||
| Residuos(t-1) | −0,047** | −0,032* | −0,032* | −0,033** | −0,032** | −0,031* | −0,030* |
| (0,019) | (0,017) | (0,017) | (0,016) | (0,016) | (0,016) | (0,016) | |
| Constante | 0,017*** | 0,009*** | 0,007*** | 0,005*** | 0,004** | 0,004*** | 0,003** |
| (0,002) | (0,002) | (0,002) | (0,002) | (0,001) | (0,001) | (0,001) | |
| Observaciones | 8.928 | 8.928 | 8.928 | 8.928 | 8.910 | 8.892 | 8.874 |
| R-Cuadrado | 0,081 | 0,177 | 0,190 | 0,200 | 0,212 | 0,215 | 0,217 |
Errores estándar robustos entre paréntesis.
Modelo de corrección de errores (variable dependiente tipo de cambio negro)
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
| ΔlnTN | ΔlnTN | ΔlnTN | ΔlnTN | ΔlnTN | ΔlnTN | ΔlnTN | |
| ΔlnTN(t-1) | −0,064 | −0,073 | −0,086 | −0,096 | −0,121 | −0,106 | |
| (0,100) | (0,104) | (0,103) | (0,102) | (0,096) | (0,086) | ||
| ΔlnTN(t-2) | 0,084** | 0,075* | 0,065* | 0,047 | 0,052 | ||
| (0,040) | (0,038) | (0,037) | (0,038) | (0,033) | |||
| ΔlnTN(t-3) | 0,081*** | 0,077*** | 0,062** | 0,065** | |||
| (0,029) | (0,024) | (0,026) | (0,026) | ||||
| ΔlnTN(t-4) | 0,076*** | 0,049 | 0,052 | ||||
| (0,025) | (0,033) | (0,033) | |||||
| ΔlnTN(t-5) | 0,031 | 0,048 | |||||
| (0,032) | (0,037) | ||||||
| ΔlnTN(t-6) | 0,056* | ||||||
| (0,033) | |||||||
| ΔlnTC | 0,207*** | 0,193*** | 0,176*** | 0,162*** | 0,146** | 0,144*** | 0,142*** |
| (0,060) | (0,065) | (0,064) | (0,061) | (0,057) | (0,055) | (0,055) | |
| ΔlnTC(t-1) | 0,177*** | 0,145** | 0,133* | 0,123* | 0,102** | 0,096** | |
| (0,067) | (0,071) | (0,070) | (0,069) | (0,050) | (0,048) | ||
| ΔlnTC(t-2) | 0,071** | 0,041 | 0,032 | 0,025 | 0,025 | ||
| (0,030) | (0,029) | (0,028) | (0,027) | (0,023) | |||
| ΔlnTC(t-3) | 0,080*** | 0,054** | 0,047** | 0,043* | |||
| (0,028) | (0,025) | (0,024) | (0,024) | ||||
| ΔlnTC(t-4) | 0,075*** | 0,055** | 0,050** | ||||
| (0,024) | (0,024) | (0,023) | |||||
| ΔlnTC(t-5) | 0,189* | 0,178* | |||||
| (0,101) | (0,104) | ||||||
| ΔlnTC(t-6) | −0,063 | ||||||
| (0,061) | |||||||
| Residuos(t-1) | 0,010 | 0,004 | 0,002 | 0,000 | 0,001 | −0,001 | 0,001 |
| (0,007) | (0,006) | (0,006) | (0,006) | (0,006) | (0,006) | (0,007) | |
| Constante | 0,017*** | 0,015*** | 0,013*** | 0,011*** | 0,009*** | 0,008*** | 0,008*** |
| (0,001) | (0,002) | (0,002) | (0,002) | (0,002) | (0,002) | (0,002) | |
| Observaciones | 8.928 | 8.928 | 8.928 | 8.928 | 8.910 | 8.892 | 8.874 |
| R-Cuadrado | 0,054 | 0,092 | 0,106 | 0,121 | 0,134 | 0,178 | 0,184 |
Errores estándar robustos entre paréntesis.
La «vida media» (del inglés half-life) estima cuánto tiempo se requiere para corregir la mitad del desequilibrio ante un shock y se define por la fórmula Vida Media=ln2lnβ, donde β es el coeficiente asociado al residuo rezagado en las estimaciones del modelo de corrección de errores. Para interpretar el resultado, supongamos que la brecha entre el tipo de cambio oficial y el tipo de cambio negro es del 50%, por ejemplo el tipo de cambio oficial es de 1peso por 1dólar, y el tipo de cambio negro es de 1,5pesos por 1dólar. Si la «vida media» es de aproximadamente 1 o 2años, esto quiere decir que al cabo de ese tiempo se revirtió la mitad de dicho desequilibrio, es decir, el tipo de cambio oficial pasó de 1peso por dólar a 1,25pesos por dólar. Al cabo de otro período de tiempo similar, el tipo de cambio oficial subirá a 1,37pesos por dólar, etc.
La conclusión que se desprende es que la causalidad va del tipo de cambio negro al tipo de cambio oficial, pero no del tipo de cambio oficial al tipo de cambio negro. Como el tipo de cambio negro se ubicaba siempre por sobre el oficial (salvo muy escasas excepciones), nuestro ejercicio empírico sugiere que las brechas se corrigieron mayoritariamente con devaluaciones del tipo de cambio oficial y no mediante caídas del tipo de cambio negro. Este proceso es relativamente veloz, ya que la «vida media» de los desequilibrios es de uno o dos años aproximadamente.
5Síntesis y conclusionesEste trabajo discute los controles de cambio en América Latina, enfatizando el problema de la unificación cambiaria. Nuestro enfoque propone una extensión del modelo de portafolio (propuesto, por ejemplo, por Dornbusch et al., 1983). Mostramos que una ligera modificación para incluir la intensidad de las regulaciones como una variable endógena puede tornar al sistema completamente inestable, lo cual es consistente con la experiencia histórica regional, en donde los controles provocaron un fenómeno del tipo «goteo» que eventualmente obligó a las autoridades a devaluar el tipo de cambio oficial.
Utilizando el panel de datos para 18 países de América Latina durante 1947 y 1998 (en base a los datos mensuales provisto por Reinhart y Rogoff, 2004), confirmamos que el tipo de cambio negro causa (en el sentido de Granger) al tipo de cambio oficial, pero no hay evidencia que permita sostener que el tipo de cambio oficial causa (en el sentido de Granger) al tipo de cambio negro.
Al contramano de buena parte de la literatura, la evidencia empírica que presentamos para América Latina sugiere que la unificación cambiaria se produce mediante aumentos del tipo de cambio oficial y no mediante reducciones del tipo de cambio negro. Debido a sus efectos perniciosos sobre el stock de reservas en poder del banco central, las grandes brechas introducen un elemento de inestabilidad macroeconómica que no debe ser menospreciado.
En América Latina, la presencia de brechas cambiarias significativas sugiere que los controles tuvieron la capacidad de influir sobre las variables reales y financieras, lo que las convertía potencialmente en un instrumento a ser considerado al menos a corto plazo. Sin embargo, los controles no pudieron prevenir grandes devaluaciones. Esto puede indicar que la presencia de brechas demasiado elevadas constituyó un problema a la hora de garantizar la sostenibilidad en el tiempo de los esquemas de control.
Para evitar ambigüedad, advertimos que en este trabajo definimos a la brecha como el logaritmo natural del tipo de cambio oficial menos el logaritmo natural del tipo de cambio negro. Como en la literatura teórica suele utilizarse el cociente entre el tipo de cambio oficial y el tipo de cambio negro, denominamos «prima cambiaria» a dicho ratio. Por otra parte, definimos al tipo de cambio como la cantidad de moneda doméstica que hay que entregar para obtener una unidad de moneda extranjera (el dólar). En consecuencia, una devaluación implica una suba del tipo de cambio.
Recientemente el Fondo Monetario Internacional parece haber reconsiderado el rol de los controles de capitales, al punto tal de aconsejarlos bajo ciertas condiciones (ver, por ejemplo, Ostry et al. (2010).
Lamentablemente, las series de tipo de cambio negro finalizan en junio de 1998, lo que impide extender el trabajo para cubrir los años 2000. De todas formas, la mayor parte de los países de la región ya habían eliminado la mayoría de las restricciones cambiarias a comienzos de dicha década, por lo que en prácticamente todos los casos el tipo de cambio negro es muy similar al tipo de cambio oficial para dicho período, con la excepción de Argentina (2011-2015) y Venezuela (desde 2003 a la fecha).
El control de cambios rompe la conexión entre la tasa doméstica y la tasa internacional, por lo que incluso autores inclinados a utilizar la paridad descubierta de tasas consideran que las ofertas relativas de activos financieros pueden tener efectos importantes incluso en una economía «abierta y pequeña» (ver, por ejemplo, Guidotti y Vegh, 1992).
Con algunas excepciones, por ejemplo Agenor (1990, 1994).
Notemos que al tomar el logaritmo natural de la prima cambiaria obtenemos lo que hemos denominado brecha cambiaria en las secciones anteriores.
Al desconocer la forma funcional de θ no es posible hallar una expresión explícita, pero debido a la continuidad de dicha función, es posible saber en qué dirección varía la tasa de crecimiento de la brecha cuando varían los argumentos.
El modelo propuesto por Dornbusch et al. (1983) sería más claro si distinguiera entre la demanda y la oferta de dólares. Como en un determinado instante temporal la oferta es fija, ambas coinciden y la prima cambiaria es tal que dicha oferta es igual a la demanda, por lo que nada se pierde al atenernos a la notación original.
Por ejemplo, mediante la subfacturación de exportaciones y la sobrefacturación de importaciones, los agentes pueden hacerse de dólares aumentando el stock de dólares en poder del sector privado. A mayor (menor) prima cambiaria, mayor (menor) es el incentivo a subfacturar y sobrefacturar.
Para una explicación detallada de cómo verificar las condiciones de estabilidad utilizando la matriz Jacobiana, véase Chiang y Wainwright (2006, cap. 19).
Ver Blanchard y Khan (1980), especialmente las proposiciones 1, 2 y 3.
Dichas condiciones son: 1)traza negativa; 2)determinante negativa; 3)menores principales positivos, y 4)la suma de las trazas de los menores principales (con el signo contrario) más el determinante debe ser positiva.
Reinhart y Rogoff (2004) encontraron un resultado con implicancias similares. Más precisamente, estos autores confirmaron que el tipo de cambio negro es un buen predictor de los valores futuros del tipo de cambio oficial, para un panel de países de todo el mundo, incluyendo el período 1946-1998 con datos mensuales.
Los resultados para los países más grandes de América Latina (no reportados en el presente trabajo, pero disponibles para quien lo solicite) se sostienen analizando cada serie individualmente.
La estimación se implementó utilizando variables dicotómicas por período, para eliminar los factores temporales que afectan al tipo de cambio oficial y al tipo de cambio negro. Los resultados no dependen de la inclusión de dichas variables.