Solvencia II transformará el sistema de determinación de las necesidades de capital del asegurador. En el nuevo marco regulatorio se propone un modelo estándar, pero al mismo tiempo se fomenta la aplicación de modelos internos de autoevaluación y gestión del riesgo. Este trabajo tiene por objeto analizar modelos alternativos propuestos en la literatura económica para la medición del riesgo de renta variable al que están expuestas las compañías de seguros. Para ello, se han utilizado datos mensuales de la serie del IBEX-35 en el período comprendido entre enero de 1992 y diciembre de 2008. Los modelos calibrados han permitido comparar los requerimientos de capital resultantes frente a la propuesta del cuarto estudio de impacto cuantitativo (QIS4). Los resultados obtenidos muestran que el capital necesario obtenido por los modelos que presentan un mejor ajuste supera considerablemente al propuesto en el modelo estándar. Esto significa que las compañías que utilicen el modelo estándar u otro basado en hipótesis similares, estarán subestimando considerablemente su exposición al riesgo de renta variable.
Solvency II will transform the system of determining capital requirements of the insurer. The new regulatory framework proposes a standard model, but at the same time, it encourages the application of internal models of self-assessment and risk management. This paper aims to examine alternative models proposed in the literature for the measurement of insurer¿s equity risk exposure. We have used monthly data series on the IBEX-35 in the period between January 1992 and December 2008. The calibrated models have allowed comparing the resulting capital requirements against the proposal of the fourth quantitative impact study (QIS4). The results show that capital requirements obtained by the better fit models are significantly greater than those of the standard model. This means that companies using the standard model or another based on similar assumptions underestimate significantly their exposure to equity risk.
La nueva regulación de solvencia de las compañías de seguros en el ámbito de la Unión Europea, denominada Solvencia II, supone la revisión de las normas de evaluación de la situación financiera con el objetivo de mejorar la medición y el control del riesgo. En la actualidad nos encontramos en la segunda fase del proyecto, iniciada en el año 2003 y que tiene por objeto la elaboración de una Directiva Marco, cuyo desarrollo se está llevando a cabo a través de estudios de impacto cuantitativo (QIS) realizados por el Comité Europeo de Supervisores de Seguros (CEIOPS). Bajo el nuevo marco, la determinación de las necesidades de capital puede realizarse mediante un modelo estándar o bien con modelos internos previamente aprobados por el reguladora.
El riesgo de inversión en renta variable, objeto de este trabajo, se incluye dentro del módulo de mercado y de acuerdo con la Propuesta de Directiva sobre Solvencia II (Comisión de las Comunidades Europeas, 2007), mide la sensibilidad del valor de los activos, los pasivos y los instrumentos financieros ante variaciones en el nivel o la volatilidad de los precios de mercado de las acciones. El modelo de rendimientos normal, implícito en el cálculo de la fórmula estándar, ha sido elegido por razones de simplicidad y transparencia. No obstante, la hipótesis de normalidad puede subestimar la cola de la distribución de pérdidas (resultados extremos) y no capturar la variabilidad que puede presentar la volatilidad, por lo que es menos apropiado para representar períodos temporales más largos (Hardy, 2001), que es a los que está expuesto el asegurador. La posibilidad de utilizar modelos internos para la determinación de las necesidades de capital, ha despertado el interés por el diseño y la selección de modelos que midan de forma más adecuada el riesgo de equity que asumen las compañías de seguros. Con este trabajo se pretende evaluar el cálculo de las necesidades de capital asociadas a la inversión en renta variable, a través de modelos alternativos al estándar. En concreto se consideran dentro de este estudio el modelo lognormal, la mixtura de distribuciones normales, los modelos GARCH, incluidos los asimétricos, y diversas variantes de modelos de cambio de régimen de Markov. Los distintos modelos han sido calibrados a la serie mensual del IBEX-35 entre enero de 1992 y diciembre de 2008 y comparados a través de diferentes criterios que muestran el grado de adecuación a las series históricas y a la cola de la distribución de pérdidas.
Este estudio contribuye a la literatura existente aportando un enfoque novedoso, que si bien ha sido aplicado en el mercado norteamericano, no ha sido realizado hasta el momento en el mercado europeo. Los resultados pueden ser de gran utilidad para la calibración del modelo estándar, ya que todavía se encuentra en proceso de evaluación. También es de interés para las compañías de seguros que deseen optar por un modelo interno de evaluación del riesgo de sus posiciones en renta variable. Por otra parte, se han utilizado datos relativos al IBEX-35, lo cual aumenta la utilidad para las aseguradoras que operan en nuestro paísb.
El trabajo se estructura en los siguientes apartados. En el apartado 2 se realiza una revisión teórica de las distintas alternativas propuestas para modelizar la renta variable en el ámbito de la actividad aseguradora y se exponen los modelos que serán objeto de análisis. En el apartado 3 se analiza la serie histórica del IBEX-35 utilizada. En el apartado 4 se procede al ajuste y evaluación de los modelos, y en el apartado 5 se hace un análisis comparativo de los resultados de aplicar los modelos propuestos frente al modelo estándar para la determinación de las necesidades de capital. Finalmente, se presentan las conclusiones.
2Revisión teórica y especificación de los modelosLa investigación sobre la distribución de los rendimientos de la renta variable se inicia con el trabajo de Bachelier (1900), quien propone un proceso de ruido blanco normal. La hipótesis de normalidad de los rendimientos ha sido la base de modelos muy importantes desarrollados en el ámbito de la teoría financiera, como son los modelos de optimización de carteras de media-varianza de Markowitz (Markowitz, 1952, 1959), el modelo de Valoración de Activos Financieros (Capital Asset Pricing Model [CAPM[) desarrollado por Sharpe (1964), Lintner (1965) y Mossin (1966) o el modelo de valoración de opciones de Black y Scholes (1973). Sin embargo, son numerosos los estudios que advierten que la distribución empírica de los rendimientos suele tener una mayor curtosis que la proporcionada por la distribución normal. Con la finalidad de superar las limitaciones del modelo de rendimientos normal, surgen nuevas propuestas que optan por el uso de distribuciones alternativas. Entre otros destacan los trabajos de Mandelbrot (1963) y Fama (1963, 1965), quienes consideraron la familia de distribuciones estables y la distribución t de Student, propuesta por Praetz (1972) y Blattberg y Gonedes (1974), que presenta unas colas mayores que las de la distribución normal. Posteriormente, Smith (1981) sugirió la distribución logística, Gray y French (1990) la distribución de error generalizada (generalized error distribution [GED]) y Eberlein y Keller (1995) la distribución hiperbólica (hyperbolic distribution). También se ha recurrido a la mixtura de distribuciones, donde el modelo más empleado es la mixtura discreta de dos distribuciones normales (Ball y Torous, 1983)c.
En el caso particular de la actividad aseguradora, recientemente han surgido distintos trabajos en el mercado norteamericano que se han interesado por la modelización del comportamiento de la renta variable con la finalidad de evaluar las necesidades de capital. No obstante, dadas las características del negocio y a diferencia de la mayor parte de los trabajos previos, el interés se ha centrado en el comportamiento del valor de la cartera a largo plazo. Este aspecto es muy importante ya que los modelos que mejor proyectan el comportamiento del activo a corto plazo, no tienen por qué ser los más adecuados para analizar el riesgo a largo plazo. Los trabajos realizados hasta el momento para analizar el riesgo derivado de la inversión en renta variable en compañías de seguros pueden englobarse dentro de dos grupos (tabla 1). Por un lado están aquellos que se integran dentro de otros más amplios que tratan de proyectar estocásticamente el comportamiento conjunto de la cartera de activos y pasivos del asegurador a medio y largo plazo. Todos ellos se caracterizan por proponer un determinado modelo, pero sin comprobar si la opción elegida es la más adecuada. Así, Schmeiser (2004) opta por el modelo de rendimientos normal, Kaufmann et al. (2001) y el modelo DynaMo 3d proponen un «modelo lineal», mientras que Hibbert et al. (2001) y Ahlgrim et al. (2004b) incorporan el modelo de cambio de régimen de Hardy (2001), justificando el mejor ajuste a las «colas gruesas» que muestran las rentabilidades históricas. Frente a estos y a raíz del trabajo de Hardy (2001), surgen diversos estudios que pretenden comparar diferentes alternativas para la modelización del riesgo a través de criterios estadísticos. En esta línea, Hardy (2001) propone un modelo de cambio de régimen lognormal (RSLN) y compara el ajuste logrado con otros modelos econométricos para los índices Standard and Poor's 500 (S&P500) y Toronto Stock Exchange 300 (TS300). En sus resultados destaca que el modelo RSLN presenta un mejor ajuste que el resto de modelos, tiene forma explícita para el cálculo del VaR y TVaR y con dos regímenes es suficiente para ajustar los datos mensuales. Una versión del modelo de Hardy que incorpora un término de reversión de los rendimientos en caso de caídas del índice es propuesta por Panneton (2003), denominada Regimen Switching Draw-Down (RSSD). Bayliffe y Pauling (2003) realizan una comparación de los modelos lognormal, lognormal autorregresivo, RSLN y GARCH, concluyendo que los modelos que presentan reversión a la media y colas gruesas son los que proporcionan mejor ajuste para datos a largo plazo. Wong y Chan (2005) emplean dos nuevos modelos, la mixtura autorregresiva (MAR) y la mixtura de ARCH (MARCH)e, cuyo ajuste comparan con el modelo lognormal, la mixtura de dos normales y el RSLN, para los datos ajustados a los índices TSE 300 y S&P 500. De su trabajo se desprende que los nuevos modelos se ajustan peor que la alternativa de cambio de régimen, si bien pueden ser útiles para la modelización de las colas. Un trabajo de características similares es el realizado por Hardy et al. (2006), quienes comparan un amplio número de modelos estimados por máxima verosimilitud para la rentabilidad del índice S&P 500. La comparación de los modelos permite concluir que los modelos GARCH presentan un buen ajuste global pero un mal ajuste en las colas de la distribución, mientras que los de cambio de régimen tienen el mejor ajuste en la cola izquierda de la distribución y por tanto una mejor adecuación a la evaluación del riesgo. Finalmente, Boudreault y Panneton (2009) realizan una comparación de distintos modelos GARCH multivariantes y modelos de cambio de régimen multivariantes para los rendimientos mensuales del mercado canadiense, americano, británico y japonés. En general se observa que los modelos GARCH tienen un mejor ajuste global que los de cambio de régimen, pero estos últimos representan mucho mejor las colas gruesas de la distribución. Los resultados alcanzados están en línea con los que se han obtenido en la literatura para los modelos univariantes.
Modelos utilizados para analizar el riesgo de equity en compañías de seguros
| Autores | Características |
| Kaufmann et al. (2001), Dynamo 3 | El modelo propuesto es denominado modelo lineal y se incluye dentro de una propuesta de análisis financiero dinámico. Se trata de una versión del CAPM en donde se correlaciona negativamente el cambio en los tipos de interés a la rentabilidad de las acciones. En este trabajo no se realiza ningún ajuste a los datos de mercado ni se compara con otras alternativas |
| Hardy (2001) | Hardy propone un modelo de cambio de régimen lognormal y compara el ajuste logrado con otros modelos econométricos para los índices S&P500 y TS300. Tras dicho análisis, concluye que el RSLN presenta un mejor ajuste que el resto de modelos y que con dos regímenes es suficiente para ajustar los datos mensuales. Otra ventaja que tiene este modelo es que presenta fórmula explícita para el cálculo de medidas del riesgo |
| Hibbert et al. (2001) | Aplican un modelo de cambio de régimen, a semejanza de la propuesta de Hardy, en el que en cada régimen el rendimiento sobre el activo libre de riesgo se distribuye normalmente. Dicho modelo se integra dentro de un modelo generación de escenarios para compañías aseguradoras |
| Panneton (2003) | Propone un modelo de cambio de régimen que permite la reversión en los rendimientos de las acciones pero preserva las colas gruesas observadas en los rendimientos mensuales de los activos. Se trata de una variante del modelo de Hardy denominada Regimen Switching Draw-Down (RSSD) que consiste en añadir un término que compensa la caída de los rendimientos. Tras calibrar el modelo al índice TSE 300, Panneton (2006) indica que dicho término resulta significativo |
| Bayliffe y Pauling (2003) | Comparan los modelos lognormal, lognormal autorregresivo, RSLN y GARCH. Los autores concluyen que los modelos de corto plazo no son necesariamente buenos modelos a largo plazo. Aquellos modelos que presentan reversión a la media y colas gruesas son los que proporcionan mejor ajuste para datos a largo plazo. Para datos mensuales el modelo RSLN es el que presenta un mejor ajuste. Además, es el único que supera el test de normalidad de los residuos |
| Schmeiser (2004) | En este trabajo, Schmeiser propone un modelo de análisis financiero dinámico (DFA) que opta por el modelo lognormal para simular los riesgos financieros y que utiliza para calcular la probabilidad de ruina de una compañía de seguros generales alemana que opta por diferentes carteras de inversión |
| Ahlgrim et al. (2004a, 2004b) | Ahlgrim et al. (2004b) desarrollan, a petición de las sociedades de actuarios americanas Casualty Actuarial Society (CAS) y Society of Actuaries (SOA), un modelo para generación de escenarios económicos para emplearse en DFA. En dicho modelo emplean la propuesta de Hardy (2001) para la renta variable. Ahlgrim et al. (2004a) comparan el «modelo lineal» con un modelo de cambio de régimen de Hardy (2001). En su estudio comprueban que la volatilidad de los rendimientos de las acciones es mayor que en la aproximación lineal, lo cual puede afectar de forma importante al asegurador que invierta un elevado porcentaje de su cartera en acciones |
| Wong y Chan (2005) | Estos autores comparan los modelos de mixtura autoregresivos (MAR) y ARCH (MARCH) con el modelo lognormal, la mixtura de dos normales, el modelo de cambio de régimen lognormal con dos regímenes (RSLN), ajustados a los índices TSE 300 y S&P 500. Utilizando diferentes criterios de comparación llegan a la conclusión de que el RSLN presenta un buen nivel de ajuste y es simple y parsimonioso. Los modelos de mixtura, a pesar de ser más complejos, presentan un peor ajuste y requieren parámetros adicionales, pero pueden ser adecuados para modelizar las colas de la distribución |
| AAA (2005). | Proponen un modelo de volatilidad estocástica lognormal (Stochastic Log-Volatility [SLV]) |
| Hardy et al. (2006) | Estos autores comparan los modelos lognormal, GARCH (1,1), diversas modalidades de modelos de cambio de régimen y un modelo de volatilidad estocástica lognormal a semejanza de la propuesta de AAA (2005) ajustados al índice S&P 500. Concluyen, mediante el análisis de los residuos y el empleo de bootstrap, que los modelos de cambio de régimen presentan un mejor ajuste en la cola izquierda de la distribución que el resto de los modelos |
| CEIOPS (2008) | La determinación del capital en el último informe de impacto cuantitativo de Solvencia II (QIS4) se basa en el modelo lognormal de precios, con media y volatilidad histórica |
| Boudreault y Panneton (2009) | En este trabajo se comparan los modelos GARCH multivariantes con los de cambio de régimen para los datos relativos a diferentes mercados (Canadá, EE. UU., Reino Unido y Japón). En general se observa que los modelos GARCH presentan un mejor ajuste global que los de cambio de régimen, pero estos últimos representan mucho mejor las colas gruesas de la distribución |
En la tabla 2 recogemos la especificación de los modelos abordados en este trabajof. El modelo de rendimientos normal, en el cual se basa el modelo estándar de Solvencia II, es de uso común en el ámbito financiero. Una aplicación interesante para el conjunto de activos financieros de una compañía de seguros puede verse en Schmeiser (2004). Este modelo cuando se aplica a períodos largos suele presentar colas menos gruesas que las que revelan los datos (Hardy, 2001). De ahí que su consideración dentro del modelo de Solvencia II pueda implicar una subestimación del riesgo realmente asumido. Una alternativa frecuentemente considerada para captar la mayor curtosis observada en los rendimientos de los activos financieros consiste en emplear una mixtura de dos o más distribuciones normales. Sin embargo, además del exceso de curtosis las series de rendimientos presentan otras propiedades como son la volatilidad no constante en el tiempo (heterocedasticidad) y la persistencia o conglomerados de volatilidad. Los modelos ARCH y GARCH modelizan de forma dinámica la propia varianza condicional en función de los valores pasados de la propia variable y fueron propuestos para explicar estas propiedades (Engle, 1982; Engle y Bollerslev, 1986). Los modelos empleados con más frecuencia para modelizar series financieras son el modelo estacionario GARCH (1,1) y el modelo no estacionario IGARCH (1,1) de Engle y Bollerslev (1986). Dichos procesos carecen de autocorrelación serial en la media. Sin embargo, en caso de que se detecte que los propios retardos de la variable de rendimientos o de las innovaciones pueden explicar su comportamiento, deben ser incorporados a la ecuación de la media dando lugar a los denominados modelos ARMA-GARCH. Los anteriores modelos tienen como principal ventaja la capacidad de generar clusters de volatilidad y distribuciones con colas gruesas. Sin embargo, una de sus limitaciones es el impacto simétrico de los shocks positivos y negativos. De esta forma, la varianza condicional depende del tamaño de las innovaciones retardadas pero no de su signo. Para incorporar los denominados efectos apalancamiento (leverage effect) observados en la series financieras se han propuesto una amplia gama de modelos GARCH asimétricos, entre los que destacan el modelo GARCH exponencial o EGARCH (Nelson, 1991) y el GJR-GARCH (Glosten et al., 1993).
Descripción de los modelos analizados en este trabajo
| Normal | yt=μ+σzt |
| Mixtura de k normales | yt=∑i=1kpi(μi+σizt); k=1,…,n; ∑i=1kpi=1 |
| GARCH (1,1) | yt=μ+εt;εt=σtzt;σt2=ω+α1εt−12+β1σt−12 |
| IGARCH (1,1) | yt=μ+εt;εt=σtzt;σt2=ω+1−β1εt−12+β1σt−12 |
| GJR-GARCH (1,1) | yt=μ+εt;εt=σtzt;σt2=ω+α1εt−1−γ1εt−12+β1σt−12 |
| EGARCH (1,1) | yt=μ+εt;εt=σtzt; logσt2=ω+α1εt−1σt−1−γ1εt−1σt−12+β1logσt−12 |
| RSLN (k regímenes) | yt=μpt+σptzt; pt=1,…,k |
| RSSD (2 regímenes) | yt=μpt+φptDt−1+σptzt; Dt=min0,Dt−1+yt; (pt=1,2) |
| RS-GARCH (1,1) | yt=μpt+εt; εt=σpttzt; σpt2=ωpt+αpt1(εt−1)2+βpt1σt−12; (pt=1,2) |
| M-GARCH (1,1) | yt=∑i=12pi(μi+εt); εt=zitσit⋅σit2=ωi+αi(εt−1)2+βiσt−12; ∑i=12pi=1 |
Siendo: yt es el rendimiento logarítmico; μ es la media, σ la volatilidad, ¿t las innovaciones, pt cada uno de los estados, zt∼N(0;1), ω, α, β y γ son parámetros por estimar.
El modelo de cambio de régimen lognormal (RSLN), propuesto por Hardy (2001), utiliza una cadena de Markov que representa la evolución del estado de la economía, que puede estar en distintas situaciones denominadas regímenes. En cada uno de los regímenes los rendimientos siguen un modelo normal independiente con parámetros distintos. Hardy (2001) considera adecuado emplear 2 regímenes para las series utilizadas del TSE 300 y del S&P 500. Los regímenes se denominan de acuerdo a su varianza como régimen 1 o de baja volatilidad y régimen 2 o de alta volatilidad. Los resultados alcanzados por Hardy (2001) muestran que la deriva o rendimiento medio esperado en el régimen 1 es positivo, mientras que en el régimen de alta volatilidad es negativo. Panneton (2002, 2003, 2006) ha propuesto una extensión del modelo RSLN para tener en cuenta las características de reversión a la media de los rendimientos, el denominado Regimen Switching Draw-Down (RSSD). El modelo establece una mayor rentabilidad esperada para el siguiente período en la medida en que el valor del índice esté por debajo de su último valor máximo (Dt). De esta forma Dt será negativa o cero, en el caso de que el mercado esté en un máximo o en el momento inicial. Es de esperar que los parámetros φa del modelo sean negativos para que se produzca la recuperación del mercado. Este modelo, si bien es muy parecido al RSLN, cuando se hacen proyecciones a largo plazo, tiende a generar una menor cola izquierda o riesgo dada la reversión de los rendimientos (Hardy et al., 2006).
Recientemente se han producido desarrollos en los modelos GARCH de cambio de régimen (Regime-Switching GARCH o RS-GARCH) donde los parámetros del modelo cambian a partir de una matriz de «estado» o «régimen» de Markov. Estos modelos permiten que la volatilidad varíe dentro de cada uno de los distintos regímenes. El modelo GARCH de cambio de régimen presenta como inconveniente, frente a los modelos GARCH y RSLN, la mayor complejidad a la hora de estimarlo. Una simplificación sobre el modelo de cambio de régimen GARCH consistiría en establecer una mixtura de los procesos. En la tabla 2 recogemos la especificación de los modelos de cambio de régimen y de mixtura para dos procesos GARCH (1,1).
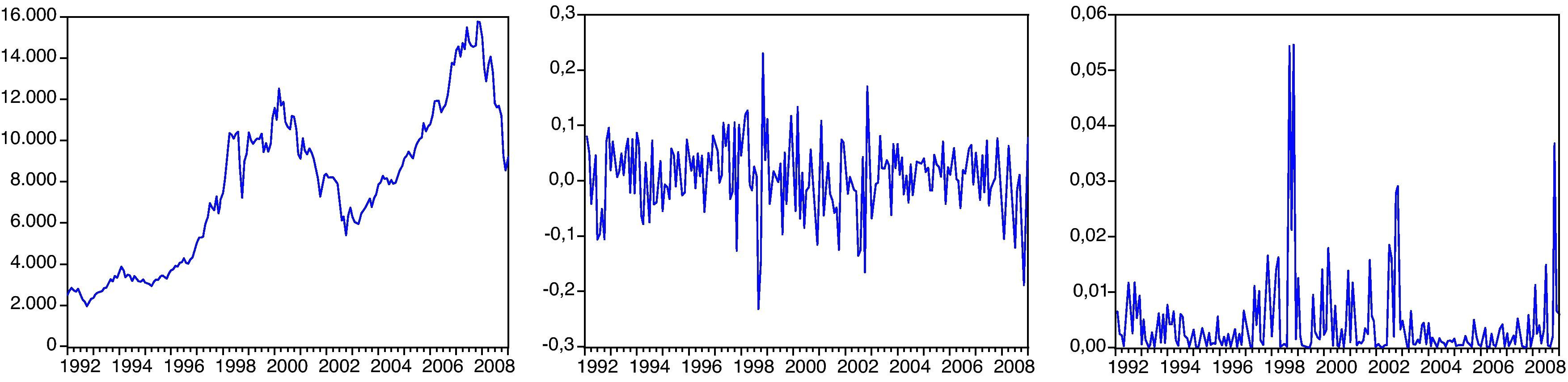
3Análisis empírico de la serieLa muestra empleada para calibrar el riesgo de inversión en renta variable es el IBEX-35 para el período enero de 1992 a diciembre de 2008 aportados por BME, por ser un índice de referencia para los aseguradores españoles. Dado que las compañías aseguradoras deben velar por los intereses de sus asegurados a medio y largo plazo, es común que los modelos de equity diseñados en el ámbito asegurador empleen una frecuencia mensual de la muestra [véase los trabajos de Hardy (2001), Panneton (2003), Wong y Chan (2005), Hardy et al. (2006) o Boudreault y Panneton (2009)], e incluso el CEIOPS ha calibrado el modelo estándar de solvencia europeo (QIS3 y QIS4) empleando una frecuencia trimestral. En la figura 1 se recoge la evolución mensual del índice, de los rendimientos logarítmicos y su cuadrado.
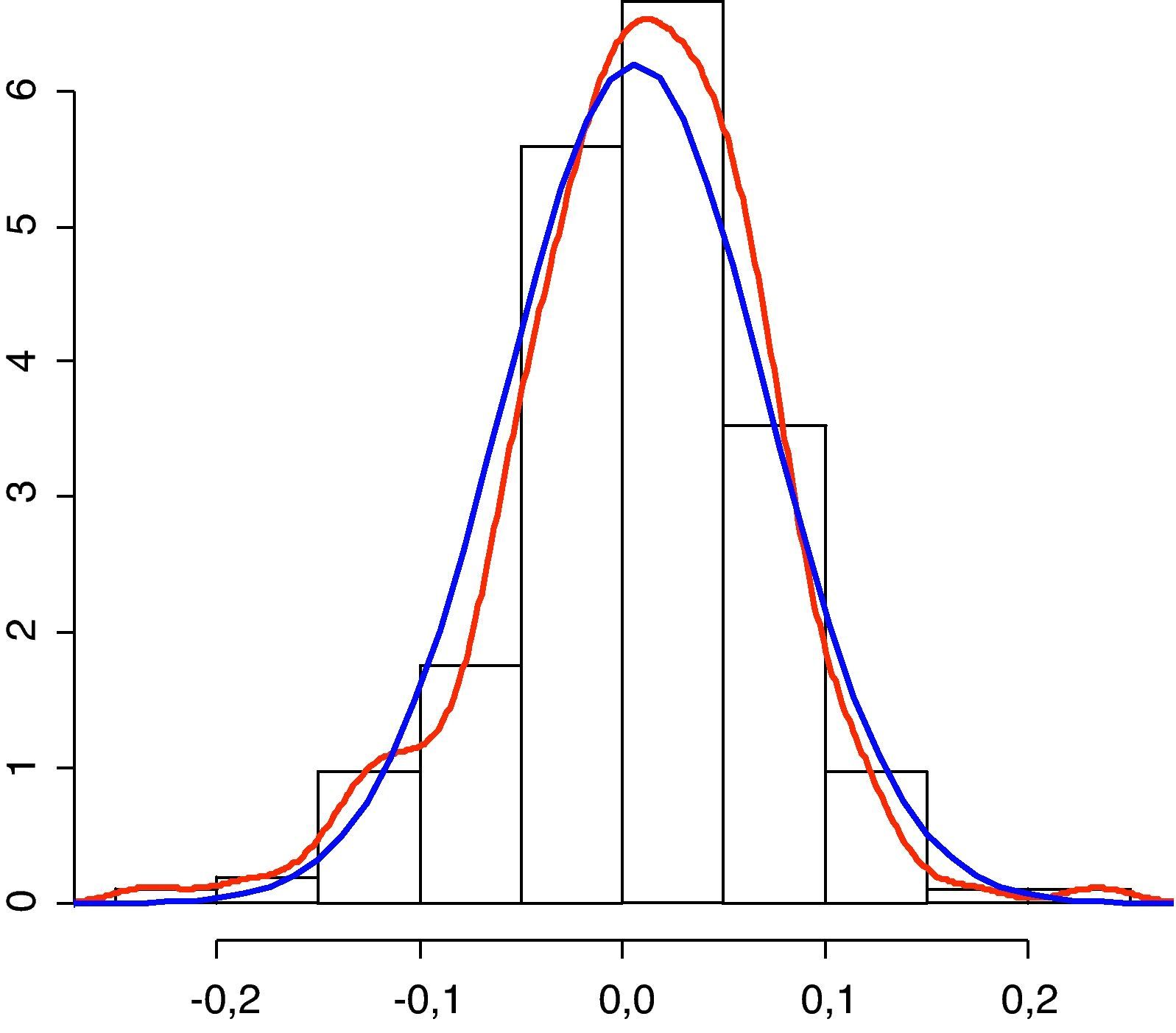
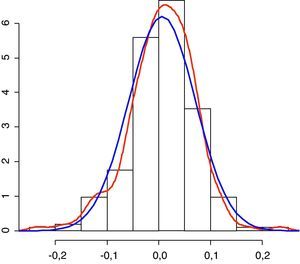
La serie analizada es claramente no estacionaria, sin embargo, no ocurre lo mismo cuando se utilizan rendimientos logarítmicos. Los rendimientos son estacionarios en media, pero presentan clusters o agrupamientos de volatilidad. Esta característica también se aprecia en el gráfico del cuadrado de los rendimientos logarítmicos. Por esta razón, es importante determinar cuál es el modelo que mejor se ajusta al comportamiento de la varianza a lo largo del tiempo. En la figura 2 se representa el histograma de los rendimientos junto con la estimación Kernel de su densidad y una densidad normal con su misma media y varianzag. Se observa como la distribución de los rendimientos mensuales es asimétrica y presenta un exceso de curtosis que llevan a rechazar la hipótesis de normalidad con la que trabaja el CEIOPS.
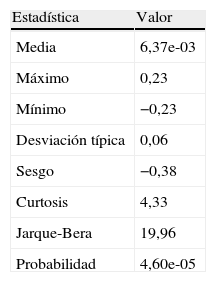
En la tabla 3 se muestran los principales estadísticos resumen de los rendimientos logarítmicos mensuales de la serie analizada, donde se puede observar el exceso de curtosis y el rechazo de la hipótesis de normalidad medida a través del test de Jarque-Bera.
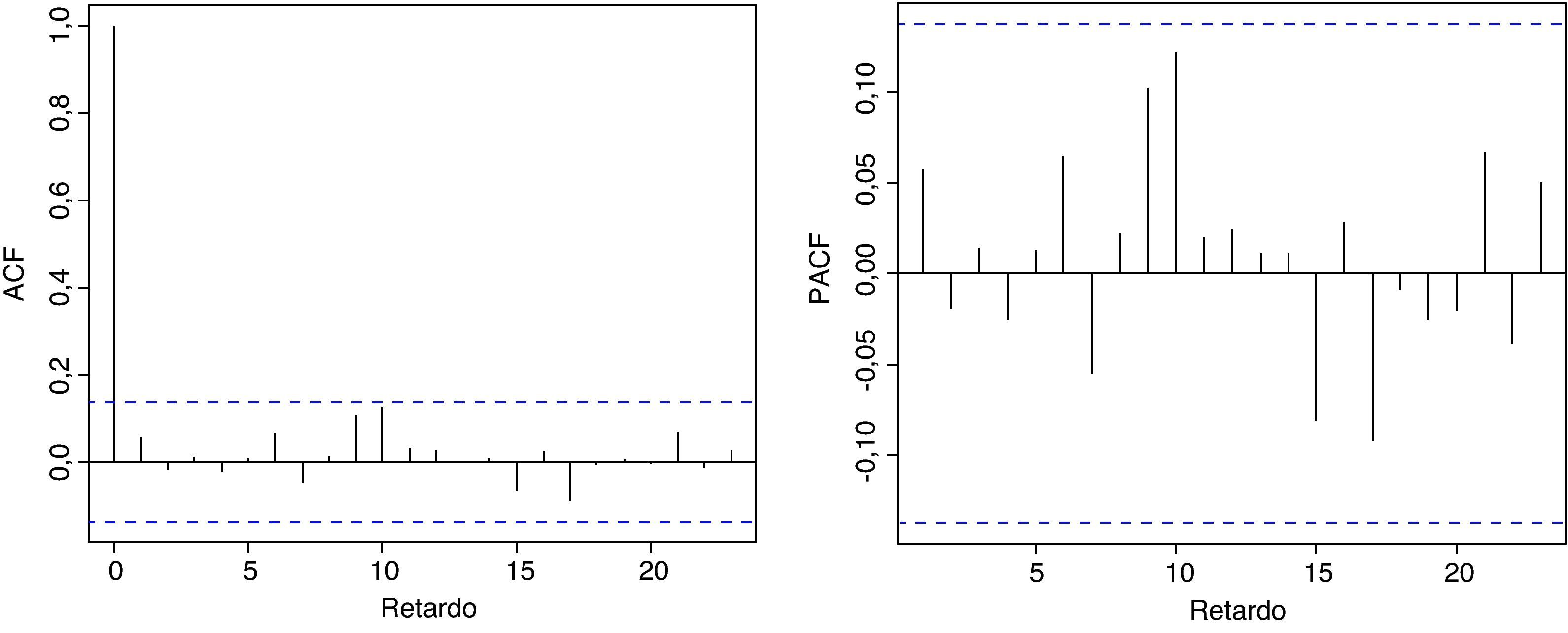
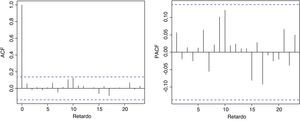
En la función de autocorrelación simple (ACF) y la función de autocorrelación parcial (PACF) de los rendimientos, representadas en la figura 3, no se observa autocorrelación lineal entre las observaciones de las rentabilidades del IBEX-35 en los diferentes desfases o retardos temporales.
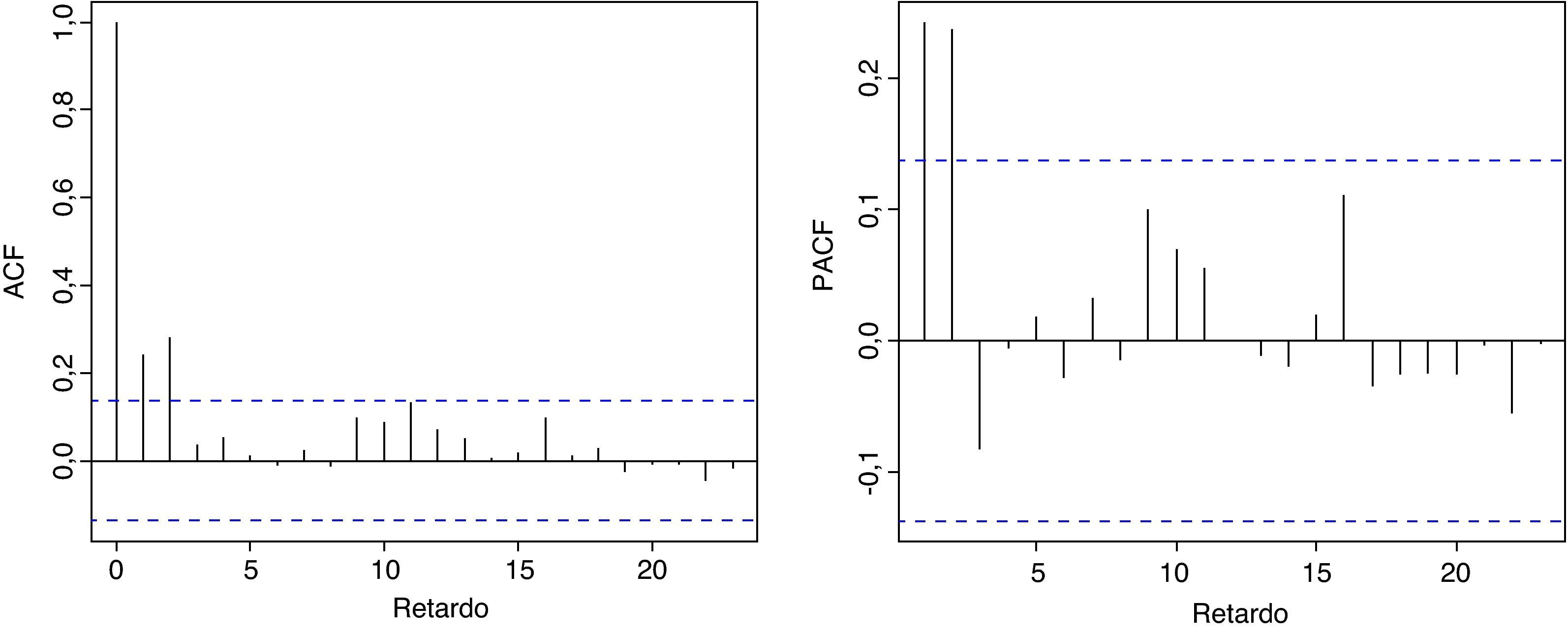
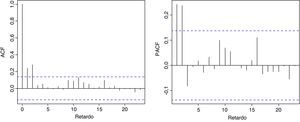
Sin embargo, la función de autocorrelación simple (ACF) y la función de autocorrelación parcial (PACF) de los rendimientos al cuadrado, representadas en la figura 4, muestran una fuerte estructura de dependencia, lo cual implica la existencia de dependencia en la varianza de los rendimientos mensuales.
4Estimación y comparación de los modelosEn este apartado exponemos los resultados de la estimación de los modelos para la serie analizada, así como la comparación de los mismos a partir de diferentes criterios estadísticos. En la tabla 4 recogemos los parámetros que resultan de la estimación por máxima verosimilitud de los distintos modelos analizados. El modelo RSLN de 2 regímenes (RSLN2), al igual que ocurre con los resultados obtenidos por Hardy (2001), proporciona un régimen estable donde la rentabilidad esperada es positiva y otro más volátil con una rentabilidad esperada negativa. Algo similar ocurre con los parámetros estimados para las medias y volatilidades en el modelo RSSD de Panneton, que son muy similares a los de RSLN, lo que concuerda con los resultados obtenidos en Hardy et al. (2006). Sin embargo, y a diferencia de estos autores, para la serie analizada, los parámetros de reversión no son relevantes e incluso toman valores positivos. Panneton (2006) obtiene un resultado similar para el índice Topix. El modelo RSSD, en principio, debiera proporcionar parámetros φi negativos en la medida en que en las situaciones en las que los índices están por debajo de su último máximo existe una presión por parte del mercado para alcanzarlos. Una vez alcanzados los valores máximos, Dt es cero por lo que el modelo se comporta como el modelo RSLN. En cuanto al modelo RSLN de tres regímenes (RSLN3), hemos restringido las probabilidades de salto o transición entre algunos regímenes (p1,2=0, p3,1=0, p2,3=0) dado que en una primera estimación dichos valores eran prácticamente nulos.
Parámetros resultantes del ajuste por máxima verosimilitud
| Modelo | Parámetros | ||
| Normal | μ=6,37e-03 | σ=0,06 | |
| Mixtura 2 normales | p=0,69 | μ1=0,02μ2=−0,02 | σ1=0,05σ2=0,09 |
| Mixtura 3 normales | p1=0,36p2=0,21 | μ1=−0,02μ2=−0,02μ2=0,04 | σ1=0,09σ2=0,03σ2=0,03 |
| GARCH (1,1) | μ=0,01ω=1,15e-04 | σ1=0,17β1=0,82 | |
| IGARCH (1,1) | μ=0,01ω=9,61e-05 | β1=0,82 | |
| GJR-GARCH (1,1) | μ=0,01ω=1,26e-04 | α1=0,17β1=0,82γ1=0,03 | |
| EGARCH (1,1) | μ=0,01ω=−0,54 | α1=0,30β1=−0,94γ1=−0,04 | |
| RSLN2 | p1,2=0,04p2,1=0,05 | μ1=−0,01μ2=0,02 | σ1=0,08σ2=0,04 |
| RSSD | p1,2=0,04p2,1=0,05 | μ1=−4,53e-03μ2=0,02 | σ1=0,08σ2=0,04φ1=3,61e-03φ2=2,24e-03 |
| RSLN3 | p1,1=0,15p2,1=0,04p2,2=0,96p2,2=0,07 | μ2=−0,12μ2=0,02μx=−1,35e-03 | σ1=0,01σ2=0,04σ2=0,09 |
| M-GARCH | p=0,94 | μ2=0,01μ2=−0,13ω1=7,04e-04 | α1=0,23α2=0,19β1=0,46 |
| RS-GARCH | p1,2=0,05p2,1=0,80 | μ1=0,01μ2=−0,13ω1=7,14e-04 | α1=0,23α2=0,20β1=0,46 |
El modelo IGARCH tiene unos parámetros muy similares al GARCH (1,1), ya que la persistencia del modelo GARCH es de α1+β1=0,99. Los modelos GARCH asimétricos no proporcionan en general un mejor ajuste. Los parámetros de efecto apalancamiento que recogen shocks asimétricos no resultan ser significativos, el p-valor asociado al parámetro γ1 del modelo GJR-GARCH es de 0,82 mientras que para el modelo EGARCH es de 0,34. El modelo RS-GARCH y M-GARCH analizados en este trabajo están formado por un proceso GARCH (1,1) y otro ARCH (1). Los parámetros en la ecuación de la media son muy diferentes bajo cada proceso, de esta forma bajo el ARCH (1) la rentabilidad logarítmica media esperada es muy negativa (μ2=−0,13) mientras que bajo el GARCH (1,1) es positiva (μ1=0,01).
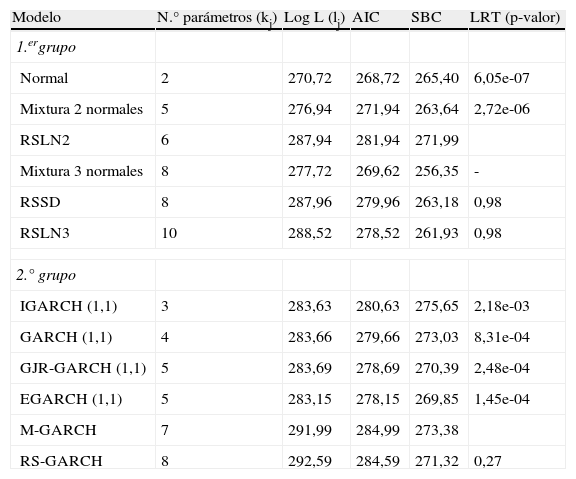
La selección entre los modelos suele realizarse utilizando el principio de parsimonia, es decir, que será preferible un modelo más sencillo a otro más complejo siempre y cuando el ajuste a los datos históricos sea similar. En el caso de que los modelos tengan el mismo número de parámetros, se suele utilizar como criterio de comparación el valor de la función de verosimilitud. Si por el contrario, los modelos presentan un número diferente de parámetros, será preciso utilizar criterios que tengan en consideración este aspecto. En concreto, en este apartado se tienen en cuenta los criterios AIC (Akaike information criteria) propuesto por Akaike (1973), el SBC (Schwartz criteria) propuesto por Schwartz (1978) y el test de la razón de verosimilitudh. El test de la ratio o razón de verosimilitud (véase por ejemplo Klugman et al., 2008) se puede emplear para comparar distintos modelos en el caso de que estos se consideren versiones reducidas o casos especiales de modelos más complejos. En este sentido se han formado dos grupos de modelos comparables. En el primer grupo se comparan los modelos respecto al RSLN2, mientras que en el segundo grupo son comparados respecto al M-GARCH. En la tabla 5 se muestran para cada modelo analizado los valores del logaritmo de la función de verosimilitud, de los criterios de Akaike (AIC) y el Criterio Bayesiano de Schwarz (SBC) así como el p-valor asociado al test LRT para cada uno de los dos grupos formados. En general, el análisis de los diferentes criterios revela que el RSLN2 mejora notablemente los resultados obtenidos por la mayoría de los modelos, siendo el modelo elegido en el primer grupo según el LRT. Centrándonos en el segundo grupo el modelo M-GARCH resulta el modelo más parsimonioso en función del AIC y LRT, pero no según SBC, que elige el modelo IGARCH.
Comparación de los modelos a través de diferentes criterios estadísticos
| Modelo | N.° parámetros (kj) | Log L (lj) | AIC | SBC | LRT (p-valor) |
| 1.ergrupo | |||||
| Normal | 2 | 270,72 | 268,72 | 265,40 | 6,05e-07 |
| Mixtura 2 normales | 5 | 276,94 | 271,94 | 263,64 | 2,72e-06 |
| RSLN2 | 6 | 287,94 | 281,94 | 271,99 | |
| Mixtura 3 normales | 8 | 277,72 | 269,62 | 256,35 | - |
| RSSD | 8 | 287,96 | 279,96 | 263,18 | 0,98 |
| RSLN3 | 10 | 288,52 | 278,52 | 261,93 | 0,98 |
| 2.° grupo | |||||
| IGARCH (1,1) | 3 | 283,63 | 280,63 | 275,65 | 2,18e-03 |
| GARCH (1,1) | 4 | 283,66 | 279,66 | 273,03 | 8,31e-04 |
| GJR-GARCH (1,1) | 5 | 283,69 | 278,69 | 270,39 | 2,48e-04 |
| EGARCH (1,1) | 5 | 283,15 | 278,15 | 269,85 | 1,45e-04 |
| M-GARCH | 7 | 291,99 | 284,99 | 273,38 | |
| RS-GARCH | 8 | 292,59 | 284,59 | 271,32 | 0,27 |
Dado que el presente trabajo tiene por objetivo el análisis del riesgo de equity, la selección de los modelos realizada exclusivamente con los criterios basados en los valores de la función de verosimilitud puede no ser adecuada. En este sentido, podría ocurrir que los modelos con mayores valores proporcionen un buen ajuste global pero no a los valores extremos, que sin embargo son determinantes para el cálculo del capital necesario. Bajo estos modelos los datos atípicos suelen ser considerados como outliers, pero desde el punto de vista de la gestión del riesgo tienen un significado crucial ya que determinan en gran medida las máximas pérdidas a las que está expuesta la compañía. Por tanto, se debe evaluar en qué medida los residuos superan el test de normalidad, especialmente en la cola izquierda de la distribución. En el caso de que los residuos no sean normales, el ajuste proporcionado por el modelo no es adecuado. Sin embargo, para los modelos de cambio de régimen y de mixturas los residuos sólo son aproximadamente N(0;1), debido a la incertidumbre asociada al proceso de cambio de régimen o de mixtura. De esta forma, en cada período temporal se establece una probabilidad de pertenecer a cada submodelo de forma que los residuos deben ser determinados en función del submodelo con el que se presupone que fueron generados. Existen dos formas de determinar los residuos a partir de los residuos condicionales a cada régimen o mixtura. El primer método consiste en asignar los residuos a cada submodelo de acuerdo a su probabilidad condicional. La segunda consiste en asociar los residuos al submodelo con una mayor probabilidad asociada. En este trabajo, a semejanza de Hardy et al. (2006), se emplean los residuos generados por el submodelo con una mayor probabilidad asociada.
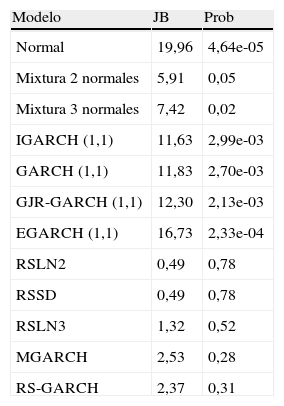
El análisis de normalidad se hace a través de cualquiera de los tests tradicionales (gráficos QQ, gráficos PP, test de Jarque Bera, Shapiro-Wilk, etc.). En el caso de que una de estas pruebas indique que el modelo no tenga residuos normales es indicativo de que el modelo no se ajusta bien a los datos, o en el caso de modelos de mixturas o de cambios de régimen que el efecto de la incertidumbre del submodelo es muy elevado. El estadístico del test de Jarque-Bera (Jarque y Bera, 1980, 1987) emplea la asimetría S y la curtosis C de los residuos y toma la expresión Q=n6S2+C−324. Bajo la hipótesis de que los residuos son normales el estadístico Q tiene una distribución χ2 con dos grados de libertad. En la tabla 6 se aprecia como los modelos normal, IGARCH, GARCH, GJR-GARCH y EGARCH no superan el test de normalidad de los residuos con un nivel de significación de 1%. Al mismo tiempo, debe apreciarse la capacidad del modelo RSLN de Hardy (2001) en sus versiones de dos y tres regímenes y con reversión a la media o modelo RSDD para superar el test. Hardy et al. (2006) encontraron que sólo los modelos de cambio de régimen analizados superan el test de Jarque-Bera. Sin embargo, nosotros encontramos que también lo superan para nuestra muestra modelos no analizados por dichos autores como son la mixtura de normales y el modelo M-GARCH.
Contrastación de hipótesis de normalidad de los residuos
| Modelo | JB | Prob |
| Normal | 19,96 | 4,64e-05 |
| Mixtura 2 normales | 5,91 | 0,05 |
| Mixtura 3 normales | 7,42 | 0,02 |
| IGARCH (1,1) | 11,63 | 2,99e-03 |
| GARCH (1,1) | 11,83 | 2,70e-03 |
| GJR-GARCH (1,1) | 12,30 | 2,13e-03 |
| EGARCH (1,1) | 16,73 | 2,33e-04 |
| RSLN2 | 0,49 | 0,78 |
| RSSD | 0,49 | 0,78 |
| RSLN3 | 1,32 | 0,52 |
| MGARCH | 2,53 | 0,28 |
| RS-GARCH | 2,37 | 0,31 |
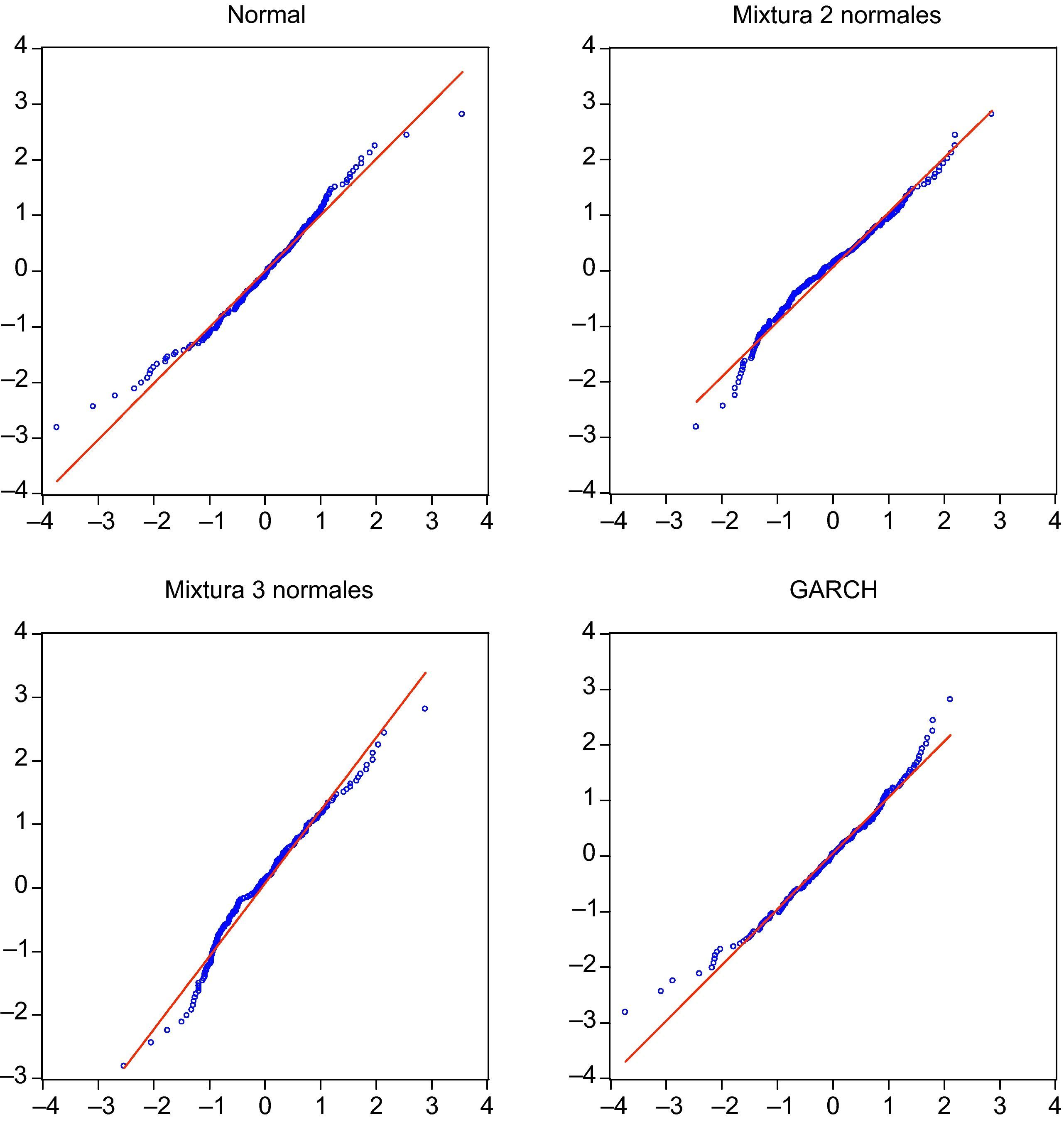
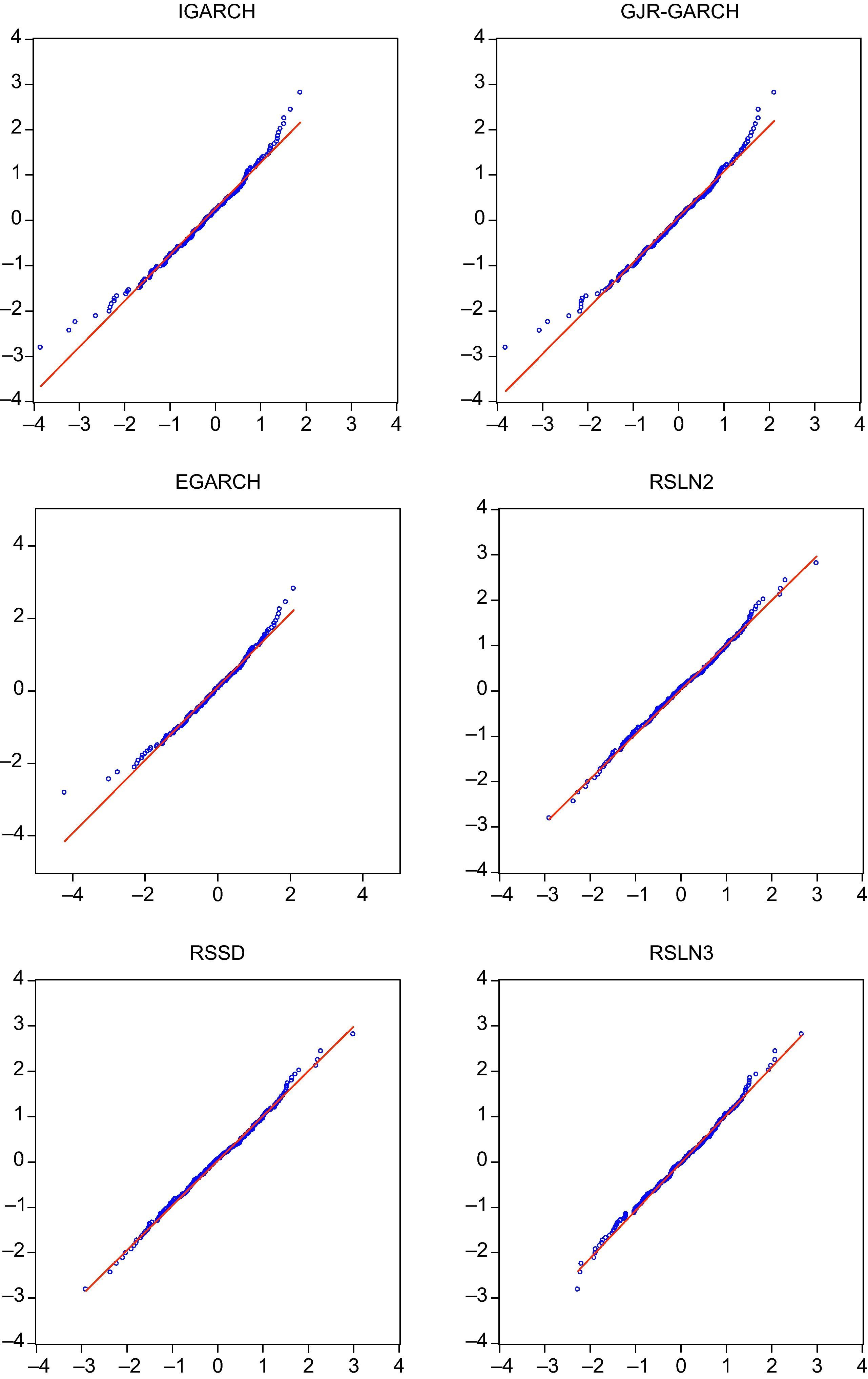
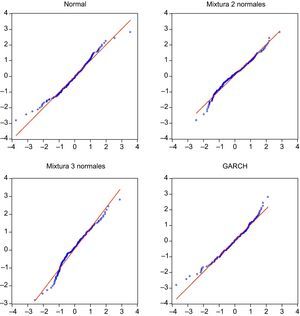
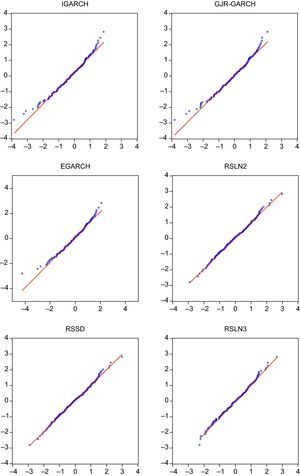
En el anexo 1 recogemos los diferentes gráficos QQ de los residuos para analizar en qué medida los cuantiles empíricos de los residuos (eje horizontal) se ajustan a los teóricos de la distribución normal. En el mismo puede apreciarse cómo los residuos de los modelos que no superan el test de Jarque Bera no proporcionan un buen ajuste a las colas de la distribución. A efectos de determinar el capital requerido a una compañía aseguradora la cola más relevante es la izquierda ya que recoge las pérdidas en la cartera. De esta forma, si un modelo infravalora dicha cola estará asignando menos capital que el necesario para soportar el riego de renta variable.
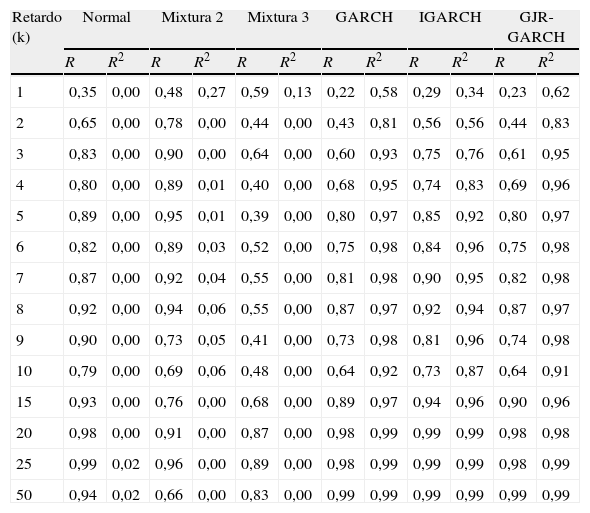
Además del análisis de normalidad, la correcta especificación del modelo estimado requiere analizar si los residuos y sus cuadrados están incorrelacionados. Un test frecuentemente empleado es la Q de Ljung y Box (1979). La hipótesis nula del test para el retardo k es que no existe autocorrelación para órdenes no superiores a k. El estadístico se define como Q=T(T+2)∑j=1kτj2τ−j, donde τj es la j-ésima autocorrelación y T es el número de observaciones. Q está asintóticamente distribuido como una χ2 con grados de libertad igual al número de autocorrelaciones. En la tabla 7 se muestran los p-valores asociados a dicho estadístico para los residuos (R) y residuos al cuadrado (R2) de distintos modelos analizados.
Probabilidad asociada al estadístico Q de los residuos (R) y sus cuadrados (R2)
| Retardo (k) | Normal | Mixtura 2 | Mixtura 3 | GARCH | IGARCH | GJR-GARCH | ||||||
| R | R2 | R | R2 | R | R2 | R | R2 | R | R2 | R | R2 | |
| 1 | 0,35 | 0,00 | 0,48 | 0,27 | 0,59 | 0,13 | 0,22 | 0,58 | 0,29 | 0,34 | 0,23 | 0,62 |
| 2 | 0,65 | 0,00 | 0,78 | 0,00 | 0,44 | 0,00 | 0,43 | 0,81 | 0,56 | 0,56 | 0,44 | 0,83 |
| 3 | 0,83 | 0,00 | 0,90 | 0,00 | 0,64 | 0,00 | 0,60 | 0,93 | 0,75 | 0,76 | 0,61 | 0,95 |
| 4 | 0,80 | 0,00 | 0,89 | 0,01 | 0,40 | 0,00 | 0,68 | 0,95 | 0,74 | 0,83 | 0,69 | 0,96 |
| 5 | 0,89 | 0,00 | 0,95 | 0,01 | 0,39 | 0,00 | 0,80 | 0,97 | 0,85 | 0,92 | 0,80 | 0,97 |
| 6 | 0,82 | 0,00 | 0,89 | 0,03 | 0,52 | 0,00 | 0,75 | 0,98 | 0,84 | 0,96 | 0,75 | 0,98 |
| 7 | 0,87 | 0,00 | 0,92 | 0,04 | 0,55 | 0,00 | 0,81 | 0,98 | 0,90 | 0,95 | 0,82 | 0,98 |
| 8 | 0,92 | 0,00 | 0,94 | 0,06 | 0,55 | 0,00 | 0,87 | 0,97 | 0,92 | 0,94 | 0,87 | 0,97 |
| 9 | 0,90 | 0,00 | 0,73 | 0,05 | 0,41 | 0,00 | 0,73 | 0,98 | 0,81 | 0,96 | 0,74 | 0,98 |
| 10 | 0,79 | 0,00 | 0,69 | 0,06 | 0,48 | 0,00 | 0,64 | 0,92 | 0,73 | 0,87 | 0,64 | 0,91 |
| 15 | 0,93 | 0,00 | 0,76 | 0,00 | 0,68 | 0,00 | 0,89 | 0,97 | 0,94 | 0,96 | 0,90 | 0,96 |
| 20 | 0,98 | 0,00 | 0,91 | 0,00 | 0,87 | 0,00 | 0,98 | 0,99 | 0,99 | 0,99 | 0,98 | 0,98 |
| 25 | 0,99 | 0,02 | 0,96 | 0,00 | 0,89 | 0,00 | 0,98 | 0,99 | 0,99 | 0,99 | 0,98 | 0,99 |
| 50 | 0,94 | 0,02 | 0,66 | 0,00 | 0,83 | 0,00 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 | 0,99 |
| Retardo (k) | EGARCH | RSLN2 | RSSD | RSLN3 | M-GARCH | RS-GARCH | ||||||
| R | R2 | R | R2 | R | R2 | R | R2 | R | R2 | R | R2 | |
| 1 | 0,28 | 0,48 | 0,79 | 0,06 | 0,79 | 0,06 | 0,97 | 0,15 | 0,67 | 0,74 | 0,67 | 0,47 |
| 2 | 0,51 | 0,78 | 0,92 | 0,00 | 0,93 | 0,00 | 0,91 | 0,28 | 0,86 | 0,93 | 0,86 | 0,77 |
| 3 | 0,70 | 0,91 | 0,80 | 0,01 | 0,79 | 0,01 | 0,97 | 0,28 | 0,96 | 0,93 | 0,96 | 0,81 |
| 4 | 0,73 | 0,96 | 0,60 | 0,02 | 0,57 | 0,02 | 0,99 | 0,43 | 0,91 | 0,86 | 0,89 | 0,76 |
| 5 | 0,84 | 0,98 | 0,73 | 0,04 | 0,71 | 0,03 | 0,99 | 0,38 | 0,96 | 0,32 | 0,95 | 0,20 |
| 6 | 0,81 | 0,99 | 0,80 | 0,06 | 0,79 | 0,05 | 0,99 | 0,51 | 0,99 | 0,22 | 0,98 | 0,15 |
| 7 | 0,88 | 0,99 | 0,88 | 0,09 | 0,87 | 0,08 | 0,96 | 0,52 | 0,99 | 0,20 | 0,99 | 0,13 |
| 8 | 0,93 | 0,97 | 0,93 | 0,12 | 0,92 | 0,11 | 0,98 | 0,61 | 1,00 | 0,28 | 1,00 | 0,19 |
| 9 | 0,87 | 0,99 | 0,87 | 0,16 | 0,86 | 0,15 | 0,91 | 0,71 | 0,68 | 0,36 | 0,62 | 0,26 |
| 10 | 0,77 | 0,90 | 0,87 | 0,22 | 0,86 | 0,21 | 0,91 | 0,75 | 0,75 | 0,43 | 0,69 | 0,32 |
| 15 | 0,95 | 0,88 | 0,93 | 0,35 | 0,93 | 0,33 | 0,78 | 0,83 | 0,90 | 0,51 | 0,86 | 0,46 |
| 20 | 0,99 | 0,93 | 0,95 | 0,27 | 0,95 | 0,26 | 0,71 | 0,73 | 0,94 | 0,77 | 0,92 | 0,71 |
| 25 | 0,99 | 0,95 | 0,93 | 0,43 | 0,93 | 0,41 | 0,80 | 0,83 | 0,97 | 0,72 | 0,96 | 0,64 |
| 50 | 0,99 | 0,98 | 0,82 | 0,38 | 0,82 | 0,36 | 0,98 | 0,84 | 0,94 | 0,40 | 0,95 | 0,34 |
Mediante el análisis del correlograma de los residuos y de los residuos al cuadrado observamos que sólo para los modelos RSLN3 y GARCH en sus distintas versiones (GARCH, IGARCH, EGARCH, GJR-GARCH, M-GARCH y RS-GARCH) los residuos están incorrelacionados y son homocedásticos. Sin embargo, puede observarse cómo los modelos normal y las mixturas de normales no recogen la volatilidad del mercado, manifiesta en las correlaciones significativas de los cuadrados de los residuos, lo cual puede tener consecuencias importantes en la estimación del riesgo de inversión. De esta forma podemos concluir que sólo el modelo RSLN de tres regímenes, el modelo M-GARCH y el modelo RS-GARCH superan los test de normalidad, incorrelación y homocedasticidad y por tanto serán los modelos considerados en el siguiente apartado. El modelo RSLN2 también será considerado dada la importancia del ajuste a la cola izquierda de la distribución de rendimientos y su parsimonia, y el modelo normal por ser la hipótesis base con la que trabaja el CEIOPS.
5Determinación del capital necesario para el riesgo de equity a través de modelos alternativos al estándarEn este apartado vamos a comparar el capital resultante de utilizar los modelos RSLN, M-GARCH y RS-GARCH evaluados con anterioridad, frente a la carga establecida en el modelo estándar. Como adelantamos en la introducción de este trabajo, en QIS4 la carga de capital para riesgo de inversión en renta variable se calcula asumiendo un shock del 32% de caída para las inversiones en índices de mercados desarrollados globales (países OCDE y EEE) y un 45% para el resto de mercados. Dichos factores permanecen inalterados desde la calibración efectuada en el tercer estudio de impacto cuantitativo (QIS3) y se alcanzó por el ajuste de los rendimientos medidos en términos nominales y netos de riesgo cambiario del índice global MSCI de mercados desarrollados para el período 1970-2005 (datos trimestrales)i. Una vez obtenidas las cantidades individuales asociadas a mercados desarrollados y resto de mercados, se agregan utilizando un coeficiente de correlación lineal de 0,75. Dado que nuestro trabajo se centra en el análisis de un sólo índice de un mercado desarrollado, los resultados obtenidos deben compararse con el factor del 32%.
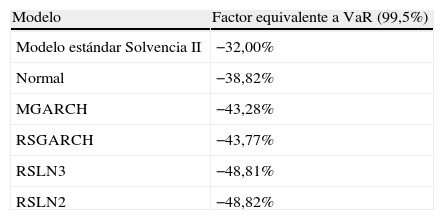
A continuación exponemos el resultado de estimar el capital necesario para una cartera invertida en IBEX-35 mediante los distintos modelos analizados. Para ello se realizó una simulación de 100.000 escenarios a un año por el método Latino hipercúbico (LHS)j. En la tabla 8 se muestran los factores que resultarían de aplicar los diferentes modelos para un VaR (99,5%). Como puede observarse tales factores superan considerablemente a la cuantía establecida en el modelo estándar. Además, el modelo de rendimientos normales, implícito en el cálculo de capital de Solvencia II, subestima de forma considerable la cifra de capital respecto al resto de los modelos. Las cargas de capital obtenidas mediante los modelos RSLN de 2 y 3 regímenes, MGARCH y RSGARCH superan en valores que van desde 4,5 a 10 puntos porcentuales el ajuste normal, y entre 13,3 y 16,8 puntos al modelo estándar. Por tanto, las compañías aseguradoras españolas que opten por el modelo estándar o simulen el comportamiento del riesgo de inversión en carteras de IBEX utilizando la hipótesis de normalidad de los rendimientos, estarían subestimando el riesgo de acuerdo con lo acontecido en el mercado en los últimos 17 años.
6ConclusionesEl modelo de rendimientos normal empleado para el cálculo de los requerimientos de capital en Solvencia II (QIS4) ha sido elegido por razones de simplicidad y transparencia. No obstante, la hipótesis de normalidad puede subestimar seriamente la cola de la distribución de pérdidas (resultados extremos) y capturar inadecuadamente la variabilidad en la volatilidad. Por este motivo en este trabajo hemos analizado la adecuación de distintos modelos susceptibles de ser utilizados como modelos internos y las necesidades de capital que resultan de su aplicación, frente a las del modelo estándar. Para ello, se han utilizado datos mensuales de la serie de IBEX-35 del período enero de 1992 a diciembre de 2008, por ser un índice de referencia para los aseguradores españoles. La comparación de los mismos atendiendo a diferentes criterios estadísticos revela que los modelos de cambio de régimen de Markov y M-GARCH son los que presentan un mejor ajuste global y son los únicos que superan el test de normalidad de los residuos. Por este motivo, representan mejor el comportamiento de los valores extremos que puede tener la cola de la distribución, y se postulan como los más adecuados para analizar el riesgo de mercado de la inversión en carteras de IBEX. Asimismo, la comparación de las cargas de capital resultantes de aplicar los modelos estimados frente a las establecidas en el modelo estándar revela una subestimación importante del riesgo de equity. En este sentido, si nos detenemos en los modelos que presentaron un mejor ajuste (RSLN de 2 y 3 regímenes, MGARCH y RSGARCH), se observa que las cargas de capital obtenidas superan entre 13,3 y 16,8 puntos al modelo estándar. Los resultados obtenidos tienen gran relevancia ya que significan que las compañías aseguradoras españolas que opten por el modelo estándar o simulen el comportamiento del riesgo de inversión en carteras de IBEX utilizando la hipótesis de normalidad de los rendimientos, estarán subestimando las necesidades de capital de acuerdo con lo acontecido en el mercado español de renta variable.
Solvencia II establecerá dos cantidades de capital: el capital económico (SCR) que es la cantidad asociada al riesgo realmente soportado por el asegurador y el capital legal o mínimo (MCR) que es la cantidad mínima que la compañía debe disponer en cada momento. El SCR puede ser calculado mediante la fórmula estándar o a través de modelos propios.
Este riesgo es particularmente relevante en el caso de las compañías de seguros generales españolas, ya que según los datos estadísticos aportados por ICEA (www.icea.es), en 2008 destinaban directamente un 15,2 por ciento de su cartera a la inversión en renta variable.
Otra familia popular de distribuciones son las distribuciones provenientes de la teoría de valor extremo: la distribución generalizada de Pareto y la distribución generalizada de valor extremo. La principal diferencia de las distribuciones de valor extremo respecto a las anteriores, es que las primeras sólo emplean para su ajuste un conjunto limitado de datos que son los máximos de bloque o los valores que superen un determinado umbral.
DynaMo es un modelo de análisis financiero dinámico (DFA) descrito en D’Arcy et al. (1997, 1998). Para una aplicación del modelo Dynamo 3 puede consultarse D’Arcy y Gorvett (2004). En la actualidad está siendo actualizado por la sociedad de actuarios americana CAS (Casualty Actuarial Society).
Wong y Li (2000) introducen los modelos autorregresivos mixtos (mixture autoregressive models [MAR]) que son la mixtura de K componentes autorregresivos, y Wong y Li (2001) los modelos de heterocedasticidad condicional autorregresiva mixtos (mixture autoregressive conditional heteroscedastic models [MARCH]), mixtura de K componentes autorregresivos con heterocedaticidad condicional autorregresiva.
Hemos ajustado los datos a múltiples distribuciones: t-Student con parámetros de localización y de escala simétrica y asimétrica, distribuciones hiperbólicas, etc., y distintos modelos GARCH con innovaciones no normales. Dado que los resultados no mejoran a los principales modelos, y por motivos de mantener la exposición centrada, hemos restringido nuestro análisis a un grupo más reducido pero lo suficientemente amplio de modelos. Sin embargo, a diferencia de Hardy et al. (2006) hemos decidido no incorporar los Modelos de Volatilidad Estocástica (SV). El lector interesado puede referirse a Ruiz y Veiga (2008), para una modelización del IBEX diario con este tipo de modelos.
El histograma se muestra en color negro, la distribución normal en color azul y el kernel en color rojo. El kernel empleado es gaussiano con un bandwidth seleccionado por el procedimiento de Silverman (1986) que toma el valor 0,01727.
El criterio de Akaike (AIC) selecciona el modelo que toma mayor valor de la diferencia entre la función de log-verosimilitud bajo el modelo j-ésimo y su número de parámetros, es decir lj−kj. El Criterio Bayesiano de Schwarz (SBC) se decanta por el modelo con mayor valor de lj−12kj⋅ln n dónde n es el tamaño muestral. El LRT se emplea cuando un modelo con k1 parámetros es un caso especial del modelo con k2 parámetros siendo k2>k1. Este test tiene como estadístico T=2(l2−l1)=2(l2/l1) que se distribuye como una χ2 con un número de grados de libertad de k2−k1. La hipótesis nula del test es que no se produce una mejora significativa del empleo del modelo más complejo.
La media aritmética anual calculada era de 11,5% y la desviación estándar era de 16,9% por lo que bajo la hipótesis de normalidad y para un VaR (99,5%) el factor a aplicar es: VaR=0,115−2,58×0,169≈−32%.
El método de simulación Latino hibercúbico (LHS) es un método de recogida de muestras por estratificación. Permite recrear una distribución con una mayor precisión para un mismo número de iteraciones que el método de Monte Carlo puro, en el que las muestras son seleccionadas de forma completamente aleatoria.