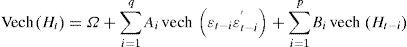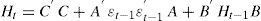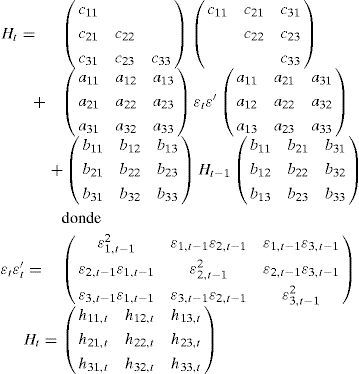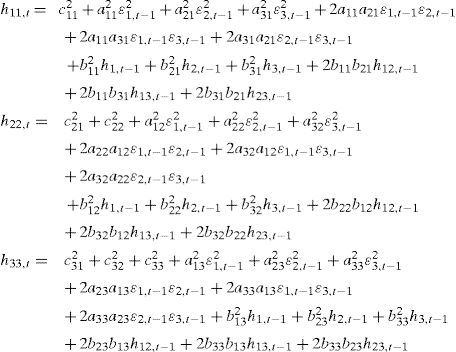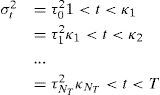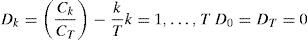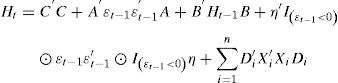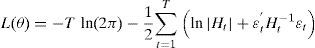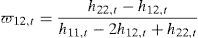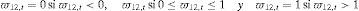En este trabajo se analiza la transmisión de información y la formación de carteras de mínimo riesgo óptimas entre las empresas de mayor, mediano y pequeño tamaño del mercado de valores español representadas, respectivamente, por los índices bursátiles IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP. La comparación de dos modelos de volatilidad, uno multivariante simétrico y otro asimétrico con cambios estructurales, muestra que existen diferencias en la transmisión de volatilidad. Las carteras de mínimo riesgo, por su parte, están formadas en todos los escenarios posibles analizados por la combinación de las empresas de mediano y pequeño tamaño (con una mayor ponderación de las empresas medianas) siendo, incluso, menor el riesgo cuando se consideran los efectos asimétricos y los cambios estructurales en la volatilidad. Estos resultados, pues, refuerzan el interés por conocer las características de este tipo de empresas frente a las que componen el IBEX 35.
This article examines the transmission of volatility and the creation of optimal risk minimizing portfolios among large-, medium- and small-capitalization companies of the Spanish stock market, which are represented by the IBEX 35, IBEX MEDIUM CAP and IBEX SMALL CAP indexes respectively. A comparison of two volatility models, a symmetric and an asymmetric multivariate GARCH model with structural changes, shows that there are differences in the transmission of volatility. We demonstrate that, in all the possible scenarios analyzed, the risk minimizing portfolio is composed of medium and small indexes with a higher weight of medium firms. The risk is even lower when asymmetric effects and structural changes are taken into account. These results therefore illustrate the importance of knowing the main characteristics of these firms with respect to those than compose the IBEX 35 index.
La modelización de la transmisión de información entre mercados bursátiles o entre sectores económicos ha sido un tema recurrente en la evidencia empírica de los últimos años. Entre las propuestas metodológicas desarrolladas podemos considerar la realizada por Ewing y Malik (2005) y Hassan y Malik (2007) que utilizan un modelo GARCH multivariante para analizar la transmisión de información entre grandes y pequeñas empresas y entre varios sectores industriales, respectivamente, considerando únicamente en el primero de los trabajos la posible existencia de cambios estructurales y sus efectos en la transmisión de información entre las carteras de diverso tamaño.
Existen en la evidencia empírica española más reciente una serie de trabajos que abordan la cuestión desde puntos de vista similares, como son los realizados por Cuñado et al (2004), Soriano y Climent (2006), Aragó y Fernández (2007), Chuliá y Torró (2007) y Pardo y Torró (2007), sin embargo este trabajo mejora la evidencia empírica previa en varios sentidos.
En primer lugar, este es el primer trabajo en el que se analizan de forma conjunta y en un mismo modelo los índices IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP, representativos de las empresas de mayor, medio y pequeño tamaño, respectivamente, del mercado bursátil española. En la actualidad todos ellos son una referencia importante a nivel nacional e internacional, además de ser la base de diferentes productos financieros como derivados, fondos de inversión o Exchange Trade Funds (ETF), por lo que resulta importante conocer en qué medida se transmiten la información y cómo se pueden conformar carteras óptimas a partir de los mismos.
En segundo lugar, se utilizan diferentes modelos de volatilidad (un modelo GARCH multivariante simétrico y un modelo GARCH multivariante asimétrico con cambios estructurales) con el objeto de comprobar los cambios en la transmisión de información.
Este estudio se complementó con la realización del análisis de la transmisión de información para cada uno de los subperíodos en los que se divide la muestra como consecuencia de la existencia de cambios estructurales en la misma. En dicho análisis se comprueba que la transmisión de información se ciñe, en todos y cada uno de los casos y para todos los períodos analizados, a los propios shocks y volatilidades retardados un período.
Finalmente, a partir de los resultados obtenidos en las estimaciones de las volatilidades se utilizan las varianzas y covarianzas condicionales para calcular los pesos o ponderaciones óptimas de los índices en orden a la formación de carteras de mínimo riesgo compuestas por dos índices, siguiendo la metodología inicialmente propuesta por Kroner y Ng (1998) e incluyendo, a diferencia de estos, diferentes supuestos en función del signo de la información transmitida. Este análisis del comportamiento del mercado bursátil español permitirá proporcionar algunas claves para comprender mejor la gestión de carteras.
La motivación de centrar nuestro trabajo en el mercado español está basada en el hecho de que en los últimos años este mercado se ha convertido en una importante referencia a nivel europeo por sus elevados niveles técnicos, operativos y organizativos. Esto ha permitido concentrar grandes niveles de volumen de inversión y mejorar la transparencia, liquidez y efectividad del mercado con lo que aumenta su atractivo a nivel inversor. En este sentido, el mercado bursátil español desempeña un papel decisivo en el conjunto de los mercados bursátiles europeos, lo que refuerza nuestro interés por enfocar el trabajo hacia el mismo. Además, tal y como apuntan Lo y Mackinlay (1990), es importante reportar resultados empíricos con datos diferentes a los trabajos iniciales con el objetivo de proporcionar robustez a la metodología original y comprobar que los resultados no corresponden al mineo de datos.
Por otro lado, la presencia de inversores institucionales (compañías de seguros, sociedades de inversión, fondos de pensiones y otras fórmulas de ahorro institucional) se ha incrementado notablemente desde finales de los noventa, situándose España dentro del conjunto de países que más inversión extranjera reciben, por lo que resulta interesante para dichos inversores proporcionar un análisis, como se hace en este trabajo, de cuáles son las carteras de mínimo riesgo a partir de la consideración de una serie de hipótesis.
Los resultados obtenidos muestran un significativo cambio en la transmisión de volatilidad e información una vez que se tienen en cuenta el comportamiento asimétrico en la volatilidad y los cambios estructurales. Sin embargo, el resultado más interesante se encuentra en la formación de las carteras de mínimo riesgo que, en cualquiera de los escenarios o metodologías, están compuestas por las medianas y pequeñas empresas, con un mayor peso de las primeras, lo que refuerza el interés por conocer las características de este tipo de empresas frente a las que componen el IBEX 35.
El resto del trabajo se estructura de la siguiente manera: en la Sección 2 se revisa la evidencia empírica previa, en la Sección 3 se describen los datos utilizados y la metodología. En la Sección 4 se muestran los resultados obtenidos. Finalmente, en la Sección 5 se exponen las principales conclusiones.
2Revisión bibliográficaUno de los principales temas en finanzas en los últimos años ha sido el análisis de la transmisión de información y volatilidad entre mercados, representados por sus índices bursátiles o sectoriales, o entre carteras, definidas por diferentes criterios como la capitalización.
Los trabajos iniciales de Hamao et al (1990), King y Wadhwani (1990) y Lin et al (1994), entre otros, fueron seguidos por otros como los de Fleming et al (1998), quienes demostraron que la diversificación de la inversión entre diferentes mercados y el hecho de compartir información conduce a la existencia de transmisión de volatilidad entre los mismos a lo largo del tiempo; o los de Chelley-Steeley y Steeley (1996) y Grieb y Reyes (2002), quienes examinaron datos del mercado británico utilizando distintas metodologías para mostrar la existencia de transmisiones de volatilidad bidireccionales entre empresas de diferentes tamaños.
Más recientemente, Malik y Hammoudeh (2007) analizaron los mecanismos de transmisión de volatilidad y shocks entre activos y mercados petrolíferos de los Estados Unidos de América y los países del Golfo. Ewing y Malik (2005) examinaron la asimetría en la predicción de la volatilidad utilizando un modelo de volatilidad bivariante y teniendo en cuenta la existencia de cambios estructurales. Finalmente, Hassan y Malik (2007) y Li y Majerowska (2008) utilizan modelos GARCH multivariantes (con más de dos variables) para analizar, respectivamente, la transmisión de información entre diferentes sectores industriales estadounidenses y entre los mercados emergentes de Polonia y Hungría y los desarrollados de Alemania y Estados Unidos.
El comportamiento de la volatilidad en el mercado bursátil español también ha sido analizado durante los últimos años en diferentes trabajos. Cuñado et al (2004) analizaron el mismo y sus cambios a la vez que identificaban las causas, llegando a la conclusión de que el mercado bursátil español está sometido a una alta volatilidad y que el volumen de negociación influye significativamente en la volatilidad.
Aragó y Fernández (2007) analizaron la influencia de los cambios estructurales en la transmisión de información entre diferentes mercados bursátiles europeos. Sus resultados sugieren que los mercados reaccionan no solo a las noticias locales sino también a las que se originan en otros mercados, especialmente cuando estas son malas. Soriano y Climent (2006) utilizan un modelo GARCH multivariante para analizar la importancia del efecto región frente al efecto industria y sus consecuencias sobre la transmisión de volatilidad. Chuliá y Torró (2007) analizan la transmisión de volatilidad entre grandes y pequeñas empresas en el mercado bursátil español utilizando un modelo CAPM condicional GARCH-M multivariante asimétrico, llegando a la conclusión de que la transmisión de volatilidad se produce tras las noticias negativas.
Finalmente, Pardo y Torró (2007) estudian la transmisión de volatilidad entre grandes y pequeñas empresas analizando la función impulso-respuesta de la volatilidad condicional siguiendo la metodología de Lin (1997) y Meneu y Torró (2003). Sus resultados muestran que existe una relación de transmisión bidireccional entre las dos carteras empleadas tras las malas noticias.
3Datos y metodología3.1DatosLos datos consisten en las rentabilidades diarias calculadas como las diferencias logarítmicas de dos cierres consecutivos de los índices IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP durante el período del 14 de enero de 1992 hasta el 31 de diciembre de 2009.
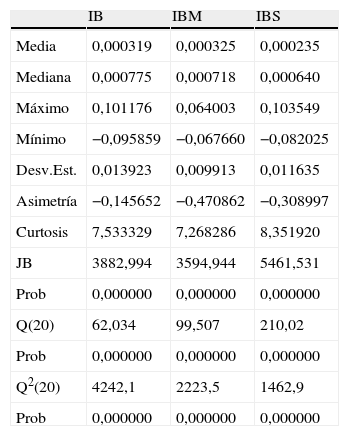
Los estadísticos básicos de las series de rentabilidad se muestran en la tabla 1. La rentabilidad del IBEX MEDIUM CAP es mayor (0,000325) que la del IBEX 35 (0,000319) y la del IBEX SMALL CAP (0,000235). Adicionalmente, su volatilidad, medida por la desviación típica, es menor (0,009913) frente a la del IBEX 35 (0,013923) y la del IBEX SMALL CAP (0,011635).
Estadísticos descriptivos
| IB | IBM | IBS | |
| Media | 0,000319 | 0,000325 | 0,000235 |
| Mediana | 0,000775 | 0,000718 | 0,000640 |
| Máximo | 0,101176 | 0,064003 | 0,103549 |
| Mínimo | −0,095859 | −0,067660 | −0,082025 |
| Desv.Est. | 0,013923 | 0,009913 | 0,011635 |
| Asimetría | −0,145652 | −0,470862 | −0,308997 |
| Curtosis | 7,533329 | 7,268286 | 8,351920 |
| JB | 3882,994 | 3594,944 | 5461,531 |
| Prob | 0,000000 | 0,000000 | 0,000000 |
| Q(20) | 62,034 | 99,507 | 210,02 |
| Prob | 0,000000 | 0,000000 | 0,000000 |
| Q2(20) | 4242,1 | 2223,5 | 1462,9 |
| Prob | 0,000000 | 0,000000 | 0,000000 |
Los términos IB, IBM e IBS hacen referencia a los índices IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente.
Los valores de la asimetría y la curtosis muestran las tres series como asimétricas a la izquierda y leptocúrticas. El estadístico Jarque-Bera rechaza en todos los casos la hipótesis nula de que las rentabilidades se encuentran distribuidas normalmente y, finalmente, el estadístico Ljung Box con 20 retardos indica la presencia de una significativa dependencia lineal y no lineal en las rentabilidades de los tres índices.
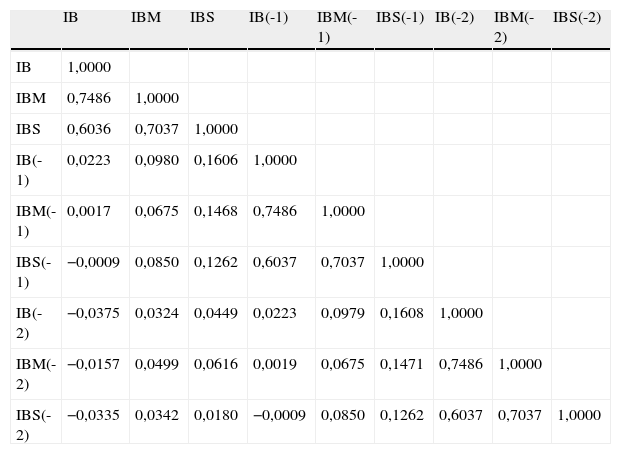
Como complemento a los datos anteriores se presenta en la tabla 2 la matriz de correlaciones entre los diferentes índices (en el mismo período y con dos retardos) para proporcionar una idea de la relación lineal entre las volatilidades de los índices. Se puede observar cómo los elevados coeficientes de correlación en el mismo período, superiores a 0,7 en los dos casos en los que se contempla el índice IBEX MEDIUM CAP, se reducen significativamente cuando se consideran los retardos, resultando incluso negativos en la mayoría de los casos cuando se toma como referencia el índice IBEX 35.
Coeficientes de correlación
| IB | IBM | IBS | IB(-1) | IBM(-1) | IBS(-1) | IB(-2) | IBM(-2) | IBS(-2) | |
| IB | 1,0000 | ||||||||
| IBM | 0,7486 | 1,0000 | |||||||
| IBS | 0,6036 | 0,7037 | 1,0000 | ||||||
| IB(-1) | 0,0223 | 0,0980 | 0,1606 | 1,0000 | |||||
| IBM(-1) | 0,0017 | 0,0675 | 0,1468 | 0,7486 | 1,0000 | ||||
| IBS(-1) | −0,0009 | 0,0850 | 0,1262 | 0,6037 | 0,7037 | 1,0000 | |||
| IB(-2) | −0,0375 | 0,0324 | 0,0449 | 0,0223 | 0,0979 | 0,1608 | 1,0000 | ||
| IBM(-2) | −0,0157 | 0,0499 | 0,0616 | 0,0019 | 0,0675 | 0,1471 | 0,7486 | 1,0000 | |
| IBS(-2) | −0,0335 | 0,0342 | 0,0180 | −0,0009 | 0,0850 | 0,1262 | 0,6037 | 0,7037 | 1,0000 |
Los términos IB, IBM e IBS hacen referencia a los índices IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente.
La aplicación de un modelo GARCH multivariante para analizar la volatilidad tiene la principal ventaja de que permite la iteracción de las varianzas condicionales y las covarianzas de las series en su estimación. Pagan (1984) demostró que este procedimiento elimina el problema asociado a las regresiones que genera la estimación en dos etapas que es utilizado en múltiples estudios. Cada ecuación de un modelo GARCH multivariante muestra cómo se transmiten los shocks y la volatilidad, en nuestro caso a través de los índices referentes de empresas de diferentes tamaños, además de mostrar la persistencia de la volatilidad en cada segmento. En relación con otros trabajos Cifarelli y Paladino (2005) sugieren que la metodología multivariante es más complicada de utilizar que la de los vectores autorregresivos (VAR) pero que, sin embargo, proporciona la información necesaria sobre la evolución de la volatilidad y su transmisión.
Existen dos procedimientos para realizar el análisis multivariante. El primero de ellos es el modelo VECH, diseñado por Bollerslev et al (1988), que se expresa como
donde Ht es la matriz de la varianza condicional de tamaño (N×N), siendo N el número de variables a introducir en el modelo; Ω representa un vector de tamaño (N (N+1)/2) × 1, A y B son matrices (N (N+1)/2) × (N (N+1)/2) y el operador VECH es un vector (N (N+1)/2) × 1.Una alternativa al modelo VECH es el modelo BEKK, que toma su nombre de las iniciales de sus creadores, Baba et al (1991). Tomado como una mejora del modelo VECH, tal y como consideran Hassan y Malik (2007), este modelo está diseñado de tal forma que la matriz de varianzas covarianzas cumple el requisito de no estimar varianzas negativas.
La matriz de covarianzas del modelo BEKK se calcula a partir de la expresión:
donde, en nuestro caso, C es una matriz (3×3) triangular inferior con seis parámetros a estimar, A y B son matrices de tamaño (3×3) que capturan, la primera de ellas, los efectos de los shocks en la volatilidad y la segunda los efectos de las varianzas condicionales retardadas, midiendo la diagonal principal de ambas los efectos de los propios shocks y varianzas, respectivamente. El número total de elementos estimados en nuestro caso, al ser utilizado un modelo trivariante, es de 24.Las varianzas condicionales se pueden expresar desarrollando las matrices como:
Sin embargo, las conclusiones alcanzadas con el modelo anterior acerca de la transmisión de información de las variables, la persistencia de la volatilidad o la formación de carteras de mínimo riesgo pueden no ser correctas si no se consideran la existencia de cambios estructurales en la varianza o las asimetrías producidas por la diferente respuesta de la volatilidad a los shocks negativos (malas noticias) o a los shocks positivos (buenas noticias). Por ello, y en orden a contrastar los resultados obtenidos en la estimación inicial, hemos considerado un modelo GARCH multivariante contemplando estos dos aspectos.
En el caso de los cambios estructurales, estos han sido definidos siguiendo la metodología del algoritmo ICSS desarrollado por Inclan y Tiao (1994), y utilizado por Aggarwal et al (1999), Malik (2003), y Ewing y Malik (2005).
La metodología asume que la serie temporal sigue una varianza estacionaria desde el período inicial hasta un momento en el que se produce un cambio repentino en la varianza. Una vez pasado el cambio la varianza vuelve a ser estacionaria hasta que se produce el siguiente cambio y así sucesivamente. Este proceso reporta una serie temporal con un número desconocido de cambios en la varianza.
Consideremos ¿t como una serie con media cero y varianza incondicional σt2. Consideremos la varianza dentro del intervalo dado por σj2, j=0, 1,..., NT donde NT es el número total de cambios en la varianza en T observaciones y 1<κ1<κ2<…<κNT
Para determinar el número exacto de cambios estructurales y el punto exacto en el que se producen se utiliza una suma acumulativa de cuadrados de residuos. De este modo Ck=∑t=1kεt2, k=1,…,T representa la suma acumulativa de cuadrados desde el inicio de la serie hasta el punto k, donde k es un posible cambio estructural y T es el número total de observaciones. A partir de este estadístico se calcula Dk como:
donde CT es la suma de los residuos al cuadrado del período completo.Si no existen cambios en la varianza el estadístico Dk oscila alrededor de 0. Sin embargo, si la serie contiene cambios en la varianza el estadístico toma valores significativamente diferentes a 0. El valor crítico basado en la distribución de Dk bajo la hipótesis de una varianza homogénea al 95% de nivel de confianza es de±1.36. De este modo si el valor de maxk(T/2)|Dk| excede el límite estaremos ante un cambio estructural en la varianzab.
En el caso de la consideración de las asimetrías existen diferentes posibilidades, tal y como muestran los trabajos de Aragó y Fernández (2007), Chuliá y Torró (2007) y Li y Majerowska (2008), sin embargo nosotros hemos optado por utilizar una variante de la especificación asimétrica de Glosten et al (1993), más conocida con GJR-GARCH.
De esta forma, el modelo que se utiliza y que considera tanto el efecto de las asimetrías como de los cambios estructurales queda como:
donde Iεt−1<0 en un vector 3×1 cuyos elementos toman el valor de 1 si la perturbación o shock en ¿t es negativa, ⊙ es el resultado del producto Hadamard (elemento a elemento), D es una matriz diagonal de parámetros de tamaño (3×3), X es un vector (1×3) que representa las dummys para cada serie representativa de cada cambio estructural, tomando el valor de 1 desde el momento del cambio hasta el final y 0 en caso contrario; finalmente, n es el número de cambios estructurales encontrados (en nuestro caso toma el valor de 3 dado que ese es el número de cambios que ha sido encontrado en cada serie).La función de máxima verosimilitud es maximizada suponiendo una distribución normal de los errores:
donde T es el número de observaciones y representa el vector de parámetros a estimar.4Resultados empíricosUno de nuestros primeros objetivos es analizar la transmisión de información entre las grandes, medias y pequeñas empresas del mercado bursátil español representadas por los índices IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente.
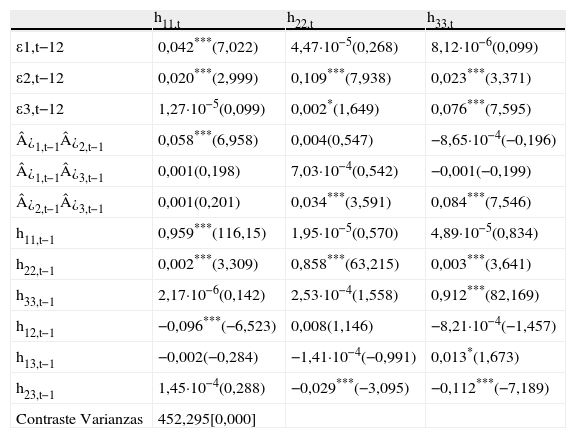
Los resultados de la estimación GARCH multivariante inicial, presentados en la tabla 3, muestran cómo en todos los casos la varianza condicional de los tres tipos de empresas están influenciados por su propia volatilidad y shocks retardados un período.
Modelo GARCH trivariante simétrico
| h11,t | h22,t | h33,t | |
| ε1,t−12 | 0,042***(7,022) | 4,47·10−5(0,268) | 8,12·10−6(0,099) |
| ε2,t−12 | 0,020***(2,999) | 0,109***(7,938) | 0,023***(3,371) |
| ε3,t−12 | 1,27·10−5(0,099) | 0,002*(1,649) | 0,076***(7,595) |
| ¿1,t−1¿2,t−1 | 0,058***(6,958) | 0,004(0,547) | −8,65·10−4(−0,196) |
| ¿1,t−1¿3,t−1 | 0,001(0,198) | 7,03·10−4(0,542) | −0,001(−0,199) |
| ¿2,t−1¿3,t−1 | 0,001(0,201) | 0,034***(3,591) | 0,084***(7,546) |
| h11,t−1 | 0,959***(116,15) | 1,95·10−5(0,570) | 4,89·10−5(0,834) |
| h22,t−1 | 0,002***(3,309) | 0,858***(63,215) | 0,003***(3,641) |
| h33,t−1 | 2,17·10−6(0,142) | 2,53·10−4(1,558) | 0,912***(82,169) |
| h12,t−1 | −0,096***(−6,523) | 0,008(1,146) | −8,21·10−4(−1,457) |
| h13,t−1 | −0,002(−0,284) | −1,41·10−4(−0,991) | 0,013*(1,673) |
| h23,t−1 | 1,45·10−4(0,288) | −0,029***(−3,095) | −0,112***(−7,189) |
| Contraste Varianzas | 452,295[0,000] |
Los subíndices 1, 2 y 3 hacen referencia a los ÍNDICES IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente. Los valores de los estadísticos t aparecen entre paréntesis. Los valores de las probabilidades asociadas a los contrastes de bondad de ajuste del modelo aparecen entre corchetes.
***, ** y * denotan niveles de significatividad del 1, 5 y 10% respectivamente.
Resulta igualmente significativa la estrecha relación entre las empresas medianas y pequeñas, ya que la varianza condicional de las medianas está significativamente influenciada, de forma directa e indirecta, por los shocks que se producen en las empresas pequeñas y de forma indirecta por la volatilidad de estas. Por su parte, las empresas pequeñas se ven influenciadas de forma significativa por la volatilidad y los shocks de las medianas tanto de forma directa como indirecta, al igual que las empresas grandes. Estas últimas apenas ejercen influencia sobre las medianas y las pequeñas, dado que únicamente es significativo el coeficiente que hace referencia a la influencia indirecta de su volatilidad su volatilidad en la volatilidad condicional de las pequeñas empresas.
Finalmente, señalar que siguiendo a Pardo y Torró (2007)c se analiza la hipótesis nula de restricción en los efectos de la varianza cruzada (H0: a12=a21=a13=a31=a23=a32=b12=b21=b13=b31=b23=b32), aparece en la tabla 3 como “Contraste Varianzas”, que es claramente rechazada por lo que no se puede ignorar la existencia de transmisión de información entre las variables.
Como se señaló al inicio del trabajo conocer las relaciones entre los índices tiene implicaciones económicas relativas a la creación de carteras de inversión óptimas. La matriz de covarianzas entre los índices calculada a partir del modelo multivariante anterior permite determinar, siguiendo la metodología empleada por Kroner y Ng (1998), Ewing y Malik (2005) y Hassan y Malik (2007), una cartera de mínimo riesgo tomando los índices como activos donde, si se asume que la rentabilidad esperada es cero, la ponderación del primer sector (ϖ12,t) con respecto al segundo en un momento t correspondería a la expresión:
donde h11,t es la varianza condicional del primer índice, h22,t es la varianza condicional del segundo índice y h12,t representa la covarianza entre los dos índices.Considerando, por tanto, una cartera que combine dos índices y asumiendo una función de utilidad de media-varianza, las ponderaciones óptimas del primer índice en la cartera de mínimo riesgo corresponderían a:
En consecuencia la ponderación en la cartera para el segundo índice sería de 1 – ϖ12,t.
A partir de los datos anteriores también se calcula el ratio de cobertura siguiendo la metodología de Kroner y Sultan (1993) quienes demostraron que para minimizar el riesgo de una cartera un inversor debería poner a corto $β del segundo índice, siendo βt=h12,th22,t, a la vez que se pone $1 a largo en el primer índice.
Los resultados de estas estimaciones, hechas sobre el modelo de volatilidad inicial, junto con las realizadas de la rentabilidad y riesgod de cada cartera (calculados ambos a partir de las expresiones del modelo de Markowitz para carteras de dos activos utilizando las ponderaciones óptimas que se extraen de la expresión 9) se muestran en la tabla 4.
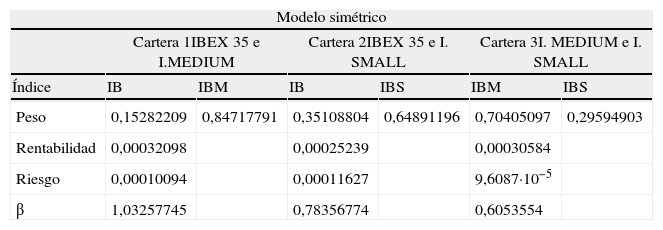
Carteras de mínimo riesgo óptimas
| Modelo simétrico | ||||||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Índice | IB | IBM | IB | IBS | IBM | IBS |
| Peso | 0,15282209 | 0,84717791 | 0,35108804 | 0,64891196 | 0,70405097 | 0,29594903 |
| Rentabilidad | 0,00032098 | 0,00025239 | 0,00030584 | |||
| Riesgo | 0,00010094 | 0,00011627 | 9,6087·10−5 | |||
| β | 1,03257745 | 0,78356774 | 0,6053554 | |||
Los términos IB, IBM e IBS hacen referencia a los índices IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente.
En el mismo se puede observar cómo la cartera de mínimo riesgo (9,6087·10-5) está compuesta por la combinación de los índices que hacen referencia a las medianas y pequeñas empresas donde el mayor peso en media corresponde al índice IBEX MEDIUM CAP (70,40%) frente a un 29,60% del IBEX SMALL CAP.
Por otro lado, la cartera con mayor rentabilidad (0,00032098) corresponde a aquella donde se combinan el índice IBEX 35 y el índice IBEX MEDIUM CAP donde, también, el mayor peso corresponde al índice relativo a las medianas empresas (84,72%) frente a un 15,28% del IBEX 35. En el lado contrario, la cartera que proporciona menor rentabilidad y mayor riesgo es la formada por los índices IBEX 35 e IBEX SMALL CAP donde la mayor ponderación corresponde al índice representativo de las pequeñas empresas (64,90% frente a 35,10%). En cuanto a los ratios de cobertura, el menor valor corresponde a la cartera de mínimo riesgo (0,6053).
Los resultados obtenidos relativos a la importancia de las medianas empresas resultan consistentes con su baja volatilidad expuesta en los estadísticos básicos y con el hecho de que su varianza condicional se encuentra menos afectada que las otras por las informaciones externas y, en todo caso, las influencias que recibe provienen de las pequeñas empresas con las que conforma la cartera de mínimo riesgo.
La evidencia empírica anterior no profundizaba más que lo expuesto en las implicaciones económicas, sin embargo, en este trabajo consideramos que resultaría interesante comprobar si la formación de la cartera de mínimo riesgo obtenida está condicionada por las diferentes noticias (positivas o negativas) que se suceden en cada índice.
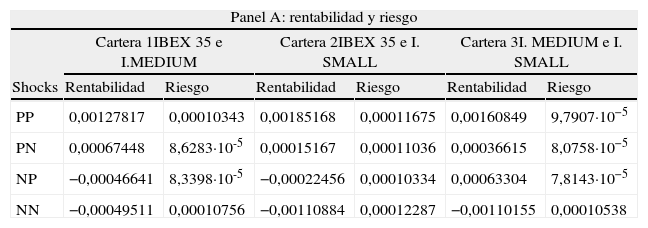
Por esa razón se agrupan los valores de las ponderaciones, rentabilidades y riesgos óptimos en función de cuatro escenarios diferentes: Buenas noticias, donde solo se consideran aquellos elementos que estén precedidos de shocks positivos (PP) en ambos índices (¿1,t−1>0;¿2,t−1>0); Noticias normales, producidas cuando uno de los shocks previos es negativo siendo contempladas, en este caso, dos posibilidades: positivo-negativo, PN, (¿1,t−1>0;¿2,t−1<0) y negativo-positivo, NP, (¿1,t−1<0;¿2,t−1>0); y, finalmente, Malas noticias, cuando los shocks previos de los dos índices por utilizar son negativos, NN, (¿1,t−1<0;¿2,t−1<0). Los subíndices 1 y 2 hacen referencia al primer y segundo índice utilizado en cada pareja de índices tal y como se muestra en la tabla 5 donde se presentan los resultados de las estimaciones realizadas.
Carteras óptimas en función de las noticias (2 shocks)
| Panel A: rentabilidad y riesgo | ||||||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Shocks | Rentabilidad | Riesgo | Rentabilidad | Riesgo | Rentabilidad | Riesgo |
| PP | 0,00127817 | 0,00010343 | 0,00185168 | 0,00011675 | 0,00160849 | 9,7907·10−5 |
| PN | 0,00067448 | 8,6283·10-5 | 0,00015167 | 0,00011036 | 0,00036615 | 8,0758·10−5 |
| NP | −0,00046641 | 8,3398·10-5 | −0,00022456 | 0,00010334 | 0,00063304 | 7,8143·10−5 |
| NN | −0,00049511 | 0,00010756 | −0,00110884 | 0,00012287 | −0,00110155 | 0,00010538 |
| Panel B: Ponderaciones de las carteras | ||||||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Shocks | IB | IBM | IB | IBS | IBM | IBS |
| PP | 0,14184603 | 0,85815397 | 0,35863634 | 0,64136366 | 0,7095475 | 0,2904525 |
| PN | 0,14540456 | 0,85459544 | 0,32094073 | 0,67905927 | 0,671476 | 0,328524 |
| NP | 0,16735917 | 0,83264083 | 0,34305067 | 0,65694933 | 0,67359409 | 0,32640591 |
| NN | 0,16174541 | 0,83825459 | 0,35799933 | 0,64200067 | 0,7195329 | 0,2804671 |
| Panel C: ratios de cobertura | |||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | |
| SHOCKS | β | β | β |
| PP | 1,0472933 | 0,79674864 | 0,62451759 |
| PN | 0,98169207 | 0,72820924 | 0,54483644 |
| NP | 0,96974256 | 0,71627892 | 0,54397231 |
| NN | 1,05012412 | 0,81668029 | 0,62710212 |
Los términos IB, IBM e IBS hacen referencia a los índices IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente.
Se analizan cuatro escenarios diferentes: Buenas noticias, donde solo se consideran aquellos elementos que estén precedidos de shocks positivos (PP) en ambos índices (¿1,t−1>0;¿2,t−1>0); Noticias normales, producidas cuando uno de los shocks previos es negativo siendo contempladas, en este caso, dos posibilidades: positivo-negativo, PN, (¿1,t−1>0;¿2,t−1<0) y negativo-positivo, NP, (¿1,t−1<0;¿2,t−1>0); y, finalmente, Malas noticias, cuando los shocks previos de los dos índices a utilizar son negativos, NN, (¿1,t−1<0;¿2,t−1<0).
P y N representan los shocks previos positivos y negativos, respectivamente siguiendo el orden de la composición de cada cartera.
En el Panel A de la tabla 5 se observa que para todos los casos posibles, ya sean las noticias buenas o malas, la cartera de mínimo riesgo es aquella formada por las pequeñas y medianas empresas, siendo incluso en un caso (aquel donde se combina un shock del IBEX MEDIUM negativo junto con un shock del IBEX SMALL positivo) la cartera que proporciona una rentabilidad mayor (en los otros casos es la segunda mejor). Con respecto a los pesos en las carteras y los ratios de cobertura, que se muestran en los paneles B y C respectivamente, no encontramos cambios significativos con los expuestos para el conjunto de las estimaciones mostradas en la tabla anterior.
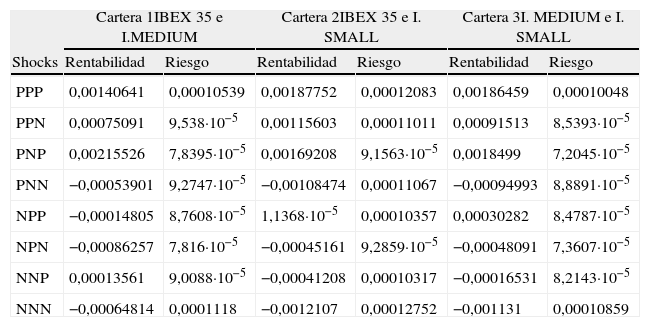
Adicionalmente, y con el objeto de contrastar la robustez de los resultados obtenidos se agrupan los valores de las ponderaciones, rentabilidades y riesgos realizados para el conjunto de los datos en función de las noticias previas de los tres índices. De este modo se contemplan 8 escenarios diferentes: Todos los shocks previos son positivos, PPP, (¿1,t−1>0;¿2,t−1>0;¿3,t−1>0); los dos primeros positivos y el tercero negativo, PPN, (¿1,t−1>0;¿2,t−1>0;¿3,t−1<0); el primero y el tercero positivo y el segundo negativo, PNP, (¿1,t−1>0;¿2,t−1<0;¿3,t−1>0); el primero positivo y los otros negativos, PNN, (¿1,t−1>0;¿2,t−1<0;¿3,t−1<0); el primero negativo y los otros positivos, NPP, (¿1,t−1<0;¿2,t−1>0;¿3,t−1>0); el primero y el tercero negativos y el segundo positivo, NPN, (¿1,t−1<0;¿2,t−1>0;¿3,t−1<0); los dos primeros negativos y el tercero positivo, NNP, (¿1,t−1<0;¿2,t−1<0;¿3,t−1>0); y, finalmente, todos negativos, NNN, (¿1,t−1<0;¿2,t−1<0;¿3,t−1<0). Al igual que en el caso anterior, los subíndices 1, 2 y 3 hacen referencia al primer, segundo y tercer índice utilizado en cada pareja de índices tal y como se muestra en la tabla 6 donde se presentan los resultados de las estimaciones realizadas.
Carteras óptimas en función de las noticias (3 shocks)
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Shocks | Rentabilidad | Riesgo | Rentabilidad | Riesgo | Rentabilidad | Riesgo |
| PPP | 0,00140641 | 0,00010539 | 0,00187752 | 0,00012083 | 0,00186459 | 0,00010048 |
| PPN | 0,00075091 | 9,538·10−5 | 0,00115603 | 0,00011011 | 0,00091513 | 8,5393·10−5 |
| PNP | 0,00215526 | 7,8395·10−5 | 0,00169208 | 9,1563·10−5 | 0,0018499 | 7,2045·10−5 |
| PNN | −0,00053901 | 9,2747·10−5 | −0,00108474 | 0,00011067 | −0,00094993 | 8,8891·10−5 |
| NPP | −0,00014805 | 8,7608·10−5 | 1,1368·10−5 | 0,00010357 | 0,00030282 | 8,4787·10−5 |
| NPN | −0,00086257 | 7,816·10−5 | −0,00045161 | 9,2859·10−5 | −0,00048091 | 7,3607·10−5 |
| NNP | 0,00013561 | 9,0088·10−5 | −0,00041208 | 0,00010317 | −0,00016531 | 8,2143·10−5 |
| NNN | −0,00064814 | 0,0001118 | −0,0012107 | 0,00012752 | −0,001131 | 0,00010859 |
Se contemplan 8 escenarios diferentes: Todos los shocks previos son positivos, PPP, (¿1,t−1>0;¿2,t−1>0;¿3,t−1>0); los dos primeros positivos y el tercero negativo, PPN, (¿1,t−1>0;¿2,t−1>0;¿3,t−1<0); el primero y el tercero positivo y el segundo negativo, PNP, (¿1,t−1>0;¿2,t−1<0;¿3,t−1>0); el primero positivo y los otros negativos, PNN, (¿1,t−1>0;¿2,t−1<0;¿3,t−1<0); el primero negativo y los otros positivos, NPP, (¿1,t−1<0;¿2,t−1>0;¿3,t−1>0); el primero y el tercero negativos y el segundo positivo, NPN, (¿1,t−1<0;¿2,t−1>0;¿3,t−1<0); los dos primeros negativos y el tercero positivo, NNP, (¿1,t−1<0;¿2,t−1<0;¿3,t−1>0); y, finalmente, todos negativos, NNN, (¿1,t−1<0;¿2,t−1<0;¿3,t−1<0).
P y N representan los shocks previos positivos y negativos, respectivamente siguiendo el orden: IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP.
Los resultados expuestos en dicha tabla confirman los obtenidos anteriormente, ya que en todos los casos posibles el menor riesgo proviene de la cartera formada por los índices que hacen referencia a las pequeñas y medianas empresase.
Los resultados anteriores, no obstante, pueden estar sobreestimados si no se tienen en cuenta la posible existencia de cambios estructurales y el comportamiento asimétrico de la volatilidad. Ewing y Malik (2005) comparan los resultados de la transmisión de información entre dos carteras de mayor y menor capitalización en el mercado bursátil norteamericano utilizando un modelo GARCH Bivariante frente a otro donde se consideraba la existencia de cambios estructurales. En dicho trabajo llegan a la conclusión de que la consideración de los cambios estructurales reduce significativamente la transmisión de volatilidad entre las carteras, por lo que si estos no son tenidos en cuenta se estaría sobreestimando la relación entre las carteras.
Por otra parte existen numerosos trabajos, como los de Pardo y Torró (2007), Chuliá y Torró (2007) o Karmakar (2010), donde se emplean modelos GARCH multivariantes asimétricos dado que se considera que la volatilidad responde de forma asimétrica a las buenas y malas noticias de igual magnitud, de forma que la volatilidad condicional tiende a crecer más ante un shock negativo que ante uno positivo.
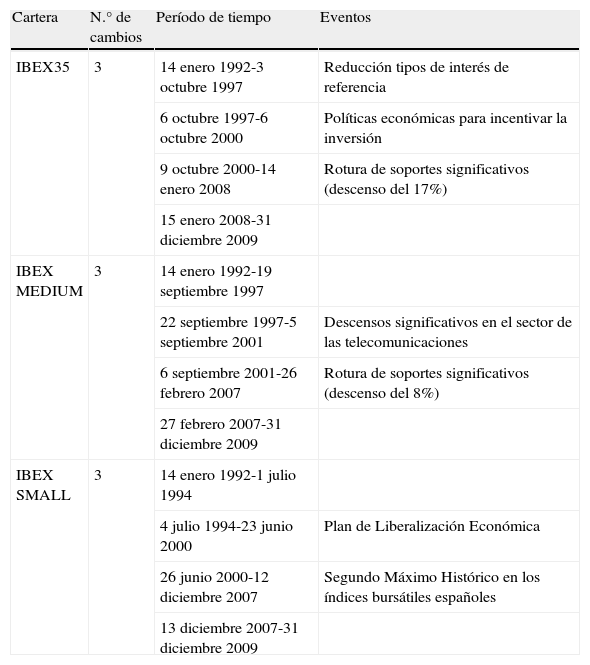
El análisis de las series para determinar la existencia de cambios estructurales mediante la metodología ICSS antes descrita denota la existencia de 3 cambios estructurales en cada índice, tal y como se muestra en la tabla 7, correspondiendo la mayoría de ellos a la respuesta de los mercados ante la toma de diferentes medidas económicas para potenciar el crecimiento económico. De este modo el índice IBEX 35 se ve afectado por la reducción de los tipos de interés de referencia o la toma de medidas económicas, por parte del gobierno, para incentivar la inversión mientras que el índice IBEX SMALL CAP, por ejemplo, presenta un cambio estructural cuando se toman las medidas económicas del Plan de Liberalización de junio de 2000.
Cambios estructurales en la volatilidad
| Cartera | N.° de cambios | Período de tiempo | Eventos |
| IBEX35 | 3 | 14 enero 1992-3 octubre 1997 | Reducción tipos de interés de referencia |
| 6 octubre 1997-6 octubre 2000 | Políticas económicas para incentivar la inversión | ||
| 9 octubre 2000-14 enero 2008 | Rotura de soportes significativos (descenso del 17%) | ||
| 15 enero 2008-31 diciembre 2009 | |||
| IBEX MEDIUM | 3 | 14 enero 1992-19 septiembre 1997 | |
| 22 septiembre 1997-5 septiembre 2001 | Descensos significativos en el sector de las telecomunicaciones | ||
| 6 septiembre 2001-26 febrero 2007 | Rotura de soportes significativos (descenso del 8%) | ||
| 27 febrero 2007-31 diciembre 2009 | |||
| IBEX SMALL | 3 | 14 enero 1992-1 julio 1994 | |
| 4 julio 1994-23 junio 2000 | Plan de Liberalización Económica | ||
| 26 junio 2000-12 diciembre 2007 | Segundo Máximo Histórico en los índices bursátiles españoles | ||
| 13 diciembre 2007-31 diciembre 2009 |
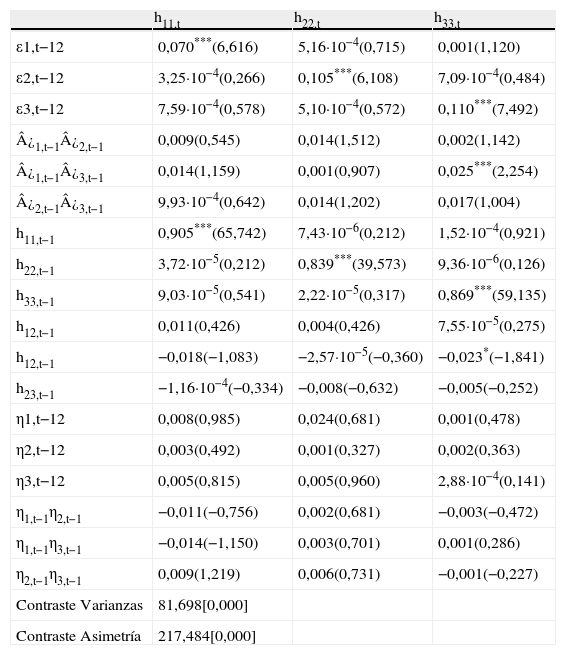
Una vez considerados estos cambios estructurales en el modelo multivariante junto con las asimetrías representadas como ηiηj observamos cómo, tal y como se había previsto, la transmisión de volatilidad se ve considerablemente reducida (ver tabla 8) entre las empresas grandes, medianas y pequeñas. Las volatilidades condicionales de las empresas grandes y medianas se encuentran únicamente influenciadas por sus propias volatilidades condicionales y sus shocks retardados un período, mientras que la volatilidad condicional de las empresas pequeñas se ve influenciada de forma directa por su propia volatilidad y shock retardados un período y de forma indirecta por la volatilidad y las innovaciones de las empresas grandes.
Modelo GARCH multivariante asimétrico con cambios estructurales
| h11,t | h22,t | h33,t | |
| ε1,t−12 | 0,070***(6,616) | 5,16·10−4(0,715) | 0,001(1,120) |
| ε2,t−12 | 3,25·10−4(0,266) | 0,105***(6,108) | 7,09·10−4(0,484) |
| ε3,t−12 | 7,59·10−4(0,578) | 5,10·10−4(0,572) | 0,110***(7,492) |
| ¿1,t−1¿2,t−1 | 0,009(0,545) | 0,014(1,512) | 0,002(1,142) |
| ¿1,t−1¿3,t−1 | 0,014(1,159) | 0,001(0,907) | 0,025***(2,254) |
| ¿2,t−1¿3,t−1 | 9,93·10−4(0,642) | 0,014(1,202) | 0,017(1,004) |
| h11,t−1 | 0,905***(65,742) | 7,43·10−6(0,212) | 1,52·10−4(0,921) |
| h22,t−1 | 3,72·10−5(0,212) | 0,839***(39,573) | 9,36·10−6(0,126) |
| h33,t−1 | 9,03·10−5(0,541) | 2,22·10−5(0,317) | 0,869***(59,135) |
| h12,t−1 | 0,011(0,426) | 0,004(0,426) | 7,55·10−5(0,275) |
| h12,t−1 | −0,018(−1,083) | −2,57·10−5(−0,360) | −0,023*(−1,841) |
| h23,t−1 | −1,16·10−4(−0,334) | −0,008(−0,632) | −0,005(−0,252) |
| η1,t−12 | 0,008(0,985) | 0,024(0,681) | 0,001(0,478) |
| η2,t−12 | 0,003(0,492) | 0,001(0,327) | 0,002(0,363) |
| η3,t−12 | 0,005(0,815) | 0,005(0,960) | 2,88·10−4(0,141) |
| η1,t−1η2,t−1 | −0,011(−0,756) | 0,002(0,681) | −0,003(−0,472) |
| η1,t−1η3,t−1 | −0,014(−1,150) | 0,003(0,701) | 0,001(0,286) |
| η2,t−1η3,t−1 | 0,009(1,219) | 0,006(0,731) | −0,001(−0,227) |
| Contraste Varianzas | 81,698[0,000] | ||
| Contraste Asimetría | 217,484[0,000] |
Los subíndices 1, 2 y 3 hacen referencia a los ÍNDICES IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente. Los valores de los estadísticos t aparecen entre paréntesis. Los valores de las probabilidades asociadas a los contrastes de bondad de ajuste del modelo aparecen entre corchetes.
***, ** y * denotan niveles de significatividad del 1, 5 y 10% respectivamente.
En ninguno de los casos posibles los coeficientes asociados con los shocks negativos que analizan la transmisión de información asimétrica resultan significativos por lo que no existe un efecto apalancamiento provocado por los shocks negativos. Estos resultados difieren, pues, de los obtenidos por Chuliá y Torró (2007) y Pardo y Torró (2007), que mostraron una mayor transmisión de información entre las empresas grandes y pequeñas en el mercado bursátil español, pudiendo estar la explicación, tal y como apuntan Chuliá y Torró (2007) en relación con sus diferencias con los resultados obtenidos previamente por Pardo y Torró (2007), en que tanto la muestra como la metodología son diferentes.
La importancia de considerar las asimetrías está apoyada por el valor del ratio del estadístico de máxima verosimilitud (LR, Likelihood Ratio) que se calcula como LR=2[L(Θ1) – L(Θ0)] donde L(Θ1) y L(Θ0) son los valores del estadístico de máxima verosimilitud obtenidos de los modelos simétrico y asimétrico, respectivamente. Este estadístico, que sigue una distribución χ2 toma el valor LR=2(46960,73-46921,07)=79,32, por lo que claramente podemos rechazar la hipótesis nula de que no existen cambios en la varianza.
Nuevamente se analiza la hipótesis nula de restricción en los efectos de la varianza cruzada (H0: a12=a21=a13=a31=a23=a32=b12=b21=b13=b31=b23=b32) que es claramente rechazada, por lo que no se puede ignorar la existencia de transmisión de información entre las variables. Igualmente es rechazada la hipótesis de la irrelevancia de los elementos asimétricos (H0: η11=η22=η33=η12=η21=η31=η23=η23=η32), especificada en la tabla como «Contraste Asimetrías», por los que los efectos asimétricos de las buenas y malas noticias no pueden ser ignorados.
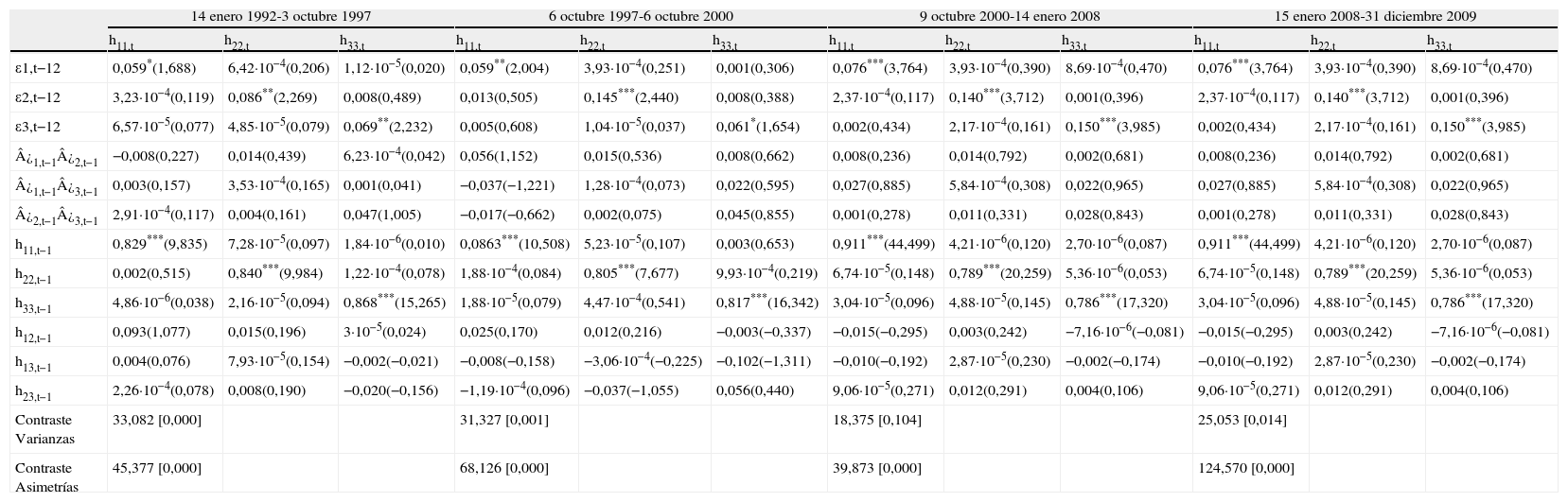
Con objeto de evaluar la robustez del modelo se estimó el mismo en cada uno de los períodos determinados conforme a los cambios estructurales, obteniéndose en todos y cada uno de ellos, tal y como se muestra en la tabla 9, los mismos niveles de transmisión de información y los mismos resultados en cuanto a la contrastación de la bondad del ajuste.
Modelo GARCH multivariante asimétrico con cambios estructurales por subperiodos
| 14 enero 1992-3 octubre 1997 | 6 octubre 1997-6 octubre 2000 | 9 octubre 2000-14 enero 2008 | 15 enero 2008-31 diciembre 2009 | |||||||||
| h11,t | h22,t | h33,t | h11,t | h22,t | h33,t | h11,t | h22,t | h33,t | h11,t | h22,t | h33,t | |
| ε1,t−12 | 0,059*(1,688) | 6,42·10−4(0,206) | 1,12·10−5(0,020) | 0,059**(2,004) | 3,93·10−4(0,251) | 0,001(0,306) | 0,076***(3,764) | 3,93·10−4(0,390) | 8,69·10−4(0,470) | 0,076***(3,764) | 3,93·10−4(0,390) | 8,69·10−4(0,470) |
| ε2,t−12 | 3,23·10−4(0,119) | 0,086**(2,269) | 0,008(0,489) | 0,013(0,505) | 0,145***(2,440) | 0,008(0,388) | 2,37·10−4(0,117) | 0,140***(3,712) | 0,001(0,396) | 2,37·10−4(0,117) | 0,140***(3,712) | 0,001(0,396) |
| ε3,t−12 | 6,57·10−5(0,077) | 4,85·10−5(0,079) | 0,069**(2,232) | 0,005(0,608) | 1,04·10−5(0,037) | 0,061*(1,654) | 0,002(0,434) | 2,17·10−4(0,161) | 0,150***(3,985) | 0,002(0,434) | 2,17·10−4(0,161) | 0,150***(3,985) |
| ¿1,t−1¿2,t−1 | −0,008(0,227) | 0,014(0,439) | 6,23·10−4(0,042) | 0,056(1,152) | 0,015(0,536) | 0,008(0,662) | 0,008(0,236) | 0,014(0,792) | 0,002(0,681) | 0,008(0,236) | 0,014(0,792) | 0,002(0,681) |
| ¿1,t−1¿3,t−1 | 0,003(0,157) | 3,53·10−4(0,165) | 0,001(0,041) | −0,037(−1,221) | 1,28·10−4(0,073) | 0,022(0,595) | 0,027(0,885) | 5,84·10−4(0,308) | 0,022(0,965) | 0,027(0,885) | 5,84·10−4(0,308) | 0,022(0,965) |
| ¿2,t−1¿3,t−1 | 2,91·10−4(0,117) | 0,004(0,161) | 0,047(1,005) | −0,017(−0,662) | 0,002(0,075) | 0,045(0,855) | 0,001(0,278) | 0,011(0,331) | 0,028(0,843) | 0,001(0,278) | 0,011(0,331) | 0,028(0,843) |
| h11,t−1 | 0,829***(9,835) | 7,28·10−5(0,097) | 1,84·10−6(0,010) | 0,0863***(10,508) | 5,23·10−5(0,107) | 0,003(0,653) | 0,911***(44,499) | 4,21·10−6(0,120) | 2,70·10−6(0,087) | 0,911***(44,499) | 4,21·10−6(0,120) | 2,70·10−6(0,087) |
| h22,t−1 | 0,002(0,515) | 0,840***(9,984) | 1,22·10−4(0,078) | 1,88·10−4(0,084) | 0,805***(7,677) | 9,93·10−4(0,219) | 6,74·10−5(0,148) | 0,789***(20,259) | 5,36·10−6(0,053) | 6,74·10−5(0,148) | 0,789***(20,259) | 5,36·10−6(0,053) |
| h33,t−1 | 4,86·10−6(0,038) | 2,16·10−5(0,094) | 0,868***(15,265) | 1,88·10−5(0,079) | 4,47·10−4(0,541) | 0,817***(16,342) | 3,04·10−5(0,096) | 4,88·10−5(0,145) | 0,786***(17,320) | 3,04·10−5(0,096) | 4,88·10−5(0,145) | 0,786***(17,320) |
| h12,t−1 | 0,093(1,077) | 0,015(0,196) | 3·10−5(0,024) | 0,025(0,170) | 0,012(0,216) | −0,003(−0,337) | −0,015(−0,295) | 0,003(0,242) | −7,16·10−6(−0,081) | −0,015(−0,295) | 0,003(0,242) | −7,16·10−6(−0,081) |
| h13,t−1 | 0,004(0,076) | 7,93·10−5(0,154) | −0,002(−0,021) | −0,008(−0,158) | −3,06·10−4(−0,225) | −0,102(−1,311) | −0,010(−0,192) | 2,87·10−5(0,230) | −0,002(−0,174) | −0,010(−0,192) | 2,87·10−5(0,230) | −0,002(−0,174) |
| h23,t−1 | 2,26·10−4(0,078) | 0,008(0,190) | −0,020(−0,156) | −1,19·10−4(0,096) | −0,037(−1,055) | 0,056(0,440) | 9,06·10−5(0,271) | 0,012(0,291) | 0,004(0,106) | 9,06·10−5(0,271) | 0,012(0,291) | 0,004(0,106) |
| Contraste Varianzas | 33,082 [0,000] | 31,327 [0,001] | 18,375 [0,104] | 25,053 [0,014] | ||||||||
| Contraste Asimetrías | 45,377 [0,000] | 68,126 [0,000] | 39,873 [0,000] | 124,570 [0,000] | ||||||||
Los subíndices 1, 2 y 3 hacen referencia a los ÍNDICES IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente. Los valores de los estadísticos t aparecen entre paréntesis. Los valores de las probabilidades asociadas a los contrastes de bondad de ajuste del modelo aparecen entre corchetes.
***, ** y * denotan niveles de significatividad del 1, 5 y 10% respectivamente.
En ambos contrastes, los pertenecientes tanto al período completo como a cada uno de los cuatro períodos en los que se divide la muestra, se puede comprobar que la persistencia de los modelos está suficientemente alejada de 1, resultado que está en línea con los encontrados por Olmeda y Pérez (1995), por lo que se cumple la condición de estacionariedad de los mismos.
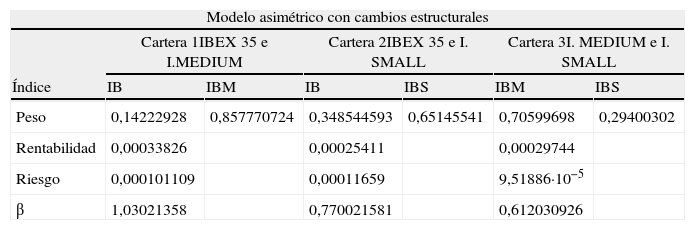
En cuanto a los efectos de la nueva matriz de covarianzas sobre las carteras de mínimo riesgo, la tabla 10 muestra cómo una vez más la cartera de mínimo riesgo se obtiene combinando las medianas y pequeñas empresas siendo, además, el único caso en el que el riesgo disminuye.
Carteras de mínimo riesgo óptimas
| Modelo asimétrico con cambios estructurales | ||||||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Índice | IB | IBM | IB | IBS | IBM | IBS |
| Peso | 0,14222928 | 0,857770724 | 0,348544593 | 0,65145541 | 0,70599698 | 0,29400302 |
| Rentabilidad | 0,00033826 | 0,00025411 | 0,00029744 | |||
| Riesgo | 0,000101109 | 0,00011659 | 9,51886·10−5 | |||
| β | 1,03021358 | 0,770021581 | 0,612030926 | |||
Los términos IB, IBM e IBS hacen referencia a los ÍNDICES IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente.
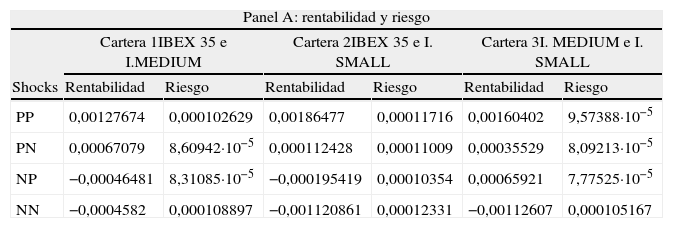
Esta situación se mantiene cuando se agrupan las carteras de mínimo riesgo en el nuevo contexto, considerando cada uno de los escenarios referentes a los shocks previos de los dos activos que componen la cartera o de los tres activos en su conjunto, tal y como se muestra en las tablas 11 y 12. En las mismas se puede observar cómo en todos los casos la cartera de mínimo riesgo es, de nuevo, aquella que combina el índice IBEX MEDIUM CAP y el índice IBEX SMALL CAP siendo este riesgo, en la mayoría de los casos, menor al estimado a partir de la matriz de covarianzas obtenida por el modelo GARCH multivariante simétrico.
Carteras óptimas en función de las noticias (2 shocks)
| Panel A: rentabilidad y riesgo | ||||||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Shocks | Rentabilidad | Riesgo | Rentabilidad | Riesgo | Rentabilidad | Riesgo |
| PP | 0,00127674 | 0,000102629 | 0,00186477 | 0,00011716 | 0,00160402 | 9,57388·10−5 |
| PN | 0,00067079 | 8,60942·10−5 | 0,000112428 | 0,00011009 | 0,00035529 | 8,09213·10−5 |
| NP | −0,00046481 | 8,31085·10−5 | −0,000195419 | 0,00010354 | 0,00065921 | 7,77525·10−5 |
| NN | −0,0004582 | 0,000108897 | −0,001120861 | 0,00012331 | −0,00112607 | 0,000105167 |
| Panel B: ponderaciones de las carteras | ||||||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Shocks | IB | IBM | IB | IBS | IBM | IBS |
| PP | 0,12827496 | 0,871725035 | 0,357686184 | 0,64231382 | 0,72097784 | 0,27902216 |
| PN | 0,13021514 | 0,869784864 | 0,319740162 | 0,68025984 | 0,68075749 | 0,31924251 |
| NP | 0,14595126 | 0,854048741 | 0,341586408 | 0,65841359 | 0,68307567 | 0,316924332 |
| NN | 0,15854429 | 0,841455712 | 0,352970203 | 0,6470298 | 0,70705958 | 0,292940422 |
| Panel C: ratios de cobertura | |||
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | |
| Shocks | β | β | β |
| PP | 1,05295116 | 0,79006425 | 0,628563069 |
| PN | 0,98906081 | 0,705483792 | 0,548986206 |
| NP | 0,97312033 | 0,700102409 | 0,545722101 |
| NN | 1,03524195 | 0,800547791 | 0,638666987 |
Los términos IB, IBM e IBS hacen referencia a los ÍNDICES IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP respectivamente.
Se analizan cuatro escenarios diferentes: Buenas noticias, donde solo se consideran aquellos elementos que estén precedidos de shocks positivos (PP) en ambos índices (¿1,t−1>0;¿2,t−1>0); Noticias normales, producidas cuando uno de los shocks previos es negativo siendo contempladas, en este caso, dos posibilidades: positivo-negativo, PN, (¿1,t−1>0;¿2,t−1<0) y negativo-positivo, NP, (¿1,t−1<0;¿2,t−1>0); y, finalmente, Malas noticias, cuando los shocks previos de los dos índices a utilizar son negativos, NN, (¿1,t−1<0;¿2,t−1<0).
P y N representan los shocks previos positivos y negativos, respectivamente siguiendo el orden de la composición de cada cartera.
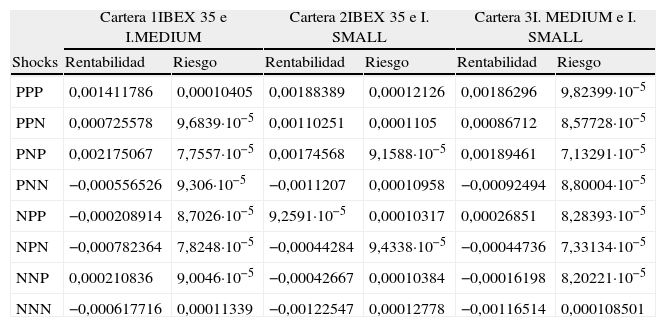
Carteras óptimas en función de las noticias (3 shocks)
| Cartera 1IBEX 35 e I.MEDIUM | Cartera 2IBEX 35 e I. SMALL | Cartera 3I. MEDIUM e I. SMALL | ||||
| Shocks | Rentabilidad | Riesgo | Rentabilidad | Riesgo | Rentabilidad | Riesgo |
| PPP | 0,001411786 | 0,00010405 | 0,00188389 | 0,00012126 | 0,00186296 | 9,82399·10−5 |
| PPN | 0,000725578 | 9,6839·10−5 | 0,00110251 | 0,0001105 | 0,00086712 | 8,57728·10−5 |
| PNP | 0,002175067 | 7,7557·10−5 | 0,00174568 | 9,1588·10−5 | 0,00189461 | 7,13291·10−5 |
| PNN | −0,000556526 | 9,306·10−5 | −0,0011207 | 0,00010958 | −0,00092494 | 8,80004·10−5 |
| NPP | −0,000208914 | 8,7026·10−5 | 9,2591·10−5 | 0,00010317 | 0,00026851 | 8,28393·10−5 |
| NPN | −0,000782364 | 7,8248·10−5 | −0,00044284 | 9,4338·10−5 | −0,00044736 | 7,33134·10−5 |
| NNP | 0,000210836 | 9,0046·10−5 | −0,00042667 | 0,00010384 | −0,00016198 | 8,20221·10−5 |
| NNN | −0,000617716 | 0,00011339 | −0,00122547 | 0,00012778 | −0,00116514 | 0,000108501 |
Se contemplan 8 escenarios diferentes: Todos los shocks previos son positivos, PPP, (¿1,t−1>0;¿2,t−1>0;¿3,t−1>0); Los dos primeros positivos y el tercero negativo, PPN, (¿1,t−1>0;¿2,t−1>0;¿3,t−1<0); el primero y el tercero positivo y el segundo negativo, PNP, (¿1,t−1>0;¿2,t−1<0;¿3,t−1>0); el primero positivo y los otros negativos, PNN, (¿1,t−1>0;¿2,t−1<0;¿3,t−1<0); el primero negativo y los otros positivos, NPP, (¿1,t−1<0;¿2,t−1>0;¿3,t−1>0); el primero y el tercero negativos y el segundo positivo, NPN, (¿1,t−1<0;¿2,t−1>0;¿3,t−1<0); los dos primeros negativos y el tercero positivo, NNP, (¿1,t−1<0;¿2,t−1<0;¿3,t−1>0); y, finalmente, todos negativos, NNN, (¿1,t−1<0;¿2,t−1<0;¿3,t−1<0).
P y N representan los shocks previos positivos y negativos, respectivamente siguiendo el orden: IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP.
Las informaciones referentes a las ponderaciones de cada índice en estas carteras y los ratios de cobertura aparecen en los Paneles B y C de la tabla 11. Los resultados no difieren de la estimación inicial, dado que se mantiene al mayor peso de las empresas medianas en las carteras de mínimo riesgo (en torno al 70% cuando se combina con las empresas pequeñas y en el entorno del 85% cuando se combina con las empresas grandes, que conforman las carteras con segundo menor riesgo en todos los casos).
En lo que se refiere a los ratios de cobertura, la cuantía necesaria para ponerse a corto en los índices IBEX MEDIUM CAP e IBEX SMALL CAP es prácticamente la misma que en la tabla 12 lo que quiere decir que, en este caso, el modelo de volatilidad condicional utilizado no influye significativamente en la cuantía a invertir a corto en cada caso.
Los resultados obtenidos añaden un importante punto de vista a la evidencia empírica previa existente sobre el análisis del efecto tamaño. Banz (1981) y Reinganum (1981) señalaron que las acciones de empresas pequeñas obtenían rendimientos sustancialmente superiores a los de las empresas grandes para periodos largos de inversión. La evidencia empírica actual muestra que el efecto tamaño sigue estando de plena actualidad en numerosos mercados bursátiles. En este sentido hay que destacar que si el estudio de las relaciones en rendimiento entre las empresas de gran tamaño y las empresas de pequeño tamaño merece especial atención, no menos importante es el análisis de la transmisión de volatilidad entre ambas.
Por otro lado, es importante destacar que la internacionalización económica y financiera ha afectado especialmente a las grandes empresas españolas tanto por cotizar en las principales bolsas mundiales como por el proceso de expansión internacional llevado a cabo, en especial en Latinoamérica. Este proceso ha provocado que dichas empresas estén más expuestas a las crisis bursátiles, económicas o sociopolíticas a nivel internacional. Las empresas pequeñas, en cambio, son menos sensibles a las crisis financieras internacionales al depender su actividad económica, en mayor medida, de factores económicos locales. Durante el período de análisis la performance de las medianas y pequeñas empresas en el mercado bursátil español, y como consecuencia los resultados obtenidos en el estudio, ha estado caracterizada por buenas perspectivas de crecimiento. Este hecho ha provocado un aumento del interés de los principales inversores nacionales e internacionales, además de los analistas, en este tipo de compañías, con lo que aumenta su atractivo y se explican los resultados obtenidos.
5ConclusionesEste trabajo analiza la transmisión de información y la formación de carteras de mínimo riesgo entre las empresas grandes, medianas y pequeñas del mercado bursátil español representadas, respectivamente, por los índices bursátiles IBEX 35, IBEX MEDIUM CAP e IBEX SMALL CAP, utilizando para ello una metodología GARCH multivariante.
Los resultados del análisis inicial realizado sobre un modelo GARCH multivariante simétrico muestran la existencia de un elevado grado de transmisión de información entre estas empresas en el mercado bursátil español. Destaca, no obstante, la importancia de las empresas medianas, ya que tanto su volatilidad condicional como sus shocks influyen significativamente de forma tanto directa como indirecta en las empresas grandes y pequeñas. Sin embargo, la posibilidad de que los resultados estuviesen sobreestimados, dado que en la metodología inicial no se contemplaron ni los cambios estructurales en la varianza ni el comportamiento asimétrico de la misma, nos condujo a reestimar el modelo considerando dichos factores. Efectivamente, la transmisión de información disminuye notablemente hasta el punto de que solo se produce una relación unidireccional indirecta de las empresas grandes a las pequeñas.
Otro resultado interesante se produce cuando se analiza la composición de la cartera óptima, ya que, tanto a partir del modelo multivariante simétrico como del modelo en el que se contemplan los cambios estructurales y las asimetrías, la cartera de mínimo riesgo en todos los casos contemplados es aquella formada por las empresas medianas y pequeñas.
Estos resultados son importantes para conocer el comportamiento del mercado de valores español y para la valoración de activos, gestión de carteras y estrategias de cobertura, ya que demuestra la importancia de las medianas y pequeñas empresas frente a las empresas grandes si se desea seguir una estrategia de mínimo riesgo.