El 23 de mayo del año 2015 fue uno de los días más tristes para economistas de todo el mundo pues se esparcía la noticia de la fatídica muerte de un gran matemático: John Forbes Nash Jr. De inmediato se comenzaron a escribir obituarios en su honor por doquier. La academia en nuestro país parece no haberse dado cuenta del suceso, o parece no haberle dado importancia. Las breves palabras siguientes se presentan para contribuir a subsanar este hecho y dar a Nash los honores que merece. Para ello, en principio se rememora su vida, luego se mencionan algunas de sus contribuciones más importantes, para cerrar, después, con unas reflexiones finales.
I. Aspectos biográficosJohn Forbes Nash Jr. nació un 13 de junio de 1928 en Bluefield, West Virginia. Fue nombrado así por su padre, un ingeniero eléctrico y veterano de la primera guerra mundial. Su madre nació también en Bluefield y, tras estudiar la universidad, se dedicó a dar clases de inglés y latín antes de casarse con Nash padre. En su lugar de nacimiento, Nash estudió la educación básica y la universidad, esta última en el Carnegie Institute of Technology (cit). En principio se matriculó para ser ingeniero químico pero luego se movió a la carrera de química, que fue sólo provisional pues al poco tiempo la dejó para cambiarse a su campo definitivo –impulsado por algunos profesores–, el de las matemáticas. Una vez en él, su avance fue tal que le dieron tanto el título de licenciado (B.S.) como el de maestro (M.S.) cuando se graduó, en 1948. Durante su estancia en el cit, Nash sólo cursó una asignatura relacionada con economía, pero eso le bastó para derivar ideas que decantaron, después, en su seminal artículo “The Bargaining Problem” publicado en 1950 (Nash, 2002).
Su paso del cit a Princeton es uno de los más impresionantes que uno pueda encontrar. De las cuatro cartas de recomendación que acompañaban los procedimientos de admisión de Nash a esa universidad, la que escribió Richard Duffin apenas contaba con escasas cinco líneas y cerraba con “[é]l es un genio matemático”. En otra, John Synge, decía que “[l]o colocaría entre lo mejor que he tenido, y posiblemente como el mejor”. En una tercera, David Moskovitz, habló de él de esta manera: “[…] si hay tal cosa como un nivel genio, su habilidad lo alcanza. No he dicho esto nunca antes de ningún otro estudiante”.1 De las pocas universidades a las que Nash pidió admisión,2 obtuvo becas para al menos dos de ellas, Harvard y Princeton, pero finalmente se decantó por la segunda, entre otras cosas porque le quedaba más cerca de su natal Bluefield (Nash, 2002). Nash entró a Princeton como John S. Kennedy Fellow, tras mucha insistencia de su parte en ser considerado para una plaza de profesor.3
Una vez en Princeton escribió su tesis doctoral en el muy joven campo de la teoría de juegos, al que había sido atraído por el trabajo del matemático John von Neumann y del economista Oskar Morgenstern. Afortunadamente el departamento de matemáticas avaló su idea –pese a que el campo de la teoría de juegos era el menos importante del departamento– y con ella obtuvo su Ph.D. en matemáticas en 1950 asesorado por Albert Tucker. Dicha tesis llevaba por nombre Non-cooperative Games y le valió pasar a la historia no sólo de las matemáticas sino también de la teoría económica, pues en parte por este trabajo es que le fue entregado el Premio Nobel varios años después.
Dado que su tesis en teoría de juegos no le dio estatus de matemático puro de primera clase, tras haber obtenido su Ph.D., se quedó en Princeton a estudiar un postdoctorado en el que produciría “Real Algebraic Manifolds” en 1952 que le garantizó tal estatus. Luego de esto, se trasladó al Instituto Tecnológico de Masachussetts (mit, por sus siglas en inglés), pues le ofrecía mejores condiciones salariales, y allí estuvo dando clases, pero sobre todo investigando,4 desde 1952 hasta 1959. Mientras tanto, pasó algunos veranos como consultor de la Corporación rand5 en Santa Mónica, California, trabajo que implicaba el uso de la teoría de jugos para el análisis de asuntos del Departamento de Defensa y de la Fuerza Aérea de Estados Unidos. Durante este período se tomó un año sabático, entre 1956 y 1957, durante el cual estuvo en el Courant Institute of Mathematical Sciences en Nueva York (Karstensson, 2002).
Nash se casó en febrero de 1957 con su antes alumna Alicia Larde, doctora en Física por el mit y originaria de El Salvador (Nash, 2002). Un año después se le tenía en el más alto estándar como uno de los jóvenes más brillantes en matemáticas. No obstante, al poco tiempo comenzó a actuar de manera extraña y pronto se le diagnosticó esquizofrenia paranoica, en abril de 1959. Este hecho coincidió con el embarazo de su esposa, por lo que decidió abandonar su puesto en el mit en junio del mismo año. A esto le siguió un período oscuro de altibajos psicológicos y delirios mentales, así como de tratamientos psiquiátricos. Alicia no soportó la situación así que se divorció de su esposo en 1963 y se separó de él, aunque sólo por algunos años pues tiempo después volvieron a vivir juntos definitivamente. Mientras tanto, Nash seguía haciendo investigación en sus breves momentos de lucidez autoinducida; su delirante actitud hizo que en Princeton le llamaran el “fantasma de Fine Hall”, el “loco de la librería” y el “genio loco de Firestone” (Karstensson, 2002).
Alrededor de 1990 su enfermedad fue mermando. Nash decía que todavía escuchaba algunas voces pero nada comparado con los delirios precedentes. Unos años más tarde, en 1994, le fue conferido, junto a John Harsanyi y Reinhard Selten, el Premio Nobel de Economía por sus contribuciones a la teoría de juegos (Nobel Media, 2014). Y como si el Nobel le hubiese devuelto la vida, Nash volvió a la actividad académica, dando conferencias, escribiendo algunos artículos, recibiendo grados honorarios de distintas universidades, incluyendo varios doctorados honoris causa; de hecho un año después del premio, la Universidad de Princeton finalmente le dio el puesto que hacía mucho tiempo merecía, el de “Senior Research Matematician” (Kelly, 2015). Los campos en los que Nash trabajó en sus últimos años fueron, sobre todo, los de teoría de juegos, relatividad general y lógica matemática, entre otros (Nash, 2009).
El 19 de mayo de 2015, junto con Louis Nirenberg, Nash recibió de las manos del Rey Harald V el Premio Abel, una de las preseas más prestigiosas en el campo de las matemáticas, por sus “notables y seminales contribuciones a la teoría de las ecuaciones diferenciales parciales no lineales y sus aplicaciones al análisis geométrico” (Abel Prize, 2015). El premio se lo dieron en Oslo, a donde fue acompañado por Alicia, con quien se había vuelto a casar en 2001. Al regresar de ese viaje, Nash y su esposa fallecieron el 23 de mayo de 2015 en un accidente automovilístico en Monroe Township, Nueva Jersey. Nash contaba 86 años y Alicia 82. Al respecto, un amigo de ellos y también profesor de matemáticas, Sergiu Klainerman dijo que “[s]us muertes al mismo tiempo, después de tan larga vida juntos de altos y bajos, pareció literaria en su tragedia y romance” (Kelly, 2015).
II. Algunos aportes a las matemáticas, la economía y la teoría de juegosNash produjo pocas publicaciones pero todas ellas de buena calidad. Su obra puede dividirse básicamente en tres grandes campos: matemáticas, economía y teoría de juegos. Entre sus escritos matemáticos más relevantes se tienen “Real Algebraic Manifolds” (1952), en el que intentó conectar a la geometría diferencial y la geometría algebraica real; “Parallel Control” (1954), que sentó un precedente para el cómputo de varios núcleos de procesamiento, y “Continuity of Solutions of Parabolic and Elliptic Equations” (1958), en el cual utilizó novedosos métodos para las ecuaciones diferenciales parciales no lineales.
En economía, sobresale un reciente artículo titulado “Ideal Money” (2002) que describe una moneda creada a partir de una canasta de divisas internacionales que fuera resistente a choques externos. Pero, como se sabe, el grueso de su obra está dedicada a la teoría de juegos y en este campo sus contribuciones más importantes fueron: “The Bargaining Problem” (1950) que dio una solución axiomática al problema de la negociación; “Equilibrium Points in n-Person Games” (1950), del que se hablará enseguida; Non-Cooperative Games (1950), su tesis de doctorado de sólo 27 páginas, en la que básicamente creó un nuevo campo dentro de la teoría de juegos y que es el que le da nombre a su trabajo; “Non Cooperative Games” (1951), artículo del mismo nombre que su tesis, con lo que Nash quiso dejar clara la diferencia entre los juegos cooperativos y los suyos, remarcando así que eran cosas muy distintas, y “Two-Person Cooperative Games” (1953), en el que extendió algunas ideas sobre el problema de la negociación.6
Es importante decir que si bien el campo de la teoría de juegos es estrictamente matemático, su aplicación tan amplia y generalizada en economía, así como en otros campos, hace que en realidad los últimos escritos mencionados puedan considerarse también aportes a la ciencia económica ya que en realidad así lo fueron. Los artículos de Nash sobre la negociación fueron utilizados como base para el estudio de situaciones en que dos agentes (o más) pueden ponerse de acuerdo para su mutuo beneficio. Los oligopolios, monopolios con monopsonios, el estado con el pueblo, etc. son tan sólo algunos ejemplos de su aplicabilidad (Rubinstein, 1995). La demostración del equilibrio (de Nash) sirvió de inspiración para otros economistas en camino de la demostración del equilibrio general. Así pues la teoría de juegos, sobre todo la originada en los juegos no cooperativos introducidos por Nash, es el fundamento de la teoría microeconómica moderna y del nuevo campo de la economía conductual, entre muchos otros nuevos campos.7
El equilibrio de Nash y el dilema del prisioneroQuizá de todas sus contribuciones la más difundida, y quizá también la más importante, sea el famoso equilibrio de Nash. El bien conocido origen de este equilibrio está en su “Equilibrium Points in n-Person Games” publicado en 1950, concepto que después sería central en su disertación doctoral. Básicamente plantea que en un juego con n jugadores en el que cada uno elige una estrategia de entre un conjunto de estrategias posibles, un equilibrio es un conjunto de estrategias, una para cada jugador, en el que la elección de estrategia de cada jugador es la mejor respuesta a las elecciones de los n-1 otros jugadores (Holg & Roth, 2004). Esta definición y su demostración de existencia, junto con la forma normal de Von Neumann, ofrecen una metodología general completa para analizar todos los juegos (Myerson, 1999).
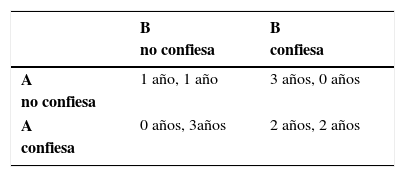
El concepto se entiende mejor con el ejemplo más conocido: el dilema del prisionero. En su origen éste fue un experimento con personas reales en el que las ganancias eran centavos de dólar pero, luego, cuando Tucker se enteró del experimento propuso una versión simple que pudiese ser entendida por un público amplio. Para esta versión se inventó una historia en la que participaban dos delincuentes que, tras delinquir, eran detenidos y separados por unos oficiales. A cada uno le ofrecían dos opciones, confesar y no confesar, y el pago por confesar era menos tiempo en prisión (Poundstone, 1993). Para este ejemplo8 añádase que a) si ninguno confiesa ambos pasan un año en prisión, b) si sólo uno confiesa, éste sale libre y el otro cubre tres años en prisión y c) si los dos confiesan, ambos pasan dos años en prisión. Siguiendo la definición de equilibrio de Nash presentada más arriba, es evidente que hay sólo un equilibrio correspondiente en el caso en que ambos confiesan.9 Se le llama dilema porque curiosamente al usar cada uno su mejor estrategia posible acaban obteniendo el peor de los resultados posibles,10 que ambos pasen dos años en prisión (véase cuadro 1).
El impacto que tuvo el equilibrio de Nash, así como el dilema del prisionero en el que se ejemplificaba fácilmente su existencia, fue enorme. Myerson (1999), dijo que “[l]a formulación del equilibrio de Nash ha tenido un impacto fundamental y penetrante en la economía y en las ciencias sociales que es comparable al del descubrimiento del adn de doble hélice en las ciencias bilógicas”. En la actualidad ya se han realizado múltiples refinamientos a su equilibrio original, los cuales han hecho de la teoría de juegos un campo mucho más amplio del que quizá pudo haber sido sin su fundamental aporte.
III. Reflexiones finalesJohn Forbes Nash fue un matemático con una historia digna de contarse, llena de muchos altibajos. Comenzó siendo raro de niño, genio de joven, esquizofrénico de adulto, y de nuevo genio en su vejez. En la universidad primero fue ingeniero, luego químico y finalmente matemático, pero a la postre de su vida terminó siendo economista. Fracasó en sus intentos de obtener grandes premios en su juventud, pero terminó ganando dos de los más importantes entre la comunidad científica. Se casó con una mujer que fue su alumna en el mit, que tuvo un hijo suyo, que se separó de él por sus delirios, que sin embargo le cuidó en su peor época sin ser su esposa, que pese a todo volvió a casarse con él en el atardecer de su vida, y que finalmente murió con él porque en realidad nunca lo abandonó. Escribió poco pero lo que hizo fue verdadera sustancia: en sólo dos hojas redactó aquello por lo que será recordado siempre, en menos de un lustro fue más prolífico de lo que muchos lo son en toda una vida; con sólo 27 páginas le dio un nuevo impulso a un campo que comenzaba a tener problemas de aplicación, y con sólo pocos años de lucidez hizo todo aquello por lo que nunca será olvidado. Nash tuvo, sin duda, una vida maravillosa.
El autor es integrante del Seminario de Credibilidad Macroeconómica de la Facultad de Economía, unam.
Las cartas, así como otros documentos personales, pueden consultarse en Princeton University, Graduate School, 2002.
Chicago, Michigan, Harvard y Princeton; fue aceptado en todas ellas.
Por poco Nash queda fuera de Princeton debido a una marcada insistencia en que le cambiaran de habitación.
Nash no tenía fama de ser buen profesor.
Abreviación de “Research And Development”, Corporación surgida en mayo de 1948.
Varias de sus obras en matemáticas y teoría de juegos se encuentran recopiladas en Nash, 1996 y en Kuhn & Nasar, 2002.
Para ver con cierta amplitud el desarrollo contemporáneo de la teoría de juegos así como sus aplicaciones a la economía véanse los 4 vols. de los Handbook of game theory with economic applications, comp. por Robert J. Aumann y Sergiu Hart.