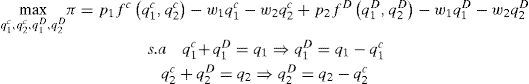El presente documento expone los principales lenguajes matemáticos utilizados en la economía desde 1838, con el trabajo de Cournot, hasta nuestros días. La exposición se estructura en tres fases: la primera, abarca de 1838 a 1947, estadio que se caracterizó por la creciente utilización del álgebra lineal y el cálculo infinitesimal; la segunda, comprende de 1948 a 1960, con el predominio de la teoría de juegos, los modelos lineales y la teoría de conjuntos convexos (lo que permitió en la década de los 50 establecer la existencia, unicidad y estabilidad del equilibrio general), y la tercera, que abarca de 1960 hasta nuestros días, destacando el desarrollo del análisis dinámico y el uso de procesos estocásticos (utilizados por la nueva economía clásica y la nueva economía keynesiana). El artículo concluye, que la economía es una ciencia social, pero que el trabajo se facilita cuando se ocupa el lenguaje sencillo, el de las matemáticas.
This paper presents the main mathematical languages used in the economy since 1838, with the work of Cournot, to this day. The exhibition is divided into three phases: the first, covering 1838 to 1947, stage was characterized by the increasing use of linear algebra and calculus; the second comprises of 1948-1960, with the predominance of game theory, linear models and the theory of convex sets (allowing establish on the 50s the existence, uniqueness and stability of general equilibrium) and the third, covering 1960 to the present, emphasizing the development of dynamic analysis and the use of stochastic processes (used by the new Classical economics and new Keynesian economics). The article concludes that economics is a social science, but the job is easier when the language is mathematic.
Debreu (1984) argumenta que las categorías básicas de la economía: precio, cantidad y valor, son cuantificables, por lo que el uso del lenguaje de las matemáticas es espontáneo en nuestra ciencia. Los modelos económicos y su consecuente aplicación de política económica dependen de la escuela de pensamiento económico que se trate. Los extremos se encuentran en los enfoques centralizado y descentralizado. En el primero, conocidos los fundamentales de la economía, existe uno o varios agentes que deciden qué producir, cómo producir y para quién producir; en contraste, en el segundo, las decisiones de los productores y los consumidores son elecciones separadas que coinciden motivadas por los precios.
Los modelos de la teoría económica pueden agruparse por diversos criterios, uno de ellos es su evolución histórica (clásico, keynesiano, síntesis neoclásica, monetarismo, poskeynesiano, elección pública, ofertista, nueva economía clásica y nuevo keynesiano), otra ruta la constituye el análisis de los modelos de expectativas (ingenuas, sensatas, adaptativas y racionales), una tercer vía es por medio del tipo de política económica (libre mercado, intervencionismo y toda mezcla de mercado-intervencionismo), y una cuarta senda la constituye el lenguaje matemático empleado.
Debreu (1984), indica que entre 1933 y 1988 el número de publicaciones técnicas en las cinco revistas más importantes de economía que emplearon el enfoque matemático se multiplicó por diez. Asimismo, Ramírez, refiere que de cuatro revistas prestigiosas de economía (Econometría eco, The American Economic Review, Journal of Political Economic y Journal of Economic Theory) de los 4,344 articulos publicados entre 1990 y 2004 la quinta parte (783) incluyó una caracterización dinámica del fenómeno bajo estudio, la proporción se eleva al eliminar los artículos cortos alcanzando un 25% del total (694), en otras palabras, uno de cada cuatro artículos incorporo un análisis dinámico (Ramírez, 2009, pág. 75). Cabe señalar que más de la mitad de los artículos corresponden a macroeconomía y teoría del crecimiento.
En este marco, el objetivo de este documento es exponer los principales lenguajes matemáticos utilizados en la economía, entre ellos el álgebra lineal y el cálculo infinitesimal, la teoría de juegos, modelos lineales, la teoría de conjuntos convexos y la dinámica.
El documento se estructura en tres apartados. En el primero, se expone la etapa del uso del álgebra lineal y el cálculo infinitesimal y abarca de 1838 a 1947; en el segundo, se muestra la aplicación de teoría de juegos, los modelos lineales y la teoría de conjuntos convexos ubicada entre 1948 y 1960 y, en el tercero, se incluye los sistemas no lineales y de análisis dinámico que inició en 1960 y continúa hasta nuestros días. Finalmente, se presentan las conclusiones.
Primera etapaLa primera etapa comprende el período de 1838 a 1947, estadio que se caracterizó por la creciente utilización del álgebra lineal y el cálculo infinitesimal (Antelo, 2005, pág. 3). En esta fase se dio forma a la teoría microeconómica basada predominantemente en la adopción de los métodos de la mecánica clásica y el uso del cálculo de variable real (Ramírez, 2009, pág. 74). Este período inició con la publicación de la obra Recherches sur les Principes Mathematiques de la Théorie des Richesses del matemático y filósofo francés Antoine-Agustin Cournot en 1838, entre sus sucesores destacan León Walras (18341910), Francis Y. Edgeworth (1845-1926) y Vilfredo Pareto (1848-1923) (Debreu, 1984, pág. 267) y termina con la aparición del libro de texto de teoría económica de Paul A. Samuelson, Foundations of Economic Analysis en 1947 (Antelo, 2005, pág. 3).
Para Andreu Mas-Collel (1999), León Walras, es uno de los más grandes economistas de todos los tiempos y su teoría de la competencia perfecta se constituye como el corazón de la economía.1Para Arrow y Hahn (1977), el análisis general competitivo es el modelo de una economía descentralizada de competencia perfecta donde los agentes eligen o toman decisiones sobre la base de ciertos axiomas de racionalidad en donde los estados de equilibrio de la producción y del intercambio son un estado ideal, no real. Pero argumentan que es el estado normal en el sentido de que es aquel hacia el cual las cosas tienden por ellas mismas bajo el régimen de libre competencia aplicada tanto a la producción como al intercambio.
Sin demeritar el trabajo de los autores mencionados, para simplificar el desarrollo expositivo de esta fase se presenta el modelo de equilibrio general de Leon Walras (1877), quien incluso reconoce en 1890, en su obra principal, que su teoría había sido desarrollada paralelamente por Jevons y Menger.2
En el equilibrio general, los precios de las mercancías3 son anunciados por el subastador y los agentes económicos deciden las cantidades que quieren vender o comprar de cada una. Los precios suben cuando el exceso de demanda es positivo y se reducen cuando el exceso de demanda es negativo (condición de un oferente neto). El problema entonces, es determinar las condiciones para que los mercados se vacíen con precios positivos y la demanda no exceda la oferta cuando los precios son nulos.
Los resultados del modelo de equilibrio general son idénticos si se trata de un modelo 1x1x1x1 que incluye un consumidor, un productor, una mercancía y un factor de la producción, o un modelo de 2x2x2x2 o de nxm (Cervantes Jiménez, 2014, págs. 345-346).
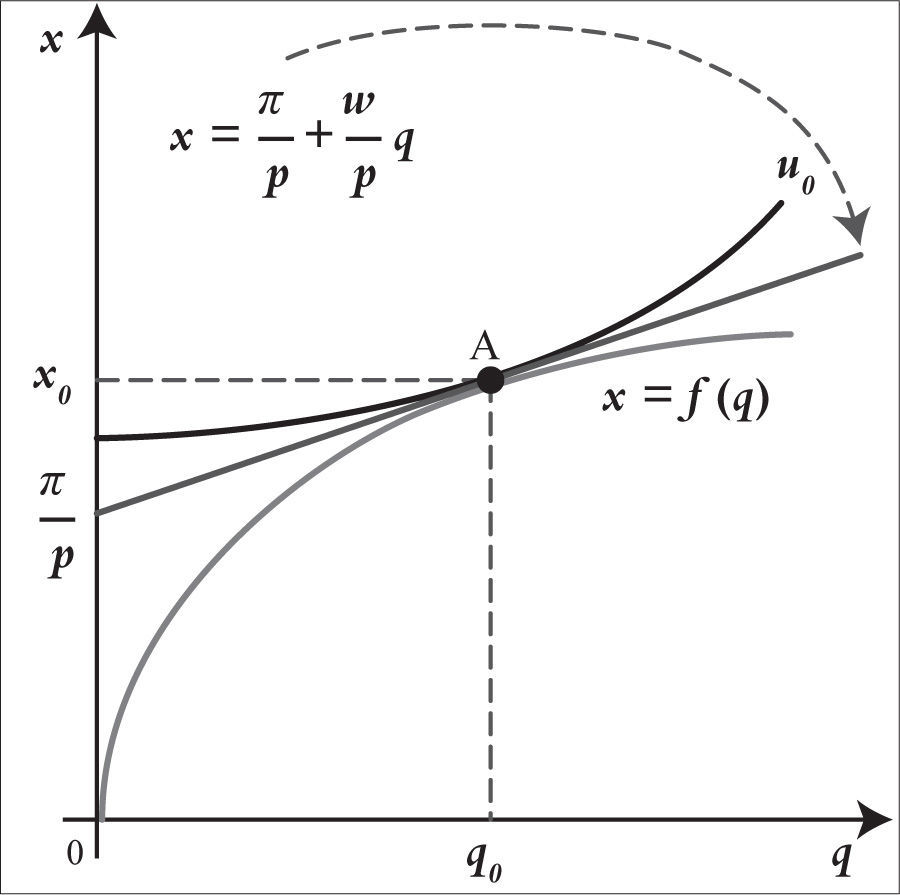
En el modelo 1x1x1x1 (Cervantes Jiménez, 2014, págs. 347-366), el productor contrata unidades de factor trabajo (q), para producir el bien de consumo (x) y la función de producción, que cumple condiciones de Inada, es x = f (q).4 El sistema de preferencias del consumidor es continúo, monótono y convexo definido en torno al consumo de ocio y de unidades del bien, así la función de utilidad del consumidor es u=uo,c=uq¯−q,c, en donde q¯ es la dotación total del tiempo disponible del agente, (q) es el tiempo de trabajo (o=q¯−q es el ocio) y (c) representa el bien de consumo perecedero con dotación inicial nula.
En el enfoque centralizado el problema del agente es maximizar su utilidad que depende de su cantidad de ocio y de consumo sujeto a la disponibilidad de tiempo y a la restricción tecnológica, a saber:
maxq,cuo,c=uq¯−q,c,s.a.x=fq. Utilizando una función auxiliar lagrangiana y sustituyendo el consumo (c) por la producción del bien de consumo (x), el problema se transforma en: maxq,c,λuq¯−q,x+λfq−x, cuya solución es f'q=UMoUMx. En el equilibrio general la productividad marginal del trabajo es igual a la relación marginal de sustitución ocio-consumo.
En el enfoque descentralizado las decisiones de producción y consumo se descomponen en dos acciones particulares que se resuelven a través del mecanismo de los precios. El productor contrata al trabajador para fabricar el bien de consumo, cuya venta genera el ingreso de la empresa. Considerando el precio del trabajo y del ocio (w) y el precio del bien de consumo (p), el problema de maximización del beneficio de la empresa es: maxqπ=px−wq, s.a. x= f(q) y sus solución es la igualdad entre el producto marginal y el precio relativo del salario nominal respecto al precio del bien: f'q=wp.
Por su parte, el consumidor enfrenta la decisión entre la cantidad de trabajo (de ocio) y su nivel de consumo, pero está restringido por su ingreso. El ingreso del consumidor (m) procede de su ingreso laboral (qw) y del beneficio (π = px - wq). Así, el problema del consumidor es elegir la canasta de consumo que maximice su utilidad restringido por la igualdad del gasto ÚMoreso, simplificando: maxq,c,λℑ=uq¯−q,x+λπ+wq−px, cuya solución es: UMoUMx=wp
Por una parte, el productor maximiza el beneficio en donde el producto marginal del trabajo es igual al salario real, por otra parte, el consumidor maximiza su utilidad sujeto a la restricción presupuestal en donde la relación marginal de sustitución ocio-consumo es igual al salario real, así que se requiere un salario real que iguale el producto marginal del trabajo con la relación marginal de sustitución ocio-consumo:
El papel de los precio es igualar las cantidades ofrecidas con las cantidades demandadas tanto en el mercado de bienes como en el mercado de factores. El rol de los precios es proporcionar los incentivos adecuados para que las decisiones de la empresa y el consumidor sean independientes, pero compatibles, lo que permite descentralizar las decisiones de la empresa y el consumidor.5
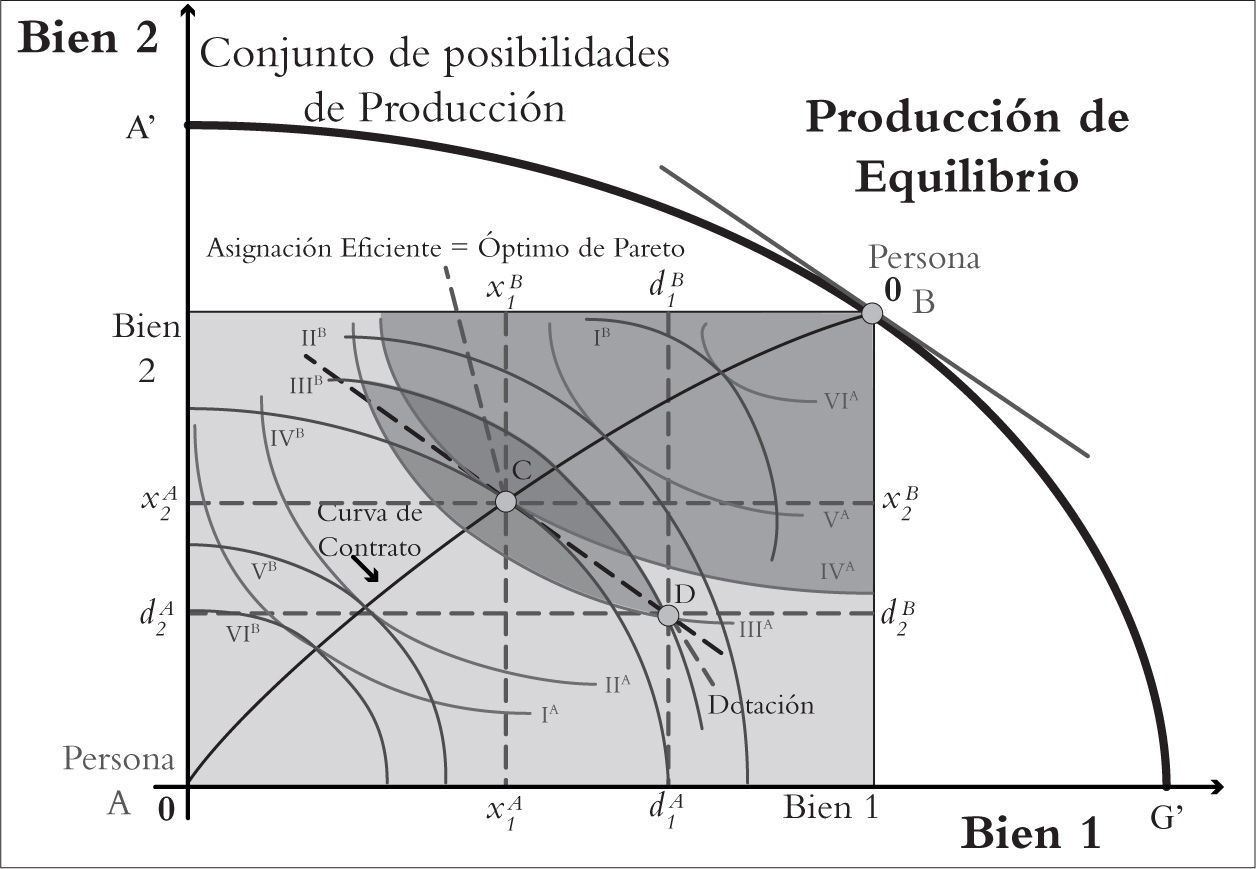
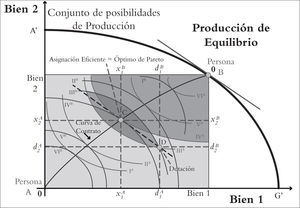
Cuando el problema se escala al modelo 2x2x2x2 se incluyen dos consumidores A y B, dos productores C y D, dos mercancías x1 y x2 y dos factores q1 y q2 (Cervantes Jiménez, 2014, págs. 373-392). El plan de producción de la economía (x, x2) y se representa por: x1=fcq1c,q2cyx2=fDq1D,q2D. Asimismo, los consumidores A y B tienen un sistema de preferencias definido en torno a los dos bienes de consumo (x1, x2), en donde: uA=uAx1A,x2AyuB=uBx1B,x2B
En el enfoque centralizado del equilibrio general el planificador central enfrenta el problema de determinar una asignación eficiente de los factores de la producción q1c,q2c,q1D,q2D y la canasta de consumo para los agentes A y Bx1A,x2A,x1B,x2B que maximicen las utilidades de cada uno de ellos agotando la cantidad total de bienes: x1=x1A+x1Byx2=x2A+x2B. Este problema se resuelve con la igualdad entre la relación marginal de transformación y la relación marginal de sustitución de ambos consumidores.
Por su parte, el enfoque descentralizado separa la decisión de producción y la de consumo.
El problema de maximización del beneficio de las empresas se representa por:
El resultado de la optimización, a saber, que la productividad marginal es igual al precio real del factor utilizado:PMq1c=w1p1PMq1D=w1p2PMq2c=w2p1PMq2D=w2p2
Por su parte, el problema de maximización de la utilidad del consumidor A es:maxx1A,x2Aλℑ=uAx1A,x2A+λw1q1A−w2q2A+θ1Aπc+θ2AπD−p1x1A−p2x2A y el de B es:maxx1B,x2Bλℑ=uBx1B,x2B+λw1q1B−w2q2B+1−θ1Bπc+1−θ2BπD−p1x1B−p2x2B.
La solución es UMx1AUMx2A=p1p2=UMx1BUMx2B=p1p2. Lo que implica que los consumidores alcanzan el equilibrio en donde la relación marginal de sustitución es igual al precio relativo de los bienes.
La solución del equilibrio general genera un vector de precio para el cual ninguna mercancía, bien o servicio, tiene exceso de demanda. De hecho, no se requieren determinar los cuatro precios, tan sólo se deben encontrar tres precios, el cuarto es el precio de la mercancía numerario; a esta condición se le conoce como la ley de Walras. Además, se generan dos teoremas de la economía del bienestar: Primer teorema de la economía del bienestar: el equilibrio generado por los mercados competitivos es óptimo en el sentido de Pareto. Este teorema garantiza que un mercado competitivo obtiene todas las ganancias derivadas del comercio y que la asignación de equilibrio lograda por un conjunto de mercados competitivos es necesariamente eficiente en el sentido de Pareto. Segundo teorema de la economía del bienestar: Si todos los agentes tienen preferencias convexas, siempre hay un conjunto de precios a los que cada asignación eficiente en el sentido de Pareto es un equilibrio de mercado para cualquier dotación. El segundo teorema implica que en cualquier asignación de la curva de contrato puede conseguirse como un equilibrio competitivo. Esto se consigue cuando las curvas de indiferencia de los consumidores son convexas. Además separa los problemas de distribución y eficiencia, es decir, para cualquier dotación de que se parta en tanto los precios sean flexibles se alcanza una asignación eficiente en el sentido de Pareto.
La exposición del equilibrio general ejemplifica el uso del cálculo infinitesimal, la que se puede generalizar utilizando el álgebra lineal.
Segunda etapaLa segunda etapa de 1948 a 1960 se marcó por la aplicación de la teoría de conjuntos convexos, la teoría de juegos y los modelos lineales (Ramírez, 2009, pág. 74). Destacan las obras de Gerard Debreu, The Theory of Value: an Axiomatic Analysis of Economic Equilibrium (1959), y de Janos Von Neumann con Oskar Morgenstern, Theory of Games and Economic Behavior6 en 1944 (Antelo, 2005, pág. 4). También destaca la disponibilidad de datos y el desarrollo de los métodos econométrico.
Gerar Debreu, (1959), demostró los aspectos axiomáticos del equilibrio general, a saber: existencia, unicidad y estabilidad. Existencia: para que el equilibrio exista se requiere que las preferencias de los consumidores sean continuas, crecientes y convexas (esta condición puede relajarse con un número grande de consumidores) y con dotaciones positivas. Asimismo, los planes factibles de producción deben ser convexos, excluyendo la posibilidad de economías de escala. Esta demostración se apoya en los teoremas de punto fijo de Brouwer y su generalización con el teorema de Kakutani (Gibbons, 1993). Unicidad: suponiendo convexidad existirá un equilibrio que generalmente será eficiente. Debreu, determinó que muchas economías se comportan de forma regular, lo que implican la existencia y unicidad del equilibrio.7 • Estabilidad: es el proceso que vacía los mercados ante choques transitorios que alteran el equilibrio, esto se resuelve a través del mecanismo de los precios.
El equilibrio general de Gerard Debreu, (1959), requiere de condiciones muy restrictivas para demostrar la existencia, unicidad y estabilidad. Por ello, se buscaron alternativas metodológicas de interdependencia estratégica, una de ellas es la propuesta por Von Neumann y Oskar Morgenstern, con la publicación en 1944 del libro seminal intitulado Theory of Games and Economic Behavior; aunque se encuentran algunos antecedentes en ideas de Cournot, Edgeworth, Borel y Zermelo, entre otros.
La teoría de juegos incluye juegos cooperativos y no cooperativos y pueden presentar estrategias dominantes, semidominantes, mixtas, maximin y equilibrios de Nash, todos en torno a juegos instantáneos o repetidos en sus versiones finitos o infinitos (Cervantes Jiménez, 2014, págs. 489-498). En la década del cincuenta del siglo pasado Kuhn (1953), estableció la mecánica para resolver juegos cooperativos y Nash extendió la teoría de juegos no cooperativos más allá de los juegos de suma cero (lo que gana un actor lo pierde el otro). El equilibrio de Nash permite alcanzar más de un equilibrio en donde la estrategia adoptada es la óptima dada la estrategia del contrincante. La teoría de juegos se utiliza en diversas disciplinas para generar hipótesis sobre guerra de precios, guerras comerciales, subastas, duopolios, oligopolios, la formación de redes sociales y sistemas de votaciones, entre otros.
Los juegos pueden ser definidos como una terna (N,Dj,φj) en donde (N) es el conjunto de jugadores, (Dj) es el conjunto de estrategias de cada jugador y (∈ℝ) es la función o matriz de pago de cada jugador perteneciente al conjunto de los números reales. En juegos con estrategia pura (σ∈D), si para cada jugador se cumple que φj (σ)≥φj (σ|σj), donde φj (σ|σj) representa el pago para el jugador cuando elige una de las posibles estrategias dada la elección de los otros jugadores, por lo que incluye el equilibrio de Nash es uno de los resultados de juego posibles dentro de esta estructura. En el caso de juegos con estrategia mixta (sin estrategia dominante o semidominante) se incluye un vector de probabilidades a cada estrategia del jugador j-ésimo (con sumatorio igual a la unidad).
La teoría de juegos modela la interdependencia entre los actores y sus resultados presentan equilibrios únicos estables, varios equilibrios estables o inestables o equilibrios estocásticos (un sistema cuyo comportamiento es intrínsecamente no determinista).
Tercera etapaLa tercera etapa inició en 1960 y continúa hasta nuestros días. En esta fase se comienzan a utilizar los modelos en los que el tiempo es una variable. La variable tiempo se presenta en tiempo discreto y continuo; el primero, corresponde a períodos (primer año, segundo año, etc.) y, el segundo, incluye al tiempo discreto y a todos los instantes intermedios. Este estadio se distingue por utilizar la tecnología matemática de las dos etapas anteriores, adicionada con modelos no lineales y análisis dinámico (Ramírez, 2009, pág. 74). En esta fase, la mayoría de los campos de la ciencia económica ocupan las matemáticas y la estadística para elaborar modelos y teorías (Antelo, 2005, pág. 5). Se usan las ecuaciones diferenciales y en diferencia, el cálculo de variaciones así como la teoría del control óptimo y programación dinámica.
Un sistema dinámico se distingue dada la relación intertemporal de las variables endógenas, la solución a este tipo de problemas requiere que las variables exógenas se mantengan constantes (en la dinámica compleja y caótica este elemento puede no incorporarse). En un sistema dinámico la relación se traslapa período a período incidiendo en la toma de decisiones de los agentes económicos. Hicks, apunta que en el método estático “el equilibrio del [período] t puede considerarse determinado únicamente por los parámetros actuales; o bien, que el equilibrio de un período individual puede manejarse como autónomo… En la estática el futuro y el presente son idénticos. Pero en la dinámica, que el presente y el futuro no sean idénticos es la esencia del problema dinámico” (Figueroa, 1993, pág. 16).
Los equilibrios dinámicos pueden ser estables o inestables. Cuando los equilibrios dinámicos son estables implican que los equilibrios estáticos también lo son, por lo que la trayectoria no se ve afectada por perturbaciones exógenas y la trayectoria temporal es convergente; en contraste, cuando los equilibrios dinámicos son inestables ante un choque externo se altera la trayectoria del sistema alejándola de sus valores de equilibrio y la trayectoria temporal es divergente, presentándose casos expansivos, cíclicos o caóticos.
Los modelos de crecimiento económico tanto endógenos como exógenos se valen de la dinámica para analizar las variables que inciden en el fenómeno al tratarse de un problema temporal. La teoría del crecimiento económico hace uso de ecuaciones diferenciales o en diferencia para analizar las trayectorias en el tiempo, ejemplos de ello son el modelo de Solow-Swan (1956), el de Ramsey (Cass-Koopmans) (1928) y el de Barro (Barro & Salai, 2004) y otros.
Hoy en día, hay dos enfoques fundamentales que constituyen la base de la macroeconomía moderna que utilizan análisis dinámico para la explicación de los fenómenos económicos, estos enfoque corresponden a la nueva economía clásica y la nueva economía keynesiana (Torres, 2004, pág. 59).
La nueva economía clásica incorporó las expectativas racionales,8 formuló la oferta agregada con microfundamentos, incluyó la crítica de Lucas para evaluar las consecuencias de medidas de política económica alternativas, estableció el principio de inefectividad de las políticas anticipadas, la inconsistencia temporal de las políticas y los modelos de ciclo económico real en condiciones de vaciado de mercado (Torres, 2004, pág. 28).
Por su parte, la nueva economía keynesiana, mantiene el principio básico de agentes racionales, pero incorpora fallos en los mercados. Su objetivo cardinal es explicar las rigideces en precios y salarios que impiden el equilibrio. Sus trabajos se desarrollan en competencia imperfecta y con información asimétrica (Torres, 2004, pág. 41).
Las principales escuelas de pensamiento económico actual están formalizando sus modelos a través de alto contenido matemático y econométrico, y aceptan los siguientes postulados generales: racionalidad de los agentes, racionalidad en la formación de expectativas, condiciones de equilibrio general y uso del agente representativo.9 Específicamente, utilizan a la microeconomía para fundamentar la macroeconomía, emplean la optimización intertemporal, incorporan las expectativas racionales10 en modelos macroeconómicos dinámicos (se puede incorporar información asimétrica), se recurre al modelo de equilibrio general, que puede ser dinámico y estocástico, con vaciado y sin vaciado de mercado (lo que conduce a mercados perfectos e imperfectos); con precios flexibles o costos de ajuste en los precios (Torres, 2004, págs. 60, 74-75).
Sobre la existencia, unicidad y estabilidad del equilibrio, este tema ha sido superada; ahora se trabaja con uno, vario o equilibrios nulos.
ConclusionesLos modelos de la teoría económica pueden agruparse por diversos criterios, se pueden discriminar por su evolución histórica, su modelo de expectativas, el tipo de política económica y el lenguaje matemático empleado. En este último, se identifican tres etapas.
La primera etapa, de 1838 a 1947, se caracterizó por la utilización del álgebra lineal y el cálculo infinitesimal, en donde sobresalen los trabajos de Antoine-Agustin Cournot, León Walras, Stanley Jevons, Karl Menger, Francis Y. Edgeworth, Vilfredo Pareto y Paul A. Samuelson.
El modelo de equilibrio general de Walras, ejemplifica el uso del cálculo infinitesimal y el álgebra lineal. Este modelo tiene dos enfoques, el centralizado y el descentralizado. En el primero, conocidos los fundamentales de la economía un planificador central determina conjuntamente las cantidades de factores requeridos para producir las mercancías y su distribución entre los consumidores; en el segundo, las decisiones de los productores y consumidores se separan y los mercados de bienes y servicios se vacían por medio del tanteo de los precios.
La segunda etapa, de 1948 a 1960, se marcó por la aplicación de la teoría de conjuntos convexos, la teoría de juegos y los modelos lineales, en donde destacan los trabajos de Gerard Debreu, Von Neumann y Oskar Morgenstern.
En esta etapa Debreu, demostró axiomáticamente que el equilibrio general cumple las condiciones de existencia, unicidad y estabilidad, pero que requiere de ciertas condiciones como continuidad y convexidad de las preferencias de los consumidores, así como convexidad en los conjuntos factibles de producción.
Ante estas condiciones restrictivas, se buscaron alternativas metodológicas de interdependencia como la Teoría de Juegos de Von Neumann y Morgenstern. Esta teoría incluye juegos cooperativos y no cooperativos con estrategias dominantes, semidominantes, mixtas, maximin y equilibrios de Nash, para juegos instantáneos o repetidos finitos o infinitos. En general, la teoría de juegos presenta resultados con equilibrios únicos estables, varios equilibrios estables o inestables o equilibrios estocásticos.
La tercera etapa, de 1960 hasta nuestros días, privilegia el uso de los modelos dinámicos en tiempo discreto y continuo con ecuaciones en diferencia y diferenciales, respectivamente.
Los equilibrios dinámicos pueden ser estables, cuando la trayectoria no se ve afectada por perturbaciones exógenas y es convergente, o pueden ser inestables ante choques externos lo altera la trayectoria del sistema alejándola de sus valores de equilibrio mostrando una trayectoria temporal divergente, presentándose casos expansivos, cíclicos o caóticos. Los modelos de crecimiento económico tanto enxógenos como endógenos se valen de la dinámica para analizar las variables que inciden en el fenómeno, tal es el caso de los modelos de Solow-Swan, Ramsey (Cass-Koopmans) y Barro, entre otros.
Hoy en día, predominan dos enfoques que constituyen la base de la macroeconomía moderna que utilizan análisis dinámico para la explicación de los fenómenos económicos, se trata de la nueva economía clásica y la nueva economía keynesiana. Ambas corrientes utilizan a la microeconomía para fundamentar la macroeconomía, emplean la optimización intertemporal, incorporan las expectativas racionales en modelos macroeconómicos dinámicos (se puede incorporar información asimétrica), se recurre al modelo de equilibrio general, que puede ser dinámico y estocástico, con vaciado y sin vaciado de mercado (con mercados perfectos e imperfectos) y precios flexibles o pegajosos.
La discusión sobre la existencia, unicidad y estabilidad del equilibrio general ha sido superada, la economía moderna considera uno, varios o equilibrios nulos. No cabe duda de que la economía es una ciencia social, pero el trabajo se facilita cuando se ocupa el lenguaje sencillo, el de las matemáticas.
Profesor de la División de Estudios Profesionales de la Facultad de Economía, unam.
Mas-Collel es coautor de Microeconomic Theory, el libro de texto más utilizado en los cursos de microeconomía de las principales maestrías y doctorados de economía.
Pese a la relevancia de sus aportación, inicialmente no se le reconoció su mérito académico y su amargura quedó plasmada en la siguiente cita: “Si Francia del siglo xix, que vio nacer la nueva ciencia, se desinteresó completamente de ella, eso se debe a una concepción, de gran estrechez burguesa, que ve la cultura intelectual dividida en dos zonas distintas: la una produciendo calculadores desprovistos de conocimiento filosóficos, morales, históricos, económicos; y otros que se destacan en las letras sin ninguna noción matemática. El siglo xx, que no está lejos, sentirá la necesidad, incluso en Francia, sentirá la necesidad de entregar las ciencias sociales a hombres de cultura general, habituados a manejar a la vez la inducción y la deducción, el razonamiento y la experiencia. Entonces la economía matemática tomará su rango al lado de la astronomía y de la mecánica matemáticas, y ese día, se nos hará justicia” (Walras, 1877, pág. xx).
Definidas espacial y temporalmente, así como por sus características físicas si son bienes y sus prestaciones cuando se trata de servicios.
La existencia del espacio se facilita cuando se supone lo siguiente:
q = {q : q es esfuerzo laboral,q∈0≤ℝ≤q¯},
x = {x: x es producción de un bien perecedero, x ∈ ℝ ≥ 0,x=f(q)},
o = {o : o es ocio, o∈0≤ℝ≤q¯,o=q¯−q,}
c = {c : c es consumo del bien perecedero, c ∈ ℝ ≥0,c =x} y
q*x = {(a, b): a ∈ q, b ∈ x } ⊂ ℝ2
Este modelo es básico en el desarrollo de la teoría macroeconómica microfundamentada de la nueva economía clásica y los nuevos keynesianos; los primeros asumen precios flexibles. y los segundos precios pegajosos (Cervantes Jiménez, 2014 (mimeo; se publicará en 2015)).
La publicación de Theory of Games and Economic Behavior, anunció una profunda y extensiva transformación en la teoría económica, siendo una motivación para la investigación el estudio de la teoría general del equilibrio económico (Debreu, Economic Theory in the Mathematical Mode, 1984, pág. 267).
Cabe señalar, que el teorema de Sonnenschein-Mantel-Debreu revela que la función de demanda agregada sólo hereda algunas de las características de la función de demanda individual, lo que no basta para asegurar la unicidad del equilibrio (Mandler, 1999).
Muth, sugiere que los agentes económicos formarán expectativas subjetivas con relación a las variables económicas futuras, equivalentes a la expectativa matemática condicional de dichas variables. Las expectativas racionales utilizan toda la información disponible por el individuo, incluido el modelo más adecuado para explicar las variables (Torres, 2004, pág. 17). El individuo carece de omnisciencia, no lo sabe todo, pero aprende y no comete errores sistemáticas (como sucede con las expectativas adaptativas).
Es pertinente señalar, que la economía con agentes representativos se comportan de manera distinta a la economía con agentes heterogéneos.
La existencia de incertidumbre y la disponibilidad de información, hacen que las expectativas sean un elemento fundamental en la modelización de la teoría económica (Torres, 2004, pág. 25). Las expectativas racionales implican que se ocupa toda la información disponible y no se comenten errores sistemáticos.