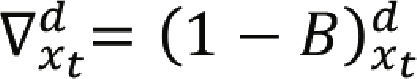El presente documento, detalla el ajuste de modelos de series de tiempo ARIMA, para la realización de pronósticos sobre el histórico de expedientes acumulados en la Comisión de Derechos Humanos del Distrito Federal (CDHDF). El propósito es comprender el comportamiento de los expedientes acumulados en el tiempo y pronosticarlos.
The document presented here, details the adjustment of ARIMA (Autoregressive Moving Average) time series models that allow to forecast the historic accumulation of files in the Mexico City Human Rights Commission. The purpose is to comprehend the behaviour of these, throughout time and to forecast the number of accumulated files.
Los modelos autoregresivos integrados de medias móviles, ARIMA por sus siglas en inglés, son los modelos de series de tiempo aditivas más populares. Son una generalización de los modelos autoregresivos de medias móviles (ARMA), útiles cuando la serie de tiempo a modelar no es estacionaria a causa de una marcada tendencia.
En la primera sección analizaremos a detalle la serie de tiempo Expedientes Acumulados en la CDHDF, misma que está compuesta por las series de expedientes acumulados en cada una de las cinco Visitadurías Generales. En la segunda sección se tratará brevemente la teoría de los modelos ARIMA, enfatizando en los requerimientos estadísticos que debe poseer la serie para un ajuste adecuado, así como la descomposición de la serie en sus componentes aditivas: tendencia, estacionalidad y componente aleatoria.
En la tercera sección, se realiza el análisis de la serie de tiempo mediante el uso del software R(library (astsa); library (forecasts)). Se pretende seguir el orden heurístico establecido en la segunda sección, en términos del análisis de los requerimientos estadísticos del modelo, en particular sobre la estacionaridad de la serie de tiempo. Es en la misma sección que se reporta el ajuste del modelo seleccionado, las características del mismo y la implementación de un modelo más parsimonioso que facilite la interpretación de los parámetros del modelo. Se realizan pruebas de normalidad y de no correlación para los errores de modelo, características que de cumplirse garantizan la eficiencia del mismo.
La cuarta sección de resultados del modelo, se realizan los pronósticos de la serie de tiempo a diferentes horizontes, estimaciones para los meses de enero a diciembre de 2016, así como su respectiva gráfica.
El presente reporte se realizó en el mes de diciembre de 2015 por la Dirección Ejecutiva de Asuntos Legislativos y Evaluación de la Comisión de Derechos Humanos del Distrito Federal.
1Expedientes Acumulados en la CDHDFLa Comisión de Derechos Humanos del Distrito Federal (CDHDF) es un organismo público autónomo que tiene por objeto la protección, defensa, vigilancia, promoción, estudio, educación y difusión de los derechos humanos en la Ciudad de México.
Algunas atribuciones de la CDHDF son: recibir quejas de presuntas violaciones a derechos humanos; conocer e investigar, a petición de parte o de oficio, presuntas violaciones de derechos humanos; formular propuestas conciliatorias entre la persona agraviada y las autoridades o servidoras o servidores públicos presuntos responsables; impulsar la observación de los derechos humanos; promover el estudio, la enseñanza y divulgación de los derechos humanos; elaborar e instrumentar programas preventivos en materia de derechos humanos, entre otras.
Cualquier persona puede acudir a la CDHDF si considera que a ella o a una tercera persona le ha sido violado alguno de sus derechos humanos, independiente de su condición social, nacionalidad, raza, religión, sexo, edad, estado civil, etcétera.
Conocer el número de expedientes acumulados en la Comisión durante un periodo mensual, o para cualquier periodo determinado, es un proceso estocástico compuesto de la adición del número de expedientes acumulados en cada una de las cinco Visitadurías Generales.
Sea Xt :el número de expedientes acumulados en la CDHDF.
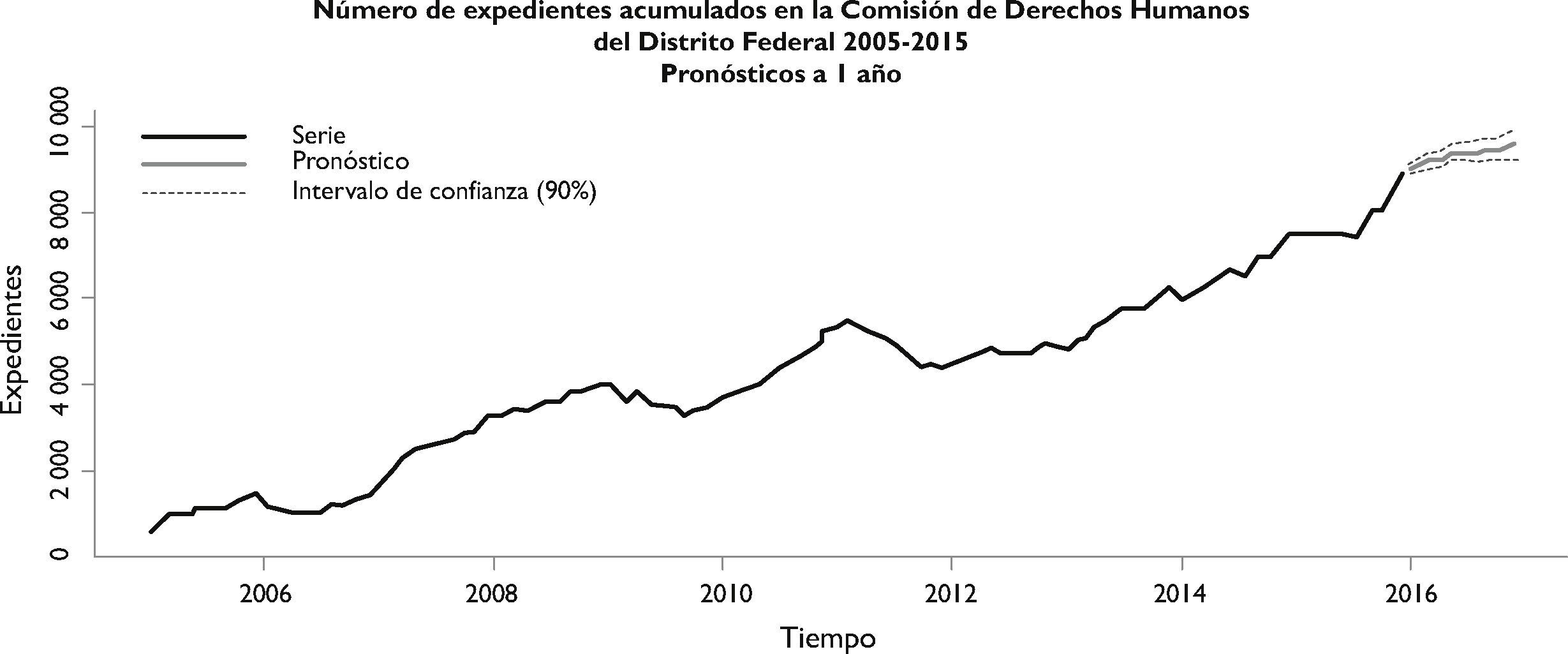
Xt = ∑(i=1)5Xt(i) donde Xt(i) es el número de expedientes acumulados en la i-ésima Visitaduría General. El comportamiento de la serie Xt puede ser observado en la figura 1.
Si una serie es considerada aditiva, cualquier modelo de serie de tiempo adecuado a ésta debe estar conformado por las componentes de: tendencia, estacionalidad y aleatoria. De tal forma que si Xt es aditiva, debe ser de la forma:
Donde T: representa la tendencia, S: la estacionalidad y E: la componente aleatoria del proceso.
En la figura 2 se puede observar la descomposición automatizada de la serie Xt en las componentes de las series de tiempo aditivas.
En la figura 3 podemos observar las gráficas de cada una de las series Xt(i), el número de expedientes acumulados por visitaduría. Es importante hacer notar que no hay similitudes en varianza en general si por pares la primera Visitaduría y la segunda visitaduría; la tercera Visitaduría y la cuarta Visitaduría.
2Modelos ARIMALos procesos ARIMA son los más populares para el modelado de procesos econométricos, financieros, meteorológicos e incluso biológicos. Son una generalización de los procesos ARMA (Auto Regresivos y de Medias Móviles), usados cuando la serie de tiempo presenta una tendencia, que la vuelve un proceso no estacionario.
La función de autocovarianzas (ACVF) es un criterio eficiente para el ajuste de un modelo de series de tiempo. La ACVF teórica está definida como la covarianza entre xt y xt+h .
Definición: La función de autocovarianza muestral es definida como:
Se observa que γ (-h) = γ (h), esto es, la función de autocovarianza es simétrica.
Consideremos xt observaciones de una serie de tiempo y wt un ruido blanco; es decir, wt es una sucesión de variables aleatorias no correlacionadas, con media cero y varianza finita.
Definición: Un modelo autorregresivo de orden p, denotado como AR(p), tiene la forma:
La función de autocorrelación parcial (facp) de un proceso AR(p) (Autorregresivo de orden p) es 0 para valores de h>p.
Definición: Un promedio móvil de orden q, MA(q) es definido como:
La función de autocovarianzas de un proceso MA(q) es 0 para valores de h>q.
Definición: Una serie de tiempo {xt ; t = 0, ±1, ±2, …} es un ARMA(p,q) si es estacionaria y si:
Con Φp ≠ 0 y θq ≠ 0. Los parámetros p y q son llamados orden autorregresivo y orden de promedio móvil respectivamente. Asumimos que wt es un ruido blanco gaussiano con media cero y varianza finita σw2.Cuando q=0 el proceso es llamado autorregresivo de orden p, AR(p) y cuando p=0 el proceso es llamado promedio móvil de orden q, MA(q).
Si suponemos que las observaciones {x1 , …,xn } no son necesariamente generadas por una serie de tiempo estacionaria, buscaremos una transformación que genere una nueva serie con las características deseadas para permitir el ajuste de un modelo ARMA, lo anterior es frecuentemente logrado mediante la diferenciación de la serie. Sin embargo, otra forma de tratar los datos, sin necesidad de aplicar transformaciones, es ajustar un modelo ARIMA.
Un ejemplo de la utilidad de los modelos ARIMA es el modelado de un proceso con deriva. Si Xt es un proceso con deriva, i.e. Xt = δ + Xt-1 + wt, entonces diferenciando el modelo Yt=∇xi obtenemos una serie de tiempo estacionaria, como en este ejemplo, en muchas otras situaciones una serie de tiempo puede ser pensada como la suma de dos componentes: una tendencia (no estacionaria) y una componente estacionaria con media cero. Los modelos ARIMA son modelos que contemplan la diferenciación de los datos.
Definición: Un proceso xt es un llamado ARIMA(p,d,q) si el proceso:
Es un ARMA(p,q) causal, en general escribiremos el modelo como:
Otros modelos de interésExisten otros modelos de series de tiempo más sencillos, pero igualmente eficientes al momento de generar pronósticos, el modelo en el que estamos interesados por su utilidad en el presente documento es el proceso Naïve Raw Drift, que significa proceso ingenuo de deriva bruta.
Las predicciones bajo el método Naïve, son simplemente el valor de la última observación, es decir yT + h = yT con yT el último valor observado.
El método Naïve Raw Drift es una variación del método Naïve, que permite a los pronósticos incrementarse en el tiempo, considerando un valor cambiante en el tiempo (llamado deriva), calculado como el cambio promedio en los datos históricos. De esta manera,
3MetodologíaComo se pudo ver en la primera sección, la serie de tiempo Xt : número de expedientes acumulados en la CDHDF está compuesta por cinco componentes, las series que reflejan el número de expedientes acumulados en cada una de las cinco Visitadurías Generales. El ajuste de un modelo adecuado al comportamiento de Xt puede hacerse en forma agregada o desagregada:
- •
La primera opción implica ajustar un modelo de series de tiempo a la serie Xt ,
- •
La segunda opción propone ajustar modelos individuales, uno a cada uno de las Xt(i), de tal manera que al poder replicar el comportamiento de cada una de ellas, la serie Xt pueda ser modelada con la suma de los procesos en los modelos individuales.
La forma de modelado desagregada es preferible, el comportamiento de las series (como puede observarse en la gráfica 3) no es el mismo en cada una de las Visitadurías Generales. Los modelos individuales replicarán o se ajustarán con mayor fidelidad al comportamiento de cada una de las series. Sin embargo, el modelado desagregado depende de una hipótesis adicional a las del agregado, la independencia mutua de los Xt(i).
Para mostrar dicha independencia, se hace uso de la función de correlación cruzada (ccf), es un criterio que no determina si dos procesos son independientes, sí refleja la posible no correlación de estos. Habiendo demostrado la no correlación de las series de tiempo, procedemos al ajuste de los modelos individuales.
Ajuste del ModeloPara realizar el ajuste de los modelos individuales, debemos retirar la componente de tendencia de cada una de las series, a fin de tener series de tiempo estacionarias. La forma de hacerlo es utilizando el operador ∇, es decir, diferenciando.
Una vez realizada la diferenciación, se grafican las funciones de autocorrelación y autocorrelación parcial, figura 5. En las gráficas de estas funciones se observa que la serie posee un comportamiento estacionario y algunas características adicionales que facilitan el ajuste de los modelos. Véanse las características de las funciones de autocorrelación y autocorrelación parcial de los modelos AR y MA explicados en la sección anterior.
Se busca que los residuales del modelo sean no correlacionados y despreciables, para lo cual se analizan las funciones de autocorrelación y autocorrelación parcial. Los resultados pueden observarse en la figura 6.
Implementación del ModeloPara la selección de los modelos individuales definitivos se compararon diversos procesos, usando los siguientes criterios: AIC, BIC, Pruebas de razón de verosimilitudes entre modelos anidados, Pruebas de Wald sobre los parámetros del modelo y Principio de Parsimonia.
Los modelos ajustados fueron los siguientes:
• Primera Visitaduría General, ARIMA (8,1,8)
• Segunda Visitaduría General, Raw Drift Model
• Tercera Visitaduría General, SARIMA(0,1,0)(1,0,2)12
• Cuarta Visitaduría General, SARIMA(0,1,3)(0,0,1)12
• Quinta Visitaduría General, SARIMA(4,1,0)(0,1,1)12
4PronósticosLos pronósticos a un año pueden consultarse en la tabla 1. Los intervalos de confianza para los pronósticos de la serie de tiempo fueron realizados a un nivel de 90% de confianza.
Pronósticos del número de expedientes acumulados en la CDHDF para el 2016
| Mes | Media | Límite Inferior | Límite Superior |
|---|---|---|---|
| Enero | 8 992 | 8 904 | 9 081 |
| Febrero | 9 100 | 8 975 | 9 226 |
| Marzo | 9 206 | 9 051 | 9 361 |
| Abril | 9 236 | 9 053 | 9 418 |
| Mayo | 9 339 | 9 132 | 9 545 |
| Junio | 9 363 | 9 136 | 9 591 |
| Julio | 9 370 | 9 123 | 9 617 |
| Agosto | 9 397 | 9 132 | 9 663 |
| Septiembre | 9 429 | 9 147 | 9 711 |
| Octubre | 9 468 | 9 170 | 9 766 |
| Noviembre | 9 518 | 9 205 | 9 831 |
| Diciembre | 9 585 | 9 258 | 9 912 |
Se ajustaron modelos de series de tiempo individuales adecuados al comportamiento del número de quejas acumuladas en cada una de las Visitadurías Generales de la CDHDF. Se presentaron pronósticos sustentados en regiones de confianza para el comportamiento de las mismas. Se mostró la validez de cada uno de los modelos mediante al análisis de residuales.
Contar con un modelo adecuado del comportamiento de las series, nos permite establecer cotas de comportamiento que sirvan como puntos de referencia para la detección de comportamientos anormales en el número de expedientes acumulado, de tal forma que se determine la llegada a valores atípicos que reflejen que el número de expedientes registrados ha aumentado significativamente, o bien que el número de expedientes concluidos es menor al esperado. De la misma manera será fácil determinar si el número de quejas es bajo, proporcionando fundamentos para la toma de decisiones.