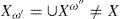El presente trabajo propone una demostración analítica de la existencia y unicidad de la función de utilidad de los consumidores. Es un ejercicio teórico que plantea la formalización de las características y definiciones matemáticas necesarias para construir una función de utilidad que represente los gustos y preferencias de cualquier individuo.
The present essay proposes an analytic proof of the existence and uniqueness of the utility function of the consumers. It is a theoretical work that presents the formalization of general characteristics and mathematical definitions needed to build an utility function that represents tastes and preferences for any individual.
El ensayo propone una reflexión analítica sobre la premisa de la teoría neoclásica, los individuos eligen las mejores cosas,1 para ello se emplea como aparato crítico el análisis del comportamiento del consumidor. A la luz de la teoría económica, se puede afirmar que el comportamiento del consumidor puede reducirse a modelar la elección de las mejores cosas, es decir, cómo los individuos seleccionan aquellos bienes y servicios que le produzcan la mayor satisfacción, con todo lo que ello implica.2 Se entiende que los gustos y preferencias de los individuos son la base de toda elección. Permítaseme un ejemplo: piense en un centro comercial. En el frenesí de consumo, es posible ver que todos los individuos eligen, pero ¿qué los conduce a elegir de tal o cual modo? Sin lugar a dudas la respuesta yace en cómo las preferencias y los gustos se estructuran y, a su vez, ordenan el conjunto de bienes que enfrenta el individuo de manera cotidiana. La naturaleza de la elección radica en la representación y posterior entendimiento de las preferencias. Tal comprensión nos proporciona una manera sencilla para explicar ese continuo buscar la combinación de bienes que genere la mayor satisfacción, siendo ahí donde la elección descansa. El ensayo desarrolla lo anterior con detenimiento.
La caracterización de las preferenciasEs momento de comenzar con los reductores de realidad. Se asume que los individuos tenemos un sistema de preferencias, generado por los gustos revelados sobre cada uno de los elementos existentes en el conjunto de los bienes, jerarquizando y ordenando uno a uno los bienes conforme con un sistema de preferencias. Basándonos en el supuesto de racionalidad del individuo, las preferencias cumplen las siguientes características:
- •
Completas
- •
Reflexivas
- •
Transitivas
- •
Completas: “∀x1, x2 ∈X se dice x1≥x2 o x1≤x2. La completud de las preferencias implica que cualesquiera dos canastas de bienes y servicios dentro del espacio de las mercancías pueden ser comparadas entre sí.
- •
Reflexivas: “∀x∈X, se dice x≥x. La reflexivilidad plantea el hecho de que cualquier canasta es al menos tan buena como ella misma.
- •
Transitivas: “∀x1, x2, x3∈X. Si x1≥x2 y x2≥x3, entonces x1≥x3. Indica que si el consumidor piensa que x1 es al menos tan buena como x2, y que x2 es al menos tan buena como x3, entonces el consumidor piensa que x1 es al menos tan buena como x3.
Las características anteriores presentan lo que se entiende como axiomas básicos o axiomas de orden, los cuales deben ser aplicables a un conjunto de elección cualquiera, permitiendo el modelaje operativo en la toma de decisiones del consumidor. En el primero la clave radica en que las canastas se pueden comparar, no existen canastas incomparables, entonces se pueden elegir entre dos canastas ya que se pueden comparar entre sí, lo que indica que siempre se puede establecer una relación de preferencias.
El segundo axioma,3 plantea que cualquier canasta es al menos tan buena como ella misma. A diferencia de los anteriores el tercero, referente a la transitividad, no es tan evidente. Este propone una hipótesis de comportamiento, entonces, no es una afirmación de lógica pura. En otras palabras, si este axioma no se cumple indica que no se están eligiendo las mejores cosas como sentencia la premisa y, por lo tanto, las preferencias del consumidor deben cumplir dicho axioma.
Siguiendo con simplificadores de realidad, es necesario que las preferencias satisfagan las siguientes características:
- •
Continuidad. ∀x1, x2 ∈X, los conjuntos {x: x1≥x2} y {x: x1≤x2} son conjuntos cerrados ⇒ los conjuntos {x: x1x2} y {x: x1<x2}son conjuntos abiertos4
- •
Monotonía débil: Si x1≥x2 ⇒ x1≥x2
- •
Monotonía fuerte: Si x1≥x2 con x1≠x2 ⇒ x1>x2
- •
Insaciabilidad local: Dado x∈X y cualquier ε<0, ⇒ ∃ un x∈X | x1-x2 |<ε ∋ x1x25.
- •
Convexidad: dados x1, x2, x3∈X, ∋ x1≥x3 y x2≥x3, entonces cumple λx1+(1-λ)x2≥x3 ∀λ∈[0, 1].
- •
Convexidad estricta:x1 ≠ x2, x3∈X, si x1≥x3 y x2≥x3. Entonces λx1+(1-λ)x2>x3 ∀λ∈[0, 1].
Ahora enunciadas las características analíticas, es menester presentar una explicación puntual. Cuando se hace referencia a la continuidad de las preferencias se nos obliga, inevitablemente, excluir todo comportamiento discontinuo en el consumidor. Permítame una explicación analítica. Si {xi} es una sucesión de canastas de consumo, donde todas son al menos tan buenas como alguna canasta x1, y si esta sucesión converge hacia una canasta x*, entonces x* es al menos tan buena como xr6 La continuidad implica lo siguiente: si x2 es una canasta estrictamente preferida a x3 y si x1 es lo suficientemente cercana a x2, entonces x1 debe ser estrictamente preferida a x3. La monotonía débil plantea que al menos mucho de todo es preferible. La monotonía fuerte es más restrictiva, dice que al menos mucho de cada bien y estrictamente más de algún bien es estrictamente mejor. La insatisfacción o insaciabilidad local plantea que podemos siempre mejorar un poco, es decir, nunca estaremos satisfechos aún y cuando estemos restringidos por pequeños cambios en la canasta de consumo. La convexidad implica que nuestro consumidor prefiere la variedad, es decir siempre preferirá medios a extremos. Este aserto generaliza el supuesto de tasas marginales de sustitución decrecientes.
Existencia de la función de utilidadYa que las preferencias del consumidor cumplen con las características expuestas en la sección anterior, es posible construir una demostración sobre la existencia de una función de utilidad. Se debe entender a la función de utilidad como la representación formal de los gustos y preferencias del individuo. Resume la manera en que cada persona interpreta su entorno, la valoración del ocio y su grado de información. Por lo tanto, se puede afirmar que es el concepto clave de la teoría económica neoclásica, ya que al definir el comportamiento del consumidor, define a la persona, las ideas y refleja su capacidad de elegir su satisfacción. La función de utilidad ui la definiremos mediante el siguiente teorema:
Sea X⊂ Rn convexo, sea ≤iun preorden de preferencias reflexivo, transitivo, completo, continuo y no saciable, definido en X. Y si ε xi∈Xi ⇒uiy es creciente y continua.
Para un mejor entendimiento de la demostración,7 es necesario dividirla en tres etapas, una que garantice la formulación de la función de utilidad, otra que hable de continuidad y la ultima que compruebe que la función de utilidad representa las preferencias. La demostración se basa en la existencia de un subconjunto numerable D de X que es denso en X.8
Si x, x’∈X satisfacen x’ ⇒ ε x∈D ∋ x’
Los cuales son disjuntos, no vacíos y cerrados en X. Dado que X es conexo no puede ser su unión,9 entonces:
Si asumimos que no hubiera ningún xÎD con la propiedad que buscamos. Esto necesariamente implicaría que D⊂Xω'∪Xω''. Por el primer aserto la adherencia10D¯, de D en X estaría contenida en la adherencia de X del conjuntoXω'∪Xω". Pero este último es cerrado ya que es la unión de dos conjuntos cerrados. Por lo que se obtendría D¯⊂Xω'∪Xω'', o dado que D=X,X=Xω'∪Xω'' lo cual es evidentemente una contradicción.
La función de utilidad a ser definida en D se denominará por u’. Si se eligen dos números reales a, b tales que a. Entonces decimos:
Si D tiene un elemento mínimo x, tomaremos u’ (x)=a.
Si D tiene un elemento máximo x, tomaremos u’(x) =b.
Extraemos de D todos los elementos indiferentes a x o a x, y llamamos D’ al conjunto restante.
Definiendo una función creciente de D’ sobre el conjunto Q’ de números racionales en el intervalo]a, b[ como sigue. Partiendo de que D’ es numerable sus elementos pueden ser ordenados (x1, x2,…, xp,…); este ordenamiento no está relacionado con el orden ≤. De modo similar, Q’ es numerable y sus elementos pueden ser ordenados (r1, r2,…, rp,…); este orden no está necesariamente relacionado con el orden ≤ Los elementos de D’ serán considerados sucesivamente; con xp se asocia un elemento rq de Q’ de tal forma que el orden se conserve y que todo elemento de Q’ acabe por ser tomado.
El proceso sería11: considerando xp, se efectúa una partición de D’ en conjuntos con las características siguientes: las clases de indiferencia de x1, x2…..xp-112, obtendríamos los intervalos de la forma] ←, xp1[, o]xpm, xpm+1 [o] xpp-1,, →] donde m xpm ≤ xpn.13 Pueden ocurrir dos casos:
Si xp está en uno de los intervalos,]xp’, xp”[ considerando el intervalo correspondiente]rqp’, rqp” [ de Q’ y seleccionando el número racional de menor rango rqp, tomando u’ (xp) =rqp.
Ahora hay que extender de D a X. Llamaremos a la función de utilidad por ser definida en X u. Si x’ pertenece a X, se escribirá el conjunto Dω'=x∈X:x≤x'yDω'=x∈X:x'≤x.
Si x es un elemento mínimo de X, tendremos u(x)=a.
Si x es un elemento máximo de X, tendremos u(x)=b.
Vamos a considerar para los casos restantes Supu’ (Dω) e Inf u’ (Dω). El siguiente paso es demostrar que ambos números son iguales.
Si x’∈Dω y x”∈Dω se tiene x’≤x”. Por lo que si r’Îu’(Dω) y r”∈u’(Dω) se tiene que r’ ≤ r” de esto se infiere directamente que Supu’(Dω) ≤ Infu’(Dω).
Supu’(Dω)<Infu’(Dω) no puede ocurrir, ya que en tal caso cualquier número racional entre ellos no sería un valor tomado de u’.
Tomando que u(x) el valor común del Sup y del Inf. Es claro que si x∈D se tiene que u’(x)=u’’(x) y u es efectivamente una extensión de D a X; en particular
Comprobando así que u es creciente
Siguiente parte verificar la continuidad de u. Sabemos que existe algún x’∈X ∋ x’∈X. Entonces utilizando la distancia euclidiana definimos d: X→R que será la función que asocia a cada x∈X la distancia entre x y x’, es decir d(x) = |x-x’|. El siguiente paso es identificar la utilidad asociada a un plan de consumo, para esto definimos un subconjunto de X, usemos C. Entonces d(C) designará la distancia entre x’ y C, en otros términos d(C) =min d(x) con x∈C. Si definimos nuestra función de utilidad, de modo que podamos comprobar mediante la función de distancias. Entonces definamos u: X→R : para cada x∈X u(x)=d[MI(x)]. En otras palabras, u(x)=min d(x’), con x’∈MI(x)14. Con esto se identifica la utilidad asociada a un plan de consumo factible con la distancia entre x’, el cual tomamos como referencia, y el conjunto de planes de consumo mejores o iguales que x. La continuidad de las preferencias y la continuidad de la función de distancia garantizan que u está bien definida para x∈X.15
Ahora la verificación de que la función de utilidad representa las preferencias. Ésta parte es bastante sencilla. Sólo es necesario probar lo siguiente: ∀x, x’∈X se cumple
La primera relación expresa de modo simple y, hasta cierto punto trivial, la definición de la función de utilidad. Indica que las alternativas mejores o iguales a x y x’ son las mismas; en este sentido se verifican uno a uno los axiomas de orden de las preferencias, entonces si las alternativas a cualesquiera dos planes de consumo son las mismas necesariamente indica que tales planes de consumo pertenecen a la misma clase de indiferencia. Por lo que se cumple la primera relación.
La segunda relación se demostrará utilizando la transitividad de las preferencias, sólo basta acotar a que sean distintos, para lo cual por tran-sitividad dos planes de consumo cualesquiera donde x>x’ necesariamente nos conduce a u(x)>u(x’). Si esto no fuera así, implicaría que x~x’ lo que violenta el orden de las preferencias y por reflexividad x>x, es decir cualquier plan de consumo es al menos tan bueno como el mismo; siguiendo con dicho razonamiento, al momento de definir ambos planes de consumo como diferentes entre si, y que la función de utilidad está definida para todo x, entonces quiere decir que los niveles de utilidad asociados a cada plan de consumo son distintos. Ahora formalicemos este razonamiento. Si x>x, tendremos x>x3x°, por transitividad se infiere MI(x)⊂MI(x’), de tal manera que u (x)>u(x’), ahora solo resta probar que sean distintos. Asumiendo u(x)=u(x’), con x~x’. Si observamos cuidadosamente u(x)=0 implica que x~x’. Para demostrarlo veamos que u(x) = 0 ⇒ d[MI(x)]=0, ∴ε x”∈MI(x)∋d(x’’)=0. Esto ocurre si x0∈MI(x), entonces tendríamos que x0≥x, y necesariamente x°~x. De aquí se infiere que si x>x’, entonces u(x)10.16 Concluyendo que sí x>x’ y u(x)=u(x’)=0 no es posible.
Es necesario llegar a una contradicción supondremos u(x)=u(x’) y sea x˜;∈X un punto ∋ dx¯=ux. Partiendo de que x˜;∈Mxsabemos que x˜;≻x≻x'. La continuidad de las preferencias, como hemos visto en la nota 28, asegura la existencia de un escalar suficientemente pequeño para determinar una combinación convexa. Sea α∈ (0,1), entonces 1−αx˜;+αx0≥x'1−αx˜;+αx0∈Mx'. Entonces decimos:
En otras palabras, u(x)≤(1-a)u(x) es únicamente posible si u(x)=0. Sabiendo que tal posibilidad ya había sido descartada, entonces x>x’ implica necesariamente que u(x)>u(x”). Quedando demostrado que la función u: Rn → R representa las preferencias del consumidor.
La última parte de la demostración consiste en probar que u es una función continua, siguiendo la lógica empleada en la prueba de la nota 28. Para cualquier escalar aeR, los conjuntos Ua+=x∈Xux≥a,Ua=x∈Xux≤a son cerrados.
Primero U(a+) es cerrado. Sea {xn}→x una sucesión en X ∋ u(xn)3a, “a, y sea x’ un punto ‘d(x’)=u (x). Por insaciabilidad sabemos que habrá algún x’’ ∈ X, arbitrariamente próximo a x’, ∋x’’>x’. La transitividad no conduce a que x’’>x. Tomando la continuidad de las preferencias asegura que a partir de un n suficientemente grande, x”≥xn. Por tanto, u(x”)≥u(xn) ≥a. Pero x’’ puede tomarse tan próximo a x’ como queramos. Como x’’>x0, d(x”)≥u(x”)>a, y por la continuidad de d(-), obtenemos que u(x’)>a. Teniendo así, u(x)=u (x’)=d (x’) ≥ a, puesto que x’~x>x0. Con lo que se prueba que el conjunto U(a+) es cerrado.
Finalmente U(a) es cerrado. Nuevamente hay que considerar una sucesión {xn}→x, pero ahora con u(xn)≤a. Sea x’n ‘d (x’n)=u(xn) para cada n. Con esto obtenemos inmediatamente que u(x’n) ≤a. Dado que la sucesión está acotada, y por ende converge a un punto x’‘u(x’) ≤a. Conforme a la segunda parte de la demostración podemos afirmar que x’n~xn ∀n, y xn→x. Tomando la sucesión {xn}→x, por continuidad sabemos que x’~x, lo que implica que u(x’)=u(x) ≤a. Con lo que se demuestra que U(a) es cerrado.
Con esto concluye la demostración, donde se prueba la existencia de una función de utilidad continua que representa las preferencias del consumidor.
La premisa completa afirma: los individuos eligen las mejores cosas con los recursos disponibles.
Es pertinente aclarar que el trabajo plantea la construcción de la función de utilidad. Esto tiene una explicación simple, es mediante esta serie de construcciones teóricas se presenta una simpliicación de la realidad que permite establecer el porqué de la elección.
Este axioma es trivial, pero hay que explicarlo, debido a que es la parte primitiva del concepto de al menos tan preferido como.
Para aquellos lectores no familiarizados les presento algunas definiciones que le serán de utilidad:
Dado un vector x∈Rn y un número real r, definimos como una bola abierta de radio r en x con Br(x) ={y∈Rn: y-x< r. A es un conjunto abierto si “∀x∈A ε algún Br(x) ∈A. Si X está en algún conjunto arbitrario y existe r>0 ‘ Br(x) ∈A entonces se dice que x está en el interior de A. El complemento de un conjunto A∈Rn consiste en todos los puntos en Rn que no están contenidos en A; y lo denotaremos como Rn/A. A es cerrado ⇔ Rn/A es abierto. Entonces, un conjunto A es acotado si existe algún x∈A y r>0 ∋ A está contenido en Br(x). Si un conjunto no vacío en Rn es cerrado y acotado se denomina compacto.
Una sucesión infinita en Rn (xi)=(x1, x2,….) es un conjunto infinito de puntos, un punto por cada posible entero, una sucesión (xi) se dice que converge a un punto x* si para cada r>0, existe un entero m ∋∀i ∀i>m, xi∈Br(x*). Podemos decir que x* es el límite de la sucesión (xi) y lo escribimos limi→∞xi=x∗. Si una sucesión converge a un punto, se le llama secuencia convergente. Podemos ahora formalizar.
Conjunto Cerrado. A es un conjunto cerrado si para cada sucesión convergente en A, converge a un punto en A.
Conjunto Compacto. Si A es un conjunto compacto, entonces cada sucesión en A tiene una subsecuencia convergente.
Expuesto lo anterior, podemos airmar que una función f(x) es continua en x* para cada sucesión (xi) que converge a x*, teniendo la sucesión (f(xi)) convergiendo a f(x*). Por lo tanto, una función que es continua en cada punto de su dominio es una función continua. Empleando cálculo se simpliica aún mas el concepto de continuidad y se deine de la siguiente forma: Sea f: R →R con regla de correspondencia (fx) y a un numero real. La función f es continua en a si se cumplen las siguientes condiciones:
- 1.
f está deinida en a, es decir existe f(a).
- 2.
Existe limi→∞fx
- 3.
limi→∞fx=fa
- 4.
Se puede ver que la deinición de continuidad de una función es respecto a un punto determinado, si se desea hablar de continuidad sin muchas complicaciones, decimos: lafunción con regla de correspondencia f(x) es continua en cada punto del dominio de la función, en donde el concepto de continua en cada punto debe cumplir las condiciones enumeradas por la definición anterior.
Aquí nuevamente me refiero a la métrica euclidiana.
Cfr. Varian, Hal R., Microeconomic Analysis, 3a. edición, WW Norton, New York, Estados Unidos 1992, p. 95.
La cual he realizado más extensa de lo que hubiese querido porque carecí de tiempo para escribirla más breve.
Todo subconjunto S de Rn contiene un conjunto numerable X ∋ S⊂X. Es decir, un conjunto arbitrario S (por lo tanto quizás no numerable) de Rn contiene un conjunto numerable X que es denso en S, es decir, ∋ para cualquier x ∈ S hay puntos de X arbitrariamente cerca de x.
Para ampliar la deinición que dimos antes decimos que un conjunto es conexo si no puede hacerse una partición del mismo en dos subconjuntos cerrados en el mismo.
Adherencia: el conjunto de los puntos adherentes a X se denomina la adherencia (cerradura) de X, se representa por x¯.
Para revisar un caso particular y, a su vez facilitar la comprensión del proceso, tendríamos que considerando x1; tomando q1=1 y u’(x1)=rq1. Considerando x2; se efectúa la partición de D’ en los siguientes conjuntos:
La clase de indiferencia de x1, los intervalos [←, x1]; y [x1, →]. Pueden ocurrir dos casos.
Si x2~x1, tomando q2=q1 y u’(x2)=rq2;
Si x2 está en uno de los intervalos, por ejemplo [←, x1], se considerará el intervalo correspondiente [a, x1] de Q’ y seleccionando en el número racional de menor rango rq2, tomaremos u’(x2]=rq2.
Es necesario destacar que el numero de conjuntos obtenidos por este método será no mayor a p-1.
Aquí se iniere que el número de intervalos no vacíos será menor o igual a p.
MI es un conjunto MI(x°)={x∈X:x≥x°}, es decir el conjunto de todas las opciones mejores o iguales que x°, dejo a usted estimado lector, la definición del conjunto de todas las opciones peores o iguales a x°.