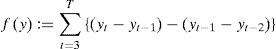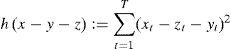La política impositiva desempeña un papel esencial para que el gobierno cumpla con sus funciones, no solo porque provee de recursos para ejercer el gasto público, sino porque los impuestos tienen efectos sobre la asignación de recursos, la distribución del ingreso y el nivel de la demanda agregada. En virtud de lo anterior, es indispensable contar con estimaciones de los ingresos que permitan tener una respuesta automática del presupuesto público ante fluctuaciones no anticipadas en el Ingreso Nacional. Por ende, en este trabajo, de acuerdo con la metodología propuesta por Engle y Granger, se propone un modelo, para estimar la recaudación del Impuesto sobre la Renta, en México.
The role of taxation is important not only because it provides resources to exercise public spending, but because taxes have effects on resource allocation, income distribution and the level of aggregate demand. In this sense, it is essential to estimate the tax collection's response to unanticipated fluctuations in the national income. Therefore, according to the methodology proposed by Engel and Granger, in this paper, a model is developed, in order to estimate and forecast the Tax Income Collection, in Mexico.
En la actualidad, la mayoría de los países tienen un sistema económico mixto, donde la distribución del ingreso no se determina, únicamente, por la forma de propiedad privada de los factores de la producción, y de sus ganancias en el mercado, sino que, también, es resultado de la intervención del Estado. El Sector Público desempeña un papel importante en el funcionamiento económico de un país, ya que determina el marco legal, para que los agentes económicos puedan desarrollar actividades productivas. Además, se encarga de proporcionar bienes públicos1 y de intervenir en los mercados en los que hay externalidades.2 Para llevar a cabo todas sus funciones, el Estado recurre a la recaudación de impuestos, mediante los instrumentos de política fiscal.
En este sentido, las funciones de la política impositiva son numerosas, pero, de acuerdo con Musgrave [1959],3 podemos mencionar las siguientes:
- 1
La provisión de bienes sociales o el proceso por el que el uso total de los recursos se divide entre bienes privados y públicos. Esta provisión se denomina función de asignación de la política impositiva. Respecto a esta función, el gobierno se preocupa por conocer los efectos de los impuestos en los precios relativos, dado que este cambio afecta la asignación de los recursos. De acuerdo con Leibfritz [1997],4 los impuestos interfieren con los incentivos a ahorrar, invertir y reducen la oferta laboral, debido al cambio en los precios relativos ocurrido cuando los impuestos son trasladados a través de las cadenas de producción y distribución. Entre más inelástica sea la oferta respecto de la demanda, la incidencia del impuesto recaerá en menor medida sobre la demanda.
- 2
Por su parte, la función de distribución es el ajuste de la distribución del ingreso y la riqueza para asegurar su adecuación a lo que se considera un estado equitativo. El gobierno se interesa en saber, ante una disminución en el gasto privado, ocasionada por impuestos, quien experimentaría una reducción en su ingreso real. En este sentido, la mayoría de los países tienen un sistema fiscal con cierto grado de progresividad. Un impuesto es progresivo si su tasa promedio se incrementa, conforme el ingreso/gasto aumenta. De acuerdo con Lewis [1984],5 si el incremento en el ingreso nacional, estuviera acompañado por un incremento en el ingreso de todas las familias, un sistema impositivo progresivo implicaría un sistema elástico respecto al ingreso.
- 3
La utilización de la política fiscal como un mecanismo para mantener un alto nivel de empleo, estabilidad de precios y una tasa de crecimiento del Producto Interno, que permita el desarrollo económico del país. Estos objetivos de la política fiscal se refieren a la función de estabilización de la política impositiva. Como menciona Capistrán, et. al. [2000],6 una regla a seguir es establecer el nivel y la composición de los ingresos de tal manera que la demanda agregada no exceda la capacidad productiva de la economía. La teoría económica indica que para cumplir con la función de estabilización, la política fiscal debe ser contra-cíclica.
Acorde con Blanchard y Fischer [1989],7 en una economía donde las fluctuaciones en el Producto Interno obedecen a cambios en la demanda agregada, la política fiscal puede ayudar a reducir los efectos en la demanda y de esta manera incrementar el Producto Interno. Sin embargo, como menciona Capistrán, una vez que se estabilizó el ingreso, es necesario considerar las distorsiones causadas por los impuestos.
A través de estas funciones, el Estado se ocupa de la división de bienes y servicios, que pueden ser producidos con los recursos disponibles, en el país, por lo que hace uso de la política fiscal y de la regulación, para lograr la asignación óptima de recursos, en el tiempo.
Descripción del Impuesto Sobre la RentaEl isr, en México, incluye el impuesto que pagan las personas físicas y el que pagan las personas morales (empresas). El isr para personas físicas grava a los residentes en México, por el total de sus ingresos percibidos, en un año calendario. Un individuo es considerado residente, en México, para efectos fiscales, en el caso en que establezca, en el territorio nacional, su casa habitación, o bien, su principal fuente de ingresos. Para el caso de los individuos no residentes en territorio nacional, la ley del isr grava, exclusivamente, los ingresos percibidos por fuente de ingresos ubicados en México. El isr de las Personas Físicas se clasifica de acuerdo con la fuente de ingreso y, en cada caso, establece requisitos específicos, para determinar la base gravable.8 Por su parte, el isr de las Personas Morales se cobra sobre la utilidad generada de la actividad empresarial. En el isr de empresas, es posible utilizar las pérdidas de un período contra las utilidades del otro, de tal manera que, visto como un flujo, se graven sólo las utilidades positivas y se tomen en cuenta las utilidades negativas. Lo anterior se logra, de manera contable, mediante la disminución de la utilidad actual, a través de la amortización de pédidas con antigüedad de 10 años, como máximo.9
En el cuadro 1, se presentan la estructuras del Impuesto Sobre la Renta, para personas físicas y morales.
Estructura del Impuesto Sobre la Renta, en México1010
La estructura corresponde a la Ley vigente para el Ejercicio Fiscal 2013. En la Iniciativa de Ley de Ingresos, para 2014, el Ejecutivo Federal propone, para el isr, diversas disposiciones tales como: restricciones al esquema de consolidación, impuestos de control sobre los dividendos y ganancias de capital, elevar la tasa marginal máxima del isr de Personas Físicas, cambios a regímenes sectoriales.
| Personas Morales | Personas Físicas | ||
| Actividades Empresariales y Profesionales | Otros Ingresos | Extranjeros confuente de ingresos en México | |
| Régimen General | Régimen General | Sueldos y Salarios | Sueldos |
| Sectoriales | Honorarios (840 mil) | Adquisición de Bienes | Honorarios |
| Consolidación | Intermedios (4 mdp) | Arrendamiento | Arrendamiento |
| Simplificado | Repecos (2 mdp) | Venta de Bienes | Venta de Bienes |
| Fines No Lucrativos | Intereses | Intereses | |
| Empresas Multinacionales | Premios | Premios | |
| Inversiones en territorios con Regímenes fiscales | Dividendos y Ganancias | Dividendos y Ganancias | |
| Maquiladoras | Otros Ingresos | Otros Ingresos | |
La idea principal en el análisis preliminar de los datos, es conocer el comportamiento de la serie, para poder aplicar apropiadamente las técnicas estadísticas. La información de la recaudación del Impuesto Sobre la Renta se encuentra disponible, con frecuencia mensual, a partir de 1990, en la página electrónica de la Secretaría de Hacienda y Crédito Público. Esta información refleja los ingresos captados por este impuesto, en flujo, es decir, conforme ingresaron en la Tesorería de la Federación. Una de las herramientas estadísticas son los gráficos de información. Por medio de la visualización de los datos, en el tiempo, se pueden detectar componentes importantes, dentro de la evolución de la serie, así como comportamientos extraños.
En el análisis gráfico, se puede observar la tendencia, que se refiere al movimiento de largo plazo de la serie, cuya característica principal es la de ser suave, en períodos largos, con relación a la unidad en que estén expresadas las observaciones de la serie. En la gráfica 1, se muestra la evolución de la recaudación de isr11 y su tendencia.12
Como se puede observar, la recaudación real sufre una caída en 1995 y 2009, debido a las crisis económicas, en ambos años. En 1995, la tasa de crecimiento real del Impuesto Sobre la Renta fue de −23.69%; mientras que, en 2009, la recaudación de isr decreció, en términos reales, 9.88%. Adicionalmente, al movimiento de largo plazo de la serie (tendencia), el análisis gráfico de los datos nos permite detectar algún tipo de comportamiento periódico de corto plazo. En particular, si la periodicidad se repite en submúltiplos del año, se puede hablar de movimientos estacionales de la serie. La estacionalidad se caracteriza por tener fluctuaciones periódicas que se repiten, cada año, en fechas e intensidad similares, que pueden medirse.
La gráfica 2 muestra el comportamiento estacional de la serie.13
El comportamiento estacional, hasta 2001, es notorio. La recaudación de Impuesto Sobre la Renta destaca en enero, abril, agosto y diciembre, debido a la estructura de los pagos provisionales. Además de la Tendencia y Estacionalidad, la variabilidad, que ha presentado la serie, no ha sido constante, ya que la crisis de 1995 afectó a la misma. La medida de variabilidad se incrementa, de manera substancial, en enero de 1995, para continuar con períodos de relativa estabilidad, hasta 2001, donde, otra vez, se presenta un incremento. Lo anterior se puede observar, en la gráfica 3.
Estimación del modelo: técnicas de relaciones causa-efectoLas relaciones causa-efecto tienen bases estructurales que pueden existir entre las variables involucradas en el análisis. En este sentido, es necesario determinar cuáles variables pueden estar o están relacionadas de forma estructural, es decir, que mantienen una relación estable de largo plazo. Este tipo de relaciones es importante en la teoría económica, dado que se condiciona el comportamiento de una variable dada con el comportamiento de otras variables. Por esto, se debe identificar a las variables que pueden determinar el comportamiento de la recaudación de Impuesto Sobre la Renta. Sin embargo, antes de iniciar con el análisis de las relaciones estructurales, las series económicas deben cumplir con ciertas características, necesarias para utilizar este tipo de modelos, en particular el de la estacionariedad o la no presencia de raíces unitarias, en la serie. En 1976, Dickey y Fuller desarrollaron una prueba para determinar si una serie es estacionaria. En el modelo general, la prueba se aplica a una regresión del tipo:
La inspección de la gráfica 3 nos advierte que el comportamiento de la serie no se da alrededor de una tendencia lineal, pero si podemos notar la presencia de un intercepto, por lo que la prueba se realizó, sin tendencia, pero con ordenada al origen. La Tabla 1 muestra los resultados para la serie de isr, en niveles.
La prueba revela que la serie de recaudación del Impuesto Sobre la Renta no es estacionaria, en niveles, es decir, no es posible rechazar la hipótesis nula de que existe, al menos, una raíz unitaria, para la serie, al nivel de significancia de 5%. Para estimar la regresión, la elección del número de rezagos, se hizo con base en la prueba de correlación serial de orden 2, es decir, se fueron aumentando rezagos hasta eliminar la correlación serial en los residuales de la ecuación 1.
En la tabla 2, se presentan los valores del estadístico de prueba, así como los valores de (n − p) R2.
En este caso, el p-valor es mayor que 0.05, por lo que No se rechaza Ho, que postula la no presencia de correlación. Concluimos que los residuales de la regresión Dickey-Fuller no presentan correlación serial. En este caso, para volver estacionaria la serie, se propone la primera diferencia regular de la Recaudación del Impuesto Sobre la Renta. La Tabla 3 muestra los resultados para la serie de isr, en primeras diferencias regulares.
Para la primera diferencia regular de la serie, el valor absoluto del estadístico dfa es mayor, en valor absoluto, a cualquiera de los valores críticos de la prueba. Por lo anterior, en primera diferencia regular, la serie no presenta raíz unitaria, por lo que, en esta situación, es estacionaria, es decir, la serie de recaudación del isr.
Si una variable x es integrada de orden d y una variable z es integrada de orden d, la combinación lineal de ambas puede resultar en una variable integrada de orden cero, es decir, estacionaria, en niveles, indicativo que x y z están co-integradas. Por lo anterior, se tiene que determinar la posible variable co-integrada con la Recaudación del isr. En este sentido, una variable que mida el desempeño de la actividad económica puede ser un fuerte candidato, para establecer una relación de equilibrio de largo plazo con la recaudación. Dada la frecuencia de observación de la serie, se considera el pib, como indicador de la actividad económica.14 En la gráfica 4, se muestra la relación entre la Recaudación del Impuesto Sobre la Renta y el Producto Interno Bruto.
Como se puede observar, existe una relación entre la evolución de la recaudación de isr y el pib, por lo que se considera que puede existir una relación de equilibrio de largo plazo entre la recaudación y el producto interno. La frecuencia mínima del pib es trimestral, por lo que el análisis de la información se hace con esta frecuencia. Se debe determinar el orden de integración de la variable, con frecuencia trimestral. En la Tabla 4, se presentan los resultados para la serie de isr y pib, en niveles.
Resultados de la Prueba de Raíz Unitaria y Correlación (cifras trimestrales)
| Serie | Estadístico dfa | Nivel de Confianza (%) | Valor Crítico | Serie | (n − p) R2 | χP2>n−pR2 |
| isr | −0.3338 | 1 | −3.52 | isr | 1.4686 | 0.479 |
| 5 | −2.90 | |||||
| 10 | −2.58 | |||||
| Serie | Estadístico dfa | Nivel de Confianza (%) | Valor Crítico | Serie | (n − p) R2 | χP2>n−pR2 |
| pib | −0.0627 | 1 | −3.52 | pib | 2.0022 | 0.36 |
| 5 | −2.90 | |||||
| 10 | −2.58 |
En ambos casos, los estadísticos dfa son, en términos absolutos, menores a los valores críticos, por lo que al menos hay una raíz unitaria, en cada serie. En la tabla 5, se muestran los resultados para la primera diferencia regular de cada serie.
Resultados de la Prueba de Raíz Unitaria y Correlación (cifras trimestrales)
| Serie | Estadístico dfa | Nivel de Confianza (%) | Valor Crítico | Serie | (n − p) R2 | χP2>n−pR2 |
| Δisr | −4.0156 | 1 | −3.52 | ΔISR | 1.142 | 0.5648 |
| 5 | −2.90 | |||||
| 10 | −2.58 | |||||
| Serie | Estadístico dfa | Nivel de Confianza (%) | Valor Crítico | Serie | (n − p) R2 | χP2>n−pR2 |
| Δpib | −4.1449 | 1 | −3.52 | ΔPIB | 1.993 | 0.369 |
| 5 | −2.90 | |||||
| 10 | −2.58 |
Dado que el isr∼i (1) y el pib∼i (1) (ambas series son estacionarias, aplicando la primera diferencia regular), es posible estimar el Modelo de Corrección de Errores, utilizando el método de estimación en dos etapas de Engle y Granger (1987).
Primera Etapa: se estima el modelo de regresión de largo plazo.
Donde Rt es la recaudación al tiempo t, VEC, es la variable explicativa co-integrada, es el error de la regresión. Adicionalmente, se añaden variables dicotómicas: i) crisis1: modela el efecto de la crisis económica de 1995 ; ii) crisis 2: modela el efecto de la crisis de 2009; iii)ietu: refleja la entrada en vigor del Impuesto Empresarial a Tasa Única; iv) Primer Trimestre: describe el pago de Renta del flujo de ingreso, generado en Diciembre y la Declaración Anual de las Personas Morales; v) Segundo Trimestre: modela la declaración anual de las personas físicas; vi) Efecto90: para reflejar el efecto de la implementación del Régimen Intermedio, para personas físicas y del Régimen Simplificado, para personas morales, en 1990; vii) Ref07: modela cambios en el Impuesto Sobre la Renta, que entraron en vigor, a partir de ese año, por ejemplo: se redujo la deducibilidad de la inversión en automóviles de 300 a 175 mil pesos; se redujo la deducibilidad de los gastos en restaurantes de 25 a 12.5 por ciento; se limitó la exención en el isr a los ingresos por la enajenación de casa habitación, a una operación por ejercicio fiscal; se eliminó la deducibilidad de las deudas de la base gravable del Impuesto al Activo impac, y se redujo su tasa impositiva de 1.8 a 1.25%; se concluyó el proceso gradual de las tasas del isr empresarial y la máxima de personas físicas, situándolas en 28%. Un resumen, con las variables indicadoras, se presenta en la tabla 6.
Variables Dicotómicas Modelo de Regresión
| Crisis1=1∀t∈1995.4−1996.20∀t∉1995.4−1996.2 | Crisis2=1∀t∈2008.2−2009.40∀t∉2008.2−2009.4 |
| ISRTrim1=1∀Trimestre=10∀Trimestre≠1 | ISRTrim2=1∀Trimestre=20∀Trimestre≠2 |
| IETU=1∀t∈2008.1−2011.40∀t∉2008.1−2011.4 | Efecto90=1∀t∈1993.1−1994.40∀t∉1993.1−1994.4 |
| Ref07=1∀t∈2007.1−2007.40∀t∉2007.1−2007.4 |
Los resultados de la regresión se reportan en la Tabla 7.
Resultados del Modelo de Regresión Largo Plazo
| Variable | Coeficiente | Desv. Est. | Estadístico t | P-Valor |
| Constante | −51,228.57 | 9,339.93 | −5.48 | 0.00000 |
| pib | 0.02 | 0.00 | 13.05 | 0.00000 |
| Crisis_2009 | −10,698.74 | 3,438.77 | −3.11 | 0.00270 |
| ietu | 20,253.94 | 3,234.76 | 6.26 | 0.00000 |
| Crisis_1995 | −8,866.21 | 4,361.75 | −2.03 | 0.04600 |
| Efecto_1990 | 14,259.89 | 2,689.34 | 5.30 | 0.00000 |
| Trimestre1 | 18,905.73 | 1,951.58 | 9.69 | 0.00000 |
| Trimestre2 | 10,931.98 | 1,903.07 | 5.74 | 0.00000 |
| Reforma07 | 12,777.12 | 3,980.28 | 3.21 | 0.00200 |
* R2=92.85 y F=108.92.
El signo de los coeficientes concuerda con lo esperado, todos los coeficientes resultaron significativos, a 95% nivel de confianza y el p-valor de la Prueba LM, con un rezago, es 0.53, indicativo que los residuales de la regresión no tienen auto-correlación de orden uno. El ajuste es relativamente bueno, ya que el coeficiente de determinación R2=0.9285; es decir; 93% de las variaciones en la recaudación de isr son explicadas por variaciones en las variables exógenas. La metodología de Engle y Granger establece que los residuales no deben presentar alguna raíz unitaria. Con este propósito, se realiza la siguiente regresión:
Bajo la hipótesis Nula. δ=0 (no cointegración). El valor crítico para T=100 y α=5% es −3.398,15 entonces 8.439>3.398. Por lo tanto, rechazamos H0, esto es, la recaudación y el pib están co-integradas, por lo que existe una relación de largo plazo entre las dos variables.
De esta manera, y considerando los resultados de la estimación, en (3), la inferencia que se extrae de ésta se puede considerar válida, para el horizonte de tiempo de la muestra.
En el cuadro 2, aparecen las auto-correlaciones generadas al especificar la el modelo (3), donde el estadístico Q de Ljung-Box confirma que los residuos no se encuentran correlacionados.
Auto-Correlaciones de los Residuos Prueba de Co-Integración
| Auto-Correlación Total | Auto-Correlación Parcial | Estadístico Q | P-Valor |
| 0.017 | 0.017 | 0.0232 | 87.90% |
| 0.126 | 0.126 | 1.2693 | 53.00% |
| 0.005 | 0.001 | 1.2717 | 73.60% |
| 0.361 | 0.351 | 11.75 | 1.90% |
| −0.141 | −0.176 | 13.37 | 2.00% |
| −0.019 | −0.095 | 13.401 | 3.70% |
| −0.017 | 0.021 | 13.426 | 6.20% |
| 0.154 | 0.048 | 15.435 | 5.10% |
| −0.001 | 0.121 | 15.435 | 8.00% |
| −0.043 | −0.066 | 15.599 | 11.20% |
| 0.103 | 0.094 | 16.544 | 12.20% |
| −0.039 | −0.143 | 16.68 | 16.20% |
| 0.011 | 0 | 16.691 | 21.40% |
| −0.169 | −0.114 | 19.381 | 15.10% |
| 0.045 | −0.016 | 19.57 | 18.90% |
| −0.189 | −0.104 | 23.047 | 11.20% |
| −0.094 | −0.142 | 23.915 | 12.20% |
Segunda Etapa: Modelo de Mecanismo de Corrección de Errores (mce)
Este modelo explica la primera diferencia regular de la serie endógena, con el error rezagado de la estimación de largo plazo (estacionario), las diferencias rezagadas de la variable exógena y de la misma endógena.
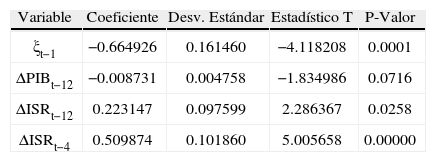
El cuadro 3 presenta los resultados de las estimaciones del modelo descrito en (4).
Todos los coeficientes son estadísticamente significativos, a 5%, con excepción del coeficiente asociado a la diferencia regular del rezago de orden 12 del pib, que es significativo a 10%. El signo negativo para el coeficiente del error rezagado actúa para restaurar el equilibrio, en el siguiente período, en este caso, trimestralmente. Si la Recaudación del Impuesto Sobre la Renta y el pib no están en equilibrio en el período t−1, entonces el mecanismo de corrección del error actúa para regresar el isr a la relación estable de largo plazo, que guarda con el pib. Para el caso de la serie de recaudación del isr, se observa que su desviación respecto del nivel de equilibrio se corrige trimestralmente en 66%, aproximadamente, es decir, la proporción del desequilibrio del isr, en t−1, corregida en t, es 66%; en otras palabras, la velocidad de ajuste, de la Recaudación de isr, hacia su valor de equilibrio de largo plazo es 66 por ciento.
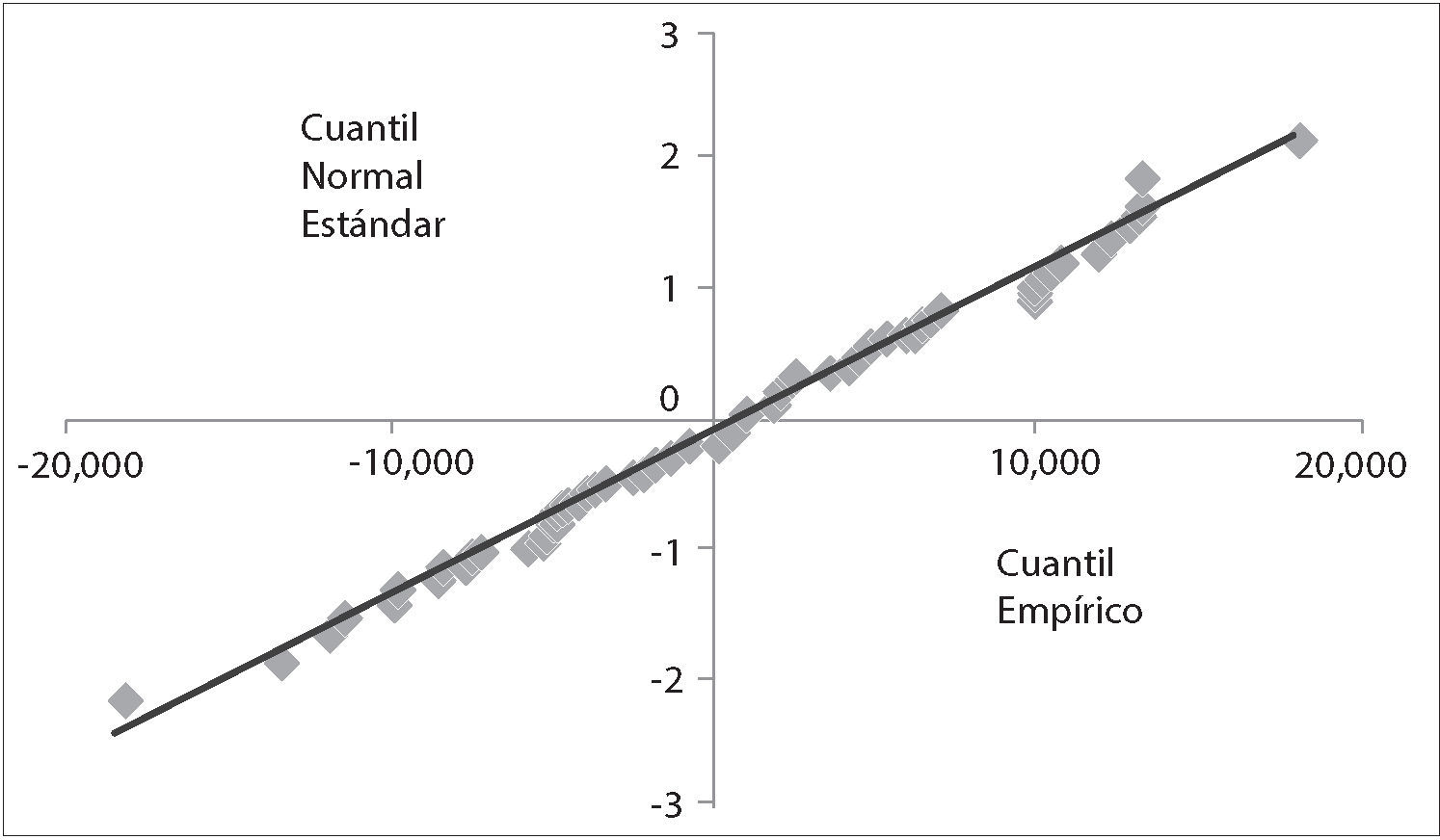
Verificación de los supuestos del modeloNormalidad en los ResidualesEn primera instancia, se realizó la gráfica de probabilidad normal (Cuantil – Cuantil), donde el eje de las frecuencias acumuladas se encuentra en una escala que corresponde al de las probabilidades acumuladas de la distribución normal, es decir, los cuantiles de la distribución normal estándar se pueden expresar como una función lineal de los cuantiles de la distribución empírica, por lo que debido a que las transformaciones lineales preservan la normalidad, si los datos ajustan a una línea recta, se puede concluir que los residuales se distribuyen de manera normal. En la gráfica 5 se observa este análisis.
Los puntos graficados presentan el comportamiento aproximado de una línea recta, teniendo pequeñas fluctuaciones, por lo que concluimos que los datos provienen de una distribución normal. La implicación de la gráfica cuantilcuantil es que si los datos, en la gráfica, estuviesen sobre una línea recta de 45 grados, las observaciones seguirían exactamente la distribución empírica propuesta, en este caso, la Normal. Si es una recta pero no de 45 grados sería indicativo que los datos deben transformarse linealmente para ajustarse a la distribución empírica. Aunado a lo anterior, el p-valor de la Prueba Jarque-Bera es 0.8327, por lo que concluimos que los Residuales se distribuyen normalmente. Por su parte, en el cuadro 4, aparecen las auto-correlaciones generadas al especificar la el modelo (4).
Auto-Correlaciones de los Residuos MCE
| Auto Correlación | Auto Correlación Parcial | Estadístico Q | P-Valor |
| −0.074 | −0.074 | 0.3604 | 54.80% |
| −0.376 | −0.383 | 9.8481 | 0.70% |
| 0.085 | 0.021 | 10.339 | 1.60% |
| 0.129 | −0.006 | 11.495 | 2.20% |
| −0.034 | 0.021 | 11.579 | 4.10% |
| −0.093 | −0.058 | 12.206 | 5.80% |
| −0.194 | −0.256 | 14.959 | 3.70% |
| 0.093 | −0.004 | 15.599 | 4.80% |
| 0.209 | 0.086 | 18.918 | 2.60% |
| −0.095 | 0.001 | 19.621 | 3.30% |
| −0.173 | −0.08 | 21.976 | 2.50% |
| 0.023 | −0.104 | 22.018 | 3.70% |
| 0.121 | −0.006 | 23.226 | 3.90% |
| 0.03 | 0.026 | 23.304 | 5.60% |
| −0.121 | −0.028 | 24.557 | 5.60% |
| −0.054 | −0.024 | 24.807 | 7.30% |
El p-valor del estadístico Q de Ljung-Box confirma que los residuos no se encuentran correlacionados. Como aproximación a la varianza de los residuales del modelo, se elevaron al cuadrado los mismos. La función de Auto-Correlación de los Residuales al cuadrado, se presenta en el cuadro 5.
Auto-Correlaciones de la Varianza para los Residuos MCE
| Auto Correlación | Auto Correlación Parcial | Estadístico Q | P-Valor |
| −0.15933 | −0.15933 | 1.67669 | 19.54% |
| 0.29668 | 0.27836 | 7.58543 | 2.25% |
| −0.09747 | −0.02114 | 8.23379 | 4.14% |
| 0.15906 | 0.07032 | 9.98983 | 4.06% |
| −0.16382 | −0.11909 | 11.88457 | 3.64% |
| 0.01643 | −0.08478 | 11.90398 | 6.41% |
| −0.07966 | −0.00711 | 12.36801 | 8.91% |
| 0.01374 | 0.00372 | 12.38206 | 13.50% |
| −0.03086 | 0.02063 | 12.45428 | 18.89% |
| −0.16081 | −0.19902 | 14.45221 | 15.33% |
| 0.00336 | −0.04085 | 14.45310 | 20.89% |
| −0.21829 | −0.17021 | 18.27904 | 10.75% |
| 0.06920 | 0.03442 | 18.67128 | 13.37% |
| −0.21122 | −0.09063 | 22.39987 | 7.08% |
De nuevo, el p-valor del estadístico Q de Ljung-Box confirma que la varianza de los residuos no presenta correlación serial, que nos haga suponer la variabilidad de la misma. Adicionalmente, se realizó la prueba dfa, en aras de establecer si la serie de residuales presenta alguna raíz unitaria.
El estadístico es mayor, en valor absoluto, a los valores críticos de la prueba, por lo que rechazamos la hipótesis nula, a favor de la estacionariedad de los residuales del Modelo de Corrección de Errores.
PronósticoUna vez que se verificó la estacionariedad y distribución de los residuales, en el Modelo de Corrección de Errores, el siguiente paso es pronosticar. El modelo se estimó hasta el último trimestre de 2011, por lo que se evaluó su capacidad predictiva, en 2012. En la gráfica 6, se presentan los valores estimados del modelo y las observaciones de la serie.
Dada la característica del Modelo de Corrección de Errores, el Pronóstico puede darse para un período, ya que depende del residual de la regresión de co-integración, con un período de rezago. No obstante, en el cuadro 6, se presenta el pronóstico con el Mecanismo de Corrección de Errores y una Combinación de Pronósticos del Método Propuesto por el autor y el Modelo Holt-Winters Multiplicativo.
Combinación de Pronósticos/1
| Tiempo | Valor Observado | Pronóstico MCE(1) | Tendencia Estacionalidad/2 (2) | Holt-Winters (3) | Combinación (2) y (3) |
| 2012 Trim1 | 150 488.21 | 149,831.67 | 154,837.31 | 147,518.50 | 150,372.83 |
| Tiempo | Valor Observado | Pronóstico MCE (1) | Tendencia Estacionalidad (2) | Holt-Winters (3) | Combinación (1) y (3) |
| 2012 Trim1 | 150 488.21 | 149,831.67 | 154,837.31 | 147,518.50 | 149,808.54 |
| Tiempo | Valor Observado | Pronóstico MCE (1) | Tendencia Estacionalidad (2) | Holt-Winters (3) | Combinación (1) y (2) |
| 2012 Trim1 | 150 488.21 | 149,831.67 | 154,837.31 | 147,518.50 | 150,482.45 |
Las técnicas de relación causa-efecto constituyen una herramienta útil, para analizar las relaciones estables de largo plazo que existen entre diversas variables económicas. Lo anterior, a través de un marco teórico consistente, propuesto por Engle y Granger, que permite resumir el efecto que tienen cambios en la actividad económica. En este trabajo, se propuso un modelo de estimación para la serie de Recaudación del Impuesto Sobre la Renta. También, dado que la combinación lineal de pronósticos permite incorporar toda la información valiosa utilizada en cada una de dichas predicciones y supera a las metodologías empleadas de manera individual, se pronosticó el comportamiento de la serie, mediante el empleo de tres modelos, incorporando la restricción de minimizar el error cuadrático, así como la no negatividad y exclusión del cero, en el dominio de los ponderadores de la combinación lineal. En este caso, podemos concluir que la mejor combinación lineal es la que incorpora las predicciones del mecanismo de corrección de errores y el método propuesto, para la extracción de la Tendencia y Estacionalidad.16
ApéndiceUn método de pronóstico, para un Modelo de Extracción de los Componentes Estacional y Tendencial, en una Serie de Tiempo.
En este trabajo, la descomposición de una serie de tiempo, en tendencia y estacionalidad se plantea como un problema de optimización. Se presenta, también, un método para pronosticar, mediante la extracción dichos componentes. En específico, se utiliza la serie del Producto Interno Bruto Trimestral en el período 1993–2012.
2. Modelo de PronósticoEl problema es descomponer una serie de tiempo {xt}t = 1, 2, … T en tendencia {yt}t = 1, 2, … T, un componente estacional {zt}t = 1, 2, … T, y un componente estocástico {ut}t = 1, 2, … T, tal que:
O de manera equivalente:
Donde x, y, z y u son vectores de dimensión T x 1. Existen ciertas características, que se deben presentar en los componentes de tendencia y estacionalidad, mencionados, en la siguiente sección.
- 1.
La suma de la tendencia y estacionalidad deben reflejar el comportamiento de la serie de la mejor manera posible, es decir, el componente estocástico u − x − y − z debe minimizarse. Se utiliza la función h: RT → R como medida de u, en específico, la suma de errores al cuadrado h(u) = uTu, la cual se minimiza.
- 2.
La tendencia requiere ser lo más suave posible, en aras de reflejar el comportamiento de largo plazo de la serie, es decir, sea la función f: RT → R una medida de la curvatura del componente tendencial. Se busca mantener lo más suave posible a f(y)
- 3.
El componente estacional debe ser estable. De nuevo, sea una función g: RT → R que mide la inestabilidad del patrón estacional, entonces se requiere minimizar g(z).
El modelo propuesto cumple con estas tres especificaciones.
- 1.
Una medida de la curvatura de la tendencia f: RT → R.
- 2.
Una medida de inestabilidad para el componente estacional g: RT → R.
- 3.
Una medida para el componente aleatorio h(u) = uTu.
La Tendencia y = y(x) y el componente estacional z = z(x) se obtienen mediante el siguiente problema de optimización:
La forma funcional, para la medida de la curvatura de tendencia es:
La medida, para la inestabilidad del patrón estacional se modela mediante:
Donde s es un número natural más grande que uno y menor que T, que denota la longitud del período estacional, por ejemplo, s=12, en el caso de datos mensuales.
La medida para el componente aleatorio se presenta, en la ecuación (6).
Dadas las formas funcionales (4), (5) y (6) el problema de optimización (3) tiene una única solución dada por el método de mínimos cuadrados.
Definimos el operador diferencial, en la ecuación (7).
De dimensiones (T+p−2, T+p) p = Períodos a Pronosticar
Sea la matriz de agregación:
Con dimensiones (T+p−s+1, T+p) s= orden del período estacional
Las matrices 7 y 8 nos permiten escribir (3) como:
Donde se incorporan columnas con valor de cero, en aras de modelar el pronóstico.
El sistema descrito en (9) se resuelve mediante mínimos cuadrados ordinarios.
Como ilustración numérica del método propuesto, se propone el siguiente vector numérico: x=(1, 2, 3, …, 10)T Con s=2.
El problema de regresión es:
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | −2 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
Para el caso del pib tenemos:
La estructura corresponde a la Ley vigente para el Ejercicio Fiscal 2013. En la Iniciativa de Ley de Ingresos, para 2014, el Ejecutivo Federal propone, para el isr, diversas disposiciones tales como: restricciones al esquema de consolidación, impuestos de control sobre los dividendos y ganancias de capital, elevar la tasa marginal máxima del isr de Personas Físicas, cambios a regímenes sectoriales.
En honor de Emilio Caballero, profesor de Estudios Profesionales de la Facultad de Economía de la unam, a quien, aunque no tuve la oportunidad de conocer, le estoy agradecido, porque su obra me ayudó a comprender la realidad tributaria de este país. Donde quiera que esté, profesor, lo saludo con admiración, respeto y agrado.
Bienes que se caracterizan por la no exclusión en su consumo y por ausencia de rivalidad, en el mismo. El elevado costo de excluir, selectivamente, del goce de un bien a quienes no pagaron por él, ocasiona que su producción no resulte atractiva, para el sector privado de la economía. Por ello, el gobierno tiene la necesidad de obtener ingresos, para proveer a la sociedad de bienes públicos que tienen una valoración, aunque no se comercialicen, en el mercado.
En ocasiones, sucede que las acciones de algunos agentes económicos afectan directamente el bienestar de otros miembros de la sociedad. La Teoría Económica conoce esto como una externalidad. Las personas afectadas no tienen influencia sobre las decisiones que alteran su bienestar, ya que son tomadas por individuos externos a ellos.
Musgrave, R.A. (1959) The Theory of Public Finance. New York.
Leibfritz, Willi, Thornton, John, y Bebbee, Alexandra (1997) Taxation and Economic Performance, oecd. Economics Department.Working Paper núm. 176, 141 p.
Lewis, Stephen R. Jr. (1984) Taxation for Development. Principles and Applications. New York.Oxford University Press.
Capistrán, Carlos (2000) Elasticidad Ingreso del isr: una aplicación de la metodología general a particular en econometría. México. Instituto Tecnológico Autónomo de México.
Blanchard, Oliver Jean, y Fischer, Stanley (1989) Lectures on Macroeconomics. eua.mit Press.
Cuando las personas físicas también tengan casa habitación, en otro país, se considerarán, para efectos fiscales, residentes en México, cuando más del 50% de sus ingresos totales tengan fuente de riqueza en México o cuando, en el país, tengan el centro principal de sus actividades profesionales.
Artículo 61 Ley del Impuesto Sobre la Renta.
Los valores de la series están expresados en millones de pesos de 2003. Para deflactar, se utilizó un índice de precios implícito, tal que la suma de los valores nominales, en el año base, sea igual con la suma de los valores en términos reales del año base.
Para la extracción de la Tendencia, se utilizó el modelo propuesto por el autor.Véase: José Alberto Bravo, “Un Método de Pronóstico, para un Modelo de Extracción del Componente de Tendencia, en una serie de Tiempo.”, Otoño de 2013. Una versión de este documento se encuentra, en el Apéndice de este ensayo.
elaboración propia, con base en cifras de recaudación reales de 2003 y el Método de Extracción, de la Estacionalidad, propuesto por el autor.