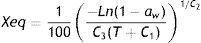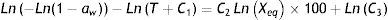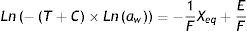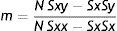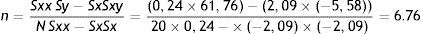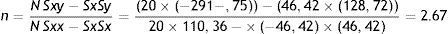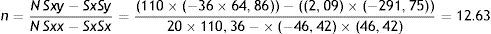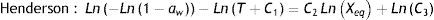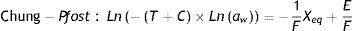Aplicación del método de los mínimos cuadrados para la obtención de los parámetros de los modelos de Henderson y Chung-Pfost

Díaz-Martín, Ricardo; Sanglier-Contreras, Gastón; Guardiola-Mouhaffel, Adib

doi:10.1016/j.eq.2015.04.008

Información del artículo

Resumen

Texto completo

Bibliografía

Descargar PDF

Estadísticas

Figuras (1)

Tablas (5)

Tabla 1. Determinación de pares de datos, a partir de resultaros empíricos, para el cálculo de parámetros por el método de mínimos cuadrados

Tabla 2. Determinación de pares de datos a partir de resultados empíricos, para los métodos de Henderson y Chung-Pfost

Tabla 3. Parámetros de mínimos cuadrados para los modelos de Chung-Pfost y de Henderson

Tabla 4. Parámetros de los modelos de Chung-Pfost y de Henderson

Tabla 5. Contenidos de humedad de equilibrio en diferentes biomasas, método de sales saturadas

Mostrar másMostrar menos

Resumen

Se desarrollan modelos matemáticos que predigan los puntos de equilibrio de humedad de los materiales higroscópicos que habitualmente se transportan, y la explicación de la obtención de los métodos de cálculo de los parámetros mediante regresión lineal de los mínimos cuadrados nos dará una comprensión complementaria.

Palabras clave:

Chung-Pfost

Henderson

Mínimos cuadrados

Astillas

Abstract

Mathematical models development to predict moisture equilibrium points in hygroscopic materials usually logistically transported. Parameters are calculated through least squares method.

Keywords:

Chung-Pfost

Henderson

Least squares

Pellets and wood chips

Texto completo

Introducción

Las astillas son un material higroscópico, lo cual indica que el agua que contiene es constante si se encuentra en equilibrio con el agua en estado de vapor del aire de la atmósfera que la rodea (Prieto García, 2006, Gordillo Martínez, Prieto Méndez, Gómez Aldapa y Román Gutérrez, 2006), de modo que las condiciones de los habitáculos o contenedores donde se transporten son determinantes para conservar su buen estado y sus propiedades.

El método de los mínimos cuadrados permite, mediante los pares compuestos por los resultados de la humedad generada por las sales y la humedad adsorbida por la biomasa, calcular los parámetros característicos de los modelos de Henderson y Chung-Pfost utilizados para predicción de estados en el transporte de esta.

Tanto las astillas como otras biomasas derivadas de la madera, como los pellets, son materiales que poseen la característica de adaptarse a la humedad del ambiente en que se encuentren; así, el contenido de humedad se adapta hasta alcanzar el equilibrio (Henderson, 1952). Las curvas de adsorción describen el cambio que sufren las biomasas al verse expuestas a condiciones higrotérmicas determinadas, de aumento progresivo hasta llegar a la humedad de equilibrio; la relación entre el contenido de humedad y la actividad del agua da la información necesaria para modelizar los materiales evaluados (García-Pérez, 2008, Cárcel, Clemente y Mulet, 2008).

Las astillas de pino resultan de introducir la madera directamente en una astilladora, la forma básica de producción de biomasa en madera, mientras que el proceso de obtención de los pellets requiere el prensado de la madera; la lignina realiza la función de aglomerante, con lo que aumenta la densidad de la madera, que no tiene que ser necesariamente de la tala de árboles, si no que se puede recuperar de carpinterías y podas.

En la madera del pino, las hemicelulosas que forman parte de la matriz junto con la lignina, donde reside la celulosa, son un 35% y donde se almacena el agua cuando se absorbe; la hemicelulosa y la lignina representan cada una un 24% de la madera.

Procedimientos experimentales

Dos baños termostáticos (a 15 y 35°C) sobre diez recipientes con diferentes humedades relativas proporcionan los datos necesarios para la regresión lineal por mínimos cuadrados.

Los datos serán la humedad relativa generada en cada recipiente y la cantidad de agua absorbida por las astillas, según el método gravimétrico estático de las sales ácidas (García Esteban, 2004, Guindeo Casasús, de Palacios y García Fernández, 2004).

Modelos matemáticos

La formación de pares entre la predicción y el estado de saturación del agua para cada sal es característico de cada modelo y dan lugar a las rectas de ajuste.

En este caso se ha elegido los modelos de Henderson y Chung-Pfost, aprobados por la Sociedad Americana de Ingenieros Agrícolas para el maíz y el arroz paddy, y los más comunes por su generalidad y relativa precisión (Muñoz et al., 1991), además de ser los únicos que tienen como variable la temperatura, dicho modelos son los únicos que consideran la temperatura en el análisis de isotermas de adsorción (García Fernández, 2013, Simón García, Esteban, de Palacios, Fernández-Golfín y Conde, 2013).

A partir de los modelos, se obtienen las respectivas ecuaciones linealizadas.

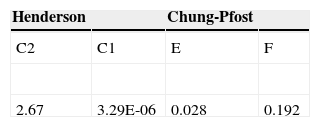
Ecuación de Henderson modificada

Fórmula 1, ecuación de Henderson modificada:

Xeq: contenido de humedad en equilibrio, %. aw: actividad del agua en el elemento. T: temperatura (°C). C1: constante de Henderson. C2: constante de Henderson. (Handbook of Industrial Drying, 2006.)

Fórmula 2, ecuación de Henderson linealizada:

Ecuación de Chung-Pfost modificada

Fórmula 3, ecuación de Chung-Pfost modificada:

Xeq: contenido de humedad en equilibrio %. aw: actividad del agua en el elemento. T: temperatura (°C). E: constante de Chung-Pfost. F: constante de Chung-Pfost. (Handbook of Industrial Drying, 2006.)

Fórmula 4, ecuación de Chung-Pfost linealizada:

Parámetros de ajuste de mínimos cuadrados

Fórmula 5, ecuación de ajuste mínimos cuadrados:

Ecuación de Chung-Pfost modificada

Fórmula 6, ecuación de ajuste mínimos cuadrados (método regresivo lineal, cálculo estadístico).

Objetivos

Explicar cómo, a partir de un procedimiento experimental de equilibrios de adsorción de humedad, podemos realizar un comportamiento predictivo de unas muestras de astillas de pino canario mediante los modelos matemáticos de Henderson y Chung-Pfost, desarrollando detalladamente la utilización de la técnica de análisis numérico de los mínimos cuadrados.

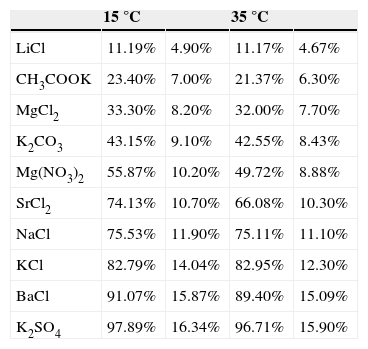
Metodología

Se ha utilizado un procedimiento de análisis gravimétrico para evaluar los porcentajes de humedad adsorbidos por las muestras, las cuales fueron previamente expuestas a diez sales ácidas (Li CL, CH3COOK, MgCl2, K2CO3, Mg (NO3)2, Sr Cl2, Na Cl, K Cl, Ba Cl, K2S O4) en recipientes cerrados hasta alcanzar su equilibrio, a las temperaturas de 15 y 35°C. Cada sal genera una humedad relativa característica en el interior de los recipientes (tablas 1 y 2).

Tabla 1.

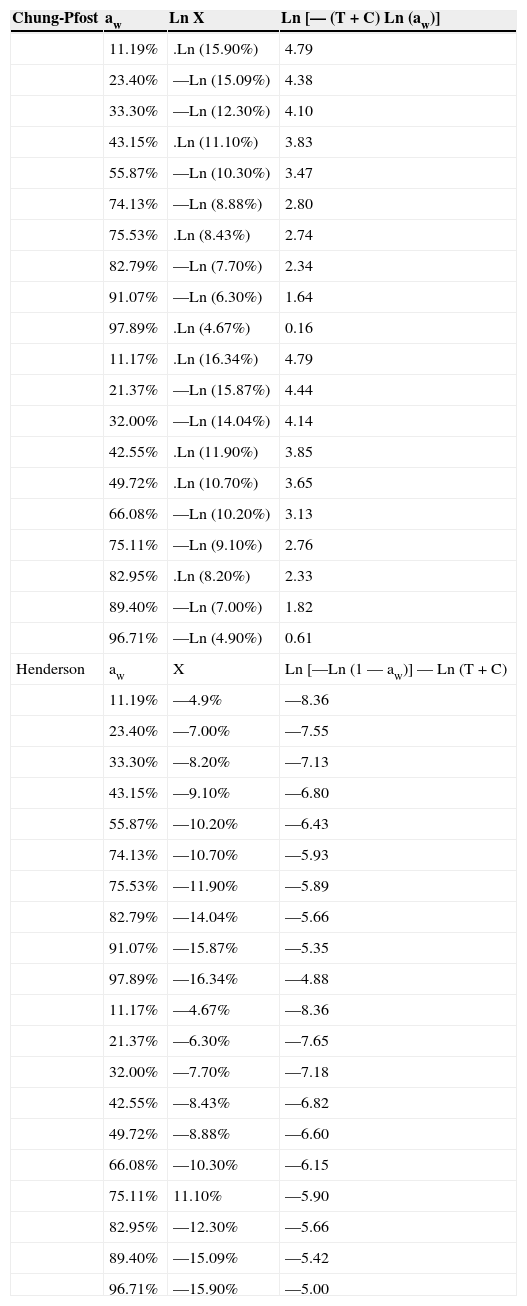
Determinación de pares de datos, a partir de resultaros empíricos, para el cálculo de parámetros por el método de mínimos cuadrados

Chung-Pfost	aw	Ln X	Ln [— (T + C) Ln (aw)]
	11.19%	.Ln (15.90%)	4.79
	23.40%	—Ln (15.09%)	4.38
	33.30%	—Ln (12.30%)	4.10
	43.15%	.Ln (11.10%)	3.83
	55.87%	—Ln (10.30%)	3.47
	74.13%	—Ln (8.88%)	2.80
	75.53%	.Ln (8.43%)	2.74
	82.79%	—Ln (7.70%)	2.34
	91.07%	—Ln (6.30%)	1.64
	97.89%	.Ln (4.67%)	0.16
	11.17%	.Ln (16.34%)	4.79
	21.37%	—Ln (15.87%)	4.44
	32.00%	—Ln (14.04%)	4.14
	42.55%	.Ln (11.90%)	3.85
	49.72%	.Ln (10.70%)	3.65
	66.08%	—Ln (10.20%)	3.13
	75.11%	—Ln (9.10%)	2.76
	82.95%	.Ln (8.20%)	2.33
	89.40%	—Ln (7.00%)	1.82
	96.71%	—Ln (4.90%)	0.61
Henderson	aw	X	Ln [—Ln (1 — aw)] — Ln (T + C)
	11.19%	—4.9%	—8.36
	23.40%	—7.00%	—7.55
	33.30%	—8.20%	—7.13
	43.15%	—9.10%	—6.80
	55.87%	—10.20%	—6.43
	74.13%	—10.70%	—5.93
	75.53%	—11.90%	—5.89
	82.79%	—14.04%	—5.66
	91.07%	—15.87%	—5.35
	97.89%	—16.34%	—4.88
	11.17%	—4.67%	—8.36
	21.37%	—6.30%	—7.65
	32.00%	—7.70%	—7.18
	42.55%	—8.43%	—6.82
	49.72%	—8.88%	—6.60
	66.08%	—10.30%	—6.15
	75.11%	11.10%	—5.90
	82.95%	—12.30%	—5.66
	89.40%	—15.09%	—5.42
	96.71%	—15.90%	—5.00

Fuente: datos propios.

Tabla 2.

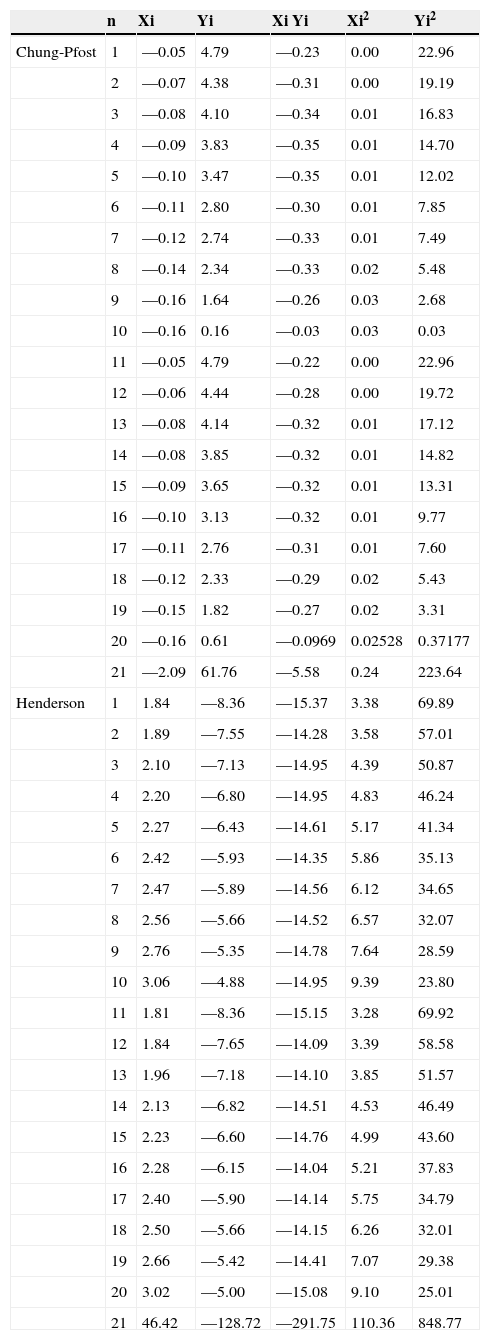
Determinación de pares de datos a partir de resultados empíricos, para los métodos de Henderson y Chung-Pfost

	n	Xi	Yi	Xi Yi	Xi2	Yi2
Chung-Pfost	1	—0.05	4.79	—0.23	0.00	22.96
	2	—0.07	4.38	—0.31	0.00	19.19
	3	—0.08	4.10	—0.34	0.01	16.83
	4	—0.09	3.83	—0.35	0.01	14.70
	5	—0.10	3.47	—0.35	0.01	12.02
	6	—0.11	2.80	—0.30	0.01	7.85
	7	—0.12	2.74	—0.33	0.01	7.49
	8	—0.14	2.34	—0.33	0.02	5.48
	9	—0.16	1.64	—0.26	0.03	2.68
	10	—0.16	0.16	—0.03	0.03	0.03
	11	—0.05	4.79	—0.22	0.00	22.96
	12	—0.06	4.44	—0.28	0.00	19.72
	13	—0.08	4.14	—0.32	0.01	17.12
	14	—0.08	3.85	—0.32	0.01	14.82
	15	—0.09	3.65	—0.32	0.01	13.31
	16	—0.10	3.13	—0.32	0.01	9.77
	17	—0.11	2.76	—0.31	0.01	7.60
	18	—0.12	2.33	—0.29	0.02	5.43
	19	—0.15	1.82	—0.27	0.02	3.31
	20	—0.16	0.61	—0.0969	0.02528	0.37177
	21	—2.09	61.76	—5.58	0.24	223.64
Henderson	1	1.84	—8.36	—15.37	3.38	69.89
	2	1.89	—7.55	—14.28	3.58	57.01
	3	2.10	—7.13	—14.95	4.39	50.87
	4	2.20	—6.80	—14.95	4.83	46.24
	5	2.27	—6.43	—14.61	5.17	41.34
	6	2.42	—5.93	—14.35	5.86	35.13
	7	2.47	—5.89	—14.56	6.12	34.65
	8	2.56	—5.66	—14.52	6.57	32.07
	9	2.76	—5.35	—14.78	7.64	28.59
	10	3.06	—4.88	—14.95	9.39	23.80
	11	1.81	—8.36	—15.15	3.28	69.92
	12	1.84	—7.65	—14.09	3.39	58.58
	13	1.96	—7.18	—14.10	3.85	51.57
	14	2.13	—6.82	—14.51	4.53	46.49
	15	2.23	—6.60	—14.76	4.99	43.60
	16	2.28	—6.15	—14.04	5.21	37.83
	17	2.40	—5.90	—14.14	5.75	34.79
	18	2.50	—5.66	—14.15	6.26	32.01
	19	2.66	—5.42	—14.41	7.07	29.38
	20	3.02	—5.00	—15.08	9.10	25.01
	21	46.42	—128.72	—291.75	110.36	848.77

Fuente: datos propios.

De tal forma utilizamos los resultados finales de los porcentajes de adsorción de humedad de cada una de las diez muestras para aplicarlos en los modelos mencionados anteriormente y confrontarlo con su valor de humedad correspondiente a la sal que haya sido expuesto, formamos pares asociados permitiéndonos desarrollar el método de los mínimos cuadrados para la obtención de los parámetros característicos de cada modelo (tablas 3 y 4).

Tabla 3.

Parámetros de mínimos cuadrados para los modelos de Chung-Pfost y de Henderson

	Chung-Pfost	Henderson
Sx	—2.09	46.42
Sy	61.76	—128.72
Sxy	—5.58	—291.75
Sxx	0.24	110.36
SYY	223.64	848.77

Fuente: datos propios.

Tabla 4.

Parámetros de los modelos de Chung-Pfost y de Henderson

Henderson		Chung-Pfost
C2	C1	E	F

2.67	3.29E-06	0.028	0.192

Fuente: datos propios.

ResultadosDeterminación de parámetros en puntos de equilibrio de adsorción

En el análisis de los resultados de la tabla 5, se obtienen los valores de contenido de humedad en equilibrio a cada temperatura. La construcción de los pares para poder aplicar el método de los mínimos cuadrados se configura de la siguiente manera. Los valores de humedad generados por las sales se le aplican las expresiones.

Tabla 5.

Contenidos de humedad de equilibrio en diferentes biomasas, método de sales saturadas

	15°C		35°C
LiCl	11.19%	4.90%	11.17%	4.67%
CH3COOK	23.40%	7.00%	21.37%	6.30%
MgCl2	33.30%	8.20%	32.00%	7.70%
K2CO3	43.15%	9.10%	42.55%	8.43%
Mg(NO3)2	55.87%	10.20%	49.72%	8.88%
SrCl2	74.13%	10.70%	66.08%	10.30%
NaCl	75.53%	11.90%	75.11%	11.10%
KCl	82.79%	14.04%	82.95%	12.30%
BaCl	91.07%	15.87%	89.40%	15.09%
K2SO4	97.89%	16.34%	96.71%	15.90%

Fuente: datos propios.

Aplicación de los datos

La disposición correlativa de los resultados para formar los pares se diferencia según la modelización lineal de los dos modelos; mientras que en el modelo de Henderson se toma el negativo del logaritmo invertido respecto a la recepción de los datos, en el modelo de Chung-Pfost se hace correlativa, tomando el mismo valor directo en valor negativo.

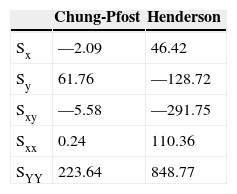
Una vez calculados los parámetros de ajuste según las fórmulas:

Parámetros Chung-Pfost:n=Sxx Sy−SxSxyN Sxx−SxSx=20×5−,58−2,09×61,7620×0,24−×−2,09×−2,09=35.18

Fórmula 7, resultados de pendiente y coeficiente anexo, para cálculo por regresión en mínimos cuadrados parámetros de la modelización de Chung-Pfost Parámetros de Henderson:

Fórmula 8, resultados de pendiente y coeficiente anexo, para cálculo por regresión en mínimos cuadrados parámetros de la modelización de Henderson.

Una vez calculadas la pendiente y la constante de la recta de ajuste de los parámetros de cada modelo, se recurre a las expresiones matemáticas lineales para determinar los parámetros característicos.

Fórmula 9, fórmulas de Henderson y Chung-Pfost, remarcando el posicionamiento de sus parámetros característicos.

En el caso de la fórmula de Henderson, el valor de C2 tiene como resultado el mismo que la pendiente de ajuste, mientras que en F de Chung-Pfost el valor es la inversa de la pendiente.

Para el segundo parámetro de los modelos, en el caso de Henderson el valor de C3 se eleva al número e; por otro lado, en Chung-Pfost la relación entre la inversa de la pendiente y la inversa del valor auxiliar de la recta da E.

Conclusiones

La precisión y la fiabilidad de un modelo matemático son fundamentales para que cumplan su función; la naturaleza de la composición de la fórmula es decisiva a la hora de encontrar su aplicación directa.

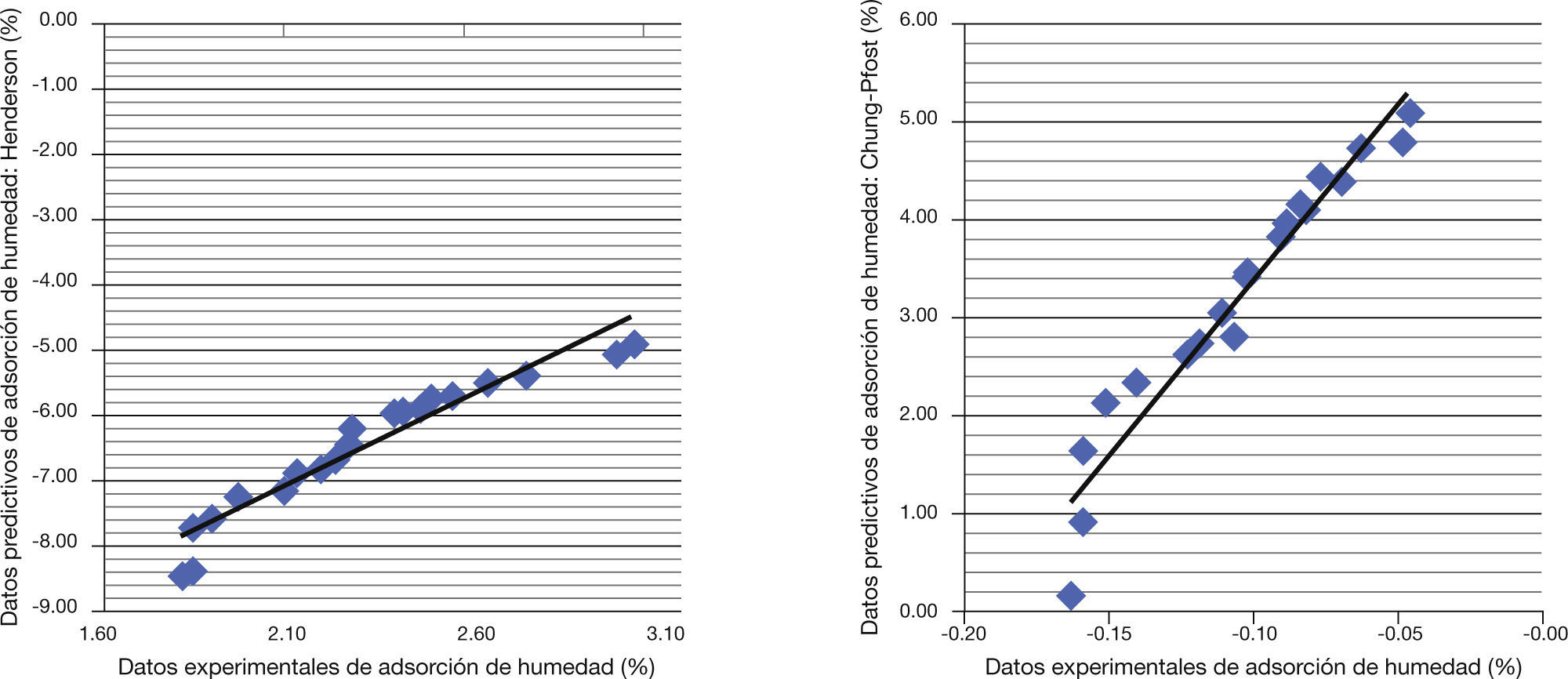
Mientras que la fórmula de Henderson pertenece a un modelo exponencial inverso, la expresión de Chung-Pfost corresponde a uno lineal, lo que condiciona la capacidad de representar parámetros de sorción de humedad con un error por debajo del 10%.

Mientras el modelo de Henderson está limitado en la modelización de biomasas que tengan sus puntos máximos de humedad de equilibrio reducido, el modelo de Chung-Pfost no es aconsejado para biomasas elevadas en puntos máximos de adsorción.

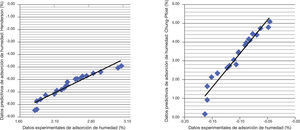
Como vemos en la figura 1, la pendiente es mayor en la modelización de Henderson, lo que indica que las mediciones son más agudas, pero no por eso más o menos precisas.

Figura 1.

Recta de ajuste de puntos de equilibrio según modelos de Henderson y de Chung-Pfost para astillas. Fuente: datos propios.

(0,19MB).

Agradecimientos

Este trabajo ha sido posible gracias al apoyo de la empresa Sedam Management, Instituto Tecnológico de Canarias y Tragsa (Empresa de transformación agraria S.A), Oliver González Arias, Miguel Pérez Afonso, Gonzalo Pierna-Vieja Izquierdo, Julián Muñoz de la Fuente.

Indexada en:

Síguenos:

Indexada en:

Síguenos:

Suscríbase a la newsletter