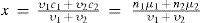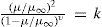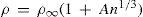Daniel Berthelot (1865-1927) used the electrical conductivity method to carry on fundamental research on the chemical equilibrium present in highly diluted electrolyte solutions, using the electrical conductivity method. In this way he was able to follow the kinetic details, particularly of the processes taking place in normal or pathological fluids of a living organism. He developed the so-called neutralization curve method, which allowed by simple inspection to judge the march of the reaction. The Académie des Sciences of France awarded him the Jecker Prize for his achievements on the subject.
Daniel Berthelot (1865-1927) usó el método de la conductividad eléctrica para realizar estudios fundamentales sobre el equilibrio químico presente en soluciones electrolíticas altamente diluídas. De esta manera fue capaz de seguir los detalles cinéticos, especialmente de los procesos que tienen lugar en los fluidos normales o patológicos de un organismo vivo. Desarrolló el llamado método de la curva de neutralización que permite observar la marcha de una reacción por simple inspección visual. La Academia de Ciencias de Francia le otorgó el Premio Jecker por sus logros en este tema.
In a previous publication we gave some details about the life and career, and the contribution of Daniel Berthelot to the subject of thermodynamics (Wisniak, 2010). Here we describe his contributions to the study of electrolyte solutions, which should be judged against the state of the art at his time. The results of this work led Berthelot to receive the 1898 Jecker Prize of the Académie des Sciences for a total of ten thousand francs awarded for work destined to the progress of organic chemistry, jointly with Joseph Louis François Bertrand (1822-1900) (for his work on soluble ferments) and Alphonse Buisine (-1918) (for his work on the chemical composition of lamb grease).
According to Berthelot (Berthelot, 1917), the study of the constitution and equilibrium of chemical compounds in solution requires the use of methods based on the physical properties of the system such as thermal, optical, electrical, etc. The first methods employed by Marcelin Berthelot (1827-1907) were calorimetric and gave a direct evaluation of the energy changes involved in the phenomena. Afterwards came measuring the electrical resistance which allowed continuing the examination of chemical reactions up to highly diluted liquors, a clear advantage in the case of substances slightly soluble in water. For most of his experiments Berthelot employed solutions containing 1/100 or 1/200 equivalent/liter of the base, acid, or salt, and in some particular cases dilutions 100 times higher. In the beginning, Berthelot was intent in studying certain chemical equilibria similar to those taking place in the human body. He believed that the electrical method was particularly applicable to the examination of reactions that take place in liquids with low concentrations of salt. When examining in the normal or in the pathological state the principal liquids of the organism, such as urine, blood, gastric fluid, etc., and also the equilibrium of several organic salts such as sodium chloride, phosphates, sodium carbonate, and bicarbonate, etc., in the presence of the above liquids, it was observed that substances having simultaneously acid and basic properties, such as glycolamine, alanine, leucine, thyrosine, serine, albumin and its derivatives, etc., played a critical role in physiological reactions. The presence in a given compound of two antagonistic functions, such as the acid and basic ones, gave place to complex equilibria. It is this coexistence of two functions that allowed Emil Fischer (1852-1919) to combine these bodies and build complex structures of polypeptides and be the first to synthesize albuminoids. The phenomena that Berthelot studied became more complicated if the reactions took place in the presence of a membrane: certain compounds were dialyzed easily and the equilibrium altered. He believed that this sort of studies would help in the search for the explanation of certain paradoxical observations, such as blood becoming more alkaline, urine becoming more acid, etc. (Berthelot, 1917).
One of the first tasks was selection of the method for measuring the conductivity of a solution. Two procedures were available, one based on alternating currents, the other on the electrometer. The first method had the advantages of being relatively fast and allowed changing the concentration of the solution in a systematic manner, without the need of preparing separately solutions of different concentration; the same advantage was present when it was necessary to mix solutions in different ratios. The method suffered of the serious inconvenience of being subject to systematic and hard to evaluate errors. The experimental evidence indicated that two repeated measurements could yield results differing by 1/40, polarization was not eliminated, only restricted to an unknown level; for highly diluted solutions it gave unreliable results, and in addition, in many situations the platinum plates serving as electrodes became corroded. The second method was the electrometric one, proposed by Gabriel Lippmann (1845-1921, 1908 Nobel Prize for Physics), based on the simultaneous use of non-polarizable electrodes and the capillary electrometer (Lippmann, 1876); it was free of the limitations of the first method and was more sensitive and precise. Its only inconvenience was in being less expedient. Berthelot chose the Lippmann method with the arrangement described by Jules Jamin (1818-1886) and Bouty (Jamin and Bouty, 1888). The unit of conductivity selected was that of an aqueous solution of KCl, containing 0.01 equivalent/L at room temperature (about 17 °C). The reason for selecting this patron was that its conductivity changed very little with temperature.
Neutralization of an acid was followed by addition of increasing amounts of base, simultaneous measurement of the electrical conductivity of the solution, and plotting the conductivity against the concentration, a method that Berthelot named neutralization curves. The shape of the curve was found to be strongly influenced by the nature of the acid or base (strong or weak), and also that there exists a certain parallelism between the electrical conductivity and the chemical strength of acids and bases, which allowed dividing electrolytes into two groups. The first group comprises the strong acids and bases, as well as their neutral salts. They are good conductors, even in concentrated solutions, and their molecular conductivity changes little with concentration. The second group comprises the weak acids (almost all of the organic acids) and the weak bases. They are poor conductors in concentrated solutions, but their conductivity changes rapidly with dilution. Well diluted they are as good conductors as the compounds in the first category (Berthelot, 1891ab, 1917).
Consider now a mixture of two electrolytes having the same molar concentration. If they belong to the first group, the conductivity x of the mixture can be calculated as the ponderated weight of the conductivities of the pure components:
where vi, ni, ci, and μi are the volume (liter), the number of moles, the specific conductivity, and the molecular conductivity, respectively of components 1 and 2. Clearly the graphical representation of the phenomenon will be a straight line. This is not the situation when mixing one electrolyte from the first class with another of the second, or two of the second group. The conductivity of the mixture cannot be calculated as above. In order to calculate it, Berthelot indicated that it was necessary to consider the following facts (Berthelot, 1917): Experience showed that the electrical conductivity did not increase indefinitely with dilution, but tended to a limit μ∞. The ratio μ/μ∞ is what Edmond Bouty (1846-1922) called the number of electrolytic molecules and Svante Arrhenius (1859-1927; 1903 Nobel Prize for Chemistry) called the number of dissociated ions per unit volume. In order to apply a proportionality rule it was necessary that both solutions A and B contain the same number of electrolyte molecules per liter. This condition was fulfilled by assuming that one molecule of the water of the B solution is withdrawn and added to the A solution. In this manner solution A becomes more diluted and its conductivity increases; at the same time, B becomes more concentrated and its conductivity decreases. A graphical representation of the results obtained with electrolytes of the second group showed that now the phenomenon was represented by a curve (instead of a straight line), which characterized the relative force of acids and bases. In every case it was possible to calculate the theoretical value of the conductivity of a mixture, assuming that there was no chemical action. The actual conductivity was now measured; any difference between the two figures was indicative of a reaction.Berthelot proceeded then to analyze and discuss the curves of neutralization for the following cases (Berthelot, 1889a): (a) Strong acid with a strong base. Here the curve of neutralization was composed of two straight lines meeting at an acute angle, so that acid liquors could be envisioned as a mixture of acid and neutral salt, and vice-versa, all alkaline liquors could be considered as a mixture of a neutral salt and a base, (b) weak acid (acetic acid) and strong base (KOH). The neutralization curve was now composed of two sections, a convex one corresponding to acid mixtures equivalent to a mixture (for example) of neutral acetate and acetic acid. The results showed that the neutral salt was stable in solution and addition of an excess of acid or alkali did not result in chemical action. The second section corresponded to alkaline liquors, representing the neutral salt and potassium hydroxide (two electrolytes of the first group). It was a straight line passing through the point corresponding to the conductivity of potassium hydroxide, and (c) weak acid (acetic acid) and weak base (ammonia). The neutral salt continued to be stable, even when diluted.
In all the above situations there was a steep change in slope at the point of neutralization. This was not the situation in the neutralization of ammonia (a poorly conducting base) by phenol (a non conducting body in solution), where the alcohol group is analogue to the acid function but weaker. The neutralization curve did not present an angular point; its two sections joined smoothly. In this situation the combination of phenol with alkali at equal number of equivalents yielded a compound mostly dissociated by the water, which tended to become complete by increasing additions of either phenol or ammonia. The same behaviour was observed when acetic acid (a weak acid and poor conductor) was neutralized with aniline (a very weak non-conducting base).
All the above observations referred only to the neutralization of monobasic acids. If the acid was dibasic (sulfuric acid, oxalic acid, etc.), then on addition to the salt formed by equivalent amounts of acid and base, there was also formation of an acid salt resulting from the combination of one equivalent of acid with one of base. In this situation the neutralization curve was composed of three straight sections, determined by the points representing oxalic acid, acid oxalate, neutral oxalate, and potassium hydroxide. If the dibasic acid was weak, for example succinic acid, part of the straight lines became curved.
Hence, examination of the curves, or comparison of the amounts observed and the calculated numbers for the mixtures, allowed an easy characterization of the basicity of an acid. If the molecular weight of the acid was known, it was enough to add to one molecule of it, 1, 2, or 3 molecules of alkali and determine where it ceased to influence the conductivity. Hence measurement of the electrical conductivity offered a new and powerful tool to determine the basicity of acids of known molecular weight. It could also be used to determine the basicity of an acid without knowing the formula of its elemental analysis.
The main subjects investigated are now presented according to the classification selected by Berthelot (Berthelot, 1917).
Neutralization of acids and basis. Study of the acid function and determination of the basicityIn the first works published by Berthelot (Berthelot, 1889ab), and which he presented as his doctoral thesis, he was intent in applying the methods of electrical conductivity to the general study of the neutralization of the principal organic acids, within the particular objective of examining the formation of neutral, acid, or basic salts, generated by mono and polybasic acids; the dissociation or the progressive recomposition, under the action of an excess of water, of the base or the acid, and finally, the possible influence exerted by other chemical functions attached to the acid one (Ditte, 1906).
Aspartic acid is one of the many compounds containing in its molecule an acid and two basic functions, and for which measurements of electrical conductivity were not available. The purpose of Berthelot's first work (Berthelot, 1889a) was to study the equilibria present in dilute solutions of aspartic acid, its neutral salts, the acid salts of sodium and potassium, and their equilibria in the presence of variable amounts of sodium hydroxide, hydrogen chloride, and potassium chloride. These equilibria depended on the presence of antagonistic acids, which in one hand could react wholly or partly with the mineral base and, on the other, to join with aspartic acid itself. They were also subordinated to the presence of an excess of mineral base forming a basic salt and to the presence of an excess of an alkaline chloride forming a double salt. Berthelot reported the conductivities of potassium chloride, aspartic acid, sodium aspartate, hydrogen chloride, sodium hydroxide and sodium chloride, and the calculated and measured conductivities of mixtures of aspartic acid and sodium chloride in different proportions, at 20 °C. The results indicated clearly that the conductivity of an equimolar solution of aspartic acid and sodium chloride was different from the calculated one. Admitting the reaction C8H7NO8 + NaCl = C8H6NaNO8 + HCl, that is, the partial formation of sodium aspartate and HCl, and that the four compounds coexisted in solution without secondary phenomena, such as the formation of a double salt, then it could be calculated that about 4% of the sodium chloride was decomposed. The difference in conductivity between the observed value and that corresponding to zero decomposition achieved a maximum value for the equimolar mixture and decreased when one of the two reagents was present in excess. Berthelot understood that this result was not strictly correct because there were other reactions taking place: aspartic acid and HCl, aspartic acid and aspartate, and aspartate and sodium chloride. Anyhow, the pertinent corrections were minimal because all these reactions occurred in the same direction and decreased the conductivity.
In a following paper (Berthelot, 1889b) presented the consequences of aspartic acid having also a basic function. The results, again expressed in terms of electrical conductivity, showed that (a) mixing one mole of HCl with one mole of aspartic acid resulted in a clear reaction; the observed conductivity decreased by about ¼ of the calculated one, indicating a decrease in the number of conducting species, that is, formation of a chlorhydrate of the basic function. Further addition of aspartic acid decreased even more the difference between the calculated and the measured conductivities, and (b) mixing two molecules of HCl with one of aspartic acid reduced the difference in conductivities to 15 of that of the equimolar mixture.
Similar experiments showed that addition of one mole of sodium aspartate to one mole of aspartic acid, led to the formation of a double salt.
Berthelot used electrical conductivity to study the effect of the presence of additional organic functions, such as phenol, alcohol, and base, in the molecule of an organic acid, with regard to the extent of the mutual influence that two functional groups exerted, according to their relative position in the molecule (Berthelot, 1890a). For this purpose he selected the three isomers of oxybenzoic acid (hydroxybenzoic acid) dissolved in water to a concentration of 0.01 equivalent/L. He reported (in four tables) the calculated and experimental conductivities, their difference, and their difference divided by μ at 100 °C of an aqueous solution of KCl containing 0.01 equivalent/L (to be used as reference by assigning to it a conductivity equal 1 unit) of aqueous solutions of KOH, NaOH, Ba(OH)2, Ca(OH)2, ammonia, and phenol (first table), of equimolar solutions of phenol + NaOH, KOH, Ba(OH)2 and Ca(OH)2 (second table), of aqueous solutions of benzoic acid (third table) or salicylic acid mixed with ½, 1, 2, and 3 moles of NaOH, and of the three isomers of oxybenzoic acid (ortho, meta and para) with 1, 2, and 3 moles of NaOH (fourth table).
The results given in the first two tables indicated that the observed conductivities were smaller than the calculated ones. The third table showed that the difference Δ between the two conductivities was the largest for the case of an equimolar mixture, corresponding to the maximum chemical combination between the two species. The last table (oxybenzoic acids) showed that the conductivities of the three isomers were quite distinct, decreasing in the order ortho, meta, and para. The conductivity of the para isomer was essentially equal to that of benzoic acid, and the value of the ratio Δ /μ for an equimolar ratio of acid + NaOH was essentially the same for the three isomers.
In a following paper Berthelot extended the results by studying the influence of two weak bases, ammonia and aniline, on the three isomers of oxybenzoic acid (Berthelot, 1890b). Again he reported the conductivities of ammonia, ammonia mixed with ½, 1 and 2 moles of phenol, with ⅓;, ½, 1, 2, and 3 moles of benzoic acid, of salicylic acid, and ammonia mixed with 1, 2, and 3 moles of ammonia, of ammonia mixed with ⅓, ½, 1, and 2 moles of m- or p-oxybenzoic acid, with aniline mixed with ⅓, ½, 1, 2, and 3 moles of benzoic acid, salicylic acid, or p-oxybenzoic acid. Once more he found that the maximum difference in conductivities occurred when the mixture was equimolar. An interesting result was that the difference between the calculated and experimental conductivities, was positive for salicylic acid, almost nil for m-oxybenzoic acid, and negative for the para isomer.
In a following work (Berthelot, 1891f) Berthelot extended his results to include the effects of ammonia and aniline on several additional acids: (a) HCl, a strong acid, (b) acetic acid, a weak acid, (c) phenol where the OH group plays the role of acid function, and (d) oxybenzoic acids, having a mixed functionality of acid and phenol. The experimental method consisted in adding to one of the acids successive amounts of the other and measuring the electrical conductivity. All the initial solutions had the same titer; initially they were acid, they became neutral when the mixture was equimolar, and from there on they became basic. The progress of the phenomenon was described by plotting the conductivity against the relative concentration. Previous results indicated that the shape of the curves changed according to the nature of the base (strong, weak) and of the acid (strong weak), and this fact allowed classifying the solutions into two large groups. The first one comprised strong acids and strong bases, and all the neutral salts. The second group encased the weak acids (almost all the organic acids) and the weak bases, which in highly diluted solution are as good conductors as the electrolytes of the first group.
His results indicated that (a) potassium formed with HCl, acetic acid, and phenol, combinations having similar conductivities, behaving like real salts, stable in solution, and not decomposed by water; (b) ammonia formed with acetic acid a stable composition and with phenol an unstable one, less conducting than neutral salts and largely decomposed by water into phenol and ammonia. The variation of its conductivity was explained by the superposition of two phenomena. In one the molecular conductivity of the salt increased with dilution and caused the decomposition of the salt (phenol is non-conducting and ammonia at medium concentrations conducts less than a neutral salt). The net effect of dissociation was then a retardation of the apparent increase in conductivity. In highly diluted solutions ammonia was less conducting than the neutral salt hence the effect of dissociation was to increase the apparent augmentation of the molecular conductivity; (c) aniline formed a stable and good conducting combination with HCl; with acetic acid the combination was unstable and mediocre conducting and with phenol the mixture was non conducting without traces of combination even at high dilution. The neutralization of HCl by aniline recalled exactly that of KOH by phenol, except that the roles of the electrolytes were interchanged; (d) the results for the three isomers of oxybenzoic acid showed that the intensity of the mutual influence of the phenol and acid groups depended on their relative position (o, m, p).
After these initial results Berthelot published a series of papers summarizing the previous conclusions, introducing the theoretical background of the calculation procedures employed, and adding the results of a large number of new measurements (Berthelot, 1891abd-g).
Friedrich Wilhelm Georg Kohlrausch (1840-1910) (Kohlrausch, 1876) had done a few measurements of the conductivity of concentrated solutions of acetic and tartaric acids, and of the acetates of potassium and sodium. Afterwards Bouty (Bouty, 1884) had measured the electrical resistance of diluted solutions of acetic, benzoic, salicylic, picric, succinic, oxalic, malic, tartaric, and oxalic acids, as well as several of their salts. All these works had shown that although organic salts have conductivities similar to those of mineral salts, the conductivity of the free acids was substantially less than that of mineral acids. They increased substantially with dilution but had different limiting values. Wilhelm Ostwald (1853-1932; 1909 Nobel Prize for Chemistry) measured the conductivity of a large number of organic acids and had tried to correlate it with the concentration of the solution, first assuming that μ2/v = constant and then with the relation m2/v (1 – m) = k (Ostwald, 1884-1885). Berthelot indicated that the purpose of his research was different, he intended to study the largest number possible of compounds in order to compare their conductivities, and study the formation of neutral, acid, and basic salts by mono and polybasic acids, the influence of water, base, or acid, on their progressive decomposition and recomposition, the influence of different chemical functions such as phenol, alcohol, alkali, present simultaneously in the molecule, etc. etc. Thus he studied 31 organic acids as well as their potassium salts, in aqueous solution, measuring the conductivity by the electrometric method with a capillary electrometer. The compounds studied were monobasic acids with simple structure (formic, acetic, and benzoic acids), dibasic acids with simple structure (oxalic, malonic, succinic, glutaric, phthalic, camphoric, fumaric, maleic, itaconic, mesaconic, and citraconic acids), and tribasic acids with simple function (tricarballylic and aconitic acids). He also studied one hexa-basic aromatic acid with simple function (mellic acid), acids having more than one function (the oxybenzoic isomers) acids having an alcoholic function (glycolic, malic, tartaric, and citric acids), and finally, basic acids (amidoacetic acid, the amidobenzoic isomers, and aspartic acid).
The method followed consisted in calculating first the conductivity of a mixture of two electrolytes assuming that there was no reaction, eq. (1), and then measuring this property. Any difference between the two figures indicated that a reaction had taken place. He then proceeded to describe the different theories available for calculating the conductivity of mixture. Assuming an aqueous solution of a substance having a volume v per mole of solute, specific electric conductivity c, and molecular conductivity μv (the quotient between c and the number of moles per liter in the solution), then μv = cv. Since it was known that the molecular conductivity increased with dilution towards a value μ∞, he called m=μv /μ∞, a ratio that tended to unity as the dilution increased.
Berthelot now reported the experimental results for the different categories of electrolytes considered, that is, the conductivity of the free acid, its neutral potassium salt, and of mixtures of the acid and KOH in different proportions. For every case he gave the values of c, μ, m, and k.
a)Monobasic acidsThe variation of conductivity followed Ostwald's equation equation m2/v (1 – m) = k, containing the two parameters k and μ∞, which can be determined from two experiences. The results indicated that for all organic acids μ∞ was about 275 at 17°C. Kohlrausch had established the rule that the conductivity of an electrolyte at infinite dilution is equal to the sum of the conductivities of the cation and the anion. Hence considering an acid RH and its potassium salt RK, these two electrolytes have a common ion R so that their limiting conductivities should correspond to the difference between the limiting conductivities of the ions H+ and K+, which at 17°C was equal to about 195 in the system of units adopted by Berthelot. This procedure was equivalent to admitting that the difference between the conductivities of the acids was the same as the difference between the conductivities of their salts. Ostwald had shown that in practice the conductivity of the salts of monobasic acids decreased as the complexity of the molecules increased, first rapidly and then slower (Ostwald, 1888), a result that led him to assign, as a first approximation, the value of the limiting conductivity according to the number of atoms present in the molecule.
b)Neutral salts of monobasic acidsIn this case the conductivity followed the law [m/(1 – m)]3= kv. In order to analyse and compare this situation with the previous one, Berthelot proceeded to measure the electrical conductivity of a large variety of acids: (1) monobasic acids (formic, acetic, and benzoic) as well as their potassium salts; (2) dibasic acids of simple functionality (oxalic, malonic, succinic, glutaric, phthalic and camphoric); (3) isomeric dibasic acids (fumaric and maleic, citraconic, mesaconic, and itaconic); (4) tribasic acids (tricarballylic, and aconitic); (5) an aromatic hexabasic acid (mellic acid); (6) phenol acids (o-, m-, p-oxybenzoic, and salicylic); (7) acid alcohols (glycolic, malic, tartaric, and citric); and (8) basic acids (amidoacetic, aspartic, and o-, m-, and p-amidobenzoic).
He summarized his findings as follows: (a) There is a substantial variation in the electrical conductivity of free organic acids, for example at a dilution of 0.01 mol, it is 239.0 for oxalic acid, 11.61 for acetic acid, and 1.13 for amidoacetic acid. No relation could be found between the conductivity and chemical constitution, a result that became more striking when comparing the conductivity of isomeric acids: 0.722 for fumaric acid and 1.773 for maleic acid. The extreme diversity for acids disappeared when considering their salts, they had very similar conductivities when compared on the basis of equivalent weights, that is, solutions containing the same weight of metal. The molecular conductivities of the neutral potassium salt of all the monobasic, dibasic, and tribasic acids varied between a maximum of 99.4 for the oxalate to 70.2 for p-oxybenzoate. Within the homologue series oxalate, succinate, glutarate, etc., the conductivity of the salt decreased in a regular form as the complexity of the molecules increased (number of atoms), a characteristic that also occurred in non homologue series, for example neutral salts of acids of the same basicity. (b) The acid salts of monobasic acids did no exist in highly diluted solutions. (c) The acid salts of dibasic acids existed in solution but not without alteration or instability. From the molecular point of view it would seem that these salts ought to have, for the same titer as neutral salts, a similar existence and stability, given that the molecule of the free acid contains two equivalents of hydrogen replaceable by a metal. There should exist two different series of salts of potassium, sodium, etc., containing either one equivalent of potassium, or one equivalent of potassium and one of hydrogen. But the study of the conductivity proved that the acid salts existed only in the state of partial dissociation into neutral salt and free acid, a result already proven by thermochemical measurements. In addition, the conductivity of acid salts increased with dilution in a different manner as simple mixtures do. The increase was different from one acid salt to another, according to the acid that generated them. The latter provided a criterion for distinguishing them from neutral salts.
When considering neutral salts in which the molecule contains the same number of atoms, but constituted of acids having different basicity, the conductivity of the neutral salt of a dibasic acid, exceeded by about 12 units that of the neutral salt of a monobasic acid. The conductivity of a tribasic acid exceed by about 6 units that of the neutral salt of a dibasic acid containing the same number of atoms (Ditte, 1906).
The results also allowed determining the basicity of an acid. For example, if the molecular weight of the acid was known, then increasing number of moles (1, 2, 3…) of alkali were added successively until they ceased to affect the conductivity. For example, for formic acid, addition of the second mole of KOH increased the conductivity by only 0.04 units. With oxalic acid, addition of the second mole of KOH increased the conductivity by 0.31 units and addition of the third mole of KOH by only 0.03 units. With citric acid the increase in conductivity was 0.31, 0.20, and 0.06, after adding the second, third, and fourth mole of KOH, respectively. When the equivalent of the acid was known but not its molecular weight, it was enough to check if addition of acid to the neutral salt resulted in the partial formation of acids salts, a phenomenon that reflected in a decrease of the conductivity of the mixture below the calculated value. For example, addition of 1 or 2 equivalents of acetic acid to the neutral acetate resulted in the conductivity being 263 and 206, against the calculated values of 265 and 207. The two sets of values are essentially the same signalling that the acid is monobasic. With regards to the presence of additional chemical functions in the molecule, the results indicated that the presence of one or more alcoholic OH groups did not influence the behaviour of diluted solutions, that is, alcoholates are totally dissociated in diluted solutions. On the other hand, the presence of a phenol group affected or not the electrical behaviour, depending on the position of the group relative to other chemical groups. The effect of a basic function, such as an amide group was variable, the conductivity changed because complex salts between antagonistic functions present in the molecule; these salts were destroyed by dilution. Initially the values of m2/v (1 – m) = k increased and eventually became constant. The basic function of acid amides became very clear in their mixtures with HCl; a chemical combination took place with formation of partly dissociated chlorhydrates.
The simple relation given by eq. (1) did not hold for the case where the mixture is composed of an electrolyte of the first group with an electrolyte of the second group. For this situation it is necessary to use the relations that Berthelot developed in the previous publication, based on the work of Bouty and Arrhenius.
Thus application of eq. (1) required that the solutions of the two (pure) components have the same number of electrolyte molecules per liter. Anyhow, the phenomenon is not represented by a straight line but by a curve that characterize the relative strength of the acids and bases. In any case, the theoretical conductivity of a mixture can always be calculated; any deviation from the measured one indicates the presence of a chemical reaction.
The unit of conductivity was again chosen as that of a solution of KCl containing 0.01 equivalent/L. All experiments were realized at 14 °C. The alkaline or acid solutions were all of the same initial concentration, 0.001 equivalent/L, so that the chemically neutral salt resulting from their mixture in equal amounts was 0.002 equivalent/L.
While the conductivities of HCl and KOH are already considerable in concentrated solutions and increase only slowly with dilution, the conductivities of acetic acid and ammonia are very weak in concentrated solutions and increase rapidly with dilution. The increase in conductivity of weak acids can be represented by the formula:
where k is a constant characteristic of the acid.The experimental results showed that the same relation could be applied to the conductivity of ammonia, with k varying between 0.201 × 10–5 and 0.193 × 10–5, assuming for μ∞ the same value as for K∫OH (185).
Berthelot compared his results with the ones obtained by Kohlrausch and Ostwald and found that they were very similar up to medium concentrations but diverged substantially as the dilution was increased. He attributed the difference to the purity of the distilled water employed, a factor which in this case was critical because of the low conductivity of ammonia. Ostwald had recognized that the water he had employed was quite impure; Kohlrausch in his calculations had subtracted from his measurements the conductivity of distilled water, an incorrect correction. Adding back this value made his results basically identically to those of Berthelot.
Study of isomerization and functional groupsThe next research subject was related to the conductivity of isomeric organic acids and their salts (Berthelot, 1891c). The series studied included simple isomers like maleic and fumaric acids, more complicated structures like itaconic, mesaconic, and citraconic acids, a more complex function presenting the three isomers, such as oxybenzoic acid, and acids presenting symmetric isomerism such as the tartaric ones. The salts studied were the potassium ones, in different molar ratios.
Berthelot concluded as follows: (a) the conductivities of the free isomeric acids differ between themselves, but is the same for their neutral salts, (c) the conductivity curves of complex acids also offers some distinctive characteristics. For example, the three oxybenzoic acids have different conductivities. In dissolved salicylic acid the role of the phenol group is small, but not so in the meta and ortho acids, where it gives place to the formation of polybasic salts. Analysis of the neutralization of these acids by ammonia justified these conclusions. The curve for salicylic acid did not justify the presence of a basic salicylate, while those for the meta and para acid showed the existence of basic salts. These ammonia salts are dissociated much more by water than the corresponding potassium salts, (b) the conductivity of diluted solutions of isomeric acids present some interesting characteristics. While fumaric acid behaves like a dibasic acid, maleic acid does not, it behaves more like a monobasic acid; its second hydrogen atom plays no part in electrolysis. These results may be explained by considering that while the two acid groups of fumaric acid may be represented by —COOH, in maleic acid only one of them may be represented so, the second is the result of the neighbourhood of a keto group with an hydroxyl one. Experience showed that the hydrogen of the hydroxyl alcoholic group did not participate in electrolysis, (b) the dextro and racemic tartaric acids have the same conductivity, (c) the equality of conductivity for the neutral salt is not altered by addition of alkali for maleates and fumarates, for the three isomers of the itaconate, and for the salts of amidobenzoic and tartaric salts. The latter result seems to indicate that the alcoholic function of the tartaric acids ceases to be of influence in diluted solutions, a conclusion also obtained from thermochemical measurements, (d) acids having a phenolic function produced neutral salts having very similar conductivities, which began to change only in the presence of an excess of alkali, (e) neutral salts of monobasic acids, on addition of an excess of the acid that formed it, behaved as simple mixtures of acid and neutral salt, (f) neutral salts of dibasic and polybasic acids behaved different because they were partially dissociated, and (g) the different behavior of the acids allowed establishing new differences between isomeric acids, and thus their identification.
Regarding the effect of the alcohol function, single or multiple, it did not multiply itself in the diluted solutions of the acids studied by Berthelot (glycolic, malic, tartaric, and citric acids); the alcoholates were totally dissociated.
The basic function present in the amido acids studied (amidoacetic, o-, p-, m-amidobenzoic, and aspartic acid), manifested itself through a series of clear characteristics. The first one was the anomaly in the variation of their conductivity, anomaly that could be explained by the formation of complex salts due to the antagonism present in the compounds. The salts were destroyed by dilution; measurement of their conductivity showed, for example, that in aspartic acid, the last traces disappeared already when the concentration became less than 1/500 equivalent/L. In aspartic acid, which is dibasic, one of the acid function was neutralized in the interior of the molecules by the basic function, so that contrary to the true dibasic acids examined (oxalic, malonic, succinic, glutaric, phthalic, camphoric, fumaric, maleic, citraconic, mesaconic, itaconic acid, etc.), it was enough to add one mole of potassium hydroxide to obtain a neutral salt, stable in solution. Addition of a second mole of potassium hydroxide produced a second neutral salt. The basic function in amido acids manifested itself even more clearly in mixtures with HCl: chlorhydrates partially dissociated are formed. In the same manner that the phenol function in oxybenzoic acids, the basic function in amidobenzoic acids was influenced by the more or less proximity of functional groups in the molecule. The weakest interaction occurred in the ortho acid.
In summary, the results Berthelot obtained employing the method of conductivity overlapped in general, those provided by thermochemistry; they could be extended to high dilutions and the examination of different problems. They offered, as well, new methods for studying the basicity of acids, their functions, and their isomers.
Phosphoric acid and phosphatesBerthelot studied in particular detail phosphoric acid and phosphates, measuring the electrical conductivity of the free acid and that of its sodium, potassium, and ammonia salts at dilutions increasing from 1/10 to 1/10,000 (Berthelot, 1891h, 1893). The available information indicated that polybasic acids seemed first to decompose according to RHn =RHn-1- +H+ (Berthelot writes H instead of H+), that is, only one hydrogen atom took place in the hydrolysis. But as the solution was diluted, there was a moment when the second hydrogen atom took part in the process; the radical RHn-1- decomposed now into RHn-2- and H. If the acid is tribasic, a third hydrogen atom would separate later on. In other words, the nature of the electrolyte changed according to the degree of dissociation; its conductivity increased uniformly and seemed to tend to the limit characteristic of monobasic acids, until the second hydrogen was released and the conductivity increased rapidly towards the limit of the dibasic acids. This was the picture emerging from the researches of Bouty (Bouty, 1844) and Kohlrausch (Kohlraush, 1876) about sulfuric acid and of Ostwald (Ostwald, 1885) about organic acids. Now, this was not the behaviour shown by phosphoric acid. Not only its conductivity did not seem to increase beyond that of monobasic acids, it varied regularly while it became more and more diluted. Although the second and third hydrogen atoms were substitutable by metal, their behaviour from the view point of electrolysis was as the hydrogen of acids do. They reminded more the behaviour of the hydrogen atoms of an OH group, which are able to form salts but do not participate in the electrolysis. It was known that the molecular conductivity of monobasic acids was quite different when in concentrated solution, but it became very similar when the dilution was increased indefinitely, tending to the value 275 for organic acids and 320 for mineral acids. Dibasic acids, on the other hand, exceeded by much this maximum; at infinite dilution the conductivity became about twice that of the monobasic acids. The conductivity of the tribasic acid increased to a much higher limit even. The conductivity of phosphoric acid at infinite dilution is only about 295, a value very similar to that of the monobasic acids. For Berthelot this result indicated that of the three hydrogen atoms present in the acid, only one took part in electrolysis, that is H3PO4 =H3PO4- +H+. The other two hydrogen atoms were not released at the negative pole; although they can be replaced by a metal, they do not behave like the hydrogen of proper acids. Their behavior reminds that of the hydrogen atoms of phenolic OH or similar compounds, capable of generating salts but not of taking part in electrolysis. Thus phosphoric acid may be compared to oxybenzoic acids, containing both the acid and the phenol function, and possessing conductivity similar to that of monobasic acids.
Measurement of the conductivity of the sodium, potassium, and ammonium salts indicated that monobasic and dibasic phosphates are stable in solution, even when diluted, while the tribasic phosphates are almost completely dissociated in dilute solution. These results showed that phosphoric acid differs completely from true tribasic acids like aconitic, citric, and tricarballylic acids, for which the monobasic and dibasic salts (acid salts) are partly dissociated by water while the tribasic salts (neutral salts) are stable in solution.
Berthelot then proceeded to measure the conductivity of the different phosphates. In order to simplify the graphical representation of the same he used the equation suggested by Bouty (Bouty, 1884):
where ρ is the molecular resistance, n the number of moles per liter, and A a constant. The factor n1/3, originally defined by Kohlrausch, had a definite physical meaning; it represented the inverse of the mean distance between the salt molecules (the proximity between molecules). Equation (3) not only gave a very good fit of the data, its graphical representation turned out to be a straight line that allowed determining the values of ρ∞ and A.Berthelot reported the conductivity and the values ρ∞ and A for monosodium orthophosphate, monopotassium and monoammonium phosphates, disodium, dipotassium, and diammonium phosphates, and sodium, tripotassium, and triammonium phosphates. A comparison of dibasic phosphates with the monobasic ones showed that with dilution the conductivity of the former changed faster than that of the latter. Alkaline tribasic phosphates were not present in the solution, but were partly decomposed by the water. Phosphoric acid differed completely from true tribasic acids such as carballylic, aconitic, and citric. The monobasic and dibasic salts of the latter are partly dissociated by water but the tribasic ones (neutral) are stable in solution.
Application to the study of organic liquidsAccording to Berthelot, his results were of particular interest to the analysis of normal and pathological fluids, as well as to the study of drugs, for example, the results regarding phosphoric acid could be used to explain the problem of the acidity of urine. Since the three acid functions present in phosphoric acid were quite different, it turned out that the weak acids present in an organism (carbon dioxide and alkaline bicarbonates in blood, lactic acid in the muscle, etc.) were unable to displace the first function, while they did so for the third, and participated together with alkaline or earth bases with the second. Also, his studies regarding the conductivity of very dilute solutions, such as those present in physiological fluids, again could be used as an example for studying the reactions of these fluids.