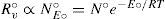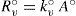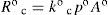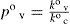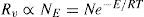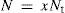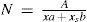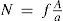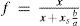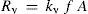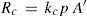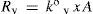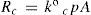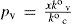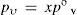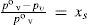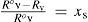Kinetic Approach for the Vapor Pressure Lowering by Non Volatile Solutes

Abstract

In most basic chemistry courses a kinetic approach is used to explain the vapor pressure lowering for solutions with a non volatile solute. This approach has been considered intrinsically incorrect for many years based on several objections. We consider that these objections are based on a misinterpretation of the kinetic model. In this paper we will show in detail this model to refute those objections and show that the kinetic approach can be a suitable teaching tool for explaining vapor pressure lowering in ideal solutions of non volatile solutes.

Introduction

Vapor pressure lowering (VPL) of a solvent as a result of dissolving a non volatile solute is a common chemical subject in undergraduate university chemical courses. Usually, quantification of VPL is performed by Raoult's law application which is rigorously valid only for ideal solutions.

Thermodynamics allows a full and clear justification of VPL just considering the lower solvent vaporization entropy at solution with respect to that of pure solvent (Peckham, 1998). Because of such thermodynamic argumentation is beyond the level of most basic chemistry courses, a kinetic approach allowing a phenomenological view, has been used as an alternative teaching tool.

However, the kinetic approach for explaining VPL has been rejected since several decades (Mysels, 1955) and recently again considered as a fallacious reasoning (Peckham, 1998). Disagreement with the kinetic approach is mainly based on the opposition to the called blocking surface theory using several arguments, that we consider as not really correct. Mainly, arguments against this theory are based on facts that theory does not invoke. Therefore, objections are sustained on the misinterpretation of the kinetic model.

In the present paper we will try to show that the kinetic approach is scientifically valid and can be used as a suitable teaching tool to depict VPL.

Some pedagogical considerations

From a didactic point of view, the possibility of using a valid kinetic approach for liquid–vapor equilibrium for a solution of a non volatile solute is a natural continuation from the description of the same phenomenon for a one component system (solvent). This option is suitable within constructivist teaching strategies. In addition kinetic model for vaporization–condensation phenomena for pure solvent is constructed from an analogy to reaction kinetics (Brennan et al., 1974; Novak, 2001) and easily extended to ideal solutions of non volatile solutes. Only if the kinetic model were out of the level of the basic chemistry course, one should discard it (not as incorrect, but as pedagogically inadequate). We think this is not the case for basic university chemistry courses.

In the following the kinetic approach for the vapor–liquid equilibrium in solutions of a non volatile solute will be presented in a deeper way than most textbooks (for example Atkins, 1998, pp. 172–173) to allow a better discussion about the objections to it.

The kinetic approach for vapor–liquid equilibrium

For a given surface area, A° of a pure solvent (we will use superscript “ ° ” in quantities corresponding to pure solvent) the vaporization rate, R°_v (mol s^–1) is proportional to the number, N°_E°, of solvent surface molecules with an energy content enough to overcome attraction energy, E°, in the form

where N° is the total number of solvent surface molecules, R is the gas constant and T is temperature. For a pure solvent composed by molecules of projected area a, N° can be expressed as A°/a and eq 1 can be reduced to

for which k°_v (that includes a⁻¹e^−E°/RT) is a temperature factor for vaporization analogous to the specific rate constant.

On the other hand, condensation rate, R°_c (mol s^–1), depends on vapor concentration molecules (at pressure p°) and is proportional to condensation surface area, then

where k°_c is the (kinetic analogous) temperature factor for condensation.

At equilibrium, rates of both processes (vaporization and condensation) are equal, and p° = p°_v, the solvent vapor pressure at T. Then equating 2 and 3, is obtained

which is a kinetic definition of vapor pressure for pure solvent.

The vaporization–condensation process for a solution of a non volatile solute can be depicted in a similar way as for pure solvent. For a given solution surface area, A, the vaporization rate, R_v (mol s^–1) is proportional to the number of solvent surface molecules, N_E, with an energy content enough to overcome attraction energy, E, thus

being N the total number of solvent surface molecules which can be expressed as a fraction of the total number of (solute plus solvent) surface molecules, N_t. Then

where x is the solvent mole fraction that accounts for the surface solvent molecular fraction.

The relationship of N with A depends on molecular areas for solvent and solute as follows

where x_s is the solute mole fraction and b is the solute molecular projected area. Finally, from eqs 6 and 7, a dependence of the total number of solvent surface molecules will be given as

where

is the fraction of the surface area taken up by solvent molecules.

Then eq 5 can be rewritten as

where k_v includes a⁻e^−E/RT.

In an analogous way as for R°_c, condensation rate, R_c (mol s^–1), depends on vapor concentration molecules (at pressure p) and is proportional to condensation surface area, A’, then

At this point it is interesting to discuss conditions for ideal behavior and their outcomes. For ideal solutions the enthalpy of mixing (if both solvent and solute are previously in the same phase as the solution) is null, then the solute–solvent energy interaction is similar to, both, solute–solute and solvent–solvent interaction energies (E = E°). But, there is an additional condition for ideality, that is solvent and solute must be similar in molecular size (Kovac, 1985). If a = b, then (eq 9) f = x. Consequently, both the similar energy interaction and equal size behaviors allow to consider that all points at solution surface are equivalent to those of pure solvent. Then can be concluded that k_v = k°_v, k_c = k°_c and A’ = A. Therefore, under ideal behavior the expressions 10 and 11 convert respectively to

and

When the vapor–liquid equilibrium is reached for a solution, vaporization and condensation rates are equal and pressure of vapor is the solution vapor pressure, p_v. From eqs 12 and 13 is derived

from which, and aided by eq 4, it can be written

which is the enunciation of Raoult's law. Taking into account that x = 1 – x_s, eq 15 can be transformed into

that is the current expression for VPL.

One possible objection to kinetic model (but not yet made) is considering first order kinetics with respect to pressure and surface area. Despite such assumption could be considered a priori very suitable from the point of view of the gas kinetic theory, it is important to point out that kinetic approach was also tested from kinetic measurements (Shapiro et al., 1975). Eq 14 can be also expressed, through eqs 2, 3, 12 and 13, as

This formulation has been successfully used (Shapiro et al., 1975) to calculate molecular weights for non volatile solutes.

Misinterpretation about the kinetic approach

The main misunderstanding about the kinetic view should be supposing it advocates a retardation effect of solute molecules on each solvent evaporation elemental event. Actually, the model shows that the presence of solute molecules at surface causes the reduction of the average molecular evaporation probability. Clearly, all solute molecules (at surface and at bulk) affect properties of solution, but for the evaporation phenomenon attention is focused at surface. For a solute molecule, evaporation probability is 0 and for a solvent molecule, the evaporation probability is π. Then for pure solvent the average molecular evaporation probability is [number of surface solvent molecules × π] / total number of surface molecules = N °π/N° = π, and for solution the average molecular evaporation probability is [number of solute molecules × 0 + number of surface solvent molecules × π] / total number of surface molecules = Nπ/N_t = x π (< π). The reduction of the global evaporation rate for solution with respect to pure solvent, then, results from a statistical factor, represented by x in eq 12. Then the term “blocking” used to represent a solute effect, must not be understood as a solute action like an additional interaction force with solvent molecules, but solute molecules “block” solvent molecular sites at surface (evaporation molecular sites). As stated above, the model (according to ideal behavior) considers solvent–solvent and solute–solvent molecular interactions as equivalent. This last feature is also very important to understand that condensation will occur with the same probability over a zone with solvent molecules, solute molecules or a mixture of both. Therefore, condensation surface area at solution surface, A’, is the total surface area, A, due to all molecular environments are equivalent.

The compatibility with the thermodynamic approach can be seen taking into account the kinetic approach is based on the lowering of solvent evaporation probability of solution, which is directly related to the lower probability of find a solvent molecule at surface. Later correspond to higher solution entropy and the subsequent lowering of evaporation entropy.

Objections to the kinetic approach and the corresponding refutations

In the following we will discuss the specific objections to the kinetic approach:

1) If a few corks are put floating on the surface of a liquid, surface sites will certainly be blocked, but the vapor pressure will obviously remain unaltered (Peckham, 1998).

This experiment would only demonstrate, as it is elementary expected, that vapor pressure of a pure liquid does not depend on total free liquid surface. Corks (macroscopic objects in other phase) cannot emulate a surface dissolved solute and consequently they cannot act as molecular condensation centers at the solution phase. Obviously, both condensation and evaporation at equilibrium occur at free liquid surface at the same rate, keeping the same vapor pressure as for liquid without floating corks. This “blocking” effect exerted by corks has not any connection (not even as analogy) with the kinetic model.

2) An insoluble material, such as cetyl alcohol, which can have no significant effect on the equilibrium vapor pressure of water, can nevertheless reduce the rate of evaporation by a factor of 6 000 as it forms a tightly packed monomolecular layer on the surface. It must therefore reduce the rate of condensation in the same proportion (Mysels, 1955).

Possibly this objection reflects better the essence of the misunderstandings of the kinetic approach. The insoluble layer offers a resistance to the transference of solvent molecules through it that controls both, evaporation and condensation processes (which could be accounted in eqs 2 and 3 with factors in the form “1/resistance”). The layer generates a retardation effect on each (vaporization or condensation) molecular event and, as a consequence, a global (macroscopic) reduction in vaporization and condensation rates occurs. Certainly, the resistance in both directions could be the same, being both rates equally reduced with respect to pure water, and vapor pressure is therefore not affected. But, as above described, the kinetic approach under ideal behavior does not invoke additional or especial forces exerted for solute molecules on solvent molecules. Even in the case of molecular resistance exerted by layer were not the same at each direction, for which vapor pressure would be different with respect to pure solvent, the corresponding phenomena is not that of depicted in the kinetic approach (despite an adaptation of the model should be account for).

3) Accumulation of molecules at the surface, such as is known to occur in solutions of surface–active agents, has no effect on the VPL of these solutions (Mysels, 1955).

The kinetic approach predicts this as the expected behavior. Dilute surfactant aqueous solutions behave as typical electrolytes solutions (Merril, 1950) because dissolved surfactant molecules at liquid surface produce the effect mentioned in the kinetic model. At greater surfactant concentration, molecules accumulated to form a layer do not act as those dissolved at surface and they will behave either as cetyl alcohol layer (objection 2) or as floating corks do (objection 1).

4) The kinetic approach implies that larger molecules which will obstruct the surface more effectively should cause a greater lowering of the vapor pressure when present in same numbers. This, of course, is contrary to Raoult's law (Mysels, 1955).

This was precisely predicted at the explanation of the kinetic approach. Such size effect, as stated above, is another factor for deviation from ideal behavior, then Raoult's law fulfillment must not be necessarily expected. It can be calculated (Kovac, 1985) that for a mole fraction of 0.05 of a solute which molecules are 10 times greater than the solvent ones, the solution vapor pressure is 10% lower than that predicted by Raoult's law (eq 15). This is understood considering that for the case of different molecular sizes between solvent and solute eq 15 must be written as p_v = fp°_v and, through eq 9 for b > a, f < x. Then, for non–ideality only due to different molecular sizes, the kinetic approach still give a description replacing in eq 12x by f. However, even in such case and for enough dilute solutions (x >> 0) f → x, and VPL would be well quantified by eq 16.

5) The explanation violates the principle of microscopic reversibility, since it makes the molecules of solute obstruct the escape but not the arrival of the molecules of solvent (Mysels, 1955).

As mentioned above, a solvent molecule at vapor phase is not obligated to condense over another solvent molecule. Such molecular event does not violate the principle of microscopic reversibility because the time reversed process does not violate any physical law.

Conclusion

The dynamic aspects of the vapor–liquid equilibrium in a solution of non volatile solute can be depicted as a simple extension of the current vaporization–condensation processes for the pure solvent. We think that the objection to the kinetic approach in order to explain vapor pressure of solution is originated in a misinterpretation of the model.

We firmly believe that the kinetic approach is the only suitable teaching tool, especially for students whose cognitive background makes pedagogically inadequate the thermodynamic explanation. If the model is used properly, it cannot provoke any misunderstanding. Moreover, a simplified version of this approach (based only in an intuitive conceptualization made about eq 12 and avoiding the full treatment included in this paper) allows a simple understanding of the phenomenon of VPL.

List of symbols

a area occupied at surface by a solvent molecule (cm²);

A° surface area for pure solvent (cm²);

A total surface area for solution (cm²);

A’ condensation surface area for solution = A (cm²);

B area occupied at surface by a solute molecule (cm²);

E molecular attraction energy for solvent molecules at solution surface (J mol ^–1);

E° molecular attraction energy for surface molecules at pure solvent (J mol ^–1);

f fraction of the surface area taken up by solvent molecules (eq 9);

k°_c temperature factor for condensation of pure solvent (mol s^–1 cm^–2);

k°_v temperature factor for vaporization of pure solvent (mol s^–1 cm^–2);

k_c temperature factor for solvent condensation for solution (mol s^–1 cm^–2);

k_v temperature factor for solvent vaporization for solution (mol s^–1 cm^–2);

N_t total number of (solute plus solvent) surface molecules at solution;

N° number of solvent molecules at pure solvent surface _E° with an energy content enough to overcome attraction energy, E°;

N_E number of solvent molecules at solution surface with an energy content enough to overcome attraction energy, E;

N° total number of solvent surface molecules;

N the total number of solvent molecules at solution surface;

p° pressure of vapor for pure solvent (= p°_v at equilibrium) (Pa);

p°_v vapor pressure of pure solvent (Pa);

p pressure of vapor for solution (= p_v at equilibrium) (Pa);

p_v vapor pressure of solution (Pa);

R gas constant (J K^–1 mol ^–1);

R_c condensation rate for a given solution surface A (mol s^–1);

R°_c condensation rate for a given pure solvent surface A° (mol s^–1);

R°_v vaporization rate for a given pure solvent surface A° (mol s^–1);

R_v vaporization rate for a given solution surface A (mol s^–1);

T temperature (K);

x solvent mole fraction (= solvent molecular fraction at surface);

x_s solute mole fraction;

π solvent molecule evaporation probability