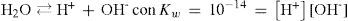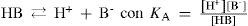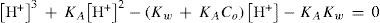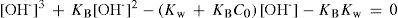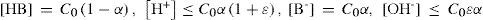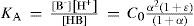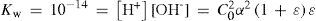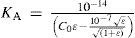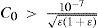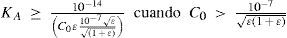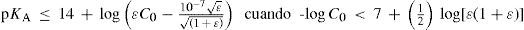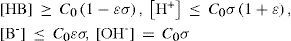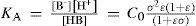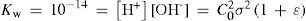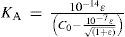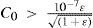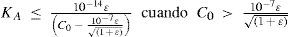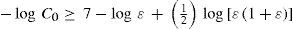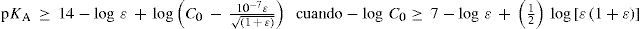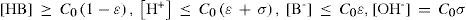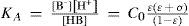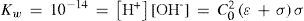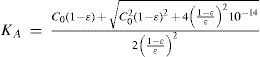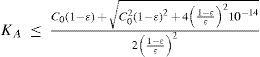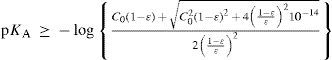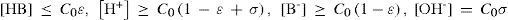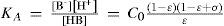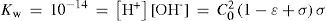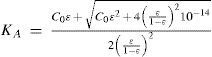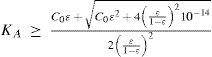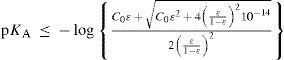La ecuación de Charlot, la gráfica de Flood y la gráfica de Gordus

Abstract

The rigorous treatment of the equilibrium state of a monoprotic acid solution (or a monoprotic base) is presented in order to justify the simplifications that permit the teaching hall presentation with a worksheet.

Introducción

El creciente poder de cálculo en velocidad, precisión y accesibilidad hace pensar que la complejidad matemática es asunto menor en el tratamiento de problemas de química analítica. Por ello, cuando se habla de cálculos de pH se tiene la falsa impresión de que no hay mucho que decir acerca del tema. Pero cuando se pretende enseñar cómo es que se realizan estos cálculos se encuentra que generalmente los algoritmos utilizados se mecanizan antes de ser conceptualizados y cabalmente comprendidos.

En este trabajo se trata de rescatar las ideas de Charlot, Flood y Gordus, acerca de cálculos de pH de los sistemas más simples: la solución acuosa de un ácido monoprótico o de una base monoprótica en concentración analítica molar C₀. Asimismo se presentan las desigualdades que subyacen en la gráfica de Gordus y se presentan hojas de cálculo, construidas ex-profeso, que permiten obtener las gráficas de Flood y Gordus para facilitar el trabajo en el aula cuando se realizan cálculos de pH para estos sistemas.

Si bien hay trabajos (Charlot, 1969; Sandoval, 2009a y 2009b; Gordus, 1987; 1991; Pérez y Carbajal, 1997, 2007a; 2007b; Galano, y col., 2009) acerca de las simplificaciones y las condiciones de su aplicación no se presenta el detalle de éstas, como se muestra a continuación.

Desarrollo

El problema didáctico: planteamiento del cálculo de pH de una solución acuosa de un ácido monoprótico (HB) en molaridad inicial o analítica C₀< 1M (soluciones diluidas)

Se tiene el sistema monoprótico HB/B/H⁺ en donde HB tiene asociado un valor de pK_A para el equilibrio de acidez.

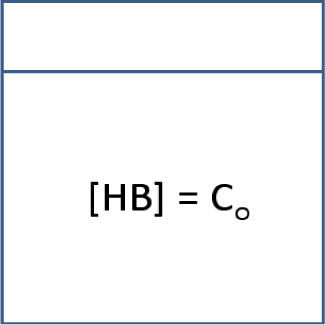
Sea la solución acuosa de HB, mostrada en el esquema 1.

Esquema 1.

Solución acuosa de un ácido monoprótico en concentración analítica molar C₀.

Se puede demostrar que en estos sistemas hay dos ecuaciones químicas independientes que contienen toda la información química del sistema. En este caso —dada la condición inicial— las ecuaciones químicas con más significado físico pueden ser la de autoprotólisis y la de acidez de HB:

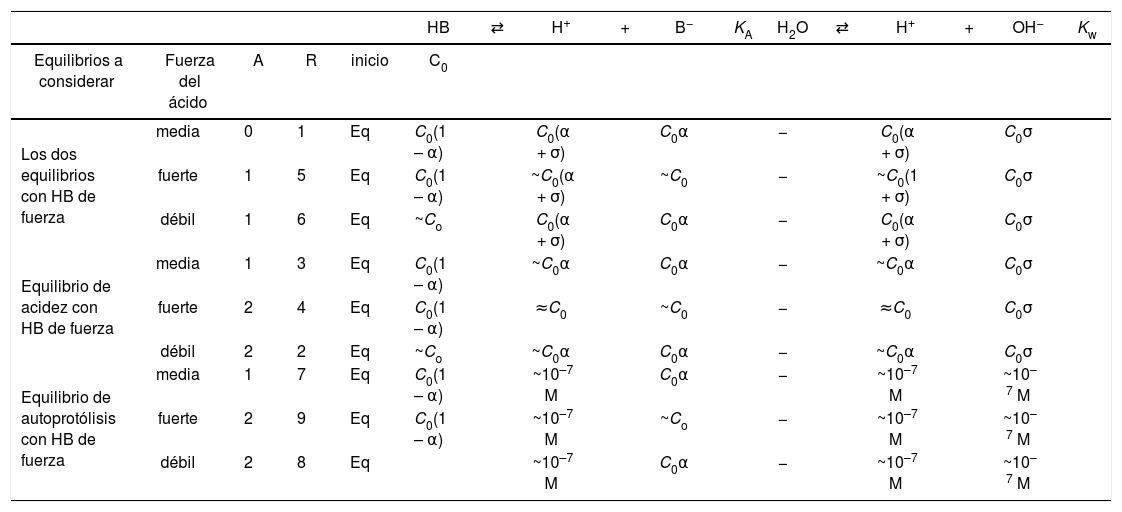
y

El estado de equilibrio del sistema, considerando ambos equilibrios independientes, se establece en la tabla 1.

Tabla 1.

Tabla de Variación de Concentraciones Molares (TVConM) para la solución acuosa de un ácido monoprótico, en concentración analítica molar C₀, considerando dos equilibrios independientes.

	HB	⇄	H^+	+	B^-	KA	H2O	⇄	H^+	+	OH^-	Kw
inicio	C0						-
equilibrio	(1-α)C0		(α+σ)C0		αC0		-		(α+σ)C0		σC0

Cálculo de pH sin aproximaciones sobre el conjunto de equilibrios independientes: Ecuación de Charlot y su representación gráfica: la gráfica de Flood

Al resolver simultáneamente el sistema de ecuaciones que resultan de aplicar la ley de acción de masas de K_A y K_w, considerando las condiciones iniciales del sistema fisicoquímico y la estequiometría de los equilibrios químicos, se obtienen ecuaciones cúbicas para calcular α o σ. Análogamente, considerando la ecuación de balance del componente B, la de electroneutralidad y las leyes de acción de masas para los equilibrios de acidez y autoprotólisis, también se encuentra una ecuación cúbica para calcular los valores de [H⁺] (ecuación 1, a veces llamada ecuación de Charlot), con parámetros que se relacionan con K_w, K_A y C₀. Las soluciones con significado físico de esta ecuación cúbica contienen las condiciones de equilibrio termodinámico del sistema.

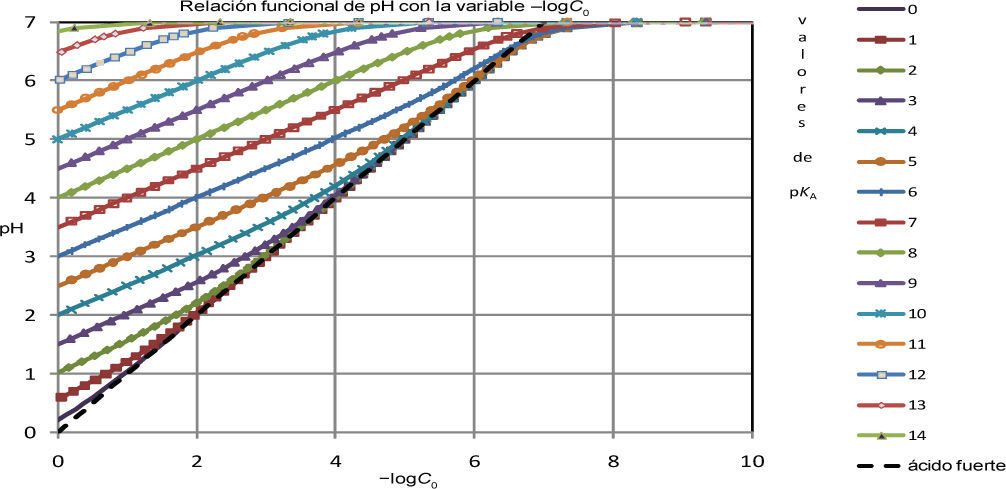
En la figura 1 se muestra una gráfica que presenta todas las soluciones posibles (con significado físico) de la ecuación 1, para valores seleccionados de pK_A.

Figura 1.

Valores de pH de soluciones acuosas del ácido monoprótico HB de molaridad inicial C₀, de acuerdo con las raíces con significado físico de la ecuación 1.

Cabe aclarar que se puede llegar a las mismas ecuaciones cúbicas —en particular a la ecuación 1— aun en el caso de ácidos monopróticos de cualquier carga eléctrica. También es importante señalar que si en el sistema se introduce al inicio solamente la base conjugada del ácido HB, la ecuación a resolver también es cúbica, e isomorfa a la ecuación 1, en donde la variable es la concentración de la especie OH^– y en lugar de la constante de acidez (K_A) aparece la constante de hidrólisis o basicidad (K_B = K_w/K_A). La ecuación 2 muestra la mencionada ecuación cúbica para las bases conjugadas de ácidos monopróticos.

Así, la gráfica de la figura 1 es exactamente la misma que se puede construir para la ecuación 2, pero el eje de las ordenadas sería de pOH (en vez de pH) y los parámetros de la misma serían valores de pK_B (en lugar de pK_A).

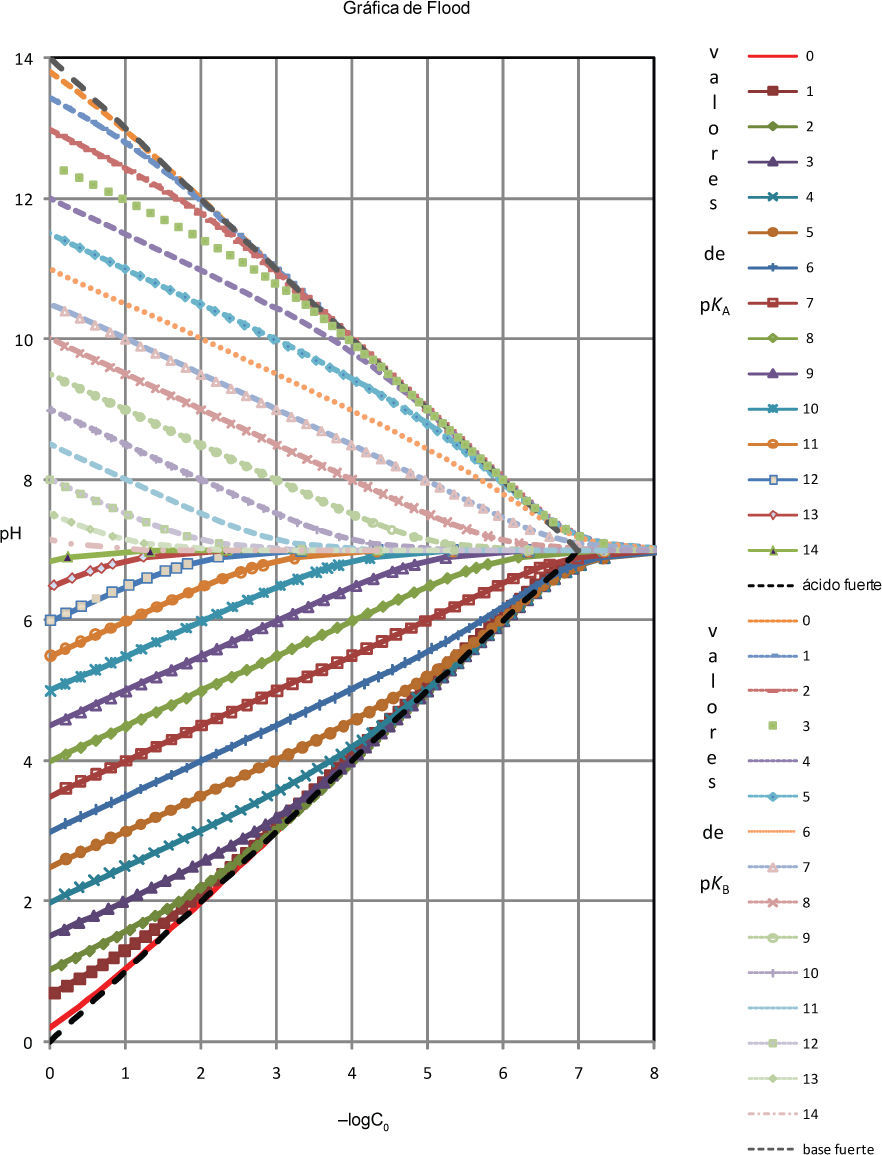
Finalmente, dado que en soluciones acuosas el pH y el pOH de la solución no son independientes y en soluciones diluidas a 25 °C pH = 14 – pOH, las soluciones de la ecuación 2 pueden expresarse en la misma representación gráfica. Esto da lugar a la llamada Gráfica de Flood, que se muestra en la figura 2.

Figura 2.

Gráfica de Flood. Esta gráfica representa todos los valores de pH de equilibrio para soluciones acuosas de ácidos monopróticos en concentración analítica molar C₀ (valores de pH < 7) o de las correspondientes soluciones acuosas de bases conjugadas en concentración analítica molar C₀ (valores de pH > 7).

Por lo tanto, la gráfica que se presenta en la figura 1 podría llamarse la “semigráfica de Flood”. La gráfica de Flood puede utilizarse para realizar cálculos de pH de soluciones acuosas de ácidos monopróticos en concentración C₀, o de sus bases conjugadas.

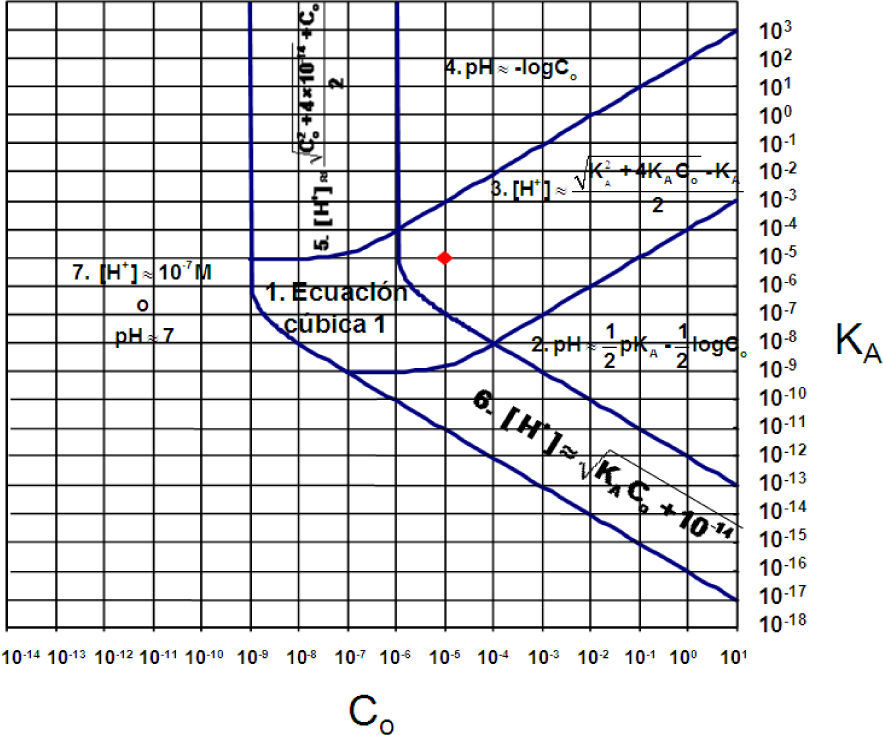
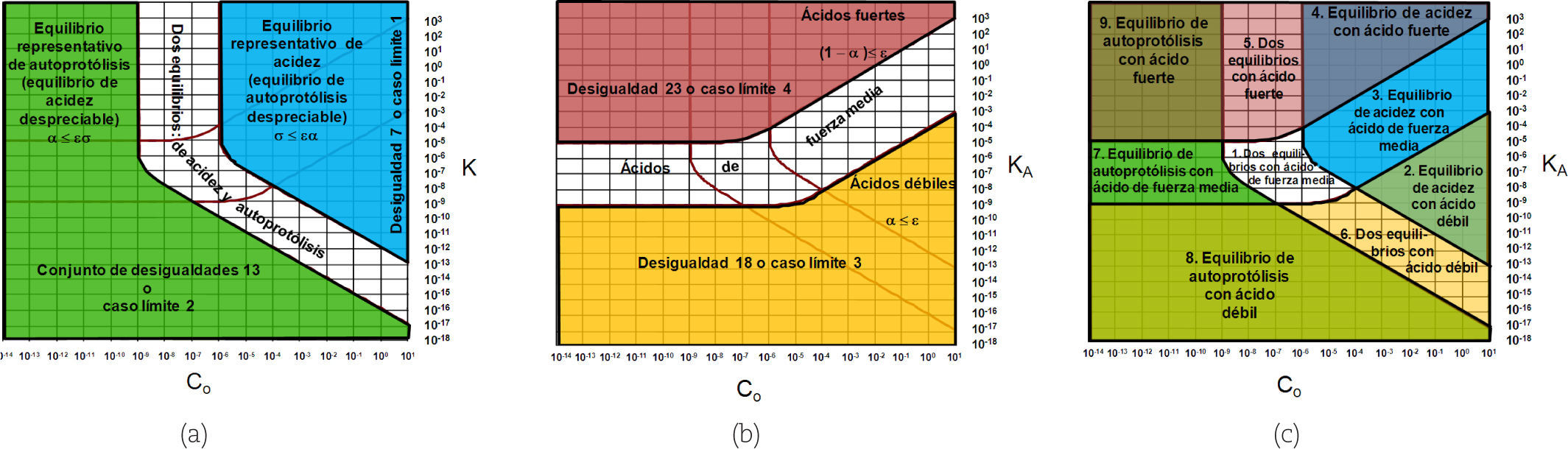
Gráfica de Gordus: establecimiento de las fronteras de importancia relativa de equilibrios, de fuerza de las especies y su relación con el error (ε) en los cálculos de concentración

La importancia relativa de los equilibrios en el sistema —mostrados en la tabla 1— depende de los parámetros; es decir, de los valores de K_w, K_A y C₀. Esto se representa en la gráfica mostrada en la figura 3 (ver Gordus, 1991). Dicha gráfica considera el 1% de error porcentual sobre las concentraciones de equilibrio en los cálculos (ε = 0.01). En la figura 3 es posible ver las regiones en donde es posible realizar aproximaciones para el cálculo de pH, cuando se está dispuesto a cometer un error no mayor que del 1% en los cálculos de las concentraciones de equilibrio.

Figura 3.

Gráfica de Gordus para una solución acuosa de un monoácido en concentración analítica molar C_o. El punto mostrado con un círculo representa un sistema en donde el ácido HB está en molaridad analítica 1 × 10^–5 M y tiene un valor de pK_A = 5.0. En cada región de la gráfica, excepto en la región 1 —numeradas de acuerdo a Gordus (1987, 1991)— se han escrito las ecuaciones que aproximadamente resuelven el pH del sistema, considerando un error máximo del 1% sobre las concentraciones de equilibrio de las especies.

El enfoque de Gordus es el mismo que hace Charlot en su libro, pero más completo, y pretende dar respuesta a las siguientes preguntas: ¿En qué condiciones es posible simplificar la solución del problema, de manera que no tenga que resolverse la ecuación 1, sino una más simple? ¿Cómo debe plantearse el problema para llegar a la gráfica mostrada en la figura 3?

Construcción de la Gráfica de Gordus, con la consideración explícita de ε

La construcción de la figura 3, considerando explícitamente ε, implica dos casos límite acerca de la importancia relativa de los equilibrios independientes del sistema, así como dos casos límite acerca de la fuerza del ácido.

Caso límite 1. Equilibrio de acidez con autoprotólisis despreciable (σ << α).

Condición de aproximación: σ ≤ εα.

Al introducir esta condición de aproximación en las condiciones de equilibrio mostradas en la tabla 1 se obtiene:

Introduciendo los valores frontera (igualdades) en las leyes de acción de masas se tiene:

y

Al despejar α de la ecuación 4 y sustituirla en la 3 se tiene

El denominador de la ecuación 5 sólo puede ser positivo definido si se cumple la desigualdad

La aproximación del equilibrio de acidez con autoprotólisis despreciable debe ser cada vez mejor cuando el valor de K_A sea mayor o igual que el otro miembro en la ecuación 5 (porque el equilibrio de acidez se hace más importante); por lo tanto:

o en forma logarítmica

Caso límite 2. Equilibrio de autoprotólisis con acidez despreciable (α << σ).

Condición de aproximación: α ≤ εσ.

Al introducir esta condición de aproximación en las condiciones de equilibrio mostradas en la tabla 1 se obtiene:

Introduciendo los valores de frontera (igualdades) en las leyes de acción de masas se tiene:

y

Al despejar σ de la ecuación 10 y sustituirla en la 9 se obtiene

Otra vez, el miembro derecho de la ecuación 11 sólo puede ser positivo definido si se cumple la desigualdad

La aproximación del equilibrio de autoprotólisis con acidez despreciable debe ser cada vez mejor cuando C₀ ≤ {10^–7ε / [(1 + ε)^1/2]} o cuando el valor de K_A sea menor o igual que el otro miembro en la ecuación 11 (porque el equilibrio de acidez se hace menos importante); por lo tanto:

o

o en forma logarítmica

o

Caso límite 3. El ácido se comporta como débil (a ≈ 0).

Condición de aproximación: a ≤ ε.

Al introducir esta condición de aproximación en las condiciones de equilibrio mostradas en la tabla 1 se obtiene:

Introduciendo los valores frontera (igualdades) en las leyes de acción de masas se tiene:

y

Despejando s de la ecuación 15 y al sustituirla en la 16 se obtiene

Ahora bien, la ecuación 17 siempre es positivo definida para cualquier valor razonable de ε ya que 0 < ε << 1. Por otra parte, la aproximación de ácido débil es buena si se cumple la desigualdad:

o en forma logarítmica:

Caso límite 4. El ácido se comporta como fuerte (α » 1).

Condición de aproximación: (1 − σ) ≤ ε; o bien, (1 − ε) ≤ α.

Al introducir esta condición de aproximación en las condiciones de equilibrio mostradas en la tabla 1 se obtiene:

Introduciendo los valores frontera (igualdades) en las leyes de acción de masas se tiene:

y

Despejando σ de la ecuación 20 y al sustituirla en la 21 se obtiene

Una vez más, la ecuación 22 siempre es positivo definida para cualquier valor razonable de ε ya que 0 < ε << 1. Por otra parte, la aproximación de ácido fuerte es buena si se cumple la desigualdad:

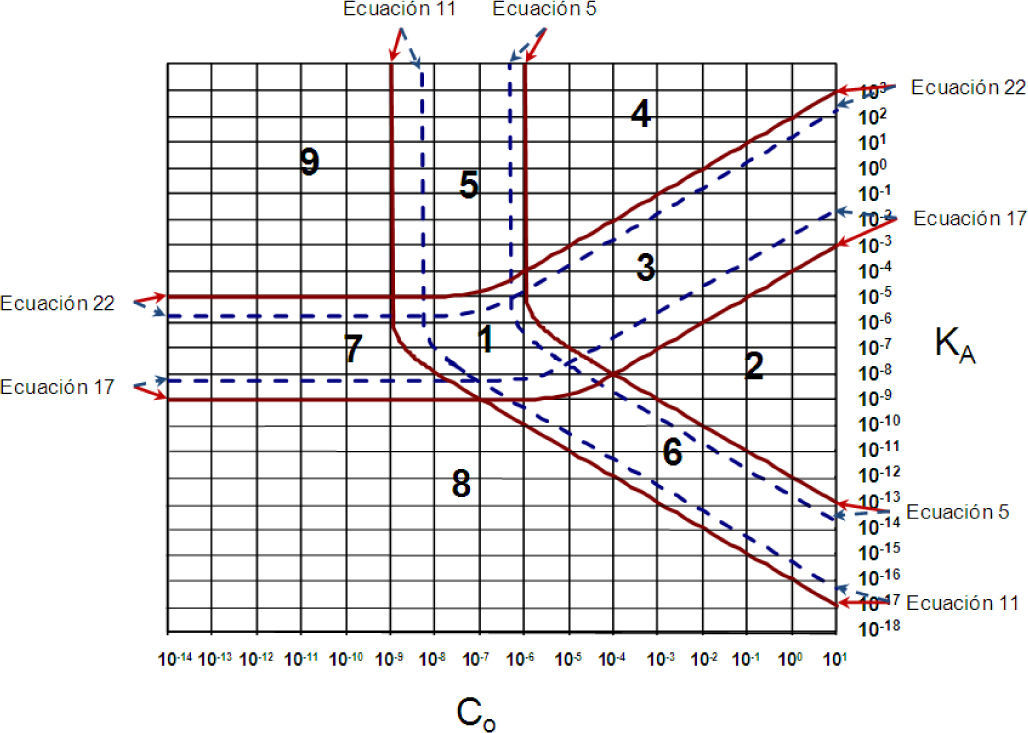
o en forma logarítmica:

Ecuaciones frontera de los casos límite para un error (ε) fijo

Si se grafican las ecuaciones 5, 11, 17 y 22 en el espacio K_A = f(C₀) con escalas logarítmicas puede obtenerse la figura 4. El conjunto de líneas en trazo continuo se ha calculado para un error del 1% (ε = 0.01), en tanto que el de líneas en trazo punteado se ha calculado para un error del 5% (ε = 0.05).

Figura 4.

Gráfica de Importancia Relativa de EQuilibrios y Fuerza de Especies (GIREQFE) para la solución acuosa de un ácido monoprótico. Las líneas continuas se calcularon con las ecuaciones correspondientes para un error del 1% (ε = 0.01), en tanto que las líneas punteadas se calcularon para un error del 5% (ε = 0.05).

Si se comparan las líneas de la figura 4 con las de la figura 3 se observa que son las mismas cuando e = 0.01, salvo que en la gráfica de Gordus la ecuación 22 sólo se grafica para valores de C₀ mayores a la concentración en donde se intersecan las ecuaciones 11 y 22, en tanto que la ecuación 17 sólo se grafica para valores de C₀ mayores a la concentración en donde se intersecan las ecuaciones 11 y 17.

Cabe señalar que la gráfica que se muestra en la figura 4 (para un valor fijo de e) puede llamarse Gráfica de Importancia Relativa de EQuilibrios y Fuerza de Especies (gireqfe) por el significado de los casos límite que se han establecido para su construcción.

También es interesante hacer notar que cuando el error que se está dispuesto a cometer en los cálculos de concentración es más grande, el área comprendida entre las ecuaciones 5 y 11 y entre las ecuaciones 17 y 22 se hace más pequeña. Esto es lógico, si se piensa que las regiones en donde se cumplen ecuaciones aproximadas —mostradas en la figura 3— deben hacerse más grandes.

Las cuatro trayectorias obtenidas en los casos límite dividen la gráfica en nueve regiones o zonas, que se han numerado de acuerdo a Gordus (1987, 1991) —con excepción de las regiones 8 y 9 que no se muestran en dicha referencia.

Regiones delimitadas en la GIREQFE para un error (ε) fijo

Para explicar mejor qué aproximaciones pueden hacerse en cada región, en la figura 5 se muestran esquemas explicativos que se relacionan con las desigualdades 7, 13, 18 y 23.

Figura 5.

Diferentes regiones de la GIREQFE con un error del 1%. (a) Aproximaciones posibles sobre la importancia relativa de equilibrios independientes; (b) Aproximaciones posibles sobre la fuerza del ácido; (c) Al sobreponer las regiones de las figuras 5a y 5b el espacio se divide en nueve regiones. En la región central (1 en la figura 4) no se pueden hacer aproximaciones para realizar cálculos precisos. En las cuatro regiones intermedias (3, 5, 6 y 7 de la figura 4) sólo se puede hacer una aproximación. En las otras cuatro regiones (2, 4, 8 y 9 de la figura 4) se pueden hacer dos aproximaciones.

La figura 5c permite deducir que en la región 1 de la figura 4 no se pueden hacer aproximaciones para realizar cálculos sobre la concentración de equilibrio de las especies del sistema con un error menor o igual al 1%; por lo tanto, habría que usar la solución (con significado físico) de la ecuación cúbica 1.

Ahora bien, la misma figura 5c permite deducir que en la figura 4 hay cuatro regiones que conllevan una aproximación. Las regiones 3 y 7 se establecen mediante una aproximación relacionada con la importancia relativa de los equilibrios de acidez y autoprotólisis, en tanto que las regiones 5 y 6 se establecen mediante una aproximación relacionada con la fuerza (el grado de disociación) del ácido.

También la figura 5c permite deducir que en la figura 4 hay otras cuatro regiones que conllevan dos aproximaciones. Las regiones 2 y 4 se establecen considerando que el equilibrio de acidez es más importante que el de autoprotólisis en tanto que la otra aproximación se relaciona con la fuerza del ácido. Asimismo, las regiones 8 y 9 se establecen considerando que el equilibrio de autoprotólisis es más importante que el de acidez en tanto que la otra aproximación se relaciona con la fuerza del ácido.

Cálculos de las concentraciones de equilibrio, con la ayuda de la GIREQFE, para un error (ε) fijo

Las aproximaciones relacionadas con las regiones 2 a 9 en la figura 4 pueden establecerse cuantitativamente sobre el estado de equilibrio mostrado en la tabla 1, despreciando los términos que son pequeños en las sumas y restas de las concentraciones de equilibrio. Así, en la tabla 2 se muestran explícitamente las aproximaciones que pueden hacerse —cometiendo un error menor o igual a ε— sobre las condiciones de equilibrio del sistema y se relacionan con las diferentes regiones de las figuras 4 y 5c.

Tabla 2.

TVConM que muestra las aproximaciones que pueden establecerse para calcular las concentraciones de equilibrio de todas las especies en la solución con un error menor o igual a ε.

					HB	⇄	H^+	+	B^−	KA	H2O	⇄	H^+	+	OH^−	Kw
Equilibrios a considerar	Fuerza del ácido	A	R	inicio	C0
Los dos equilibrios con HB de fuerza	media	0	1	Eq	C0(1 – α)		C0(α + σ)		C0α		−		C0(α + σ)		C0σ
	fuerte	1	5	Eq	C0(1 – α)		~C0(α + σ)		~C0		−		~C0(1 + σ)		C0σ
	débil	1	6	Eq	~Co		C0(α + σ)		C0α		−		C0(α + σ)		C0σ
Equilibrio de acidez con HB de fuerza	media	1	3	Eq	C0(1 – α)		~C0α		C0α		−		~C0α		C0σ
	fuerte	2	4	Eq	C0(1 – α)		≈C0		~C0		−		≈C0		C0σ
	débil	2	2	Eq	~Co		~C0α		C0α		−		~C0α		C0σ
Equilibrio de autoprotólisis con HB de fuerza	media	1	7	Eq	C0(1 – α)		~10^–7 M		C0α		−		~10^–7 M		~10^–7 M
	fuerte	2	9	Eq	C0(1 – α)		~10^–7 M		~Co		−		~10^–7 M		~10^–7 M
	débil	2	8	Eq			~10^–7 M		C0α		−		~10^–7 M		~10^–7 M

A = Número de aproximaciones realizadas.

R = Región de las figuras 4 y 5c en donde se cumple la condición de equilibrio mostrada.

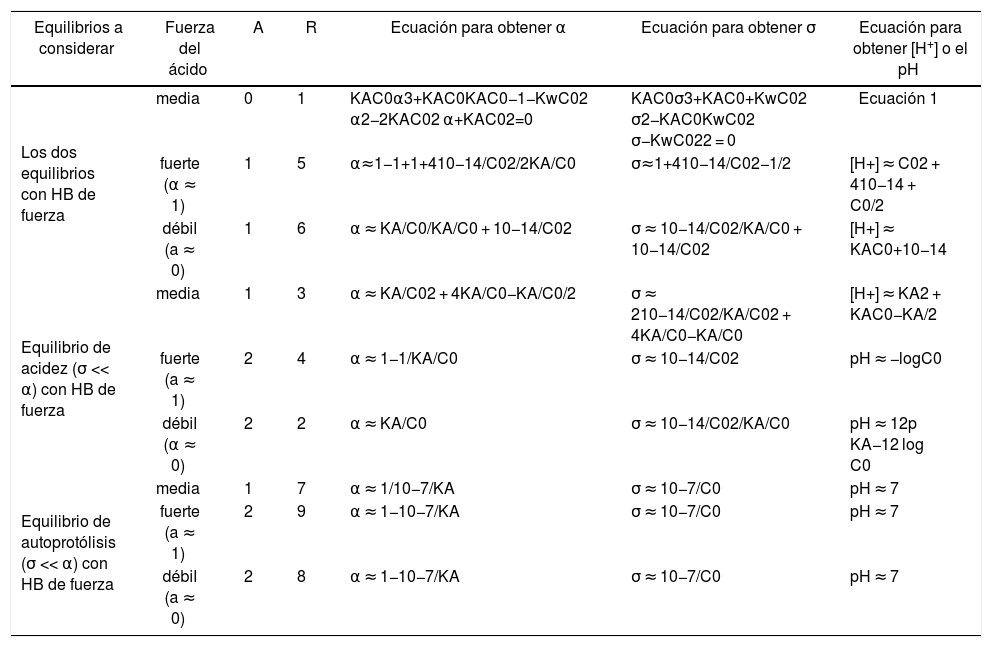
Como se muestra en la tabla 2, para conocer las concentraciones de equilibrio de todas las especies en la solución en cada caso particular es necesario calcular los valores de la fracción disociada del ácido (α) y del grado de autoprotólisis (σ). Es por ello que en la tabla 3 se muestran las expresiones algebraicas que permiten calcular a y s, al resolver el sistema de ecuaciones correspondiente, con un error menor o igual a ε. Con los valores de estas variables calculadas con las ecuaciones de la tabla 3 y las expresiones de la tabla 2 se pueden conocer todas las concentraciones de equilibrio de las especies en el sistema para cualquier condición inicial de una solución acuosa de un ácido monoprótico.

Tabla 3.

Cálculos exacto y aproximados para determinar las concentraciones de equilibrio de todas las especies en el sistema de la solución acuosa de un ácido monoprótico de molaridad analítica C_o considerando un error máximo igual a ε.

Equilibrios a considerar	Fuerza del ácido	A	R	Ecuación para obtener α	Ecuación para obtener σ	Ecuación para obtener [H^+] o el pH
Los dos equilibrios con HB de fuerza	media	0	1	KAC0α3+KAC0KAC0−1−KwC02 α2−2KAC02 α+KAC02=0	KAC0σ3+KAC0+KwC02 σ2−KAC0KwC02 σ−KwC022 = 0	Ecuación 1
	fuerte (α ≈ 1)	1	5	α≈1−1+1+410−14/C02/2KA/C0	σ≈1+410−14/C02−1/2	[H+] ≈ C02 + 410−14 + C0/2
	débil (a ≈ 0)	1	6	α ≈ KA/C0/KA/C0 + 10−14/C02	σ ≈ 10−14/C02/KA/C0 + 10−14/C02	[H+] ≈ KAC0+10−14
Equilibrio de acidez (σ << α) con HB de fuerza	media	1	3	α ≈ KA/C02 + 4KA/C0−KA/C0/2	σ ≈ 210−14/C02/KA/C02 + 4KA/C0−KA/C0	[H+] ≈ KA2 + KAC0−KA/2
	fuerte (a ≈ 1)	2	4	α ≈ 1−1/KA/C0	σ ≈ 10−14/C02	pH ≈ −logC0
	débil (α ≈ 0)	2	2	α ≈ KA/C0	σ ≈ 10−14/C02/KA/C0	pH ≈ 12p KA−12 log C0
Equilibrio de autoprotólisis (σ << α) con HB de fuerza	media	1	7	α ≈ 1/10−7/KA	σ ≈ 10−7/C0	pH ≈ 7
	fuerte (a ≈ 1)	2	9	α ≈ 1−10−7/KA	σ ≈ 10−7/C0	pH ≈ 7
	débil (a ≈ 0)	2	8	α ≈ 1−10−7/KA	σ ≈ 10−7/C0	pH ≈ 7

A = Número de aproximaciones realizadas.

R = Región de las figuras 4 y 5c en donde se cumplen las ecuaciones mostradas.

La tabla 3 también muestra una columna con las ecuaciones, exacta y aproximadas, para cálculos de la [H⁺] o el pH, tal como aparecen en la figura 3. Esto se debe a la importancia que tiene este cálculo para sistemas ácido-base de Br&b.phiv;nsted.

Finalmente, cabe aclarar que la gráfica de Gordus sólo presenta una región 7, que se presenta para valores de C₀ muy pequeños o valores de pK_A muy grandes, en donde el pH es aproximadamente igual a 7 (porque el equilibrio más importante es entonces el de autoprotólisis). El que aparezcan las regiones 8 y 9 desde la figura 4 se relaciona con aproximaciones para el mejor cálculo de α con ecuaciones aproximadas, como se observa en la tabla 3.

Hojas de cálculo de Excel para la construcción de la gráfica de Flood y la GIREQE para una solución acuosa de un ácido monoprótico en molaridad analítica C0

Aunque las gráficas de Flood y de Gordus aparecen en algunas publicaciones, consideramos conveniente construir unas hojas de cálculo para poder aprovechar estas herramientas, de manera más versátil, haciendo uso de los recursos computacionales.

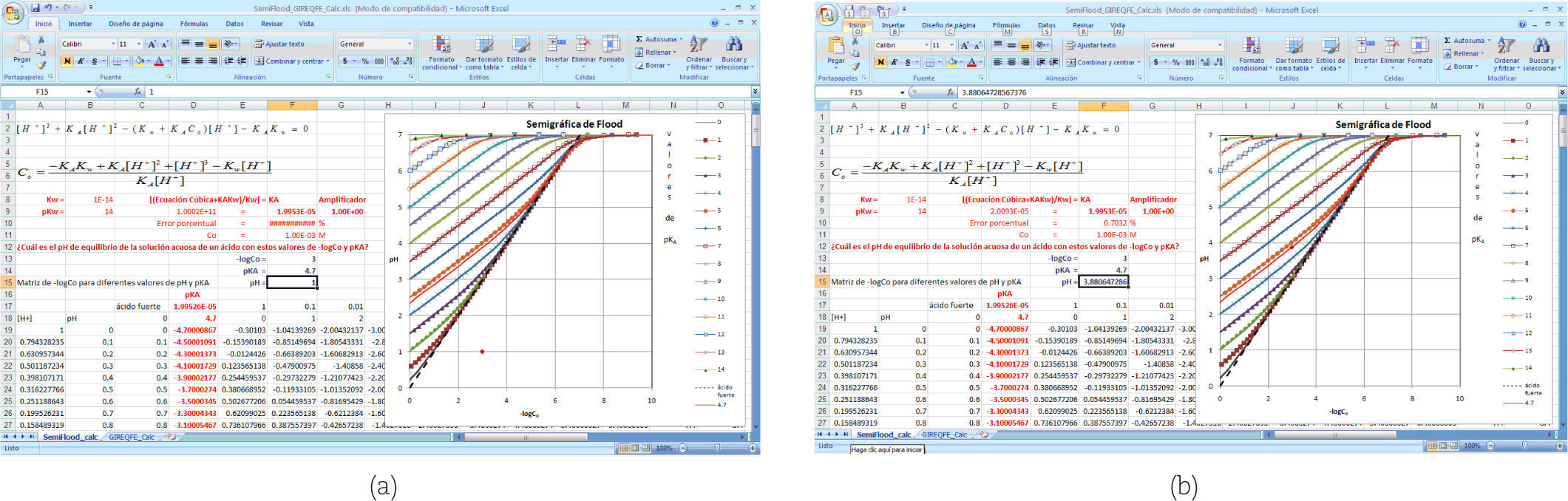
En la figura 6 se presentan detalles de la hoja de cálculo SemiFlood_calc que se encuentra en el libro SemiFlood_GIREQFE_Calc.xls del programa Excel de Microsoft para Office 2007. En el lado izquierdo, en la parte superior, se muestran la ecuación 1 y el despeje de C₀ como función de [H⁺] a partir de dicha ecuación. En la hoja de cálculo se construye entonces una matriz en donde se calculan los valores de C₀ para diferentes valores de pK_A para valores de pH en el intervalo de 0 a 14, con incrementos de 0.1. Los datos de esta matriz se grafican como se muestra en la misma figura 6, dando lugar a la semigráfica de Flood. La hoja se hizo con la finalidad de resolver, por aproximaciones sucesivas, la pregunta: ¿cuál es el pH de equilibrio de la solución acuosa de un ácido con estos valores de –logC₀ y pK_A? Las coordenadas iniciales del punto mostrado en la figura 6a como un rombo (rojo en la pantalla a color) son –logC₀ = 3 y pH = 1, para un pK_A = 4.7. Por aproximaciones sucesivas hay que acercar el rombo a la línea continua (una curva delgada ubicada entre las curvas de pK_A = 4 y pK_A = 5, que también es de color rojo en la pantalla a color) para resolver el problema. El punto puede llevarse cerca de la línea cambiando el valor de pH en la celda F13 y luego utilizar la rutina Solver de Excel, aunque la rutina no converge a una solución muy cercana para resolver este problema cuando se tiene un valor calculado (celda D9) muy diferente al valor del K_A (celda F9)). Así, la respuesta obtenida para este problema es pH = 3.8806472858934, después de haber acercado el rombo a la curva de pK_A = 4.7 cambiando el valor de pH a 3.85. El error cometido en la aproximación es 0.5406%.

Figura 6.

Hoja de cálculo para realizar cálculos de pH con la semigráfica de Flood. (a) Situación inicial de la hoja cuando se plantea la pregunta, y (b) Solución obtenida para este problema con la ayuda de la rutina Solver de Excel.

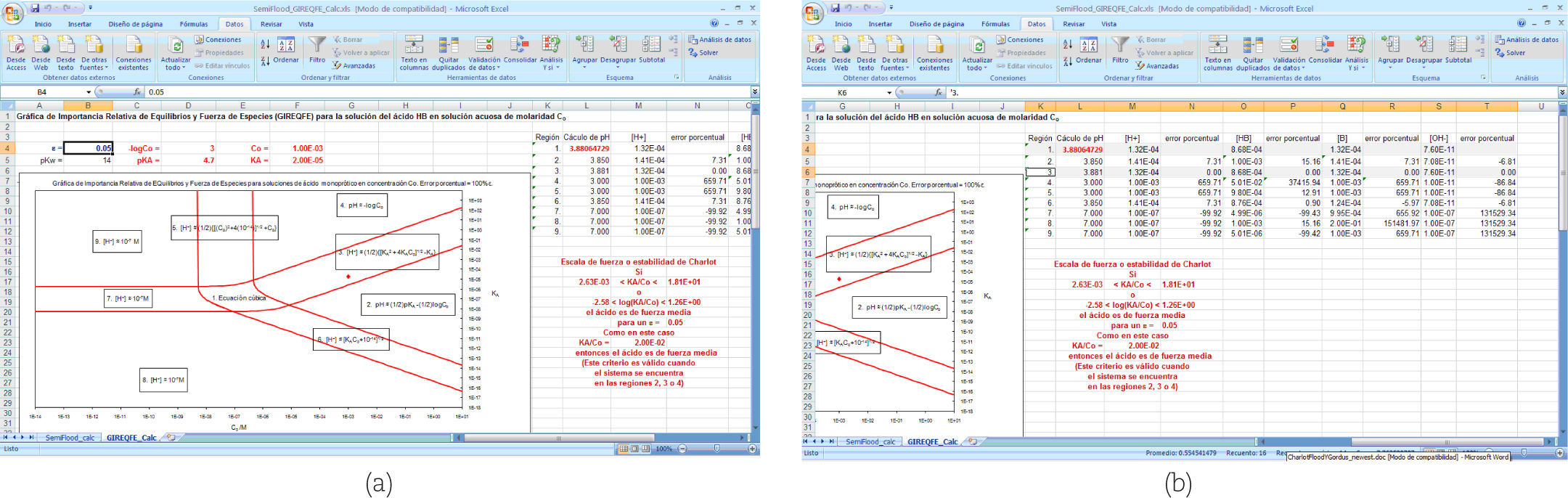
Ahora bien, en la figura 6 se observa que el libro Semi-Flood_GIREQFE_Calc.xls tiene también una hoja de cálculo, llamada GIREQFE_calc que aprovecha la solución a la ecuación cúbica obtenida en la hoja SemiFlood_calc para explicar el uso de la gráfica de Gordus. Entonces, en la figura 7 se observa el contenido de la hoja GIREQFE_calc después de haber obtenido una solución al pH de la solución que se estudió en la hoja Semiflood_calc en la figura 6b.

Figura 7.

Contenido de la hoja GIREQFE_calc (del libro SemiFlood_GIREQFE_Calc.xls) después de haber obtenido una solución aceptable en la hoja SemiFlood_calc mostrada en la figura 6b. a) Presentación de la GIREQFE asociada al problema mostrado en la figura 6, y b) Los cálculos de la tabla muestran que la mejor solución aproximada es, efectivamente, la que se presenta para la región 3.

Las coordenadas del punto (C₀, K_A) del problema que se está estudiando se representan por medio del rombo (de color rojo en la pantalla a color) en la figura 7a; que en este caso cae en la región 3 para un valor de error igual a 0.05. El valor del pH calculado se encuentra en la celda L4 (también en color rojo en la pantalla a color). En la figura 7b se observan todas las concentraciones de equilibrio de las especies relevantes en el problema y es evidente que el valor calculado en forma aproximada con las ecuaciones de la región 3 son las que tienen un error porcentual menor o igual al 5%.

En la figura 7 también se muestra que en la hoja GIREQFE_calc aparece la escala de fuerza de ácidos de Charlot, con el parámetro K_A/C₀, que es una manera equivalente de tratar el problema del grado de disociación del ácido que en la gráfica de Gordus, en las regiones 2, 3 y 4.

Aquellos lectores interesados en recibir el archivo de Excel con el que se realizaron todas estas figuras del artículo, pueden solicitarlo por correo electrónico al primer autor: Alberto Rojas H. . Resulta interesante tenerlo para cambiar alguno de los datos iniciales y ver los resultados.

Conclusiones

Este trabajo muestra las ideas fundamentales de la solución exacta al problema de cálculo del pH de equilibrio para una solución acuosa de un ácido monoprótico o de una base monoprótica. Se recuerda cómo se construyen e interpretan las gráficas de Flood y de Gordus y, finalmente, se presenta una hoja de cálculo que puede ser utilizada en los cursos de química analítica (material disponible con los autores).

En un segundo artículo de esta sección explotaremos el potencial de este tratamiento mediante el planteo de problemas y su resolución con los instrumentos aquí presentados.