The Nobel Prize in Physics for 2012 was awarded to Serge Haroche and David J. Wineland “for ground-breaking experimental methods that enable measuring and manipulation of individual quantum systems”. The former deals with photons and measures them with atoms and the latter deals with ions and manipulates them with photons. The potential and actual applications of handling quantum systems are on their way to revolutionize not only technology but the way we understand the microscopic world.
Desde el advenimiento de la mecánica cuántica y a lo largo de la historia de su desarrollo se ha tenido que lidiar con fenómenos y propiedades que nos son ajenos por la escala a la que interactuamos cotidianamente (Tegmark & Wheeler, 2001). La dualidad onda-corpúsculo y el principio de indeterminación son conceptos pilares que nos ayudan a entender la estructura atómica y molecular en términos de orbitales. No obstante, los más recientes avances y experimentos nos hablan de una gran lista de cualidades que podríamos calificar, cuando menos, como desconcertantes. Los “misterios” cuánticos han inspirado publicaciones como El mensaje del cuanto (Zeilinger, The message of the quantum, 2005) donde pueden leerse las provocativas frases: “…para el evento individual en física cuántica, no sólo se desconoce la causa, no hay causa” y “la suposición de que la partícula posee tanto posición como momento, antes de la medición, es errada.”
Dentro de dicha lista se encuentra la superposición de estados. Por ejemplo la proyección para el espín de un electrón puede ser positiva (apuntar “hacia arriba”), negativa (apuntar “hacia abajo”) o una superposición de ambos. En el último caso esto implica que al medir se puede obtener cualquiera de ambos resultados, cada uno con cierta probabilidad. Lo último suele interpretarse como que el espín electrónico se encuentra en ambos estados simultáneamente mientras no sea medido, pues en la medición se selecciona sólo una de las contribuciones a la superposición (Peña, 2003).
Tomemos ahora una molécula de H2 en estado electrónico singulete, es decir que los espines de ambos electrones se encuentran en orientaciones opuestas. Si dicha molécula se disocia en el vacío se obtendrán dos átomos de hidrógeno con la peculiaridad de que el espín del electrón en uno de ellos será opuesto al del electrón en el otro átomo; en otras palabras, si al determinar la proyección del espín en el átomo A ésta sale negativa, entonces se puede asegurar que la correspondiente en el átomo B será positiva. Sin embargo, para satisfacer el requerimiento de antisimetría que da lugar al principio de exclusión de Pauli, el estado singulete en la molécula original corresponde a una superposición de las dos combinaciones de espín posibles: (↑,↓) y (↓,↑). Esto significa que al medir la componente de espín sobre el átomo A, los estados sobre los cuales se hará la selección son moleculares, ¡a pesar de que ya no existe enlace covalente!, y no sólo eso sino que el átomo B “se enterará” del estado seleccionado sin que se haya interactuado directamente con él. En este ejemplo se han ilustrado el entrelazamiento y la no localidad (Peña, 2003).
Se dice que los átomos se encontraban en un estado entrelazado porque la medición sobre el átomo A implicó la definición de la propiedad en el átomo B sin tener que hacer ninguna medida sobre éste; es decir, que a pesar de lidiar con sistemas separados éstos se comportan como uno solo y toda la descripción se hace para el sistema diatómico y nunca para cada átomo por separado. Y se habla de no localidad ya que la acción sobre el átomo A tuvo una consecuencia sobre el átomo B sin importar que éstos ya no tuvieran una comunicación o contacto directo, en este caso, sin importar que ya no existiera enlace químico.
Éstas y otras peculiaridades no sobreviven hasta la escala macroscópica ya que la mera interacción de dos sistemas diferentes implica que éstos “se miden” mutuamente; si hablamos de moles de sistemas entonces el número de mediciones efectuadas terminará colapsando las superposiciones y separando entrelazamientos. Este proceso se llama decoherencia y dadas las condiciones usuales de un sistema clásico bajo régimen térmico, es casi omnipresente y su acción sumamente rápida (Tegmark & Wheeler, 2001). Incluso Erwin Schrödinger llegó a afirmar: “Nunca experimentamos con sólo un electrón o átomo o molécula (pequeña). A veces suponemos que lo hacemos en experimentos pensados, esto invariablemente conlleva a consecuencias ridículas” (Schrödinger, 1952). 77 años después, los galardonados al premio Nobel de Física en 2012 lograron desarrollar métodos experimentales que permiten acceder a las propiedades cuánticas a pesar de la diferencia de escalas y de la decoherencia (Nobel Foundation, 2012). Veamos cómo lo hicieron.
Fotones en cavidadesUna realización de sistema cuántico es un fotón, y la óptica cuántica se encarga de su estudio (Vicent, et al., 2008). A grandes rasgos, las técnicas experimentales de esta disciplina se basan en el uso de espejos semitransparentes (reflejan y dejan pasar porciones iguales de la luz incidente) y retardadores de onda (cristales que alteran la propagación de la luz en una fracción controlada del ciclo de onda) para determinar la interferencia entre fotones individuales, es decir que no pertenecen a un haz. Los resultados experimentales logrados hasta la fecha han tenido enorme relevancia tanto para la indagación y comprobación de aspectos fundamentales en la teoría cuántica como para el desarrollo de nuevas y prometedoras tecnologías tales como encriptación cuántica (diseño de códigos secretos) y teleportación (traslado instantáneo de información) (Zeilinger, 2000), incluso se han logrado aprovechar para realizar cálculos de estructura electrónica (Lanyon, et al., 2012). Sin embargo, en todos esos experimentos aunque los fotones puedan ser manipulados durante la trayectoria, están condenados a desaparecer al momento de la medición.
El gran logro de Serge Haroche y sus colaboradores Jean-Michel Raimond y Michel Brune en la École Normale Supérieure de París ha sido encontrar formas de medir estados de fotones individuales sin destruirlos en el proceso (Nogues, et al., 1999).
Con este objetivo, el primer paso consiste en lograr fotones de “vida larga”, para lo cual se recurre a una cavidad esférica cuyo interior se encuentra forrado de Nb pulido a espejo. De esta forma, efectuando los experimentos a temperaturas cercanas al cero absoluto se puede garantizar: primero, que la contribución por radiación térmica al interior de la cavidad es despreciable, y segundo, que el forro será superconductor estabilizando el campo eléctrico. Como consecuencia, los fotones que rebotan en la cavidad tienen una vida media de más de 10 órdenes de magnitud mayor que en cualesquiera otras condiciones.
Los fotones confinados adquieren una longitud de onda del tamaño de la cavidad, es decir en las microondas. Un átomo dentro de la cavidad sería, en principio, insensible a este tipo de radiación, por lo cual los átomos se preparan en estados de Rydberg. En éstos, el átomo de valencia de un átomo alcalino (el grupo de Haroche emplea Rb) se encuentra en un estado excitado de tan alta energía que el conjunto de electrones internos y el núcleo quedan tan lejanos que el sistema se asemeja a un átomo hidrogenoide, lo que facilita su descripción (Kleppner, Littman, & Zimmerman, 1981); además, los número cuánticos elegidos para este caso particular: n=50 y l=|ml|=49, son idóneos para que el átomo interactúe con la radiación en la cavidad mediante la transición al estado excitado con n=51. Sin embargo, el dispositivo está diseñado para que la frecuencia de los fotones en la cavidad no coincida exactamente con la diferencia en energía de los niveles atómicos en cuestión. De esta manera, el átomo no absorbe la radiación permitiendo la subsistencia de los fotones, y es su interacción con el campo eléctrico lo que modifica los niveles energéticos (efecto Stark) y, por ende, su función de onda, dejándolo en un estado cuya medición revelará los detalles de la interacción con los fotones.
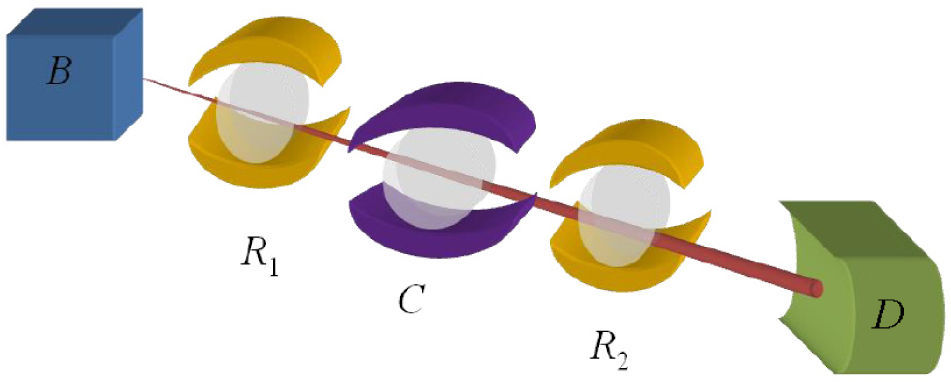
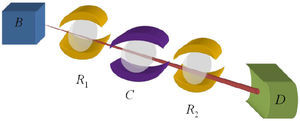
Un diagrama del dispositivo empleado por el grupo de Haroche se muestra en la figure 2. En la caja B se crea el estado de Rydberg para un haz de átomos de Rb mediante un láser pulsado. En la cavidad auxiliar R1 se tiene una población conocida y controlada de fotones de tal forma que se modifica la función de onda del átomo construyendo una superposición entre los estados con n=50 y 51. En la cavidad C ocurre la interacción con la radiación de interés de forma que se genera una fase (desproporción) en la superposición. La cavidad auxiliar R2 tiene las mismas características que R1 pero al lidiar con un estado de entrada diferente arrojará una superposición distinta. Y por último el detector D permite identificar las componentes de la superposición.
Al no absorberse el fotón, éste puede hacerse interactuar con un tren de átomos, lo que permite caracterizar el estado final con mayor certidumbre. Recientemente esta metodología se ha empleado para observar el proceso de decoherencia: en C se produce radiación controlada en estados cuánticos conocidos y se efectúa la medición con el proceso descrito mientras el sistema evoluciona de una superposición de estados a una mezcla clásica (Deléglise, et al., 2008).
Iones atrapadosLa sección anterior nos sugiere que los átomos e iones individuales también son sistemas a los que vale la pena mirar como dispositivos con aplicaciones cuánticas. Desde hace tres décadas se han desarrollado técnicas con la finalidad de controlar partículas individuales. La más empleada es el enfriamiento Doppler, método propuesto por Theodor W. Hänsch, los laureados Arthur L. Schalow y Hans G. Dehmelt, y el que nos ocupa actualmente David J. Wineland (Hammerich, 2010).
El procedimiento consiste en iluminar el átomo con un láser cuya frecuencia se encuentre ligeramente por debajo de la frecuencia de resonancia del átomo; de esta forma, gracias al corrimiento hacia el azul, el átomo sólo absorberá fotones que se le aproximen y será transparente para aquellos que se alejen de él. La emisión de los fotones absorbidos ocurrirá en todas direcciones aleatoriamente de manera que por conservación de la cantidad de movimiento el átomo terminará con una velocidad mucho menor que la que tenía antes de interactuar con el láser. Sin embargo, en ocasiones la transferencia de momento implica un aumento en el movimiento del átomo, poniendo una cota inferior al enfriamiento. Con ayuda de campos magnéticos (trampa de Pinning) o de campos eléctricos estáticos (trampa de Paul), la técnica puede aplicarse para atrapar partículas cargadas individuales, o conjuntos pequeños que permiten la manipulación de sus estados cuánticos. De esta manera, Wineland y sus colaboradores lograron el enfriamiento de iones Mg+ en 1978 y el atrapamiento de iones individuales con una trampa de Pinning en 1981.
Después del enfriamiento Doppler, un ion atrapado puede describirse en términos tanto de sus niveles electrónicos como de las oscilaciones de éste dentro de la trampa; tal movimiento se encuentra cuantizado en niveles vibracionales.
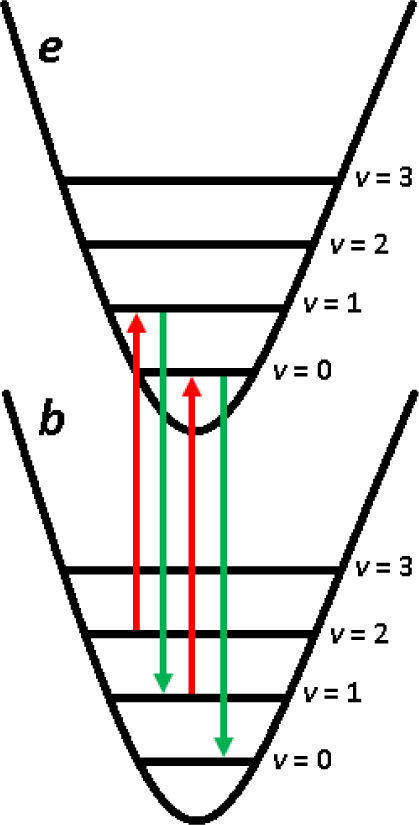
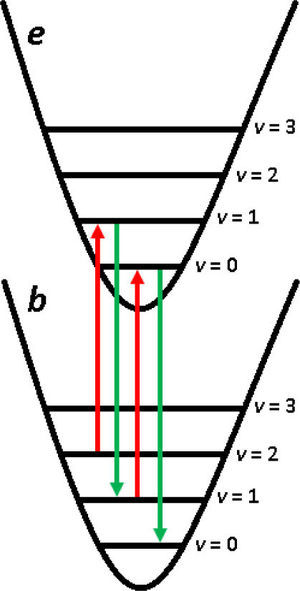
Para llevar el sistema al estado base se efectúa una técnica conocida como modulación de banda lateral, la cual consiste en hacer pasar al ion desde el estado electrónico basal (b) a un estado excitado (e) pero con un estado vibracional menor que el inicial; de esta manera, cuando el ion se relaje, llegará al estado b con la frecuencia de oscilación disminuida. Una secuencia alternada de excitaciones y decaimientos llevan finalmente al sistema a su estado base vibracional (v=0). Al conseguir tener a la partícula cargada en su estado basal (b,0) se puede proceder a la manipulación.
En el National Institute of Standards and Technology (NIST) en Colorado, el grupo de Wineland ha logrado una transferencia de estados superpuestos propuesta por Juan I. Cirac y Peter Zoller en 1995. Al ion en estado (b,0) se le hace incidir un pulso de láser de forma que su función de onda quede en términos de una superposición de los estados electrónicos basal y primer excitado, pero ambos bajo el mismo estado vibracional basal (b+e,0). Un segundo pulso de banda lateral produce la transición de la componente electrónica excitada al estado basal electrónico pero con v=1, de forma que el sistema queda como (b,0+1). De esta forma la manipulación sobre los estados electrónicos genera superposición de los estados vibracionales, los cuales son compartidos por los iones en la trampa.
De computadoras, gatos y relojes¿Y para qué sirve tanta sofisticación y control sobre este tipo de sistemas? Una de las perspectivas para la manipulación de los sistemas cuánticos individuales es el desarrollo de computadoras cuánticas, en las cuales la información se codifica en bits cuánticos (qubits), como el espín o la polarización, cuya capacidad de procesamiento está sujeta a las reglas del mundo cuántico, lo que hace que estas computadoras, de construirse, serían mucho más poderosas que las actuales.
El último experimento descrito en la sección anterior es aprovechado para generar una puerta lógica conocida como Control-NOT (CNOT) la cual efectúa la operación NOT sobre un qubit a reserva del estado en que se encuentre un qubit entrelazado con el primero (Amador Bedolla & Aspuru Guzik, 2008). En el experimento de Wineland, el par de qubits entrelazados los conforman el estado electrónico y el estado vibracional del ion atrapado.
La indagación sobre aspectos fundamentales de la física es también una aplicación directa de estos sistemas, que si bien no llevan a productos comerciales, resuelven o generan nuevos cuestionamientos que conducen a un subsecuente progreso. En particular podemos mencionar al gato de Schrödinger: éste es un experimento pensado, en el cual un gato se encuentra encerrado en una caja con un dispositivo que producirá su muerte dependiendo del resultado de un proceso cuántico; si la parte cuántica del sistema se encuentra en una superposición, entonces Schrödinger plantea la pregunta de si es posible que el gato se encuentre en una superposición de estados vivo-muerto. Ahora sabemos que esta situación es imposible debido a la decoherencia, pero a raíz de este planteamiento, los estados superpuestos se han denominado genéricamente como estados de gato (Haroche, 1998). El experimento mencionado al final de la sección dedicada a Haroche es un ejemplo del grado de control que se tiene para tratar con este tipo de estados. Tener la capacidad de caracterizar y darle seguimiento al proceso de decoherencia con tanto detalle ha puesto como nuevo objetivo revertir dicho proceso con la finalidad de estabilizar las propiedades cuánticas del sistema y lograr la persistencia de los estados de gato.
En un último ejemplo el equipo de Wineland ha construido relojes ópticos de iones que logran una precisión dos órdenes de magnitud mayor que el estándar actual de frecuencia basado en relojes de Cs (Nobel Foundation, 2012). Esto se debe a que las transiciones entre niveles electrónicos ocurren a energías mucho mayores que el decaimiento de átomos en un reloj de Cs. Su construcción se basa en el empleo de una transición estrecha (prohibida) en un ion individual, lo cual genera complicaciones debido a que se necesitan fuertes transiciones permitidas que posibiliten el enfriamiento y la detección; esta dificultad se sortea entrelazando iones que proveen la transición espectroscópica requerida [1S0 → 3P1 en 27Al+ (267nm)] con iones que permiten las transiciones de enfriamiento (9Be+).
¿Y la Química?Si bien en particular para los experimentos aquí detallados la intervención química es apenas apreciable, hablando en general de la manipulación de sistemas individuales el panorama pinta muy diferente.
Comenzando por la óptica cuántica, se requieren fuentes de fotones individuales, los cuales pueden ser semiconductores o materiales con propiedades ópticas no lineales; la investigación sobre la producción de ambos tipos de sistemas tiene una actividad intensa en la actualidad. Los últimos incluso han pasado de ser propiedad exclusiva del estado sólido a un interés compartido con la síntesis orgánica.
Otros fuertes candidatos para figurar en este marco son las resonancias magnéticas: los espines nucleares y electrónicos proveen de una base cuántica intrínseca para la manipulación de información (Stamp & Gaita-Ariño, 2009). Por lo tanto, el diseño racional de moléculas orgánicas que permitan maniobrar con los espines nucleares mediante RMN es una actividad muy prometedora. También en el campo del magnetismo molecular se han registrado importantes avances como la generación de moléculas magnéticas individuales y ya está en proceso el desarrollo de un procesador cuántico formado a partir de cúmulos de coordinación conocidos como Cr7Ni (Troiani, et al., 2005).
Además, la química puede salir beneficiada desde el punto de vista de que los simuladores cuánticos prometen una nueva vía para cálculos de estructura electrónica que en principio arrojarán resultados más exactos y en menor tiempo que cualquier recurso computacional actual (Lanyon, et al., 2012). Cabe mencionar que los primeros avances significativos en esta área están siendo logrados por el grupo de Alán Aspuru, egresado de la Facultad de Química de la UNAM, en Harvard.
Por último, queda mencionar que México no se encuentra relegado en la investigación de este tipo de temas. Existe la División de Información Cuántica de la Sociedad Mexicana de Física, la cual cuenta con miembros en instituciones de todo el país: el CINVESTAV, el INAOE, el ITESM, el CENAM, la UASLP y la UNAM, por mencionar algunos. Se han hecho importantes trabajos en óptica cuántica, atrapamiento de iones, resonancias magnéticas, acoplamiento con cavidades, relojes ópticos, etc.
Sin lugar a dudas el mundo cuántico ya no es terreno exclusivo de la teoría, y hoy en día no sólo somos capaces de explorarlo sino de modificarlo. Estas expediciones con sabor a conquista prometen, y ya están cumpliendo, llevarnos muy lejos; nos permitirán construir dispositivos más precisos y poderosos de lo que solíamos imaginar, así como profundizar en la comprensión de la intimidad del universo, tema que hoy por hoy mientras más estudiamos, al parecer, menos entendemos.