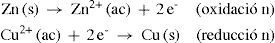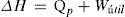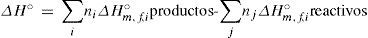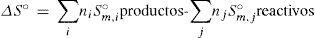A class activity for General Chemistry students is proposed. In this class the equation relating Gibbs energy with useful work in reversible processes is verified. For this purpose, literature thermochemical data and values of the electromotive force (EMF) of redox reactions are employed. The EMF values can be obtained either from experimental measurements of several galvanic cells, or alternatively by the use of computer simulations which can be found in the internet. We expect this activity will help students to better understand the meaning of useful work and to connect different topics developed within the General Chemistry course.
La termodinámica es un tema fundamental en los cursos de química general básica universitaria para la formación de los alumnos que estudian las ciencias químico-biológicas y físicomatemáticas, debido a que brinda a los alumnos herramientas para obtener información sobre los cambios energéticos que acompañan a las reacciones químicas y para la predicción de la espontaneidad de las mismas en distintas condiciones. Estas herramientas serán retomadas en cursos posteriores para aplicarlas a sistemas más complejos.
Es muy común que los docentes tiendan a ejemplificar el concepto de trabajo con el de expansión y compresión de un gas (trabajo mecánico tridimensional) en los cursos de química general, mientras que en los cursos de física clásica se ejemplifica con el trabajo mecánico unidimensional realizado por una partícula. Esta situación puede provocar que los alumnos adopten una idea errónea de que los únicos tipos de trabajo que se consideran en la expresión que representa la primera ley de la termodinámica (llamada también ecuación energética), son los dos tipos de trabajo antes mencionados, dificultando la comprensión de este concepto y fomentándose el desconocimiento de la existencia de las otras variedades de trabajo.
Debemos destacar que el trabajo útil (Wútil) se refiere a todo tipo de trabajo distinto del de expansión (Wexp). Ejemplos de trabajo útil son el trabajo mecánico producido por el vapor generado a partir de la combustión del petróleo. Otros ejemplos son el trabajo eléctrico que se puede obtener de una celda electroquímica, el trabajo magnético y el trabajo superficial. Varios libros de Química General (Chang, 1992, pp. 777-803; Mortimer, 1983, pp. 459-494; Whitten, Gailey y Davis, 1992, pp. 600-634), relacionan trabajo máximo con la variación de energía de Gibbs en procesos a temperatura y presión constantes; sin embargo, en la mayoría de los casos no aclaran el origen de esta relación. Tampoco estos libros diferencian entre trabajo de expansión y trabajo útil.
En electroquímica, uno de los temas incluidos en la currícula de los cursos de química general básica universitaria, se muestra cómo a partir de medidas de fuerza electromotriz puede obtenerse el trabajo útil (trabajo eléctrico) de una celda galvánica, como veremos más adelante. Por ello, éste será el tipo de trabajo útil que emplearemos en este trabajo.
Si bien hay otros trabajos de Educación Química donde se ha abordado el análisis de datos termodinámicos a partir de medidas electroquímicas, algunos de ellos (Salt y Etzler, 1984; Vincent, 1970) proponen actividades como la medida de la fuerza electromotriz de celdas galvánicas a distintas temperaturas para la obtención de parámetros termodinámicos para cursos de Fisicoquímica, y otros se enfocan principalmente en el cálculo de la variación de entropía del universo (Bindel, 2000). No se han encontrado trabajos en los que se propongan actividades de laboratorio que vinculen medidas electroquímicas con parámetros termodinámicos dirigidos a cursos básicos de Química.
Los objetivos de este trabajo se listan a continuación.
Objetivo generalSe propone la realización de una actividad experimental que les permita a los alumnos una mejor comprensión del concepto de trabajo (específicamente el trabajo eléctrico), su relación con la ecuación energética y con la variación de la energía de Gibbs en procesos reversibles a temperatura y presión constantes.
Objetivo específicoEl objetivo específico de este trabajo es realizar el cálculo de la variación de la energía de Gibbs por dos caminos; uno a partir de datos calorimétricos y el otro utilizando datos de potenciales de óxido-reducción en condiciones estándar, de algunas celdas electroquímicas elegidas.
Para ello se propone la construcción de celdas electroquímicas para obtener los valores de los potenciales eléctricos de las mismas experimentalmente y compararlos con los valores teóricos calculados previamente.
Además, se propone la utilización de simulaciones de las celdas electroquímicas o pilas propuestas para comparar el valor de su potencial eléctrico obtenido con el valor experimental.
Fundamentos teóricosPilas o celdas electroquímicasUna celda galvánica o pila es un dispositivo que permite la generación de una corriente eléctrica a partir de una reacción redox espontánea (Chang, 1992, pp. 777-803; Mortimer, 1983, pp. 459-494; Whitten, Gailey y Davis, 1992, pp. 600-634). Estas celdas constan de dos compartimientos (semiceldas) en los que se colocan soluciones acuosas de un electrolito y allí se sumergen sendos electrodos. En la figura 1 se muestra a modo de ejemplo un esquema de la pila de Daniell, en la que el electrodo donde se produce la oxidación (ánodo) es un electrodo de cinc sumergido en una solución de ZnSO4 y el electrodo en el que ocurre la reducción (cátodo) es un electrodo de cobre sumergido en una solución de CuSO4. Se indica la convención de signos para el ánodo y cátodo respectivamente.
Las semirreacciones de cada semicelda son las siguientes:
La reacción global es:
La notación habitual de una celda galvánica es la que se muestra a continuación para la celda de Daniell:
En esta notación se ubica al electrodo que funciona como ánodo a la izquierda y al cátodo a la derecha. Las barras verticales representan las interfases de separación sólido/líquido y la doble barra vertical simboliza al puente salino, que permite la conducción electrolítica.
Trabajo eléctricoPara una celda galvánica o pila el trabajo eléctrico (Welec) se define como:
donde n es el número de cargas eléctricas intercambiadas en la reacción electroquímica que se efectúa en la pila, F es la constante de Faraday (96484,56 C) y E es la fuerza electromotriz que produce la pila (Atkins, 1990, pp. 260).Relación entre el trabajo eléctrico y la variación de la energía de GibbsDe acuerdo con la primera ley de la termodinámica aplicada para sistemas cerrados:
donde ΔU representa la variación de energía interna, Q es el calor absorbido o cedido por el sistema y W es el trabajo realizado sobre el sistema o sobre los alrededores.En la tabla 1 se presenta la convención de signos para el calor y el trabajo:
Convención de signos para trabajo y calor
| Tipo de energía: | Signo: | Significado: |
|---|---|---|
| Trabajo | W < 0 | El sistema hace trabajo sobre los alrededores. |
| W > 0 | Los alrededores hacen trabajo sobre el sistema. | |
| Q < 0 | El sistema transfiere calor hacia los alrededores. | |
| Calor | Q > 0 | Los alrededores transfieren calor hacia el sistema. |
Por la definición de entalpía (H), H = U + pV, donde p y V son la presión y el volumen, respectivamente, la variación de entalpía en un proceso se calcula como:
Si consideramos que el trabajo W = Wexp+ Wútil, donde Wexp es el trabajo de expansión-compresión, mientras que Wútil corresponde a un tipo de trabajo distinto al de expansión-compresión (que es un tipo de energía útil), la ecuación 2 se transforma en:
A presión constante, Wexp = –pΔV y Q = Qp (el subíndice p indica que la presión es constante) y la ecuación 2 toma la siguiente forma:
Si el único trabajo es el de expansión-compresión, Wútil = 0. Al comparar las ecuaciones (3) y (5), se puede concluir que ΔH = Qp
Si hay trabajo útil (Wútil ≠ 0) y si la presión se mantiene constante, la ecuación 4 toma la siguiente forma:
Sustituyendo la ecuación 6 en la ecuación 3, y como la presión es constante Δ(pV) = p ΔV, se obtiene:
La variación de energía de Gibbs (ΔG) para un proceso a temperatura y presión constantes (Atkins, 1990, pp. 116) está dada por:
Pero ΔS = Qrev/T, donde Qrev es la cantidad de calor transferida durante un proceso isotérmico reversible entre los estados inicial y final. Si este proceso tiene lugar a presión constante, ΔS = Qp/T, por lo tanto, Qp= TΔS y al sustituir esta expresión en la ecuación 7, se obtiene:
Igualando las ecuaciones 8 y 9, se tiene que:
Como la variación de la energía de Gibbs es aplicable para procesos reversibles a temperatura y presión constantes; por lo tanto, el trabajo útil será el máximo trabajo que puede realizar el sistema en un proceso reversible. Esto quiere decir que:
Como ya se mencionó anteriormente, para una pila o celda electroquímica, el trabajo eléctrico puede calcularse como:
Como el trabajo eléctrico realizado por la pila es el máximo, además de ser un tipo de trabajo útil en un proceso reversible, entonces:
Esto quiere decir, que a temperatura y presión constantes, las ecuaciones (11) y (13) son equivalentes:
A condiciones estándar (298,15 K y 1 bar y para soluciones a una concentración 1 M), la fuerza electromotriz producida por la pila será la estándar (E°), y la ecuación (12) se transforma en:
En el caso de una pila, podemos aproximarnos experimentalmente a la situación de reversibilidad si conseguimos que la intensidad de corriente que circula por el circuito al que se encuentra conectada sea muy pequeña. Esto se logra si se emplea un instrumento con resistencia eléctrica interna muy grande al medir la diferencia de potencial entre los electrodos de la pila. De esta forma, la diferencia de potencial medida se aproximará al valor de la fuerza electromotriz producida por la pila (E°), o llamada también potencial óxido-reducción.
A 1 bar y 298,15 K, la variación de la energía de Gibbs corresponderá a su valor estándar ΔG°. Al igualar las ecuaciones (14) y (15) a condiciones estándar se llega a la siguiente expresión:
A condiciones estándar, la variación de la energía de Gibbs para una reacción de óxido-reducción puede calcularse empleando la ecuación (8):
Con ayuda de la ecuación (17) y de los datos termoquímicos estándar de entalpía ΔH° y entropía ΔS° de reacción (Handbook of Chemistry and Physics, 1981, pp. D-85/ D-87) y a partir de la ecuación (16) empleando los datos electroquímicos de potenciales óxido-reducción estándar, (Handbook of Chemistry and Physics, 1981, pp. D-155/ D-157) se calculará la variación de la energía de Gibbs ΔG° de tres celdas electroquímicas, cuyos valores serán comparados con aquellos obtenidos experimentalmente.
La elección de las reacciones electroquímicas se hizo teniendo en cuenta que las celdas electroquímicas (Cu-Zn o celda de Daniell, Ag-Cu y Ag-Zn) pueden construirse de forma experimental y además que sus potenciales estándar se pueden simular en la página de internet (Chemistry Experiment Simulations and Conceptual Computer Animations, 2010). De esta manera se pueden comparar los potenciales eléctricos estándar obtenidos experimentalmente contra los valores que se obtienen directamente de la simulación.
Metodología experimentalMateriales, equipos y reactivos
- •
Láminas de Cu, Zn y Ag (de 20 mm ancho, 30 mm de largo y 2 mm de espesor).
- •
Sales: CuSO4·5H2O, ZnSO4, AgNO3, KNO3 (esta última sal para construir el puente salino).
Se debe emplear una sal de Hg2+ [como Hg(NO3)2] para amalgamar la lámina de zinc y estabilizar este metal para que se lleve a cabo la reacción redox deseada. De lo contrario, la fuerza electromotriz producida por estas pilas será muy variable, ya que el Zn es muy inestable en agua y se puede formar hidrógeno (reacción indeseable). Por ello, el Zn se amalgama por medio de inmersión durante varios segundos en solución de Hg(NO3)2. Así se forma una gota de Hg sobre la superficie, y la misma se frota con papel de filtro hasta cubrir de manera uniforme la superficie del electrodo con la amalgama de Zn (Burmístrova, 1977, pp. 330).
- •
Agua destilada.
- •
Gel de agar para la construcción del puente salino.
- •
Tubos de vidrio en forma de U.
- •
Cables con conexión de “banana” y “caimanes” (rojo y negro) (esto es para conectar los electrodos y las terminaledel multímetro digital)
- •
Polvo abrasivo.
- •
Multímetro digital con resolución de 0,01 V.
Como primera actividad, se propone construir las siguienteceldas electroquímicas mostradas en la tabla 2:
Para ello se procederá de la siguiente manera:
- 1.
Pulir las láminas de Cu, Zn y Ag con polvo abrasivo, las cuales servirán como electrodos.
- 2.
Enjuagar los electrodos con agua destilada y secarlos. Ver más arriba el tratamiento del electrodo de Zn.
- 3.
Preparar 100 mL de las soluciones de CuSO4 (1M), ZnSO4 (1M) y AgNO3(1M) (por pesada de 24,95 g de CuSO4·5H2O; 16,14 g de ZnSO4 y 16,98 g de AgNO3, respectivamente).
- 4.
Verter en seis vasos de precipitados, aproximadamente 50 mL de las soluciones de: CuSO4 (1 M), ZnSO4 (1 M) y AgNO3 (1 M).
- 5.
Los electrodos de Cu y Zn deben sumergirse en las soluciones correspondientes para el armado de la pila I, los electrodos de Cu y Ag en sus soluciones correspondientes para la pila II, y los de Zn y Ag en las soluciones correspondientes para la pila III.
- 6.
El puente salino se preparó por disolución de 2 g de gel de agar y 15 g de KCl en 100 mL de agua en ebullición. Llenar el tubo en forma de U y dejar enfriar hasta que solidifique.
- 7.
Conectar los cables con caimanes a ambos electrodos de acuerdo a la convención de colores existente (cable rojo al cátodo y cable negro al ánodo), asegurando que exista buen contacto eléctrico.
- 8.
Conectar el otro extremo de los cables con conexión de banana al voltímetro y realizar la lectura de la diferencia de potencial. Recuerde que en una pila el electrodo positivo es el cátodo.
- 9.
Retirar el puente salino y enjuagarlo con agua destilada.
- 10.
Proceder en forma similar a los pasos 4-9 para el armado de las pilas II y III. 4
Se determinarán los valores de E° para las reacciones electroquímicas que se llevan a cabo en las pilas I, II y III, empleando los dispositivos que se muestra en las figuras 1-3.
A partir de los datos de Eo medidos experimentalmente, se les pedirá a los alumnos que calculen ΔG° con ayuda de la ecuación (16).
2) Determinación de ΔG° a partir de datos termoquímicosComo siguiente actividad, se propone a los alumnos el cálculo de ΔG° a 298,15 K y 1 bar, de acuerdo con la ecuación (17) para las reacciones que tienen lugar en las celdas electroquímicas mostradas en la tabla 2 (ver tabla 3), empleando los datos de las entalpías molares de formación y entropías absolutas molares a condiciones estándar informados en la tabla 4. Las entalpías (Atkins, 1990, pp. 51) y entropías de reacción (Atkins, 1990, pp. 95) pueden calcularse utilizando las siguientes ecuaciones:
donde ΔH°m,f,i y ΔH°m,f,j representan las entalpías molares estándar de formación de reactivos y productos respectivamente; y ni y nj son los respectivos coeficientes estequiométricos. S°m,i y S°m,j son las entropías absolutas molares estándar.Entalpías de formación y entropías absolutas estándar a 298,15 K y 1 bar a
| Sustancia | ΔH°m,f/(kJ/mol) | S°m/(J/K mol) |
|---|---|---|
| Cu (s) | 0 | 33,15 ± 0,08 |
| Cu2+ (ac) | 65,69 ± 0,80 | –97,1 ± 1,2 |
| Zn (s) | 0 | 41,63 ± 0,13 |
| Zn2+ (ac) | –153,39 ± 0,20 | –109,6 ± 0,7 |
| Ag (s) | 0 | 42,55 ± 0,21 |
| Ag+ (ac) | 105,750 ± 0,085 | 73,38 ± 0,40 |
Por otra parte, se les solicitará a los alumnos que calculen los valores de E° para las pilas I, II y III mostradas en la tabla 2 a partir de los datos de los potenciales óxido-reducción estándar mostrados en la tabla 5, teniendo en cuenta la siguiente ecuación:
donde E°ox/red (cátodo) y E°ox/red (ánodo) son los potenciales óxido-reducción estándar para las semirreacciones catódica y anódica respectivamente. A partir de estos valores calcularán ΔG°, empleando la ecuación (16).Resultados y discusiónPara evaluar los resultados se les pedirá a los alumnos que confeccionen una tabla comparativa donde se informen los resultados de las ΔG° para las tres pilas: a) a partir de datos termoquímicos; b) a partir de datos electroquímicos, y c) medidos experimentalmente, tal como se muestra en la tabla 6.
Valores de parámetros termodinámicos para las reacciones de la Tabla 3
| Pila: | Reacción: | Datos termoquímicos: | Datos electroquímicos: | Datos experimentales(a): | ||||
|---|---|---|---|---|---|---|---|---|
| ΔH° /(kJ) | ΔS°/(J/K) | ΔG°/(kJ) | E°/(V) | ΔG°/(kJ) | E°/(V) | ΔG°/(kJ) | ||
| I | Cu2+ (ac, 1M) + Zn (s) d Zn2+ (ac, 1M) + Cu (s) | 219,08 | –20,98 | –212,8 | 1,103 | –212,8 | ||
| II | 2 Ag+ (ac, 1M) + Cu (s) d Cu2+ (ac, 1M) + 2 Ag (s) | –145,81 | –191,9 | –88,6 | 0,4594 | –88,6 | ||
| III | 2 Ag+ (ac, 1M) + Zn (s) d Zn2+ (ac, 1M) + 2 Ag (s) | –364,89 | –212,89 | –301.4 | 1,5624 | –301,4 | ||
Como se ve hay un acuerdo excelente entre los valores de energía de Gibbs obtenidos a partir de datos termoquímicos y los obtenidos a través de datos electroquímicos para las tres pilas propuestas. En el caso de los datos de ΔG° calculados en base a los datos experimentales de potencial se les pedirá a los alumnos que calculen el error relativo de acuerdo a la siguiente ecuación:
tomando como valores verdaderos a los hallados a partir de datos de literatura.Para reforzar los conocimientos adquiridos por los estudiantes, se pueden determinar los valores de E° para las tres pilas estudiadas en este trabajo, sin realizar el experimento, empleando la simulación que se encuentra en internet (Chemistry Experiment Simulations and Conceptual Computer Animations, 2010), en la sección electrochemistry y ejecutando el archivo Voltaiccell20.swf siguiendo las instrucciones del tutorial (figura 4).
Es importante mencionar que para la simulación de la pila Ag-Cu (ver figura 4), la conexión de los electrodos con las terminales del multímetro están invertidas, y ésa es la razón por las que produce un potencial óxido-reducción negativo. Para esta pila el metal que funciona como ánodo es el Zn y el que funciona como cátodo es la Ag, tal como se verifica según el código de colores (cátodo conexión con alambre rojo, ánodo, conexión con alambre negro).
Como se ve, hay un muy buen acuerdo entre los valores de potenciales óxido-reducción observados en las simulaciones y los calculados teóricamente. Si bien en la tabla 6 no se incluyen los valores experimentales obtenidos con nuestro multímetro, los valores son muy próximos tanto a los teóricos como a los simulados.
ConclusionesA través de una propuesta experimental y una simulación pudimos darle generalidad al término de trabajo en la expresión de la Primera Ley de la termodinámica y ejemplificar el concepto de trabajo útil asociado a trabajo eléctrico. Para tales efectos, se verificó la ecuación que vincula la variación de la Energía de Gibbs con el trabajo útil en un proceso reversible, comparando los resultados obtenidos con los que se derivaron de medidas electroquímicas.
La propuesta desarrollada en el aula cumplió con los objetivos propuestos y hubo un aprendizaje significativo por parte de los alumnos, verificado a través de encuestas y discusiones en el aula.