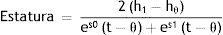Validar ecuaciones de regresión que predicen el estado de madurez (EM) para evaluar el crecimiento físico y adiposidad corporal de niños y adolescentes chilenos.
Material y métodosSe efectuó un estudio transversal en 8.094 escolares de entre 6,0 y 18,9 años. Se evaluó el peso, la estatura de pie, la estatura sentada y la circunferencia de cintura (CC). El pico de velocidad de crecimiento (PVC) se estimó por el modelo matemático 1 de Preece-Baines (MPB). Para estimar el EM, se utilizaron las ecuaciones de Mirwald (basadas en edad, peso, estatura de pie, estatura sentada y longitud de piernas) y las ecuaciones de Moore (basadas en edad, peso y estatura de pie). Se calculó el índice de masa corporal (IMC).
ResultadosEl MPB evidenció que el PVC en hombres fue de 10,33±0,29años y en mujeres fue a los 12,81±0,27años. Por medio de la ecuación de Mirwald, los hombres alcanzaron el EM a los 14,09±0,8APVC y las mujeres los 11,6±0,9APVC, mientras que, por la ecuación de Moore, los hombres alcanzaron a los 13,7±0,6APVC y las mujeres a los 12,1±0,6APVC. Hubo diferencias significativas entre el MPB con Mirwald, MPB con Moore y entre Mirwald con Moore (p<0,001). Los valores de explicación por categoría de EM fueron: ecuación de Mirwald [hombres (precoz R2=0,81, promedio R2=0,69 y tardío R2=0,09) y mujeres (precoz R2=0,83, promedio R2=0,83 y tardío R2=0,77)], ecuación de Moore [hombres (precoz R2=0,93, promedio R2=0,70 y tardío R2=0,79) y mujeres (precoz R2=0,89, promedio R2=0,89 y tardío R2=0,83)]. Se crearon percentiles para peso, estatura, CC e IMC.
ConclusiónSe verificó que las ecuaciones de Moore y Mirwald difieren con el modelo matemático MPB en ambos sexos, aunque, la ecuación de Moore podría ser útil para la evaluación del EM en niños y adolescentes chilenos.
To validate regression equations that predict the state of maturity (MS) to evaluate the physical growth and body fatness of Chilean children and adolescents.
Material and methodsA transversal study was carried out in 8,094 school children between 6.0 and 18.9 years old. Weight, standing height, sitting height, and waist circumference (WC) were evaluated. Peak growth rate (PVC) was estimated by the mathematical model 1 of Preece-Baines (MPB). Mirwald's equations (based on age, weight, standing height, sitting height, and leg length) and Moore's equations (based on age, weight, and standing height) were used to estimate MS. The body mass index (BMI) was calculated.
ResultsThe BMP showed that the PVC in men was 10.33±0.29 years and in women was 12.81±0.27 years. Using Mirwald's equation, men reached MS at 14.09±0.8APVC and women at 11.6±0.9APVC, while using Moore's equation, men reached 13.7±0.6APVC and women at 12.1±0.6APVC. There were significant differences between MPB with Mirwald, MPB with Morre, and between Mirwald and Moore (p<0.001). Explanation values by MS category were Mirwald's equation [men (early R2=0.81, mean R2=0.69 and late R2=0.09) and women (early R2=0.83, mean R2=0.83 and late R2=0.77)], Moore's equation [men (early R2=0.93, mean R2=0.70 and late R2=0.79) and women (early R2=0.89, mean R2=0.89 and late R2=0.83)]. Percentiles were created for weight, height, CC and BMI.
ConclusionIt was verified that Moore's and Mirwald's equations differ with the mathematical model MPB in both sexes. However, Moore's equation could be useful for the evaluation of MS in Chilean children and adolescents.
El crecimiento físico se considera un proceso dinámico, complicado y largo, que continúa durante toda la infancia, la niñez y la adolescencia1, mientras que la maduración es un proceso de importantes cambios fisiológicos que se manifiestan de forma más intensa durante la adolescencia.
Ambos son procesos fisiológicos complejos que son controlados o afectados por factores hormonales, ambientales y genéticos2 y ocurren simultáneamente3.
Evidentemente, la infancia, niñez y adolescencia son etapas de gran interés para la investigación en las ciencias de la salud, especialmente en la evaluación y seguimiento del crecimiento físico, el estado nutricional, cambios en el estado de madurez (EM), estilos de vida, entre otros aspectos.
Durante estas etapas se crean oportunidades para que el individuo pueda expresar su potencial genético, pero a su vez, este puede ser modificado por el medio ambiente. De hecho, estudiar estos factores es relevante para la investigación pediátrica, ya que conllevan un constante control, diagnóstico y seguimiento del proceso de crecimiento y maduración biológica, cuyo objetivo es identificar niños con riesgo nutricional4. En ese sentido, algunos estudios recientes destacan que la pubertad temprana está asociada con un mayor grado de riesgo de sobrepeso y obesidad5,6. Por lo que incluir indicadores de EM durante la evaluación del crecimiento y la composición corporal es una necesidad urgente, puesto que puede proporcionar un medio de ajuste más preciso en la evaluación del estado nutricional durante la etapa del crecimiento y desarrollo.
En general, los métodos de evaluación del EM (edad esquelética y características sexuales secundarias, edad de la menarquia, porcentaje de estatura adulta), a menudo son poco prácticos y son considerados invasivos7–9. Esto es una gran desventaja para las investigaciones epidemiológicas, lo que impide su uso y aplicación a grandes poblaciones.
Como tal, en los últimos años se han propuesto dos técnicas no invasivas, basado en indicadores somáticos que permiten predecir el EM de niños y adolescentes. El primero, propuesto por Mirwald et al.10, basado en variables de edad, peso, estatura, estatura sentada y longitud de las piernas (diferencia entre estatura y estatura sentada) y el segundo, propuesto por Moore et al.11, en el que utiliza edad cronológica, peso y estatura, respectivamente.
Ambas técnicas proceden de la misma base de datos, y han sido muy utilizadas en estudios que tienen que ver con el control y participación en programas de actividad física12, seguimiento del crecimiento físico13, entrenamiento de fuerza en atletas14, en la detección de talentos deportivos15, entre otros estudios.
Recientemente, Malina y Koziel16 han validado ambas técnicas en niños y adolescentes polacos utilizando un criterio longitudinal, destacando que las ecuaciones de Moore et al.11 a pesar de tener limitaciones importantes son útiles para niños y adolescentes; sin embargo, hasta donde se sabe, en América del Sur y específicamente en Chile, ningún estudio ha comparado y validado estas ecuaciones de forma transversal y/o longitudinal, por lo que identificar la técnica que más se ajuste a la población chilena podría ayudar a interpretar los parámetros de crecimiento físico y adiposidad corporal en poblaciones pediátricas.
En consecuencia, basados en estas premisas, este estudio tiene como objetivo: validar las ecuaciones de regresión que predicen el EM en una muestra de niños y adolescentes chilenos (ecuaciones de Mirwald et al.10 y Moore et al.11), considerando como método criterio el modelo matemático 1 de Preece-Baines17 para muestras transversales (MPB). Este modelo permite estimar la velocidad de crecimiento, especialmente cuando el tamaño de la muestra en niños y adolescentes es grande18.
Esta información puede ayudar a clasificar el riesgo nutricional en niños que están avanzados en cuanto a su madurez6, ya que la intensidad y la duración de la pubertad son específicas en cada individuo y pueden variar considerablemente entre ellos13.
MétodosTipo de estudio y muestraSe efectuó un estudio transversal (comparativo) en niños y adolescentes de la región del Maule (Chile). La población de la muestra estaba compuesta por 31.696 estudiantes con edades comprendidas entre los 6,0 y 18,9 años. Los escolares pertenecían a 4 provincias de la región del Maule (Cauquenes, Curicó, Linares y Talca). Los escolares asistían a 12 colegios municipales del nivel básico y medio. El muestreo probabilístico (aleatorio) se utilizó para calcular el tamaño de la muestra, lo que resultó en una muestra de 8.094 sujetos [4.260 (13,43%) hombres y 3.834 (12,0%) mujeres] con un IC del 95%.
Los padres y/o tutores de los alumnos firmaron el consentimiento informado y cada alumno el asentimiento informado. El estudio se llevó a cabo de acuerdo con la Declaración de Helsinki para seres humanos y a las sugerencias del comité de ética de la Universidad Autónoma de Chile (protocolo n.o 238/2013). Se incluyó a los escolares que aceptaron participar voluntariamente y a los que completaron las evaluaciones antropométricas. Fueron excluidos los que no asistieron el día de la evaluación y los que no completaron las evaluaciones antropométricas.
Técnicas y procedimientosLas variables antropométricas se midieron en las instalaciones de los colegios durante horario escolar (8:00-12:30h y 14:30-18:00h) y de lunes a viernes. Se realizó durante los años 2015 y 2016. Para evaluar, se conformó un equipo de 6 evaluadores experimentados y entrenados en evaluaciones antropométricas. Todas las variables fueron evaluadas dos veces y los errores técnicos de medida (ETM) intra- e interevaluador oscilaron un 1-2%.
Las mediciones antropométricas se evaluaron siguiendo las recomendaciones de Ross y Marfell-Jones19. Se midió sin zapatos y con la menor cantidad de ropa posible (solo una camiseta ligera, pantalones cortos y sin zapatos). Se evalúo el peso corporal (kg) usando una balanza electrónica (Tanita, Reino Unido) con escala de 0 a 150kg y con precisión de 100g. La estatura de pie con un estadiómetro portátil (Seca Gmbh & Co. KG, Hamburgo, Alemania) con precisión de 0,1mm, según el plano de Frankfurt. La estatura sentada se midió en un banco de madera (caja plana de 50cm de altura) con un estadiómetro (SECA, Hamburgo, Alemania) con 0,1mm de precisión. La circunferencia de la cintura CC (cm) se midió en el punto medio entre las costillas inferiores y la parte superior de la cresta ilíaca con una cinta de medición antropométrica de metal, marca Seca, graduada en milímetros con una precisión de 0,1cm. El índice de masa corporal (IMC) se calculó utilizando la fórmula: IMC=peso (kg)/estatura2 (m).
El método criterio para evaluar el pico de velocidad de crecimiento (PVC) de niños y adolescentes fue el modelo matemático 1 de Preece-Baines (MPB)17. Este modelo se utiliza en estudios de crecimiento transversal y longitudinal20 y sirve para hacer inferencia de la aceleración del crecimiento y para determinar la edad en que se alcanza la estatura adulta. Este modelo logístico exponencial multiplicado fue:
Este modelo representa 5 parámetros: h1 representa la asíntota superior (estatura adulta), hθ se relaciona con la estatura, S0 y S1 se relacionan con los incrementos medios en el estirón (forma del pico) y el parámetro θ se relaciona con la edad de hθ.
El EM de los escolares estudiados se determinó mediante los años del pico de velocidad de crecimiento de la estatura (APVC). Se calculó por medio de la ecuación de regresión propuesta por Mirwald et al.10. Este método incluye la estatura de pie, la estatura sentada, la longitud de las piernas (estatura de pie−estatura sentada) y sus interacciones:
Mujeres: Estado de madurez (años)=−9,376+(0,0001882×(longitud de piernas×estatura sentada))+(0,0022×(edad×longitud de piernas))+(0,005841× (edad×estatura de pie))−(0,002658×(edad×peso))+(0,07693× (relación peso por estatura×100)).
Hombres: Estado de madurez (años)=−9,236+((0,0002708×(longitud de piernas×estatura sentada))+(−0,001663×(edad×longitud de piernas))+(0,007216× (edad×estatura de pie))+(0,02292× (relación peso por estatura×100)).
Las ecuaciones propuestas por Moore et al.11 utilizan la edad y la estatura de pie para ambos sexos:
Mujeres: Estado de madurez (años)=−7,709133+(0,0042232×(edad×estatura)).
Hombres: Estado de madurez (años)=−7,999994+(0,0036124×(edad×estatura)).
Para clasificar el EM, se utilizó la sugerencia descrita por Malina y Koziel16, considerando a los jóvenes con maduración promedio dentro de −1 a +1APVC, inferiores a −1APVC como precoz, y superiores a +1APVC como tardío.
EstadísticaLa normalidad de datos se verificó por medio de Kolmogórov-Smirnov (K-S). Se efectuaron los cálculos de estadística descriptiva (promedio, desviación estándar, rango, frecuencia y porcentaje). Las diferencias entre ambos sexos se efectuaron por medio del test t para muestras independientes. Las comparaciones entre MPB y las ecuaciones de regresión se efectuaron por medio del test para muestras relacionadas. Las relaciones entre variables fueron verificadas por medio de Pearson, R2 ajustado y error estándar de estimación (EEE). En todos los casos se consideró p<0,05 como significativo. Los cálculos se efectuaron en planillas de Excel y SPSS 18.0. El cálculo del modelo MPB y la gráfica del PVC se efectuaron en el Software R.
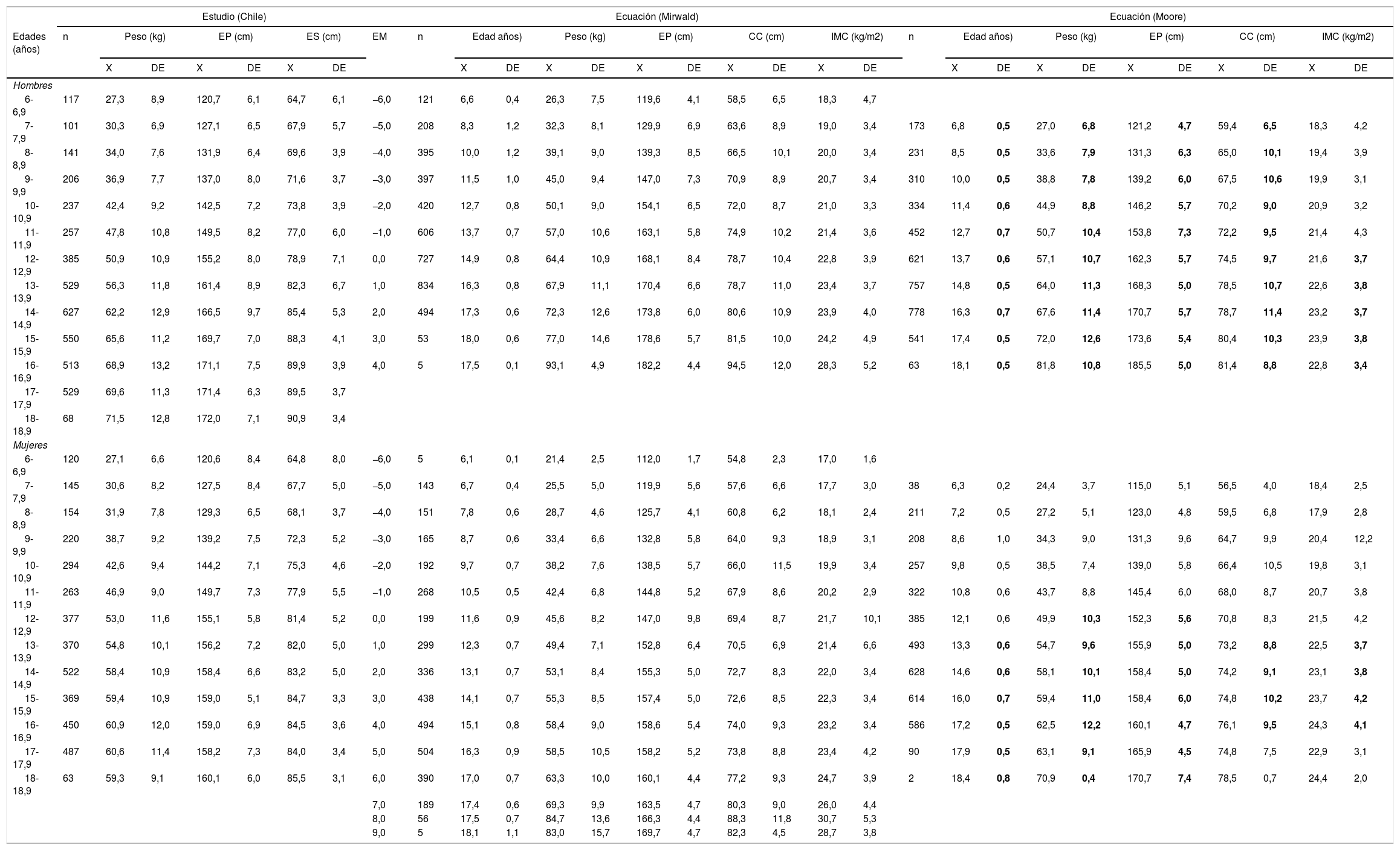
ResultadosLa tabla 1 muestra las comparaciones de las variables de crecimiento físico y adiposidad corporal, alineadas por EM para ambas ecuaciones. Para la ecuación de Mirwald, el EM en hombres oscila desde −6 hasta +4APVC y en mujeres va desde −6 hasta +9APVC; sin embargo, en la ecuación de Moore, en hombres, los valores del EM oscilan desde −5 hasta +5APVC, y en mujeres, desde −5 hasta +6APVC.
Variables de crecimiento físico y adiposidad corporal, alineadas por edad cronológica y EM en niños y adolescentes de ambos sexos
| Estudio (Chile) | Ecuación (Mirwald) | Ecuación (Moore) | ||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Edades (años) | n | Peso (kg) | EP (cm) | ES (cm) | EM | n | Edad años) | Peso (kg) | EP (cm) | CC (cm) | IMC (kg/m2) | n | Edad años) | Peso (kg) | EP (cm) | CC (cm) | IMC (kg/m2) | |||||||||||||
| X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | X | DE | |||||
| Hombres | ||||||||||||||||||||||||||||||
| 6-6,9 | 117 | 27,3 | 8,9 | 120,7 | 6,1 | 64,7 | 6,1 | −6,0 | 121 | 6,6 | 0,4 | 26,3 | 7,5 | 119,6 | 4,1 | 58,5 | 6,5 | 18,3 | 4,7 | |||||||||||
| 7-7,9 | 101 | 30,3 | 6,9 | 127,1 | 6,5 | 67,9 | 5,7 | −5,0 | 208 | 8,3 | 1,2 | 32,3 | 8,1 | 129,9 | 6,9 | 63,6 | 8,9 | 19,0 | 3,4 | 173 | 6,8 | 0,5 | 27,0 | 6,8 | 121,2 | 4,7 | 59,4 | 6,5 | 18,3 | 4,2 |
| 8-8,9 | 141 | 34,0 | 7,6 | 131,9 | 6,4 | 69,6 | 3,9 | −4,0 | 395 | 10,0 | 1,2 | 39,1 | 9,0 | 139,3 | 8,5 | 66,5 | 10,1 | 20,0 | 3,4 | 231 | 8,5 | 0,5 | 33,6 | 7,9 | 131,3 | 6,3 | 65,0 | 10,1 | 19,4 | 3,9 |
| 9-9,9 | 206 | 36,9 | 7,7 | 137,0 | 8,0 | 71,6 | 3,7 | −3,0 | 397 | 11,5 | 1,0 | 45,0 | 9,4 | 147,0 | 7,3 | 70,9 | 8,9 | 20,7 | 3,4 | 310 | 10,0 | 0,5 | 38,8 | 7,8 | 139,2 | 6,0 | 67,5 | 10,6 | 19,9 | 3,1 |
| 10-10,9 | 237 | 42,4 | 9,2 | 142,5 | 7,2 | 73,8 | 3,9 | −2,0 | 420 | 12,7 | 0,8 | 50,1 | 9,0 | 154,1 | 6,5 | 72,0 | 8,7 | 21,0 | 3,3 | 334 | 11,4 | 0,6 | 44,9 | 8,8 | 146,2 | 5,7 | 70,2 | 9,0 | 20,9 | 3,2 |
| 11-11,9 | 257 | 47,8 | 10,8 | 149,5 | 8,2 | 77,0 | 6,0 | −1,0 | 606 | 13,7 | 0,7 | 57,0 | 10,6 | 163,1 | 5,8 | 74,9 | 10,2 | 21,4 | 3,6 | 452 | 12,7 | 0,7 | 50,7 | 10,4 | 153,8 | 7,3 | 72,2 | 9,5 | 21,4 | 4,3 |
| 12-12,9 | 385 | 50,9 | 10,9 | 155,2 | 8,0 | 78,9 | 7,1 | 0,0 | 727 | 14,9 | 0,8 | 64,4 | 10,9 | 168,1 | 8,4 | 78,7 | 10,4 | 22,8 | 3,9 | 621 | 13,7 | 0,6 | 57,1 | 10,7 | 162,3 | 5,7 | 74,5 | 9,7 | 21,6 | 3,7 |
| 13-13,9 | 529 | 56,3 | 11,8 | 161,4 | 8,9 | 82,3 | 6,7 | 1,0 | 834 | 16,3 | 0,8 | 67,9 | 11,1 | 170,4 | 6,6 | 78,7 | 11,0 | 23,4 | 3,7 | 757 | 14,8 | 0,5 | 64,0 | 11,3 | 168,3 | 5,0 | 78,5 | 10,7 | 22,6 | 3,8 |
| 14-14,9 | 627 | 62,2 | 12,9 | 166,5 | 9,7 | 85,4 | 5,3 | 2,0 | 494 | 17,3 | 0,6 | 72,3 | 12,6 | 173,8 | 6,0 | 80,6 | 10,9 | 23,9 | 4,0 | 778 | 16,3 | 0,7 | 67,6 | 11,4 | 170,7 | 5,7 | 78,7 | 11,4 | 23,2 | 3,7 |
| 15-15,9 | 550 | 65,6 | 11,2 | 169,7 | 7,0 | 88,3 | 4,1 | 3,0 | 53 | 18,0 | 0,6 | 77,0 | 14,6 | 178,6 | 5,7 | 81,5 | 10,0 | 24,2 | 4,9 | 541 | 17,4 | 0,5 | 72,0 | 12,6 | 173,6 | 5,4 | 80,4 | 10,3 | 23,9 | 3,8 |
| 16-16,9 | 513 | 68,9 | 13,2 | 171,1 | 7,5 | 89,9 | 3,9 | 4,0 | 5 | 17,5 | 0,1 | 93,1 | 4,9 | 182,2 | 4,4 | 94,5 | 12,0 | 28,3 | 5,2 | 63 | 18,1 | 0,5 | 81,8 | 10,8 | 185,5 | 5,0 | 81,4 | 8,8 | 22,8 | 3,4 |
| 17-17,9 | 529 | 69,6 | 11,3 | 171,4 | 6,3 | 89,5 | 3,7 | |||||||||||||||||||||||
| 18-18,9 | 68 | 71,5 | 12,8 | 172,0 | 7,1 | 90,9 | 3,4 | |||||||||||||||||||||||
| Mujeres | ||||||||||||||||||||||||||||||
| 6-6,9 | 120 | 27,1 | 6,6 | 120,6 | 8,4 | 64,8 | 8,0 | −6,0 | 5 | 6,1 | 0,1 | 21,4 | 2,5 | 112,0 | 1,7 | 54,8 | 2,3 | 17,0 | 1,6 | |||||||||||
| 7-7,9 | 145 | 30,6 | 8,2 | 127,5 | 8,4 | 67,7 | 5,0 | −5,0 | 143 | 6,7 | 0,4 | 25,5 | 5,0 | 119,9 | 5,6 | 57,6 | 6,6 | 17,7 | 3,0 | 38 | 6,3 | 0,2 | 24,4 | 3,7 | 115,0 | 5,1 | 56,5 | 4,0 | 18,4 | 2,5 |
| 8-8,9 | 154 | 31,9 | 7,8 | 129,3 | 6,5 | 68,1 | 3,7 | −4,0 | 151 | 7,8 | 0,6 | 28,7 | 4,6 | 125,7 | 4,1 | 60,8 | 6,2 | 18,1 | 2,4 | 211 | 7,2 | 0,5 | 27,2 | 5,1 | 123,0 | 4,8 | 59,5 | 6,8 | 17,9 | 2,8 |
| 9-9,9 | 220 | 38,7 | 9,2 | 139,2 | 7,5 | 72,3 | 5,2 | −3,0 | 165 | 8,7 | 0,6 | 33,4 | 6,6 | 132,8 | 5,8 | 64,0 | 9,3 | 18,9 | 3,1 | 208 | 8,6 | 1,0 | 34,3 | 9,0 | 131,3 | 9,6 | 64,7 | 9,9 | 20,4 | 12,2 |
| 10-10,9 | 294 | 42,6 | 9,4 | 144,2 | 7,1 | 75,3 | 4,6 | −2,0 | 192 | 9,7 | 0,7 | 38,2 | 7,6 | 138,5 | 5,7 | 66,0 | 11,5 | 19,9 | 3,4 | 257 | 9,8 | 0,5 | 38,5 | 7,4 | 139,0 | 5,8 | 66,4 | 10,5 | 19,8 | 3,1 |
| 11-11,9 | 263 | 46,9 | 9,0 | 149,7 | 7,3 | 77,9 | 5,5 | −1,0 | 268 | 10,5 | 0,5 | 42,4 | 6,8 | 144,8 | 5,2 | 67,9 | 8,6 | 20,2 | 2,9 | 322 | 10,8 | 0,6 | 43,7 | 8,8 | 145,4 | 6,0 | 68,0 | 8,7 | 20,7 | 3,8 |
| 12-12,9 | 377 | 53,0 | 11,6 | 155,1 | 5,8 | 81,4 | 5,2 | 0,0 | 199 | 11,6 | 0,9 | 45,6 | 8,2 | 147,0 | 9,8 | 69,4 | 8,7 | 21,7 | 10,1 | 385 | 12,1 | 0,6 | 49,9 | 10,3 | 152,3 | 5,6 | 70,8 | 8,3 | 21,5 | 4,2 |
| 13-13,9 | 370 | 54,8 | 10,1 | 156,2 | 7,2 | 82,0 | 5,0 | 1,0 | 299 | 12,3 | 0,7 | 49,4 | 7,1 | 152,8 | 6,4 | 70,5 | 6,9 | 21,4 | 6,6 | 493 | 13,3 | 0,6 | 54,7 | 9,6 | 155,9 | 5,0 | 73,2 | 8,8 | 22,5 | 3,7 |
| 14-14,9 | 522 | 58,4 | 10,9 | 158,4 | 6,6 | 83,2 | 5,0 | 2,0 | 336 | 13,1 | 0,7 | 53,1 | 8,4 | 155,3 | 5,0 | 72,7 | 8,3 | 22,0 | 3,4 | 628 | 14,6 | 0,6 | 58,1 | 10,1 | 158,4 | 5,0 | 74,2 | 9,1 | 23,1 | 3,8 |
| 15-15,9 | 369 | 59,4 | 10,9 | 159,0 | 5,1 | 84,7 | 3,3 | 3,0 | 438 | 14,1 | 0,7 | 55,3 | 8,5 | 157,4 | 5,0 | 72,6 | 8,5 | 22,3 | 3,4 | 614 | 16,0 | 0,7 | 59,4 | 11,0 | 158,4 | 6,0 | 74,8 | 10,2 | 23,7 | 4,2 |
| 16-16,9 | 450 | 60,9 | 12,0 | 159,0 | 6,9 | 84,5 | 3,6 | 4,0 | 494 | 15,1 | 0,8 | 58,4 | 9,0 | 158,6 | 5,4 | 74,0 | 9,3 | 23,2 | 3,4 | 586 | 17,2 | 0,5 | 62,5 | 12,2 | 160,1 | 4,7 | 76,1 | 9,5 | 24,3 | 4,1 |
| 17-17,9 | 487 | 60,6 | 11,4 | 158,2 | 7,3 | 84,0 | 3,4 | 5,0 | 504 | 16,3 | 0,9 | 58,5 | 10,5 | 158,2 | 5,2 | 73,8 | 8,8 | 23,4 | 4,2 | 90 | 17,9 | 0,5 | 63,1 | 9,1 | 165,9 | 4,5 | 74,8 | 7,5 | 22,9 | 3,1 |
| 18-18,9 | 63 | 59,3 | 9,1 | 160,1 | 6,0 | 85,5 | 3,1 | 6,0 | 390 | 17,0 | 0,7 | 63,3 | 10,0 | 160,1 | 4,4 | 77,2 | 9,3 | 24,7 | 3,9 | 2 | 18,4 | 0,8 | 70,9 | 0,4 | 170,7 | 7,4 | 78,5 | 0,7 | 24,4 | 2,0 |
| 7,0 | 189 | 17,4 | 0,6 | 69,3 | 9,9 | 163,5 | 4,7 | 80,3 | 9,0 | 26,0 | 4,4 | |||||||||||||||||||
| 8,0 | 56 | 17,5 | 0,7 | 84,7 | 13,6 | 166,3 | 4,4 | 88,3 | 11,8 | 30,7 | 5,3 | |||||||||||||||||||
| 9,0 | 5 | 18,1 | 1,1 | 83,0 | 15,7 | 169,7 | 4,7 | 82,3 | 4,5 | 28,7 | 3,8 | |||||||||||||||||||
La negrita indica diferencia significativa en relación con la ecuación de Mirwald según el estado de madurez.
CC: circunferencia de la cintura; DE: desviación estándar; EM: estado de madurez; EP: estatura de pie; ES: estatura sentada; X: media aritmética; IMC: índice de masa corporal.
Se observaron diferencias significativas en hombres; los valores del EM calculado por Mirwald fueron superiores en edad, peso y estatura en relación con la ecuación de Moore en todos los niveles. Pero en la CC las diferencias se observan desde −5 hasta 0APVC, y desde +2 hasta +4APVC; y en el IMC, desde 0 hasta +5APVC. No hubo diferencias en el IMC desde −6 hasta −1APVC (p>0,05).
En mujeres, no hubo diferencias significativas en la edad, peso y estatura desde −5 hasta −1APVC; sin embargo, las diferencias empiezan a aparecer desde 0 hasta +6APVC en las variables de crecimiento físico (edad, peso y estatura) (p<0,05), mientras que en las variables adiposidad corporal (CC e IMC) se determinaron diferencias desde +1 hasta +4APVC, donde la ecuación de Moore presentó valores superiores en relación con la de Mirwald. Además, no hubo diferencias significativas en las variables de adiposidad desde −5 hasta 0APVC y +5 y +6APVC (p>0,05).
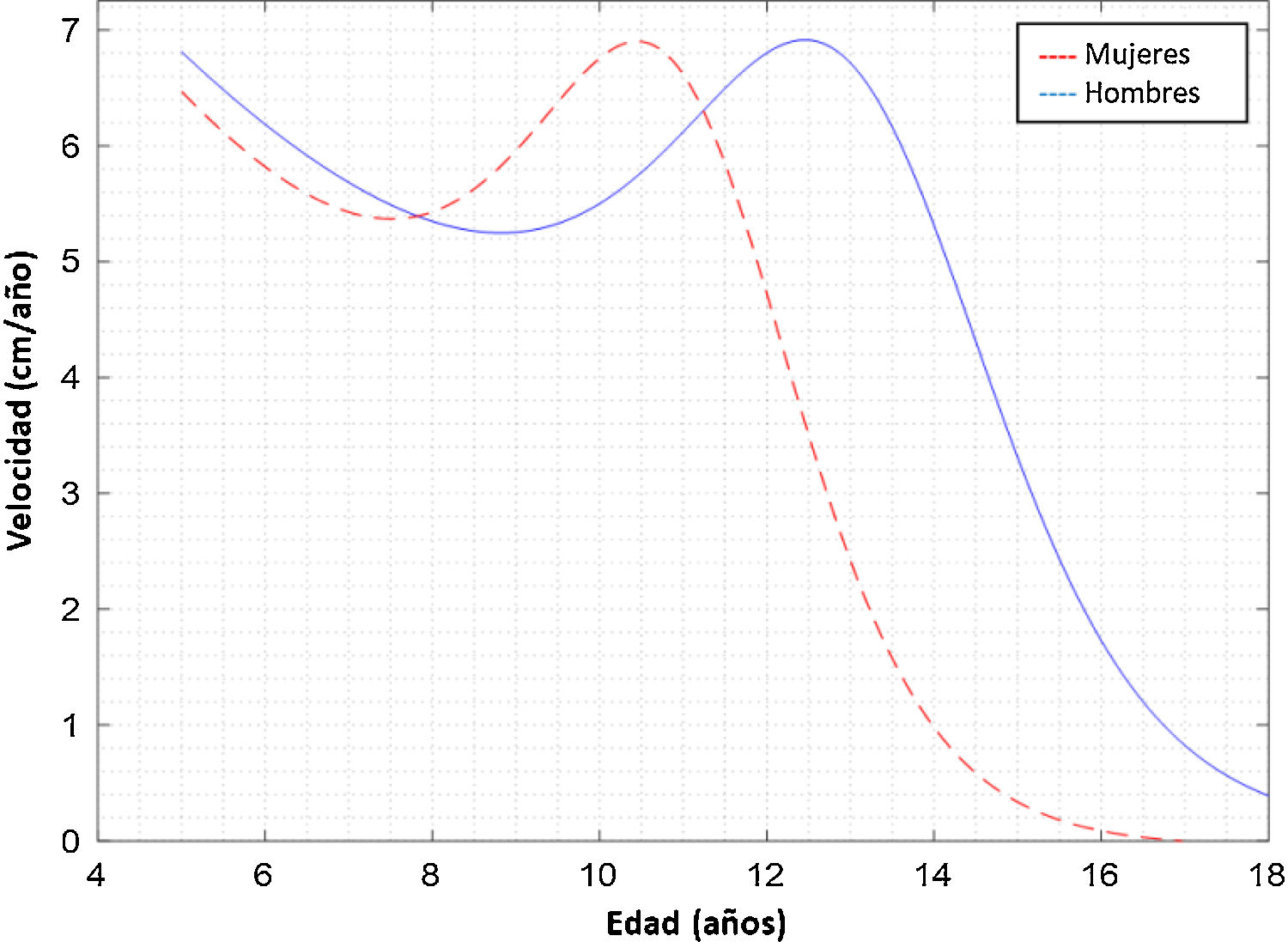
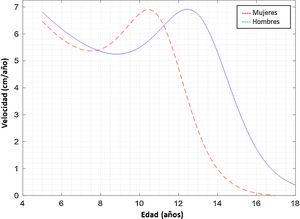
La curva del PVC en función de la edad cronológica determinada por MPB se observa en la figura 1. Nótese que en las mujeres el PVC se determinó a los 10,33±0,29 años y en hombres a los 12,81±0,27 años. La velocidad de crecimiento en las mujeres fue de 6,90±0,96 cm/año y en hombre fue de 7,11±1,47 cm/año.
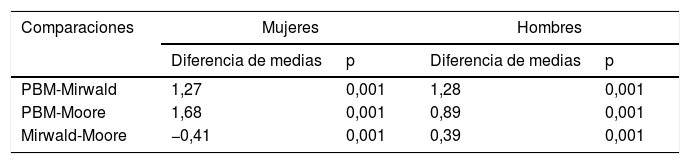
La tabla 2 muestra las comparaciones entre el MPB con la ecuación de Mirwald y Moore para ambos sexos. El MPB difiere significativamente con ambas ecuaciones y en ambos sexos (p<0,001); además, hubo diferencias entre Mirwald y Moore en ambos sexos (p<0,001).
Comparación de los valores medios del pico de velocidad de crecimiento (PVC) en niños y adolescentes de ambos sexos
| Comparaciones | Mujeres | Hombres | ||
|---|---|---|---|---|
| Diferencia de medias | p | Diferencia de medias | p | |
| PBM-Mirwald | 1,27 | 0,001 | 1,28 | 0,001 |
| PBM-Moore | 1,68 | 0,001 | 0,89 | 0,001 |
| Mirwald-Moore | −0,41 | 0,001 | 0,39 | 0,001 |
PBM: Modelo Preece-Baines.
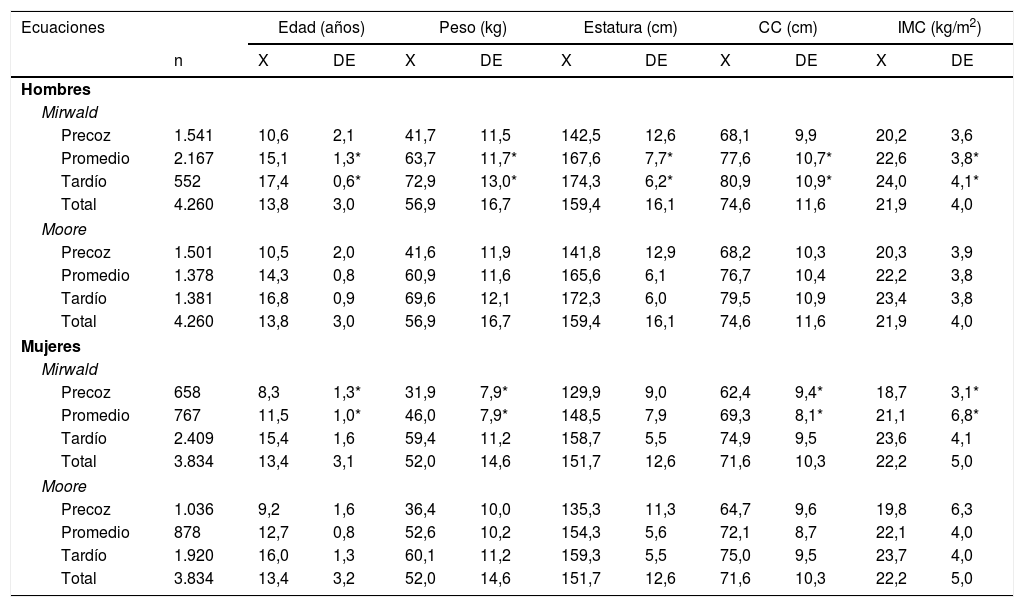
Las categorías del EM en función de las variables del crecimiento físico y adiposidad corporal para ambas ecuaciones se observan en la tabla 3. En ambos sexos se determinaron diferencias significativas entre las dos ecuaciones. En hombres, la ecuación de Mirwald mostró valores superiores de edad, peso y estatura en las categorías promedio y tardío (p<0,05), mientras que en la categoría precoz no hubo diferencias significativas (p>0,05). En las mujeres, la ecuación de Moore presentó valores superiores en la edad, peso y estatura en las categorías precoz y promedio; sin embargo, en la categoría tardío, no hubo diferencias significativas entre ambas ecuaciones (p>0,05).
Comparación de las variables de crecimiento físico y adiposidad corporal, categorizadas por EM para ambos sexos y ecuaciones
| Ecuaciones | Edad (años) | Peso (kg) | Estatura (cm) | CC (cm) | IMC (kg/m2) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| n | X | DE | X | DE | X | DE | X | DE | X | DE | |
| Hombres | |||||||||||
| Mirwald | |||||||||||
| Precoz | 1.541 | 10,6 | 2,1 | 41,7 | 11,5 | 142,5 | 12,6 | 68,1 | 9,9 | 20,2 | 3,6 |
| Promedio | 2.167 | 15,1 | 1,3* | 63,7 | 11,7* | 167,6 | 7,7* | 77,6 | 10,7* | 22,6 | 3,8* |
| Tardío | 552 | 17,4 | 0,6* | 72,9 | 13,0* | 174,3 | 6,2* | 80,9 | 10,9* | 24,0 | 4,1* |
| Total | 4.260 | 13,8 | 3,0 | 56,9 | 16,7 | 159,4 | 16,1 | 74,6 | 11,6 | 21,9 | 4,0 |
| Moore | |||||||||||
| Precoz | 1.501 | 10,5 | 2,0 | 41,6 | 11,9 | 141,8 | 12,9 | 68,2 | 10,3 | 20,3 | 3,9 |
| Promedio | 1.378 | 14,3 | 0,8 | 60,9 | 11,6 | 165,6 | 6,1 | 76,7 | 10,4 | 22,2 | 3,8 |
| Tardío | 1.381 | 16,8 | 0,9 | 69,6 | 12,1 | 172,3 | 6,0 | 79,5 | 10,9 | 23,4 | 3,8 |
| Total | 4.260 | 13,8 | 3,0 | 56,9 | 16,7 | 159,4 | 16,1 | 74,6 | 11,6 | 21,9 | 4,0 |
| Mujeres | |||||||||||
| Mirwald | |||||||||||
| Precoz | 658 | 8,3 | 1,3* | 31,9 | 7,9* | 129,9 | 9,0 | 62,4 | 9,4* | 18,7 | 3,1* |
| Promedio | 767 | 11,5 | 1,0* | 46,0 | 7,9* | 148,5 | 7,9 | 69,3 | 8,1* | 21,1 | 6,8* |
| Tardío | 2.409 | 15,4 | 1,6 | 59,4 | 11,2 | 158,7 | 5,5 | 74,9 | 9,5 | 23,6 | 4,1 |
| Total | 3.834 | 13,4 | 3,1 | 52,0 | 14,6 | 151,7 | 12,6 | 71,6 | 10,3 | 22,2 | 5,0 |
| Moore | |||||||||||
| Precoz | 1.036 | 9,2 | 1,6 | 36,4 | 10,0 | 135,3 | 11,3 | 64,7 | 9,6 | 19,8 | 6,3 |
| Promedio | 878 | 12,7 | 0,8 | 52,6 | 10,2 | 154,3 | 5,6 | 72,1 | 8,7 | 22,1 | 4,0 |
| Tardío | 1.920 | 16,0 | 1,3 | 60,1 | 11,2 | 159,3 | 5,5 | 75,0 | 9,5 | 23,7 | 4,0 |
| Total | 3.834 | 13,4 | 3,2 | 52,0 | 14,6 | 151,7 | 12,6 | 71,6 | 10,3 | 22,2 | 5,0 |
CC: circunferencia de la cintura; DE: desviación estándar; EM: estado de madurez; IMC: índice de masa corporal; X: media aritmética.
En las variables de adiposidad corporal (CC e IMC), en hombres, la ecuación de Mirwald evidenció valores significativos más altos en relación con la ecuación de Moore en las categorías promedio y tardío para la CC e IMC (p<0,05). No hubo diferencias en la categoría precoz en ambos indicadores de adiposidad (CC e IMC) (p>0,05). En las mujeres, la ecuación de Moore reflejó valores superiores a la de Mirwald en la CC e IMC en las categorías precoz y promedio (p<0,05). Pero en la categoría tardío no se observaron diferencias significativas, ni en la CC ni en el IMC (p>0,05).
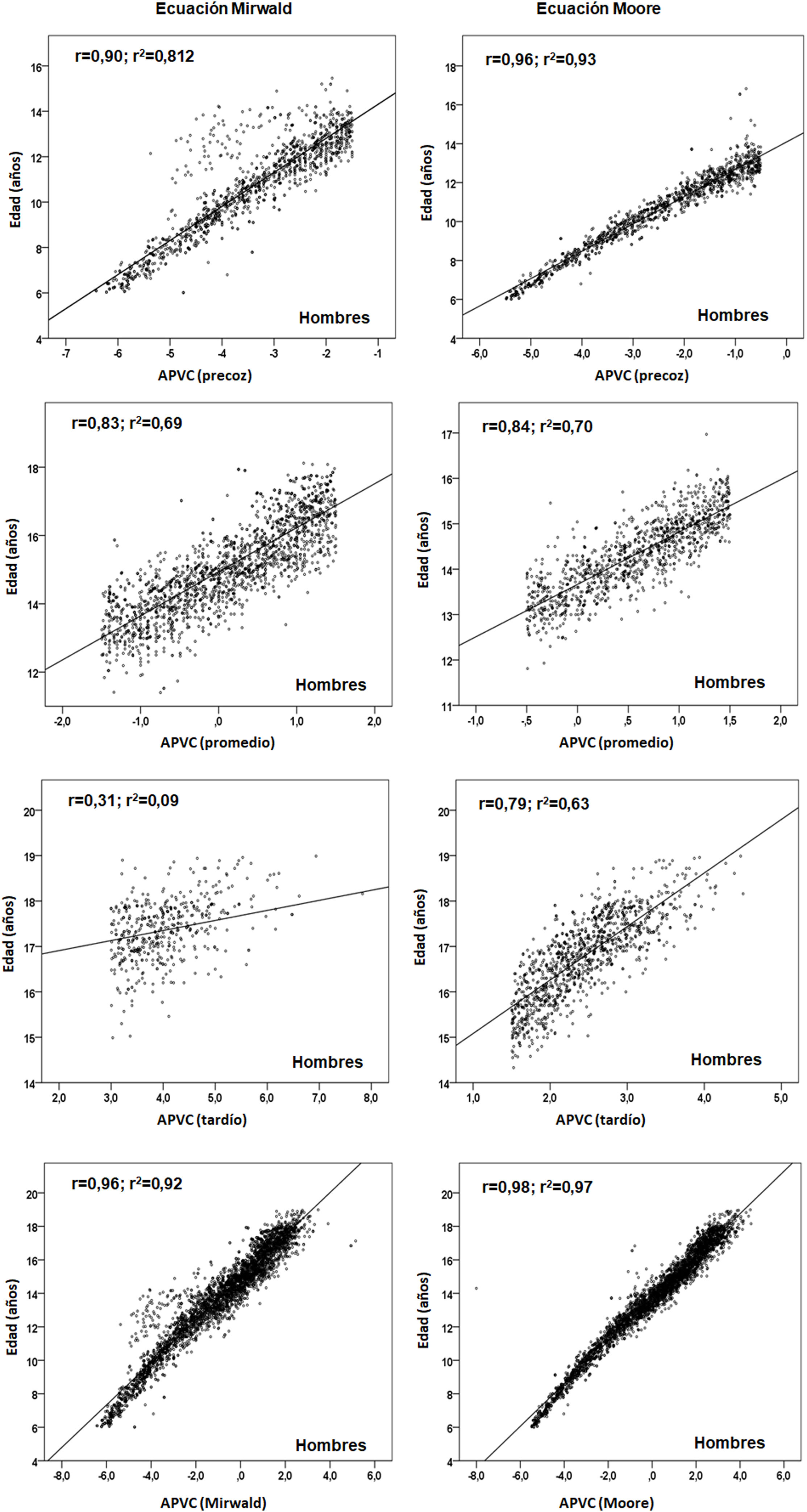
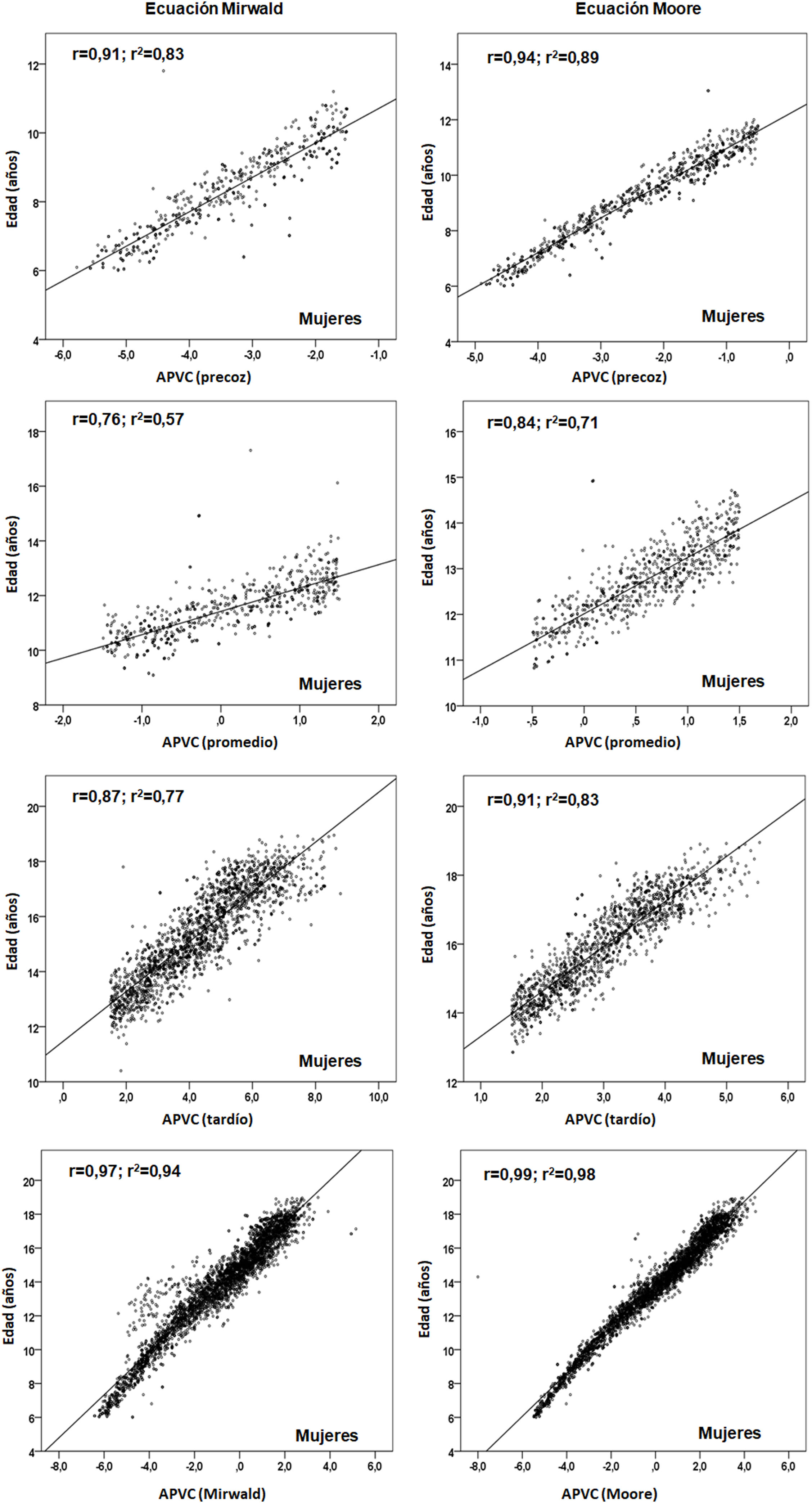
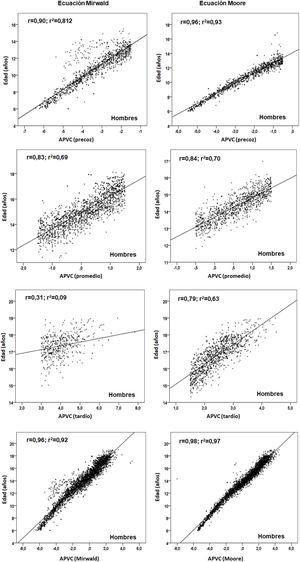
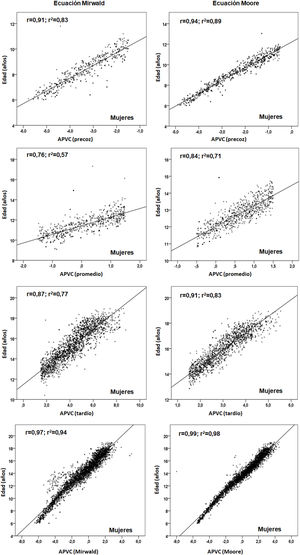
Las relaciones entre edad cronológica con cada categoría del EM se observan en las figuras 2 y 3. Los valores del coeficiente de determinación por categoría de EM, a través de la ecuación de Mirwald, fueron relativamente inferiores respecto a la ecuación de Moore en ambos sexos. Por la ecuación de Mirwald los valores de R2 oscilaron entre 0,09 y 0,81 en hombres y entre 0,57 y 0,83 en mujeres. Por la ecuación de Moore, los valores oscilaron entre 0,63 y 0,93 en hombres y entre 0,71 y 0,98 en mujeres.
Los resultados del estudio han demostrado diferencias significativas entre el MPB con la ecuación de Mirwald y Moore en ambos sexos. Estos hallazgos indican que ambas ecuaciones antropométricas que predicen el EM de niños y adolescentes no podrían ser aplicadas a los niños y adolescentes chilenos.
De hecho, los APVC determinados por MPB reflejaron edades mucho antes que las ecuaciones de regresión, siendo a los 10,33±0,29 años en mujeres y a los 12,81±0,27 años en hombres, por lo que existe una diferencia de medias superiores cuando se predice por medio de Mirwald y Moore (∼0,89 a ∼1,68 años).
También se ha verificado que los APVC de este estudio determinados por MPB fueron similares a los reportados en muestras de estudios transversales de Perú21 y México22, con lo cual estas evidencias confirman que las niñas generalmente tienen un crecimiento más temprano y alcanzan el tamaño final antes que sus contrapartes de los hombres.
Por otro lado, confirmamos también que hubo diferencias significativas entre ambas ecuaciones de regresión, tanto en hombres como en mujeres. La ecuación de Mirwald reflejó valores superiores en hombres (en las variables de crecimiento y adiposidad) en las categorías promedio y tardío en relación con la ecuación de Moore; por el contrario, en mujeres, la ecuación de Mirwald evidenció valores inferiores (peso, estatura, CC e IMC) en las categorías precoz y promedio respecto a la ecuación de Moore. No hubo diferencias en los hombres cuando se clasificó con madurez tardía, mientras que en mujeres no hubo diferencias cuando se clasificó con madurez precoz.
En consecuencia, tras verificar las diferencias entre ambas ecuaciones, se procedió a relacionar la edad cronológica con cada categoría del EM (precoz, promedio y tardío) para verificar el grado de asociación en cada ecuación. Se evidenció que las ecuaciones de Moore en ambos sexos reflejaron valores relativamente más altos que la ecuación de Mirwald en las tres categorías del EM. Esta información podría sugerir su aplicación a muestras de niños y adolescentes chilenos, a pesar de que ambas ecuaciones en sus estudios presentan similares poderes de explicación (89 y 90%).
Estos resultados obtenidos en este estudio podrían estar asociados a un menor EEE en la ecuación de Moore en relación con la ecuación de Mirwald, puesto que estudios anteriores previamente ya habían alertado de algunas limitaciones en la ecuación de Mirwald10,23, sobre todo en individuos que se encuentran más alejados de los APVC16,23.
De hecho, las regresiones observadas en este estudio indican que en la categoría del EM tardío, el % de explicación en ambos sexos fueron inferiores respecto a la ecuación de Moore, especialmente en hombres, lo que ratifica un menor poder de explicación en los jóvenes con APVC más avanzados, como se observó en algunos estudios10,24.
Hasta la fecha, la ecuación de Mirwald se ha generalizado en cuanto al uso y aplicación en diversas poblaciones a nivel mundial13,24,25 y en Chile26,27, tal vez por ser la más antigua y difundida desde su publicación, ya que la propuesta de Moore fue publicada hace 5 años y es posible que demore más tiempo para una mayor difusión y conocimiento en el ámbito de las ciencias de la salud y del deporte.
Destacamos en ese sentido, que el EEE de las ecuaciones propuestas para determinar el EM de forma no invasiva y el número de predictores seguirán siendo motivo de investigaciones en diversos contextos socioculturales, puesto que el interés común es alcanzar valores precisos y exactos en sus estimaciones, y consecuentemente la validez externa, aunque, por otro lado, es necesario que cada población genere sus propias ecuaciones10, acordes a su realidad.
También es necesario aclarar que la maduración es un proceso biológico de progreso hacia la madurez y varía entre los sistemas corporales16. Este implica dos aspectos relevantes, el estado y el tiempo. El primero se refiere al nivel de maduración en el momento de la observación y el segundo a la edad en que ocurre la maduración específica3. Pues las ecuaciones investigadas en este estudio abordan los APVC alcanzados para una determinada edad cronológica, sin embargo, el estado de madurez no es posible determinarlo por medio de las ecuaciones analizadas, lo cual es una brecha importante para seguir investigando.
Así pues, controlar el efecto de la madurez y el rango sustancial, en el ritmo y el momento del crecimiento en poblaciones pediátricas, sigue siendo un desafío11, especialmente en el ámbito de la investigación, pues abre nuevas posibilidades y perspectivas entre los profesionales para seguir proponiendo alternativas no invasivas y de fácil uso en las ciencias de la salud y del deporte.
En general, este estudio presenta varias fortalezas que están relacionadas con el tamaño y tipo de selección de la muestra, así como con la fiabilidad de las medidas antropométricas, que presentaron valores inferiores al 2% en el ETM; inclusive es el primer estudio a gran escala que se llevó a cabo en Chile controlando el EM, sin embargo, futuros estudios deben prestar atención a otros criterios de validación de las ecuaciones de regresión para estimar el EM, puesto que esta investigación únicamente se limitó a validar a través de un modelo matemático MPB, ya que no se disponía de muestras longitudinales. Futuros estudios deben preocuparse en estudiar a los niños y adolescentes chilenos de forma longitudinal, con lo cual es posible proponer nuevas ecuaciones específicas para poblaciones regionales.
ConclusiónEn conclusión, se verificó que las ecuaciones de Moore y Mirwald difieren con el modelo matemático MPB en ambos sexos, aunque la ecuación de Moore podría ser útil para la evaluación del EM en niños y adolescentes chilenos, en vista de que presenta un menor error de estimación en sus ecuaciones propuestas.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.