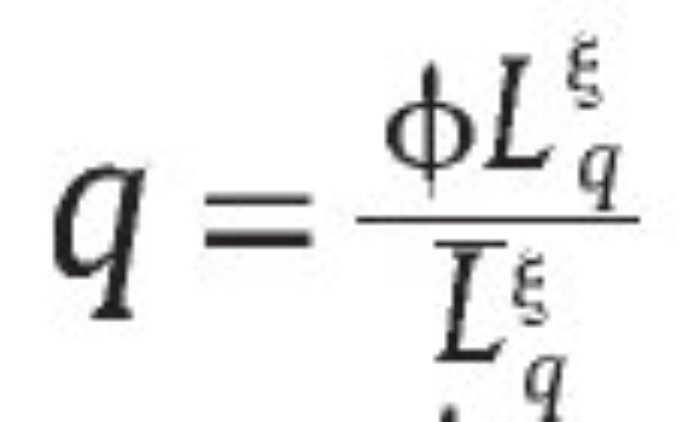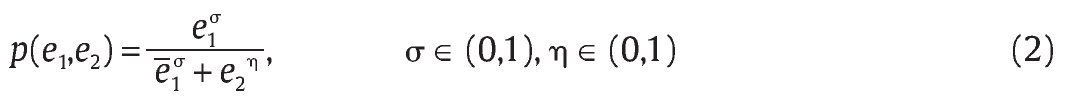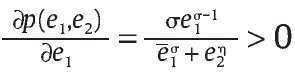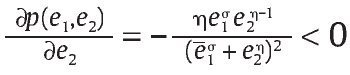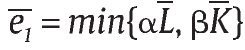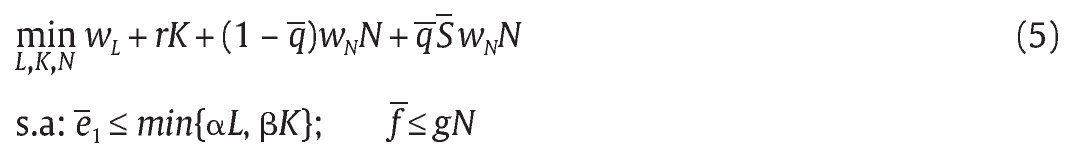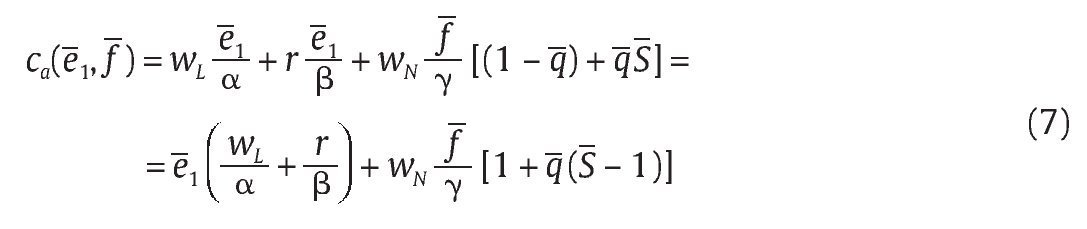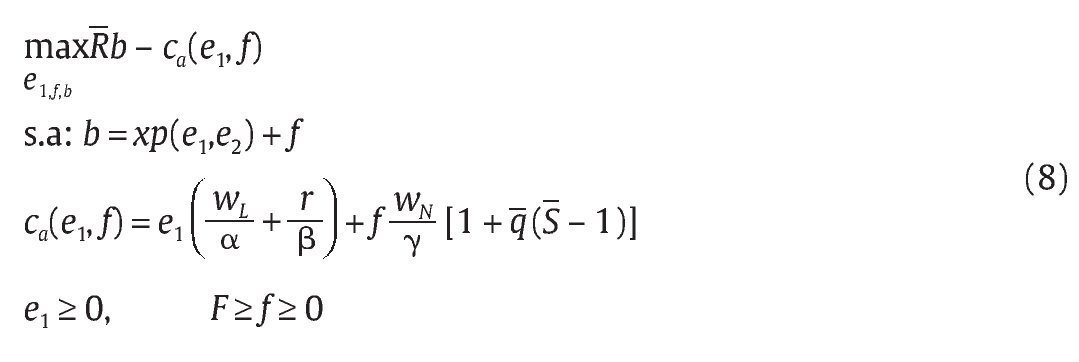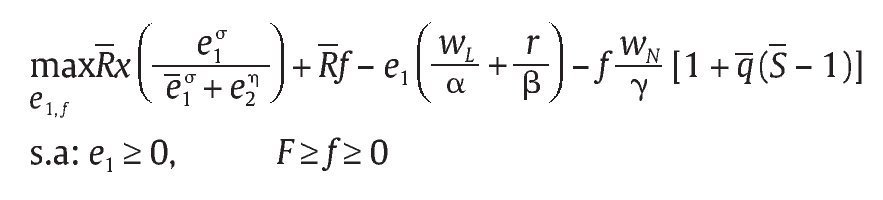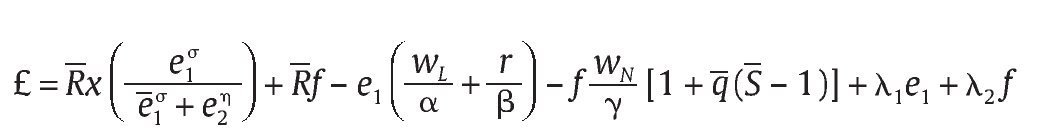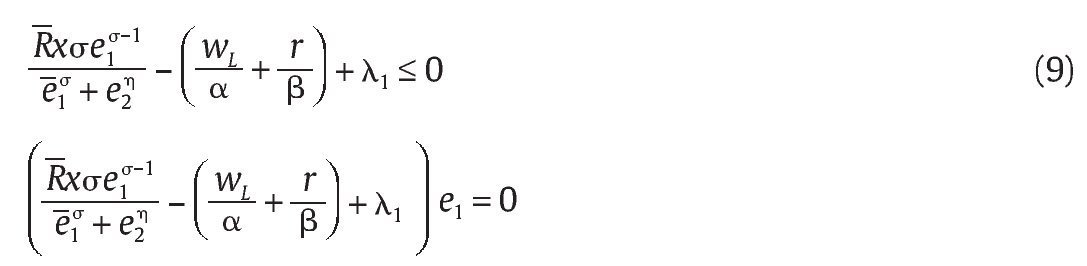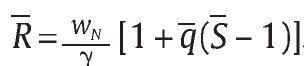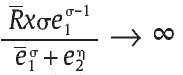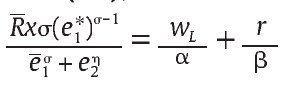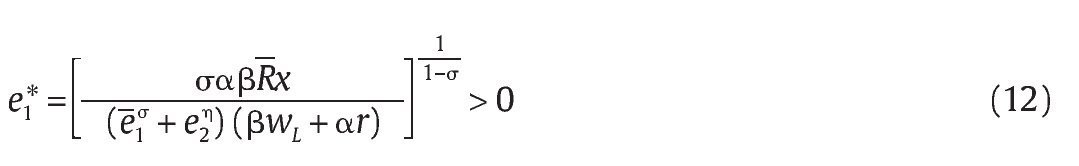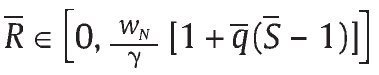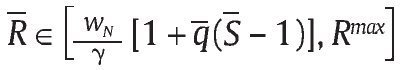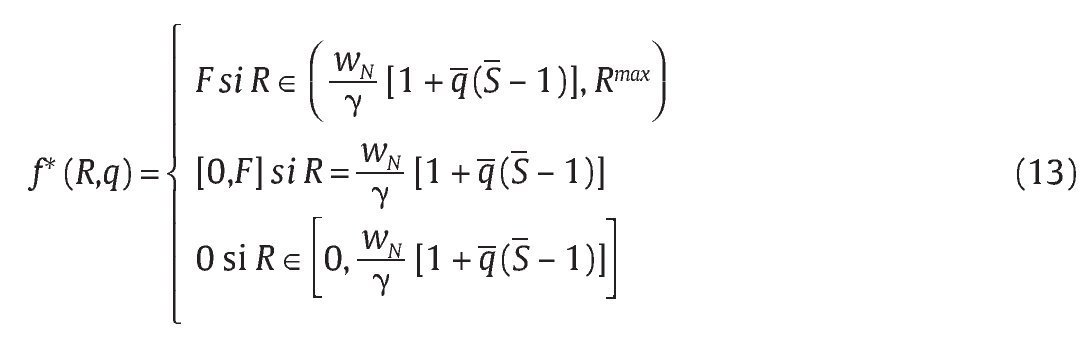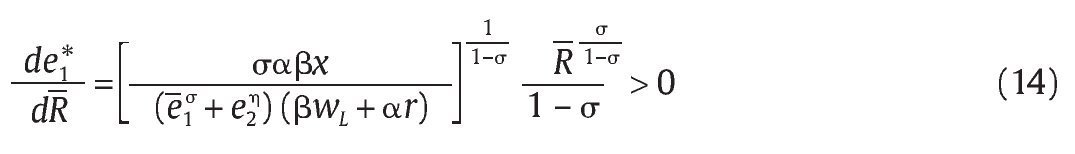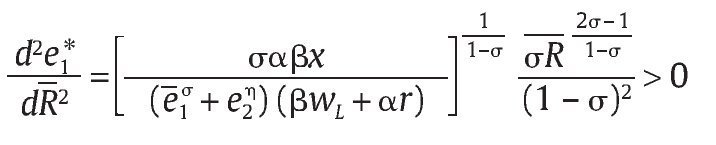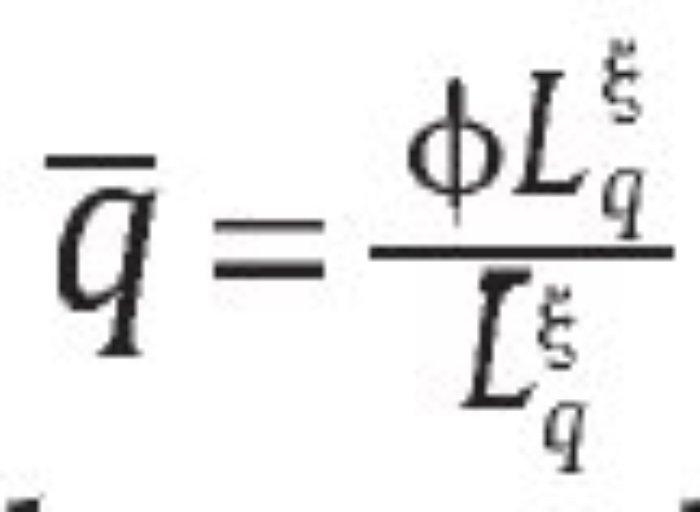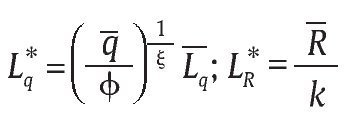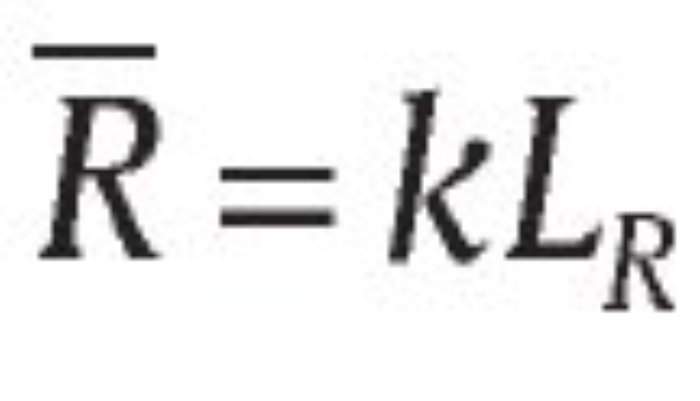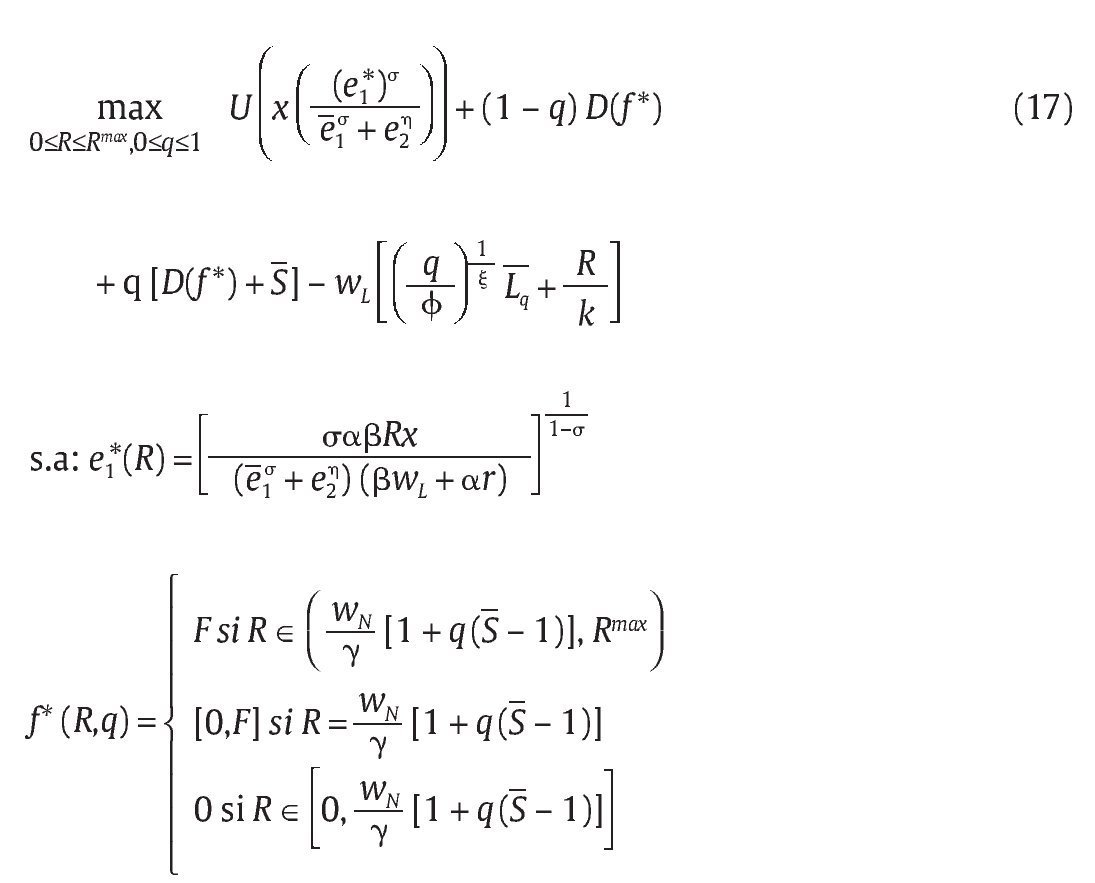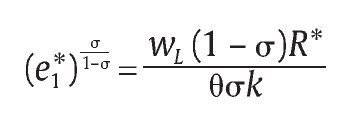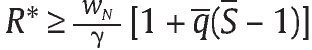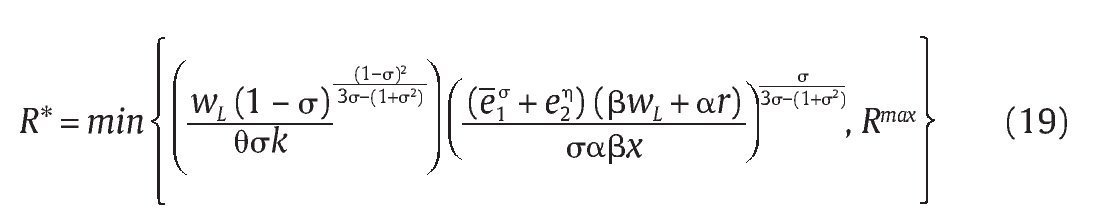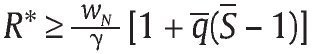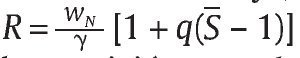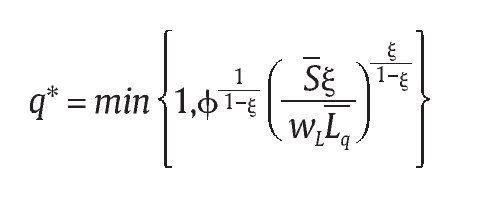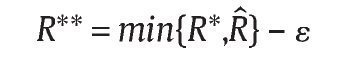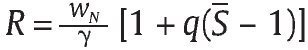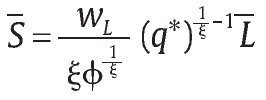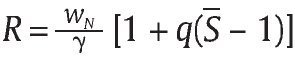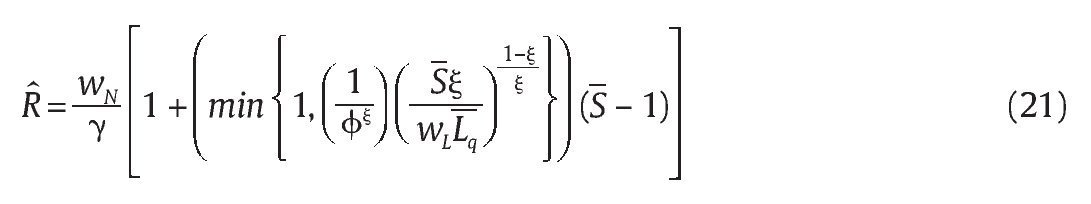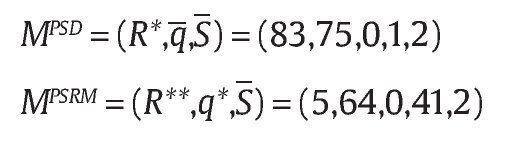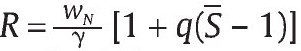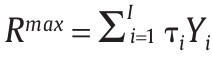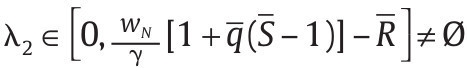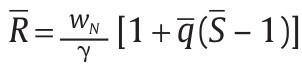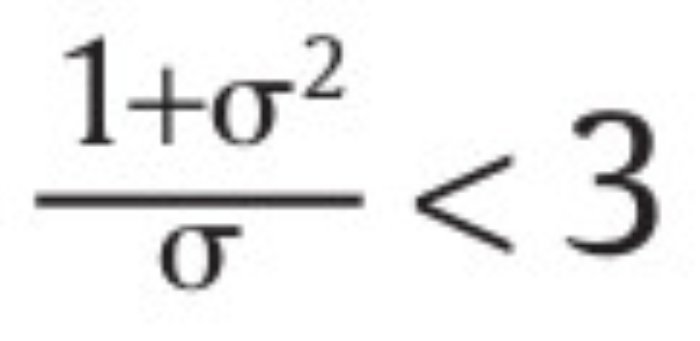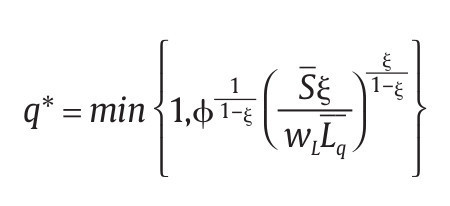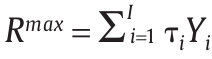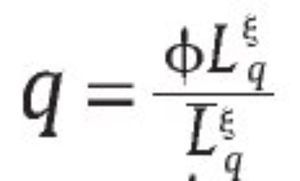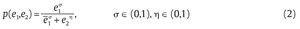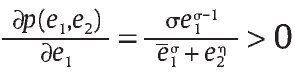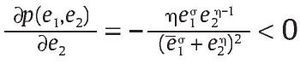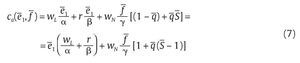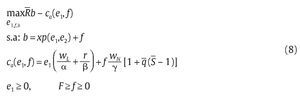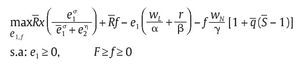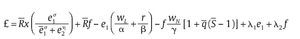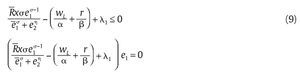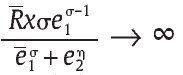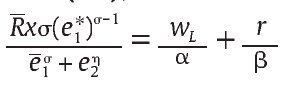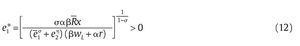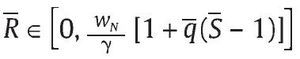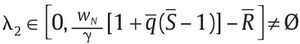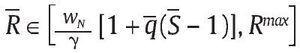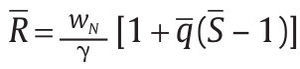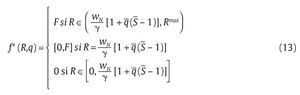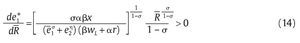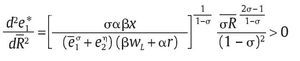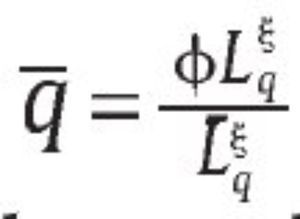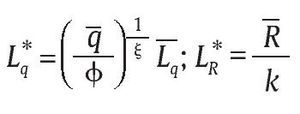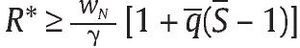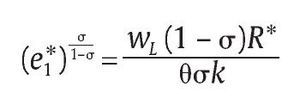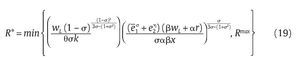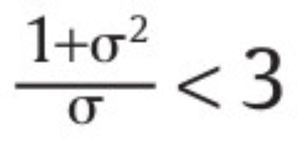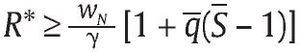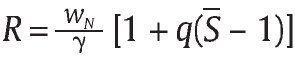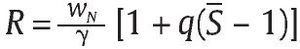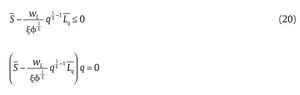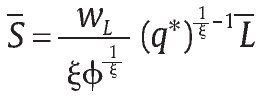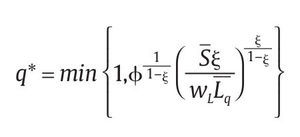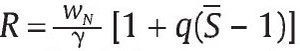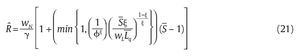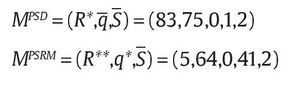Este artículo formaliza a través de un mecanismo de principal-agente la política de seguridad democrática del Gobierno de Uribe, y muestra su relación con el incremento de las víctimas de ejecuciones extrajudiciales llamados "falsos positivos". El modelo explica las fallas de la política de seguridad democrática al compararla con una política contrafáctica alterna que involucre un nivel óptimo de auditoría a las unidades militares para evitar falsos positivos. Se encuentra que esta política contrafáctica aumentaría el bienestar de la sociedad
This article, through a principal-agent mechanism, constructs a model of the democratic security policy of the Uribe Government, and shows its relationship with the increase in victims of extra-judicial executions called "false positives". The model explains the failures of the democratic security policy by comparing it with an alternative counterfactual policy that involves an optimum level of audit of military units to avoid false positives. It was found that this counterfactual policy could increase the well-being of society.
"En la paz, los hijos entierran a los padres; la guerra altera el orden de la naturaleza y hace que los padres entierren a sus hijos". Herodoto
"Actualmente, para muchos economistas, la economía es en gran parte un problema de incentivos: incentivos para trabajar con ahínco, para producir productos de buena calidad, para estudiar, para invertir, para ahorrar, etc. ¿Cómo diseñar instituciones que provean los incentivos correctos a los diferentes agentes económicos?, se ha convertido en una pregunta fundamental en economía". Laffont y Martimort (2002, p. 1.)
1. Introducción
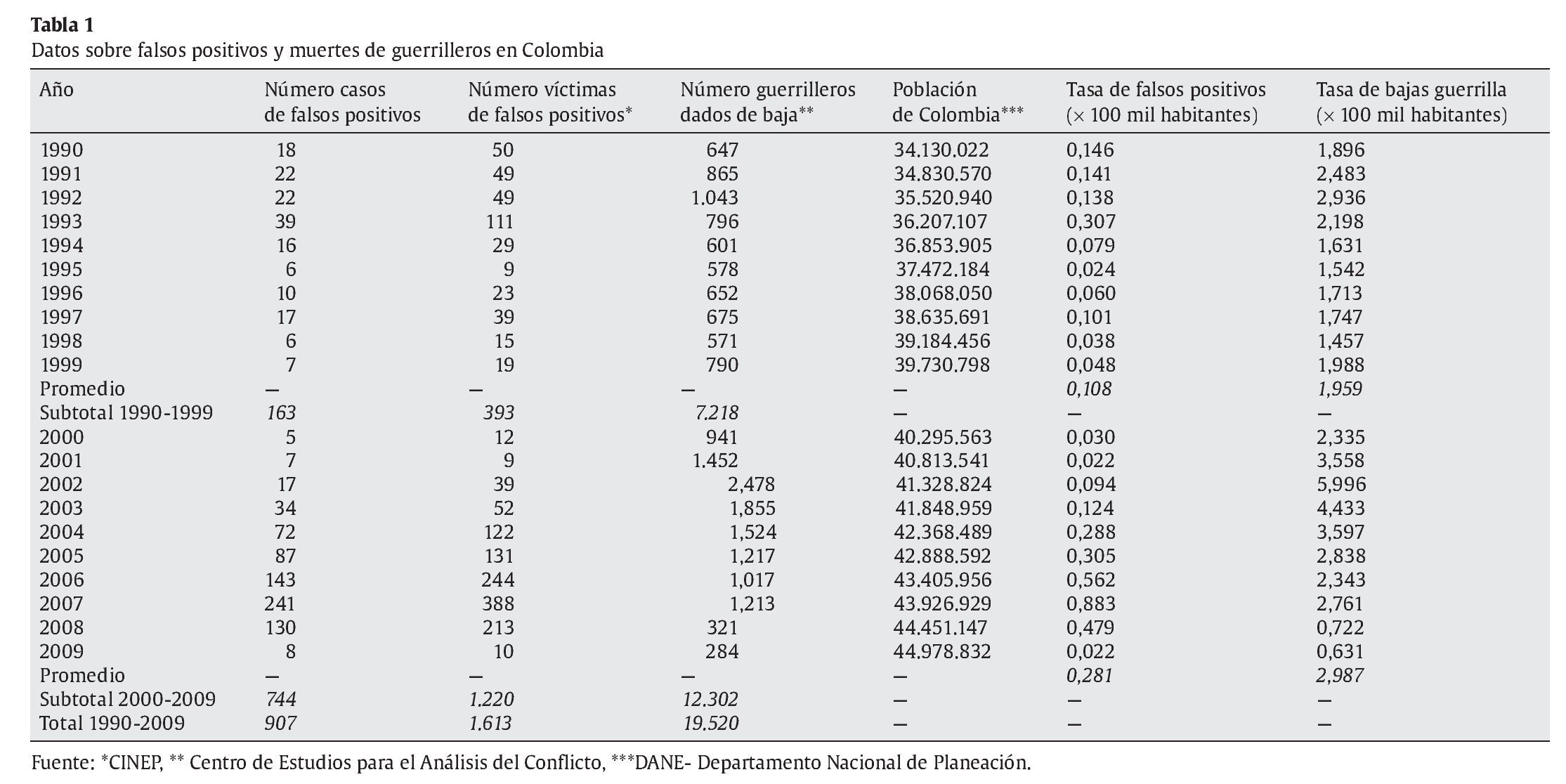
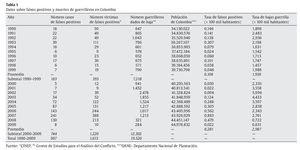
Las cifras sobre ejecuciones extrajudiciales o mal llamados falsos positivos son indignantes1. Según el Centro de Investigación para la Educación Popular, el número de víctimas asciende a 1.613 entre 1990 y 2009. La Fiscalía, por su parte, reporta 2.799 víctimas de este comportamiento, mientras que la Oficina del Alto Comisionado para los Derechos Humanos de la Organización de las Naciones Unidas habla de 3.000 víctimas entre 2004 y 2008. Es claro que los denominados falsos positivos no son algo nuevo en nuestro país, pero también es claro que el problema se exacerbó durante la implementación de la política de seguridad democrática (PSD) entre 2002 y 2010. Por ejemplo, con base en los datos reportados en la tabla 1, la tasa promedio de falsos positivos por cada 100.000 habitantes tuvo un incremento del 154%, pasando de 0,11 en la década comprendida entre 1990 y 1999 a 0,28 entre 2000 y 2009. Comportamiento similar al que presenta la tasa de guerrilleros dados de baja que aumentó en 52% pasando de 1,96 en la década de los noventa a 2,99 en la siguiente década. En términos absolutos, el número de falsos positivos pasa de 393 a 1.220 entre las mismas 2 décadas, mientras que el número de guerrilleros dados de baja pasa de 7.218 a 12.302 en el mismo período. Estas cifras sugieren un aumento de la intensidad del conflicto en Colombia entre la década de los noventa y la primera década del nuevo milenio2 acompañado de una mayor victimización de la población civil reflejada en el incremento de falsos positivos (tabla 1).
La primera década del nuevo milenio transcurre, en su mayoría, bajo la denominada PSD, implementada a partir de mediados del 2002 bajo el primer Gobierno de Álvaro Uribe Vélez; política "cuyo objetivo general es la protección de los colombianos y el fortalecimiento del Estado de derecho y la autoridad democrática en todo el territorio"3. Esta política se concibió "...como una política para la protección de la población, donde la seguridad es entendida como la presencia permanente y efectiva de la autoridad democrática en todo el territorio. En este sentido, dado que los derechos humanos son fundamento y razón de ser del ordenamiento constitucional, según la PSD su vigencia requiere ante todo de la plena soberanía democrática y de la capacidad del Estado de hacer prevalecer el orden jurídico en todo el territorio"4.
Para dar cumplimiento a esta política era indispensable recuperar el control estatal sobre el territorio nacional que se había debilitado tanto por los intentos anteriores de diálogos de paz, como los llevados a cabo por Andrés Pastrana en el Caguán durante su mandato, y por el avance mismo de las acciones de la guerrilla. Luego de recuperar el control territorial, la PSD prevé el fortalecimiento del aparato judicial que garantice el control estatal en todo el territorio nacional. En cumplimiento de sus objetivos, la PSD afirma que en sus acciones, las fuerzas militares cumplirán con la ley y respetarán los derechos humanos sancionando a quienes los incumplan. Debe notarse que la PSD en sí misma no propone un mecanismo específico para fortalecer el sistema judicial que permita verificar y controlar las acciones de las Fuerzas Armadas, es decir, se da por sentado que las fuerzas militares acatarán las leyes y que el sistema judicial actual es competente para controlarlas.
Este vacío institucional, a nuestro juicio, es un elemento importante a la hora de establecer la relación entre la PSD y el aumento de los falsos positivos porque implica un desconocimiento de los incentivos que determinan el comportamiento final de los militares. De hecho, la PSD propuso al Congreso, en 2003, un polémico estatuto antiterrorista con el cual se pretendía fortalecer las acciones de las Fuerzas Armadas a través de la conformación de unidades especiales, configuradas por personal de la fiscalía y de la fuerza pública, y que facultaba a soldados para realizar levantamiento de cadáveres, interrogar sospechosos y recaudar pruebas contra las personas que detenían; estatuto que finalmente fue declarado inexequible por la Corte Constitucional en agosto de 2004, debido a que el estatuto daba vía libre a posibles abusos cometidos por parte de la fuerza publica y la posible violación de derechos fundamentales y tratados internacionales firmados por Colombia. Además, la oposición consideraba que su aprobación era el camino hacia el autoritarismo, el abuso y las arbitrariedades por parte de la fuerza pública.
Al dar por sentado que las fuerzas militares acatarán las leyes y que el sistema judicial actual está en capacidad de controlar sus acciones, la PSD se enfoca principalmente en ofrecer incentivos a los militares específicamente a través de recompensas monetarias, permisos para los soldados y felicitaciones, ascensos o capacitaciones en el exterior a los militares de más alto rango. Este tipo de incentivos generó un afán desmedido por mostrar resultados satisfactorios en la lucha contra los grupos al margen de la ley tal y como lo evidencian, entre otros, testimonios como los consignados en el estudio «Colombia: la guerra se mide en litros de sangre»5.
"Uno de los incentivos que nos otorgaban a los comandantes de contraguerrilla de cada batallón era una licencia por todo el mes de diciembre a los pelotones que más sumaran muertos en el año, o sea que si mi pelotón del Batallón Calibío era el que más había dado muertos en el año, yo y mi gente salíamos todo el mes de diciembre [...] También se dijo que el soldado que más diera bajas sería incentivado con enviarlo al Sinaí o a un curso fuera del País"6.
"Se [implantó] un problemático esquema de evaluación [de desempeño]: valora excesivamente —y, a veces, exclusivamente— las bajas del oponente, y castiga desproporcionadamente los propios fracasos operacionales. Consecuencia: tendencia a que se logren bajas sin asumir riesgos, sin exponerse demasiado o, mejor, nada. Resultados: civiles indefensos que aparecen muertos en combates que nunca existieron"7.
"Nos dijo mi Coronel Ramírez, cada comandante de compañía me debe responder por 1 muerto en combate cada mes y la sección segunda me debe responder por 3 muertos al mes, en este momento la guerra se mide en litros de sangre, el comandante que no tenga resultados de muertos por mes tendrá la sanción correspondiente y se verá reflejado en su folio de vida [...]"8.
Los datos en la tabla 1 muestran una relación positiva entre la tasa de falsos positivos y la implementación de la PSD en el período 2002-2009. En particular, nótese que la tasa de falsos positivos para el año 2002 era de 0,094, la cual es muy cercana al promedio de la década anterior, y que a partir de 2003 se observa un incremento continuo y significativo de la misma hasta 2007. En este sentido, conjeturamos que la PSD exacerbó el número de falsos positivos debido al vacío institucional derivado de no tener un mecanismo apropiado de control de las acciones de las Fuerzas Armadas.
Con base en lo anterior, este artículo propone entender el problema de los falsos positivos como el resultado de un perverso mecanismo de incentivos de la PSD en el que se motiva, con retribuciones monetarias y de otra índole, la sustitución de guerrilleros muertos en combate por personas ajenas al conflicto9. El modelamiento detallado de los incentivos perversos que causan este tipo de problemática implica, además, proponer mecanismos alternativos que permitan atenuar y/o solucionar el problema. Al final, proponemos una política de seguridad con responsabilidad militar (PSRM), la cual contempla explícitamente un mecanismo de control sobre las acciones de las Fuerzas Armadas para lograr sus objetivos sin gene-rar incentivos que transgredan los derechos fundamentales de los ciudadanos.
El documento continúa de la siguiente manera. La segunda sección justifica la teoría del pricipal agente como una herramienta apropiada para entender el problema de los falsos positivos, mien-tras que el modelo propiamente dicho se presenta en la tercera sección. Finalmente, se presentan las conclusiones del trabajo.
2. Diseño de mecanismos
El diseño de mecanismos o teoría de la implementación es una parte de la teoría de juegos y tiene por objetivo el diseño de un mecanismo o juego que permita implementar un resultado que se considera a priori como deseado por uno de los participantes. Diseñar este tipo de mecanismos, cuando se prevé de antemano que durante el desarrollo de la interacción se presentarán asimetrías de información, es lo que técnicamente se denomina el problema de principal-agente. El nombre principal-agente evoca la idea de un principal, que es quien conoce el resultado que se desea implementar, que para llevar a cabo su objetivo se ve en la necesidad de contratar un agente proveyéndole incentivos adecuados a través de un mecanismo diseñado por él para que el agente implemente el resultado deseado. La literatura técnica distingue entre 3 posibles problemas de información que enfrenta el principal a la hora de diseñar un mecanismo: los resultantes de acciones del agente que no pueden ser observadas por el principal (acción oculta), los resultantes de información solo accesible al agente en el desarrollo de la interacción (información oculta) y los resultantes de acciones del agente que están enmarcadas en un contexto de responsabilidad limitada (limited liability). El primero de estos casos es conocido también bajo el nombre de riesgo moral, mientras que el segundo se denomina de selección adversa.
En este artículo, la PSD del Gobierno de Álvaro Uribe Vélez se formaliza a través de un modelo principal-agente en donde el principal corresponde al Gobierno y el agente a una unidad militar. Dentro de la teoría del diseño de mecanismos, una relación principal-agente bajo riesgo moral aparece cuando el principal no es capaz de observar las acciones que realiza el agente y, en consecuencia, enfrenta problemas de información asimétrica que deben ser tenidos en cuenta a la hora de crear los incentivos para este último. Creemos que el fenómeno de falsos positivos puede entenderse como un problema de información asimétrica con riesgo moral por parte del Gobierno. Para entender esto conceptualizamos de manera general al Gobierno como el principal que desea implementar un objetivo deseable de antemano, a saber: debilitar grupos armados al margen de la ley. Para lograr dicho objetivo, el principal propone a las unidades militares, que corresponden a los agentes, un mecanismo específico denominado PSD el cual provee incentivos para que las unidades militares actúen de manera acorde con la consecución del objetivo deseado por el Gobierno.
Una vez que el Gobierno imparte la política a las unidades militares (agentes) para combatir a los grupos armados, y sugiere acciones encaminadas al cumplimiento del objetivo planteado, las unidades militares con el ánimo de optimizar su propia utilidad escogen una acción para realizar dentro de un conjunto posible de acciones. Sin embargo, la acción escogida por las unidades militares puede ser acorde o no con el objetivo planteado por el Gobierno. De hecho, la unidad militar presenta y reporta el número total de bajas que son atribuidas a su acción sin que el Gobierno pueda distinguir si las bajas provienen de miembros del grupo al margen de la ley o de falsos positivos. A pesar de esto, la unidad militar recibe la compensación pactada con el Gobierno dado el número de bajas totales reportadas. Es importante aclarar que la compensación puede o no ser monetaria, puede entenderse, por ejemplo, en términos de felicitaciones oficiales, días de vacaciones o ascensos de grados militares.
En esta relación principal-agente, el Gobierno no puede observar directamente las acciones llevadas a cabo por el agente-unidad militar en el cumplimiento de su tarea, es decir, no tiene certeza de si las bajas presentadas por el agente son realmente provenientes de com bates o son realmente falsos positivos. Este es el problema de información que enfrenta el Gobierno en la implementación de la PSD, el cual es un problema de riesgo moral.
Es importante mencionar que trabajos como los de Mitchell y Carey (2012) y Rivera (2012) abordan una problemática similar a la de los falsos positivos en un ambiente tipo principal-agente. Sin embargo, dichos estudios no proponen un modelo microfundamentado a la hora de su análisis, como tampoco se hace en la literatura que conocemos en torno al tema específico de los falsos positivos.
2.1. Infograma de los falsos positivos
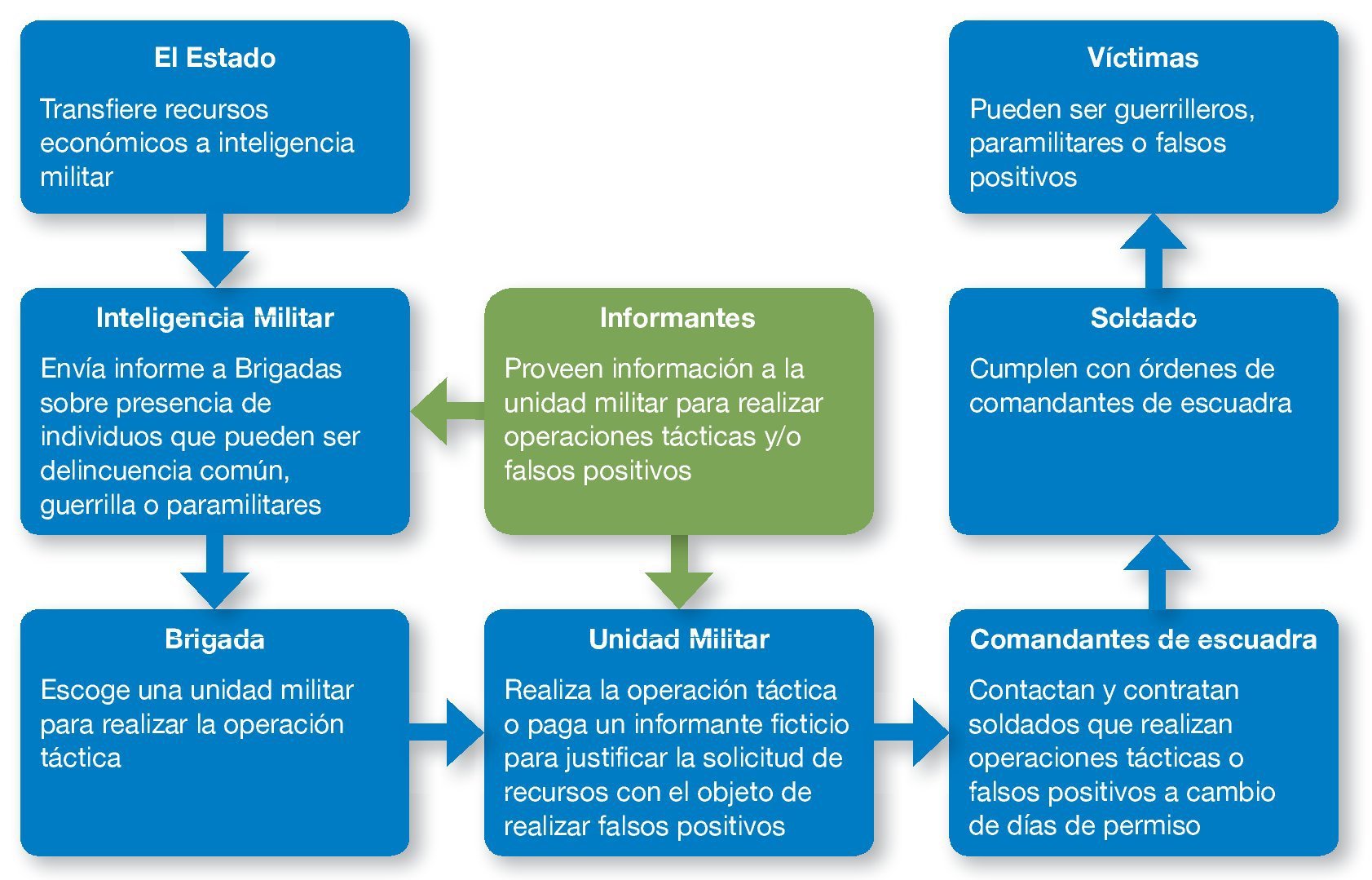
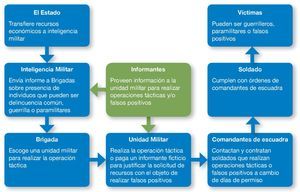
La historia de los falsos positivos puede ser contada brevemente de la siguiente manera: el dinero de los falos positivos salía de lo que el Gobierno giraba para la inteligencia militar. Inteligencia militar informaba sobre la presencia de individuos sospechosos en determinados lugares, quienes podían ser delincuencia común, guerrilla o paramilitares, planeaba la operación y enviaba un informe a la brigada. Esta seleccionaba la unidad militar que hacía la opera-ción o misión táctica, y que era la que finalmente realizaba el falso positivo. Cuando la unidad militar no obtenía resultados, y decidía realizar operaciones de falsos positivos, pagaba a un informante ficticio para justificar su solicitud de recursos. Del dinero recibido, el informante ficticio recibía una parte, mientras que el resto iba para los comandantes de escuadra quienes a su vez asignaban presupuesto para los soldados que podían conseguir las víctimas y las armas configurando así los denominados falsos positivos. Finalmente, los soldados recibían de 15 a 20 días de permiso y los oficiales recibían felicitaciones. Este infograma se representa en la figura 1.
Figura 1. Infograma de falsos positivos.
3. Modelo
En esta parte, proponemos un modelo de principal-agente que permite capturar los ingredientes fundamentales de los problemas de información y los incentivos para generar los llamados falsos positivos. El modelo no tiene la intención de ser una representación totalmente realista del proceso descrito en la figura 1, aunque pretende capturar los rasgos mas importantes del fenómeno para poder discutir posibles soluciones al problema de los falsos positivos. Para ello, debemos modelar la forma en que una unidad militar enfrenta al grupo al margen de la ley y su relación con los incentivos que provee el Gobierno para lograr este objetivo. En esta relación, debemos mostrar la aparición de los llamados falsos positivos.
3.1. Supuestos
Con este escenario en mente construimos un modelo principal-agente que permite formalizar los incentivos que generan falsos positivos. Como se ha argumentado arriba, suponemos que el principal es el Gobierno, mientras que el agente es la unidad militar. Del Gobierno asumimos que su objetivo es el de alcanzar el máximo bienestar posible para la sociedad que gobierna y que dicho bienestar depende positivamente del debilitamiento de grupos armados al margen de la ley. En particular, para el Gobierno la forma más efectiva de debilitar estos grupos es aumentar el número esperado de bajas en combate. Por otro lado, suponemos que el bienestar de la socidad decrece con el número esperado de víctimas de los falsos positivos y, además, que el bienestar de la sociedad decrece con el costo de la supervisión de la unidad militar para el cumplimiento de sus funciones. Esto lo representamos por medio de una función de bienestar10 reducida
donde g es el número de bajas esperadas en combate con grupos armados al margen de la ley que proporciona la unidad militar, f es el número de falsos positivos, S es un parámetro exógeno que representa la sanción a los militares que incurran en conductas no deseadas y C es una función de costos de supervisión del agente; estos términos se precisarán más adelante. Se supone que esta función de bienestar reducida es separable en g y f donde U'(g) > 0, U"(g) < 0, D'(f) < 0 y D(0) = 0 . Por simplicidad, asumimos unas condiciones límite sobre U y D: limg→0U'(g) = ∞ y limf→0(-D'(f)) = ∞. La primera condición significa que el bienestar incrementa significativamente con un aumento marginal en g partiendo de g = 0, mientras que la segunda significa que cuando partimos de una situación de f = 0 el bienestar se ve negativa y significativamente afectado por un caso marginal de falso positivo. El problema de información que enfrenta el Gobierno es que observa el número total de bajas esperadas b = g + f pero no puede distinguir de este total cuáles corresponden a falsos positivos y cuales a bajas en combate entre la unidad militar y el grupo armado al margen de la ley.
El mecanismo propuesto por el Gobierno para llevar a cabo su objetivo de debilitar los grupos armados al margen de la ley lo modelamos de la siguiente forma: consiste en realizar una transferencia R ε [0,Rmax] a la unidad militar basada en el número de bajas presentadas por esta, donde el valor Rmax > 0 es la cantidad de recursos económicos máxima que puede transferir el Gobierno a la unidad militar para implementar su política y una auditoría de los procedimientos de la unidad militar con base en un sistema judicial establecido representado por una probabilidad de auditoría q ε (0,1) y una sanción a los infractores S. Suponemos que el recaudo fiscal de los recursos transferibles a la unidad militar Rmax viene de una función tributaria
donde τi ε (0,1) es la tasa de impuestos para la política de seguridad sobre el ingreso total Yi (laboral y no laboral) del i-ésimo contribuyente de la sociedad civil conformada por I contribuyentes. Sin embargo, obtener un recaudo de tamaño R ε (0,Rmax] requiere contratar funcionarios que lo realicen en representación del Gobierno, así que suponemos que el recaudo es una función de producción lineal en el número de funcionarios gubernamentales contratados LR, es decir, kLR donde k > 0 es la productividad de los funcionarios del Gobierno (es decir, funcionarios de la Dirección de Impuestos y Aduanas Nacionales) para recaudar el monto R.
De otra parte, el sistema judicial preestablecido se modela como una sanción S > 1 para la unidad militar si es encontrada culpable de falsos positivos, que son detectados con probabilidad q. En caso de que q = 0, entonces suponemos que no habría sanción para la unidad militar es decir, S = 0. Para el Gobierno, como representante de la sociedad, una mayor sanción a los responsables de los falsos positivos debe representar un aumento del bienestar social, lo que se refleja en la función 1. Sin embargo, tomamos S como dado exógenamente por la sociedad a través de su sistema judicial, el cual no es alterado por el Gobierno en la implementación de su política de seguridad. De otro lado, asumimos que generar un nivel de probabilidad de auditoría q ε (0,1] también se puede ver como una función de producción porque requiere contratar funcionarios gubernamentales Lq, lo que se modela a través de la función de producción
para Lqε [0,Lq] y φ ε (0,1), ξε (0,1).
Dados estos elementos, denotaremos el mecanismo del Gobierno para implementar su política de seguridad como una tripla M = (R,q,S). El objetivo del Gobierno para implementar su política se puede representar a través de la escogencia óptima de R y q para la maximización de la función de bienestar social (1) teniendo en cuenta el comportamiento óptimo por parte de la unidad militar. En este contexto, conceptualizamos la PSD del Gobierno de Álvaro Uribe como una tripla MPSD = (R,q,S) donde se toma como dado tanto S como q, y tan solo utiliza la variable R para lograr su objetivo del debilitamiento de grupos al margen de la ley. Debido a que durante el Gobierno de Álvaro Uribe no se realizaron reformas en la justicia, de tal manera que existiera un control especial sobre los militares en la PSD, asumimos que tanto S como q son exógenas. Compararemos este mecansimo de PSD con uno que incorpore, además, responsabilidad militar, es decir, que tenga en cuenta q en el momento de escoger óptimamente R.
Por su parte, la unidad militar toma como dado el mecanismo propuesto por el Gobierno para escoger su nivel óptimo de esfuerzo para combatir los grupos armados al margen de la ley y el número esperado de bajas que puede presentar al Gobierno como resultado de su actividad. Simplificaremos el modelo suponiendo que solamente existe un grupo armado al margen de la ley que debe ser debilitado por la unidad militar. En particular, suponemos que las bajas en combate por parte de la unidad militar ocurren con probabilidad de éxito p(e1,e2) ε [0,1]. Esta probabilidad de éxito está en función de e1 que denota la eficiencia en combate de la unidad militar y de e2 que denota la eficiencia en combate del grupo al margen de la ley. Suponemos que esta función tiene la siguiente forma funcional:
para todo e1 ε [0,e1] y e2 ε [0,e2]. Nótese que esta función satisface unos supuestos razonables de la lógica de la guerra: p(0, e2) = 0 para todo e2 ≥ 0 y p(e1, 0) = 1, es decir, si la unidad militar no tiene ninguna eficiencia militar, su probabilidad de éxito es nulo, mientras que si el grupo al margen de la ley no tiene ninguna eficiencia militar y el Gobierno escoge la máxima eficiencia militar posible, entonces su probabilidad de éxito deber ser 1. Por otra parte, suponemos que la función (2) satisface
0 y
decir, una mayor eficiencia de la unidad militar en combate implica una mayor probabilidad de obtener bajas del grupo al margen de la ley, y a su vez un aumento en la eficiencia en combate del grupo armado al margen de la ley disminuye la probabilidad de bajas de la unidad militar. Más aún, p(e1, e2) en (2) es una función cóncava estricta en e1 lo que significa que la probabilidad de éxito crece con e1 pero marginalmente cada vez menos. Asumimos, además, que e2 > 0 es exógena ya que no estamos interesados en modelar el comportamiento del grupo armado al margen de la ley.
Por otra parte, suponemos que e1 es determinada óptimamente por la unidad militar al escoger los niveles de capital y trabajo requeridos para obtener un nivel determinado de eficiencia en el combate. El nivel e1 viene determinado a través de una función de producción que por simplicidad suponemos que tiene la forma tipo Leontief, así:
donde α > 0, β > 0, L ε [0,L] es el número de soldados y K ε [0, K] es la tecnología de combate que son utilizados por la unidad militar. Al asumir que la función de producción es de tipo Leontief, estamos suponiendo que no hay sustitución entre soldados y tecnología militar11.
Con probabilidad p(e1, e2) > 0, la unidad militar da de baja a x combatientes del grupo al margen de la ley donde x > 0 es la productividad en combate de la unidad militar, la cual se asume como dada, mientras que con probabilidad (1 - p(e1, e2)) no obtiene bajas en combate. Nótese que la máxima probabilidad que la unidad militar tiene de éxito es p(e1, e2) para un nivel dado de e2, donde e1 = min{αL, βK}. El número esperado de bajas en combate del grupo armado al margen de la ley por parte de la unidad militar se define como g = xp(e1, e2). Los precios de K y L se representan como r y wL, respectivamente, los cuales son tomados exógenamente por el Gobierno y la unidad militar.
Finalmente, la unidad militar puede reportar bajas que no corresponden a bajas en combate contra el grupo armado al margen de la ley, sino a ejecuciones extrajudiciales de civiles. Esta labor la realiza la unidad militar con certeza a través de una función de producción lineal en el número de soldados N utilizados,
los cuales reciben un ingreso wN > wL por cada falso positivo y donde γ > 0 es una constante que respresenta la productividad en este tipo de labores. Suponemos que existe un máximo de soldados N que podrían hacer esta labor tal que el número de falsos positivos está acotado por F ≡ γN. Asumimos esta cota como determinada exógenamente a través, por ejemplo, de la propia ética de militares (comandantes y soldados) que no se prestarían a la realización de este tipo de actividades, así como por los niveles de resistencia de las comunidades de las cuales se obtienen los falsos positivos.
3.2. Comportamiento de la unidad militar
El comportamiento de la unidad militar involucra 2 partes: i) la unidad militar debe escoger óptimamente los niveles de L, N y K para lograr un nivel de bajas esperado b = g + f, tomando como dado el mecanismo diseñado por el Gobierno, y ii) una vez que ha determinado estos niveles óptimos, maximiza su beneficio económico que depende de las transferencias que el Gobierno le hace en función de las bajas presentadas. Formalmente, caracterizamos el primero de estos problemas a través del siguiente conflicto de minimización de costos:
donde e1 y f son los niveles dados de eficiencia de la unidad militar para producir bajas en combate y falsos positivos, respectivamente.
Dados los niveles e1 y f que se desean producir, la solución al problema de minimización es trivial debido a que las restricciones se satisfacen como igualdades y a que la función de tipo Leontief va a implicar que aL = bK. Así, la solución viene dada por:
La función de costos de la unidad militar para producir e1 y f se encuentra reemplazando (6) en la función que se ha de minimizar en (5) y está dada por:
Una vez determinada la función óptima de costos, la unidad militar determina óptimamente su nivel de efectividad militar e1 para obtener bajas en combate de grupos armados al margen de la ley, el nivel f de falsos positivos y, por ende, el total esperado de bajas b = xp(e1,e2) + f. Para ello, la unidad militar soluciona el siguiente problema de maximización tomando como dado el mecanismo M = (R,q,S):
Reemplazando b, ca(e1, f) y p(e1,e2) en la función objetivo podemos expresar el problema de maximización de la unidad militar como:
donde la función objetivo es estrictamente cóncava en e1 y tan solo cóncava en f debido a la linealidad asumida en f. La función lagrangiana correspondiente al problema esta dada por:
donde λ1 ≥ 0 y λ2 ≥ 0 son multiplicadores de Lagrange. Las condiciones de primer orden de Kuhn-Tucker correspondientes son:
Nótese que si R = 0 la escogencia óptima de la unidad militar es e1* = 0 y f * = 0 ya que si la unidad militar escoge algo diferente su beneficio sería estrictamente negativo. Para valores de R estrictamente positivos se puede mostrar que e1* > 0. Para ver esto, nótese que si e1* = 0, entonces
∞ dado que σ ε (0,1) y así la condición de primer orden en (9) no podrá satisfacerse, lo que implica una contradicción; por lo tanto, debe tenerse e1* > 0. Dado esto, y bajo la condición de primer orden (11), entonces se debe tener l =, además por (9) se debe tener λ =, además por (9) se debe tener
con lo cual al despejar se obtiene que:
Por otra parte, la solución f* = 0 ocurre si
para
que es consistente con las condiciones de primer orden (10) y (11). Además, la solución f* = F ocurre con λ2* = 0 por la condición (11) y si los parámetros en la condición de primer orden (10) satisfacen
, dado que esta condición de primer orden no depende de f. Finalmente, si
entonces f* ε [0,F] lo que significa que f* queda indeterminado. Este comportamiento de la solución f* se debe a que la función objetivo es lineal en f.
Resumiendo, podemos caracterizar la función de reacción de la unidad militar para f de la siguiente manera:
Nótese que la función (12) es creciente en R dado que
lo que significa que la eficiencia militar de la unidad aumenta con los recursos R que se le proveen para cualquier nivel de eficiencia militar e2 que tenga el grupo al margen de la ley. Más aún, el nivel óptimo de eficiencia militar e1* es una función convexa en R. Para ver esto, nótese que
lo que significa que en un mecanismo como M = (R,q,S) en donde solamente se incremente R, las ganancias marginales en el número esperado de bajas en combate a través de una mayor eficiencia en combate de la unidad militar e1* aumentan.
3.3. Comportamiento del Gobierno
El comportamiento del Gobierno también involucra 2 partes: i) minimizar los costos de la implementación de la política, representados aquí por el gasto en mano de obra para la recaudación de los ingresos fiscales para un nivel dado de transferencia R y del gasto en mano de obra para auditar a la unidad militar a través de la detección de falsos positivos, para algún nivel dado de la probabilidad de auditoría q, y ii) encontrar un nivel de gasto óptimo R y una probabilidad óptima de q que le permita debilitar a los grupos armados al margen de la ley para aumentar al máximo el bienestar esperado de la sociedad de acuerdo con la función reducida de bienestar dada en (1). Po demos formalizar el primero de estos problemas de la siguiente forma:
para algún 0 ≤ q ≤ 1 y algún R ≥ 0. Este problema tiene en cuenta que para producir un nivel de auditoría q y recaudo R el Gobierno debe contratar funcionarios públicos de la fiscalía y la Direccion de Impuestos y Aduanas Nacionales. Nótese que para solucionar este problema de minimización, las restricciones se deben satisfacer como igualdades, es decir, y
dado que Lq y LR son recursos costosos. Por tanto, las demandas óptimas de trabajo están dadas por:
La función óptima de costos viene dada por:
Ahora bien, el Gobierno debe determinar el nivel óptimo de (R,q) del mecanismo M = (R,q,S) para implementar su política. En concreto, este segundo problema del principal viene dado por la maximización del bienestar esperado:
donde las funciones e1* y f * son las respuestas óptimas por parte de la unidad militar para cualquier nivel de (R,q) propuesto por el Gobierno correpondiente al mecanismo M = (R,q,S). Nótese que los tér-minos (1 - q) D(f *) + q[D(f *) + S] terminan siendo tan solo D(f *) + qS para cualquier nivel de f *.
En lo que sigue, resolvemos 2 casos: i) la PSD del Gobierno de Uribe donde el mecanismo es de la forma MPSD = (R,q,S), lo que significa que la solución del problema (17) utiliza únicamente el instrumento R y se toman como dados q y S, y ii) la PSRM de un Gobierno interesado en evitar falsos positivos a través de un mecanismo que tome en cuenta tanto R como q, es decir, MPSRM = (R,q,S).
Caso 1: Política de seguridad democrática
Consideremos el mecanismo MPSD = (R,q,S) y resolvamos (17) de la siguiente forma: obtenemos R* óptimo sin considerar el comportamiento de f * y luego si
se concluye que f * = F, de lo contrario f * = 0. Para esto reemplacemos e1*(R) en la función objetivo en (17), donde se debe notar que la función objetivo es cóncava estricta en R. Por tanto, las condiciones de primer orden con respecto a R son necesarias y suficientes:
Nótese que R* = 0 no puede ser solución a este problema ya que si lo fuera, entonces e1* = 0 y, por tanto, g = 0. Como por hipótesis tenemos que limg→0U'(g) = ∞, entonces la condición de primer orden en (18) no se satisface, lo cual es una contradicción. Por tanto, concluimos que R* > 0. Así, utilizando la ecuación (14) para reemplazarla en la ecuación (18) y especializando la función U(g) = u ln g con u > 0, la cual satisface los supuestos hechos arriba para U(g), obtenemos la igualdad siguiente:
la cual al utilizar la ecuación (12) y despejar R* obtenemos,
donde suponemos que σ satisface
tal que R* sea creciente en wL y e2h. El operador min aparece porque el valor R* no puede superar la cota superior Rmax. Si el valor de R* encontrado en (19) satisface
, entonces f* = F, de lo contrario f* = 0. Así, la PSD del Gobierno de Uribe es el mecanismo MPSD = (R*,q,S) para algún valor q ε (0,1].
Caso 2: Política de seguridad con responsabilidad militar
Consideremos el mecanismo MPSRM = (R,q,S) en el cual un Gobierno interesado en evitar falsos positivos utiliza R y q como instrumentos para su política de seguridad. La solución de este caso requiere considerar q* dentro del problema de optimización (17). Por un lado, nótese que e1* depende solo de R y no de q, aunque f* sí depende tanto de R como de q. Por otro lado, la aparición de falsos positivos f* > 0 depende crucialmente de la condición
, la cual establece una relación creciente entre R y q para que la unidad militar no opte por falsos positivos.
Así, la forma de solucionar el problema es imponer 2 condiciones adicionales a la condición (19) encontrada en el caso anterior. La primera es obtener el q* a través de condiciones de primer orden del problema (17), ignorando en principio y momentáneamente los términos relacionados con f*, mientras que la segunda es imponer la condición
que relaciona la escogencia óptima de R y q para la aparición o no de falsos positivos. Derivando la función objetivo en (17) con respecto a q se obtiene la siguiente condición de primer orden:
La solución debe involucrar q* > 0 porque de lo contrario la primera condición en (20) no se podría satisfacer dado que j ε (0,1) y S > 1 lo cual es una contradicción. Esto implica que
de la cual se despeja,
donde el operador del mínimo aparece ya que se debe satisfacer q* ε (0,1].
Ahora bien, al imponerse la condición
al problema, obtenemos un valor crítico Rˆ dado por,
y por tanto, el valor óptimo de R sería,
R** = min{R*,Rˆ} – ε
para un valor de « > 0 pequeño que genere f* (R**,q*). Esto implica que la solución de un Gobierno que desea implementar una PSRM es nMPSRM = (R**,q*,S).
Las soluciones MPSD = (R*,q,S) y MPSRM = (R**,q*,S) se pueden ilustrar en la figura 2 con los siguientes valores de los parámetros: wL = 2, wN = 4, x = 1,5, r = 2,5, θ = 1, D = -1 si f* = F, mientras que D = 0 si f* = 0, F = 1,6, σ = 0,5, ξ = 0,5, k = α = γ = β = 1, e1 = 20, e2h = 5, φ = 0,9, S = 2, Lq = 1.
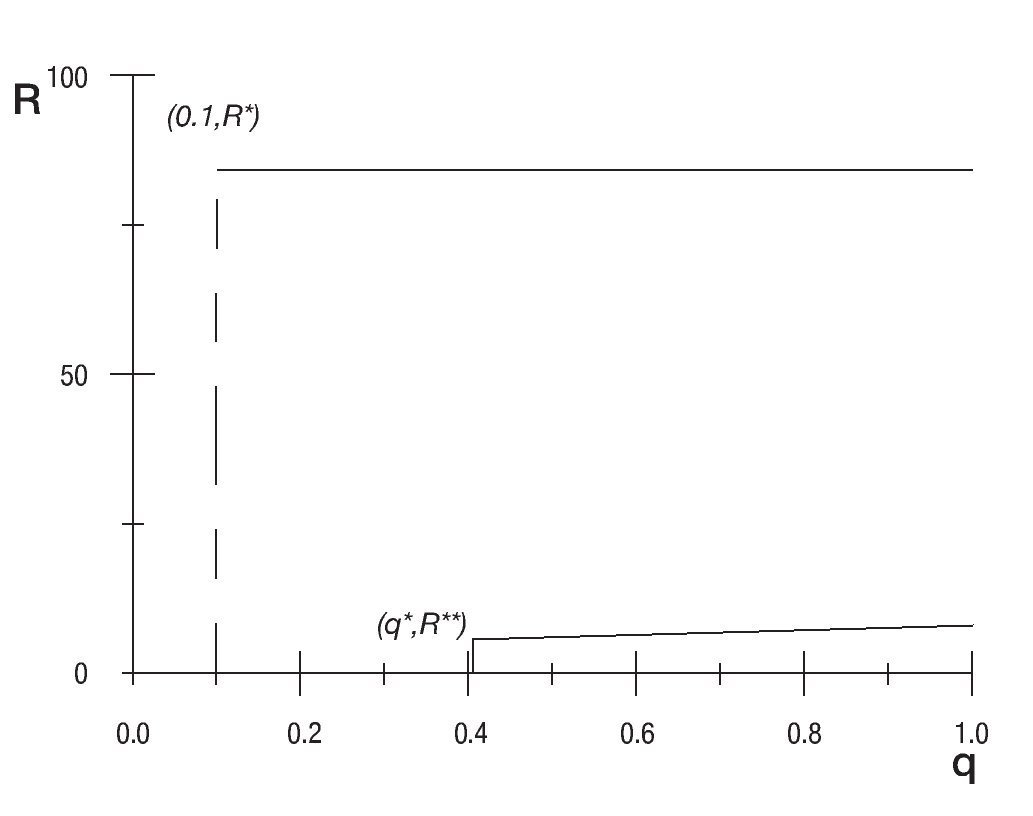
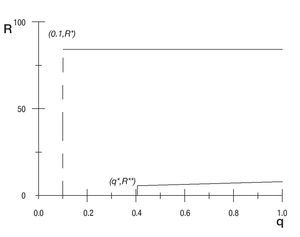
Figura 2. Resultado óptimo de las políticas: política de seguridad democrática y política de seguridad con responsabilidad militar.
Algunos de estos valores se justifican de la siguiente forma. Dados los supuestos del modelo, el valor de wN es superior en 100% al valor de wL, lo cual es razonable dado que para realizar ejecuciones extrajudiciales seguramente se requieren mayores incentivos que los que se proveen usualmente para combatir a la guerrilla. El número de bajas del grupo al margen de la ley x = 1,5 corresponde al promedio nacional anual entre 2003 y 2008 de guerrilleros dados de baja por combate que se obtuvo de las cifras reportadas por el Centro de Estudios para el Análisis del Conflicto. La tasa de interés r = 2,5 del capital corresponde al promedio anual de la tasa de interés real para el período 2003-2008 calculado con base en las cifras reportadas del Departamento Nacional de Planeación. El valor de u es el de las preferencias de la sociedad con respecto al número esperado de bajas del grupo al margen de la ley relativo al peso dado a falsos positivos. Suponemos justificado por nuestra ignorancia que θ = 1, que significa que la valoración de un muerto dado de baja justamente al grupo al margen de la ley es valorado con signo contrario pero con igual magnitud por la sociedad que un muerto de un civil como falso positivo, lo cual viene dado por D = -1 si f* = F y D = 0 si f* = 0. El supuesto F = 1,6 está basado en el promedio anual de falsos positivos por caso de ejecuciones extrajudiciales reportados en la tabla 1 entre el 2003 y 2008. Los demás parámetros del modelo garantizan las condiciones asumidas sobre las respectivas funciones y no tienen un soporte empírico, pero se jusifican tan solo por requerimientos técnicos propios de la estructura teórica del modelo.
Bajo los valores de los parámetros obtenemos,
donde por simplicidad se supuso q = 0,1 en la PSD del Gobierno de Uribe. La figura 2 muestra el resultado óptimo de las 2 políticas. Para la PSD, el nivel de R es R* = 83,75 y corresponde a la línea continua en la figura 2 que intersecta con la línea punteada vertical de q = 0,1. Mientras que en la PSRM el nivel de R es R** = 5,64 con el valor óptimo correspondiente q* = 0,41. Nótese que en la PSRM el valor de R** es < R* debido a que se determina endógenamente el nivel de auditoría a las unidades militares. La línea recta con pendiente positiva es la curva de incentivos
definida en q ε [q*,1] que corresponde al conjunto factible de probabilidades de auditoría de las cuales se puede escoger en la PSRM. Debemos notar que bajo esta especificación paramétrica el bienestar social bajo la política MPSD es estrictamente menor (B* = -166,78) que el bienestar social bajo la política MPSRM (B* = -12,477) ilustrando la ganancia en bienestar de una PSRM.
4. Conclusiones
El presente artículo utiliza un modelo principal-agente para modelar la PSD del Gobierno de Álvaro Uribe como un mecanismo entre el Gobierno nacional (principal) y las unidades militares (agente) en el cual solo se tiene en cuenta una parte de los incentivos a los militares (es decir, la zanahoria) con el objetivo de debilitar a los grupos armados al margen de la ley a través del combate militar. La política omite la otra parte necesaria de los incentivos a los militares (es decir, el garrote) dado que existe un problema de información en la relación, ya que que el Gobierno no observa directamente si las bajas presentadas por las unidades militares provienen de combates con grupos al margen de la ley o no. Esta omisión en la PSD del Gobierno de Uribe genera resultados no deseados por la sociedad civil en su conjunto, a saber: un número alto de ejecuciones extrajudiciales, los llamados falsos positivos. El problema fundamental de la PSD es la falta de control de las acciones de las unidades militares, las cuales son no observables directamente por el Gobierno.
Adicionalmente, se modela una propuesta de política de seguridad alterna, denominada PSRM, que reduce el problema de las ejecuciones extrajudiales al tener en cuenta los 2 tipos necesarios de incentivos del Gobierno para las unidades militares dados los problemas de información existentes en su interacción (es decir, la zanahoria y el garrote). Este mecanismo alterno determina óptimamente un nivel de auditoría que, aunque costoso para el Gobierno, aumenta el bienestar social a través de una mayor probabilidad en la detección de ejecuciones extrajudiciales por parte de las fuerzas militares. En términos del diseño de mecanismos, esta política de seguridad alterna tiene en cuenta la posibilidad de que el agente-unidad militar puede tener incentivos para desviarse de la acción deseada por el principal.
La conclusión de la política de seguridad contrafáctica con responsabilidad militar se discute bajo el supuesto, debatible, de que el enfrentamiento militar es una política conveniente para la sociedad civil para atenuar el conflicto armado en Colombia.
Agradecimientos
Los autores agradecen la colaboración de Federico Corredor como asistente de investigación del Centro de Investigación en Economía Política de la Universidad Externado de Colombia. Evidentemente, los errores son únicamente nuestros.
1. El término "falsos positivos" hace referencia en lenguaje castrence al hecho de presentar como muertos en actividades propias de una acción militar a quienes en realidad no lo son. En sentido más amplio, el término más apropiado quizá sea el de víctimas de ejecuciones extrajudiciales. Sin embargo, y en atención al mayor uso cotidiano del primer término, nos referiremos en el artículo a las víctimas de ejecuciones extrajudiciales como falsos positivos.
2. Es de notar que la tasa promedia de militares dados de baja (× 100.000 habitantes) en combate terminó cayendo de 1,1 a 0,9, lo que podría reflejar una mayor tecnología de combate por parte de las Fuerzas Armadas.
3. "Política de Defensa y Seguridad Democrática", Ministerio de Defensa (2003).
4. idem.
5. Federación Internacional de Derechos Humanos 2012. "Colombia. la guerra se mide en litros de sangre".
6. ibíd p. 9.
7. ibíd p. 10.
8. ibíd p. 10
9. Según el CINEP, los falsos positivos se definen como un mecanismo ficticio para obviar la ilegalidad del acto, recurriendo a la única circunstancia en la que el asesinato puede evadir ser un acto punible: cuando se mata en combate.
10. Las funciones de bienestar social han sido criticadas extensamente por diferentes motivos, especialmente por implicar comparaciones interpersonales de utilidad. Somos conscientes de estas limitaciones del concepto, sin embargo, utilizamos una función de bienestar social que capture que a la sociedad le disgustan los falsos positivos y que aplaude hasta cierto punto los muertos en combate de los integrantes del grupo al margen de la ley.
11. Asumir una tecnología diferente, por ejemplo, una que permita algún grado de sustitución entre soldados y tecnología militar afectaría el nivel óptimo de esfuerzo por parte de la unidad militar, presumiblemente a la baja, pero no alteraría los resultados sustanciales del modelo en términos de falsos positivos porque la diferencia sustancial, manteniendo la misma tecnología en las 2 politicas que se van a modelar, es la determinación endógena de la probabilidad para detectar falsos positivos en la segunda de ellas a diferencia de la primera, en donde se asume como dada.
INFORMACIÓN DEL ARTÍCULO
Historia del artículo:
Recibido el 20 de noviembre de 2012
Aceptado el 20 de febrero de 2013
* Autor para correspondencia.
Correo electrónico: ernesto.cardenas@uexternado.edu.co (E. Cárdenas).
Bibliografía
CINEP (2011). Colombia, deuda con la humanidad 2: 23 años de falsos positivos, Bogotá: Editorial Códice ltda.
Elespectador.com.co (2011). Del Estatuto de Seguridad a la Seguridad Democrática. Bogotá, elespectador.com.co [en línea], [consultado 15 Jul 2012], Disponible en: http://m.elespectador.com/impreso/judicial/articuloimpreso-del-estatuto-deseguridad-seguridad-democratica
Eltiempo.com.co (2011). Radiografía de los Falsos Positivos, Bogotá, eltiempo.com. co [en línea], [consultado 25 Jul 2012] Disponible en: http://www.eltiempo.com/ Multimedia/infografia/falsos_positivos/
Federación Internacional de Derechos Humanos (2012).Colombia. La guerra se mide en litros de sangre.
Laffont, J. J. y Martimort, D. (2002). The Theory of Incentives: The Principal Agent Model, Princenton University Press.
Mitchell, N. y Carey, S. (2012). Delegating repression: the effect of pro-government militias on human rights violations. Documento de Trabajo. Julio de 2012. Presidencia de la República. Ministerio de Defensa. (2003). Política de Defensa y
Seguridad Democrática, [consultado 15 Jul 2012]. Disponible en: http://www. oas.org/csh/spanish/documentos/Colombia.pdf
Rivera, M. (2012). Violence Breeds Violence: How Violent Crime Affects Repression in Democratic Regimes. Trabajo de tesis doctoral, Departamento de Gobierno. Universidad de Essex.