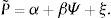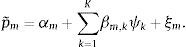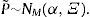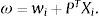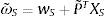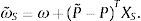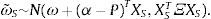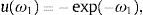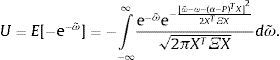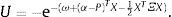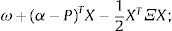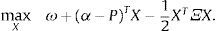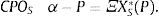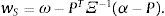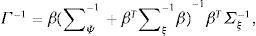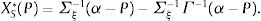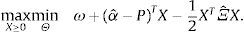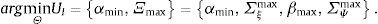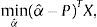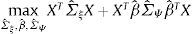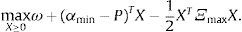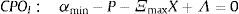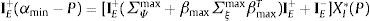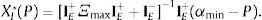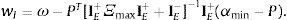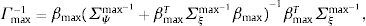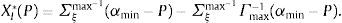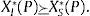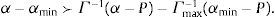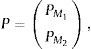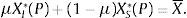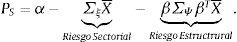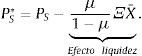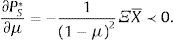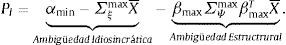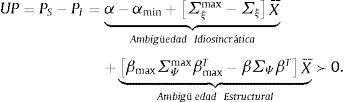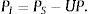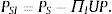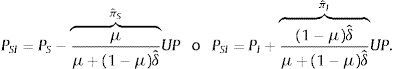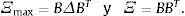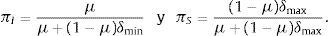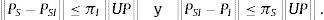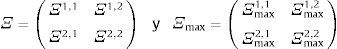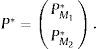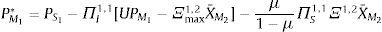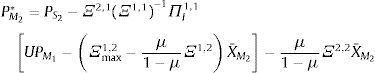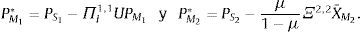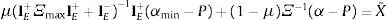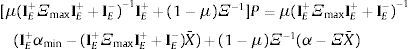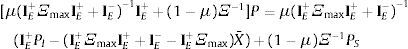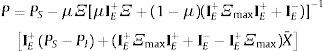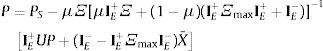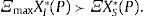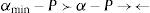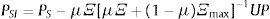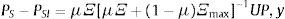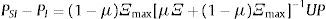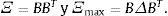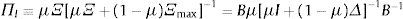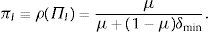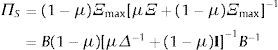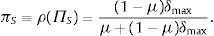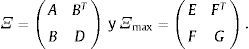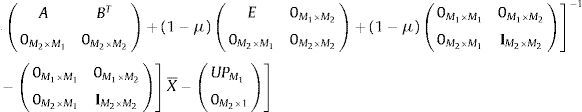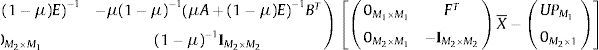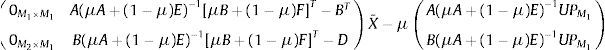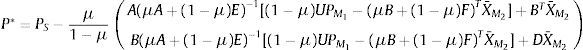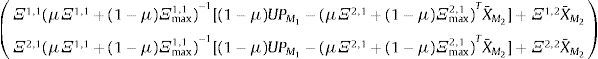Precios de los activos bajo ambigüedad estructural: portafolios cautelosos, prudenciales y conservadores

Resumen

Este artículo analiza los efectos extensivo (portafolio conservador) e intensivo (portafolios cauteloso y prudencial) generados por 2 tipos de ambigüedad: idiosincrática y estructural. Bajo estas formas de ambigüedad los agentes no participan en algunos mercados de activos, lo cual reduce los precios de los activos por la liquidez que deja de inyectarse en estos mercados. De otro lado, al incorporar ambigüedad estructural existe una prima de ambigüedad descontada sobre los precios y, en equilibrio, un canal de trasmisión de estos efectos sobre los precios a través de los diferentes mercados. Al introducir ambigüedad estructural, considerada como ambigüedad sobre la sensibilidad de los precios a las macroinnovaciones que se agregan desde un nivel micro, es posible identificar los vínculos entre los diferentes segmentos del mercado de activos riesgosos. Con estas características, este artículo argumenta que los precios reaccionan suavemente a macroinnovaciones si el peso relativo de los agentes aversos a la ambigüedad es bajo y el vínculo objetivo entre los mercados es débil.

Abstract

This paper studies the extensive (conservative portfolio) and intensive (cautious and prudential portfolios) effects emerging from two kinds of ambiguity: idiosyncratic and structural. Both kinds of uncertainty induce investors not to participate in some asset markets, which reduces prices through liquidity reduction in those markets. On the other hand, structural uncertainty implies an ambiguity premium discounted from prices and, in equilibrium, a channel of transmission of both effects across assets. The novelty of this paper is that structural uncertainty results from ambiguity on asset sensitivities to macro news aggregated from a micro level, which allows us to identify the macroeconomic linkages among market segments. Using this feature of the model, this paper concludes that current prices react slowly to macro news if the relative weight of ambiguity-averse agents is lower and the objective linkages among assets are weak.

«We perceive the world before we react to it, and we react not to what we perceive, but always to what we infer».

(Knight, 1921, p. 201)

En el análisis convencional, la elección del portafolio óptimo requiere el conocimiento de los riesgos implícitos en cada activo que puede componerlo; sin embargo, en ciertos contextos, la existencia de información idiosincrática y de interconexiones entre los mercados oscurece el proceso de evaluación de las pérdidas o ganancias y del grado de exposición a las distintas formas de riesgo. Este tipo de escenarios se configuran por transformaciones en las relaciones que determinan el entorno de decisión (Caballero y Krishnamurthy, 2008) e implican que no todas las formas de riesgo pueden ser caracterizadas a través de una única distribución de probabilidad, fenómeno denominado ambigüedad.

Este artículo contribuye a esta discusión, desarrollando un modelo estático con ambigüedad en 2 niveles: idiosincrática (microeconómico) y estructural (macroeconómico). La ambigüedad idiosincrática deviene del conocimiento impreciso del valor fundamental y de los riesgos que enfrenta un activo individualmente considerado. La ambigüedad estructural tiene como fuente la percepción del entorno macroeconómico, es decir, deviene del conocimiento impreciso del grado de interconexión entre los diferentes segmentos del mercado de activos. Este tratamiento resulta novedoso porque permite evaluar los efectos de la ambigüedad entre los diferentes segmentos del mercado de activos riesgosos a luz de la interconexión entre estos segmentos. Al introducir estas características, este artículo argumenta que los precios reaccionan suavemente a macroinnovaciones si el peso relativo de los agentes aversos a la ambigüedad es bajo y el grado de interconexión objetivo entre los mercados es débil. Eventualmente, el peso relativo de los agentes aversos a la ambigüedad aumenta incrementando los problemas de liquidez y las distorsiones en los precios.

En el modelo, mientras que una proporción de los agentes, denominados sofisticados, observa una única distribución de los precios futuros, la proporción restante, denominados ingenuos, enfrenta un escenario de planeación ambiguo, es decir, observa un conjunto de distribuciones de los precios futuros. Como sugiere Ellsberg (1961), al enfrentar escenarios ambiguos los agentes prefieren loterías con probabilidades conocidas frente a loterías con resultados desconocidos, es decir, los agentes ingenuos son aversos a la ambigüedad. Gilboa y Schmeidler (1989) muestran que este fenómeno puede modelarse usando una regla maxi-mínimo, es decir, permitiendo que los agentes ingenuos usen una heurística para seleccionar los parámetros que caracterizan el escenario de planeación sobre el cual eligen un portafolio óptimo.

Una aclaración necesaria en este punto es la diferencia entre aversión a la ambigüedad y aversión al riesgo infinita. Para ilustrar dicha diferencia supongamos de existen 2 estados de naturaleza «bueno» y «malo». Un agente con aversión infinita al riesgo elige considerando únicamente el escenario «malo», aunque este ocurre con una probabilidad conocida q, y el «bueno», con probabilidad 1-q (Gennaioli, Slheifer y Vishny, 2012). Por el contario, un agente averso a la ambigüedad observa múltiples probabilidades asociadas a cada estado de naturaleza, y elige asociando la probabilidad más alta al estado «malo» q_max y 1 – q_max al «bueno» (Barberis y Thaler, 2003; Guidolin y Rinaldi, 2010).

La aversión a la ambigüedad implica que los agentes ingenuos participan en los mercados de activos si el rendimiento esperado compensa la interacción de las distintas formas de ambigüedad. De esta manera, la composición de sus portafolios difiere del portafolio de los agentes sofisticados, porque la ambigüedad reduce las posiciones en los activos riesgosos (efecto intensivo) e inhibe la participación en los mercados de estos activos (efecto extensivo). En el contexto de este artículo, estos efectos permiten caracterizar 3 tipos de comportamiento en los agentes ingenuos: cauteloso, prudencial (efecto intensivo) y conservador (efecto extensivo).

Los trabajos de Easley y O’Hara (2009, 2010) y Pritsker (2012, 2013) contienen los ingredientes del modelo planteado. Easley y O’Hara (2009, 2010) examinan el papel de la ambigüedad idiosincrática como inhibidora de la participación de los agentes en el mercado, en consecuencia, la mayor ambigüedad en un mercado induce a que la riqueza que se deja de invertir en ese mercado sea conservada en efectivo. El presente artículo extiende los trabajos de Easley y O’Hara (2009, 2010), porque enfatiza la relevancia de las macroinnovaciones como fuente de la ambigüedad estructural y su papel en la elección del portafolio y su efecto sobre los precios de los activos Para tal fin incorpora la agregación de los macrorriesgos desde el nivel microeconómico propuesta por Pritsker (2012, 2013). Agregación que considera la relevancia de una noticia macroeconómica para el precio futuro de cada activo y que posibilita la evaluación de los efectos sobre los precios en atención a la interconexión entre los diferentes segmentos del mercado.

En equilibrio, el efecto de la ambigüedad depende del peso relativo de cada tipo de agente, así como de sus percepciones respecto a la varianza y a la media de los precios futuros. Cuando el grado de ambigüedad es bajo, los agentes ingenuos participan inyectando liquidez a los mercados y menguando el efecto de sus percepciones sesgadas al interactuar con los agentes sofisticados. En consecuencia, los precios presentes reflejan una ponderación de las creencias sobre los parámetros; este resultado muestra el papel de los mercados para ponderar cierta información sesgada.

Cuando la ambigüedad se extiende en un segmento del mercado inhibe la participación y reduce la liquidez en ese segmento, los agentes ingenuos retornan a los activos familiares, contexto en el cual las distorsiones en los precios dependen de la existencia de agentes aversos a la ambigüedad, mientras que el canal de transmisión de estos efectos depende del grado de interconexión «objetivo» entre los mercados.

El texto se organiza de la siguiente manera. La sección 1 sintetiza la literatura relacionada. La sección 2 presenta las características de la distribución de los precios y de la riqueza. La sección 3 obtiene los portafolios óptimos de los agentes sofisticados e ingenuos, para el portafolio de estos últimos da cuenta de la existencia 3 tipos de comportamientos: cauteloso, prudencial y conservador. La sección 4 caracteriza el equilibrio en términos de los efectos de dichos comportamientos sobre los precios de los activos riesgosos. La sección 5 discute los resultados a la luz de la literatura. La sección vi concluye.

1

Revisión a la literatura

La literatura relacionada proviene de 2 fuentes: empírica y teórica. Vinculada con la relevancia de la información macroeconómica, la literatura empírica apunta en direcciones contrarias. De un lado, el comportamiento de los precios con respecto a las macroinnovaciones no es exclusivo de grandes, e infrecuentes, anuncios de los hacedores de política. Webb (1994), Webb y Smith (1994), Engle, Ito y Lin (1990), y Fleming y Lopez (1999) proveen evidencia de que este fenómeno es la respuesta usual de los precios a los anuncios de carácter macroeconómico y revela que los «participantes en el mercado esperan ansiosamente estos anuncios, en búsqueda de una señal que indique la dirección del mercado» (Webb, 1994, p. 2). En general, estos autores proveen evidencia de clústeres de volatilidad en los precios de los activos, los días en que ciertos anuncios de política se presentan y argumentan que la labor de identificar la información realmente nueva en estos es complicada, entre otras razones, porque al formar sus proyecciones mucha de esta información en sopesada por el consenso y la percepción de los agentes con respecto a las relaciones macroeconómicas (Webb, 1994, p. 6).

De otro lado, Klibanoff, Lamont y Wizman (1998), y Cutler, Poterba y Summers (1989) señalan que en el mercado de valores las noticias generadas por cambios en el valor fundamental y las noticias cualitativas no parecen explicar grandes movimientos en los precios de los activos. Sin embargo, los primeros encuentran evidencia en favor de la hipótesis de que inversionistas individuales asignan más importancia a las noticias más prominentes y menos a aquellas menos prominentes, incluso si las 2 piezas de información implican el mismo efecto sobre el valor fundamental¹. En una semana típica, los precios subreaccionan a cambios en los fundamentales; en semanas con noticias que aparecen en la portada de The New York Times los precios exhiben una reacción mayor.

Esta literatura empírica está vinculada con el argumento teórico de la hipótesis de los mercados eficientes, en el cual los precios corrientes deberían ser un estadístico suficiente para estimar los parámetros involucrados en la elección del portafolio, en ausencia de: 1) costos de transacción; 2) costos de producción y diseminación de la información, y 3) desacuerdos entre los inversionistas respecto de la distribución de los precios futuros (Bray, 1981; Grossman, 1989; Webb, 1994).

Con respecto a esta literatura empírica y teórica, este artículo argumenta que la información contenida en los precios corrientes refleja el desacuerdo con respecto a los parámetros que delimitan el escenario probabilístico de elección. Dicho desacuerdo es inducido por la aversión a la ambigüedad de una masa de los agentes en el mercado. En otras palabras, el presente artículo se centra en la presencia de sesgos en la información transmitida, los efectos de equilibrio general inducen la trasmisión de información y diluyen estos sesgos solo de manera parcial. En esta perspectiva, los resultados aquí presentados pueden considerarse como un equilibrio informacional interim, donde la incorporación de información acerca de las creencias de los agentes es sopesada en el mercado.

Por otro lado, se encuentra la amplia literatura sobre aversión a la ambigüedad, de la cual una síntesis detallada se encuentra en Guidolin y Rinaldi (2010). Aquí se consideran los trabajos de Easley y O’Hara (2009, 2010) y Pritsker (2012, 2013) porque contienen los ingredientes esenciales del modelo planteado. Easley y O’Hara (2009, 2010) examinan el papel de la ambigüedad idiosincrática como inhibidora de la participación de los agentes en el mercado, estos autores excluyen la posibilidad de correlaciones entre los precios futuros de los activos, por esta razón, la mayor ambigüedad en un mercado, induce a que la riqueza que se deja de invertir en ese mercado sea conservada en efectivo.

El presente artículo extiende el trabajo de Easley y O’Hara (2009) porque las interconexiones entre los mercados implican que al no participar o reducir sus posiciones en los activos riesgosos, los agentes ingenuos eliminan ciertos riesgos de su portafolio e inducen un efecto de transmisión de las restricciones de liquidez a lo largo de los mercados de activos. Adicionalmente, se incorpora el papel de las restricciones en las posiciones cortas, las cuales generan un costo de participación que activa el escenario probabilístico donde las innovaciones macroeconómicas son de mayor relevancia. En esta línea, Paiella (2007) analiza la importancia empírica de estas restricciones en el contexto de la participación y sus implicaciones sobre los precios.

Pritsker (2012, 2013) plantea la existencia de ambigüedad estructural en los mercados de crédito interbancario, en particular, la ambigüedad emana del conocimiento incompleto, por parte de los prestamistas, de las exposiciones de los prestatarios a las diferentes formas de riesgo. En su modelo, los macrorriesgos son correctamente identificados; sin embargo, los prestamistas no saben a ciencia cierta si los prestatarios eligen el portafolio óptimo sobre la frontera de media varianza o un portafolio situado sobre una recta que pasa por este. Usando la noción de ambigüedad estructural y la agregación de los macrorriesgos desde el nivel microeconómico propuesta por Pritsker (2012, 2013), este artículo enfatiza la relevancia de las macroinnovaciones como fuente de la ambigüedad estructural, para determinar el papel que desempeña en la elección del portafolio óptimo y su efecto sobre los precios de diferentes tipos de activos.

La huida a la calidad es un caso extremo del portafolio conservador, en el cual un mayor grado de ambigüedad se disemina a través de los mercados e implica que los precios de los activos se ven afectados por la menor liquidez inyectada al sistema. En un artículo relacionado, Caballero y Krishnamurthy (2008) muestran que la ambigüedad, respecto a la probabilidad de recibir una oleada de choques, tiene efectos expansivos asociados a episodios de fligth to quality y a las restricciones de liquidez que se diseminan a lo largo de los mercados. Este resultado es similar al planteado por Gennaioli et al. (2012), quienes argumentan que la omisión de riesgos incentiva la innovación financiera, la cual incrementa la fragilidad del sistema; una vez los riesgos omitidos son, súbitamente, incluidos se presentan episodios de fligth to quality, induciendo, así, al colapso de los mercados financieros. Con respecto a estos artículos, la novedad del presente reside en el tratamiento de las macroinnovaciones, su papel en las tenencias de activos y la trasmisión de los sesgos a lo largo del mercado.

2

El modelo

Siguiendo a Easley y O’Hara (2009), este artículo adapta el modelo «CARA-normal» de elección de portafolio propuesto por Lintner (1969) e implementado en el clásico The informational role of prices de Grossman (1989). Este modelo consiste de 2 periodos. En el primer periodo t = 0, se seleccionan los portafolios óptimos y se realizan operaciones de compra y venta de activos, y en el segundo t = 1, se realizan los pagos.

Existen M activos riesgosos, en t = 0 todos los agentes observan el vector M × 1 de precios presentes P y saben que el vector de precios futuros P˜ se distribuye normalmente, pero algunos agentes no observan una única distribución de P˜. Adicionalmente, existe un activo libre de riesgo (efectivo), cuya oferta neta es cero con precio constante e igual a la unidad.

En t = 1 los precios de los M activos riesgosos están dados por el vector aleatorio:

Donde ξ ∼ N_M(0, Σ_ξ) es el vector M × 1 de choques idiosincráticos, independientes entre sectores² y Ψ ∼ N_K(0, Σ_Ψ) es el vector K × 1 de innovaciones (noticias) macroeconómicas, independientes entre ellas³. En general, estas noticias pueden ser positivas o negativas, así, β es una matriz M × K sensibilidades de los precios a la información macroeconómica, tal que β_m,k ≥ 0, ∀m = 1, ....., M y ∀k = 1, ....., K. Para evaluar las implicaciones de estos supuestos, considere el precio del m-ésimo activo:

El precio futuro de cada activo depende de las desviaciones con respecto a su valor fundamental α_m, inducidas por los riesgos idiosincráticos y macroeconómicos. El supuesto de normalidad de los choques idiosincráticos y estructurales implica que con probabilidad distinta de cero existen realizaciones negativas de los precios futuros, en otras palabras, este supuesto significa que no existe responsabilidad limitada. Sin embargo, como muestra Lintner (1969) el supuesto de normalidad permite obtener soluciones cerradas tales que los portafolios óptimos y los precios presentes de equilibrio son funciones de la media y varianza de los precios futuros. Por estas razones, la existencia de precios futuros negativos no afecta los resultados y se obtienen soluciones cerradas sin necesidad de recurrir al teorema de separación de Tobin⁴.

Esta parametrización de los macrorriesgos, agregados desde el nivel micro (Pritsker, 2013), permite evaluar las interconexiones entre los sectores e introduce una tecnología de incorporación de innovaciones macroeconómicas basada en su relevancia: para todos los agentes una realización ψ¯k<0 es una mala noticia, la cual tendrá un efecto negativo sobre p_m, si β_m,k > 0, o nulo, si β_m,k = 0. En este sentido, β_m,k evalúa si una noticia macroeconómica es irrelevante, β_m,k = 0, para el m-ésimo activo, o relevante, β_m,k > 0, de tal forma que entre mayor es este parámetro, mayor la relevancia de la noticia. Bajo este supuesto, la fuente de ambigüedad será la relevancia de una macro-innovación, y no la dirección del efecto sobre los precios⁵.

Bajo estas condiciones, el vector de precios futuros se distribuye normalmente:

Donde Ξ = βΣ_Ψβ^T + Σ_ξ, es una matriz M × M simétrica, no negativa y definida positiva. Una manera intuitiva de visualizar esta matriz es considerar el mercado de activos compuesto de 2 segmentos M = M₁ + M₂, así, Ξ puede escribirse como una matriz en bloques:

La matriz Ξ2,1=(Ξ1,2)T captura la correlación entre los segmentos M₁ y M₂, la cual depende del efecto cruzado de las macroinnovaciones en cada segmento. Si las macroinnovaciones son irrelevantes para el segmento M_i, no existe interconexión entre los segmentos, Ξ^2,1 = 0. De manera análoga, si las macroinnovaciones son relevantes para los 2 segmentos del mercado, estos estarán interconectados, Ξ^2,1 ≻ 0. En adelante, las matrices A y B, M × N, satisfacen A ≻ B si a_mn > b_mn, ∀m = 1,…, M y ∀n = 1,…, N. Si N = 1 se trata de vectores columna.

En los mercados para los M + 1 activos existen 2 tipos de inversionistas una fracción 1-μ de sofisticados (S) y μ de ingenuos (I). Mientras que los primeros conocen los parámetros de la única distribución de los precios de los activos riesgosos, los segundos observan un conjunto de estos parámetros asociados a un conjunto de distribuciones. Formalmente, el conjunto de parámetros observado por los agentes sofisticados es Θ_S = {α,Ξ}. Mientras que el conjunto de parámetros de los agentes ingenuos Θ_I es tal que: α_min, α_max, Ξ_min, Ξ_max ∈ Θ_I, con α_min ≺ α ≺ α_max y Ξ_min ≺ Ξ ≺ Ξ_max.

En t = 0, los agentes satisfacen la restricción de presupuesto dada su riqueza inicial ωy los precios de mercado P:

Para los agentes i = S, I la riqueza inicial es la misma y en t = 0 deben distribuirla entre los M activos riesgosos X_i y el activo libre de riesgo w_i.

En t = 1 la riqueza futura de los agentes sofisticados es la variable aleatoria:

Como estos agentes deben satisfacer su restricción de presupuesto, se tiene:

Para los agentes sofisticados los precios futuros siguen una distribución normal multivariada con media α y matriz de varianzas y covarianzas Ξ, así, para un portafolio X_S, su riqueza futura se distribuye normalmente:

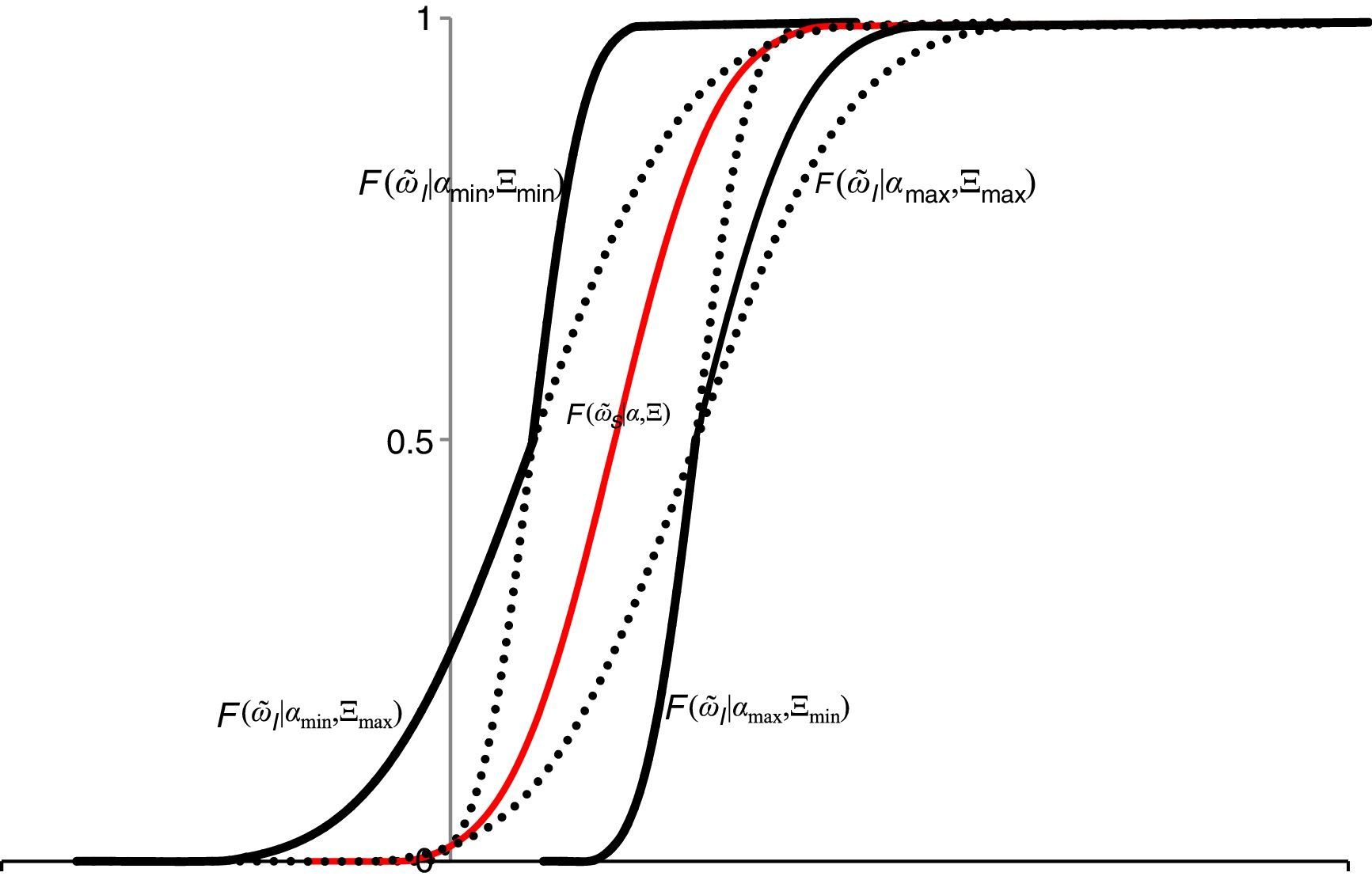
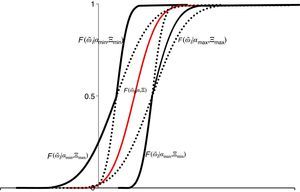
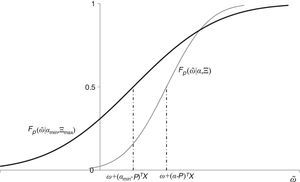
Aunque los agentes ingenuos saben que las innovaciones macroeconómicas e idiosincráticas tienen media cero y que los precios se distribuyen normalmente, no observan de manera precisa los parámetros de la distribución de los precios, es decir, operan en un escenario ambiguo. Bajo las condiciones impuestas sobre Θ_I, la figura 1 muestra el espacio de las diferentes funciones de distribución acumulada de la riqueza aleatoria ω˜I observadas por los agentes ingenuos para el portafolio X_I.

Figura 1.

Distribuciones de probabilidad acumulada para ω˜I.

En el proceso de toma de decisiones un agente sofisticado enfrenta riesgo estructural e idiosincrático, los resultados de sus decisiones son al azar, pero conoce los parámetros de la única distribución de probabilidad. Estos parámetros están asociados a los elementos específicos de un activo y la sensibilidad de su precio futuro a las innovaciones macroeconómicas y la volatilidad de estas innovaciones.

Un agente ingenuo enfrenta ambigüedad idiosincrática, porque observa múltiples distribuciones para el vector de precios futuros, fenómeno que desde la perspectiva de los agentes ingenuos dificulta el proceso de evaluación de los riesgos. Como muestra la figura 1, los agentes ingenuos poseen una gran cantidad de información que deben seleccionar a fin de determinar su escenario para la elección de un portafolio. Bajo el supuesto de normalidad esta información se refleja en múltiples distribuciones acumuladas, en las cuales el riesgo es capturado por las diferentes percepciones de la volatilidad de la riqueza asociada a innovaciones idiosincráticas y estructurales. De esta manera, este supuesto permite capturar el complejo de interrelaciones estructurales en un contexto simple.

3

Ambigüedad y elección del portafolio

Suponemos que todos los agentes exhiben una función de utilidad Bernoulli con coeficiente de aversión absoluta al riesgo igual a 1:

este supuesto y ω = ω_I = ω_S permiten que las diferencias en la elección del portafolio resulten de la las diferentes opiniones en cuanto a la información, y no de la postura de los agentes frente al riesgo o de diferencias en el nivel de riqueza.

Bajo este supuesto la función de utilidad esperada es:

La cual es la función generadora de momentos de una variable distribuida normalmente con media ω + (α − P)^TX y varianza X^TΞX, entonces:

Así, la utilidad esperada puede escribirse como una transformación estrictamente creciente (-ln[-U]) de la expresión:

y el problema de elección de portafolio para los agentes sofisticados es equivalente a:

La condición de primer orden de los agentes sofisticados es:

De donde el portafolio óptimo de los agentes sofisticados es el rendimiento esperado ajustado por riesgo⁶:

Este portafolio debe satisfacer la restricción de presupuesto (3) para el nivel de riqueza ω; así, las tenencias del activo libre de riesgo wS satisfacen:

Dado que Ξ es una matriz no negativa y definida positiva, α ≻ P es la condición necesaria, más no suficiente, para que los agentes sofisticados asuman posiciones largas en todos los activos, XS*(P)≻0. Viceversa, α ≺ P es la condición necesaria, más no suficiente, para que los agentes sofisticados tomen un posición corta en todos los activos, XS*(P)≺0.

Recordando que Ξ = β∑_Ψβ^T + ∑_ξ, para simplificar la notación:

y usando la identidad de Woodbury (Brandt y Syskind Perdersen, 2012) el portafolio óptimo de los agentes sofisticados puede escribirse:

Con ello, si α ≻ P y α − P ≻ Γ⁻¹(α − P), los agentes sofisticados toman posiciones largas en todos los activos, XS*(P)≻0. Intuitivamente, esta condición dice que el exceso de retorno esperado debe compensar la interacción entre las distintas formas de riesgo capturada por Γ⁻¹.

Los agentes ingenuos eligen si participar o no en cada mercado, sujetos a restricciones para tomar posiciones cortas. En la medida en que tomar una posición corta implica la capacidad de tomar prestado y un proceso de negociación con los operadores financieros (D’Avolio, 2002), estas restricciones se asocian a la existencia de costos de participar y los agentes ingenuos se identifican con aquellos que tienen un rezago de experiencia o de capital humano para realizar dicha transacción (Easley y O’Hara, 2009; Paiella, 2007)⁷.

Bajo estas condiciones, los agentes ingenuos determinan simultáneamente el escenario de planeación y el portafolio óptimo:

En este contexto, el problema práctico de inferencia que resuelven los agentes ingenuos, en una situación particular, tiene que ver con cuáles son las características relevantes y cuáles las circunstancias bajo las que realizan su elección (Knight, 1921). Gilboa y Schmeidler (1989) proporcionan la base axiomática para este problema de determinación del escenario probabilístico de planeación, donde los agentes ingenuos, quienes consideran múltiples distribuciones (fig. 1) sobre el estado de las variables económicas, son aversos a la ambigüedad y toman decisiones óptimas basadas en la creencia de que el peor de los casos impera (Ghirardato et al., 2004; Klibanoff et al., 2005). Dado que X ≥ 0 y que Ξˆ es positiva y definida positiva, la solución al problema de minimización que define el escenario de planeación es:

Para interpretar esta solución es conveniente evaluar cada uno de los términos de la minimización. El primer componente de este problema es el retorno medio del portafolio X:

α_m,min es la solución a este problema, si los agentes ingenuos toman una posición larga en el m-ésimo activo, y α_m,max si toman una posición corta. Cuando existen restricciones a las posiciones cortas el vector de valores fundamentales α_min, caracteriza el escenario de elección.

El segundo componente del problema está asociado a la varianza de la riqueza, la cual depende de la relevancia de las macroinnovaciones, y de la varianza al nivel estructural e idiosincrático, problema que es equivalente a:

Al evaluar este programa en el conjunto de parámetros los agentes ingenuos asignan máxima volatilidad al choque idiosincrático sobre el activo m, es decir, σ_m,max, para m = 1, ....., M, es la varianza asociada al choque específico, independientemente de si la posición es larga o corta en cada activo. Esto ocurre porque la elección de este parámetro no está atada a la posición en los otros activos, por tanto, Σξmax es la matriz de varianzas que caracteriza el escenario de planeación con respecto a los choques idiosincráticos.

Caracterizar el escenario de planeación en términos de la ambigüedad estructural resulta más complejo, porque existen interconexiones entre los mercados que implican que mayor volatilidad o relevancia de las macroinnovaciones no necesariamente es perjudicial. En este caso, si los agentes ingenuos asumen la misma posición, corta o larga, en todos los activos, entonces el escenario probabilístico de planeación, caracterizado por máxima volatilidad (ΣΨmax) y relevancia de las macroinnovaciones (β_max) es el usado para determinar el portafolio óptimo.

Ahora bien, el efecto de la ambigüedad estructural puede mitigarse tomando una posición corta en el activo m y una larga en el activo m ', en este caso, el escenario de planeación incorporaría parámetros intermedios entre mínima y máxima relevancia, y volatilidad de las macroinnovaciones. En esta perspectiva, las restricciones a las posiciones cortas se acompañan de transformaciones en las relaciones que determinan el entorno de decisión⁸, induciendo a los agentes ingenuos a considerar escenarios de planeación donde las macroinnovaciones exhiben máxima relevancia y volatilidad.

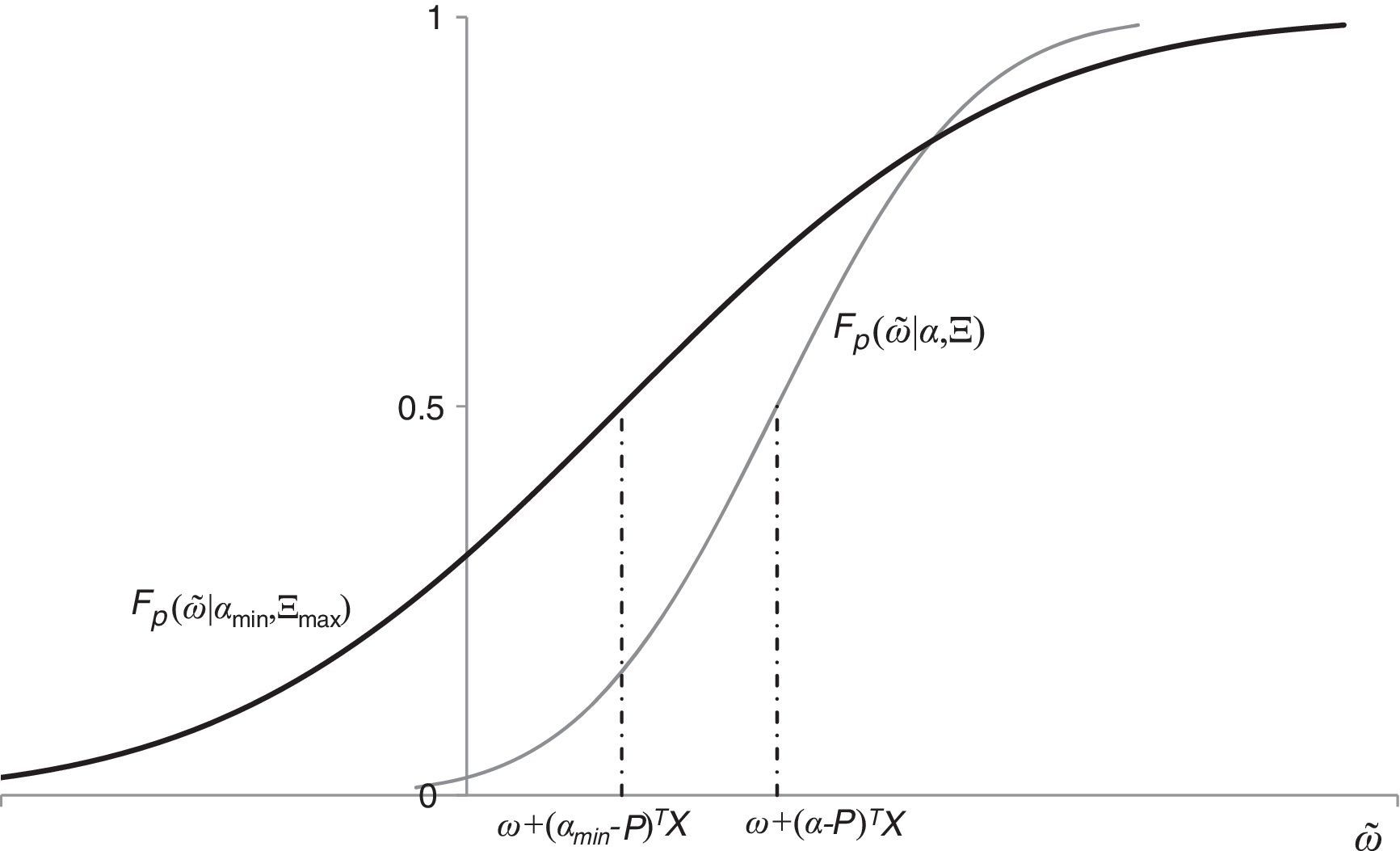
Bajo estas consideraciones, los agentes ingenuos usan un escenario probabilístico de planeación caracterizado por la media más baja de los precios futuros, máxima volatilidad de los choques específicos y de las innovaciones macroeconómicas, y, finalmente, máxima relevancia de las innovaciones macroeconómicas. La figura 2 describe el escenario probabilístico de planeación en términos de la distribución acumulada de la riqueza futura; y compara un agente ingenuo con uno sofisticado, quienes evalúan portafolio X ≻ 0 a los precios P ≺ α_min ≺ α.

Figura 2.

Distribución acumulada de la riqueza: agentes ingenuos versus sofisticados.

Los agentes ingenuos asignan máxima relevancia a las innovaciones macroeconómicas, así como, máxima volatilidad a estas (máxima correlación entre los precios de los activos), haciendo más pesadas las colas de la distribución (Barberis, 2013). De igual forma, se asigna una mínima media al precio de los activos, desplazando la distribución acumulada hacia la izquierda. En términos de la distribución acumulada los parámetros que caracterizan el escenario probabilístico de planeación inducen un fenómeno de «colas pesadas»: como resultado de la aversión a la ambigüedad, los agentes asignan probabilidades altas a los peores escenarios y bajas a los mejores. Como ilustra la figura 2, PrI(ω˜≤ω0)>PrS(ω˜≤ω0), para todo ω0≤E[ω˜], donde E[ω˜] es la verdadera media de la riqueza.

Estas características del escenario probabilístico de planeación, el problema de elección de portafolio de los agentes ingenuos se transforma en:

Así, la condición de primer orden para los agentes ingenuos es:

Donde Λ es el vector M × 1 de multiplicadores de Lagrange, y satisface Λ≻_0 y λm'xI,m'*=0, cada elemento de este vector puede leerse como la pérdida sombra asociada a las restricciones para tomar prestado en el mercado. Con ello, α_m',min ≤ p_m' es una condición necesaria para que los agentes ingenuos no participen en el m ' -ésimo mercado. Viceversa, si α_m,min > p_m es una condición necesaria para que los agentes ingenuos participen en m-ésimo mercado.

Sea la función indicadora 1λm, tal que 1λm=1 si λ_m = 0, y 1λm=0 si λ_m > 0, entonces pueden escribirse las matrices indicadoras IE+=diag(1λ1,.....,1λM) y IE−=I−IE+. La matriz IE− indica los mercados en los cuales la restricción está activa o inactiva⁹. Con ello, la condición de primer orden puede escribirse como:

Este sistema de ecuaciones es recursivo en bloques, es decir, los agentes ingenuos descartan participar en los M^' mercados donde α_m',min ≤ p_m', y evalúan si participar o no en los siguientes. De donde el portafolio óptimo de los agentes ingenuos está dado por:

Este portafolio debe satisfacer la restricción de presupuesto (3), de donde se obtienen las tenencias del activo libre de riesgo wI:

La expresión (12) es análoga a la obtenida para los agentes sofisticados (8); en este caso, el portafolio óptimo de los agentes ingenuos se ajusta al riesgo en situación de estrés financiero.

Usando la identidad de Woodbury, la matriz indicadora IE+=I, y la matriz

el sistema de demanda (12) puede escribirse como:

De donde las condiciones necesarias y suficientes para la participación de los agentes ingenuos en los M mercados son:

Participación 1: α_m,min > p_m ∀m = 1, ....., M.

Participación 2: (αmin−P)≻Γmax−1(αmin−P).

Estas condiciones de participación establecen que los agentes ingenuos participan en un mercado, si el rendimiento esperado es positivo (Dow y da Costa, 1992) y suficiente para compensar la interacción de las distintas formas de riesgo en un escenario aversión a la ambigüedad, interacción capturada por Γmax−1. A fin de simplificar la caracterización del equilibrio, se supone que la segunda condición se satisface, por tanto, la ecuación (12) determina el portafolio óptimo de los agentes ingenuos, con 1λm=1, si α_m,min > p_m, y 1λm=0 si α_m,min ≤ p_m.

El rasgo que muestra los efectos de la ambigüedad reside en que si α_m,min < p_m < α_m los ingenuos no participan y los sofisticados tienen incentivos para hacerlo. En este contexto, la interacción entre las diferentes formas de ambigüedad implica el siguiente resultado:

Proposición 1 (portafolio cauteloso): si los agentes sofisticados e ingenuos participan en todos los mercados tomando posiciones largas, XS*(P)≻0 y XI*(P)≻0, entonces sus portafolios no satisfacen:

Prueba: véase el anexo.

En un contexto de aversión a la ambigüedad, no puede ocurrir que para todos los mercados las tenencias de activos de los agentes ingenuos sean mayores o iguales a las tenencias de los sofisticados. Esto ocurre porque la existencia de interconexiones en los mercados induce un efecto diversificación, los agentes ingenuos pueden reducir sus tenencias en esos segmentos donde la ambigüedad es mayor sin castigar sus participaciones en otros segmentos del mercado. Un caso especial de este comportamiento emerge cuando, respecto de los agentes sofisticados, los agentes ingenuos exhiben mayores tenencias del activo libre de riesgo y menores tenencias en todos los activos riesgosos:

Corolario 1 (portafolio prudencial): si los agentes sofisticados e ingenuos participan en todos los mercados tomando posiciones largas, XS*(P)≻0 y XI*(P)≻0, entonces sus portafolios son tales que XS*(P)≻XI*(P) y wI*(P)>wS*(P), si se satisface la siguiente condición sobre el sesgo de los agentes ingenuos:

Prueba: se obtiene de las ecuaciones (8′) y (12′).

Esta condición sugiere que la interacción entre las formas de ambigüedad puede inducir a una evaluación de los rendimientos esperados en escenarios de mayor estrés, menguando, así el efecto diversificación asociado a la interconexión entre los mercados.

En la práctica, el conocimiento preciso de la exposición al riesgo puede llegar a ser importante cuando el grado de interconexión entre los sectores oscurece el proceso de evaluación de las pérdidas y del grado de exposición de los activos a las distintas fuentes de riesgo, lo cual induce un comportamiento más cauteloso que reduce la disposición a transar en un segmento del mercado. En esta perspectiva, el mercado de activos puede dividirse en 2 segmentos: participación M₁ y no participación M₂, con M = M₁ + M₂ y

la distinción entre cada segmento y su tamaño depende de la magnitud del sesgo sobre el valor fundamental, entre menor el precio esperado de los activos en un segmento del mercado, mayores los incentivos de los agentes ingenuos para no participar en este segmento y, por tanto, mayor su tamaño. Este resultado se sintetiza en la siguiente proposición:

Proposición 2 (portafolio conservador): si β_max ≻ 0, un mayor grado de ambigüedad en el segmento M₂, tal que αM2,min pasa a αM2,min≺_PM2, entonces, las tenencias de los M₂ activos riesgosos caen a cero en ese segmento XI,M2*=0, mientras que incrementan las tenencias en el activo libre de riesgo y en los activos del segmento M₁.

Prueba: se obtiene al reescribir la ecuación (11) para los M₁ activos riesgosos en función de los restantes M₂, y evaluar las condiciones de holgura complementaria.

La intuición detrás de esta proposición es que entre mayor el grado de ambigüedad, en cuanto al rendimiento de los activos en el segmento M₂, los cuales son vistos como más riesgosos, mayores los incentivos para que los agentes ingenuos se abstengan de participar en ese segmento del mercado, al hacer esto eliminan el efecto de la ambigüedad estructural en M₂ mercados sobre el portafolio en conjunto, razón por la cual incrementan las tenencias en el activo libre de riesgo y en los activos del segmento M₁, vistos como menos ambiguos, fenómeno denominado retorno a la familiaridad («flight to familiarity») (Guidolin y Rinaldi, 2010).

4

Ambigüedad y precios de equilibrio

Notando la oferta per cápita exógena de cada activo como x¯m>0 y el vector de ofertas como X¯≻0. Para la fracción μ de agentes ingenuos y 1 − μ de sofisticados, la condición de equilibrio es:

Las demandas por activos riesgosos a los precios de equilibrio deben satisfacer la restricción de presupuesto (3) dado el nivel de riqueza ω, así la demanda per cápita del activo libre de riesgo en equilibrio es:

Para caracterizar el vector de precios de equilibrio, se procede evaluando 4 casos de referencia, sobre los cuales se definen casos generales en las proposiciones 3 y 4.

Caso 1: (valuación «correcta» de los activos: μ = 0) XS*(PS)=X¯ y α > P_S, entonces:

En este caso, el mercado está poblado únicamente por agentes sofisticados, así, P_S representa el precio de mercado asociado a la valuación correcta de los activos (Lintner, 1969), es decir, el precio de mercado de cada activo en t = 0 es la media de su precio en t = 1 descontando el riesgo estructural y sectorial.

Caso 2: (no participación:IE+=0) 0 < μ < 1 y αmin≺_PS*≺α, entonces XI*(PS*)=0, XS*(PS*)=X¯≻0, y:

En este escenario extremo, el efecto de la ambigüedad sobre los parámetros de la distribución inhibe la participación de los agentes ingenuos en todos los mercados, razón por la cual las tenencias de activos de los agentes ingenuos se limitan al activo libre de riesgo (Routledgea y Zin, 2009). En consecuencia, los precios caen por un efecto liquidez, tal que entre mayor es la proporción de agentes ingenuos que no participan, menor es la liquidez inyectada al sistema y, por ende, menor el precio de cada activo:

Caso 3: (valuación bajo aversión a la ambigüedad: μ = 1) XI*(PI)=X¯≻0 y α_min ≻ P_I, entonces IE+=I y el vector de precios satisface:

Con este vector de precios la prima de ambigüedad puede definirse como:

Con ello, en un escenario de aversión a la ambigüedad, el vector de precios puede escribirse como el vector de precios bajo valuación «correcta» descontando la prima de ambigüedad:

Caso 4: (precios portafolio cauteloso:IE+=I) 0 < μ < 1 y α ≻ α_min ≻ P_SI, entonces XS*(PSI)≻0, XI*(PSI)≻0, y el vector de precios:

Alternativamente: P_SI = P_I + Π_SUP

Donde Π_I = μΞ(μΞ + (1 − μ)Ξ_max)⁻¹ y Π_S = I − Π_S.

Este sistema de ecuaciones para los precios permite evaluar el papel de la interacción entre los 2 tipos de agentes en el mercado. Por ejemplo, considere que el sesgo de los agentes ingenuos en términos de la varianza es tal que: Ξmax=δˆΞ, con el escalar δˆ>1, entonces:

Donde los escalares que premultiplican a UPπˆS y πˆI son los radios espectrales de las matrices Π_I y Π_S, respectivamente, y constituyen una medida del peso de los agentes ingenuos, relativa a la magnitud del sesgo inducido por la aversión a la ambigüedad. Note que 0<πˆS<1 y 0<πˆI<1.

En este caso, si bien, en el mercado, las percepciones de los agentes ingenuos inducen un comportamiento cauteloso o prudencial, mercado a mercado sobre los precios solo se descuesta una fracción de la prima de ambigüedad. En otras palabras, los precios no alcanzan el nivel de valuación «correcta» (PS−PSI=πˆSUP), aunque la interacción de los agentes en el mercado mengua el efecto de la prima de ambigüedad (PI−PSI=πˆIUP).

En este sentido, es posible evaluar el efecto de la interacción de los agentes en el mercado calculando una medida del peso de los agentes ingenuos, relativa a la magnitud conjunta del sesgo sobre la varianza.

Para obtener la magnitud conjunta del sesgo sobre la varianza, debe notarse que Ξ_max y Ξ son definidas positivas, entonces existen una matriz B no singular, y una matriz diagonal Δ, con elementos δ_m > 1, tales que:

Donde Δ es la matriz de valores propios de Ξ_maxΞ⁻¹. Para el m-ésimo activo, el elemento δ_m de Δ es una medida del grado de ambigüedad en los parámetros asociados a la varianza. Mientras que la distancia entre δ_max y δ_min es una medida conjunta del grado de ambigüedad¹⁰.

Para evaluar el peso de cada tipo de agente, relativo al sesgo inducido por la ambigüedad, se calcula la norma matricial, inducida por la norma euclidea, de las matrices Π_I y Π_S¹¹, esto es sus radios espectrales, respectivamente:

Con ello el equilibrio de participación plena bajo el portafolio cauteloso satisface.

Proposición 3: en el equilibrio de portafolio cauteloso, el vector de precios satisface:

para la norma matricial •2 inducida por la norma euclidea en R^M.

Prueba: véase el anexo.

Esta proposición plantea que en el mercado la interacción entre los 2 tipos de agentes mengua el efecto de los comportamientos cauteloso y prudencial, es decir, reduce el efecto de la prima de ambigüedad, pero no lo elimina.

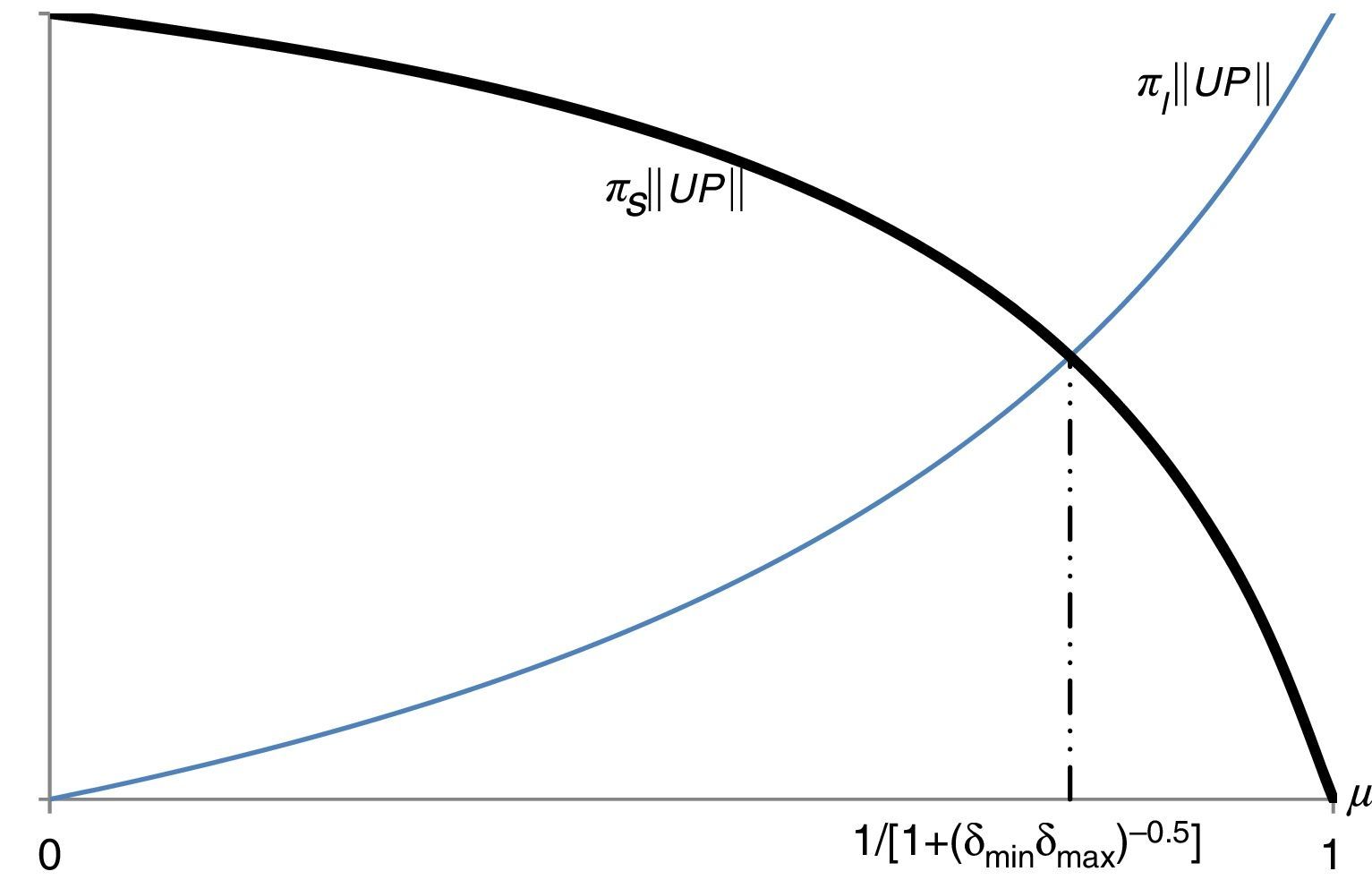
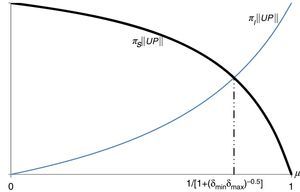
La figura 3 muestra un resultado intuitivo, entre mayor es la masa de agentes ingenuos, mayores las distorsiones en los precios de los activos riesgosos: si cuando la masa de agentes ingenuos se acerca a la unidad, la cota superior para PS−PSI se acerca a UP, y más cerca estarán los precios de aquellos que se corresponden con un equilibrio de valuación bajo aversión a la ambigüedad, PSI−PI≈0.

Figura 3.

Cotas superiores para PS−PSI y PSI−PI.

En el escenario anterior, el grado de ambigüedad es suficientemente bajo como para que los agentes ingenuos participen en todos los mercados. De manera tal que, la interacción entre los diferentes tipos de agentes mengua el efecto liquidez inducido por el retorno al activo libre de riesgo. Ahora bien, es posible que el grado de ambigüedad sea tal que el comportamiento conservador inhiba la participación de los agentes ingenuos, en un segmento del mercado M₂, talque M = M₁ + M₂.

Al descomponer el mercado en 2 segmentos, Ξ y Ξ_max pueden escribirse como las matrices en bloques:

Ξ2,1=(Ξ2,1)T captura la correlación entre los 2 segmentos M₁ y M₂, y Ξmax2,1=(Ξmax1,2)T la percepción de esta correlación por parte de los agentes ingenuos. De igual forma, el vector de precios de equilibrio puede escribirse como:

Con esta notación, el equilibrio inducido por el comportamiento conservador en el segmento M₂, puede caracterizarse así:

Proposición 4 (precios bajo portafolio conservador): si 0 < μ < 1, entonces el equilibrio es único y para cada segmento del mercado es alguno de los siguientes:

• 1.

  Participativo: si para el segmento M₁ se satisface αM1≻αM1,min≻PM1*, entonces para estos para M₁ mercados las tenencias de activos son XS1*(P*)≻0 y XI1*(P*)≻0, y el vector de precios satisface:

  

  Donde ΠI1,1=μΞ1,1(μΞ1,1+(1−μ)Ξmax1,1)−1 y ΠS1,1=I−ΠI1,1.

• 2.

  No participativo: si para M₂ activos se satisface αM2≻PM2*≻_αM2,min, entonces para estos para M₂ mercados las tenencias de activos son tales que XS2*(P*)≻XI2*(P*)=0 y el vector de precios satisface:

  

  Prueba: véase el anexo.

Para el segmento M₁, el vector de precios está dado por el precio de valuación correcta descontando una combinación convexa entre la prima de ambigüedad y el efecto liquidez, este último inducido por la no participación en el segmento M₂. Los agentes ingenuos no participan en los mercados donde la ambigüedad es alta, generando efectos que se realimentan.

Si la relevancia de las macroinnovaciones tiende a cero Ξ^2,1 sería una matriz nula y como en Easley y O’Hara (2009, p. 1827) los precios para cada segmento son:

Lo cual implica que se anula el canal de trasmisión del comportamiento cauteloso del primer al segundo segmento, así como el efecto del comportamiento conservador del segundo al primer segmento. En este sentido, la magnitud de las distorsiones en precios depende de la existencia de agentes aversos a la ambigüedad, mientras que el canal de transmisión de estas percepciones depende del grado de interconexión «objetivo» entre los mercados.

5

Discusión

La proposición 1 y el corolario 1 muestran los efectos intensivos generados por la interacción entre ambigüedad estructural e idiosincrática; estas proposiciones implican que los agentes ingenuos asignarían una menor riqueza financiera a los activos riesgosos, resultado para el cual Dimmock, Kouwenberg, Mitchell y Peijnenburg (2013) proveen evidencia empírica. Usando datos de una encuesta representativa para Estados Unidos, estos autores muestran que la aversión a la ambigüedad se asocia negativamente con la fracción de la riqueza financiera asignada en renta variable.

Por su parte, la proposición 2 sugiere que la ambigüedad inhibe la participación en los mercados financieros. Con respecto a este efecto extensivo, Dimmock et al. (2013) encuentran la tasa de participación es 4,3 puntos porcentuales más baja para los agentes aversos a la ambigüedad. Adicionalmente, estos autores muestran que los individuos con una mayor aversión a la ambigüedad son más propensos a vender activamente las acciones durante la crisis. En el contexto de la crisis de 2008-2009, un aumento de una desviación estándar en la aversión a la ambigüedad se asocia con un incremento de 3,3 puntos porcentuales en la probabilidad de venta de acciones.

La literatura asocia este tipo efectos extensivos en un contexto de crisis con episodios de fligth to quality (Caballero y Krishnamurthy, 2008; Gennaioli et al., 2012). En el contexto de la proposición 2 existen 3 escenarios donde estos episodios se configuran. En primer lugar, los segmentos M₁ y M₂ pueden estar desconectados desde la perspectiva de los agentes ingenuos, es decir, K macroinnovaciones son irrelevantes en el segmento M₂, en este escenario, la creciente ambigüedad en el segmento M₂, incrementa las tenencias de efectivo. En segundo lugar, si el segmento M₂ copa el mercado de activo riesgosos, M₂ = M, así, los agentes ingenuos no participan en los mercados de activos riesgosos, y aumentan sus tenencias de efectivo. Finalmente, si β_max = 0 la tenencia de cada activo depende únicamente de la ambigüedad idiosincrática, los mercados están desconectados, por esta razón, el incremento de la ambigüedad idiosincrática en el segmento induce una huida al activo libre de riesgo (Easley y O’Hara, 2009, 2010).

La proposición 3 tiene implicaciones desde las perspectivas de los oferentes, del agente representativo en el mercado y de la eficiencia informacional de los mercados.

Desde la perspectiva de los oferentes, la proposición 3 significa que el descuento sobre el precio se reduce al emparejarse aleatoriamente a un agente ingenuo con probabilidad μ. Para el caso de los mercados de crédito interbancario europeos, Pritsker (2013) argumenta que el reciente auge de los mercados negociados (brokered market) es una respuesta endógena a la creciente ambigüedad: la presencia de intermediarios entre compradores y vendedores incrementa la eficiencia del mercado, porque los acuerdos de crédito interbancario se establecen de manera anónima, es decir, el prestamista se asigna aleatoriamente a un prestatario, proceso que incrementa la liquidez y el volumen de transacciones.

Desde la perspectiva del mercado, como sugieren Campbell y Mankiw (1989), el agente representativo, más que ser un agente plenamente racional¹², es una combinación lineal entre un agente racional y un agente siguiendo una regla de dedo. Los resultados sugieren que el agente representativo puede construirse como una combinación lineal entre un sofisticado y uno ingenuo, con pesos relativos π_S y π_I, respectivamente. Cuando el peso relativo del agente ingenuo es bajo, las macroinnovaciones explican muy poco de la variabilidad de los precios (Cutler et al., 1989). Por el contrario, si el peso relativo del agente ingenuo es alto, los precios reaccionan de manera más aguda a las macroinnovaciones; como sugieren Klibanoff et al. (1998) la relevancia de los macrorriesgos puede estar relacionada con la fuente de la noticia. En una semana típica los precios reaccionan suavemente a las noticias macroeconómicas, mientras que en semanas donde una macronoticia aparece en la portada del Times, o es anunciada por el presidente de la FED o por una calificadora de riesgos como Moody's, es mayor la reacción de los precios. Entre mayor credibilidad o sobresaliencia de la fuente, mayor π_I y, por tanto, menor el precio de los activos.

Desde la perspectiva de la eficiencia informacional de los mercados, los precios corrientes reflejan el desacuerdo con respecto a los parámetros que delimitan el escenario probabilístico de planeación; en este artículo dicho desacuerdo es inducido por la aversión a la ambigüedad de una masa de los agentes en el mercado. En otras palabras, el presente artículo se centra en la presencia de sesgos en la información transmitida, los efectos de equilibrio general inducen la trasmisión de información y diluyen estos sesgos solo de manera parcial. Este resultado es similar al encontrado en la literatura de arbitraje limitado: en el mercado, los agentes sofisticados no pueden inducir que el precio de los activos corresponda con el precio de valuación correcta (Shleifer, 2000). En esta perspectiva, los resultados presentados en el presente artículo pueden considerarse como un equilibrio informacional interim, donde la incorporación de información acerca de las creencias de los agentes es sopesada en el mercado (Grossman, 1989; Epstein y Wang, 1994; Epstein y Schneider, 2007).

La proposición 4 sugiere que el canal de trasmisión de los efectos de la ambigüedad está asociado a la relevancia «objetiva» de las macroinnovaciones; en este caso la pregunta en torno a qué determina esta interconexión queda abierta, lo cual invita a considerar los efectos de la innovación financiera o la concentración de los mercados en pocos operadores en términos de incrementar o reducir la interconexión entre los diferentes segmentos que componen el mercado de activos (Pritsker, 2013; Caballero y Simsek, 2010).

6

Conclusiones

Este artículo presenta un modelo donde la indeterminación de las relaciones que definen el entorno de decisión, induce a la reevaluación de los modelos para evaluar las distintas formas de riesgo, en particular, en contextos donde la información existente sobre elementos idiosincráticos y sobre las interconexiones entre los mercados dificulta el proceso de evaluación de las pérdidas o ganancias y del grado de exposición a las distintas formas de riesgo. La presencia de estos riesgos denominada ambigüedad, implica que los agentes en el mercado toman decisiones basados en parámetros de la distribución de los precios futuros, asociados a los peores estados de naturaleza. Así, con creencias motivadas por la posibilidad de fenómenos de «cola izquierda», las precauciones tomadas por los agentes aumentan, afectando negativamente la disposición a realizar transacciones en los mercados financieros, en este sentido, se discute las condiciones bajo las cuales los agentes aversos a la ambigüedad invierten menos en un segmento del mercado (comportamiento cauteloso o prudencial) o se abstienen de participar en algunos segmentos del mercado (comportamiento conservador o flight to quality).

Una vez se plantea una taxonomía del comportamiento de los agentes ingenuos, se evalúa el comportamiento de los precios de los activos, en el equilibrio. En un escenario donde todos los agentes participan, se muestra que al sopesar las creencias de los agentes en el mercado se mengua el efecto de las distintas formas de ambigüedad. Sin embargo, cuando los agentes aversos a la ambigüedad se abstienen de participar en algunos segmentos del mercado, las creencias inducidas por la presencia de colas anchas en la distribución de los precios futuros generan efectos que se realimentan entre los segmentos que componen el mercado de activos, lo cual amplifica el efecto de la ambigüedad dependiendo del grado de interconexión que existe entre los mercados. En esta perspectiva, una línea de investigación que queda abierta es la manera en que los agentes actualizan sus creencias, a medida que obtienen nueva información en el mercado, es decir, la incorporación del proceso de actualización dinámico y la influencia que este tiene sobre los precios. En esta perspectiva, una ventaja del modelo propuesto es el uso de distribuciones normales para los precios, lo cual sugiere que puede implementarse un proceso browniano para el proceso de actualización. El reto de esta línea emerge al considerar una ampliación constante del conjunto de información, lo cual puede acarrear mayor ambigüedad en la medida en que los agentes evalúan la información nueva con un sesgo preexistente.

Conflicto de intereses

El autor declara no tener ningún conflicto de intereses.

Agradecimientos

Agradezco los comentarios de José Miguel Torres, Sonia Di Giannatale, Jorge Fernández y Stephen McKnight. La presente versión se enriquece con los valiosos comentarios de los evaluadores externos de la revista Ensayos sobre Política Económica.