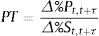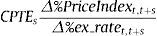Revisión de algunas estimaciones recientes del traspaso del tipo de cambio a los precios en México

Resumen

Este trabajo muestra que las estimaciones de la elasticidad de traspaso del tipo de cambio a los precios en México reportadas en algunos trabajos de investigación recientes se derivan de cálculos erróneos. La Junta de Gobierno del Banco de México ha utilizado estas estimaciones durante varios años para tomar decisiones de política monetaria.

Abstract

This article shows that estimates of the elasticity of pass-through from exchange rate to prices reported in some of the recent literature are derived from erroneous calculations. The Board of Bank of México has been using these estimates for several years to make decisions on monetary policy.

1

Introducción

Algunos trabajos de investigación recientes sobre el traspaso del tipo de cambio a los precios en México contienen un error metodológico. Este error se presentó por primera vez en Banco de México (2011), posteriormente en Capistrán, Ibarra y Ramos-Francia (2012) y Cortés (2013a), y más recientemente en Guillermo y Rodríguez (2014) y Rodríguez (2015). En este trabajo se explica el error metodológico que contienen los trabajos mencionados, con especial atención en Capistrán et al. (2012) y Cortés (2013a), cuyos resultados se replican. También se documenta que las conclusiones de estos trabajos forman parte de los parámetros que utiliza desde hace varios años la Junta de Gobierno del Banco de México para tomar decisiones de política monetaria.

Todos los trabajos mencionados en el párrafo anterior utilizan el mismo procedimiento para estimar la elasticidad de traspaso del tipo de cambio a los precios, el cual incluye 3 etapas: 1) estimación de modelos de vectores autorregresivos (VAR) con datos de tasas de inflación y depreciación, además de otras variables; 2) a partir de los modelos VAR estimados, se obtienen las funciones de respuesta de la tasa de inflación y la tasa de depreciación ante un impulso (o choque) en la tasa de depreciación; finalmente 3) se utilizan estas series de impulso-respuesta para calcular la inflación acumulada y la depreciación acumulada después del choque. La elasticidad de traspaso acumulado se obtiene del cociente de la inflación acumulada dividida por la depreciación acumulada.

El procedimiento descrito ha sido utilizado anteriormente en muchos trabajos de investigación, pero en los que se analizan aquí hay una característica que conduce a un error de cálculo. Esta característica consiste en utilizar para la estimación de los modelos VAR datos mensuales de tasas de crecimiento anual. Como se demuestra más adelante, el error en que incurren los autores mencionados consiste en que la evaluación de la inflación y la depreciación acumuladas después de un choque son incorrectas, y esto invalida el cálculo de la elasticidad de traspaso.

Los resultados de Banco de México (2011), Capistrán et al. (2012) y Cortés (2013a) son de especial interés porque, de acuerdo con las Minutas de las reuniones de política monetaria de la Junta de Gobierno del Banco México, estos resultados son utilizados en la toma de decisiones de política monetaria¹.

En la sección 2 se explica en detalle el error que contienen los cálculos de la elasticidad de traspaso de los trabajos mencionados. Para ilustrar el error, se replican las estimaciones de Capistrán et al. (2012) y Cortés (2013a). La sección 3 muestra cómo puede calcularse correctamente dicha elasticidad utilizando los mismos modelos de los autores mencionados. La sección 4 verifica si el error metodológico que se explica puede encontrarse en la literatura previa. En la sección 5 se demuestra que la Junta de Gobierno del Banco de México ha utilizado durante varios años estimaciones incorrectas de la elasticidad de traspaso para tomar decisiones de política monetaria. La sección 6 presenta las conclusiones.

2

Análisis de estimaciones del traspaso del tipo de cambio a los precios en México

A continuación se analiza el método utilizado en los trabajos mencionados para calcular la elasticidad de traspaso del tipo de cambio a los precios con el fin de mostrar el error metodológico. Este error se deriva de que la elasticidad se calcula como el cociente de sumas (o sumatorias) de los valores obtenidos en las funciones de impulso-respuesta que resultan de los modelos VAR, los cuales son estimados con datos mensuales de tasas anuales de depreciación y de inflación además de otras variables².

Específicamente, Capistrán et al. (2012) presentan la siguiente expresión para calcular la elasticidad de traspaso acumulado en τ periodos después de un choque en la tasa de depreciación (págs. 825-826):

«La elasticidad de traspaso acumulado (PT) en el periodo τ se calcula de la siguiente manera:

en la que Δ%P_t,t+τ es el cambio porcentual en el nivel de los precios τ periodos después del choque, y Δ%S_t,t+τ denota el cambio porcentual en el tipo de cambio en el mismo periodo.»

Una primera observación que debe hacerse a esta formulación es que debe hacer explícito que el horizonte de tiempo para el cual se calcula la elasticidad de traspaso es variable y se representa con el subíndice τ. Específicamente, la expresión correcta para el lado izquierdo de la ecuación debe mostrar ese subíndice: PT_τ.

Como se muestra con detalle más adelante, los cambios porcentuales acumulados que utilizan los mencionados autores para el numerador y el denominador de la elasticidad de traspaso son obtenidos acumulando los impulso-respuesta derivados de sus modelos VAR. Este procedimiento es incorrecto porque los impulso-respuesta necesariamente tienen las mismas unidades y la misma frecuencia que los datos originales (ver Hamilton, 1994, pág. 323). Es decir, los impulso-respuesta contienen tasas anuales de depreciación y de inflación.

Es obvio que al acumular tasas de depreciación (inflación) anual a lo largo de un cierto número de meses consecutivos no es posible obtener la depreciación acumulada (inflación acumulada). Para demostrar este punto, basta recordar que es posible sumar tasas de crecimiento de periodos consecutivos para obtener el crecimiento porcentual acumulado solamente cuando coinciden la frecuencia de las observaciones y la periodicidad de la tasa de crecimiento (calculada como diferencia de logaritmos). Por lo anterior, tanto el numerador como el denominador de la expresión utilizada por Capistrán et al. (2012) para calcular la elasticidad de traspaso acumulado están evaluados incorrectamente y, en consecuencia, el cociente no es la elasticidad que los autores pretenden calcular.

A continuación se replican los resultados de Capistrán et al. (2012) y Cortés (2013a) para mostrar en detalle el procedimiento que utilizan para calcular la elasticidad de traspaso. En este punto, es muy importante aclarar que el presente trabajo tiene como único objetivo hacer notar un error metodológico en el cálculo de la elasticidad de traspaso y no pretende evaluar la especificación o la estimación de sus modelos VAR.

No es necesario repetir la descripción detallada del modelo de Capistrán et al. (2012) en el presente artículo. Basta con mencionar que las variables endógenas son los siguientes indicadores de la economía mexicana: el índice global de la actividad económica (IGAE), la tasa de interés de los Certificados de la Tesorería (CETES), el tipo de cambio nominal (pesos por dólar) y diferentes índices de precios que utilizan alternativamente. El índice de mayor importancia es el Índice Nacional de Precios al Consumidor (INPC), el cual incluyen en su modelo base³. Las variables exógenas son: el índice de producción industrial, el índice de precios al consumidor y la tasa de bonos del Tesoro, todas ellas de Estados Unidos, además del índice de precios internacionales de las materias primas⁴.

Todas las variables incluidas en la estimación, excepto las tasas de interés, son tasas de crecimiento anual calculadas con diferencias logarítmicas con respecto al mismo mes del año anterior, y la frecuencia de las observaciones es mensual. En este punto, es conveniente citar a los autores: «Todas las variables se expresan en tasas de crecimiento anual, a excepción de la tasa de interés» (Capistrán et al., 2012, pág. 822).

Después de estimar el modelo VAR, se obtienen las series de impulso-respuesta de la tasa de inflación del INPC y de la tasa de depreciación del tipo de cambio ante un choque en la propia tasa de depreciación, y con estas series se calcula la elasticidad de traspaso tal y como lo hicieron los autores del Banco de México con el fin de obtener el mismo resultado y, de ese modo, ilustrar claramente el error⁵.

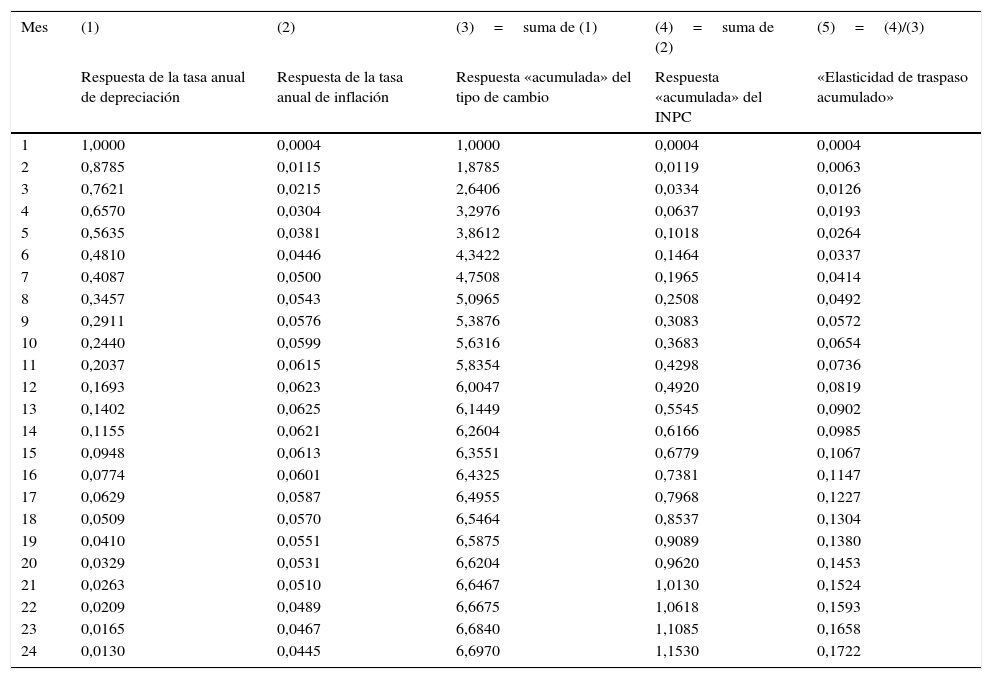
La columna 1 de la tabla 1 muestra la respuesta de la tasa anual de depreciación del tipo de cambio en los meses posteriores a un choque de un punto porcentual en la propia tasa de depreciación. La columna 2 de la tabla 1 muestra la respuesta de la tasa de inflación anual ante el mismo choque. Para calcular la elasticidad de traspaso acumulado es necesario calcular las tasas de crecimiento porcentual acumulado del INPC y del tipo de cambio después del choque. Estas tasas de inflación y depreciación acumuladas se utilizan en el numerador y denominador, respectivamente, del cociente que representa la elasticidad de traspaso. El error metodológico de Capistrán et al. (2012) se presenta al calcular estas tasas de inflación y depreciación acumuladas.

Tabla 1.

Cálculo de la elasticidad de traspaso de Capistrán et al. (2012) (muestra: enero 1997 a diciembre 2010, unidad: puntos porcentuales)

Mes	(1)	(2)	(3) = suma de (1)	(4) = suma de (2)	(5) = (4)/(3)
	Respuesta de la tasa anual de depreciación	Respuesta de la tasa anual de inflación	Respuesta «acumulada» del tipo de cambio	Respuesta «acumulada» del INPC	«Elasticidad de traspaso acumulado»
1	1,0000	0,0004	1,0000	0,0004	0,0004
2	0,8785	0,0115	1,8785	0,0119	0,0063
3	0,7621	0,0215	2,6406	0,0334	0,0126
4	0,6570	0,0304	3,2976	0,0637	0,0193
5	0,5635	0,0381	3,8612	0,1018	0,0264
6	0,4810	0,0446	4,3422	0,1464	0,0337
7	0,4087	0,0500	4,7508	0,1965	0,0414
8	0,3457	0,0543	5,0965	0,2508	0,0492
9	0,2911	0,0576	5,3876	0,3083	0,0572
10	0,2440	0,0599	5,6316	0,3683	0,0654
11	0,2037	0,0615	5,8354	0,4298	0,0736
12	0,1693	0,0623	6,0047	0,4920	0,0819
13	0,1402	0,0625	6,1449	0,5545	0,0902
14	0,1155	0,0621	6,2604	0,6166	0,0985
15	0,0948	0,0613	6,3551	0,6779	0,1067
16	0,0774	0,0601	6,4325	0,7381	0,1147
17	0,0629	0,0587	6,4955	0,7968	0,1227
18	0,0509	0,0570	6,5464	0,8537	0,1304
19	0,0410	0,0551	6,5875	0,9089	0,1380
20	0,0329	0,0531	6,6204	0,9620	0,1453
21	0,0263	0,0510	6,6467	1,0130	0,1524
22	0,0209	0,0489	6,6675	1,0618	0,1593
23	0,0165	0,0467	6,6840	1,1085	0,1658
24	0,0130	0,0445	6,6970	1,1530	0,1722

Para tratar de calcular el crecimiento porcentual del índice de precios al consumidor en los 24 meses posteriores al choque en el tipo de cambio, Capistrán et al. (2012) acumulan, suman, las 24 tasas anuales que obtienen en el impulso-respuesta de la tasa de inflación (último renglón de la columna 4) y colocan esa cantidad en el numerador del cociente que usan para calcular la elasticidad de traspaso. Para el denominador acumulan las 24 tasas de crecimiento anual del tipo de cambio que obtienen después del choque (último renglón de la columna 3). Con estas 2 cantidades calculan el cociente que presentan como la elasticidad de traspaso del tipo de cambio a los precios acumulado en los 2 años posteriores al choque. Este resultado se replica en el último renglón de la columna 5 de la tabla 1.

Al repetir el cálculo erróneo descrito anteriormente el valor de la «elasticidad» de traspaso acumulado 24 meses después del choque que se obtiene es 0,17, el cual es prácticamente igual al que reportaron Capistrán et al. (2012): «En el largo plazo esta elasticidad es de aproximadamente 0,16» (pág. 826). Dicha «elasticidad» se muestra en el último renglón de la columna 5 de la tabla 1. Como es obvio, el cálculo corresponde a 24 meses, a pesar de que los autores lo llaman «de largo plazo».

Es importante replicar este resultado en particular porque es el que resaltan los autores mencionados en el resumen de su trabajo (pág. 813) y también porque este resultado se resalta en el «Capítulo Técnico» del Informe Sobre la Inflación Enero-Marzo de 2011 del Banco de México (pág. 58).

Como es obvio, no es correcto sumar tasas de crecimiento anual de meses consecutivos para tratar de calcular el crecimiento porcentual acumulado. Como regla general, debe recordarse que es válido acumular tasas de crecimiento calculadas con logaritmos naturales siempre y cuando coincidan la periodicidad de las tasas de crecimiento y la frecuencia de los datos.

Finalmente, cabe mencionar que Capistrán et al. (2012) presentan un gran número de estimaciones de elasticidades de traspaso utilizando diferentes índices de precios y periodos de muestra. En total, presentan 17 «elasticidades» calculadas con el mismo método erróneo descrito anteriormente.

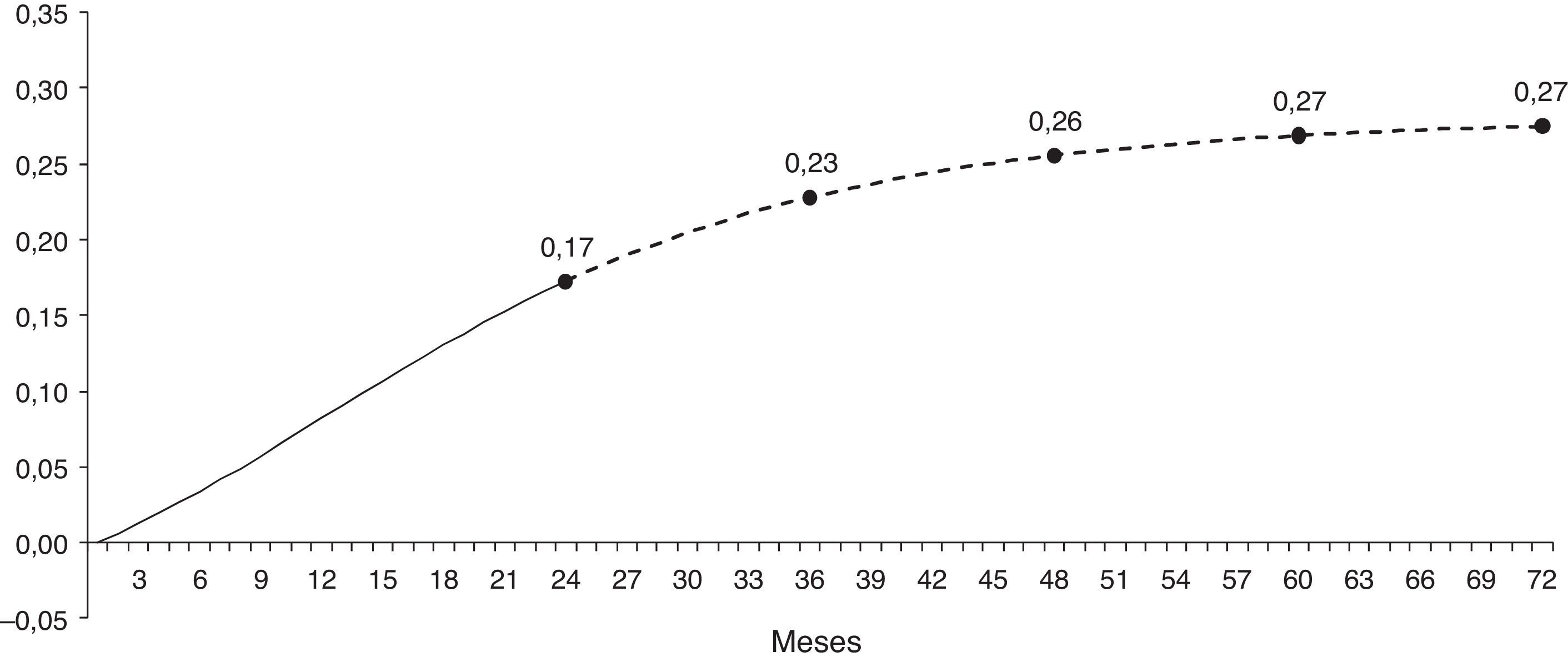
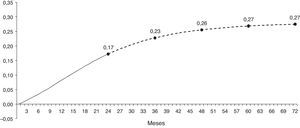
Además del error metodológico explicado antes, otra observación importante que debe hacerse sobre los resultados que presentan Capistrán et al. (2012) es que, como se hizo notar antes, los autores llaman «de largo plazo» a una «elasticidad» que calculan para un periodo de 24 meses. A este respecto, es necesario aclarar que el término elasticidad de largo plazo debe referirse solamente a aquella elasticidad cuya magnitud se mantiene estable independientemente del horizonte de tiempo para el cual se calcula. En este caso es necesario extender varios años más los impulso-respuesta y los cálculos que hacen los mencionados autores para observar que el valor de la «elasticidad» se estabiliza después de 5 años en un nivel de 0,27. Es decir, en realidad la «elasticidad» de largo plazo tal y como la calculan (erróneamente) Capistrán et al. (2012) es del 27%, no del 16%. La figura 1 muestra con una línea sólida la elasticidad calculada hasta 24 meses tal y como la reportaron los mencionados autores (ver su figura 3.c, pág. 825), y con línea punteada se muestra la extensión de los cálculos necesaria para obtener la elasticidad de largo plazo, la cual se observa a partir del quinto año y tiene un nivel del 27%.

Figura 1.

Elasticidad de traspaso después de 24 meses y de largo plazo (calculada como en Capistrán et al., 2012).

El error en el cálculo de la elasticidad de traspaso descrito antes se repitió posteriormente en el trabajo de Cortés (2013a). Este autor estima el traspaso del tipo de cambio al INPC y sus subíndices siguiendo la metodología de Capistrán et al. (2012) y utiliza también observaciones mensuales de tasas de crecimiento anual. Para demostrar que Cortés (2013a) repite el error que se explicó anteriormente, en este trabajo se replica una de las numerosas estimaciones que presenta.

Específicamente, se replica el cálculo de la elasticidad que corresponde al INPC con una muestra que va de junio de 2001 a diciembre de 2010, la cual se encuentra en el primer renglón de su cuadro 1 (pág. 328). Esta elasticidad corresponde al traspaso acumulado 12 meses después de un choque en la tasa de depreciación y merece especial atención porque también se reportó previamente en Capistrán et al. (2012). Al respecto, es conveniente citar directamente a Cortés (2013a): «Como informaron Capistrán et al. (2012), en 2010 la elasticidad de traspaso de los movimientos en el tipo de cambio sobre la inflación general de precios al consumidor era de 0,02 a un año del choque» (pág. 327)⁶.

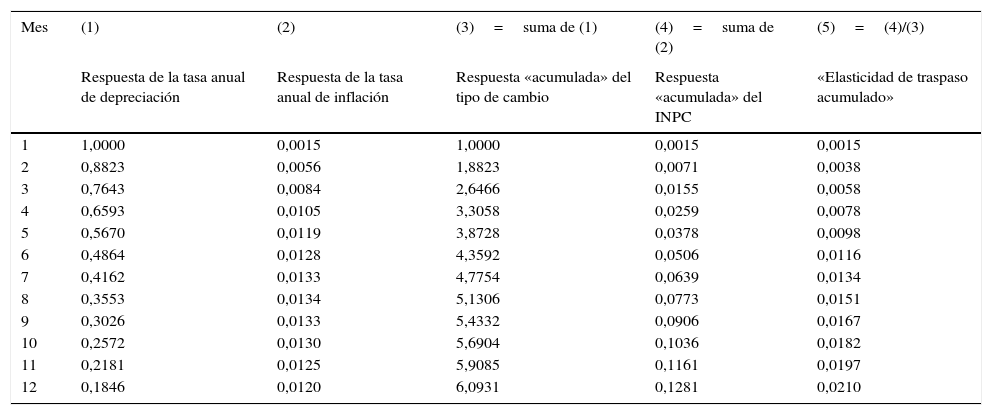
Para repetir el cálculo de Cortés (2013a), la columna 1 de la tabla 2 muestra la respuesta de la tasa anual de depreciación ante un choque de un punto porcentual en la misma tasa de depreciación. La columna 2 presenta la respuesta de la tasa de inflación anual del INPC ante el mismo choque. Las columnas 3 y 4 muestran las respuestas «acumuladas» tal y como las calcula Cortés (2013a), es decir, sumando las respuestas obtenidas del modelo VAR. Finalmente, la columna 5 muestra la «elasticidad de traspaso acumulado», que es el cociente de las columnas 4 y 3. El último renglón de la columna 5 muestra una «elasticidad» 12 meses después del choque de 0,021. Este resultado es igual al reportado por Cortés (2013a), lo cual corrobora que siguió el mismo método erróneo de Capistrán et al. (2012)⁷.

Tabla 2.

Cálculo de la elasticidad de traspaso de Cortés (2013a) (muestra: junio 2001 a diciembre 2010, unidad: puntos porcentuales)

Mes	(1)	(2)	(3) = suma de (1)	(4) = suma de (2)	(5) = (4)/(3)
	Respuesta de la tasa anual de depreciación	Respuesta de la tasa anual de inflación	Respuesta «acumulada» del tipo de cambio	Respuesta «acumulada» del INPC	«Elasticidad de traspaso acumulado»
1	1,0000	0,0015	1,0000	0,0015	0,0015
2	0,8823	0,0056	1,8823	0,0071	0,0038
3	0,7643	0,0084	2,6466	0,0155	0,0058
4	0,6593	0,0105	3,3058	0,0259	0,0078
5	0,5670	0,0119	3,8728	0,0378	0,0098
6	0,4864	0,0128	4,3592	0,0506	0,0116
7	0,4162	0,0133	4,7754	0,0639	0,0134
8	0,3553	0,0134	5,1306	0,0773	0,0151
9	0,3026	0,0133	5,4332	0,0906	0,0167
10	0,2572	0,0130	5,6904	0,1036	0,0182
11	0,2181	0,0125	5,9085	0,1161	0,0197
12	0,1846	0,0120	6,0931	0,1281	0,0210

Más recientemente, Guillermo y Rodríguez (2014) y Rodríguez (2015) utilizaron el mismo método para estimar elasticidades de traspaso del tipo de cambio a los precios en México. Los resultados de estos autores no se replican en el presente trabajo. Es suficiente verificar que ellos también utilizan un modelo VAR estimado con datos mensuales de tasas anuales de inflación y depreciación, entre otras variables, y siguen el procedimiento descrito antes para calcular la elasticidad de traspaso. A continuación se cita directamente el artículo de Guillermo y Rodríguez (2014)⁸:

«… the data set for our model consists of monthly observations of annual growth rates» (pág. 22).

«… we calculated the cumulative elasticity of each price index with respect to the exchange rate shock as suggested by Capistrán et al. (2012). The cumulative exchange rate pass-through elasticity (CPTE) s periods after a shock that took place at time t is defined as follows:

Where Δ%PriceIndex_t,t+s is the cumulative inflation change (in the corresponding prices, i.e. import, producer and consumer) s periods after the shock, and Δ%ex_rate_t,t+s is the cumulative exchange rate depreciation change s periods after the shock. In other words, the CPTE at period s is the ratio of the cumulative response of the corresponding price inflation to the cumulative response of the exchange rate depreciation, both evaluated s periods after the exchange rate shock» (pág. 26).

3

Presencia del error de estimación en otros trabajos

Con el fin de investigar si el error metodológico explicado antes proviene de otros trabajos de investigación, a continuación se verifica si pueden encontrarse errores similares en los trabajos que sirvieron de referencia a los autores del Banco de México. La conclusión es que dicho error no se encuentra en la literatura consultada por los autores mencionados pero sí se encuentra en otros trabajos previos.

McCarthy (2000) y Hahn (2003) utilizan tasas de crecimiento trimestral (calculadas con diferencias logarítmicas) con frecuencia trimestral y calculan los efectos acumulados sumando las tasas de crecimiento trimestrales obtenidas en los impulso-respuesta de sus modelos VAR. Choudhri, Faruqee y Hakura (2005) también utilizan datos trimestrales de tasas de crecimiento trimestral (diferencias logarítmicas) y los efectos en los niveles de los índices de precios se obtienen acumulando los impulso-respuesta. Por su parte, Stulz (2007) incluye en sus modelos VAR datos mensuales de tasas de crecimiento mensual (diferencias logarítmicas) y calcula correctamente la inflación acumulada después de un choque en la tasa de depreciación sumando las tasas mensuales que obtiene en los impulso-respuesta. En todos estos casos los autores acumulan correctamente tasas de crecimiento calculadas con diferencias logarítmicas, ya que coinciden la periodicidad de las tasas de crecimiento y la frecuencia de los datos.

En contraste, Winkelried (2003) utiliza datos mensuales de tasas trimestrales de inflación y depreciación para estimar modelos VAR (ver su anexo 1, pág. 24) y acumula las respuestas obtenidas para la inflación y la depreciación para tratar de obtener la inflación y la depreciación acumuladas, y con ellas calcula la elasticidad de traspaso como el cociente de inflación acumulada dividido por depreciación acumulada. Es decir, este autor comete el mismo error que Capistrán et al. (2012) y Cortés (2013a). Aunque este autor no utiliza tasas de inflación y depreciación anuales sino trimestrales, es claro que no es posible acumular observaciones mensuales de tasas trimestrales para calcular la inflación o depreciación acumuladas. Como se ha explicado antes, y como se muestra en los trabajos descritos en el párrafo anterior, solamente pueden acumularse tasas de crecimiento calculadas con diferencias logarítmicas que tengan una frecuencia igual que el horizonte para el cual se calcularon las tasas de crecimiento.

Un punto importante que debe tenerse en cuenta con respecto a varios trabajos mencionados en los párrafos anteriores es que se enfocan en economías avanzadas en las que las variaciones del tipo de cambio y los precios tienden a ser relativamente pequeñas. En estos casos, la aproximación de las variaciones porcentuales utilizando diferencias logarítmicas es correcta. Sin embargo, si las variaciones no son pequeñas, debe preferirse el cálculo directo de las tasas de crecimiento utilizando la formulación usual, Δ%Y_t = ((Y_t–Y_t-1)/Y_t-1)*100, porque la aproximación logarítmica tiende a subestimar las tasas de crecimiento cuando no son pequeñas. Ilustración: una tasa de crecimiento del 2% resulta ser del 1,98 cuando se calcula con diferencias logarítmicas, una tasa de crecimiento del 5% se aproxima como 4,88 y una tasa del 10% se aproxima con 9,53 cuando se utilizan diferencias logarítmicas.

4

Evaluación del efecto del cálculo incorrecto de la elasticidad de traspaso

Para evaluar el efecto que tiene el cálculo incorrecto de la elasticidad de traspaso deben compararse los resultados que presentan Capistrán et al. (2012) con los resultados que se obtienen cuando se calcula correctamente dicha elasticidad. Los cálculos que se presentan a continuación tienen como objetivo solamente mostrar cuál es la única interpretación válida que puede hacerse de sus funciones impulso-respuesta para calcular la elasticidad de traspaso acumulado. Este ejercicio no constituye de ninguna manera un aval de su modelo, el cual, como se dijo antes, no se pretende evaluar en el presente trabajo.

La única manera de calcular correctamente una elasticidad de traspaso acumulado utilizando los impulso-respuesta de los autores mencionados es la siguiente. Para ilustrar el cálculo se utilizan las columnas 1 y 2 de la tabla 1, las cuales contienen tasas anuales de depreciación y de inflación. La elasticidad de traspaso acumulado 12 meses después del choque se calcula fácilmente con el cociente de la observación número 12 en la columna 2 (tasa de inflación anual 12 meses después del choque) dividida por la observación número 12 de la columna 1 (tasa de depreciación anual 12 meses después del choque). Estas 2 cifras son tasas anuales de inflación y de depreciación, y por tanto su cociente es la elasticidad de traspaso acumulado en 12 meses. El valor que se obtiene es 0,0623 / 0,1693 = 0,37. Esto significa que después de un año el 37% de la depreciación del tipo de cambio se ha traspasado a la inflación del INPC.

La elasticidad de traspaso también puede calcularse correctamente para un periodo de 24 meses. Primero es necesario calcular correctamente las tasas de depreciación y de inflación acumuladas en los 24 meses posteriores al choque. Estas tasas acumuladas pueden obtenerse fácilmente para cada variable sumando las tasas anuales correspondientes a los meses 12 y 24 en las columnas 1 y 2 de la tabla 1. Esta suma de tasas anuales es correcta porque están separadas por 12 meses, y gracias a ello es posible hacer la eliminación aritmética necesaria para obtener la tasa de crecimiento porcentual en los 24 meses, como se ilustra a continuación utilizando la variable Y. La eliminación de términos redundantes es obvia.

Al realizar los cálculos correctamente con base en las columnas 1 y 2 de la tabla 1 se obtiene que la tasa de inflación acumulada durante los 24 meses posteriores al choque es: 0,0623 + 0,0445 = 0,1068 y la tasa de depreciación del tipo de cambio acumulada en el mismo periodo es: 0,1693 + 0,0130 = 0,1823. En consecuencia, el cálculo correcto de la elasticidad de traspaso del tipo de cambio a los precios al consumidor es: 0,1068 / 0,1823 = 0,586. Esto significa que en un plazo de 2 años el 59% de la depreciación del tipo de cambio se traspasa a la inflación de los precios al consumidor.

Es muy importante notar que la elasticidad de traspaso calculada correctamente es equivalente a 3,4 veces la cifra de 0,16 que reportaron los autores mencionados. Es decir, interpretando correctamente los impulso-respuesta de Capistrán et al. (2012) se encuentra que el error de cálculo resulta en una importante subestimación de la elasticidad de traspaso.

El método ilustrado anteriormente, que consiste en agregar las respuestas de las variables que se obtienen cada 12 meses, puede utilizarse para calcular correctamente las elasticidades de traspaso para cualquier horizonte de tiempo, siempre y cuando las cifras utilizadas correspondan a observaciones que sean múltiplos de 12.

5

Incidencia en la política monetaria

Es natural que los trabajos de investigación del Banco de México aspiren a contribuir a la formulación de la política monetaria. Así lo expresan claramente los autores mencionados.

Capistrán et al. (2012) concluyen su artículo diciendo: «Los resultados respecto al comportamiento de los índices de precios agregados y de los precios individuales serán útiles en la construcción de modelos macroeconómicos estructurales que pueden ser usados para la elaboración de pronósticos, así como para el análisis de la política monetaria en México» (pág. 837).

Por su parte, Cortés (2013a) concluye su artículo de la siguiente manera: «En este trabajo empírico se presenta evidencia sobre la relación entre el tipo de cambio y los precios al consumidor en México, la cual puede aportar elementos importantes y servir como marco de referencia en varias dimensiones para modelos estructurales y de equilibrio general. Adicionalmente, brinda herramientas de análisis que pueden ser utilizadas en la toma de decisiones de política monetaria» (pág. 342).

Desafortunadamente, los cálculos de la elasticidad de traspaso que se han descrito anteriormente forman parte de los parámetros que utiliza la Junta de Gobierno del Banco de México para determinar su política monetaria. Esto se corrobora al revisar la Minutas de sus reuniones para tomar decisiones de política monetaria:

Minuta 9 (febrero 2012): «En cuanto al impacto del tipo de cambio sobre los precios en México, algunos miembros de la Junta citaron trabajos de investigación del Banco de México para argumentar que el traspaso ha sido limitado en el pasado» (pág. 18).

Minuta 17 (febrero 2013): «… en caso de existir una preocupación por una posible depreciación del tipo de cambio, dicho miembro [de la Junta de Gobierno] indicó que debe considerarse que actualmente se tiene evidencia de que el traspaso hacia los precios es reducido, por lo que el efecto sobre la inflación sería reducido aun de manifestarse un choque de esa naturaleza» (pág. 20).

Minuta 27 (mayo 2014): «… un miembro [de la Junta de Gobierno] enfatizó que el riesgo de mayor inflación por una posible depreciación es acotado dado el documentado bajo traspaso de las variaciones del tipo de cambio a la inflación» (pág. 23).

Minuta 33 (febrero 2015): «Todos los integrantes [de la Junta de Gobierno] coincidieron en que a pesar de la evidencia de varios años de que el traspaso de movimientos cambiarios a los precios ha sido bajo y que su efecto sobre la inflación tiende a ser transitorio, la posibilidad de que el tipo de cambio permanezca en los niveles actuales por un periodo prolongado o que incluso el peso registre depreciaciones adicionales, representa un riesgo para la inflación» (pág. 17)⁹.

Como se demostró antes, la evidencia utilizada en las reuniones de la Junta de Gobierno del Banco de México consiste en estimaciones incorrectas de la elasticidad de traspaso.

6

Conclusión

Este trabajo muestra que las estimaciones de la elasticidad de traspaso del tipo de cambio a los precios en México reportadas primero en Banco de México (2011) y posteriormente en varias publicaciones académicas se derivan de cálculos erróneos.

Dichos cálculos resultan de una característica peculiar de los trabajos revisados: utilizan datos mensuales de tasas anuales de depreciación y de inflación para estimar modelos VAR (además de otras variables). Esta inusual combinación de frecuencia de datos y periodicidad de tasas de crecimiento conduce a un error de cálculo que tiene consecuencias graves.

Primera. El error de cálculo descrito invalida los resultados reportados en Banco de México (2011), Capistrán et al. (2011, 2012), Cortés (2013a,b), Guillermo y Rodríguez (2014) y Rodríguez (2015).

Segunda. De acuerdo con las réplicas de las estimaciones de Capistrán et al. (2012) y Cortés (2013a) que se presentan en este trabajo, el error de cálculo resulta en un importante sesgo a la baja en la estimación de la elasticidad de traspaso del tipo de cambio a los precios.

Tercera. En términos de política económica las consecuencias son de lo más importante. La Junta de Gobierno del Banco de México ha utilizado sistemáticamente durante varios años estimaciones erróneas del traspaso del tipo de cambio a los precios para tomar decisiones de política monetaria¹⁰.

Comentario final. La estimación correcta de la elasticidad de traspaso del tipo de cambio a los precios en trabajos futuros requerirá no solamente corregir el error metodológico que se ha explicado en el presente trabajo. En particular, no bastará con estimar modelos similares utilizando tasas de crecimiento mensual. Será necesario, por ejemplo, incluir en el modelo una estimación de la brecha del producto. Sin embargo, debe reconocerse que la estimación de la brecha del producto requiere a su vez hacer una evaluación y selección de los diferentes filtros estadísticos disponibles para estimar el producto potencial. También deberá determinarse nuevamente el mejor número de rezagos para estimar el modelo y probar si diferentes ordenamientos de las variables en el modelo VAR producen resultados distintos. Es suma, se requerirá una discusión amplia del modelo VAR que debe estimarse. El presente trabajo no aborda estos temas pero deja abierto un campo fértil para futuras investigaciones.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.