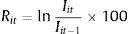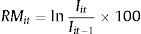Este documento tiene por objetivo probar la existencia de los efectos estacionales del día de la semana, mes del año, cambio de mes, fin de diciembre y superstición en los mercados de capitales de la Alianza del Pacífico durante el período 2002-2014. Para esto se emplea una metodología econométrica de estadísticos tradicionales y no paramétricos. Se pudo concluir que existe un efecto día de la semana para los mercados chileno, colombiano y peruano, el cual se comporta, en general, como lo sugiere la literatura, y un efecto cambio de mes para los mercados mexicano y peruano, que se comporta según lo sugerido por la literatura. No se detectó ningún efecto mes del año, fin de diciembre o superstición.
This document aims at testing the existence of the seasonal effects day of the week, month of the year, change of month, end of December and superstition in the capital stock markets of the countries belonging to the Pacific Alliance, during 2002-2014. For this, parametric and no parametric statistics econometric methodology were used. The results demonstrated that the day of the week effect existed in the Chilean, Colombian, and Peruvian markets, whose behavior, in general, agrees with the literature. In addition, change of month effect existed in the Mexican and Peruvian markets, whose behavior also agrees with the literature. The month of the year, end of December and superstition effects were not detected.
O objetivo deste documento é provar a existência dos efeitos sazonais do dia da semana, o mês do ano, a mudança de mês, o final de dezembro e a superstição nos mercados de capitais da Aliança do Pacífico durante o período 2002-2014. Para isso, é utilizada uma metodologia econométrica de estatísticos tradicionais não paramétricos. Concluiu-se que existe um efeito dia da semana para os mercados do Chile, da Colômbia e do Peru, que se comporta geralmente como sugerido pela literatura, e um efeito mudança de mês para os mercados mexicano e peruano, que se comporta como é sugerido pela literatura. Não foi detectado efeito mês do ano nenhum, nem final de dezembro ou superstição.
Motivada por la necesidad de conocer con mayor profundidad las características de las bolsas de valores que hacen parte de la Alianza del Pacífico, y en particular del Mercado Integrado Latinoamericano (MILA), la presente investigación buscó probar la existencia de 5 efectos calendario en estos mercados accionarios en el período 2002-2014.
Debe tenerse presente que, desde su apertura en 2011, el MILA se ha posicionado como el segundo mercado por capitalización bursátil de América Latina (MILA, 2015) y cobra aún más relevancia con la incorporación de la Bolsa Mexicana de Valores (BMV) en 2015. Aun así, es importante tener en cuenta que el MILA no es más que una autopista tecnológica que conecta las 4 bolsas de valores que lo componen, de modo que cada plaza bursátil sigue siendo independiente y, por ende, tiene características propias y, posiblemente, niveles de eficiencia y de estacionalidades diferentes (Worthington y Higgs, 2006).
Para Romero-Álvarez, Ramírez-Atehortúa y Guzmán-Aguilar (2013), el MILA permite mayor diversificación, pero los beneficios de esta no son tan evidentes, debido a los efectos de la integración de los mercados. La explicación más común para este fenómeno es que los riesgos para los inversionistas tienden a parecerse entre estos mercados (Romero-Alvarez, 2013), que tienen características importantes que los diferencian de los demás mercados latinoamericanos, como los menores costos de transacción asociados a la liquidez, las cuales justifican su integración (Agudelo, Barraza, Castro y Mongrut, 2012).
Figueroa (2014) considera que el MILA es una importante oportunidad para los inversionistas estadounidenses, al poder invertir simultáneamente en 4 (con la integración de México) de los países latinoamericanos más promisorios y con mayor potencial de crecimiento de sus mercados de capitales. Por su parte, Romero Tapia (2014) afirma que el MILA es el motor que dinamizará la Alianza del Pacífico, siempre y cuando se hagan reformas que permitan mayor profundidad de los mercados; esto porque uno de los retos más importantes que tiene este mercado integrado es el de la circulación y disponibilidad de la información (Seraylán, 2012).
Pese a la creciente importancia del MILA, la revisión de literatura muestra que no hay grandes avances académicos1 con respecto a él; además, si bien en América Latina se han desarrollado investigaciones sobre efectos estacionales, estas no han abarcado los 5 fenómenos que de manera conjunta se abordaron en esta investigación, ni han hecho énfasis en los 4 mercados aquí estudiados, pues la tendencia ha sido evaluar los efectos o los países por separado (French, 1980; Gibbons y Hess, 1981; Keim y Stambaugh, 1984).
Este trabajo se basa en el artículo sobre los efectos estacionales de Agrawal y Tandon (1994), en el cual los autores estudian estos 5 efectos para 18 países a nivel mundial. Así pues, un análisis que siga el formato de Agrawal y Tandon (1994), en el que se compilen varios efectos y países en un mismo documento, es poco frecuente a nivel general y completamente innovador para una investigación centrada en el MILA.
Una contribución de este trabajo consiste en que los fenómenos de calendario abren la posibilidad de que haya arbitraje en los mercados financieros y que los agentes del mercado, ajustando sus estrategias de inversión, puedan hacerse con retornos fruto de los efectos estacionales. Otra contribución de este artículo es la validación de la aplicabilidad de la hipótesis de mercados eficientes (HME) con datos empíricos en los mercados del MILA.
En el desarrollo de la investigación se encontró una limitación referida a la disponibilidad de los datos. Si bien los mercados estudiados en conjunto constituyen el segundo mercado por capitalización bursátil de América Latina, muchos de los títulos allí transados presentan problemas de liquidez, y estos mercados no son tan profundos como los de países desarrollados; aún más, no se asemejan en tamaño al mercado de Brasil, el más grande de la región.
Los resultados de esta investigación prueban la existencia del efecto día de la semana en los mercados de capitales chileno, colombiano y peruano; igualmente, muestran la existencia del efecto cambio de mes en las bolsas de México y Perú. Los efectos mes del año, fin de diciembre y superstición no se encontraron para ningún mercado.
El presente artículo está compuesto por 5 secciones; la segunda sección presenta la revisión de literatura, la tercera detalla la metodología, la cuarta expone y analiza los resultados y la quinta presenta las conclusiones.
2Revisión de literaturaEn esta sección se presenta la HME como el fundamento teórico que sustenta la investigación. Se revisa en particular la literatura que prueba el cumplimiento de esta hipótesis, desde la perspectiva del análisis de los efectos estacionales. De la misma manera, se explican los efectos estacionales y se hace referencia a los pocos estudios que hay para el caso latinoamericano. Dentro de esta revisión se destacan las metodologías que se han usado para calcular los efectos estacionales y se mencionan algunas de sus posibles causas.
2.1Hipótesis de mercados eficientesLos efectos estacionales en las bolsas de valores han recibido la atención de los investigadores especializados en la línea de estudio de la eficiencia de los mercados bursátiles, pero es uno de los temas menos estudiados; apenas el 9%, en promedio, de las publicaciones en el área lo han tratado (Duarte Duarte y Mascareñas, 2013).
Los estudios de la HME han derivado en diversas críticas. Cortés y Corzo (2009) hacen una revisión de las principales críticas a la HME, las cuales se resumen en 3 aspectos: primero, la presencia de autocorrelaciones en los rendimientos de los activos; segundo, la evidencia empírica de la sobrerreacción de los agentes del mercado, y tercero, el supuesto de las expectativas racionales, que no es suficiente para que los precios de los activos reflejen toda la información. A pesar de las críticas, estos autores coinciden en que la literatura reconoce una enorme dificultad de hacer predicciones en el mercado. Martínez Barbeito (2014) expresa que parte de la explicación de las anomalías presentadas en la literatura se encuentra en la ausencia de estudios sobre el efecto del análisis técnico y la lectura de charts, aunque reconoce que estas técnicas tienen limitaciones.
Por otra parte, Agudelo y Gutiérrez (2011) señalan que para el período 2003-2010 los mercados latinoamericanos no reaccionan con total eficiencia a los anuncios macroeconómicos, y en algunos casos solo incorporan la información con posterioridad a los anuncios. Por su parte, Aranda y Jaramillo (2010) recomiendan el uso de técnicas de evaluación que incorporen la no linealidad de las series financieras, puesto que su estudio para el mercado chileno se caracteriza por patrones no lineales.
Los autores Ojeda y Castaño (2014) encuentran que la hipótesis de eficiencia débil no se cumple en el caso del mercado colombiano, cuando se aplican pruebas paramétricas y se asume inexistencia de costos de transacción. Sin embargo, Olasolo, Ruiz y Pérez (2008) señalan que cuando las pruebas de mercados eficientes toman en cuenta los costos de transacción, la HME no se puede rechazar.
En general, Lobejón (2011) considera que la crisis ha hecho que la teoría de los mercados eficientes sea cuestionada y requiera de nueva evidencia empírica que la sustente desde sus mismas bases. De esta forma, para mercados con activos poco transados, como los latinoamericanos, resulta necesario utilizar información privilegiada para valorar los activos financieros (Londoño y Cuan, 2011).
2.2Efectos estacionalesLos efectos estacionales se refieren a comportamientos atípicos en ciertas fechas de los retornos de los activos que se transan en el mercado. Estos comportamientos contradicen la HME y permiten establecer predicciones sobre el comportamiento de los activos (Rivera, 2009). De esta forma se encuentran distintos tipos de efectos, que se abordan en esta investigación.
En primer lugar, el efecto día de la semana consiste en que los retornos diarios de los mercados siguen un patrón particular; se señala que los retornos de los lunes son particularmente bajos y los de los viernes, anormalmente altos; además, que el efecto lunes podía prolongarse a martes en algunos mercados determinados, elemento sujeto al huso horario de la plaza bursátil (Agrawal y Tandon, 1994). Este fenómeno es originalmente descubierto por Fields (1934) en el mercado accionario americano; tras él, otros académicos, como French (1980) y Gibbons y Hess (1981), prueban que el efecto realmente existe. Keim y Stambaugh (1984) encuentran que este efecto está presente para todos los tamaños de firmas, sin importar dónde se transen las acciones.
Rivera (2009) encontró que el efecto día de la semana se presentaba en Colombia antes de que las bolsas de valores del país se fusionaran, y que persistió después de la fusión; de esta forma, históricamente el martes ha sido el día de menores rendimientos, mientras que el viernes presenta mayores rendimientos; sus resultados son confirmados por Pérez y Mendoza (2010), quienes, además de usar pruebas paramétricas, emplean pruebas no paramétricas sobre una versión ampliada del índice de la bolsa, por considerar que el número de acciones de este es limitado. Los resultados de Rivera también están en línea con los de Ortiz, Peña y Espitia (2016), con la única diferencia de que el retorno de los días martes presenta un comportamiento favorable, mientras que el del lunes es desfavorable.
Para América Latina, Kristjanpoller (2012a) encuentra que el efecto día de la semana persiste en el mercado argentino, brasileño, chileno, colombiano y peruano, pero García (2010) considera que este efecto ya ha desaparecido (se basa en el índice LATIBEX), y coincide parcialmente con ciertos hallazgos de Rojas y Kristjanpoller (2014).
Algunos artículos recientes argumentan que el efecto día de la semana ha desaparecido en ciertos mercados desarrollados, donde las opciones sobre acciones son activamente transadas (Chen y Singal, 2003); esta posición es apoyada por el trabajo de Hansen, Lunden y Nason (2005), salvo en las firmas de baja capitalización, donde el efecto no ha decrecido. Algunas de las causas que han sido sugeridas para explicar este fenómeno son que los fines de semana no se transa (Latif, Arshad, Fatima y Farooq, 2011), diferencias de tiempo entre trading y settlement (Gibbons y Hess, 1981), malas noticias dadas por las firmas al final del viernes, anuncios macroeconómicos según el día de la semana que son realizados, posiciones cerradas por short sellers antes del fin de semana y teorías conductuales sobre el comportamiento de inversionistas individuales (Draper y Paudyal, 2002; Singal, 2004).
En segundo lugar, el efecto mes del año consiste en que los retornos de los mercados suelen seguir un patrón según el mes en el que se esté transando; normalmente se establecen retornos superiores a la media en enero e inferiores en diciembre (Agrawal y Tandon, 1994); Rozeff y Kinney (1976) encuentran este efecto para el mercado accionario americano. Posteriormente, Ariel (1987) realiza un estudio según el cual el fenómeno solo es válido para las pequeñas firmas, en la misma línea que García (2008); afirmación que contradicen Lakonishok y Smidt (1988). Loughran (1997) encuentra que los efectos mensuales varían si la acción es considerada una value stock o una growth stock, siendo más pronunciados en este último tipo. Para el caso de Latinoamérica, López y Rodríguez (2010) encuentran evidencia mixta del efecto mes del año, pero indican que existe cuando los índices se calculan en moneda local y deja de existir para algunos países cuando el índice se convierte a dólares.
En tercer lugar, sobre el efecto cambio de mes, el estudio más importante en la literatura es el de Lakonishok y Smidt (1988), quienes hallan que en el mercado americano el precio de las acciones alrededor del último día de trading del mes es mucho mayor que en el resto de los días. Por su parte, Kolahi (2006) encuentra resultados acordes con esta definición del efecto para los mercados accionarios europeos; su investigación coincide parcialmente con Agrawal y Tandon (1994), quienes notan que el efecto existe, pero únicamente por un período de tiempo. Por el contrario, Patel (2012) considera que el efecto ya no existe para varios índices de países desarrollados y emergentes. En este sentido, estudios más específicos, por características de las acciones, como los de Sharma y Narayan (2014), encuentran que el efecto sigue presente en el mercado americano, pero varía según la industria y el tamaño de la firma. Algunos estudios, como el de Kunkel, Compton y Beyer (2003), incluyen países de América Latina y hallan el efecto de cambio de mes; otros, como García (2010), consideran que este fenómeno ha decrecido en los últimos tiempos y ya no existe en la región, mientas que Kristjanpoller y Arenas (2015) prueban que el efecto aún persiste en Latinoamérica y hacen énfasis en su presencia en las principales acciones de la región.
En cuarto lugar, también se han conducido estudios sobre el efecto fin de diciembre y día feriado (en el que se incluyen los días anteriores a la Navidad y el Año Nuevo), los cuales han probado que existe en varios países (Kristjanpoller, 2012b); aun así, García (2010) no lo halla. El fin de diciembre y el día feriado son fenómenos que empiezan a ser notados por Lakonishok y Smidt (1988), quienes encuentran que para el período entre Navidad y Año Nuevo, y para los días de trading antes de estos días feriados, los retornos son anormalmente altos con respecto al resto del año en el mercado estadounidense. Ariel (1990) soporta este hallazgo y encuentra que los retornos son superiores a la media a lo largo de todo el día anterior a los diferentes festivos del año. Complementando lo anterior, Agrawal y Tandon (1994) encuentran que este efecto está presente en la mayoría de los países de su muestra, incluyendo México. Pese a esta línea de coincidencias en los diferentes estudios académicos, Chong, Hudson, Keasey y Littler (2005) consideran que el efecto ha desaparecido en los mercados desarrollados que ellos estudian, por la creciente sofisticación de las plazas bursátiles. Por otra parte, Edil (2012) encuentra que en firmas pequeñas del mercado asiático el efecto es más grande, pero la liquidez de la acción no lo afecta.
Por último, el efecto superstición es de los menos estudiados y, posiblemente, el que genera más dudas sobre su existencia (Lucey, 2000). En su estudio, Kolb y Rodriguez (1987) notan que los retornos de los viernes trece difieren negativamente de los retornos de otros viernes en el mercado americano. De otro lado, Dyl y Maberly (1988) encuentran que los resultados de los viernes 13 no son realmente diferentes, hallazgo que va en línea con Lakonishok y Smidt (1988), quienes consideran que la evidencia sobre este efecto se origina por un sesgo de selección. Agrawal y Tandon (1994) no encuentran este efecto, pero Keef y Khaled (2011) encuentran que existe para ciertos países de una muestra de 62 índices accionarios, en la que se incluían países como Chile, México y Perú. En contraste, Lucey (2000) halló este efecto en 11 de los 19 países que estudió, pero en el sentido contrario, es decir, se dan mayores retornos los viernes 13. Dado lo anterior, no hay estudios sobre este efecto según las características propias de las acciones, ni tampoco en América Latina o la Alianza del Pacífico.
En la evaluación de los efectos estacionales se usaban estadísticos tradicionales para comparar los retornos según el día (pruebas F y T), pero tras las críticas de Chang, Pinegar y Ravichandran (1993), quienes argumentan que los supuestos de estas pruebas hacen que sus resultados no sean realmente robustos, se proponen cálculos de White, correcciones de Cochrane y test estadísticos no paramétricos para el día de la semana (Chang et al., 1993; Pérez y Mendoza, 2010) y mes del año (Camilleri, 2008). En años recientes se ha popularizado el uso de modelos GARCH, porque permiten modelar la varianza del error, donde residen fuertes supuestos de los test estadísticos tradicionales (Kristjanpoller, 2012a; Kristjanpoller y Arenas, 2015; López y Rodríguez, 2010).
El modelo usado para entender el fenómeno de superstición considera estadísticos tradicionales (Kolb y Rodriguez, 1987), pero autores como Lucey (2000) han preferido incorporar pruebas no paramétricas en su investigación; la causa de este fenómeno sería enteramente psicológica y estaría asociada a la percepción que se tiene sobre fechas como el viernes 13 (Lucey, 2000). En la literatura reciente, posterior a 2000, no hay claridad sobre la existencia (ni dirección) de este fenómeno de superstición; por lo tanto, su causa sería enteramente psicológica.
3MetodologíaSe hace un análisis de series de tiempo de los retornos de los índices accionarios de Chile, Colombia, México y Perú, obtenidos en la plataforma Bloomberg. Dicho análisis se lleva a cabo en moneda local y en dólares, de la manera en que lo realizan López y Rodríguez (2010). Estas series se dividen en 2 periodos, del 2002 al 2008 y del 2009 al 2014, para entender si hay cambios en el tiempo, como lo proponen Agrawal y Tandon (1994) en su trabajo.
En este orden de ideas, los retornos diarios de los mercados son calculados mediante la siguiente ecuación:
donde Rit son los retornos diarios, Iit es el valor de cierre del índice e Iit−1 es el valor del día anterior. Para el caso de los retornos mensuales, la fórmula que se emplea es:RMit son los retornos mensuales, Iit es el valor en el último día transable del mes al que corresponda el retorno e Iit−1 es el valor en el último día transable del mes anterior.Se utilizaron regresiones por mínimos cuadrados ordinarios (MCO) con especificaciones diferentes, dependiendo del efecto por estudiar (tabla 1), tal como lo sugiere la literatura en este campo.
Modelos econométricos empleados para cada efecto
| Efecto | Modelo | Descripción |
|---|---|---|
| Día de la semana (Agrawal y Tandon, 1994) | Rit=a1D1t+a2D2t+a3D3t+a4D4t+a5D5t+et | Rt es el retorno del día; las variables D1t, D2t,…, D5t representan los días lunes, martes, miércoles, jueves y viernes, respectivamente; et corresponde al término del error |
| Mes del año (Sánchez, 2006) | Rit=b1DM1t+b2DM2t+b3DM3t+⋯+b11DM11t+b12DM12t+et | La variable DMnt es una dummy que se ajusta el mes n (n=1,2,…,12). Rit para este fenómeno son los retornos mensuales de los índices a estudiar, y et es el término del error |
| Cambio de mes (Kolahi, 2006) | Rit=β0+β1DTOMt+et | Donde Rit son los retornos para el periodo estudiado; DTOMt es una variable dummy cuando los retornos corresponden al período de 4 días de trading anteriores y posteriores al último día de trading del mes (− 4, +4) |
| Fin de diciembre y día feriado* (Agrawal y Tandon, 1994; Sánchez, 2006) | Rit=θ0+θ1DDt1+θ2DDt2+θ3DDt3+et | Donde Rit corresponde a los retornos del mercado; DDt1 es una variable dummy que se activa cuando el retorno se da en el período (1) que se quiere estudiar, DDt2 se activa para el período (2) y DDt3 para el período (3); et es el término del error |
| Superstición (Lucey, 2000) | Rit=ϕ0+ϕ1DSt+et | DSi es una variable dummy que marca 1 si el viernes analizado es 13 y 0 si es un viernes pero no es 13. Rit son los retornos diarios de los viernes, y et es el término del error |
Fuente: elaboración propia.
Cada modelo expuesto previamente se resuelve usando 2 técnicas: estadísticos tradicionales y estadísticos no paramétricos. El uso de estas 2 técnicas garantiza la triangulación metodológica por la que abogan Hussey y Hussey (1998), de manera tal que los resultados son más confiables. Lucey (2000) considera que por medio de esta triangulación y el uso de ambos tipos de estadísticos los resultados cobran especial robustez. Por otra parte, como segunda fase en la resolución de los modelos se sigue la metodología de pruebas no paramétricas sugerida por Chukwuogor (2007), Kunkel et al. (2003), Lucey (2000) y Pérez y Mendoza (2010).
Para solucionar el supuesto de la distribución normal del error se usa la prueba no paramétrica de Kruskal-Wallis2. Como elemento adicional a esta, puede resultar necesario realizar una prueba post-hoc que dictamine cuáles son las medias diferentes. El test post-hoc utilizado en este artículo es la prueba de Dunn-Bonferroni3, que es de las pruebas más usadas tras realizar un test de Kruskal-Wallis (Balluerka y Vergara, 2005).
Para los efectos cambio de mes y superstición se realiza únicamente una prueba de Kruskall-Wallis de una variable (la cual es igual a la prueba de Mann-Whitney), puesto que solamente hay una variable en la regresión.
4Resultados y análisisEsta sección presenta, en primer lugar, una subsección con el análisis descriptivo de los datos, lo cual facilita su comprensión y permite hacerse una idea general de los resultados. Posteriormente se presentan 5 subsecciones que dan cuenta de los resultados de las pruebas paramétricas y no paramétricas, en la búsqueda de cada uno de los efectos estacionales estudiados. Finalmente, se presentan las implicaciones de los resultados de la investigación.
4.1Estadísticas descriptivasEsta investigación trabajó con los índices generales de las bolsas de valores de los 4 países de la Alianza del Pacífico (tabla 2): Índice General de Precio de Acciones (IGPA, Chile), Índice General de la Bolsa de Valores de Colombia (IGBC, Colombia), Índice de Precios y Cotizaciones (MEXBOL, México) e Índice General de la Bolsa de Valores de Lima (IGBVL, Perú). Los índices generales son proxys del mercado sobre el que transan, y en teoría reflejan la canasta mejor diversificada del mercado (Berk y DeMarzo, 2007).
Estadísticas descriptivas de los retornos diarios de los índices (2002-2014)
| Retornos índice | Obs | Promedio | Desviación estándar | Varianza | Oblicuidad (Skewness) | Curtosis | |
|---|---|---|---|---|---|---|---|
| IGPA | Local | 3.247 | 0,0385 | 0,7884 | 0,6216 | −0,1801 | 13,9916 |
| USD | 3.247 | 0,0407 | 1,1529 | 1,3291 | −0,4559 | 12,0437 | |
| IGBC | Local | 3.171 | 0,0761 | 1,3228 | 1,7497 | −0,3069 | 15,5723 |
| USD | 3.171 | 0,0749 | 1,6611 | 2,7593 | −0,3954 | 11,9424 | |
| MEXBOL | Local | 3.275 | 0,0582 | 1,2796 | 1,6374 | 0,0630 | 8,7455 |
| USD | 3.275 | 0,0435 | 1,6291 | 2,6539 | −0,1249 | 10,1334 | |
| IGBVL | Local | 3.251 | 0,0778 | 1,4930 | 2,2291 | −0,5308 | 13,8333 |
| USD | 3.251 | 0,0822 | 1,5848 | 2,5116 | −0,5382 | 13,6529 | |
La información estadística descriptiva de cada índice se presenta en su moneda local (primera línea) y en dólares americanos (segunda línea).
Fuente: elaboración propia
Sobre las estadísticas descriptivas de los datos, se puede destacar que al analizar los retornos diarios de cada mercado los índices cuyas desviaciones estándar son más altas no son necesariamente los que más retornos generan; esto podría darse fruto de la llamada «anomalía de la baja volatilidad», según la cual portafolios con menor desviación estándar pueden obtener retornos superiores en el largo plazo, rompiendo con la teoría del Capital Asset Pricing Model (CAPM) (Haugen y Heins, 1975).
Por otra parte, son evidentes las diferencias entre los retornos en moneda local y en dólares, lo cual muestra la necesidad de realizar los análisis de los efectos en ambas.
Respecto a los retornos según el día de la semana, llama la atención que los lunes hay retornos más pequeños (menos para el IGBVL) y los viernes retornos superiores (menos para el MEXBOL). Con respecto a los retornos mensuales en moneda local, los valores para los meses de marzo del MEXBOL y el IGBVL son superiores. Los retornos del IGBC en los meses de julio parecen ser considerablemente superiores al resto de meses, y los retornos de noviembre para la IGBVL son bastante negativos; igualmente, destacan las fuertes fluctuaciones que presenta el índice peruano, en moneda local y en dólares (figs. 1-4). Por lo tanto, no parece haber evidencia que soporte el efecto mes del año sugerido por la literatura.
Según las estadísticas descriptivas, es posible que existan los efectos estacionales en los mercados del MILA; este hecho resulta más plausible para el caso del efecto día de la semana; por otro lado, es posible que exista un efecto mes del año de manera diferente al que tradicionalmente se presenta en estos mercados.
4.2Efecto día de la semanaLos estadísticos tradicionales (tabla 3) muestran que existe el efecto día de la semana en los mercados chileno y colombiano, y en menor medida en el peruano. En Chile, el efecto persiste con un nivel de significancia del 5% durante todos los períodos de tiempo, en moneda local y en dólares; en línea con la literatura revisada, los días lunes y martes existe una correlación negativa con los retornos, y los viernes, positiva. Para Colombia, el efecto se encuentra en 2002-2014 y en 2002-2008 en moneda local y en dólares; dado que en 2009-2014 no se encontró el efecto, es probable que esté desapareciendo; adicionalmente, la prueba de estabilidad de Chow4 rechaza la hipótesis de estabilidad en los parámetros en ambos períodos, lo que indica un cambio estructural en 2008. En el caso del mercado peruano, en el período 2002-2014 los retornos de los días lunes, martes y miércoles tienen un coeficiente negativo, mientras que los viernes el coeficiente es positivo; en este caso, la inconsistencia entre los resultados de la prueba F y la prueba T puede deberse a las restricciones de los estadísticos tradicionales, aunque cabe destacar que la prueba de multicolinealidad Variance Inflation Factors (VIF) no es preocupante.
Pruebas estadísticas tradicionales para el efecto día de la semana
| Día | IGPA | IGBC | MEXBOL | IGBVL | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | |||||||||
| Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef, | p>t | Coef, | p>t | |
| dlunes | −0,16844 | 0,000* | −0,21546 | 0,001* | −0,31915 | 0,000* | −0,41543 | 0,000* | −0,03005 | 0,673 | −0,11714 | 0,196 | −0,20376 | 0,014* | −0,23460 | 0,008* |
| dmartes | −0,09527 | 0,029* | −0,14844 | 0,020* | −0,23747 | 0,001* | −0,28408 | 0,002* | 0,00383 | 0,957 | −0,08436 | 0,348 | −0,22096 | 0,008* | −0,25592 | 0,004* |
| dmiercoles | −0,04566 | 0,296 | −0,08984 | 0,160 | −0,09364 | 0,198 | −0,14963 | 0,101 | 0,01927 | 0,785 | −0,07619 | 0,396 | −0,17196 | 0,038* | −0,18985 | 0,031* |
| djueves | −0,03096 | 0,479 | 0,05682 | 0,373 | −0,12385 | 0,090 | −0,14330 | 0,119 | −0,01268 | 0,858 | −0,11953 | 0,186 | −0,12663 | 0,128 | −0,13821 | 0,118 |
| dviernes | 0,10624 | 0,001* | 0,11955 | 0,008* | 0,22524 | 0,000* | 0,26584 | 0,000* | 0,06194 | 0,217 | 0,12278 | 0,054 | 0,22297 | 0,000* | 0,24652 | 0,000* |
| Prueba F | 0,0013* | 0,0001* | 0,0002* | 0,0002* | 0,9687 | 0,6816 | 0,0587 | 0,0296* | ||||||||
| dlunes | −0,17898 | 0,003* | −0,20862 | 0,019* | −0,48907 | 0,000* | −0,58320 | 0,000* | −0,04238 | 0,643 | −0,16304 | 0,198 | −0,13801 | 0,245 | −0,17214 | 0,168 |
| dmartes | −0,09289 | 0,120 | −0,17874 | 0,042* | −0,44328 | 0,000* | −0,52626 | 0,000* | −0,10843 | 0,229 | −0,19115 | 0,126 | −0,22370 | 0,059 | −0,27608 | 0,026* |
| dmiercoles | −0,00555 | 0,926 | −0,08640 | 0,326 | −0,21346 | 0,066 | −0,32234 | 0,024* | 0,01535 | 0,865 | −0,08147 | 0,515 | −0,16378 | 0,166 | −0,18574 | 0,135 |
| djueves | 0,01818 | 0,761 | 0,05399 | 0,538 | −0,20504 | 0,079 | −0,33576 | 0,019* | −0,07397 | 0,414 | −0,20063 | 0,110 | −0,15691 | 0,188 | −0,19006 | 0,129 |
| dviernes | 0,09320 | 0,028* | 0,12619 | 0,043* | 0,37869 | 0,000* | 0,46251 | 0,000* | 0,08551 | 0,183 | 0,16687 | 0,061 | 0,23939 | 0,004* | 0,27310 | 0,002* |
| Prueba F | 0,0045* | 0,0112* | 0,0002* | 0,0006* | 0,6269 | 0,4491 | 0,4198 | 0,2631 | ||||||||
| dlunes | −0,15683 | 0,015* | −0,22306 | 0,017* | −0,11977 | 0,156 | −0,21704 | 0,054 | −0,01932 | 0,856 | −0,07805 | 0,544 | −0,27876 | 0,015* | −0,30567 | 0,013* |
| dmartes | −0,09827 | 0,124 | −0,11286 | 0,224 | 0,00452 | 0,955 | 0,00073 | 0,995 | 0,10044 | 0,343 | 0,00732 | 0,954 | −0,21789 | 0,058 | −0,23256 | 0,060 |
| dmiercoles | −0,09259 | 0,148 | −0,09366 | 0,314 | 0,04769 | 0,552 | 0,05383 | 0,614 | 0,02255 | 0,831 | −0,07180 | 0,574 | −0,18137 | 0,113 | −0,19452 | 0,115 |
| djueves | −0,08913 | 0,164 | 0,06019 | 0,518 | −0,02708 | 0,737 | 0,08324 | 0,438 | 0,04023 | 0,706 | −0,04974 | 0,700 | −0,09156 | 0,427 | −0,07817 | 0,528 |
| dviernes | 0,12172 | 0,008* | 0,11166 | 0,092 | 0,04468 | 0,433 | 0,03442 | 0,650 | 0,04184 | 0,578 | 0,08520 | 0,348 | 0,20391 | 0,012* | 0,21566 | 0,014* |
| Prueba F | 0,0041* | 0,0268* | 0,3668 | 0,0748 | 0,8252 | 0,9412 | 0,1214 | 0,097 | ||||||||
En la primera columna se encuentran los períodos para los cuales se realizó el análisis. La siguiente columna muestra el coeficiente de la regresión por MCO que se encontró para cada día y a continuación se encuentra el valor p de la prueba T (y de la prueba F cuando la línea corresponde a este test). Las columnas muestran los retornos tanto en moneda local como en dólares de cada índice general.
Fuente: elaboración propia
Los resultados de la prueba de Kruskal-Wallis (tabla 4) coinciden en su mayoría con los estadísticos tradicionales. El efecto existe para el IGPA, menos para el periodo 2009-2014, en moneda local; está presente en el IGBC en ambas monedas para 2002-2014 y 2002-2008, mientras que en Perú existe únicamente en 2002-2014. Al realizar la prueba de contrastes de Dunn-Bonferroni (tabla 5) y revisar las diferencias en las medias de los rangos, los resultados para el mercado chileno son similares a los estadísticos tradicionales: parece existir una diferencia constante (y negativa) entre los retornos de los lunes y los de los jueves y viernes. Con los estadísticos no paramétricos, esta diferencia pierde significancia.
Prueba de Kruskal-Wallis para el efecto día de la semana
| Período | IGPA | IGBC | MEXBOL | IGBVL | ||||
|---|---|---|---|---|---|---|---|---|
| RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | |
| Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | |
| 2002-2014 | 0,0001* | 0,0001* | 0,0004* | 0,0011* | 0,9549 | 0,5903 | 0,0278* | 0,0093* |
| 2002-2008 | 0,0001* | 0,0003* | 0,0001* | 0,0006* | 0,9551 | 0,9066 | 0,1302 | 0,0562 |
| 2009-2014 | 0,1123 | 0,0016* | 0,3785 | 0,1253 | 0,8074 | 0,5085 | 0,2436 | 0,1977 |
En la primera columna se encuentran los períodos para los cuales se realizó el análisis. En las siguientes columnas se encuentran cada uno de los índices generales con sus retornos tanto en moneda local como en dólares, cada casilla refleja el valor p encontrado usando la prueba de Kruskal-Wallis entre días para cada uno de los períodos.
Fuente: elaboración propia
Prueba Dunn-Bonferroni para el efecto día de la semana
| Prueba Dunn-Bonferroni de contrastes: P-Valor | IGPA | IGBC | IGBVL | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | |||||||
| 2002-2014 | 2002-2008 | 2002-2014 | 2002-2008 | 2008-2014 | 2002-2014 | 2002-2008 | 2002-2014 | 2002-2008 | 2002-2014 | 2002-2014 | ||
| Lunes | Martes | 0,571 | 0,908 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Lunes | Miércoles | 0,001* | 0,001* | 0,104 | 0,273 | 1 | 0,08 | 0,587 | 0,27 | 1 | 1 | 1 |
| Lunes | Jueves | 0,001* | 0* | 0* | 0,002* | 0,001* | 0,053 | 0,15 | 0,05 | 1 | 1 | 1 |
| Lunes | Viernes | 0* | 0,002* | 0* | 0,018* | 0,037* | 0* | 0,001* | 0,001* | 0,005* | 0,188 | 0,095 |
| Martes | Miércoles | 0,54 | 0,254 | 1 | 0,771 | 1 | 1 | 0,506 | 1 | 1 | 1 | 1 |
| Martes | Jueves | 0,356 | 0,112 | 0,001* | 0,012* | 0,179 | 0,692 | 0,115 | 0,563 | 0,572 | 1 | 1 |
| Martes | Viernes | 0,06 | 0,339 | 0,032* | 0,072 | 1 | 0,016* | 0* | 0,031* | 0,001* | 0,015* | 0,004* |
| Miércoles | Jueves | 1 | 1 | 0,056 | 1 | 0,151 | 1 | 1 | 1 | 1 | 1 | 1 |
| Miércoles | Viernes | 1 | 1 | 0,803 | 1 | 1 | 1 | 0,282 | 0,923 | 0,116 | 0,592 | 0,462 |
| Jueves | Viernes | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0,342 | 0,952 | 0,589 |
Las primeras 2 columnas muestran los días que son comparados por medio de la prueba post-hoc. Las siguientes columnas reflejan los valores p de cada test según los días que estén siendo comparados y según los retornos de los índices donde la prueba Kruskal-Wallis haya sido significativa al 95%.
Fuente: elaboración propia
Dado lo anterior, se concluye que el efecto día de la semana existe en los mercados chileno, colombiano y peruano; estos hallazgos coinciden con el estudio de Pérez y Mendoza (2010) para el caso colombiano. Por otra parte, el rezago del efecto a los días martes va en línea con lo encontrado por Agrawal y Tandon (1994).
Kristjanpoller (2012a) halla el efecto día de la semana para el mercado chileno, colombiano y peruano, al igual que en este estudio; no obstante, Rojas y Kristjanpoller (2014) encuentran parcialmente el efecto en estos mercados. Pese a estas similitudes, García (2010) no encuentra efecto día de la semana para el índice LATIBEX.
La explicación económica de este efecto se ha sustentado en la diferencia proveniente de los días no transables del fin de semana (Latif et al., 2011) en los mercados de la región, diferencias de tiempo entre trading y settlement (Gibbons y Hess, 1981), anuncios macroeconómicos según el día de la semana que son realizados, posiciones cerradas por short sellers antes del fin de semana y teorías conductuales sobre el comportamiento de inversionistas individuales (Draper y Paudyal, 2002; Singal, 2004); en la misma línea de la interpretación hecha por Mills, Siriopoulos, Markellos y Harizanis (2000), se podría pensar que las malas noticias dadas por las firmas al final del viernes en los mercados objeto de estudio repercuten en los retornos diarios de los índices.
4.3Efecto mes del añoA partir de los resultados de las pruebas F, en ninguno de los países estudiados parece existir el efecto mes del año. Para el caso de las pruebas específicas, solo 2 meses parecen ser significativos, pero los signos de ambos hallazgos van en contra de lo sugerido por la literatura académica revisada (el análisis VIF mostró que la multicolinealidad de la muestra no era preocupante). Al realizar la prueba de Kruskal-Wallis se encuentra que no existe este efecto. Se concluye, entonces, que los retornos de los mercados del MILA no varían según el mes del año, lo cual está en línea con los hallazgos de García (2010) y de Rojas y Kristjanpoller (2014), así como con el estudio de López y Rodríguez (2010) para los retornos en dólares, pero con resultados diferentes para el caso de la moneda local. En síntesis, ningún mercado de la Alianza del Pacífico presenta estacionalidades mensuales.
4.4Efecto cambio de mesLos estadísticos tradicionales (tabla 6) indican que el efecto cambio de mes existe para los mercados mexicano y peruano, tanto en dólares como en moneda local, pero parece que ha tendido a desaparecer5. Para el caso del MEXBOL, se encuentra una correlación positiva en el momento del cambio de mes, tanto en dólares como en pesos mexicanos, durante 2002-2014; cuando se realiza el mismo análisis para los 2 subperíodos, únicamente se encuentra el efecto para 2002-2008, en moneda local. Para el IGBVL se encuentra una correlación positiva (y con coeficiente superior al resto de mes) en el momento del cambio de mes para ambas monedas, tanto en 2002-2014 como en 2002-2008.
Pruebas estadísticas tradicionales para el efecto cambio de mes
| Período | Período del mes | IGPA | IGBC | MEXBOL | IGBVL | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | ||||||||||
| Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | Coef. | p>t | ||
| 2002-2014 | Cambio de mes | 0,0197733 | 0,479 | 0,0417781 | 0,307 | 0,0469592 | 0,321 | 0,0456592 | 0,442 | 0,1087679 | 0,016* | 0,130326 | 0,023* | 0,1149589 | 0,030* | 0,1154627 | 0,040* |
| Resto de mes | 0,0299831 | 0,102 | 0,0226688 | 0,398 | 0,0553944 | 0,078 | 0,0547016 | 0,166 | 0,0117241 | 0,691 | −0,0122402 | 0,745 | 0,0282734 | 0,415 | 0,0324713 | 0,378 | |
| 2002-2008 | Cambio de mes | 0,0115302 | 0,764 | 0,0339962 | 0,546 | 0,0542972 | 0,474 | 0,0434807 | 0,640 | 0,1314258 | 0,053 | 0,1336954 | 0,103 | 0,18126 | 0,016* | 0,1899754 | 0,017* |
| Resto de mes | 0,0372933 | 0,139 | 0,0284703 | 0,441 | 0,0923005 | 0,067 | 0,0980047 | 0,113 | 0,0148354 | 0,737 | −0,0101307 | 0,850 | 0,0243184 | 0,624 | 0,025874 | 0,619 | |
| 2009-2014 | Cambio de mes | 0,0294678 | 0,469 | 0,0509109 | 0,391 | 0,0387091 | 0,456 | 0,0484988 | 0,484 | 0,0825272 | 0,153 | 0,1264521 | 0,114 | 0,0380393 | 0,604 | 0,0290285 | 0,713 |
| Resto de mes | 0,0213712 | 0,425 | 0,0158343 | 0,685 | 0,0122997 | 0,722 | 0,0041371 | 0,928 | 0,0080599 | 0,831 | −0,0147246 | 0,779 | 0,0328407 | 0,494 | 0,04009 | 0,438 | |
La primera columna muestra los períodos que son analizados. La segunda columna indica si el coeficiente de la columna 3 para el momento de cambio de mes o para el resto del mes. Las siguientes columnas tienen los datos de cada índice tanto en moneda local como en dólares. La columna llamada Coef. muestra los coeficientes de la regresión por MCO para cada momento del mes, la columna siguiente refleja el valor p de la prueba T para cada uno de esos momentos.
Fuente: elaboración propia
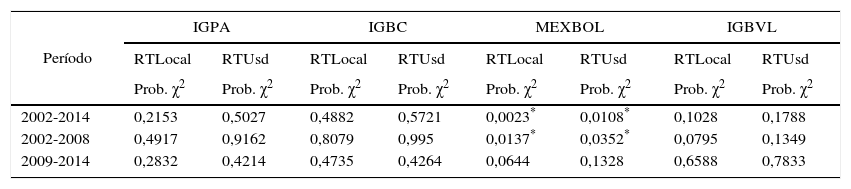
Cuando se realiza este mismo análisis por medio de la prueba de Mann-Whitney, el efecto cambio de mes se encuentra únicamente para el mercado mexicano al 95% (tabla 7). Según la literatura, entre las causas de este fenómeno están las fechas de los anuncios macroeconómicos, el flujo periódico de fondos a los mercados, la estandarización de los sistemas de pago y razones conductuales sobre el comportamiento de inversionistas, esperando cambios positivos y nueva información en el mes siguiente (Latif et al., 2011; Nikkinen, Sahlström, Takko y Äijö, 2009).
Prueba de Mann-Whitney para el efecto cambio de mes
| Período | IGPA | IGBC | MEXBOL | IGBVL | ||||
|---|---|---|---|---|---|---|---|---|
| RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | RTLocal | RTUsd | |
| Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | Prob. χ2 | |
| 2002-2014 | 0,2153 | 0,5027 | 0,4882 | 0,5721 | 0,0023* | 0,0108* | 0,1028 | 0,1788 |
| 2002-2008 | 0,4917 | 0,9162 | 0,8079 | 0,995 | 0,0137* | 0,0352* | 0,0795 | 0,1349 |
| 2009-2014 | 0,2832 | 0,4214 | 0,4735 | 0,4264 | 0,0644 | 0,1328 | 0,6588 | 0,7833 |
La primera columna indica el período que es analizado. Las siguientes columnas muestran los índices generales tanto en moneda local como en dólares. De la cuarta a la novena línea se muestran los resultados del valor p de la prueba de Mann-Whitney.
Fuente: elaboración propia
La evidencia sugiere que este efecto cambio de mes existe, aunque con una tendencia a desaparecer.
Se puede concluir con certeza que el efecto cambio de mes existe en el mercado mexicano y posiblemente en el peruano, en ambos casos de la manera clásica. También se puede afirmar que ni en Chile ni en Colombia hay indicios de que este fenómeno exista. Este hallazgo coincide con los resultados de Kunkel et al. (2003) y Kristjanpoller y Arenas (2015) sobre México (y Perú para este último estudio), pero dista para los demás países.
4.5Efecto fin de diciembre y día feriadoLos resultados de los estadísticos tradicionales muestran la posible existencia del efecto fin de diciembre únicamente para el IGBC (Colombia), aunque para ningún caso el estadístico de la prueba F es significativo. Cuando se realiza la prueba de Kruskal-Wallis no se encuentra que el efecto exista. Este hallazgo coincide con los resultados de García (2010). Kristjanpoller (2012b) encuentra que el efecto día feriado existe para Chile y Perú. Luego el efecto fin de diciembre y día feriado, para Año Nuevo y Navidad, no existe en el MILA.
4.6Efecto supersticiónLos estadísticos no son significativos para ninguno de los países estudiados, en ninguno de los períodos y en ninguna de las monedas. La prueba de Mann-Whitney muestra que el efecto superstición no existe para ninguno de los países. Este hallazgo va en línea con los resultados de Agrawal y Tandon (1994) para México, pero es diferente a lo hallado por Lucey (2000). En general, no existe ningún trabajo que se enfoque en este efecto para América Latina ni para la Alianza del Pacífico.
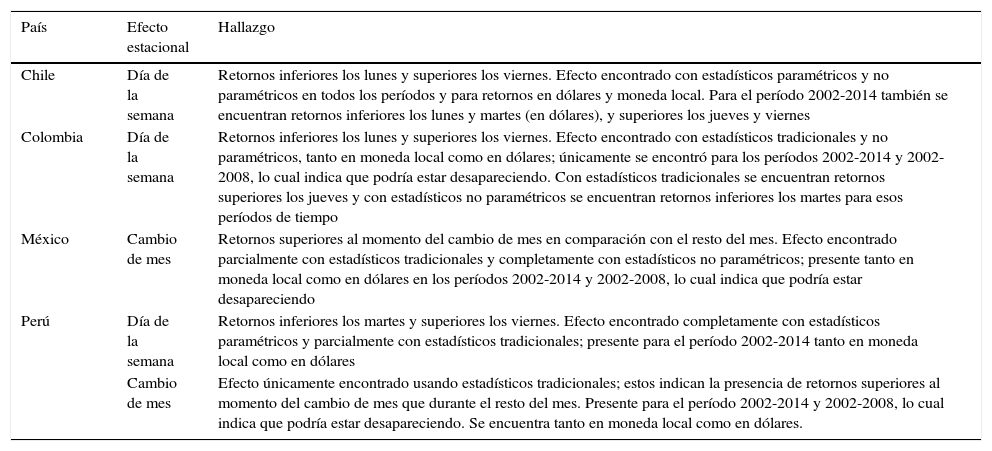
En síntesis, existen ciertas estacionalidades para los 4 mercados de la Alianza del Pacífico. Sin embargo, se debe tener en cuenta que las economías latinoamericanas han experimentado una mejora en su eficiencia de mercado en los últimos 10años (Duarte Duarte y Mascareñas, 2014). En la tabla 8 se hace un resumen de los resultados encontrados para cada país.
Resumen de los hallazgos por país
| País | Efecto estacional | Hallazgo |
|---|---|---|
| Chile | Día de la semana | Retornos inferiores los lunes y superiores los viernes. Efecto encontrado con estadísticos paramétricos y no paramétricos en todos los períodos y para retornos en dólares y moneda local. Para el período 2002-2014 también se encuentran retornos inferiores los lunes y martes (en dólares), y superiores los jueves y viernes |
| Colombia | Día de la semana | Retornos inferiores los lunes y superiores los viernes. Efecto encontrado con estadísticos tradicionales y no paramétricos, tanto en moneda local como en dólares; únicamente se encontró para los períodos 2002-2014 y 2002-2008, lo cual indica que podría estar desapareciendo. Con estadísticos tradicionales se encuentran retornos superiores los jueves y con estadísticos no paramétricos se encuentran retornos inferiores los martes para esos períodos de tiempo |
| México | Cambio de mes | Retornos superiores al momento del cambio de mes en comparación con el resto del mes. Efecto encontrado parcialmente con estadísticos tradicionales y completamente con estadísticos no paramétricos; presente tanto en moneda local como en dólares en los períodos 2002-2014 y 2002-2008, lo cual indica que podría estar desapareciendo |
| Perú | Día de la semana | Retornos inferiores los martes y superiores los viernes. Efecto encontrado completamente con estadísticos paramétricos y parcialmente con estadísticos tradicionales; presente para el período 2002-2014 tanto en moneda local como en dólares |
| Cambio de mes | Efecto únicamente encontrado usando estadísticos tradicionales; estos indican la presencia de retornos superiores al momento del cambio de mes que durante el resto del mes. Presente para el período 2002-2014 y 2002-2008, lo cual indica que podría estar desapareciendo. Se encuentra tanto en moneda local como en dólares. |
Fuente: elaboración propia.
Los hallazgos de este estudio contradicen la HME en los mercados referenciados; aunque algunos de los efectos estudiados parecen desaparecer, otros se han mantenido a lo largo del período de estudio. Esta persistencia implica que tales efectos constituyen una anomalía, puesto que no parecen corregirse con el paso del tiempo.
La principal implicación de este comportamiento es que los agentes de mercado pueden intervenir de manera activa para conseguir oportunidades de arbitraje. En un mercado eficiente, dichas oportunidades de arbitraje desaparecerían. Sin embargo, los resultados encontrados tienen, en consecuencia, una segunda implicación, que consiste en que los agentes de mercado no actúan de manera racional, o su racionalidad es limitada.
Algunos estudios señalan la imposibilidad de asegurar la existencia de los efectos tratados, debido a problemas con el uso de los datos o a los sesgos metodológicos derivados de cada estudio; sin embargo, esta investigación demuestra la existencia de tales efectos con pruebas paramétricas y no paramétricas, además de establecer diferencias en los períodos considerados.
Como resultado de estas anomalías, se espera que agentes del mercado puedan beneficiarse de retornos extraordinarios mediante el uso de estrategias de inversión que se ajusten a la existencia de tales anomalías.
5ConclusionesEs posible evidenciar diferencias entre las estacionalidades de las plazas bursátiles de los países de la Alianza del Pacífico y, en particular, del MILA. Se puede concluir que existe un efecto día de la semana para los mercados chileno, colombiano y peruano, el cual se comporta, en general, como lo sugiere la literatura académica. Por otro lado, se pudo hallar un efecto cambio de mes para los mercados mexicano y peruano; en ambos casos, el efecto se comporta según lo sugerido por la literatura. No se detectó ningún efecto mes del año, fin de diciembre o superstición en los mercados de la Alianza del Pacífico.
El hecho de que existan efectos estacionales en la región conduce a rechazar la HME en su forma más débil. Pese a toda la literatura académica existente sobre estos fenómenos, los mercados del MILA aún no han interiorizado estas oportunidades de arbitraje. La existencia de ciertos efectos calendario en los mercados aquí estudiados es un hallazgo importante que puede ser utilizado con fines económicos por inversionistas especializados en procesos de arbitraje; el hecho de que existan efectos periódicos predecibles abre la puerta para que comisionistas de bolsa u otras entidades financieras encuentren oportunidades de obtener beneficios extraordinarios por ineficiencias del mercado.
Con la metodología que siguió este trabajo, fundamentada en las sugerencias de Hussey y Hussey (1998), Lucey (2000) y Pérez y Mendoza (2010), se pretendía realizar una triangulación de pruebas estadísticas para que los resultados fueran robustos, pero es necesario mencionar que los estadísticos tradicionales manejan supuestos fuertes. Igualmente, los estadísticos no paramétricos pueden ser más flexibles, pero pierden cierto nivel de confianza; por ende, no deja de ser importante anotar que ambas pruebas estadísticas tienen limitaciones.
Finalmente, para futuras investigaciones podría resultar interesante conocer las causas de los efectos calendario en la región, como método para validar las diferentes hipótesis que existen sobre su origen. Igualmente, se podría estudiar qué sucede con los efectos cuando los mercados de la Alianza del Pacífico profundicen su integración. Una línea inmediata de aplicación de estos resultados puede ser la definición de portafolios de inversión que se ajusten a la existencia de las anomalías aquí encontradas. Mediante la simulación de los rendimientos de estos portafolios se puede probar la existencia de posibilidades de arbitraje.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Algunos de los artículos más importantes en el tema son el de Uribe y Mosquera (2014) y el de Vargas y Bayardo (2013).
Este artículo se basa en el trabajo de grado que desarrolló David Arbeláez Gracía, bajo la tutoría del profesor John Rosso, para optar al título de economista en la Universidad de Los Andes.
La prueba de Kruskal-Wallis es una herramienta estadística que permite probar la igualdad de medias sin asumir la normalidad del error. Si la prueba rechaza la hipótesis nula (según la cual las medias son iguales), únicamente se puede afirmar que existe diferencia entre las medias; no se puede determinar qué grupo de medias son diferentes.
Como ventaja, esta prueba controla la tasa de error cuando las comparaciones se plantean a priori (Balluerka y Vergara, 2005).
Esta es una prueba que se usa en series de tiempo para determinar si los parámetros del modelo permanecen constantes a lo largo del tiempo (Gujarati, 2004).