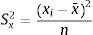El desarrollo que ha presentado el mercado mayorista de energía en Colombia ha permitido que hoy en día se estén negociando futuros de electricidad en el mercado de capitales local. Este trabajo tiene como objetivo diseñar un producto derivado en el que subyace el precio de la electricidad. Para esto, se analiza la serie de tiempo del precio de la electricidad para modelar su volatilidad; y a partir de esta, se diseña una opción exótica tipo barrera que muestra cómo se pueden usar este tipo de productos financieros en la cobertura de riesgos de los agentes del mercado.
The development of the Colombian wholesale energy market has currently allowed it to trade electricity futures in local capital markets. This work aims to design a derivative, which has the price of electricity as the underlying. For this, we analyzed the time series of electricity price volatility modeling, and from this, an exotic barrier‐type option was designed that shows how to use this type of financial products to cover risks from market agents.
O desenvolvimento que o mercado grossista de energia na Colômbia apresentou permitiu que hoje em dia se estejam a negociar futuros de electricidade no mercado local de capitais. Este trabalho tem como objectivo desenhar um produto derivado que tem como subjacente o preço da electricidade. Para tal, analisa‐se a série de tempo do preço da electricidade para modelar a sua volatilidade; e a partir desta desenha‐se uma opção singular, tipo barreira, que mostra como se podem usar este tipo de produtos financeiros na cobertura de riscos dos agentes do mercado.
El sector energético siempre ha sido uno de los más importantes para el desarrollo de un país. Desde la década de los 90, y específicamente desde 1993 con la promulgación de la llamada Ley Eléctrica, la industria de la energía eléctrica nacional ha sufrido constantes cambios que permiten considerarla hoy en día una de las industrias más modernas y desarrolladas no solo del país, sino de toda América Latina. Dentro de los avances más importantes se encuentra el progreso en los instrumentos que tienen los operadores generadores y comercializadores para realizar las diferentes transacciones. Por ejemplo, el naciente mercado de derivados sobre productos energéticos (DERIVEX) abre la puerta para que se estructuren diferentes productos que ayuden a los operadores del mercado en la minimización de riesgos financieros y en la maximización de sus utilidades.
En este sentido, este trabajo busca hacer aportes en el diseño y uso de productos derivados, que tengan como subyacente el precio de la electricidad, para el mercado mayorista de energía en Colombia. De esta forma, en este documento de investigación se diseña una estrategia de cobertura con aplicación de productos derivados y análisis de riesgos basados en la modelación de la tendencia y volatilidad del precio spot de la energía eléctrica para el corto plazo. Es decir, se considera que los factores fundamentales y estructurales del mercado los recoge el comportamiento de los precios; por ende, una modelización del precio spot para el corto plazo se considera suficiente para estimar su volatilidad con el fin de establecer coberturas.
Para esto, el documento se desarrolla de la siguiente forma. La primera sección es esta introducción. En la segunda se estiman modelos econométricos de series de tiempo, modelo autorregresivo integrado de media móvil (ARIMA, del inglés autoregressive integrated moving average) y modelos autorregresivos con heterocedasticidad condicional (ARCH, del inglés, autorregresive conditional heteroscedasticity)‐GARCH con el fin de establecer el proceso estocástico que da origen a la serie de precio spot de la electricidad, de tal forma que sea posible estimar su tendencia y su volatilidad. En la tercera sección, se hace uso de los procedimientos y metodologías propias de la ingeniería financiera para estructurar un producto derivado que sirva de cobertura frente al riesgo de mercado identificado en la sección anterior; para esto, se calcula la prima que tendría una opción exótica tipo barrera. En la cuarta sección se incluyen las conclusiones.
2Modelo para el cálculo de la volatilidad diaria de la energía eléctrica en el mercado mayorista de energía en ColombiaCasi todas las distribuciones pueden ser descritas dentro de 4 momentos (algunas distribuciones requieren un momento, mientras que otras requieren 2, y así sucesivamente). Las estadísticas descriptivas capturan cuantitativamente estos momentos.
El primer momento describe la ubicación de una distribución y es interpretado como un valor esperado, ganancias esperadas, o el valor promedio de los sucesos. El segundo momento mide la dispersión o el ancho de una distribución, y es frecuentemente descrito utilizando medidas tales como la desviación estándar y la varianza. La desviación estándar indica el promedio de desviación de todos los datos respecto a su media y es una medida popular que está asociada con el riesgo (una desviación estándar alta significa una distribución más abierta y dispersa, o también una dispersión más extensa de datos alrededor de la media, por consiguiente un riesgo más alto) y sus unidades son idénticas a los datos originales. El cálculo de la varianza es el siguiente:
Otros elementos estadísticos para analizar la forma de la distribución son la curtosis y el sesgo. La curtosis mide qué tanto se levantan los datos respecto al eje horizontal e indica la concentración de la distribución; si el coeficiente es mayor que cero, igual a cero o menor que cero, la serie es leptocúrtica (colas delgadas), mesocúrtica y platicúrtica (colas gordas), respectivamente.
También se puede referenciar con valores positivos y negativos; así, un valor positivo en la curtosis indica una distribución relativamente acentuada y una curtosis negativa indica una distribución relativamente plana. La curtosis medida aquí ha sido centrada en cero. Aun cuando ambas son igual de válidas, centrándola alrededor de cero lleva una interpretación más sencilla. Una curtosis muy negativa indica una distribución muy aplanada (platicúrtica o con colas gordas). Esto indica una probabilidad más alta de eventos extremos (por ejemplo, eventos catastróficos, ataques terroristas, caídas en el precio de la bolsa de energía) que se predicen en una distribución normal. Por último, el sesgo indica el grado de asimetría de una distribución alrededor de su media. Un sesgo positivo indica una distribución con una cola asimétrica extendiéndose hacia valores positivos y un sesgo negativo indica una distribución con una cola asimétrica extendiéndose hacia valores negativos.
Esta sección está subdividida en 3 partes que permitirán abordar la construcción del modelo para estimar la volatilidad del precio de la electricidad. En primer lugar se realiza un análisis gráfico de la serie de precio diario de la electricidad y sus retornos. En segundo lugar, se hacen pruebas de estacionaridad, y por último, se estiman los modelos ARIMA y ARCH‐GARCH.
2.1Análisis de la serieEl primer paso para hacerse una idea del comportamiento del precio de la energía eléctrica es observar su gráfica para el año 2009 (fig. 1).
Como se observa en la figura 1 son muy marcados los cambios de precio de un día para otro en diferentes momentos del horizonte. El precio muestra en su comportamiento los efectos complejos de la actividad de oferta, demanda y la regulación, puesto que todos estos recogen la influencia de sus determinantes operacionales –tecnológicos, organizacionales– administrativos y regulatorios. Los precios de la energía eléctrica presentan un comportamiento complejo, explicado por la presencia de los siguientes eventos: los ciclos estacionales de periodicidad diaria, semanal, mensual, junto con cambios en los determinantes del precio, sugieren que tales ciclos influyen en gran medida en la media y la volatilidad.
Por el lado de la oferta, la electricidad se debe generar para suplir la demanda inmediata ya que es imposible su almacenamiento, lo cual implica que el mercado debe poseer suficientes activos de generación para satisfacer el consumo diario. Las características de producción de energía y las limitaciones para su almacenamiento hacen que la oferta tenga que responder rápidamente a los cambios bruscos de la demanda puesto que un déficit en la generación de electricidad causa picos inmediatos en los precios, los cuales vuelven rápidamente a niveles normales.
En un mercado altamente hidroeléctrico como el colombiano, el factor clima tiene una importante influencia en la capacidad efectiva de generación, lo cual produce variaciones estacionales en los precios. Las épocas climatológicas muy secas provocan unos precios extremadamente altos, ya que la demanda pasa a ser atendida por las plantas térmicas cuyo costo de operación es muy alto. Por el contrario, cuando hay abundante caudal en los ríos del país, disminuyen los costos porque es ahí donde las hidroeléctricas funcionan y las térmicas no.
En definitiva, la alta dependencia de diversos factores de índole económica y meteorológica, que resultan impredecibles, que tienen la demanda de electricidad y los precios sumada a la imposibilidad de almacenamiento de la energía es lo que determina su comportamiento altamente volátil. De igual manera, el efecto de la liberalización del mercado en los años 90 con la implantación de la ley eléctrica produjo cambios repentinos en los precios de manera intempestiva ya que los consumidores hoy en día no cuentan con una tarifa única regulada y fijada para diferentes periodos de tiempo.
Lo anterior provoca una alta incertidumbre entre los agentes para predecir sus flujos de ingresos esperados por su actividad, y de igual manera, una dificultad para establecer y proyectar costos de abastecimiento por parte de los agentes que integran la demanda, siendo esto una justificación para el uso de instrumentos de cobertura disponibles en el mercado de derivados organizados.
Otro elemento del análisis de la serie de precios que resulta de gran importancia para establecer patrones de comportamiento es la estacionalidad, la cual se genera por pautas de comportamiento temporal de la serie diaria, explicada por altibajos en el consumo de energía en distintos momentos de la semana. Este tipo de estacionalidad (días de la semana) está marcada por el hecho de la reducción en el consumo de electricidad en los fines de semana, con la lógica disminución del precio de bolsa explicada por el descenso de la actividad productiva nacional en los días festivos de nuestro calendario, mientras que los días entre semana presentan una mayor demanda de energía y es por ello que suele haber picos en dicha franja semanal.
Los picos en la serie de precios se producen de manera instantánea e imprevisible, generando grandes saltos hasta cantidades muy elevadas en intervalos cortos de tiempo; en el caso de la serie analizada, de un día para otro se observan cambios que a simple vista resultan inexplicables, pero que son naturales en este tipo de mercado.
Dichos picos se producen por anomalías en el sistema de producción y de transmisión, como la pérdida momentánea de la capacidad de generación o congestiones en las redes de transmisión del sistema interconectado nacional, por lo tanto, entra otro factor de análisis para explicar el comportamiento de la serie y es la dependencia del precio ante factores tecnológicos del sistema; es decir que en la medida en que los procesos inmersos en la cadena de generación‐transmisión estén funcionando con tecnología punta y se estén monitorizando continuamente para corregir fallas de índole técnico, el precio de la electricidad en bolsa va a presentar un comportamiento moderadamente volátil (León y Rubia, 2001).
Otro elemento importante para explicar el comportamiento impredecible de la serie de precios de la electricidad es su componente estocástico. De manera general, los procesos estocásticos se dividen en procesos estacionarios en covarianza o débilmente estacionarios y en procesos no estacionarios. Los procesos débilmente estacionarios son aquellos en los que el comportamiento es aleatorio y con reversión a la media, mientras que los no estacionarios son aquellos en los cuales la media del proceso cambia a lo largo del tiempo. Según esto, la serie de precios de la electricidad es evidentemente un proceso débilmente estacionario ya que cada vez que se observa un salto brusco en el precio luego tiende a corregirse hacia los niveles normales del mismo en el horizonte de tiempo.
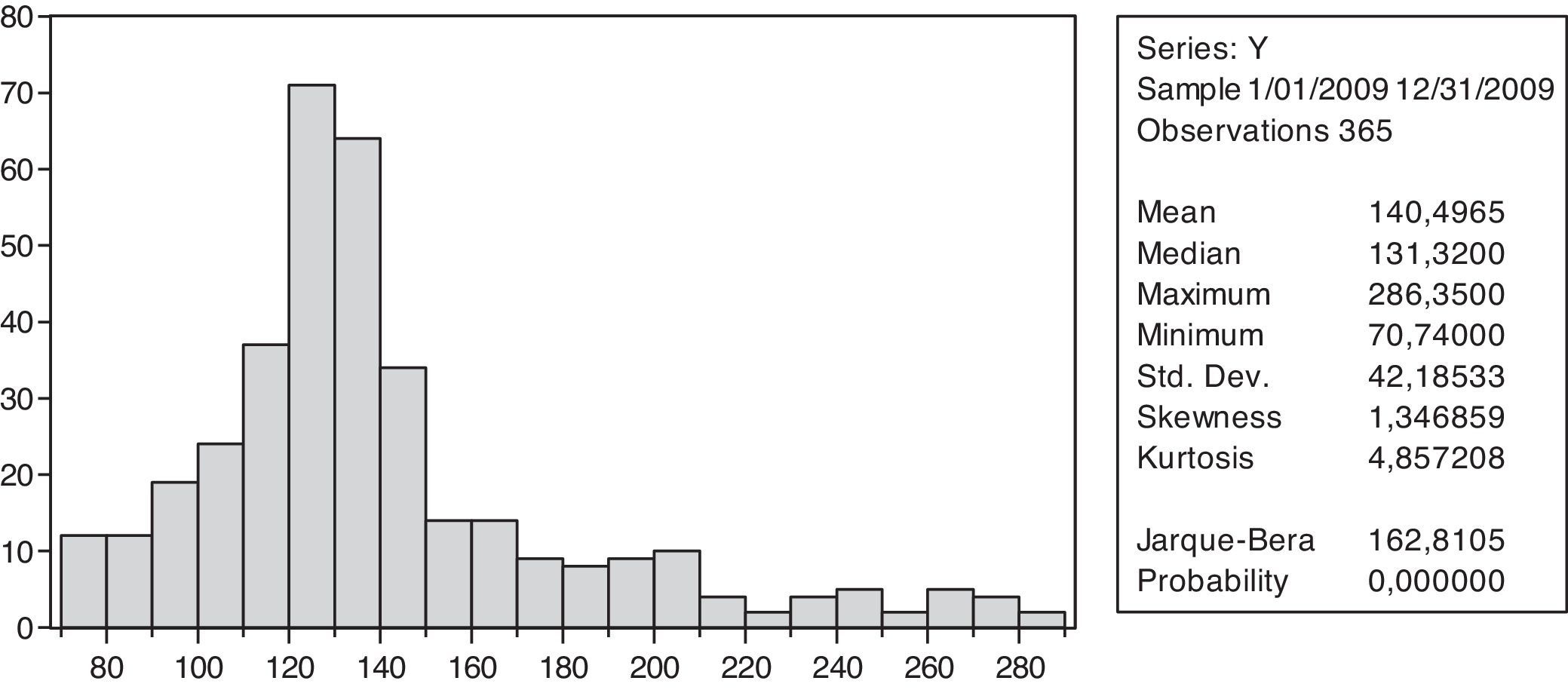
En la figura 2 se puede observar que el histograma de la serie en niveles ($/Kwh), evidencia la poca relación de la misma con cualquier distribución estadística conocida. La distribución muestra asimetría en sus datos con un sesgo a la derecha ya que los datos están concentrados a la izquierda.
En la figura 3 se observa cómo los retornos logarítmicos de la serie muestran estacionaridad en media y es posible observar los agrupamientos de volatilidad.
De la misma forma, el histograma de frecuencias de los retornos logarítmicos (fig. 4), deja ver una alta frecuencia entorno a la media de la serie, lo cual indica que es leptocúrtica; sin embargo, para corroborar la aparente normalidad de la misma se prueba con el estadístico Jarque‐Bera.
El valor de probabilidad del estadístico Jarque‐Bera rechaza la hipótesis de normalidad de la serie.
El correlograma de la serie de precio spot de electricidad en niveles (fig. 5) demuestra que la serie no es estacionaria. Básicamente, se observa que el comportamiento de la columna de la autocorrelación va disminuyendo lentamente, mientras la autocorrelación parcial tiene en su primer nivel una barra prolongada, lo cual indica su no estacionaridad.
2.2Prueba de raíz unitariaPara realizar la prueba de raíz unitaria se estima una regresión por mínimos cuadrados ordinarios de la serie en niveles y su rezago en la cual la variable dependiente es el precio y la independiente o explicativa es su rezago de un periodo. Con este modelo se prueba la hipótesis nula de que el coeficiente de la variable dependiente rezagada es significativo. Si se rechaza la hipótesis se estaría frente a una serie con presencia de raíz unitaria. El modelo que se estima es el siguiente:
Donde ¿t son los residuos que se distribuyen normalmente y no presentan correlación serial. Los resultados de la estimación se encuentran en la tabla 1.
Como se observa en la tabla 1, se rechaza la hipótesis nula y por lo tanto la variable rezagada en t −1 resulta significativa para explicar su propio valor en t, lo que evidencia presencia de raíz unitaria en la serie y no estacionaridad de la misma. Igualmente se realiza la prueba de Dickey‐Fuller aumentada. El estadístico de contraste de la prueba de Dickey‐Fuller aumentada es el estadístico t de la estimación por mínimos cuadrados ordinarios del parámetro π en la siguiente regresión auxiliar:
asumiendo la hipótesis nula de raíz unitaria π=0 (León y Rubia, 2001). Los resultados de esta prueba están en la tabla 2. Dados los resultados de la prueba se concluye que la serie tiene raíz unitaria y por ende no es estacionaria.Ya que la serie en niveles ($/Kwh) resulta no estacionaria, se sigue el análisis con los rendimientos logarítmicos del precio de la electricidad. Los resultados de la prueba de Dickey‐Fuller aumentada que se muestran en la tabla 3 evidencian que el rendimiento logarítmico no tiene raíz unitaria, lo cual indica que la serie es estacionaria.
2.3Modelo autorregresivo integrado de media móvil y modelos autorregresivos con heterocedasticidad condicionalAhora bien, con el correlograma de los rendimientos de la serie (fig. 6) se observa que las barras de la autocorrelación (MA) sobresalen en el rezago 1, 11 y 21. Igualmente, en la autocorrelación parcial (AR) sobresalen en los rezagos 1, 11 y 21, lo cual es un indicio de los posibles rezagos para estimar los modelos autorregresivos y de medias móviles.
Luego de estimar diferentes combinaciones se pudo concluir que el modelo más apropiado es un modelo autorregresivo de orden 1 a 8 con una media móvil de 8 periodos, ya que sus coeficientes son altamente significativos y posee los menores criterios de información Akaike‐Schwarz; sin embargo, la decisión final se complementa observando el correlograma de los residuos de dicho modelo, el cual corrige la correlación parcial de los errores del modelo haciéndola nula. En la tabla 4 se muestra la estimación del modelo ARIMA identificado por criterios de información y significación de sus coeficientes.
Modelo ARIMA
| Variable dependiente: Retornos del precio spot de la electricidad | ||
| Variable | Coeficiente | Prob. |
| AR (1) | 0,220809 | 0,0000 |
| AR (2) | −0,364306 | 0,0000 |
| AR (3) | −1,341660 | 0,0000 |
| AR (4) | −1,316915 | 0,0000 |
| AR (5) | −1,220789 | 0,0000 |
| AR (6) | −1,168312 | 0,0000 |
| AR (7) | −1,112057 | 0,0000 |
| AR (8) | −0,243992 | 0,0000 |
| MA (8) | −0,858650 | 0,0000 |
| Muestra | 349 | |
| Durbin‐Watson | 1,994347 | |
| Akaike criterion | −2,039864 | |
| Schwarz criterion | −1,940450 | |
Fuente: elaboración propia.
Con la transformación de la serie del precio de la electricidad por medio de sus retornos logarítmicos se logró una estacionaridad en la media pero no en la varianza; si se observa la figura 3 de los retornos logarítmicos es posible percibir que la varianza de los datos es variable a lo largo del horizonte temporal. Este problema se puede eliminar modelando la varianza de manera que sea constante mediante los procesos ARCH‐GARCH. No obstante, los procesos ARCH‐GARCH también deben ser identificados de manera que, bajo los supuestos del modelo, se encuentren los rezagos que afecten el comportamiento de la varianza, y sobre estos construir el modelo que permita calcular la volatilidad de la serie. El objetivo de los modelos ARCH‐GARCH es determinar un patrón de comportamiento estadístico para la varianza dado por las siguientes expresiones:
Para verificar la presencia de efectos ARCH–GARCH en los residuos del modelo ARIMA se presenta en la tabla 5 la prueba de multiplicador de Lagrange para probar la hipótesis nula de ausencia de comportamiento ARCH‐GARCH en la varianza de los residuos.
Dado que con esta prueba se confirma la presencia de efecto ARCH‐GARCH evaluando al 5% de significación, se estima un modelo ARCH (0) GARCH (1) o lo que es igual, un modelo ARCH‐GARCH (tabla 6).
Los resultados de la estimación del modelo ARCH‐GARCH arrojan una volatilidad diaria para la serie estimada en 9,07039%
Con este resultado, en la figura 7 se encuentran los rendimientos del precio de la electricidad con las 2 bandas de volatilidad.
De esta manera es posible apreciar que el modelo econométrico captura la mayor parte del comportamiento de los rendimientos del precio, siendo esto una gran ayuda para los agentes comercializadores, y generadores en sus exposiciones en bolsa de energía ya que, por ejemplo, muchas veces por distintas razones la demanda en una región se dispara sin que la compañía eléctrica del sector cuente con reservas suficientes para suplir esa distribución y debe acudir a comprar la energía que necesita a cualquier precio. Es en estos casos en donde se hace necesario que los departamentos de riesgo tengan presente el análisis de volatilidad para controlar sus inversiones y puedan tener planes de contingencia cuando el precio alcance picos por las causas expuestas anteriormente.
3Propuesta de cobertura con productos derivados: opción exótica tipo barreraPara definir la estrategia de cobertura es necesario avanzar en el proceso de administración del riesgo desde los pasos descritos en la figura 8.
Con los resultados obtenidos de la medición del riesgo de mercado se puede concluir que una forma de mitigar el riesgo de precio de la energía eléctrica es con una estrategia de cobertura en el mercado de derivados. Esta cobertura puede hacerse con futuros u opciones. Dado que el propósito es proponer un ejercicio cobertura con un derivado diferente al que se negocia actualmente el mercado, se optó por la opción barrera.
En este sentido, en esta sección se toma como insumo la volatilidad diaria calculada en la sección anterior y se realizan los cálculos del valor en riesgo de una posición larga en energía eléctrica, cuyo resultado mostrará el camino a seguir en el diseño del producto derivado para la cobertura de esta posición. Por último, se muestra el modelo con el que se diseña un producto derivado estructurado, en este caso una opción exótica tipo barrera, para realizar una óptima cobertura en un producto tan volátil como la energía eléctrica.
3.1Valor en riesgoEn la administración del riesgo, en la etapa de medición o valoración, es indispensable contar con suficientes técnicas que permitan calcular la pérdida esperada en la posición que se tenga. El valor en riesgo (VaR, por sus siglas en inglés value at risk) es hoy en día una de las medidas de riesgo más empleadas por los actores de los mercados financieros en el mundo entero. Según De Lara (2004), esta medida estadística, de riesgo de mercado, estima la perdida máxima que podría registrar un portafolio en un intervalo de tiempo con cierto nivel de probabilidad o confianza.
Para Alonso y Berggrun (2008), el VaR condensa en un único valor el riesgo total de un activo o portafolio, que facilita la toma de decisiones. Es importante escoger correctamente los 2 parámetros que conforman el VaR: el horizonte de tiempo y el nivel de confianza. El horizonte de tiempo, al igual que el nivel de confianza, se escoge dependiendo del uso que se le da a la medida, ya que esta puede afectar el modelo y los supuestos que se empleen en el momento del cálculo del VaR.
Como metodologías para el cálculo del VaR se utilizan los métodos paramétricos, los métodos no paramétricos (simulación histórica) y los métodos mixtos (simulación de Montecarlo). El utilizado en este trabajo es el paramétrico.
El método paramétrico tiene como característica principal el supuesto de que los rendimientos del activo siguen una distribución normal. Sin embargo, la mayoría de los activos no siguen un comportamiento normal sino un comportamiento aproximado, por lo tanto los resultados obtenidos son una aproximación.
Donde Z es el factor de nivel de confianza, Va corresponde al monto total de la inversión o exposición total al riesgo, a precios de mercado, σ es la diferencia y t es el horizonte de tiempo para el que se calcula el VaR.Para el caso de la presente investigación se calculó el VaR en una compra de energía de 360.000kw/h a un precio de $120,70kw/h, es decir una transacción de $43,452.000, con un nivel de confianza del 95% y con un horizonte de tiempo diario. En este sentido se empleó la volatilidad calculada por el modelo ARCH‐GARCH, llegando a los siguientes resultados:
Este resultado indica que con un nivel de confianza del 95% la pérdida esperada para la posición de compra de 360.000kw/h es de aproximadamente $6.482.805, lo que representa una pérdida del 14,92% de la inversión inicial. Para que un comprador de energía eléctrica cubra su riesgo de precio, expresado por el VaR, puede utilizar como estrategia una opción tipo barrera.
3.2Cobertura con opciones exóticas: tipo barreraLas opciones son contratos que a diferencia de los futuros se pueden negociar en un mercado over the counter, o en el mercado organizado. Al ser opción da derecho al comprador de ejercer la compra o la venta del activo subyacente si le conviene y por ello paga una prima. Según Crespo (1998), en las opciones exóticas la estructura de los resultados es diferente a la de las opciones tradicionales, y han surgido con el propósito de abaratar el valor de las primas de las opciones tradicionales o para ajustarse más a determinadas situaciones.
Ahora bien, el valor de los instrumentos derivados debe ser calculado teniendo en cuenta el comportamiento del activo subyacente. La volatilidad es una variable crucial en los mercados de opciones y se refiere, principalmente, al posible rango de variaciones de los precios del subyacente. Palazzo (2000) expresa que estadísticamente es la dispersión del rendimiento del activo subyacente, definiendo como rendimiento las variaciones del precio. A mayor volatilidad del subyacente, el rango de precios al vencimiento de la opción será mayor, lo que implica un riesgo superior para los vendedores de opciones y mayores probabilidades de beneficio para los compradores de opciones. El mercado de opciones traducirá los aumentos de volatilidad en incrementos de precios y a la inversa.
Específicamente, la opción exótica tipo barrera es aquella que se cancela o se activa dependiendo de si el precio del subyacente alcanza cierto valor durante un periodo de tiempo determinado, independientemente del valor que tenga el activo subyacente al vencimiento de la opción. Estas opciones también pueden ser europeas o americanas, y clasificarse en: opciones abajo y de salida down‐out, o abajo y de entrada down‐in; en estas opciones la barrera se encuentra por debajo del nivel inicial del activo subyacente. Igualmente, pueden ser arriba y de salida up‐out o arriba y de entrada up‐in; en estas opciones la barrera está por encima del nivel inicial del activo, esto se traduce en 8 tipos distintos de opciones tipo barrera, teniendo en cuenta que pueden ser call o put. La tipología anteriormente descrita tiene las siguientes características:
- •
Opciones tipo knock‐in: estas opciones tienen derecho a ejercerse si durante el periodo determinado el precio del activo subyacente alcanza un determinado valor, es decir, pasa de ser una opción condicional a una opción simple de compra o venta. Estas se clasifican en 2 tipos: una de ellas son las opciones up‐in, las cuales se activan o adquieren el derecho a ser ejercidas al vencimiento si el precio del activo subyacente se ubica por encima de un determinado nivel o barrera durante la vida de la opción. La otra se refiere a las opciones down‐in, que se activan o adquieren el derecho a ser ejercidas al vencimiento si el precio del activo subyacente cae por debajo de un determinado valor que constituye la barrera, que estará por debajo del precio del subyacente en el momento de pactar la opción.
- •
Opciones tipo knock‐out: estas opciones tienen derecho a ejercerse si durante el periodo de vida de la opción el precio del activo subyacente no alcanza la barrera, es decir, que la opción pierde el derecho a ser ejercida si durante la vida de la misma el precio del subyacente toca la barrera. Se clasifican en 2 tipos, las opciones up‐out, que se pierden el derecho de ser ejercidas si el valor del activo subyacente alcanza determinado nivel durante el periodo de vida de la opción; y las opciones down‐out, que pierden el derecho de ser ejercidas si el valor del activo subyacente cae por debajo del nivel establecido como barrera, que estará por debajo del precio del subyacente al inicio de la vida de la opción.
Para el presente trabajo la opción propuesta es una call barrera. Esta opción tendrá un nivel de barrera por encima del precio spot, y se activará cuando toque la barrera; su tipología sería call up‐in (CUI). El modelo de valoración utilizado es el Black‐Scholes.
El modelo Black‐Scholes original para valoración de opciones de tipo europeo es un modelo que trabaja con distribuciones continuas para el comportamiento del precio (lognormal) y los rendimientos (normal). Este modelo se desarrolla bajo algunos supuestos, entre otros, el precio del activo subyacente sigue un camino aleatorio, lo que supone la eficiencia en los mercados. Sin embargo, este supuesto no se cumple en su totalidad aun en mercados desarrollados.
Por lo anterior es importante reconocer que, en la propuesta de cobertura por medio de opciones barrera para el riesgo de precio de la energía eléctrica en Colombia, la prima calculada por el modelo Black‐Scholes es solo un referente de negociación que permite la evaluación de la relación beneficio‐costo en la gestión del riesgo.
Para valorar opciones exóticas tipo barrera por el método de Black‐Scholes, las ecuaciones tienen cierta modificación, y en esto influye la relación entre la barrera (B) y el precio de ejercicio (K); es decir, B≥K o B≤K, lo que genera 16 distintas modalidades de opciones barrera. Para la propuesta solo se presenta la opción barrera de interés, CUI.
Para la valoración se utiliza el siguiente modelo que presenta una aplicación con aplicación a derivados energéticos.
De tal forma que:
Donde, B es el valor de la opción barrera, K es el precio de ejercicio, t es el tiempo al vencimiento, σ es la volatilidad y N (di) denota la distribución normal acumulada.
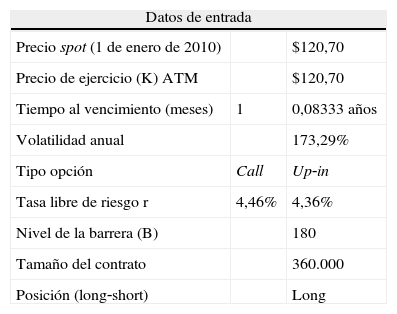
En la tabla 7 se incluye la información para realizar la valoración a partir de los datos históricos hasta el 1 de enero de 2010, donde el precio spot del kw/h de la energía eléctrica es $120,7
Datos para valoración Black‐Scholes
| Datos de entrada | ||
| Precio spot (1 de enero de 2010) | $120,70 | |
| Precio de ejercicio (K) ATM | $120,70 | |
| Tiempo al vencimiento (meses) | 1 | 0,08333 años |
| Volatilidad anual | 173,29% | |
| Tipo opción | Call | Up‐in |
| Tasa libre de riesgo r | 4,46% | 4,36% |
| Nivel de la barrera (B) | 180 | |
| Tamaño del contrato | 360.000 | |
| Posición (long‐short) | Long | |
Fuente: elaboración propia.
El nivel de barrera se estableció teniendo en cuenta el precio promedio de los últimos 3 meses (90 días) (1 de octubre de 2009 a 1 de enero de 2010).
Los resultados obtenidos para cada uno los parámetros del modelo Black‐Scholes se muestran en la tabla 8.
Estimación de parámetros
| λ | d1 | d2 | d3 | d4 | d5 | d6 | d7 | d8 | |
| 0,029061 | 0,257391 | −0,242853 | −0,541517 | −‘1,041761 | −0,556055 | −1,056299 | −1,354962 | −1,855206 | |
| N (d) | 0,601561 | 0,40406 | 0,294076 | 0,148761 | 0,289087 | 0,145416 | 0,087715 | 0,031783 | |
| N (‐d) | 0,398439 | 0,59594 | 0,705924 | 0,851239 | 0,710913 | 0,854584 | 0,912285 | 0,968217 |
Fuente: elaboración propia.
Con los anteriores parámetros se aplica la fórmula para la opción exótica barrera CUI:
El resultado del modelo de valoración se presenta en la tabla 9.
Valoración Black‐Scholes
| Si Barrera≤E | Si Barrera≥E | ||||||
| Opciones call | Opciones put | Opciones call | Opciones put | ||||
| Tipo | Valor | Tipo | Valor | Tipo | Valor | Tipo | Valor |
| Down‐in | Up‐out | Down‐in | Up‐out | ||||
| Down‐out | Up‐in | Down‐out | Up‐in | ||||
| Up‐out | Down‐in | Up‐out | Down‐in | ||||
| Up‐in | Down‐out | Up‐in | 21,8686 | Down‐out | |||
Fuente: elaboración propia.
El valor de la prima aumenta cuando se disminuye el valor de la barrera; con una barrera de 130 la prima de la opción CUI se iguala al valor de la opción call clásica 23,88. A medida que aumenta la barrera la prima disminuye; por ejemplo si toma el promedio del último mes que es 194, la prima de la opción barrera es 20,33. Teniendo en cuenta que el precio del kw/h para la energía eléctrica en los últimos 3 meses osciló entre 120,7 y 286,35, se toma otro escenario con un valor de barrera de 200 y la prima es de 19,59.
4ConclusionesEl objetivo principal de este trabajo es el diseño de un producto derivado para administrar el riesgo inherente a la negoción de un commodity como la energía eléctrica. Para lograr el objetivo, se procedió a estimar los modelos econométricos que sirvieran de insumo para el diseño de la estrategia de negociación a largo plazo. La utilización de la metodología ARCH‐GARCH para la modelación de la volatilidad en los precios intradía de la energía eléctrica, para el caso colombiano, arrojó como resultado la presencia de altas volatilidades intradía en el mercado energético, las cuales podrían estar explicadas por el comportamiento pasado del precio y por la volatilidad pasada del mismo. Por ello es de valiosa importancia el pasado de la variable en el comportamiento pasado y futuro de la misma.
Igualmente, la medición del riesgo realizada a través de la metodología VaR permitió observar la pérdida máxima a la que se enfrenta un agente del mercado eléctrico como producto de la alta volatilidad que presenta este activo, por lo cual se explica la iniciativa primordial de los agentes en realizar contratos de tipo financiero y contratos a largo plazo donde se asegure un precio y se evite la exposición a la variabilidad de la cotización en bolsa; sin embargo, la escasez o los excedentes de los agentes que son cubiertos o demandados en la bolsa de energía representan una necesidad de los agentes a acudir al mercado y exponerse al riesgo en los precios.
A partir del cálculo de la volatilidad generada por el modelo ARCH‐GARCH se diseñó una opción exótica tipo barrea que se valoró, y se calcularon las primas a partir del modelo Black‐Scholes. Se concluye que cuanto más tiempo se tome para la cobertura menos confiable va a ser la estrategia debido al alto nivel de volatilidad que presenta el mercado; por tal motivo, es necesario realizar operaciones a corto plazo, ya que cuando se toma una cobertura a largo plazo los rangos que genera la volatilidad son muy altos, ocasionando la probabilidad de que los precios crezcan de forma no coherente con los precios reales.
Por último, las conclusiones y el diseño del producto derivado que se plantea en este trabajo tiene la limitación de ser un ejercicio netamente teórico, ya que en la actualidad no se negocian opciones sobre energía eléctrica en el mercado colombiano y no se tiene una serie de precios futuros lo suficientemente consistente como para realizar algún tipo de verificación. En este sentido, los espacios académicos tienen la posibilidad de hacer sus aportes desde la ingeniería financiera, la econometría o la economía de mercados energéticos para que se haga una importante contribución al desarrollo de los mercados y a tener mecanismos transparentes y eficientes en la formación de precios.