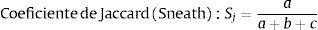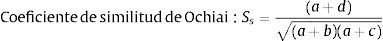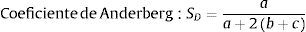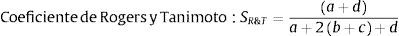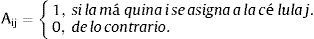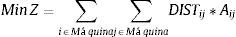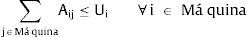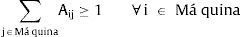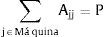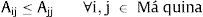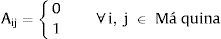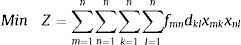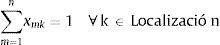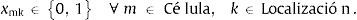Metodología de distribución de plantas en ambientes de agrupación celular

Resumen

Este artículo propone una metodología para la distribución de plantas en sistemas de manufactura flexible, basada en métodos cuantitativos para agrupación de familias, formación de células de manufactura y el uso de técnicas multicriterio. Respecto a la agrupación de productos, se consideraron criterios geométricos y se usó un modelo p-mediana modificado para la creación de células. De esta forma, la distribución de planta apropiada se escogió utilizando el proceso analítico jerárquico, evaluando diferentes alternativas obtenidas con el modelo Quadratic Assignment Problem, que considera el número deseado de células a formar y los coeficientes de similitud empleados para la agrupación celular. La metodología propuesta se probó a través de un caso real, verificándose la conveniencia del procedimiento en una empresa colombiana del sector metalmecánico.

Abstract

This article proposes a plant layout methodology for flexible manufacturing systems, based on quantitative methods used to clustering product families, manufacturing cell formation and finally using multicriteria techniques. Fore product clustering, geometric criteria were taken into account and a modified p-median model was used for the formation of cells. Thus, the appropriate layout of facilities was chosen using the Analytic Hierarchy Process, evaluating different alternatives obtained from the Quadratic Assignment Problem model, which takes into account the desired number of cells to be created and the similarity coefficients used for cell clustering. The proposed methodology was tested through an actual case, being verified the suitability of the procedure in a Colombian company from the metalworking sector.

Resumo

Este artigo propõe uma metodologia para a distribuição de plantas em sistemas de fabricação flexível baseada em métodos quantitativos para a agrupação de famílias, a formação de células de fabrico e a utilização de técnicas multicritério. Em relação à agrupação de produto, foram considerados critérios geométricos e foi usado um modelo de p-meio modificado para a criação de células. Assim, a distribuição apropriada de planta foi escolhida utilizando o Processo Analítico Hierárquico avaliando diferentes alternativas obtidas com o modelo de Quadratic Assignment Problem, que leva em consideração o número de células desejado de células para formar e os coeficientes de similaridade utilizados para a agrupação celular. A metodologia proposta foi testada através de um caso real verificando-se a adequação do procedimento em uma empresa colombiana do sector metalúrgico.

1

Introducción

En mercados que exigen gran competitividad, la administración de los negocios se enfrenta a decisiones y problemas que deben resolverse de manera estratégica para el mantenimiento exitoso de las compañías. Entre esas decisiones es de gran relevancia el satisfacer las necesidades de los clientes externos en cuanto a la calidad del producto y al servicio, siendo el cumplimiento en las entregas un elemento de gran impacto (Davis-Sramek, Mentzer y Stank, 2008).

El cumplimiento en las entregas se asocia en gran medida a la organización de los procesos de manufactura, que a su vez contribuye a la mejor utilización de recursos de una planta. Una de las herramientas para la mejora de los procesos es la planificación del layout, con la cual se pueden mejorar los tiempos de producción, la productividad y la eficiencia, pudiéndose además disminuir los costos de manejo de materiales (Drira, Pierreval y Hajri-Gabouj, 2007).

Debido a la flexibilidad que requieren los mercados actuales, que tienen gran variedad de productos y bajos volúmenes de producción, se aplica ampliamente la filosofía de la manufactura celular y flexible (Mahdavi, Teymouria, Baher y Kayvanfar, 2013; Dixit y Gupta, 2013), la cual permite agrupar un número de piezas comunes para procesarlas en una célula compuesta de las máquinas necesarias para producirlas. En especial, se aplica en sectores como el metalmecánico, utilizando la distribución celular, lo que le permite mejorar la eficiencia de los procesos (Wemmerlov y Johnson, 1997)

Los entornos metalmecánicos son regularmente del tipo Job Shop y pueden contar con gran número de máquinas y gran variedad de productos que se caracterizan por tener diferentes rutas de paso, aspecto que dificulta el acomodar las máquinas en un orden específico de flujo. Esto obliga a preguntarse dónde ubicar cada máquina teniendo en cuenta que puede ser usada por distintos productos, con diferentes rutas y demandas. Lo anterior conlleva un problema de localización de máquinas, problema que tradicionalmente se ha resuelto con métodos heurísticos y exactos, donde uno de los más conocidos es el Quadratic Assignment Problem (QAP) (Koopmans y Beckmann, 1957; Liggett, 2000). Según Liggett (2000), el QAP tiene una alta complejidad que puede desencadenar infactibilidades y altos tiempos computacionales. Es por ello que las agrupaciones de productos y de máquinas, previo al uso del QAP, representan estrategias de disminución de complejidad.

En este artículo se presenta una metodología para distribución en planta útil en ambientes de manufactura flexible, siendo posible trabajar con un gran número de máquinas, factor que usualmente incrementa la complejidad haciendo difícil el uso aislado del algoritmo QAP, que ha demostrado ser No Polinomial-duro (NP-duro) en cuanto a su complejidad (Cela, 2013), requiriéndose en este caso nuevas estrategias de solución. Por lo tanto, se propone una estrategia metodológica novedosa, agrupando primero las máquinas mediante un modelo p-mediana modificado, ajustando el modelo p-mediana tradicional de Kusiak (1987), para luego aplicar el QAP a un problema más reducido.

El p-mediana modificado propuesto, que es distinto al formulado por Won y Lee (2004), permite agrupar más de una misma máquina en una célula o grupo, y el agrupamiento está influenciado por distintos coeficientes de similaridad (Yin y Yasuda, 2006). El presente artículo muestra por primera vez un proceso de solución en cascada, donde con cada coeficiente de similaridad se obtiene, a través del modelo p-mediana modificado propuesto, un nuevo agrupamiento, y cada agrupamiento alimenta el algoritmo QAP que arroja una configuración óptima de máquinas. Las configuraciones así obtenidas, cambiando el coeficiente de similaridad, son comparadas y rankeadas con el método multicriterio Analytic Hierarchy Process (AHP) (Yang y Kuo, 2003; Hadi-Vencheh y Mohamadghasemi, 2013), para finalmente decidir por la mejor distribución de la planta.

En la literatura revisada sobre metodologías de distribución en planta no se ha encontrado una asociación similar a la antes presentada entre un método multicriterio y el QAP con un enlace con el modelo p-mediana modificado desarrollado, y para ello se puede revisar, por ejemplo, a Yang y Kuo (2003), Yang y Hung (2007a), Salazar, Vargas, Añasco y Orejuela (2010) y Karande y Chakraborty (2014).

Dado lo anterior, el artículo se esquematiza de la siguiente manera: la sección 2 explica de manera ampliada el esquema metodológico elegido, en la sección 3 se explica el p-mediana modificado, y la sección 4 explica el método QAP y el método multicriterio. La sección 5 presenta los resultados de la aplicación de la metodología propuesta en un caso de estudio real, y la sección 6 muestra las conclusiones.

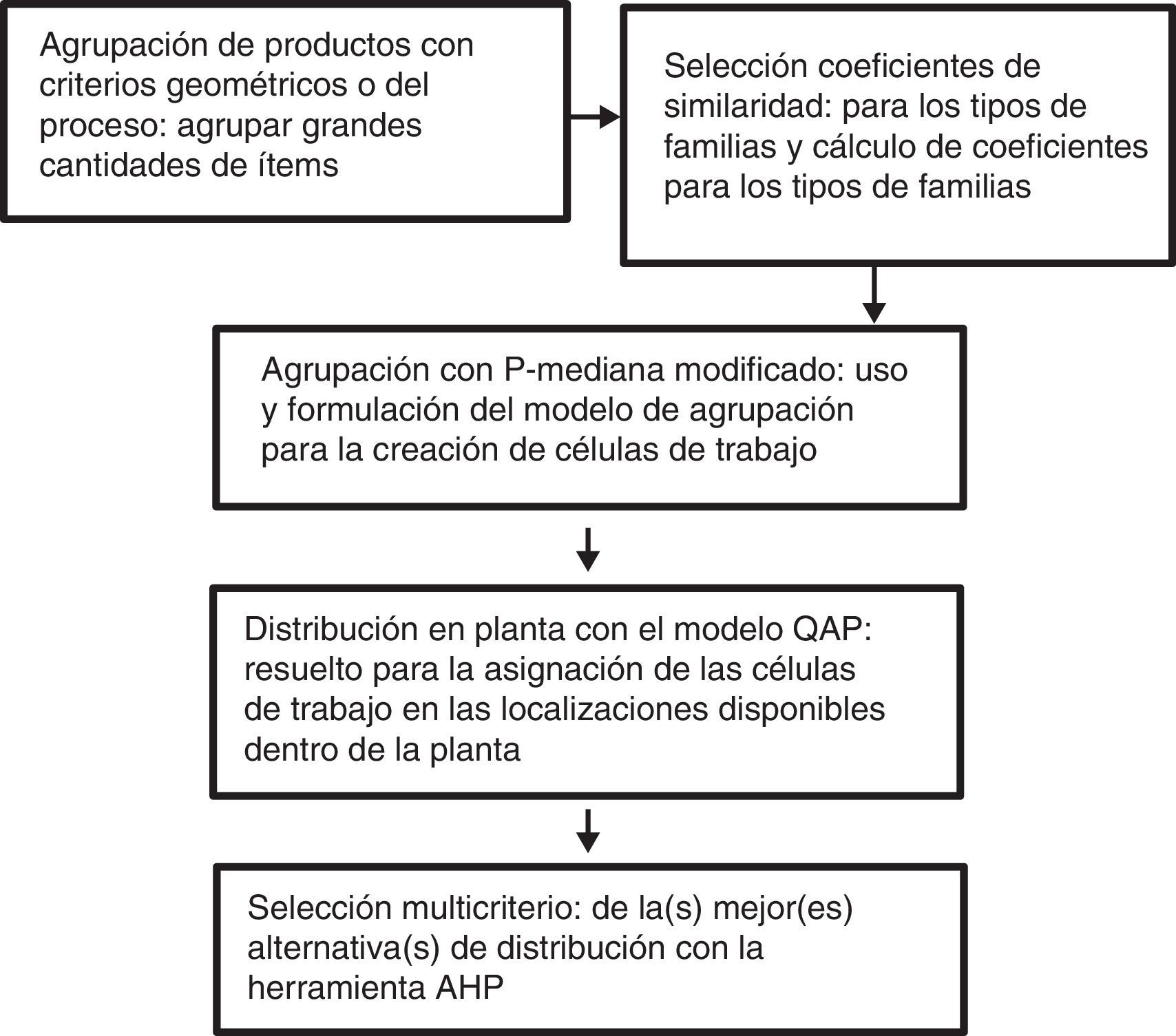
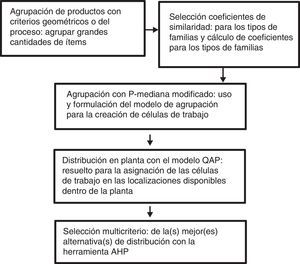
2

Metodología

Se propone una metodología basada en la combinación de varios métodos que abordan de manera jerárquica y concatenada una serie de subproblemas asociados a la elección de la mejor distribución de planta. La figura 1 esboza la estrategia metodológica general.

Figura 1.

Metodología propuesta.

Fuente: elaboración propia.

Teniendo como referente de un sistema de manufactura flexible a cualquier empresa del sector metalmecánico, se tiene que ellas manejan grandes cantidades de ítems, y por ello se establece conveniente empezar por hacer un primer tipo de agrupamiento de los productos «por criterios geométricos» (Kusiak, 1987). Esto tiene como finalidad hacer un agrupamiento preliminar, reduciendo el número de ítems para facilitar los posteriores desarrollos numéricos con los modelos p-mediana y QAP. Este primer agrupamiento consideró los siguientes criterios:

• ∘

  Geometría de las piezas: tamaño, forma, etc.

• ∘

  Funciones de los componentes: mango, abrazadera, etc.

• ∘

  Según el tipo de fabricación: tamaño del lote, ruta del proceso, etc.

• ∘

  Material de la pieza.

Partiendo de la agrupación hecha en el paso anterior se seleccionaron los coeficientes de similaridad teniendo en cuenta los siguientes criterios:

• ∘

  Coeficientes que según el estado del arte tuvieran mayor aplicación en la tecnología de grupos.

• ∘

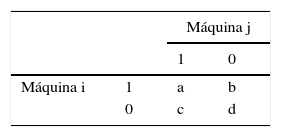
  Usar coeficientes de similaridad basados en las tablas de contingencia (Warrens, 2008), las cuales tienen la estructura mostrada en la tabla 1.

  Tabla 1.

  Estructura de tablas de contingencia

  		Máquina j
  		1	0
  Máquina i	1	a	b
  	0	c	d

  Fuente: adaptado de Warrens (2008).
• ∘

  Se incluyeron además coeficientes basados en distancia (Selim, Askin y Vakharia, 1998) y otros de asociación para poder hacer un estudio comparativo.

Considerando la tabla 1, puede decirse que en los modelos más comunes los coeficientes de similaridad se calculan sobre caracteres de dos estados, cada uno de los cuales se registra como 1 o 0 (presencia o ausencia), donde a es el número de productos que tienen operaciones en ambas máquinas, b es el número de productos presentes en la máquina «i» pero no «j», c es el número de productos presentes en la máquina «j» pero no «i», y d es el número de productos ausentes en ambas máquinas. Algunos de las expresiones de los coeficientes elegidos se muestran a continuación, y para mayor información pueden verse las investigaciones de Yin (2006) y Warrens (2008):

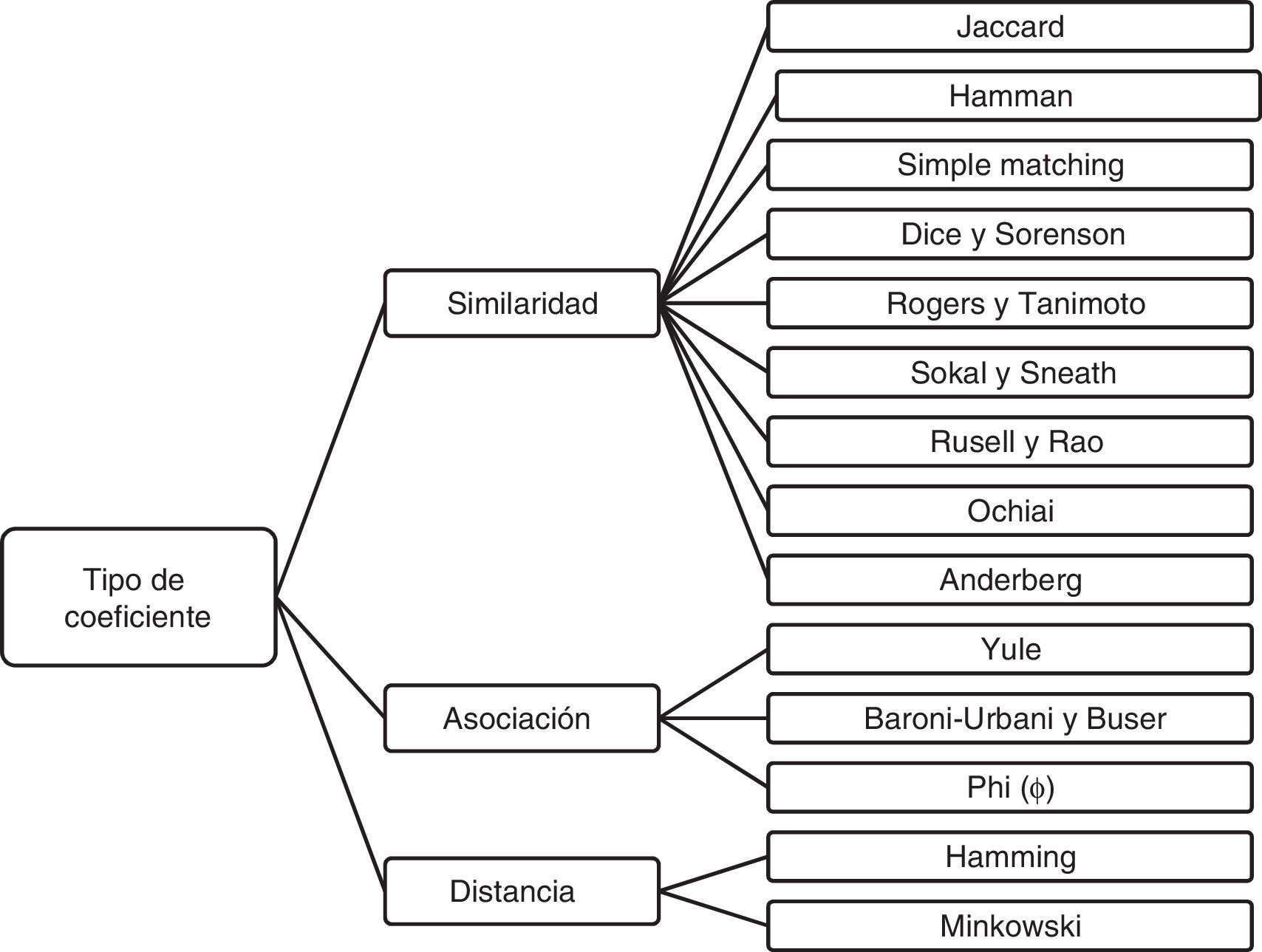
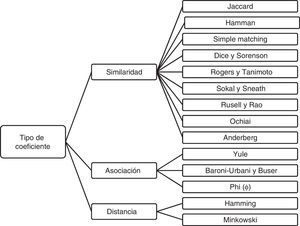
Los coeficientes de similaridad finalmente seleccionados se muestran en la figura 2, y se calcularon según sus fórmulas existentes. Es claro que la elección de alguno de ellos puede inducir un distinto agrupamiento de las máquinas, y en ese sentido se empleó el modelo p-mediana para cada coeficiente, arrojando en cada caso agrupamientos de máquinas que serían luego aprovechados por el procedimiento basado en el QAP de distribución de planta.

Figura 2.

Tipo de coeficientes.

Fuente: elaboración propia.

3

Modelo p-mediana modificado

Partiendo del modelo p-mediana de Kusiak (1987) se propone un modelo con una función objetivo flexible, la cual maximiza la similaridad o minimiza la distancia, dependiendo del coeficiente de la figura 2 que se utilice. Se elabora y propone entonces un modelo p-mediana modificado que posee características deseables y ajustadas al sector en estudio.

Dadas las características del sector es posible que se cuente con varias máquinas del mismo tipo, esto debido a que cuando se desea incrementar capacidad en algún cuello de botella, estos incrementos se planifican a mediano plazo, se hacen de manera discreta y se logran generalmente comprando más máquinas de la misma clase. En el modelo propuesto se asume que existe un límite superior e inferior de máquinas de cada tipo, permitiendo que un tipo de máquina se pueda asignar a más de una célula. Esto implica cambiar el modelo original de Kusiak, modificando la primera restricción y adicionando una restricción que involucre los límites mencionados, tal como se verá a continuación.

Índices y parámetros del modelo modificado:

• ∘

  i, j = índices de máquinas.

Parámetros:

• ∘

  N = número de máquinas en la planta.

• ∘

  P = límite de células a formar.

• ∘

  DIST_ij = medida de distancia entre las máquinas i y j.

• ∘

  SIM_ij = medida de similaridad entre las máquinas i y j.

• ∘

  U_i = máquinas disponibles del tipo i.

Variable de decisión:

Función objetivo:

Restricciones:

Las expresiones (6) y (7) representan la función de desempeño la cual puede ser distancia (6) o similaridad (7), según sea el tipo de coeficiente de similaridad que esté evaluándose. La desigualdad (8) garantiza que el total de máquinas de un mismo tipo no supere el número total máximo de máquinas de ese tipo, mientras que la ecuación (9) garantiza que al menos se asigne una máquina de cada tipo en el sistema. La ecuación (10) restringe el número de células a abrir, y la (11) condiciona a que solo se puedan asignar máquinas a células abiertas. Finalmente, la ecuación (12) define la variable. Hay que tener en cuenta que el modelo aquí presentado es distinto a la propuesta de Won y Lee (2004), quienes en contraste consideran que una máquina solo puede asignarse a una sola célula.

4

Uso del Quadratic Assignment Problem (QAP) y selección multicriterio

Dependiendo de la función de desempeño (similaridad o distancia) y el valor de p empleado en el modelo de p-mediana modificado, se genera una distribución de planta a través del modelo QAP (Drira et al., 2007), resultando al final múltiples distribuciones de planta, una para cada coeficiente y para cada valor de p que se elija considerar. Finalmente, estas posibles distribuciones se priorizan con el método multicriterio AHP.

En el modelo QAP empleado, se asume que cada localización tiene la capacidad suficiente para albergar cualquiera de las células; sin embargo, en caso contrario se adiciona una restricción de capacidad para cada localización.

Índices y parámetros del QAP:

• ∘

  f_mn es el flujo de la célula m a la n.

• ∘

  d_kl es la distancia de Manhattan del centroide de la localización k al de la localización l.

Variables:

Función objetivo:

Restricciones:

La función objetivo (13) del QAP define la distribución de planta óptima, para cada agrupación, de acuerdo al criterio de «costo de manejo de materiales» (CMM). Sin embargo, la elección de la mejor distribución debería considerar, según la literatura, múltiples criterios, tal como se presentan en Altuntas, Selim y Dereli (2014), Chiang, Kouvelis y Urban (2006), Hosseini y Seifbarghy (2016), Karande y Chakraborty (2014), Matai (2015), Raman, Nagalingam y Lin (2009); Salazar et al. (2010), Saraswat, Venkatadri y Castillo (2015), Xu, Liu y Lei (2016), Yang y Hung (2007b), Yang y Kuo (2003), entre otros. En este artículo se propone escoger la mejor alternativa a través de cinco criterios seleccionados de la literatura, uno de los cuales es el CMM aportado por el QAP. Los otros cuatro criterios fueron (Yin, 2006) y serán utilizados en el AHP:

• ∘

  Elementos excepcionales (EE): se refiere al número de movimientos intercelulares.

• ∘

  Índice de capacidad de agrupación (ICG): es una formulación obtenida de restar a una eficiencia máxima del 100%, la relación de elementos excepcionales frente a todos los procesos de los productos (Yin, 2006).

• ∘

  Porcentaje de utilización de las máquinas (UM) (Miltenburg y Zhang, 1991): es el promedio global de la utilización de las células.

• ∘

  Proximidad del espacio (PR): es el indicador que calcula la eficiencia de la distribución en planta teniendo en cuenta los costos de los viajes en vacío, el flujo de material, el flujo de información y el flujo de personal, según Raman, Nagalingam y Chiu (2005).

De esta forma, la ecuación (14) garantiza que toda célula sea asignada a solo una localización, la ecuación (15) garantiza que toda localización tenga asignada una y solo una célula.

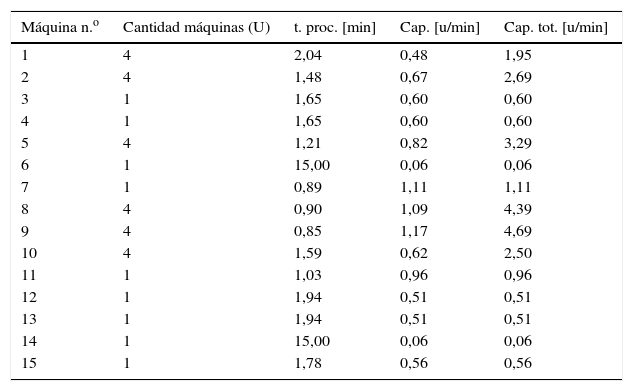
5

Caso de estudio y análisis de resultados

La metodología se validó en una compañía del sector metalmecánico especializada en autopartes metalmecánicas. El portafolio actual de productos de la compañía seleccionada es de 30.000 ítems creados y sus procesos principales son corte, conformado, perforación, tratamiento térmico, acabado y lijado. La cantidad de máquinas disponibles de cada tipo (U), el tiempo necesario en cada operación, el tiempo de proceso (t. proc.) y la capacidad unitaria por máquina (Cap.) y la del total de máquinas (cap. tot.), se muestran en la tabla 2.

Tabla 2.

Características de capacidad de las máquinas/procesos comunes

Máquina n.^o	Cantidad máquinas (U)	t. proc. [min]	Cap. [u/min]	Cap. tot. [u/min]
1	4	2,04	0,48	1,95
2	4	1,48	0,67	2,69
3	1	1,65	0,60	0,60
4	1	1,65	0,60	0,60
5	4	1,21	0,82	3,29
6	1	15,00	0,06	0,06
7	1	0,89	1,11	1,11
8	4	0,90	1,09	4,39
9	4	0,85	1,17	4,69
10	4	1,59	0,62	2,50
11	1	1,03	0,96	0,96
12	1	1,94	0,51	0,51
13	1	1,94	0,51	0,51
14	1	15,00	0,06	0,06
15	1	1,78	0,56	0,56

Fuente: elaboración propia.

La planta tiene un espacio disponible de 2.286 m². Las células creadas (el parámetro p del modelo p-mediana) deben ser como mínimo igual a 2 para que la filosofía de la estructura celular tenga sentido y como máximo 5 por disponibilidad actual de espacio. Teniendo en cuenta las características del caso de estudio, a continuación se desarrolla la metodología antes propuesta.

5.1

Agrupación con criterios geométricos o de su proceso de fabricación

De los 30.000 ítems creados se seleccionaron los ítems «activos» o cuya demanda en el último año hubiese sido mayor a cero, quedando elegidos 3.787 productos. Los productos que seguían el mismo proceso de fabricación se agruparon, obteniendo 120 familias.

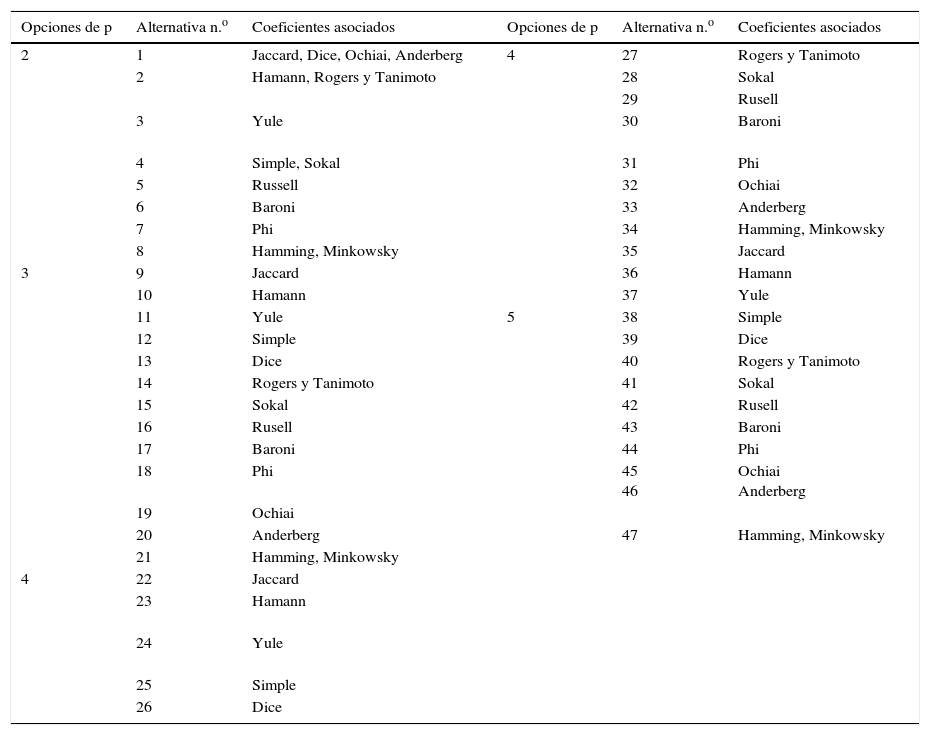
5.2

Agrupamientos celulares obtenidos variando los coeficientes de similaridad y los valores de p

La tabla 3 muestra las alternativas de agrupamiento celular arrojadas por el modelo p-mediana modificado, obtenidas combinando los valores de p y los coeficientes de la figura 2. Se obtuvieron en algunos casos agrupaciones (o células) idénticas con distintos coeficientes. Por ejemplo, para la alternativa 1 de la tabla 3, la conformación de las células fue igual para los coeficientes de Jaccard, Dice, Ochiai y Andeberg, y otras, como la 27 con el coeficiente de Rogers y Tanimoto, tuvieron una única agrupación. Fueron en total 47 agrupamientos diferentes.

Tabla 3.

Alternativas de agrupación como entrada al modelo de distribución en planta

Opciones de p	Alternativa n.^o	Coeficientes asociados	Opciones de p	Alternativa n.^o	Coeficientes asociados
2	1	Jaccard, Dice, Ochiai, Anderberg	4	27	Rogers y Tanimoto
	2	Hamann, Rogers y Tanimoto		28	Sokal
				29	Rusell
	3	Yule		30	Baroni
	4	Simple, Sokal		31	Phi
	5	Russell		32	Ochiai
	6	Baroni		33	Anderberg
	7	Phi		34	Hamming, Minkowsky
	8	Hamming, Minkowsky		35	Jaccard
3	9	Jaccard		36	Hamann
	10	Hamann		37	Yule
	11	Yule	5	38	Simple
	12	Simple		39	Dice
	13	Dice		40	Rogers y Tanimoto
	14	Rogers y Tanimoto		41	Sokal
	15	Sokal		42	Rusell
	16	Rusell		43	Baroni
	17	Baroni		44	Phi
	18	Phi		45 46	Ochiai Anderberg
	19	Ochiai
	20	Anderberg		47	Hamming, Minkowsky
	21	Hamming, Minkowsky
4	22	Jaccard
	23	Hamann
	24	Yule
	25	Simple
	26	Dice

Fuente: elaboración propia.

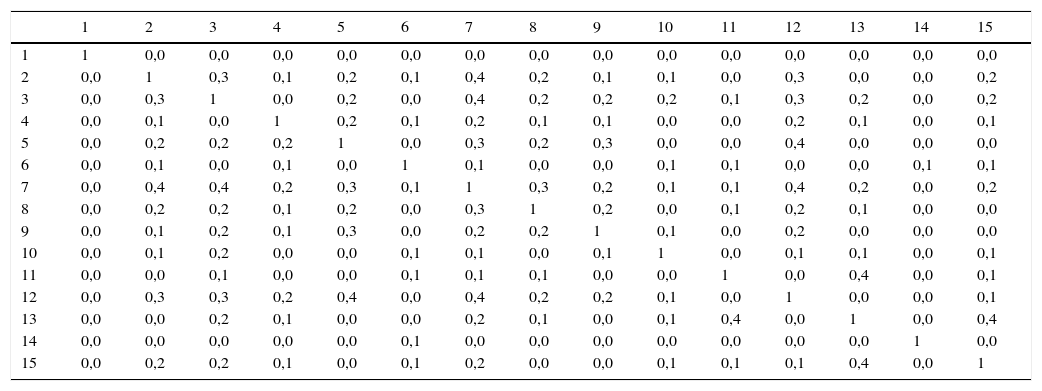
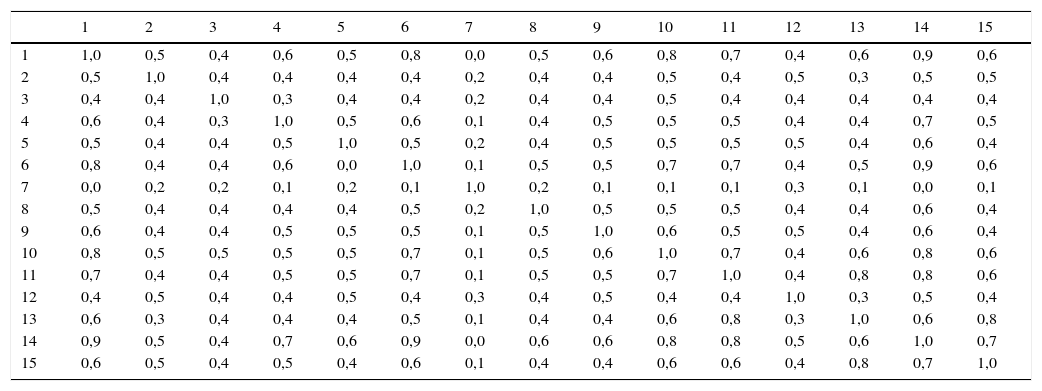
Los coeficientes de similaridad se calcularon teniendo en cuenta las tablas de contingencia. Como ejemplo se muestra el resultado del coeficiente de Jaccard para la alternativa 1 (tabla 4) y el de Rogers y Tanimoto para la alternativa 27 (tabla 5).

Tabla 4.

Resultados coeficiente de similaridad de Jaccard para la alternativa 1

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	1	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0	0,0
2	0,0	1	0,3	0,1	0,2	0,1	0,4	0,2	0,1	0,1	0,0	0,3	0,0	0,0	0,2
3	0,0	0,3	1	0,0	0,2	0,0	0,4	0,2	0,2	0,2	0,1	0,3	0,2	0,0	0,2
4	0,0	0,1	0,0	1	0,2	0,1	0,2	0,1	0,1	0,0	0,0	0,2	0,1	0,0	0,1
5	0,0	0,2	0,2	0,2	1	0,0	0,3	0,2	0,3	0,0	0,0	0,4	0,0	0,0	0,0
6	0,0	0,1	0,0	0,1	0,0	1	0,1	0,0	0,0	0,1	0,1	0,0	0,0	0,1	0,1
7	0,0	0,4	0,4	0,2	0,3	0,1	1	0,3	0,2	0,1	0,1	0,4	0,2	0,0	0,2
8	0,0	0,2	0,2	0,1	0,2	0,0	0,3	1	0,2	0,0	0,1	0,2	0,1	0,0	0,0
9	0,0	0,1	0,2	0,1	0,3	0,0	0,2	0,2	1	0,1	0,0	0,2	0,0	0,0	0,0
10	0,0	0,1	0,2	0,0	0,0	0,1	0,1	0,0	0,1	1	0,0	0,1	0,1	0,0	0,1
11	0,0	0,0	0,1	0,0	0,0	0,1	0,1	0,1	0,0	0,0	1	0,0	0,4	0,0	0,1
12	0,0	0,3	0,3	0,2	0,4	0,0	0,4	0,2	0,2	0,1	0,0	1	0,0	0,0	0,1
13	0,0	0,0	0,2	0,1	0,0	0,0	0,2	0,1	0,0	0,1	0,4	0,0	1	0,0	0,4
14	0,0	0,0	0,0	0,0	0,0	0,1	0,0	0,0	0,0	0,0	0,0	0,0	0,0	1	0,0
15	0,0	0,2	0,2	0,1	0,0	0,1	0,2	0,0	0,0	0,1	0,1	0,1	0,4	0,0	1

Fuente: elaboración propia.

Tabla 5.

Resultados coeficiente de Rogers y Tanimoto para la alternativa 27

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	1,0	0,5	0,4	0,6	0,5	0,8	0,0	0,5	0,6	0,8	0,7	0,4	0,6	0,9	0,6
2	0,5	1,0	0,4	0,4	0,4	0,4	0,2	0,4	0,4	0,5	0,4	0,5	0,3	0,5	0,5
3	0,4	0,4	1,0	0,3	0,4	0,4	0,2	0,4	0,4	0,5	0,4	0,4	0,4	0,4	0,4
4	0,6	0,4	0,3	1,0	0,5	0,6	0,1	0,4	0,5	0,5	0,5	0,4	0,4	0,7	0,5
5	0,5	0,4	0,4	0,5	1,0	0,5	0,2	0,4	0,5	0,5	0,5	0,5	0,4	0,6	0,4
6	0,8	0,4	0,4	0,6	0,0	1,0	0,1	0,5	0,5	0,7	0,7	0,4	0,5	0,9	0,6
7	0,0	0,2	0,2	0,1	0,2	0,1	1,0	0,2	0,1	0,1	0,1	0,3	0,1	0,0	0,1
8	0,5	0,4	0,4	0,4	0,4	0,5	0,2	1,0	0,5	0,5	0,5	0,4	0,4	0,6	0,4
9	0,6	0,4	0,4	0,5	0,5	0,5	0,1	0,5	1,0	0,6	0,5	0,5	0,4	0,6	0,4
10	0,8	0,5	0,5	0,5	0,5	0,7	0,1	0,5	0,6	1,0	0,7	0,4	0,6	0,8	0,6
11	0,7	0,4	0,4	0,5	0,5	0,7	0,1	0,5	0,5	0,7	1,0	0,4	0,8	0,8	0,6
12	0,4	0,5	0,4	0,4	0,5	0,4	0,3	0,4	0,5	0,4	0,4	1,0	0,3	0,5	0,4
13	0,6	0,3	0,4	0,4	0,4	0,5	0,1	0,4	0,4	0,6	0,8	0,3	1,0	0,6	0,8
14	0,9	0,5	0,4	0,7	0,6	0,9	0,0	0,6	0,6	0,8	0,8	0,5	0,6	1,0	0,7
15	0,6	0,5	0,4	0,5	0,4	0,6	0,1	0,4	0,4	0,6	0,6	0,4	0,8	0,7	1,0

Fuente: elaboración propia.

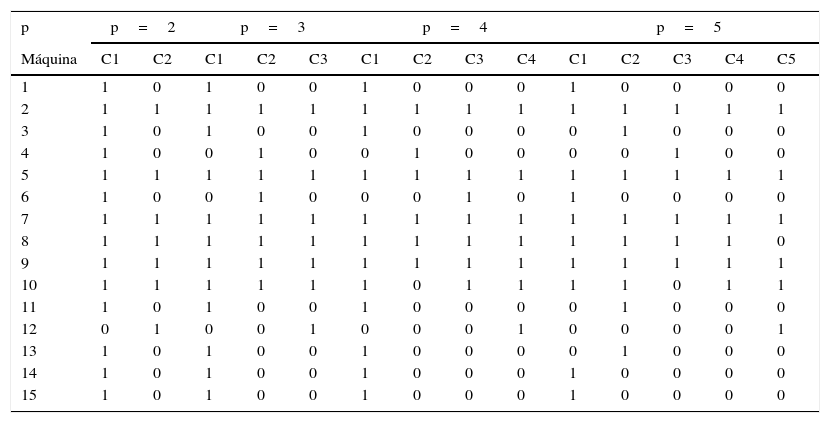
En la tabla 6 se muestra como ejemplo el agrupamiento obtenido con el modelo p-mediana modificado usando el coeficiente de Jaccard, para los diferentes p.

Tabla 6.

Células creadas con el modelo p-mediana modificado usando el coeficiente de Jaccard (1: asignada; 0: no asignada)

p	p = 2		p = 3			p = 4				p = 5
Máquina	C1	C2	C1	C2	C3	C1	C2	C3	C4	C1	C2	C3	C4	C5
1	1	0	1	0	0	1	0	0	0	1	0	0	0	0
2	1	1	1	1	1	1	1	1	1	1	1	1	1	1
3	1	0	1	0	0	1	0	0	0	0	1	0	0	0
4	1	0	0	1	0	0	1	0	0	0	0	1	0	0
5	1	1	1	1	1	1	1	1	1	1	1	1	1	1
6	1	0	0	1	0	0	0	1	0	1	0	0	0	0
7	1	1	1	1	1	1	1	1	1	1	1	1	1	1
8	1	1	1	1	1	1	1	1	1	1	1	1	1	0
9	1	1	1	1	1	1	1	1	1	1	1	1	1	1
10	1	1	1	1	1	1	0	1	1	1	1	0	1	1
11	1	0	1	0	0	1	0	0	0	0	1	0	0	0
12	0	1	0	0	1	0	0	0	1	0	0	0	0	1
13	1	0	1	0	0	1	0	0	0	0	1	0	0	0
14	1	0	1	0	0	1	0	0	0	1	0	0	0	0
15	1	0	1	0	0	1	0	0	0	1	0	0	0	0

Fuente: elaboración propia.

5.3

Obtención de las distribuciones de planta con el modelo Quadratic Assignment Problem (QAP) y selección multicriterio Analytic Hierarchy Process (AHP)

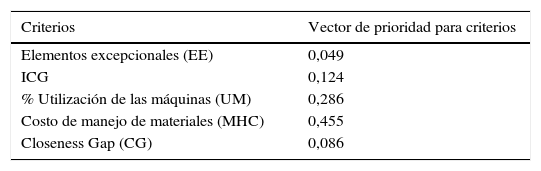
El modelo QAP se resolvió en el software AMPL^® para las distintas alternativas de células, arrojando 47 alternativas diferentes de distribución en planta. La tabla 7 muestra el vector de prioridad de criterios que se obtuvo considerando el concepto de los expertos al interior de la empresa objeto de estudio, con una consistencia de 0,056.

Tabla 7.

Vector de prioridad de criterios

Criterios	Vector de prioridad para criterios
Elementos excepcionales (EE)	0,049
ICG	0,124
% Utilización de las máquinas (UM)	0,286
Costo de manejo de materiales (MHC)	0,455
Closeness Gap (CG)	0,086

Fuente: elaboración propia.

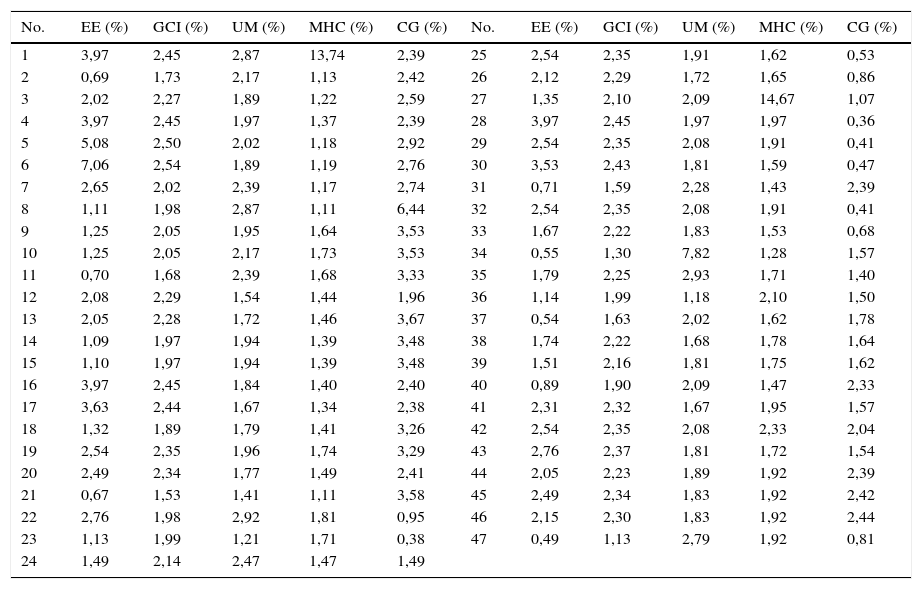
Adicionalmente, se realizó la matriz de comparación de las alternativas para cada criterio, obteniéndose las ponderaciones que se muestran en la tabla 8.

Tabla 8.

Resultados de los indicadores por alternativa

No.	EE (%)	GCI (%)	UM (%)	MHC (%)	CG (%)	No.	EE (%)	GCI (%)	UM (%)	MHC (%)	CG (%)
1	3,97	2,45	2,87	13,74	2,39	25	2,54	2,35	1,91	1,62	0,53
2	0,69	1,73	2,17	1,13	2,42	26	2,12	2,29	1,72	1,65	0,86
3	2,02	2,27	1,89	1,22	2,59	27	1,35	2,10	2,09	14,67	1,07
4	3,97	2,45	1,97	1,37	2,39	28	3,97	2,45	1,97	1,97	0,36
5	5,08	2,50	2,02	1,18	2,92	29	2,54	2,35	2,08	1,91	0,41
6	7,06	2,54	1,89	1,19	2,76	30	3,53	2,43	1,81	1,59	0,47
7	2,65	2,02	2,39	1,17	2,74	31	0,71	1,59	2,28	1,43	2,39
8	1,11	1,98	2,87	1,11	6,44	32	2,54	2,35	2,08	1,91	0,41
9	1,25	2,05	1,95	1,64	3,53	33	1,67	2,22	1,83	1,53	0,68
10	1,25	2,05	2,17	1,73	3,53	34	0,55	1,30	7,82	1,28	1,57
11	0,70	1,68	2,39	1,68	3,33	35	1,79	2,25	2,93	1,71	1,40
12	2,08	2,29	1,54	1,44	1,96	36	1,14	1,99	1,18	2,10	1,50
13	2,05	2,28	1,72	1,46	3,67	37	0,54	1,63	2,02	1,62	1,78
14	1,09	1,97	1,94	1,39	3,48	38	1,74	2,22	1,68	1,78	1,64
15	1,10	1,97	1,94	1,39	3,48	39	1,51	2,16	1,81	1,75	1,62
16	3,97	2,45	1,84	1,40	2,40	40	0,89	1,90	2,09	1,47	2,33
17	3,63	2,44	1,67	1,34	2,38	41	2,31	2,32	1,67	1,95	1,57
18	1,32	1,89	1,79	1,41	3,26	42	2,54	2,35	2,08	2,33	2,04
19	2,54	2,35	1,96	1,74	3,29	43	2,76	2,37	1,81	1,72	1,54
20	2,49	2,34	1,77	1,49	2,41	44	2,05	2,23	1,89	1,92	2,39
21	0,67	1,53	1,41	1,11	3,58	45	2,49	2,34	1,83	1,92	2,42
22	2,76	1,98	2,92	1,81	0,95	46	2,15	2,30	1,83	1,92	2,44
23	1,13	1,99	1,21	1,71	0,38	47	0,49	1,13	2,79	1,92	0,81
24	1,49	2,14	2,47	1,47	1,49

Fuente: elaboración propia.

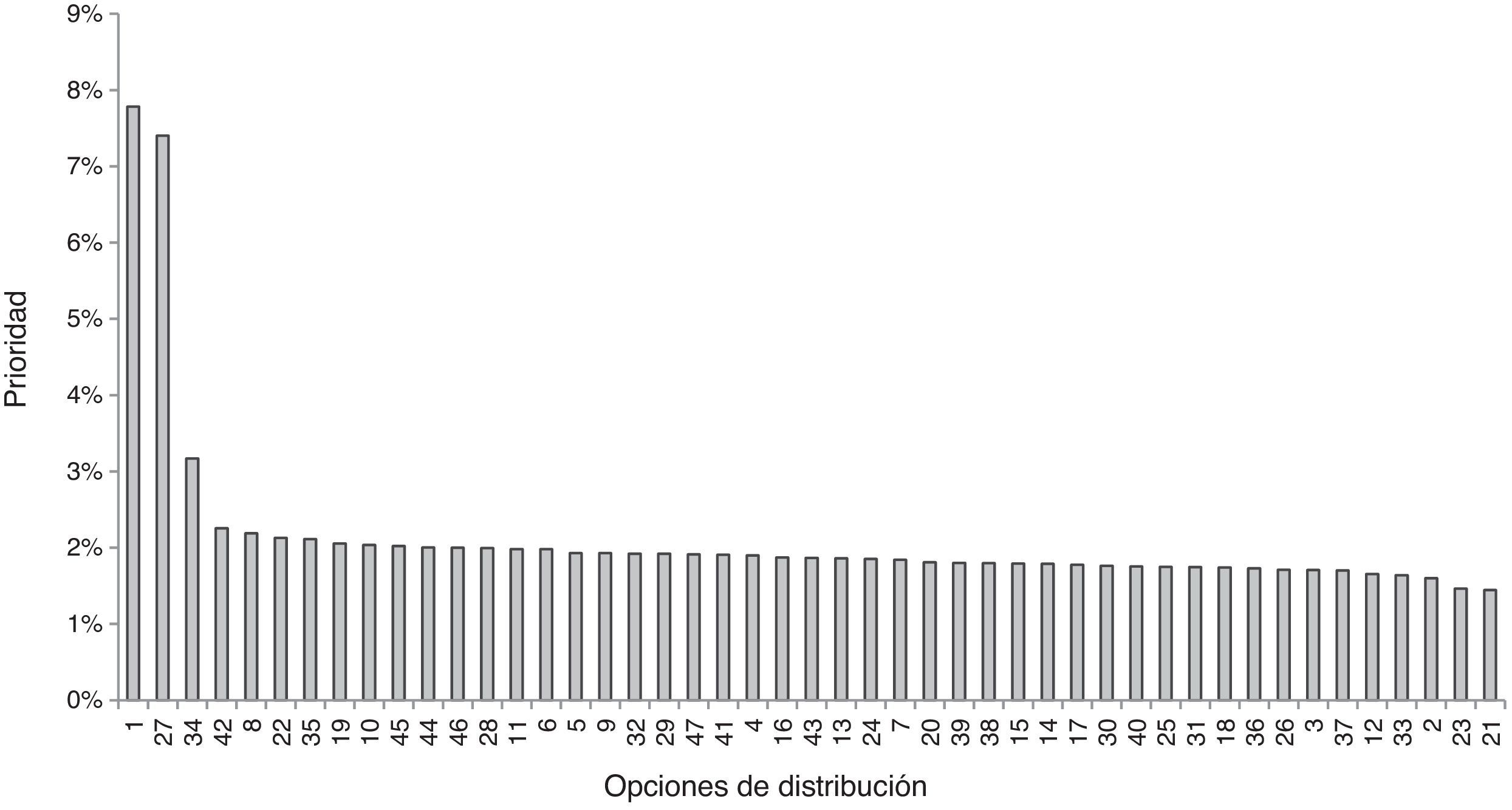
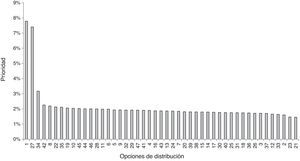
Con el vector de prioridad para los criterios y los resultados de la priorización de alternativas por criterio, se obtiene la priorización de alternativas mostradas en la figura 3. Las mejores alternativas son las números 1 y 27, cuya diferencia porcentual es mínima. En cuanto al número de células a formar en el espacio disponible, se deben tomar como mejores distribuciones las número 1 y 27.

Figura 3.

Priorización de las alternativas.

Fuente: elaboración propia.

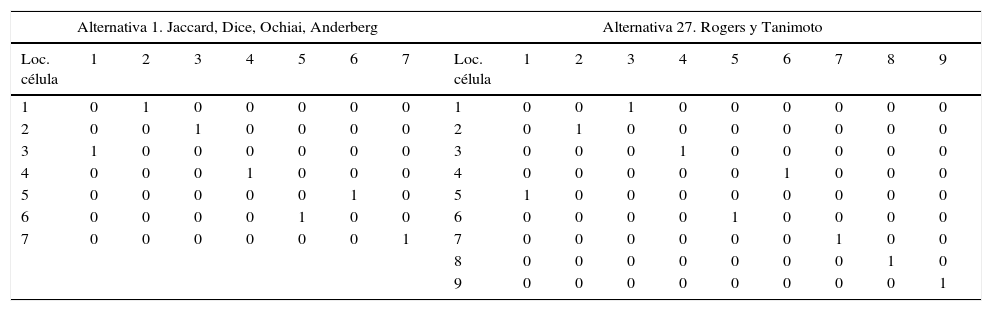
En la tabla 9 se presenta la formación de las células para las dos mejores alternativas y el proceso de asignación de QAP para estas.

Tabla 9.

Número de células y distribución de las alternativa 1 y 27

Alternativa 1. Jaccard, Dice, Ochiai, Anderberg								Alternativa 27. Rogers y Tanimoto
Loc. célula	1	2	3	4	5	6	7	Loc. célula	1	2	3	4	5	6	7	8	9
1	0	1	0	0	0	0	0	1	0	0	1	0	0	0	0	0	0
2	0	0	1	0	0	0	0	2	0	1	0	0	0	0	0	0	0
3	1	0	0	0	0	0	0	3	0	0	0	1	0	0	0	0	0
4	0	0	0	1	0	0	0	4	0	0	0	0	0	1	0	0	0
5	0	0	0	0	0	1	0	5	1	0	0	0	0	0	0	0	0
6	0	0	0	0	1	0	0	6	0	0	0	0	1	0	0	0	0
7	0	0	0	0	0	0	1	7	0	0	0	0	0	0	1	0	0
								8	0	0	0	0	0	0	0	1	0
								9	0	0	0	0	0	0	0	0	1

Fuente: elaboración propia.

La alternativa 1 presenta levemente mejores características frente a la 27 debido a que salen menos los ítems de una célula hacia otra con esta configuración. Adicionalmente, el índice de capacidad de agrupación es mayor para este caso. Es decir, las alternativas 1 y 27 son las que tienen el mayor porcentaje en el costo de manejo de materiales (MHC) con valores de 13,74 y de 14,67, respectivamente, siendo este el criterio con más peso en el porcentaje de prioridad, con un valor de 45,5%. El siguiente criterio en importancia es el porcentaje de utilización de máquinas, con un peso porcentual de 28,6%, en el que la alternativa 1 toma 2,87% y la 27 toma 2,09%. El criterio GCI, tercero en importancia, tiene un peso de 12,4%, donde la alternativa 1 presenta un valor del 2,45% y la 27 con el 2,10%.

Si bien es cierto que la alternativa 1 es más costosa en el manejo de materiales, lo cual le da una ponderación menor en ese indicador, los otros indicadores la favorecen con respecto a la alternativa 27. Es claro que si el proceso de toma de decisiones se basa solo en criterio del costo de manejo de materiales, entonces la alternativa 1 no sería seleccionada. La estrategia multicriterio empleada no solo permite seleccionar dicha alternativa, sino que también ofrece todo un ranking para todas, lo cual brinda una mejor información en el proceso de toma de decisiones.

6

Conclusiones

El presente artículo propone una metodología que combina la agrupación de productos en familias, el uso de un modelo p-mediana modificado asociado al uso de coeficientes de similaridad para el agrupamiento de máquinas en células, el empleo del QAP y el uso del AHP para definir la distribución de planta óptima, procedimiento útil en sistemas de manufactura flexible con múltiples ítems y múltiples máquinas. Según la revisión de literatura, se identifica esta combinación metodológica como única, y se pudo comprobar la viabilidad de su implementación en un caso real relacionado con una empresa metalmecánica del sector autopartes. La complejidad del caso analizado se pudo abordar satisfactoriamente con la combinación de las técnicas empleadas, dejando un precedente importante para el sector económico analizado, pudiéndose usar estrategias computacionales de fácil implementación y solución. Esto es de significativa importancia conociendo la complejidad que implica el implementar el QAP en casos de tamaño real como el estudiado. Sin embargo, es necesario complementar los análisis realizando variaciones a los parámetros de los modelos empleados.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.

Agradecimientos

El presente trabajo ha recibido el apoyo de la Escuela de Ingeniería Industrial de la Universidad del Valle.