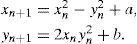Después de una breve explicación sobre el significado de los fractales en las Ciencias de la Tierra, se presenta una modificación de la famosa iteración de Mandelbrot. El resultado tiene un cierto parecido con una hoja de gingko, el cual es una especie de árbol singular, no solo en la botánica sino en la cultura y la filosofía oriental. Se presentan algunas de las características inusuales del nuevo fractal “hoja de gingko”.
After shortly explaining the significance of fractals in the geosciences I present a modification of the famous Mandelbrot iteration. The result bears a certain resemblance to a gingko leaf. The gingko tree is special in botany, in cultural history and in philosophy. Some unusual features of the new gingko-leaf fractal are presented.
This special article out of competition does not directly concern geophysics but indirectly by presenting a special new fractal (the gingko-leaf fractal) and beyond that by enabling the view on beauty of science and connections to philosophy, art, and nature.
It is well-known that fractals surround us everywhere [see e. g. Mandelbrot (1977) and Barnsley (1988)]. The concept of fractals was introduced into science by Mandelbrot (1967) in a geological context. Later it became more and more evident that fractals are very important for geophysics and geology. That is small wonder because following Scholz and Mandelbrot (1989) one possible broad explanation of the role of fractals in geophysics may be found in probabilistic limit theorems, and in the existence of classical “universality classes” related to them. A second possible explanation may come from deterministic chaotic dynamics. Additionally, Turcotte (1989) pointed out that scale invariance has long been recognized as an important feature of many geological problems. A fractal distribution is the only distribution that is scale invariant. Thus it is not surprising that many geological and geophysical data sets are fractals. In this context, fractals are a method of empirically correlating a variety of quantitative observations. But in addition to being appropriate for empirical correlations fractals also result from several classes of theoretical studies. Dimri has devoted the first chapter of his book[Dimri (2005)] the fractals in geophysics and seismology. The applications in seismology range from the size-frequency distribution of earthquakes, Omori’s law and the analysis of aftershock data even up to the forcasting of tsunami. For completeness, we cite here also two articles which analyse the fractal geometry and seismicity in the Mexican subduction zone[Angulo-Brown et al. (1998)] and fracture arrays in Baja California Sur, Mexico, by using fractal analysis[Nieto-Samaniego et al. (2005)].
One of the most prominent fractals is without doubt the Mandelbrot set. After Taylor and Sprott (2008) Mandelbrot saw this set for the first time at 1 March 1980. It must have been an indescribably great feeling to see that whole cosmos of wonderful and unimaginably fragile structures. The author of the present article was also surprised in suddenly seeing the gingko-leaf fractal (see Figure 2) for the first time about 25 years ago. It has not those fine ramifications and complexity of the Mandelbrot set which is following Dewdney (1985) “the most complex object in mathematics”. But the gingko-leaf set is complex enough and has its own specialities and beauties as we will see later. We start with a short description of the gingko tree’s prominence.
The gingko treeIt is well known that the gingko tree (Ginkgo biloba) is a “living fossil” because of its special botanic history. It is a medical plant with botanical and historico-cultural significance. The German curatorship “Baum des Jahres” (tree of the year) has declared it as the “tree of the millennium”. It is a great symbol for our world, a tree of the world and a symbol of strength and hope. The far eastern philosophy considers the tree, among other things because of its splited leaves, as an incarnation of the famous Ying-Yang principle and connected with that it is also considered as a symbol for harmony and fertility. Last but not least the people are fascinated from the special beauty of the leaves. Nobody less than Johann Wolfgang von Goethe (1749-1832) was also fascinated from this tree and its leaves and initiated the growing of a gingko in the botanical garden in Jena, which is now the oldest gingko tree in Thuringia. He even wrote a poem “Gingo Biloba” [Goethe (1819)] which he devoted to his muse Marianne von Willemer (1784-1860) (see Figure 1) and whose rough English translation is (see en.wikipedia.org/wiki/Gingo_biloba):
Gingo BilobaThis leaf from a tree in the East, Has been given to my garden. It reveals a certain secret, Which pleases me and thoughtful people. Is it a living being, Which has separated in itself? Or are these two, who chose To be recognized as one? Answering this kind of question, Haven’t I found the proper meaning, Don’t you feel in my songs, That I’m one and double?
It is well-known that the Mandelbrot set consists of all points c=a+ib=ˆ(a,b) of the complex plane for which the quadratic recurrence equation
does not tend to infinity, i. e. ∀n, n>0, zn ≠ ∞. It can be also written in real notation with z=x+i y:
There are a lot of generalizations of (1), e. g. with higher polynomials instead of (1) or with bicomplex numbers in order to produce Mandelbrot sets in dimensions three and four[Rochon (2000)] among many others. All these generalizations do not create the elementary beauty of the original Mandelbrot set, the so-called apple-man.
We apply now another special generalization of (1) which leads to a structure which can be considered as a stylized gingko leaf (see Figure 2). It is defined as follows:
where the star means complex conjugation. We call it gingko-leaf iteration. It is a polynomial of third order in zn and Zn*. However, the cubic terms in xn and yn cancel. By using the real notation we see immediately what is going on here in contrast to (2):
That means, the only third order term is the mixed term xn2yn.
A visualization of the Mandelbrot set together with the new gingko-leaf set is presented in Figure 3. It shows the approximate border strip of the apple-man together with the gingko leaf. Figure 3 was calculated with Mathematica and for the reader’s convenience we present here the main features of the program without explanation:
CompiledMandel=Compile[{{c, _Complex}}, Length[FixedPointList[#ˆ2+c &, c,25, SameTest ->(Abs[#2]>2.0 &)]]]; CompiledGingko=Compile[{{c, _Complex}}, Length[FixedPointList[#ˆ2+Im[#ˆ2]* (Re[#] – 1)*I+c &, c, 25, SameTest ->(Abs[#2]>2.0 &)]]]; g=DensityPlot[compiledGingko[x+I y], {x, -2, 0.6}, {y, -1.3, 1.3}, PlotPoints ->500, Mesh ->False, Frame ->False, AspectRatio ->Automatic, ColorFunction ->(If[#=1, RGBColor[0.3, 0.7, 0], RGBColor[1, 1, 1]] &)]; c=ContourPlot[compiledMandel[x+I y], {x, -2, 0.6}, {y, -1.3, 1.3}, PlotPoints ->300, Frame ->False, AspectRatio ->Automatic, ContourShading ->False, Contours ->{13}];
Obviously, the gingko-leaf set is symmetric concerning the x-axis. The proof for that behaviour is simple and is omitted here. It can be carried out similarly as for the Mandelbrot set.
Some features of the gingko-leaf setThe Mandelbrot set has a rich structure at its border line and also in the outer regions not belonging to the set. The latter structure can be visualized by using so-called velocity diagrams, where the number of iterations necessary for exceeding a given limit is colour-coded [see e. g. Peitgen and Richter (1986)]. The same is true for the gingko-leaf set especially within the regions A and B of Figure 2 and we present some examples. A very convenient and effective vehicle for visualizing these structures is the “Fractalizer” of Sontheimer (2007), which was used for painting figures 6- 9. Additionally we have investigated also the inner region of the set (Figure 4) with Turbo Pascal by using the following colour-code, where t=xn2+yn2:
It could be carried out with Mathematica as well by using e. g. the RasterArray command.
The stalk (region A) is characterized by the occurrence of so-called satellites which are typical for the antenna of the Mandelbrot set and which have now the form of stylized gingko leaves in the broadest sense (Figure 5).
The colour-code for Figure 5 is:
The nodality in region A has also a nice structure which we demonstrate with the “landscape” in Figure 6. The black parts belong to the gingko-leaf set.
Very interesting and beautiful structures occur in region B nearby the sawtooth-like indentations at the right end of the gingko leaf. In Figure 7 we see a stylized winter rose (Euphorbia pulcherrima), whose origin is Mexico. It occurs in many places of region B.
Another winter rose from region B is presented in Figure 8. It is interesting to note that contrary to Figure 7 we find here parts of it which belong to the gingko-leaf set (in black).
It remains unclear wether similar to the Mandelbrot set the isolated parts of the set are all connected with the main body by very thin fibres or not.
MiscellaneousIt is well-known [see e. g. Peitgen and Richter (1986)] that by changing the role of c and z in (1) we can assign each point of the complex plane a corresponding Julia set. The same is true for the gingko-leaf set. Especially for points from region A and B interesting figures are obtained. Without going into details we present two examples from region B in Figure 9.
I have called the left figure “throne of Cuauhtémoc” and the right figure “bad ghost”. Note that on both sides of the throne again winter roses occur.
Finally, let us demonstrate that by changing the gingko-leaf iteration only a little bit, we get a completely different set. By replacing (4) by
we obtain a set (Figure 10) which I call “ugly duckling”.
Obviously, the symmetry concerning the x-axis is completely broken.
ConclusionsWe have presented a less-known part of the enormously multiform world of fractals. It is not excluded, that the properties of the gingko-leaf set follow from already existing mathematical theorems about more general fractals. This might require closer examination. It is also not excluded that a similar kind of feedback mechanism, which produces the gingko-leaf fractal, is also responsible in the broadest sense for “producing” the nice gingko leaves in nature. At the same time a formal but pretty “connection” between the gingko and the Mexican winter rose is accomplished.
Hopefully, this article will attract attention of all people fascinated by the beauty of science.
A special word of thanks goes to Robert Sontheimer (Hohenstein/Germany) who modified his program Fractalizer for the investigation of the gingko-leaf set and carried out a lot of test calculations. Without his help this article would not have been possible in the present form.
I devote this article to the memory of my honoured former colleague Dr. Erhard Unterreitmeier (1939-1997), who encouraged me to publish the gingko fractal under the title “Gingko from Jena” already about 25 years ago. Additionally, I devote it to my mother Alice Malischewsky nee Auning (1903-1995), who followed my efforts about fractals with great interest.


















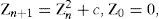
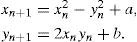

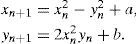

![Color-coded range a∈[−1.4366,−1.4360], b∈[−0.0069,−0.0064] within region A. Color-coded range a∈[−1.4366,−1.4360], b∈[−0.0069,−0.0064] within region A.](https://static.elsevier.es/multimedia/00167169/0000005300000001/v2_201505081401/S001671691471493X/v2_201505081401/en/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)


![Colour-coded range a∈[−1.8,−1.5], b∈[−0.01, 0.01] within region A with Turbo Pascal. Colour-coded range a∈[−1.8,−1.5], b∈[−0.01, 0.01] within region A with Turbo Pascal.](https://static.elsevier.es/multimedia/00167169/0000005300000001/v2_201505081401/S001671691471493X/v2_201505081401/en/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![The winter rose in region B out of the gingko-leaf set with a∈[0.4507, 0.4528], b∈[−0.2148, 0.2132]. The winter rose in region B out of the gingko-leaf set with a∈[0.4507, 0.4528], b∈[−0.2148, 0.2132].](https://static.elsevier.es/multimedia/00167169/0000005300000001/v2_201505081401/S001671691471493X/v2_201505081401/en/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Winter rose in region B for a∈[0.386232, 0.386246], b∈[−0.135391,−0.135381]; the black forms belong to the gingko-leaf set. Winter rose in region B for a∈[0.386232, 0.386246], b∈[−0.135391,−0.135381]; the black forms belong to the gingko-leaf set.](https://static.elsevier.es/multimedia/00167169/0000005300000001/v2_201505081401/S001671691471493X/v2_201505081401/en/main.assets/thumbnail/gr8.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)