Dynamics of internal waves generated by mountain breeze in Alchichica Crater Lake, Mexico

Resumen

Mediciones hidrofísicas realizadas en el lago cráter profundo Alchichica, México, mostraron la presencia de ondas internas intensas con período de un día, generadas por la influencia regular de la brisa de montaña. Las ondas diurnas generan ondas internas semidiurnas, las cuales tienen periodos cercanos a las oscilaciones de resonancia del lago. Las ondas internas rompen cerca de la orilla y en el fondo del lago, causando circulación baroclínica y mezcla de masas de agua. De acuerdo con los datos obtenidos con un ADCP, dos ondas inclinadas diurnas y dos semidiurnas se propagan en el lago unas hacia las otras en profundidad y pueden producir fluctuaciones de un modo vertical, cuando la profundidad del lago es un múltiplo de la semilongitud de onda vertical. Esta multiplicidad se aplica tanto a las ondas diurnas como a las semidiurnas. La existencia simultánea de modos horizontales y verticales corresponde a un modo volumétrico, o fluctuaciones resonantes de la laguna. Las ondas colapsan cerca del talud y del fondo del lago, induciendo circulación baroclínica y mezcla local.

Abstract

Hydrophysical measurements carried out in the deep tropical crater lake Alchichica, Mexico, showed the presence of intense internal waves with a one-day period, generated by the regular influence of a mountain breeze. The diurnal waves effectively generate semidiurnal internal waves that are close to the resonance oscillations of the lake. The internal waves brake close to the shoreline and into the lake's bottom, which generates baroclinic circulation and water masses mixing. According to the data obtained with a ADCP, two diurnal and two semidiurnal inclined waves propagate in the lake towards each other in depth and can form fluctuations of a vertical mode, if the depth of the lake is a multiple of one-half the vertical wavelength. This multiplicity applies to both the diurnal and semidiurnal waves. The simultaneous existence of horizontal and vertical modes corresponds to a volumetric mode, or resonant lake oscillation. The waves collapse near the shore slopes and the lake's bottom, inducing baroclinic circulation and local mixing.

Introduction

Internal oscillations in density stratified lakes depend on the lake shape, the bottom relief and the wind force which causes these oscillations. In large lakes the sporadic wind force creates nonlinear asymmetric internal waves which propagate in lake (Farmer, 1978). In circular lakes, the pulsating wind forces internal seiches with a horizontal modal structure (MacIntyre and Flynn, 1999; Csanady, 1973). Above the sloping bottom internal Kelvin waves or the Poincaré waves can be formed (Antenucci et al., 2000; Saggio, Imberger 1998). The periodic wind generates internal waves that give rise to nonlinear harmonics and a wide spectrum of internal waves (Monismith, 1985; MacIntyre and Flynn, 1999). The presence of internal waves has been reported in Lake Alchichica (Filonov and Alcocer, 2002).

Though wind-forced motions in stratifi lakes near sea level have been previously studied and modeled (Monismith, 1985; Imberger, 1985), there have been few investigations of lakes in volcanic craters located in high altitude tropical zones. Research of the physical processes associated with mountain breezes has been discussed in relation to Santa Maria del Oro (Serrano et al., 2002), volcanic Mexican lake situated at a height of 1500 m above sea level.

The objective of the present study was to provide physical experimental evidence on the causes and dynamics of the internal waves generated in Lake Alchichica by mountain breezes.

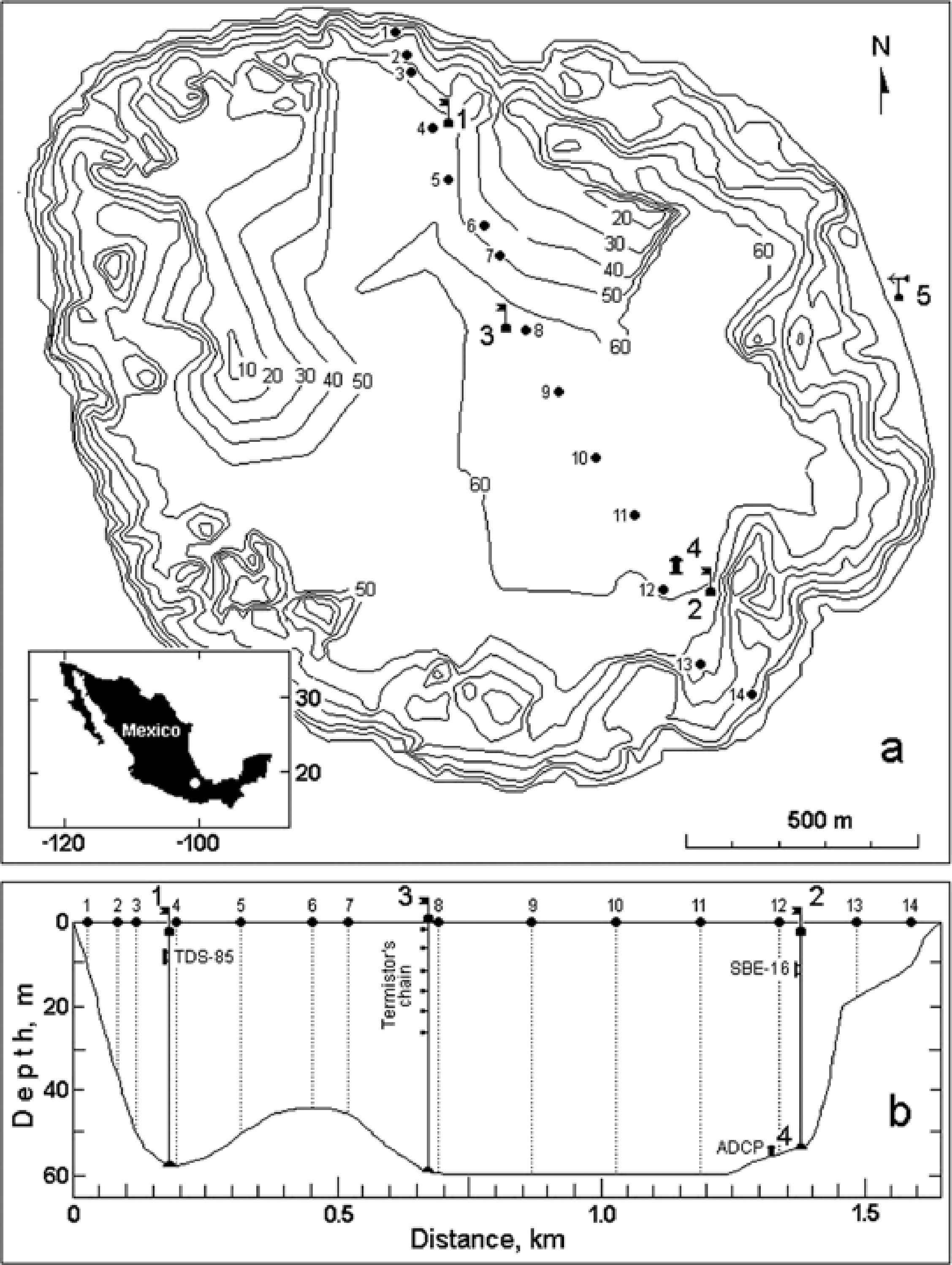
Study area

Lake Alchichica is a typical saline crater lake of the Mexican plateau, with circular shape, steep coastal slopes, more than 1.5 km diameter and 60 m depth (Figure 1a). Alchichica is one of the deepest natural lake in Mexico. It is located at an elevation of 2350 m above sea level. Its coordinates are 19° 24.7‘N and 97° 24.0’W. Alchichica has an area of 2.3 km² with a volume of 94,214,000 m³ and an average depth of 40.9 m (Filonov et al., 2006). The water has a salinity of 8.5 g/L and a pH 8.7-9.2, dominated by sodium-magnesium and chloride- bicarbonate ions. Water salinity varies little with depth. Annual air temperature fluctuates from –5.5 to 30 °C with a mean value of 14.4 °C (Filonov and Alcocer, 2002). An arid climate, with an annual precipitation regime of less than 500 mm and an annual evaporation rate of 1690 mm characterizes the area. Alchichica is warm-monomictic (monomictic lakes are lakes that mix from top to bottom during one mixing period each year). Mixing takes place from late December to early March, during the cold, dry season, and it remains stratifi d throughout the rest of the year (from late March to early December) during the warm, rainy season (Alcocer et al., 2000). The lake's diameter is less than the internal Rossby radius (7.3 km), so the influence of the Earth's rotation is negligible.

Figure 1.

a) The bottom's relief and the instruments’ position in lake. The large numbers show the position of buoys 1, 2 and 3; the ADCP (4) and the meteorological station (5). Circles with small numbers show the casts’ position during the fourth survey 10.05.2004 from 14:14 until 15:02. b) The bottom profile on the line of CTD casts and the position of devices in the water column.

Hydrographic and meteorological measurements

The experiment at the lake was carried out from May 8 till May 11, 2004. Temperature fluctuations were measured by three mooring instruments (Figure 1). Buoy 1 was equipped with a temperature meter TDS-85 (made by UABC, Mexico) at horizon 8 m, with a measuring precision of 0.02 °C. The buoy 2 was equipped with a conductivity-temperature-depth (CTD) meter SBE-16 (made by Sea-Bird Electronics) at horizon 12.5. The buoy 3 was equipped with a chain of Waterpro thermistors (Onset Computers Corp., Massachusetts, USA) deployed at depths of 1, 5, 10, 15, 20 and 25 m with a 0.2 °C resolution. On this mooring temperature was measured hourly during 3 month (from March 24 to May 20, 2002).

Five temperature surveys were made on a line between moorings, approximately at 30 degree angle from the average wind direction (Figure 1). Each survey lasted about one hour. During a survey a CTD profi er SBE-19 fell manually from the boat with a speed of about 1 m/s and a 0.5 seconds sampling rate. A Global Position System (GPS) fixed the coordinates of the sounding points.

An Acoustic Doppler Current Profiler (600 kHz ADCP, RD-Instruments) was placed at the bottom. During 2.6 days, it measured the vertical profile of three current speed components with a vertical resolution of 1 m (Figure 1). The sampling rate was 0.5 minutes. The speed's time series were smoothed out with an interval 2.5 hrs.

Meteorological measurements were hourly conducted on the lake from January 2003 to December 2004, using Davis GroWeather automatic weather station mounted at a height of 4 m on the east coast of the lake.

The acquired data were analyzed using unified standard methods and spectral analysis techniques (Jenkins and Watts, 1968). To calculate two-dimensional spectra for temperature, wind and water current fluctuations, we followed the methods described in Konyaev (1990).

For calculation of vertical deviations of the water layers on data of temperature sections the following algorithm was used (Filonov and Konyaev, 2003): all vertical temperature- pressure profiles Tj(pj) are interpolated onto a single depth grid Tj(z) and the mean temperature profile is computed as: Tz=1J∑jTjz where j = 1:J is the profile index. The mean profile T_j(z) describes the unperturbed position of water layers. The inverse functions z_j(T) and z(T) exist if the original profiles T_j(z) and the mean profile T(z) are monotone functions as it is in our case.

Vertical deviations of water layers from the unperturbed position are defined as Δhjz=zT−zjT. Next, temperature is replaced with depth by means of the mean profile z(T) to give the relationship between deviation and depth Δhjz. The layers’ position is then obtained as h_j(z) = z − Δh_j(z).

Each sounding consists of two temperature profiles T_dj(z) and T_uj(z), which correspond to the descending and ascending track of the profiler respectively. The difference between these profiles d_hj(T) = z_uj(T) − z_dj(T) is accounted for by rapid (small-scale) disturbances of water layers. Temperature T is then replaced with depth z with the use of the mean profile z(T) to give the dh_j(z) difference. It is then normalized by Δt_j(z), which is the time interval between the observations made on downward and upward sounding profiles: w_j(z) = dh_j(z)/Δt_j(z). The normalized difference has the units of velocity. However, this vertical velocity is accounted for not only by the vertical motion of layers but by their horizontal advection as well.

The geographical coordinates are transformed to along-leg coordinate x, which is assigned to each profile. In this way, three vertical-cross sections are generated: the layers’ position h(x, z), their deviation Δh_j(x, z) and vertical velocity w(x, z).

Results

Mountain breeze circulation

Analysis of a two-year series of meteorological observations at the lake showed that the presence of mountain winds is relatively constant from day to day in the area of the lake. Lake Alchichica lies in a volcanic crater in the mouth of a wide mountain valley that extends north to south with slopes as high as 300-500 m. To the north, there is an extensive saline plain spanning nearly 200 km². These topographic features provide suitable conditions for local atmospheric circulation between the mountain and the saline valley over the entire length of the lake.

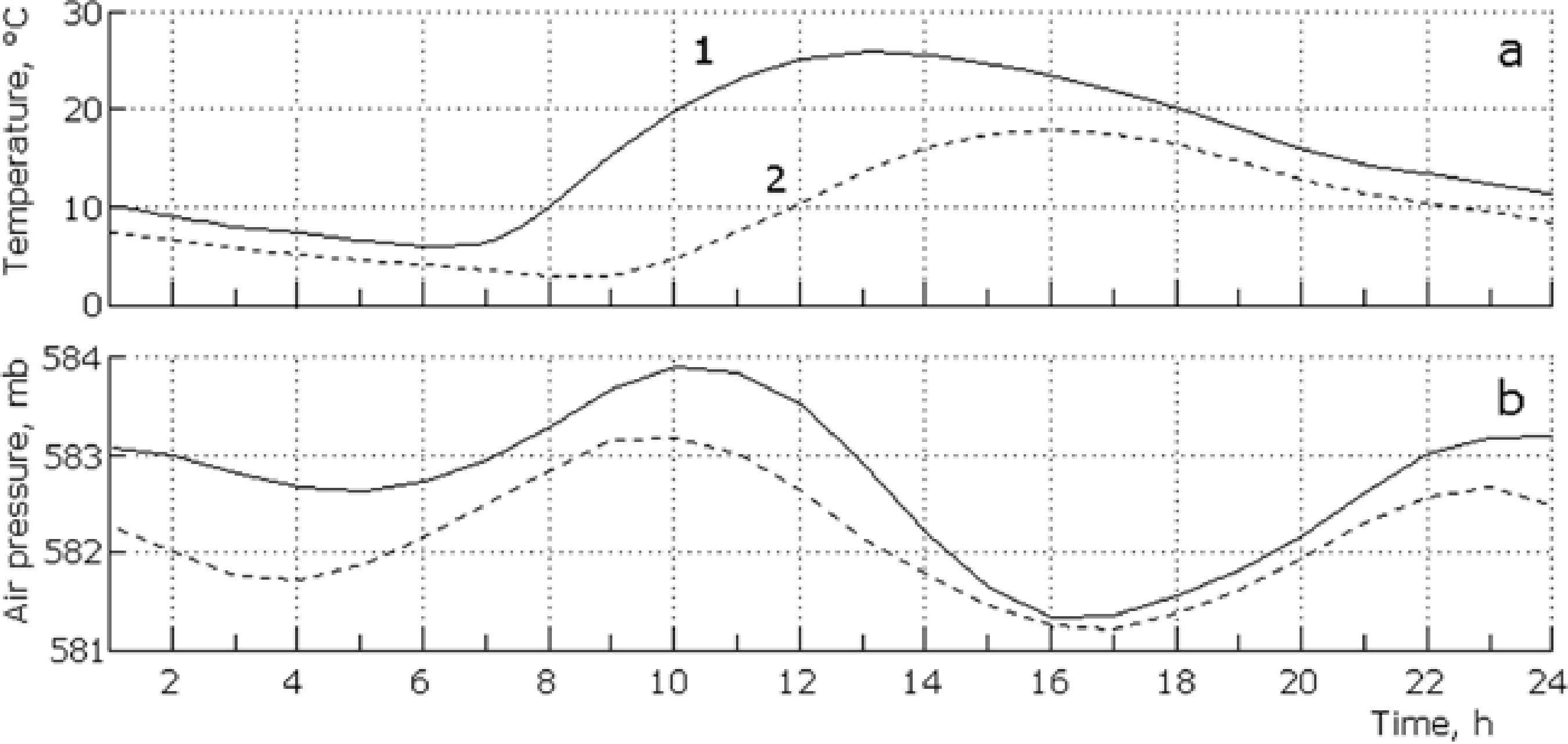
During the day, temperature differences between the saline valley and the main zone create a reverse pressure gradient. As a result, the wind is directed upwards along the main slopes from the north. The daily course of the wind over the lake dictates daily fluctuations in the air temperature and atmospheric pressure (Figure 2 a, b).

Figure 2.

a) Hourly average fluctuation of air temperature, b) atmospheric pressure for the dry (1) and wet (2) seasons in a year.

From 22:00 until 13:00 hours, the weak wind above the lake does not exceed 1 m/s. Its speed grows quickly during the afternoon and reaches an average hourly speed of 5-6 m/s with pulses up to 10-12 m/s at approximately 17:00 hours (see in the upper right corner of the. As of 22:00 hours, the wind begins to rapidly return back to nocturnal normal values. The wind's direction throughout the day varies insignificantly and remains within the N-NNO range, and presents a non-daily clockwise rotation, typical for a sea breeze or for a breeze on such large Mexican lakes such as Chapala (Filonov, 2002).

Stratification

Long-term measurement of the thermistor chain in the center of the lake (mooring 3) showed that due to the considerable water transparency (euphotic zone 14-38 m) and the action of wind and internal waves, daily solar warming penetrates to a depth of about 10 m. The total heat infl is small as the rapid increase in temperature of the top layer in the first half of the day is offset by a similarly swift downturn in the second half of the day. Wide variability in daily air temperature is important for heat absorption and emission in a high-mountain tropical plateau. Wind waves on the lake are small (length 5-7 m and height less than 0.5 m) and they create a mixing that does not likely penetrate deeper than a few meters. At midday, the surface temperature decreases slightly with the onset of the breeze.

During our experiment the density stratifi of the lake was defi by the temperature decrease with depth from 19.5 °C on the surface to up to 14.7 °C near the bottom. Salinity decreased insignificantly from 7.58 psu at the surface to 7.52 psu on the bottom (Figure 3). Thus, vertical change in water density is completely determined by temperature. The thermocline with the maximal buoyancy frequency N(z) = [(g/ ρ)· (∂ρ/ ∂z)]1/2 of 20 cycle/h, settles down between horizons 10 and 18 m. The buoyancy frequency in the deep layers is decreased to 1 cycle/h.

Figure 3.

a) Mean vertical profiles of temperature, salinity and buoyancy frequency (data from five repetitive cuts, just 48 casts).

Temperature fluctuations in two separate points (moorings 1 and 2)

Despite the difference in depth of the devices, the average temperature measured by both of them was identical and equal to 18.9 °C. Hence, on average, under action of the wind, the thermocline is tilted. In the lake's northern part (mooring 1) the thermocline is raised with respect to the southern part (mooring 2) around 4.5 m. The towing of the temperature gauge on a line between moorings has shown, during the maximal wind speed (after midday), that the water temperature at a depth of 0.2 m increases monotonously from 19.3 °C near mooring 1 to up to 20.2 °C near mooring 2.

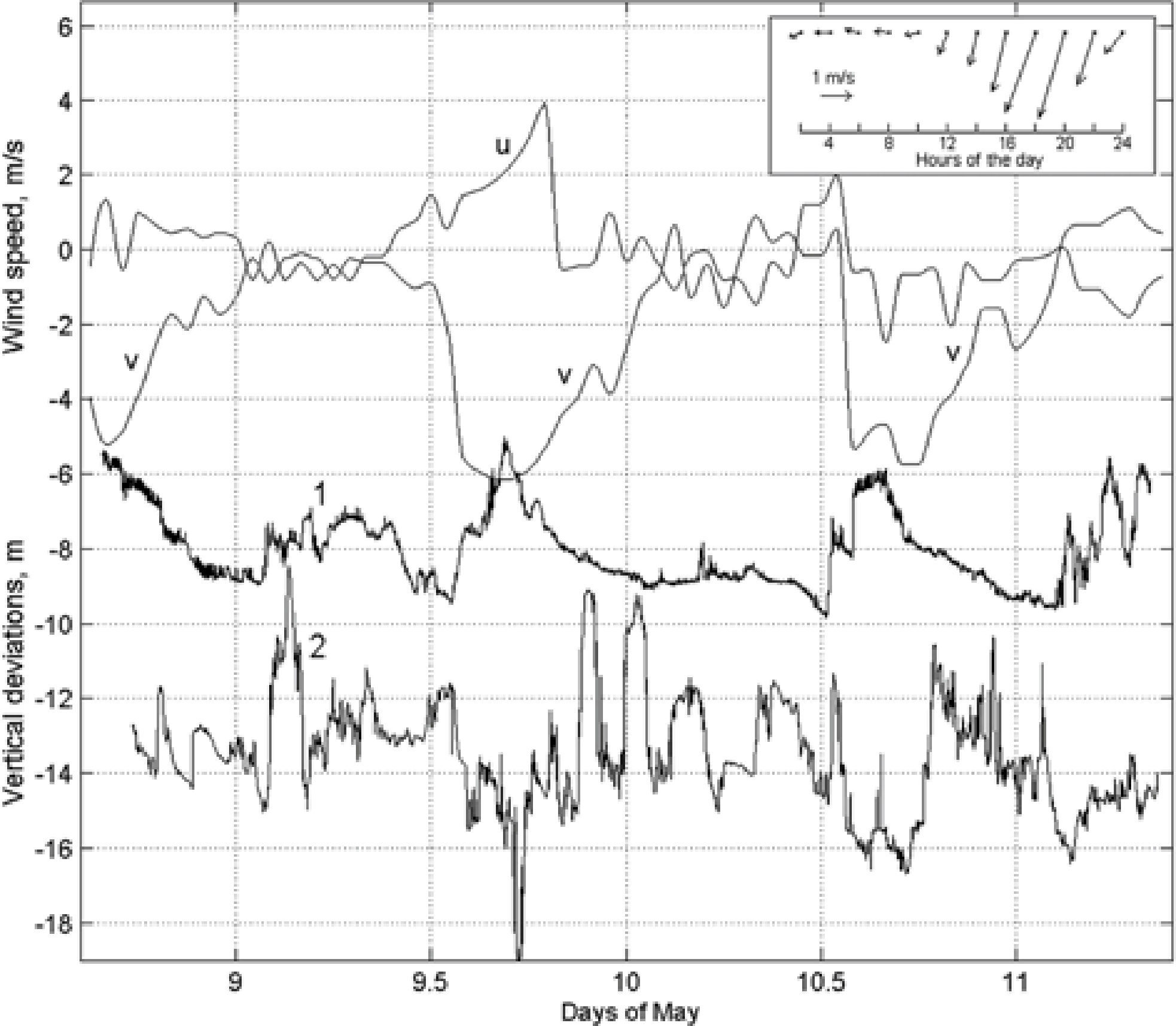
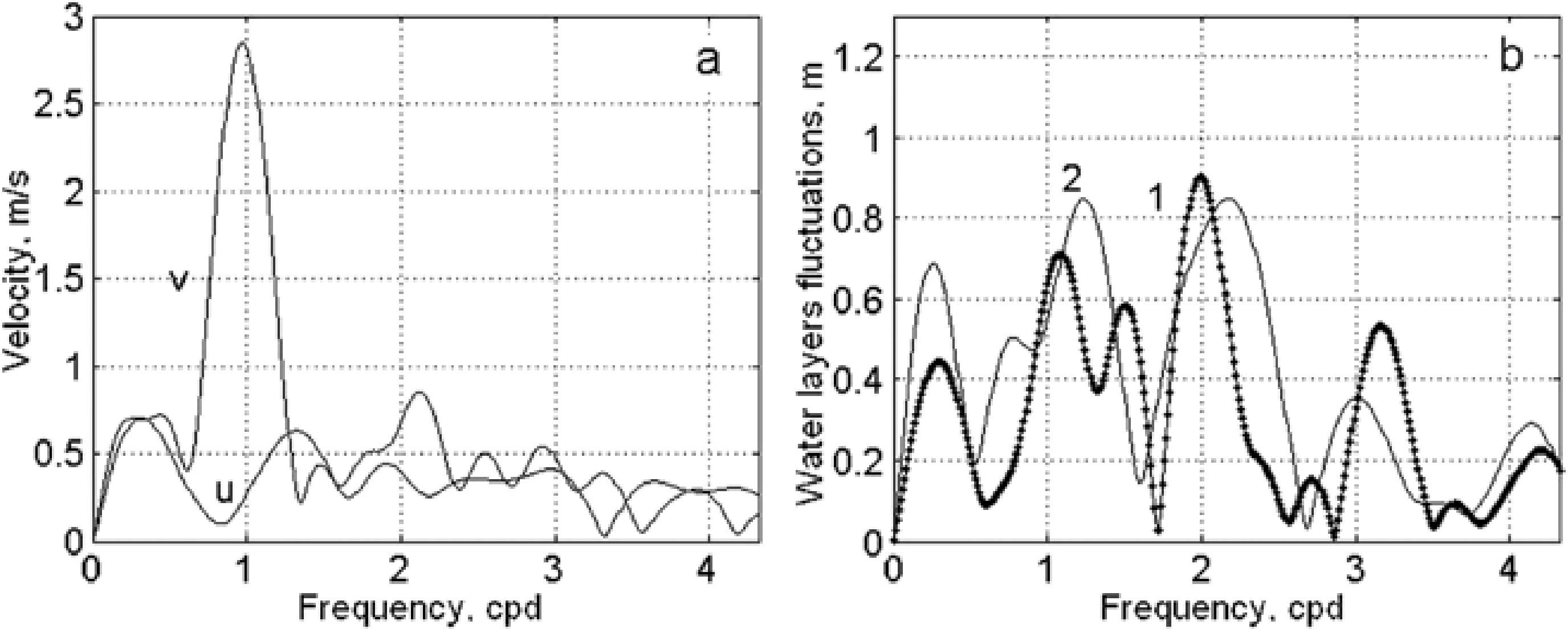
The fluctuations in the water layers at the moorings have large amplitude and complex form with the predominance of diurnal and semidiurnal oscillations. There are high short bursts and groups of bursts with a height of up to 3 m (Figure 4). On the basis of the temperature fluctuations at each mooring and the average temperature profi the vertical water layer deviations were determined at the depths where the thermographs were deployed. The structure of the deviation spectra was similar at the two moorings (Figure 5). The greatest peak is on the semidiurnal frequency. Another peak of almost the same height is on the diurnal frequency.

Figure 4.

Horizontal wind speed components and vertical deviations of water layers at mooring 1 (horizon 8 m) and mooring 2 (horizon 12.5 m). The numbers of the curves correspond to the buoys 1 and 2. Daily average wind velocity from January to May 2002 in Lake Alchichica is presented in the rectangle in the superior right corner.

Figure 5.

Spectra of the wind speed components (а) and water layers fluctuations near buoy 1 and 2 (b). The spectral density of the peaks is numerically equal to the oscillations’ amplitude with the appropriate frequency.

From here and subsequently, the spectrum is calculated as the module of a Fourier transformation without squares it. Thus, spectral density in the spectrum peaks is numerically equal to the amplitude of fluctuations on the appropriate frequencies, and it is possible to present the axis of spectral density in the same units in which the time series is measured (Figure 5).

The diurnal oscillations alone are dominant in the correlation function between vertical deviations of water layers under the buoys and the v-component (northern component) of the wind. The correlation between vertical deviations and the u-component (eastern component) of the wind is relatively small. Hence, the diurnal internal waves are created by the wind, which direction coincides with the axis v.

As shown by the correlation analysis, the oscillations on the two buoys are in an opposite phase as it occurs in oscillations with horizontal mode. It is possible to assume that between the two moorings only half of the diurnal wavelength settles down (first horizontal mode with antinodes of vertical deviations and nodes of horizontal orbital speed at opposite sides of the lake).

Oscillations of water layers on a line survey

Five temperature surveys were made on a line between moorings. They were performed every day in the middle of the day. The survey's data processing consisted of a number of procedures:

• -

  Elimination of inversions in temperature and salinity profiles;

• -

  Interpolation of the data in a uniform scale of depth;

• -

  Calculation of mean vertical profiles of temperature, salinity, density and buoyancy frequency;

• -

  WKB - normalization of the temperature profiles (Filonov and Lavin, 2003);

• -

  Transition from temperature to pressure profiles by means of an average temperature profile;

• -

  Calculation of pressure deviations (vertical deviations of the water layers).

The detailed description of these procedures can be found in (Filonov and Konyaev, 2003).

Vertical deviations of the water layers form the two-dimensional fi ld on a depth- horizontal plane. This field has periodicity, which precisely comes to light by means of a two-dimensional (vertical and horizontal wave numbers) deviations’ spectrum (Figure 6). The maximum positive deviation on one end of the survey is accompanied by the maximum negative deviation on the other end.

Figure 6.

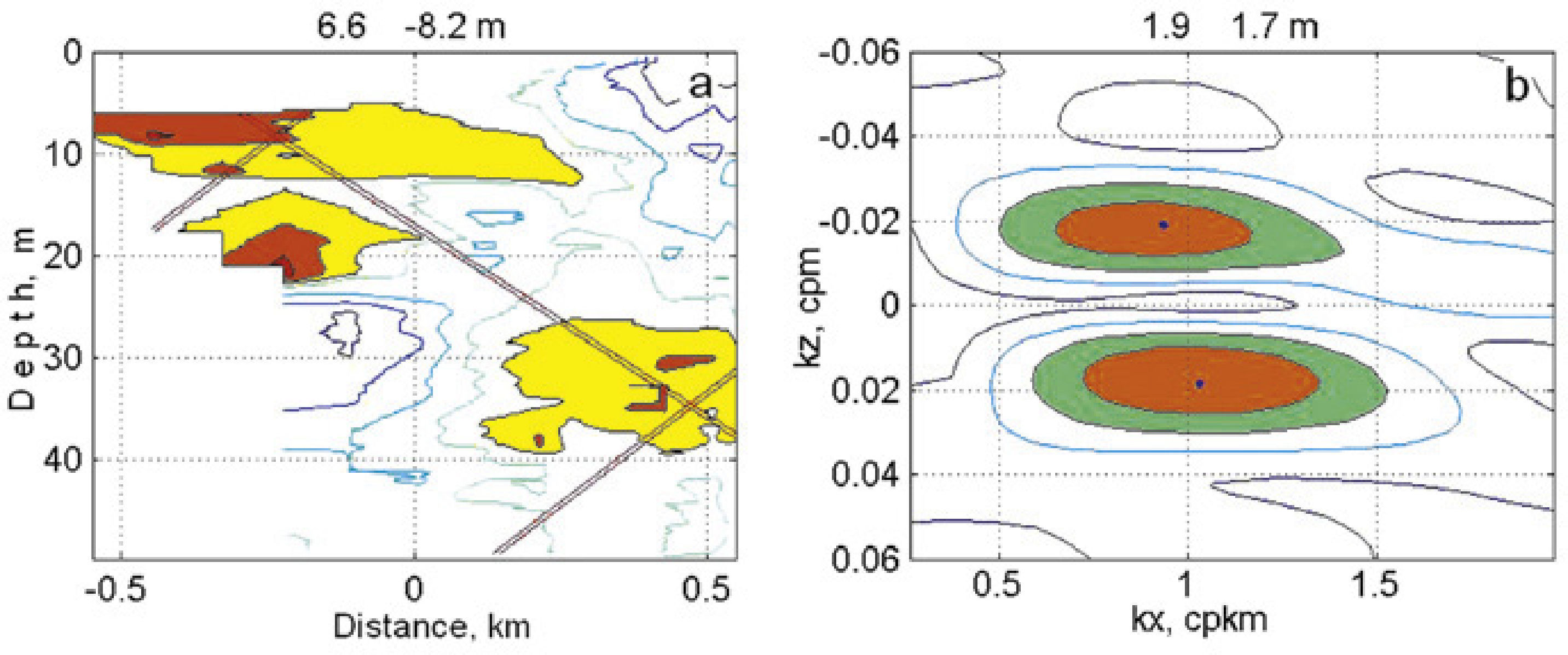
Deviations of water layers on the data of fourth survey (a) and two-dimensional spectra of these deviations (b). The axis x is directed from mooring 1 to 3. The straight lines show crests of two waves corresponding to the basic peaks of the spectra (b). Above the figures the maximum and minimum deviations (a) and the amplitude of the basic fluctuations (b) are showed. Isolines on Figure (a) are plotted with a 0.3 step from a maximum. Here, the levels above 0.3 are shaded. Isolines on Figure (b) Isolines are plotted with a 0.2 step from a maximum; the levels above 0.6 are shaded.

The spectrum contains two basic peaks with different vertical wave number. The estimations of the horizontal wavelengths spectrum present two peaks at 1.3 and 1.5 km for survey 3 and at 1.1 and 1.8 km in average for all four surveys. The systematic difference in the measured wavelengths could arise as a result of the Doppler's effect at the survey. The difference of the measured horizontal wave numbers, when the diurnal or semidiurnal waves (f =1 or 2 cycle/day) move towards each other and the boat speed of V = 1 km/h, is equal to Δkx = 2 f / V = 0.08 or 0.16 cycle/km, that is close to the observable shift (Figure 6). Hence, the waves move horizontally towards each other and form a horizontal mode of oscillations.

In the ocean there is usually a vertical mode of internal waves formed as a result of the reflection of waves from the bottom and the surface. In our case, a horizontal mode can be formed by reflection from the sloping shores, whose inclination considerably exceeds the inclination of the internal waves.

Current speed

The speeds’ fi is transformed to depth-constant buoyancy frequency (WKB-normalization) maintaining the thickness of the observed water layer. After the WKB-normalization, the internal waves’ beams and crests become rectilinear, and the basic spectrum peaks become more compact (Filonov and Lavin, 2003).

The normalized field is subjected to further analysis. Previously, the average values of the current speed are removed from the current's time series components on each horizon. The field of the horizontal u-component of the speed vector on a depth-time plane contains a characteristic interference structure (the u-component is directed towards the east, v - towards the north) (Figure 7a). The crest's inclination determines the vertical phase speed of the diurnal and semidiurnal waves, which is equal to 0.055 and 0.075 cm/s. Tilting diurnal wave crests on the vertical-horizontal plane by the temperature recording is 2.3 degrees, so that the horizontal diurnal wave phase velocity is 1.4 cm/s.

Figure 7.

а) A u-component of current speed after WKB-normalization and crests of diurnal and semidiurnal waves propagate in opposite directions on depth (inclined lines). Isolines are plotted with a step 0.2 from a maximum, the positive deviations are shaded. b) The spectra of the u-component (positive semi axis of frequency) and v-component of the speed (negative semi axis). Isolines are plotted with a step 0.1 from a maximum; the levels above 0.7 are shaded. The waves moving up marked by symbols and by symbols - moving down.

In a spectrum of the u-component there are two peaks with a diurnal frequency and two with semidiurnal frequency (Figure 7b). Each pair of peaks corresponds to two inclined waves on a depth-time plane. The waves propagate in opposite directions on depth. More intensive waves propagate downwards (group movement), less intensive - upwards. Oscillations of the v-component of the speed are significantly less intensive, so the orbital movements in the waves occur on the strongly extended orbits on a west-east direction.

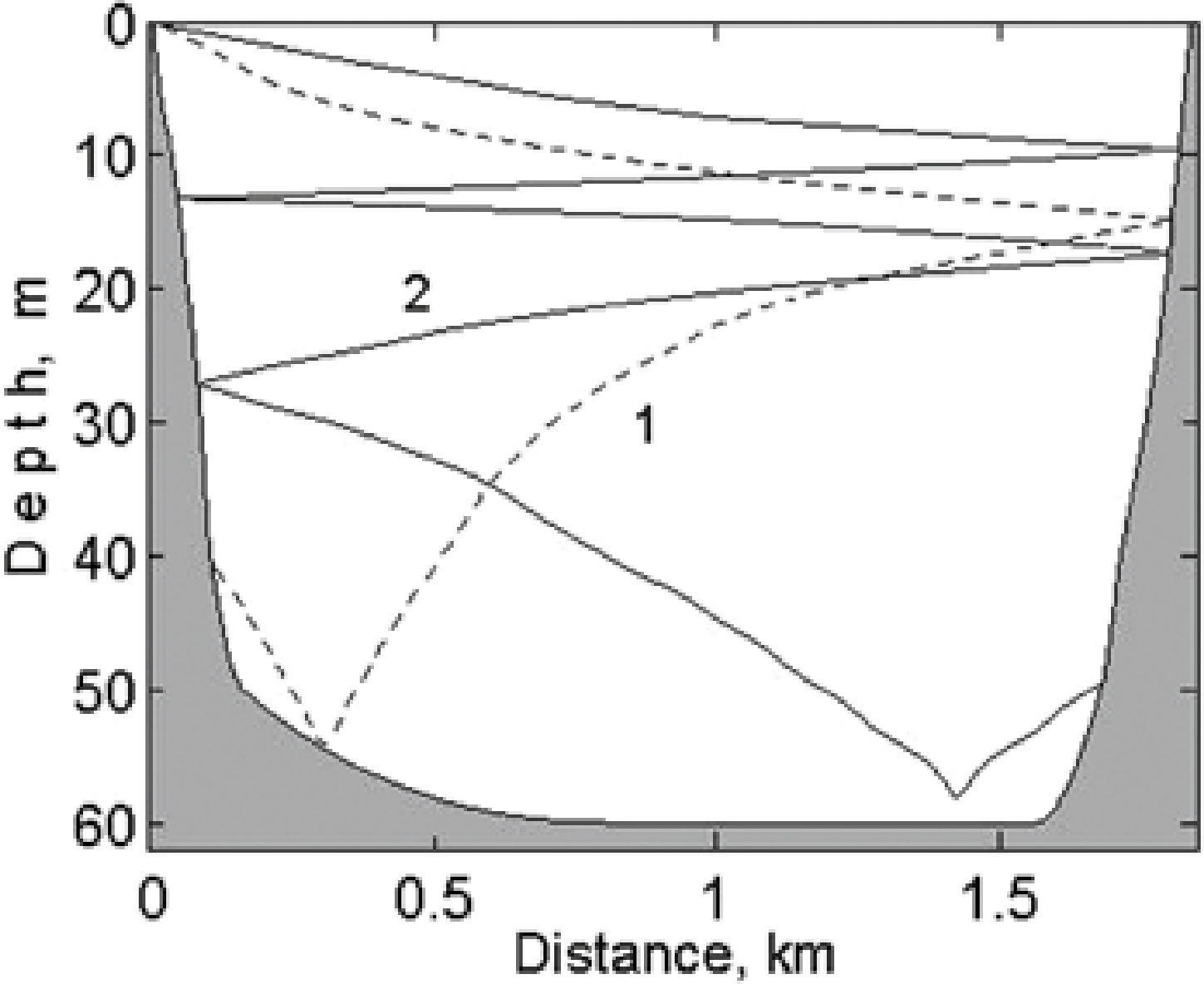
Trajectories of beams

It is convenient to treat the inclined wave in the terms of beams, or characteristics. The beam's angle of inclination is defined by the buoyancy frequency N(z), the inertial frequency F = 0.66 cycle/day and the wave frequency f : α(z) = arctg(f 2 − F2)/(N(z)2)f 2)1/2. The trajectory of a beam comes out by integrating on depth xz=x0±∫0zctgαzdz where x₀ defines the beam's location on the x axis. The crests and troughs of a wave extend along the beam; the group velocity is directed along the beam.

Taking a vertical section of the lake, on a line from west to east, two characteristics for the diurnal and semidiurnal waves were calculated (Figure 8). Two and a half vertical lengths of a diurnal wave and one length of a semidiurnal wave fit from the surface of the lake to the bottom. Steep side slopes and a practically flat bottom create conditions for the arising of resonance for internal waves.

Figure 8.

The characteristics beam of diurnal (1) and semidiurnal (2) internal waves.

Discussion

The mountain breeze, which blows with diurnal periodicity, serves as the causing force and as the source of energy for all movements in the lake. In the afternoon the wind drives warm water on the surface to one of the lake's edges. The movements in a thin top layer of the lake serve as a wave generator, creating an internal wave with a diurnal period.

On the data obtain with the mooring instruments, vertical fl ctuations of temperature at opposite edges of the lake are in an opposite phase, so two waves form horizontal mode with antinodes of vertical fluctuations at opposite edges of lake (Figure 7). The waves’ horizontal length is approximately equal to twice the lake's diameter.

From the ADCP's data, we found that both diurnal and semidiurnal oscillations are formed by two inclined waves (four waves in all). Pair of inclined waves moves towards each other, on depth. On the temperature survey data (taking into account the Doppler Effect) only two inclined internal waves move towards each other on a horizontal plane.

It is possible that diurnal and semidiurnal waves are not determined by the survey because they might have a different orientation relative to the survey line.

Diurnal oscillations are forced ones; their horizontal wavelength is imposed by the lake's diameter. Semidiurnal oscillations arise originally as a result of nonlinear distortions of large diurnal oscillations. However, the amplitude of the semidiurnal oscillations ranges up and even exceeds the amplitude of the diurnal ones. This can be a result of the proximity between semidiurnal oscillations and resonance ones in the lake.

Conclusion

Solar warming creates and supports steady density stratification on in the lake. The daily change in temperature in the top water layer is very large, but the daytime heat influx is compensated, to a great extent, by its loss at night. The stratification interferes with a vertical exchange inside the lake. In the afternoon, the wind drives warm water on the lake surface, causing an inclination of the thermocline. Water surge on the surface is created by friction forces. The mountain breeze blows over Lake Alchichica with diurnal periodicity and generates diurnal internal waves with large amplitude. The second harmonic of the diurnal oscillations arises due to nonlinear distortions of the diurnal oscillations and reaches large amplitude presumably because semidiurnal frequency is close to the lake's resonance one. The internal waves partially break especially near the coastal slopes in the thermocline's area, providing local mixing of the lake's waters.

The water volume of the lake Alchichica looks like a vertical cylinder that allows the occurrence of both horizontal and vertical modes of internal waves and, as a result, cavity resonator for the waves. As far as we know the cavity resonance of internal waves in a natural basin was first observed. The generation mechanism of semidiurnal internal waves by forcing of the diurnal frequency is new for natural hydrophysical objects. It seems likely that the discovered effects are rare for the natural basins as their water volumes have irregular forms. In this regard the interesting exceptions may be among the volcanic lakes of Mexico.

Referencias no citadas

Thorpe, 1998.

Acknowledgements

This project was fi ncially supported by Consejo Nacional de Ciencia y Tecnología (CONACyT) projects No.41667 and No.33667-T. The authors thank Dr. K. Konyaev† for a discussion the results. The authors also thank Laura Peralta and Luis A. Oseguera (FES Iztacala, UNAM) for helping in the field work