Usamos registros de algunas estaciones de la base de datos de la OTSN para caracterizar su respuesta de sitio y para analizar los límites y alcances del modelado de Rayleigh para los cocientes espectrales H/V.
Las estaciones que consideramos en este trabajo pueden ser agrupadas, según su respuesta sísmica, como sitios en roca dura y como sitios con algún efecto de sitio. A partir de estos resultados proponemos modelos de velocidades que están basados en el modelado de Rayleigh (cálculo de la elipticidad teórica).
Los resultados muestran que para los sitios con algún efecto de sitio los cocientes espectrales H/V pueden ser modelados a partir del cálculo de la elipticidad teórica de un modelo de velocidades. Sin embargo, para los sitios en roca dura, en los que los cocientes espectrales son bastante planos, el modelado a partir de la elipticidad teórica de ondas de Rayleigh no resuelve de manera satisfactoria. Esto puede deberse a que las condiciones generales para que los cocientes H/V proporcionen un pico definido, cercano a la frecuencia fundamental de resonancia de ondas S, y por tanto que este pico se pueda asociar con una medida de la elipticidad de las Ondas de Rayleigh no se cumple en sitios de roca dura.
We use records from the East Thuringian Seismic Network (OTSN, Ostthüringer Seismisches Netzwerk) to characterize the site response for each station, and to analyze the scope and limits of the Rayleigh modeling for H/V spectral ratio. The stations considered in this work can be classified by their seismic response as hard rock sites or as sites with some site effect. From these results we propose velocity models based on Rayleigh modeling (theoretical Rayleigh wave ellipticity).
Our results show that for locations affected by site effects the H/V spectral ratio can be modeled by the theoretical ellipticity of layered velocity models. For hard rock sites the spectral ratio is rather flat and the modeling with the theoretical ellipticity was not very clear. This may be explained by the fact that for hard rock sites the conditions for a clear fundamental frequency associated with S-wave resonance, and therefore with Rayleigh wave ellipticity, are not fulfilled.
Seismic noise can be analyzed in different ways depending on the objective of the study (ChávezGarcía, 2009). A popular analysis method is the H/V spectral ratio method. This method was first proposed by Nogoshi and Iragashi (1971) and years later it was summarized by Nakamura (1989). During the decade of the 1990′ s almost 80% of published works about seismic noise were using the H/V spectral ratio method (Bard, 1998; Bonnefoy-Claudet et al., 2006).
It is widely accepted that this method can provide reliable estimates of S wave resonant frequency, especially in places with large amplification and simple subsoil geology (Bard, 1998; Chavez-García, 2009; SESAME, 2004; Bonnefoy-Claudet et al., 2006; Malischewsky and Scherbaum, 2004). However, it is also accepted that a theoretical model for the interpretation of the H/V measurements from seismic noise still has to be developed and analyzed.
One way to interpret the H/V spectral ratios is to assume that the seismic field is diffuse and contains all types of elastic waves, therefore the H/V spectral ratio could be computed in terms of the imaginary part of the Green’s Function (Kawase et al., 2011; Sánchez-Sesma et al., 2011a; Sánchez-Sesma et al., 2011b).
On the other hand, Malischewsky and Scherbaum (2004) proposed that H/V spectral ratios could be modeled as measurements of Rayleigh wave ellipticity, assuming that seismic noise is dominated by surface waves. They propose an exact formula to calculate the theoretical ellipticity for a given velocity model, which can be either a single layer over a half-space or a multilayered model (Malischewsky et al., 2010; Tran et al., 2011). The same authors have discussed the conditions required to model H/V spectral ratios in terms of theoretical ellipticity, with special emphasis on velocity contrast and values of the Poisson ratio ν.
In this study, we use data from some stations of the East Thuringian Seismic Network, OTSN, and we discuss H/V spectral ratios modeling in terms of theoretical Rayleigh wave ellipticity. We show and discuss the results for noise records and for explosion events from the mining district of Western Silesia, Poland and from Thuringia, in Germany. The local seismic events from Thuringia cannot be used because they are deep and produce no surface waves.
As a first step we classify the stations from the OTSN according to their seismic response as defined by the H/V spectral ratios. Then we suggest some velocity models following Malischewsky and Scherbaum (2004), Malischewsky et al. (2010) and Tran et al. (2011), to discuss the possibilities of this modeling.
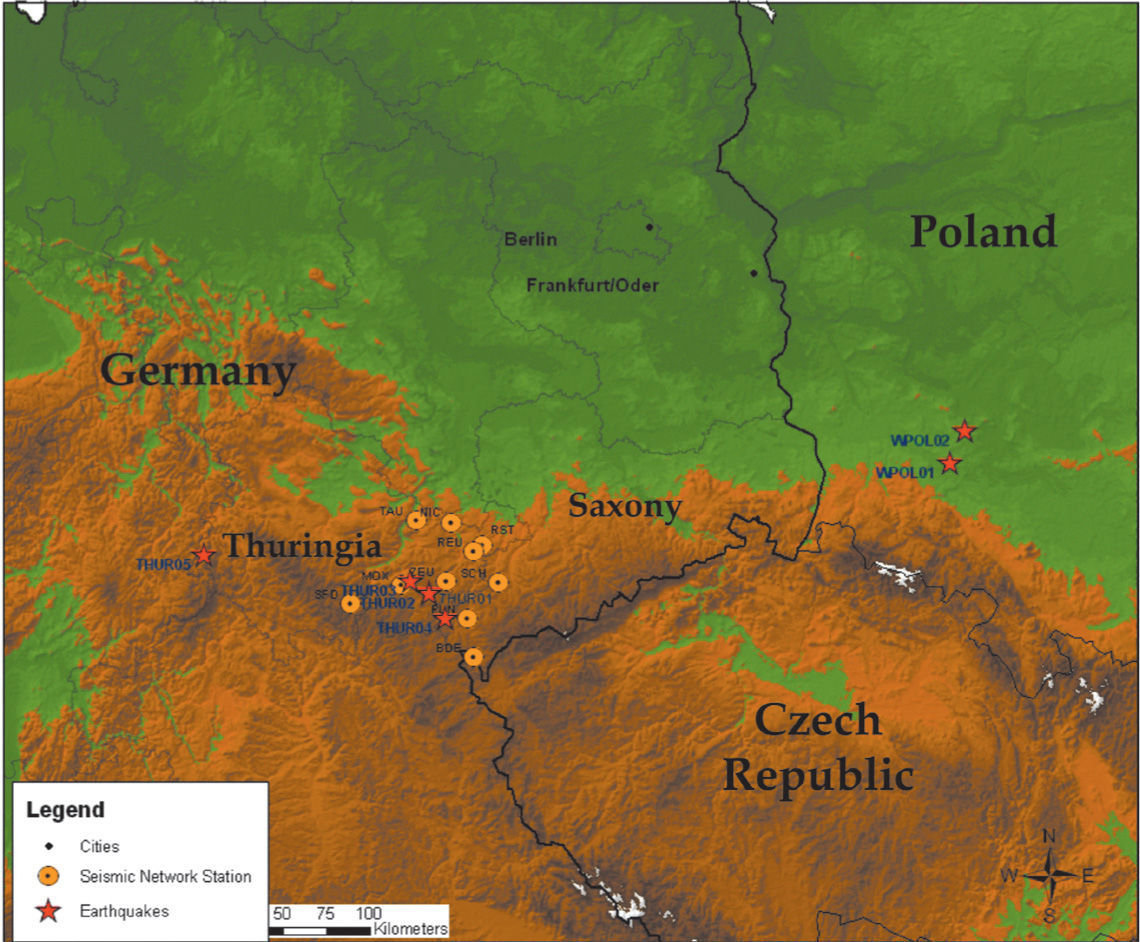
The East Thuringian Seismic Network (OTSN)The OTSN (Figure 1, Table 1) was installed in 1997 to investigate local seismicity and its relation with the stress field, recent tectonics and the local crustal structure, and to estimate seismic risk in Eastern Thuringia (Kracke et al., 2000).
Location of the OTSN stations.
| Station code | Town | Lat°N | Long°E | Altitude (m) |
|---|---|---|---|---|
| BDE | Bad Elster | 50.29 | 12.22 | 420 |
| MOX | Moxa | 50.65 | 11.62 | 455 |
| NIC | Nickelsdorf | 50.98 | 12.01 | 250 |
| PLN | Plauen | 50.49 | 12.16 | 432 |
| PST | Posterstein | 50.86 | 12.26 | 270 |
| REU | Reust | 50.83 | 12.19 | 454 |
| SCH | Schönfels | 50.68 | 12.40 | 435 |
| SFD/SCHD | Schmiedefeld | 50.54 | 11.21 | 761 |
| TAU | Tautenburg | 50.98 | 11.71 | 330 |
| ZEU | Zeulenroda | 50.67 | 11.98 | 331 |
Most of the stations are located on rock outcrops, sometimes with a thin sedimentary layer. Therefore, some stations may have site effects which are not important in terms of motion amplification, but they yield a good opportunity to test H/V spectral ratio in terms of theoretical ellipticity.
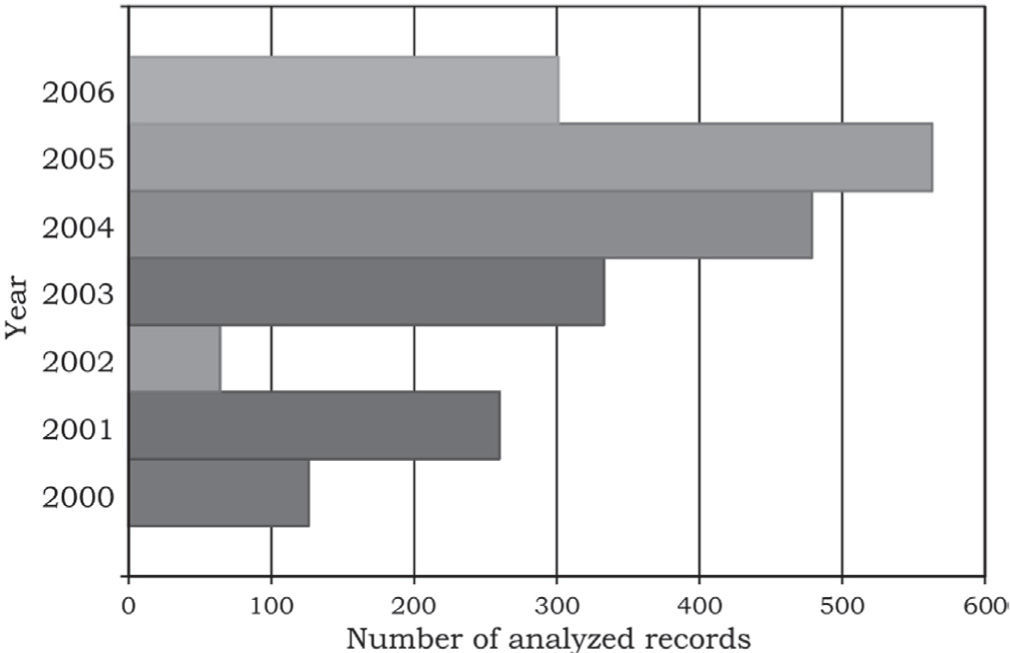
We worked with the OTSN database in the period from 2000 to 2006. During this period the OTSN does not provide continuous records. In the first stage of the study we selected records which did not contain any seismic event but only seismic noise. In a second stage we used the software developed by Tran et al. (2011) to obtain Rayleigh wave theoretical ellipticity for a given velocity model and to compare this solution with the actual H/V spectral ratio. Finally, we present some preliminary results of H/V spectral ratio analysis for explosions from the mining district of Western Silesia (Poland) and from Thuringia (Germany).
We selected those stations with most stable behavior in terms of spectral ratios: BDE, MOX, PLN, NIC and REU.
Noise analysisFor each month of the analysis we selected those records with noise data. Figure 2 shows the number of records analyzed per year. For year 2005 we had the largest quantity of noise records, but the most representative of our analysis for the whole period are those for year 2004. In the next sections we show the results for this year, meaning that each of the spectral ratio curves corresponds to a monthly average during the year 2004.
For each selected file we used three 20 seconds windows considered from the beginning of the record with 20% overlap. This analysis section was done with Seisan (Ottemöller et al., 2011).
Noise H/V spectral ratio resultsFrom the results of the spectral ratio we may classify the OTSN stations according to their site response into two groups:
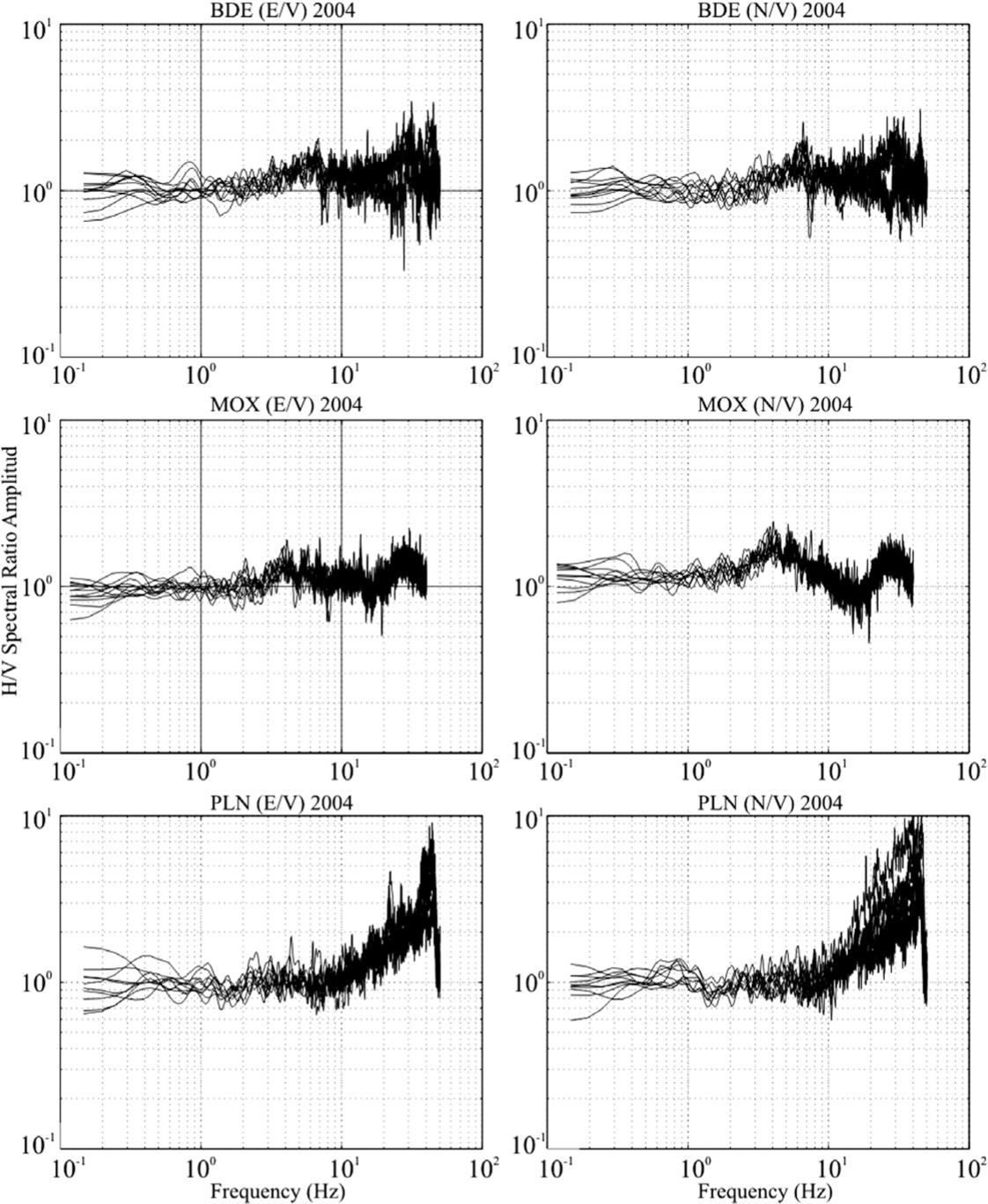
Group I. The spectral ratio amplitudes are close to one from 0.1 to 10 Hz. We propose that these amplitudes correspond to stations on bedrock. This group includes MOX, BDE and PLN (Figure 3).[/sp]
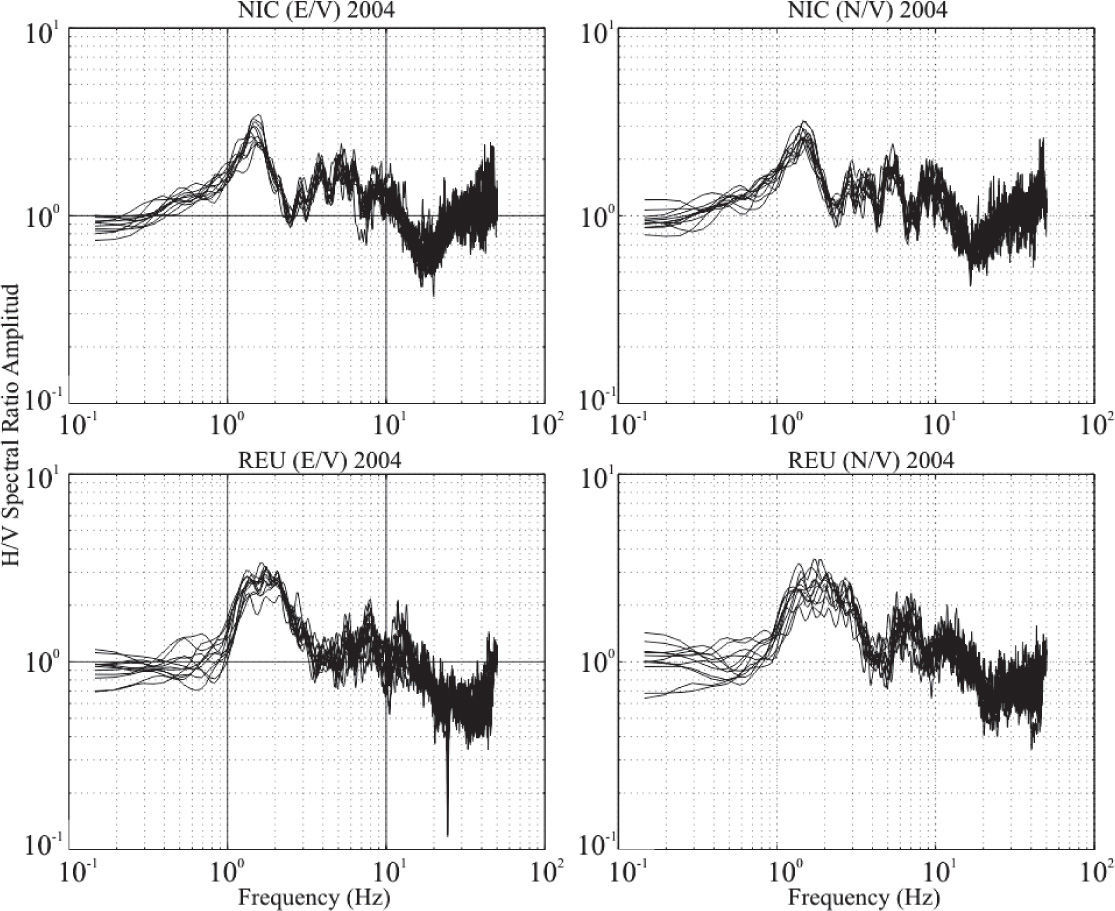
Group II. The spectral ratios show at least one well defined peak. The stations in this group are REU and NIC (Figure 4). These stations, though on bedrock have a thin sedimentary layer which causes a small site effect (low amplitude) in the seismic response. But it also implies a contrast on the physical properties.
In Figure 3 the spectral ratio at BDE is quite stable in both components; the amplitude is close to one for up to 1 Hz and then increases, reflecting anthropogenic activities. At MOX, although the amplitude is also close to one in most part of the spectrum, the H/V ratio has a small peak between 3 and 5 Hz, although the amplitude is not important. Finally, for PLN the spectral ratio amplitude is close to one up to 1 Hz and then it increases reflecting anthropogenic activity.
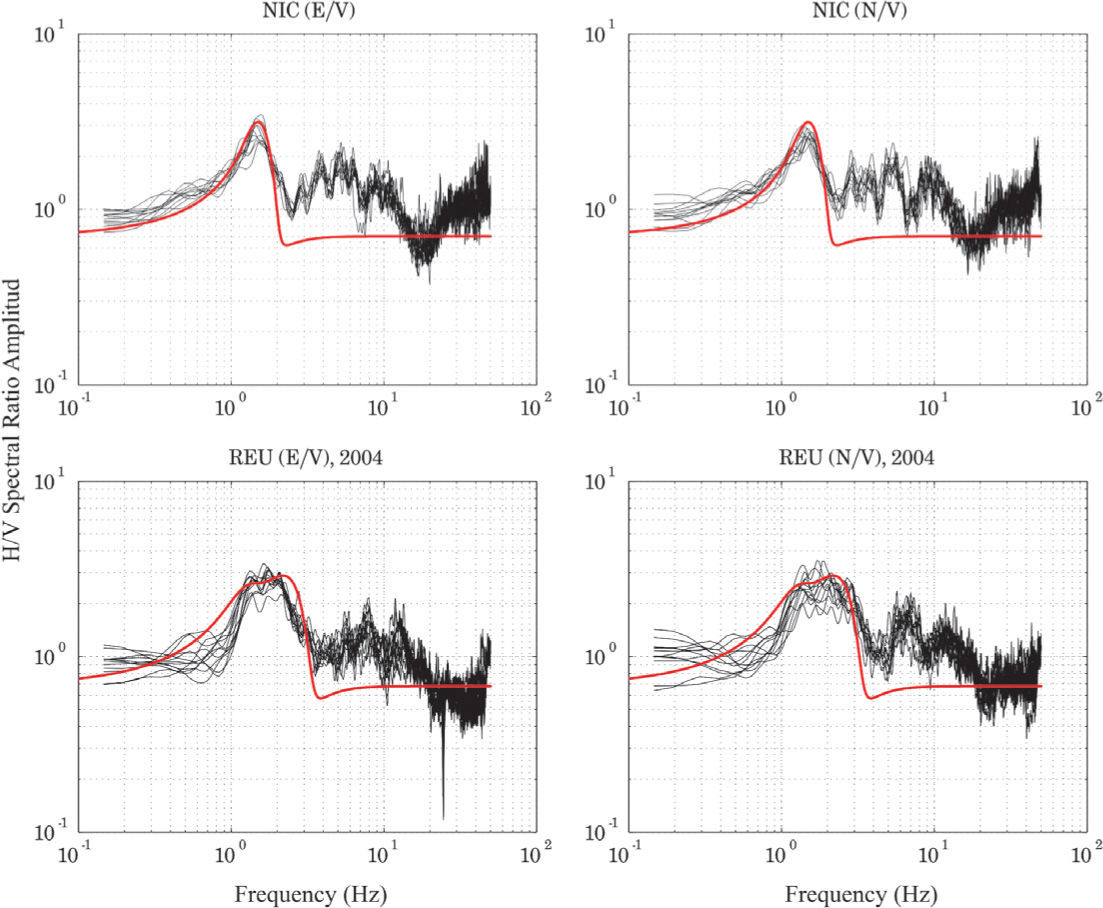
For stations in Group II (Figure 4), the station NIC shows a similar behavior in the spectral ratio of the two components: in both cases we found a fundamental frequency at 1.46 Hz with amplitude of 2.7, and then the spectral ratio display three peaks at: 2.82, 3.8 and about 5 Hz, with amplitudes between 1.5 and 1.8. As mentioned in Malischewsky et al. (2010), this may be due to the value of Poisson’s ratio for the shallower layers of the velocity structure.
For station REU, it is not easy to define the fundamental frequency; rather we can define a plateau between 1 and 3 Hz, where the amplitude is close to 3. Later, between 6 and 7 Hz a peak is observed with amplitude of about 2.
Theoretical EllipticityAssuming that the noise wavefield is dominated by surface waves, the H/V spectral ratio would measure the Rayleigh wave ellipticity. Some conditions have to be fulfilled in order to have a good coincidence between the fundamental frequency of the H/V spectral ratio (main peak) and the singularity of the theoretical ellipticity.
Considering a layer over a half space model the velocity contrast must be higher than 3.5; and the ratio d/λβ1 must be fulfilled, where d is the thickness of the layer and λβ1 is the wavelength in the layer (Scherbaum et al., 2003; SESAME, 2004; Malischewsky and Scherbaum, 2004; Tran et al., 2011).
Malischewsky and Scherbaum (2004) presented an exact formula to calculate the theoretical ellipticity of Rayleigh waves for a single layer over a half-space model. The theory for layered models was later proposed by Malischewsky et al. (2010) and Tran et al. (2011).
In some cases the H/V spectral ratio might show more than one peak after the main peak (as in NIC station, Figure 4). Malischewsky et al. (2010) propose that the following maximum may be associated with deeper layers resonance frequencies. In addition, Tran et al. (2011) report that for special Poisson’s ratio two peaks of the theoretical ellipticity may exist for a model with a layer over a half-space.
Considering the conditions for the physical parameters described above and previous velocity models for the OTSN stations, obtained by the geological conditions and by the models used to locate the local earthquakes, we propose velocity models for the stations we worked with and in some cases modified them by trial and error to adjust the observed H/V spectral ratio. We show and discuss the results for the stations classified into the two groups previously defined.
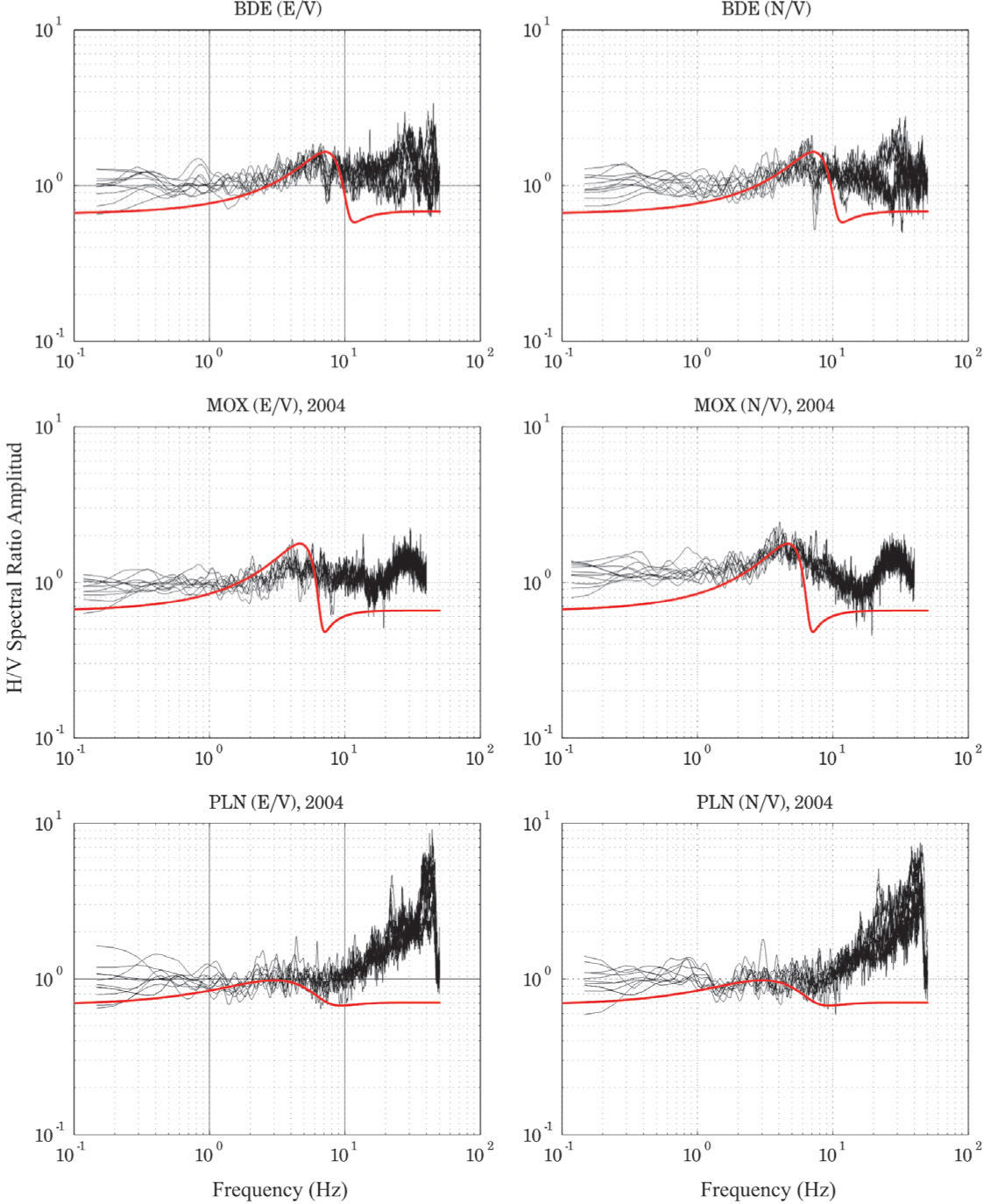
In Table 2 we show the velocity profiles for the stations on Group I and on Figure 5 the H/V spectral ratio and with thick red line the theoretical ellipticity for the velocity models of each station from this group.
H/V spectral ratio for BDE, MOX and PLN for year 2004 and with thick red line the theoretical ellipticity of the models showed in table 1.
The stations in Group I are characterized by a quite flat seismic response within a large frequency interval. This implies that there might not be a large impedance contrast between the shallower layers and the basement.
However, on Figure 5 we can see that Rayleigh modeling fits well below 1 Hz. The difference between the ratios of the horizontal component may be due to directional noise sources that affect more one motion direction than the other. This problem could be solved using the combination of the horizontal motion components before calculating the H/V spectral ratio (SESAME, 2004). We still consider both horizontal components separately to characterize the differences in them.
For station PLN the behavior in high frequencies is probably due to anthropogenic activities and more exploration on this effect is beyond the scope of this work.
In Table 3 we show the velocity models for the stations NIC and REU in group 2. For station REU we propose a more detailed velocity model because the H/V spectral ratio is more like a plateau. In Figure 6 we show the H/V spectral ratio for stations NIC and REU and with a thick red line the theoretical ellipticity for the velocity models in Table 2. As we can see in Figure 6 the fit between the H/V spectral ratio and the theoretical ellipticity for the station NIC is good for the fundamental frequency, in terms of shape and amplitude. For station REU the fitting is also good considering the plateau shape and that there is not a single fundamental frequency.
H/V Spectral ratio for NIC and REU for the year 2004 and with thick red line the theoretical ellipticity for the models showed in table 2.
The peaks in higher frequencies in both stations require more attention to be modeled as they can be related to higher propagation modes.
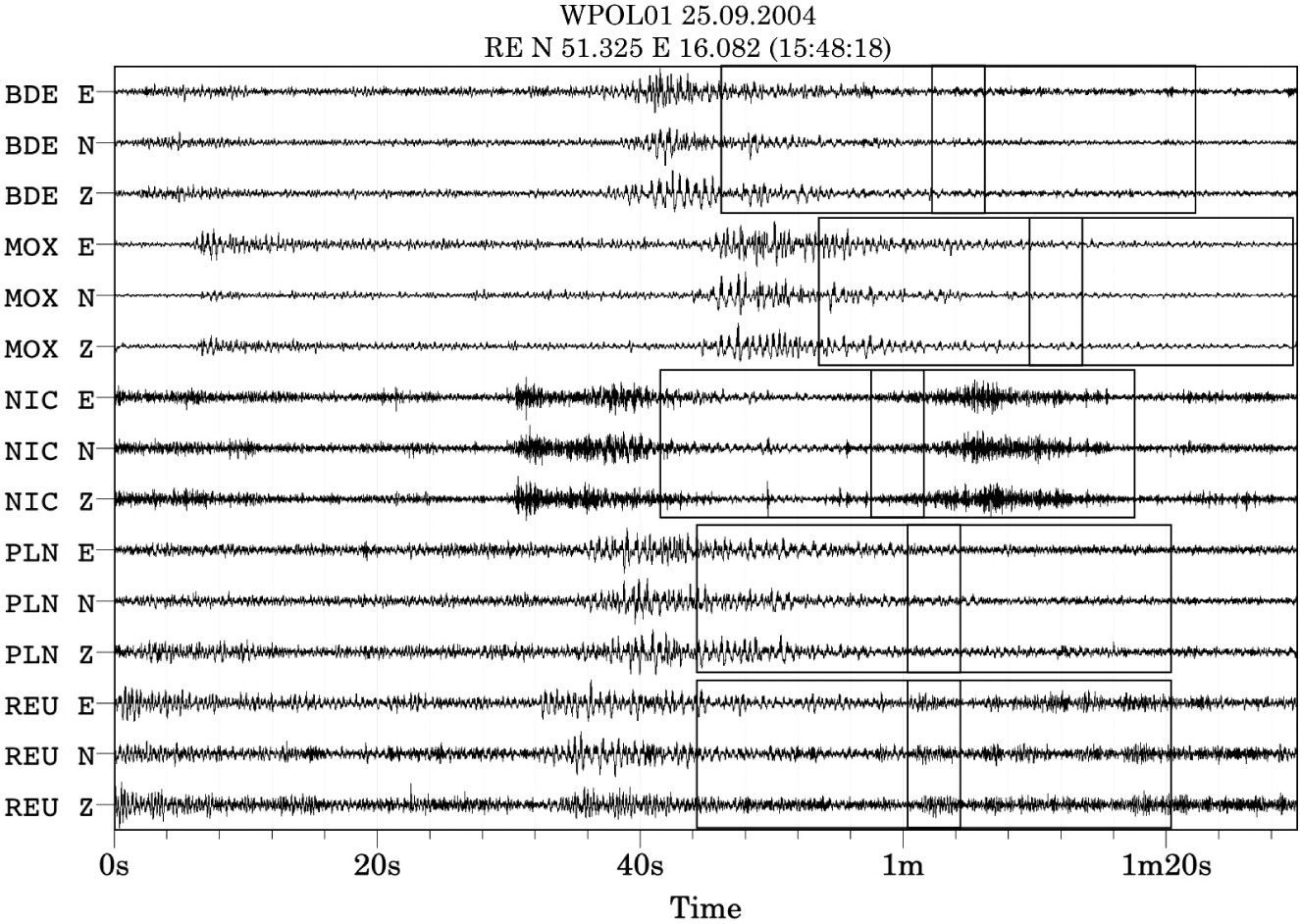
Explosion events Coda H/V spectral ratioExplosion seismic events due to mining activities are quite superficial and rich on surface waves. Therefore, we selected five of these events (Table 4): three coming from Western Silesia mining district, in Poland, and two coming from Thuringian mining area, in Germany. In Figure 7 we show the location of these events. In Figure 8 we show the record for event WPOL01 in the stations of the OTSN and the windows we used containing surface waves.
Date, time and location for explosion events. WPOLXX refers to events from Western Silesia, Poland; and THURXX refers to events from Thuringia, Germany.
| Explosion events | Date (dd.mm.yyyy) | Time (hh:mm:ss) | Lat N | Lon E |
|---|---|---|---|---|
| WPOL01 | 25.09.2004 | 15:48:18 | 51.325 | 16.082 |
| WPOL02 | 26.09.2004 | 19:32:23 | 51.489 | 16.202 |
| THUR01 | 02.04.2004 | 12:22:04 | 50.617 | 11.843 |
| THUR02 | 06.05.2004 | 11:58:11 | 50.613 | 11.842 |
| THUR03 | 08.07.2004 | 12:06:02 | 50.673 | 11.683 |
| THUR04 | 30.11.2004 | 14:20:06 | 50.489 | 11.985 |
| THUR05 | 22.09.2005 | 04:00:00 | 50.750 | 10.007 |
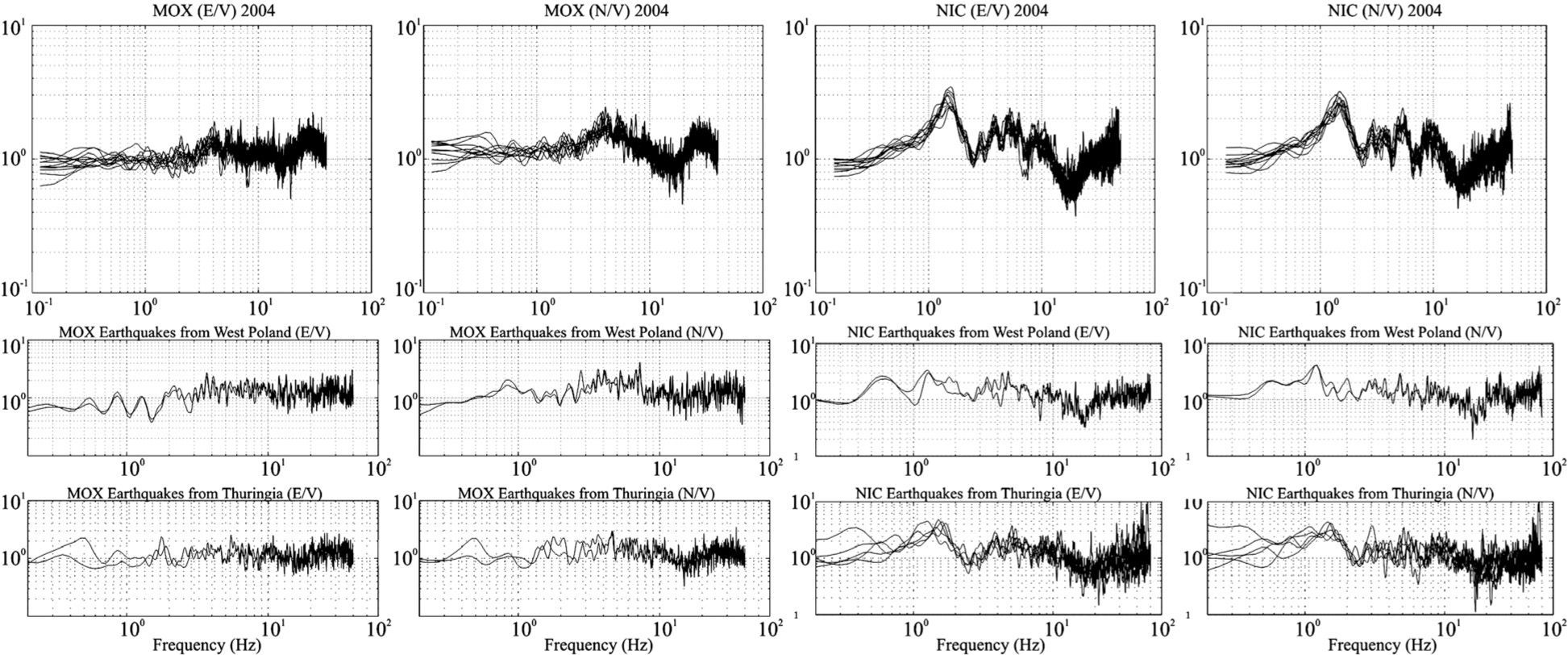
In Figure 9 we show a comparison between the H/V spectral ratio from noise data vs. the spectral ratio from explosion events for MOX and NIC stations. For MOX station we can see that the spectral ratios for explosion events are quite similar to those from noise data. For NIC station, though the behavior is also quite similar the fundamental frequency is not so clear, especially for those events coming from Western Silesia. For these events we can see that low frequencies are more excited. It would require analyzing more explosion events for these stations to find out if there is coincidence with noise H/V spectral ratio or not.
ConclusionsFrom the analysis of the OTSN data base from 2000 to 2007, we obtained the seismic response for some of the stations. We defined two groups in terms of H/V spectral ratio results: group I formed by stations BDE, MOX and PLN, characterized by a flat spectral ratio in most of the frequency interval. For station PLN we interpret the amplitude increase in frequencies higher than 1Hz as due to anthropogenic activities. Stations in group II, NIC and REU, are characterized by small site effects (motion amplification) either in a single frequency (NIC) or in a plateau (REU).
For stations in Group I there is not a big velocity contrast between the layer and the half space; therefore the H/V spectral ratio does not show a clear fundamental frequency. This also implies certain difficulties to model the spectral ratio in terms of theoretical ellipticity. However, we could model some part of them with acceptable results below 1 Hz.
On the other hand, for stations in Group II we have two different behaviors. First, the classic one with a well-marked fundamental frequency at station NIC; though it also shows some more maxima in higher frequencies that can be due to surface waves higher modes or also to Poisson’s ratio conditions that could not be modeled. These maxima in higher frequencies were also found in the spectral ratio for station REU; however for this station the plateau shape of the spectral ratios shows also that the velocity contrast is not high.
The results for the spectral ratio from explosion events are quite similar to those from noise records. However, the possibility of using surface waves from explosion events has to be more explored and this would be a good opportunity to use the data from the actual Thuringian Seismic Network (TSN), which has continuous records.
The stations of the OTSN were installed to measure small regional and local earthquakes; therefore they were supposed not to show any site effect. Probably the same kind of analysis using data from places with a known and strong site effect (due to geological conditions) would enlighten more the scope of the H/V spectral ratio modeling in terms of theoretical ellipticity.
We are especially grateful to Dr. Cinna Lomnitz for his encouragement and support of many years. DAAD supported Hortencia Flores as scholar at the Friedrich Schiller University Jena where this research was performed. We thank Prof. Michael Korn from Leipzig University for his review and constructive comments as well as two anonymous reviewers.