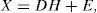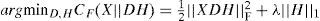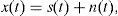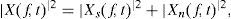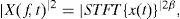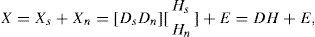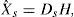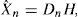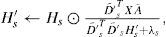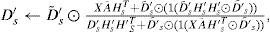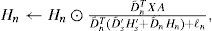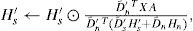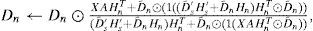Reducing wind noise in seismic data using Non-negative Matrix Factorization: an application to Villarrica volcano, Chile

Resumen

La separación de distintas fuentes existentes en una sola señal sísmica es un problema interesante y al mismo tiempo difícil. En este trabajo presentamos un método semi-ciego para la separación de un solo canal sísmico para mejorar la parte de señal de origen volcánico. En este método, el esquema de descomposición de las fuentes se basa en una factorización en matrices dispersas y non-negativas (Non-negative Matrix Factorization, NMF) de la representación tiempo-frecuencia del único canal sísmico vertical. Como caso de estudio se presenta una aplicación a partir de datos sísmicos registrados en el volcán Villarrica, Chile, uno de los más activos de los Andes meridionales. Los datos analizados están fuertemente contaminados por el ruido del viento y el procedimiento propuesto se utiliza para separar un componente de origen volcánico de otro de origen meteorológico.

Abstract

Single channel source separation of seismic signals is an appealing but difficult problem. In this paper, we introduce a semi-blind single-channel seismic source separation method to enhance the components of volcanic origin. In this method, the source decomposition scheme is addressed as a Sparse Non-negative Matrix Factorization (NMF) of the time-frequency representation of the single vertical seismic channel. As a case study we present an application using seismic data recorded at Villarrica volcano, Chile, one of the most active in the southern Andes. The analysed dataset is strongly contaminated by wind noise and the procedure is used to separate a component of volcanic origin from another of meteorological origin.

Introduction

Villarrica volcano (Chile), located in the southern Andes (39.42º S, 71.93º W) has more than 60 important historical eruptions (Casertano, 1963). As other volcanoes of basic composition (Behncke et al., 2003; Behncke, 2009), Villarrica can not only produce effusive and moderate explosivity activity, but also pyroclastic flows that represent the most dangerous scenario (Moreno, 1998). It is currently characterized by the presence of a small (30-40 m wide) summit lava lake which produces a persistent volcanic tremor and discrete events associated to strombolian activity (Ortiz et al., 2003; Tárraga et al., 2008). In November 2004 we installed an L22 three-component geophone (f₀ = 2.0 Hz) approximately 800 m from the summit crater. The seismometer recorded continuously for a period of 10 days, between November 8, 2004 and November 17, 2004.

Noise often affects records of volcanic tremor or ambient ground-motion recordings used e.g. for HVSR estimates of seismic site amplification. Benson et al. (2007) introduce several methods to reduce the effects of local, non-stationary noise sources, earthquakes and instrumental irregularities on ambient noise. Lambert et al. (2011) propose four methodologies focused on the removal of the effects of anthropogenic noise. In this work, we apply an innovative wind noise reduction procedure to the tremor recorded at Villarrica, based on Non-negative Matrix Factorization with Sparse Coding (Hoyer, 2002) and on the construction of a wind noise dictionary which is estimated from the available seismic recording itself. The presented procedure can be extended to the filtering of wind noise in other volcanic geophysical time series, such as the ones recorded by infrasonic sensors (Ichihara et al., 2012).

A two training step strategy to Single-Sensor Seismic Analysis

In this paper, we extend the Non-negative Matrix Factorization (NMF) and Sparse Coding (SC) procedure introduced in (Cabras et al., 2012), where the basic idea is that we can obtain a meaningful part-based factor decomposition (Lee & Seung, 1999) from a single-channel time series imposing only the constraints of non-negativity and sparseness of the data. For a general discussion on NMF and SC, see Cichocki et al. (2009). As we will describe in detail below, the main contribution with respect to the original procedure (Cabras et al., 2012) lies in the training stage, where we learn two sets of basis components in two steps directly from the available dataset: in the first training step we learn an approximate volcanic-set basis components (or preliminary volcanic-set dictionary), D′˜;s, selecting a non windy data-set for training; in the second training step we learn the wind-set basis components (or noise-set dictionary), D_n, selecting a windy data-set for training. The separation stage remains the same of (Cabras et al., 2012), providing a fixed wind-set basis components, D_n to the constrained sparse NMF learning loop.

We can state an NMF problem as follows: given a non-negative data matrix X∈ℝ+F×T (with x_ft ≥ 0 or equivalently X ≥ 0) and a reduced rank K (K ≤ min(F,T)), find two non-negative matrices D∈ℝ+F×K, called dictionary or basis components and H∈ℝ+K×T′, called sparse code or weights, which factorize X as well as possible, that is:

where E∈ℝ+F×T represents the approximation error to minimize. The meaning of dictionary matrix D, sparse code matrix H and rank K depends on the specific application and signal representation. To estimate the parameters of NMF, (i.e. the factor matrices D and H), we need to minimize the measure of similarity (or cost function C) between the data matrix X and the estimated model matrix Xˆ=DH the simplest and widely used measure is the squared Euclidean distance (or Frobenius norm):

where λ ia a non-negative regularization parameter that controls the tradeoff between sparseness and reconstruction error and ||H||1 is an ℓ₁ norm regularization function proposed in Hoyer (2002).

Cabras et al. (2012) adopted the single channel enhancement model originally developed for processing audio records (Cabras et al., 2010) to separate a “high convective”, relatively transient, seismic source of interest from a “low convective”, relatively continuous, “noise” in a single-sensor seismic time series recorded at Erta ’Ale volcano (Harris et al., 2005). Erta ’Ale is characterized by the presence of a permanent lava lake that produces, in a similar way to Villarrica, at least part of a continuous volcanic tremor (Jones et al., 2006), which is really characterized by a superposition of different independent sources (Jones et al., 2012). In the Erta ’Ale case study, we learned the basis components of the noise n(t), denoted by D_n, in a single step training stage, because in our data-set we have segments of pure “low convective noise” for training.

In the present case study of Villarrica volcano, this strategy is not directly applicable. In fact, our data-set is characterized by a relatively continuous “volcanic tremor”, our source of interest, immersed in a relatively transient “wind” noise that we want to suppress. Wind components change rapidly in time and wind gusts can show very high energy, with comparable or greater energy than the volcanic tremor background, which is always present. This implies that we have no samples of pure “wind” noise for training. Both tremor and wind are non-stationary broad-band sources, with overlapping components in time and frequency as in the daily data-set shown in Figure 1. Focusing our attention to power spectral density of a windy day and a few hours of tremor signal registration without wind present, we recognize that most of the energy overlaps in the low frequency range, while high frequency range is dominated by wind components, as depicted in Figure 2. Our final task is to reduce wind noise in single-channel volcanic seismic recordings by means of a classical refiltering technique as suppression rule, such as a Wiener one (see Figure 3).

Figure 1.

Spectral analysis of one day data-set, in the center-bottom panel, a full day time-series registration showing largest amplitudes in presence of wind noise; in the center-medium panel, the spectrogram showing a highly non-stationary broad-band wind noise and relatively continuous broad-band tremor with a peak at approximately 7 Hz; in the left-center panel, the power spectral density (psd) shows the average broad-band spectrum of the signal with a peak of energy centered again at about 7 Hz; in the center-top panel, marginal time-slice energy distribution at a given frequency (e.g. 25 Hz) is shown, pointing out the non-stationary character of the recorded signal at a given frequency.

Figure 2.

Power Spectral Density of the windy day data-set of Figure 1 (blue line) and a few hours of volcanic tremor without wind of another day data-set available (red line). Both records are broad-band signals with a peak of energy centered at about 7 Hz, attributable to tremor. Windy record is characterized by a constant high energy broad-band noise. At f > 10 Hz, tremor energy decays rapidly and wind noise dominates, masking anything volcanic in this frequency range.

Figure 3.

General scheme of the target enhancement model FT/BT. Preliminary precompute background target dictionary Ds′ when non-overlapped to foreground noise, learn foreground noise dictionary (D_n) from mixed recording, learn background target dictionary (D_s) from mixed recording (Foreground Training and Background Learning, FT/BL).

As in the Erta ‘Ale case (Cabras et al., 2012), we aim to estimate the undesired components, or interference, n(t) and the source of interest, or target, s(t) directly from the observable data mix in the time domain, with minimal a priori knowledge. A common technique to manipulate a time-varying observed signal consists in transforming it into a time-frequency representation. Assuming that saturation effects are absent in the mixed observable x(t):

and assuming that s(t) and n(t) are uncorrelated, we can extend linearity in the power spectral domain and transform the data into a nonnegative representation suitable for NMF scheme:

where the observable signal x(t) and the sources s(t) and n(t) are transformed into a complex time-frequency representation X(f, t), X_s(f, t) and X_n(f, t) respectively. The most commonly used time-frequency representation is the Short-Time Fourier Transform (STFT) which transforms a discrete time signal into a complex spectrogram.

In the following a more general element-wise exponentiated STFT was adopted:

where β is an important parameter to NMF performance, not only in audio application as shown in Schmidt et al. (2007), but also on seismic time-frequency signal representation.

In a time-frequency representation, the k columns of the dictionary matrix D in Eq. 1 constitute the characteristic frequency components of the spectrogram amplitude, while the k rows of the sparse code matrix H contains the weights of corresponding components of the dictionary matrix used in each time frame of the spectrogram amplitude.

Assuming the additivity of sources, the dictionary of the mixed signal of Eq. 1 can be seen as the horizontal concatenation of the individual source dictionaries. Moreover, the sparse code of the mixed signal can be seen as the vertical concatenation of the individual source sparse codes:

where all matrices are non-negative.

In order to estimate the magnitude of true sources X_s and X_n, we use a constrained sparse NMF (NMF^*) to compute the dictionary of the target source D_s and the sparse code of both sources H_s and H_n assuming the dictionary D_n known a priori (Cabras et al., 2010). Finally we estimate the spectrogram of tremor source as:

and the spectrogram of the wind noise as:

Three strategies can be adopted to learn dictionaries D_s and D_n depending on available mixed and unmixed training data, characterizing the following enhancement models:

• a)

  Precompute all dictionaries (D_s andD_n or in generalD₁, D₂, …, D_N) in non-overlapping time-series (Sources Training, ST enhancement model);

• b)

  Precompute background noise dictionary (D_n) when non-overlapped to target and learn target dictionary (D_s) from mixed recording (Background Training and Foreground Learning, BT/FL enhancement model);

Preliminary precompute background target dictionary (D’_s) when non-overlapped to foreground noise, learn foreground noise dictionary (D_n) from mixed recording, learn background target dictionary (D_s) from mixed recording (Foreground Training and Background Learning, FT/BL enhancement model).

A limitation of the Sources Training enhancement model strategy is that each source dictionary D₁, D₂, …, D_N, must be modeled prior to the separation. This approach was followed by Mehmood et al. (2012) in a seismic footstep detection based system to separate the human footstep signatures from the horse footstep spectral signatures. However, the availability of non-overlapping time series for all the different sources rarely applies to natural seismic datasets. Background Training and Foreground Learning is a more realistic strategy when background noise is more stationary than the foreground signal of interest and we can easily recognize enough samples of background noise-only to learn D_n. Schmidt et al., (2007) suggest to pre-compute D_n, an approach followed also by (Cabras et al., 2012), then learn D_s(f, m), H_s(m, t) and H_n(k, t) with a modified constrained NMF, where m is the number of user defined components of the target source dictionary and k is the number of user defined components of the noise dictionary.

But if we are interested in a Background Source more stationary than the Foreground Noise, it will be probably very difficult to find samples of noise-only components to carry out the training. An alternative approach has then to be followed, where a first training step on background source-only samples is followed by a learning step of noise components which determines the new 2 steps foreground noise training (FT in Figure 3) while in Cabras et al. (2012) background noise was trained in one single step, because of noise-only samples availability. The estimation of a priori noise dictionary, D_n, is modeled by a two step sparse NMF computation, where equations are similar to the equations described in Cabras et al. (2012) but switching the index definitions of “noise” (n) and “source” (s) and shortly reformulated here for clarity. In the first step the sparse NMF algorithm starts with randomly initialized matrix, Ds′ and H′′, and alternates the following updates until convergence:

where ⊙ operator indicates element-wise multiplication, the fraction line element-wise division between two matrices, D′˜;s is the Euclidean column-wise normalization of the dictionary to prevent joint numerical drifts D′s in Hs′ and (Eggert and Körner, 2004), 1 is a suitable size square matrix of ones and A is the activity diagonal binary square matrix, explained in more detail in the discussion section. The parameter λ_s determines the degree of sparsity in the code matrix. The trained preliminary dictionary of target source D′s is the a priori knowledge to learn the noise dictionary D_n, which can be trained directly from selected time sections of the available noisy signal using a constrained sparse NMF (NMF^*) model estimation, so that only D_n, H_n and Hs′ are estimated, while D′s is predefined and left unchanged by the following updating equations until convergence:

The resulting noise dictionary, D_n, is the a priori estimated information needed by the final Background Learning step (BL) as shown in Figure 3. BL is the final Blind Source Separation step (BSS) which assigns the decomposed parts to the source of interest and discards the interference source described in Cabras et al. (2012) with a solution based on a constrained sparse Non-negative Matrix Factorization (NMF) model estimation and prior knowledge on undesired component.

A case study: Villarrica wind noise reduction

For illustrative purposes, we applied our methodology to a seismic dataset recorded at Villarrica volcano.

Datasets

The analyzed dataset consists of 10 full day records of a single L22 short period vertical sensor component (f₀=2.0 Hz) sampled at 100 Hz. Each record exhibits non stationary high frequency non volcanic signal contamination, presumably determined by strong wind. No additional a priori information, such as a wind gauge, is available. Figure 1 shows an example of a full day record spectral analysis. The Power Spectrum Density (PSD) of Figure 2 shows that the wind energy recorded from the vertical sensor component dominate in frequency > 10 Hz, while overlaps with tremor energy in the low frequency range.

Parameters

In order to process the dataset with the NMF algorithm, volcanic recordings are analyzed by an 8192 point Hamming windowed with β = 1/3 exponentiated STFT and 50% overlap (Eq. 4). This heuristic value of β, which corresponds to the cube root compression, is quite important to achieve good NMF data decomposition in terms of SNR, our experimental results confirm that the more common value β = 1 produces worse separation results.

The number of components in the target source dictionary, m, and the number of components in the noise source, k, are very important parameters which depend highly to the true but unknown sources, since all these components concur to model the sources. Using too few components results in a poor model of the sources which show strong evidence only for a limited set of data; conversely, more complex models (i.e. with many components) can always fit the data, but we must avoid implausible over-parameterized models, following the principle of parsimony, i.e. finding the model that most simply accounts for the observed dataset. With our seismic datasets, we get plausible dictionaries with k and m in the range of 32-64 components.

The sparsity regularization parameter enforces sparseness (i.e. simplicity) to learn the preliminary volcanic dictionary and controls the tradeoff between sparseness and reconstruction error. Increasing the sparseness term, the dictionary solution becomes less fragmented, since the decomposition algorithm tends to encode the input matrix using less dictionary components. Good solutions are achieved with λ_s = 0.5.

In a similar way, sparseness regularization parameter enforces sparseness to learn the wind noise dictionary D_n, in our experimental datasets; good results were obtained for λ_{s =} 0.5.

Results and discussion

In order to estimate the preliminary target dictionary D′s, we analyze several 1 day records (8.64 Msamples@100Hz sampling frequency) to catch some temporal frames without wind, as at 5 hrs of Figure 1, where Power Spectral Density is similar to the red line of Figure 2. It is evident that a major requirement for the method to work properly is the availability and the recognition by the user of a time period for which there is only “source” signal, i.e. without wind contamination. This training period should be chosen by careful examination of the spectral content time evolution and/or, if available, using additional data such as datasets from pressure sensors, microphones, infrasound sensors or anemometers. Visual spectrogram screening can be a subjective and an error prone selection activity which must be taken in account and reduced adopting a statistical estimation algorithm, in figure 3 we call it Statistical Foreground Activity Detector, which detect and flag the active frames (if frame t is active: A_{tt =} 1, otherwhise 0), implemented as a time-recursive averaging algorithm based on signal-presence uncertainty, similar to statistical Voice Activity Detector (VAD) used in speech enhancement methods (Cabras et al, 2010). With the selected temporal frames we apply a sparse NMF to preliminary train the tremor dictionary shown in bottom left panel of Figure 4. This pre-estimated source model is then used to estimate the wind noise dictionary applying a sparse NMF^* learning algorithm on a strong windy day data-set; the resulting D_n is depicted in the top right panel of Figure 4. This is a definitive wind noise dictionary for our data-set and is very important to prevent volcanic tremor components amongs D_n components. The further learning step (BL in Figure 3) was applied to all records of the data-set to estimate D_s, H_s and H_n and estimate the tremor source spectrogram (Eq. 7) and the noise source spectrogram (Eq. 8). Figure 5 shows the estimated spectrogram sources of a full day recording. The dataset tremor dictionary D_s is shown in the right bottom of Figure 4. It is similar to but smoother, depending on more data frames, and it differs greatly from D_n, although it points out some frequency superposition.

Figure 4.

Observed signal spectrogram X (top left panel), characterized by 2 windy temporal windows; preliminary tremor dictionary Ds′ estimated in a short, wind free, temporal window (bottom left); wind noise dictionary D_n estimated in the second windy temporal window (top right); dataset tremor dictionary D_s estimated in the full day.

Figure 5.

Spectrograms of a wind corrupted signal X (top panel), estimated tremor source Xˆs (center panel) and estimated wind noise Xˆn (bottom panel) of a 24 hours of Villarrica vertical sensor component. Foreground Training (FT) was applied in the temporal window between 5^*10⁴ s and 7.5^*10⁴ s.

Conclusions

We have presented an automatic method for wind noise reduction of volcanic tremor based on estimating the noise components dictionary by means of sparse NMF algorithms. The novel idea is to pre-compute a preliminary dictionary model only for the target source and infer the dictionary model of the noise from a suitable representation of a signal mixture. Notwithstanding the obvious drawback that the user must be able to highlight a time period where source signal is not affected by wind (if possible with the help of additional wind-affected sensors), experiments on a real world seismic-only dataset recorded at Villarrica volcano contaminated by strong wind noise show that sparse NMF algorithms and our method are quite effective to reduce wind noise in single channel seismic recordings and can be succesfully used to better investigate the time evolution of tremor spectral content.

Acknowledgments

We are grateful to Dr. Jeff Witter for assistance with location and deinstallation of the seismometer site.