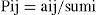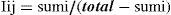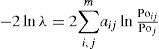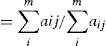Stratigraphic Columns Modeling and Cyclicity Analysis of the Misoa Formation, Maracaibo Lake, Venezuela, using Markov Chains

Resumen

Se realiza en este trabajo la caracterización estocástica de un yacimiento constituido por una secuencia de areniscas intercaladas con limolitas y lutitas. La unidad estratigráfica estudiada corresponde a la arena C4 de la formación Misoa, Campo Lama, Lago de Maracaibo (Venezuela). Se desarrolló un algoritmo de Cadenas de Markov, basado en la definición de relaciones genéticas entre litofacies en una columna estratigráfica. La aplicación del método de Monte Carlo utilizando este algoritmo en 11 pozos en el área, permitió obtener pseudo-secuencias en 20 nuevas localizaciones. El algoritmo fue capaz de modelar, apropiadamente, pseudos-secuencias estratigráficas y cuantificar la proporción relativa de facies, mostrando un 82% de certidumbre en términos del contenido relativo de sedimentos en un pozo de prueba. El mapa de arena neta generado integrando las columnas estratigráficas obtenidas de la información de pozos y las pseudo-columnas Markovianas, sugiere la presencia de cuerpos de arena con orientaciones noreste-suroeste, coincidentes con estudios geológicos previos en el área. Este mapa puede ayudar a definir zonas prospectivas en el campo. La aplicación del algoritmo indicó la existencia de memoria estratigráfica a lo largo de las columnas analizadas. El método de Columnas de Markov embebidas usado en el análisis de ciclicidad de toda el área indica que se presentan transiciones cíclicas sólo de areniscas a limolitas y de lutitas a limolitas. Por tanto, para el área de estudio, en promedio, pueden identificarse con el análisis Markoviano procesos de afinamiento hacia arriba y engrosamiento hacia arriba, como era de esperarse para el sistema deltaico dominado por mareas asociado al reservorio analizado.

Abstract

A stochastic characterization of a hydrocarbon reservoir, constituted by a sedimentary sequence of sandstones interbbeded with siltstones and shales, has been performed. The stratigraphic unit studied here mainly comprises the C4 sands of the Misoa Formation, located in the Lama Field, Maracaibo Lake (Venezuela). A Markov Chain algorithm, based on the definition of genetic lithofacies relationships along stratigraphic columns, was developed. The application of the Monte Carlo stochastic method using this algorithm, to log data from 11 wells, allowed the generation of pseudo sequences at 20 new locations. This algorithm was able to properly model pseudo stratigraphic sequences and to quantify the relative facies percentage, showing a 82% confidence level related to the proportional content of sediments at a test well. The net sand map obtained integrating the stratigraphic columns, derived from the well information, and the Markov pseudo-columns, suggests the presence of sand bodies with a northeast-southwest orientation that agree with previous geological studies in the area. This map could help in the definition of prospective zones in the field. The existence of stratigraphic memory along the evaluated columns was recognized after applying the algorithm. The embedded Markov method used in the cyclicity analysis of the whole area indicates cyclic transitions just from sandstones to siltstones and from shales to siltstones. Hence for the study area, on average, fining upward and coarsening upward processes can be identified with the Markovian approach, as was expected for the tide-dominated deltaic system associated to the analyzed reservoir.

Introduction

The knowledge or understanding of the facies architecture of the subsurface is a key aspect in many geological and geophysical problems as, for example, hydrocarbon reservoir characterization. In a reservoir, an alternation of diverse lithological intervals (e.g. sandstones, shales, coals, and/or siltstones) can be observed as a result of the different sedimentation processes involved (Eidsvik et al., 2002; Sinvhal & Sinvhal, 1992). This information is usually obtained from the different well logs and core information of the study area. To completely characterize the reservoir, this information, available just at the well locations, should be extended to the whole area or volume of interest. Different geostatistical techniques have been used to mathematically model and characterize reservoir heterogeneities, in order to obtain representative facies alternation that are geologically possible (Elfeki and Dekking, 2001). Some of these techniques use variogram, autocorrelation or autocovariance functions. In these cases, to model the spatial variability from the fitting of the variograms, intensive data sets are needed (Carle and Fogg, 1996).

Markov Chains represent an alternative way to model the spatial structure of a reservoir and have been applied in geology to model lithologies or facies that constitutes discrete variables or categorical data (Elfeki and Dekking, 2001). The Markovian analysis is a statistical technique that enables the definition and description of the facies associations along a stratigraphic sequence. Hence, Markov chains allow modeling stratigraphic sequences through a probabilistic analysis (Miall, 1973; Eidsvik et al. 2002; Eidsvik et al., 2004a). Within a Markov chain, the transition probability from a discrete state to the next depends on the previous state (Till, 1974). Therefore the occurrence of a particular facies depends, in a certain way, on the previous facies. This dependence suggests that the sedimentary processes that could control at a specific time the facies distribution, have memory (Leeder, 1982). This memory is useful as it might support the environmental interpretation that could be demonstrated analyzing adjacent sections (Suarez, 1997). As gradual changes along a well can be recognized in terms of the different lithologies observed, Markov Chains may be used as a tool for the indirect determination of facies type, thickness and alternation along it (Doveton, 1994; Sinvhal & Sinvhal, 1992; Eidsvik et al., 2002; Eidsvik et al., 2004a).

This stochastic technique can also be used to model complex geologic processes that are related to agents not precisely identified (e.g. sedimentary cycles) (Kulatilake, 1987). In fact, the Markovian analysis allows evaluating the state of change in terms of its relative probability of occurrence. The lithologies are not only repeated vertically, but partially depend from one another. Hence, a sedimentary sequence cycle can be described as a series of rocks or beds which overlay or underlay one another with a predictable probability pattern (Schwarzacher, 1975; Sinvhal and Sinvhal, 1992). Different studies have used this approach for cyclicity analysis of stratigraphic sequences (e.g. Miall, 1973; Kulatilake, 1987). Suarez (1997) used a Markovian analysis to define the lithofacies genetic relationships along the sedimentary column of the Rio Negro Formation, Venezuela. Just one section was included in that study due to the absence of any detailed bibliography about the Uribante Through. Suárez (1997) was able to quantitatively represent a stratigraphic sequence useful for the interpretation of the sedimentary environments of the study area. His results demonstrated the presence of stratigraphic memory within the tested column, even though just one column was analyzed. The inclusion of one column could be a limitation regarding the definition of the stratigraphic memory. Nevertheless, this kind of studies is considered useful in the definition of the genetic relationships among the lithofacies (Miall, 1973) and in the paleo-environmental interpretation (Suárez, 1997).

The main purpose of the present study is to develop and to apply a Markov Chain algorithm in order to model the geological setting and to stochastically characterize a reservoir, located at the Lama Field, Maracaibo Lake, Venezuela, considering the possible cyclicity of the strata of interest. Mathematical simulation and pattern recognition techniques were applied, trying to understand and predict the vertical and horizontal lithological variations at the study area in order to diminish the uncertainty in the stochastic characterization of a hydrocarbon reservoir. The studied reservoir belongs to the C4 sands of the Misoa Formation, which comprises thick layers of sandstones interbedded with thin layers of siltstones and shales. The algorithm will be used to model pseudo stratigraphic sequences and to quantify the relative facies proportion along the reservoir. The Markovian property, and hence the stratigraphic memory of the section analyzed, will be evaluated, as well as the confidence of the algorithm in terms of the relative facies proportion obtained at test wells. The nature of the cyclic sedimentation processes in the area will be analyzed by means of the Markov approach, using more than only one sedimentary sequence, as the information derived from all the wells available for this study will be integrated.

Geographical and Geological setting

The study area is located in the central part of the Maracaibo Basin, specifically at the Lama Field, southeast of Block IX, Venezuela (seeFigure 1).

Figure 1.

Geographic location of the Lama Field (After Cedillo et al., 2004)

The west part of the Lama Field is one of the largest hydrocarbon accumulations within the central part of the Maracaibo Lake Basin. This area is in contact with the west boundary of the Lama-Icotea Fault, and it is limited by an inverse northwest-southeast fault system. A series of antithetic normal faults toward the Icotea fault are present along the study area (Arminio et al., 1994; Delgado, 1993). In the central and south parts of the field, a different structural tendency can be observed, characterized by the presence of inverted faults to the west southwest – east northeast direction (Delgado, 1993). The major geological feature in the area is a north-northeast-trending anticlinal dome (Ambrose and Ferrer, 1997). Several structural compartments were created between intersecting faults of diverse age, due to the complex tectonic development of the Maracaibo Lake (Ambrose and Ferrer, 1997). Structurally, the main traps are located along the Icotea high, with Cretaceous and Eocene reservoirs (Yoris and Ostos, 1997).

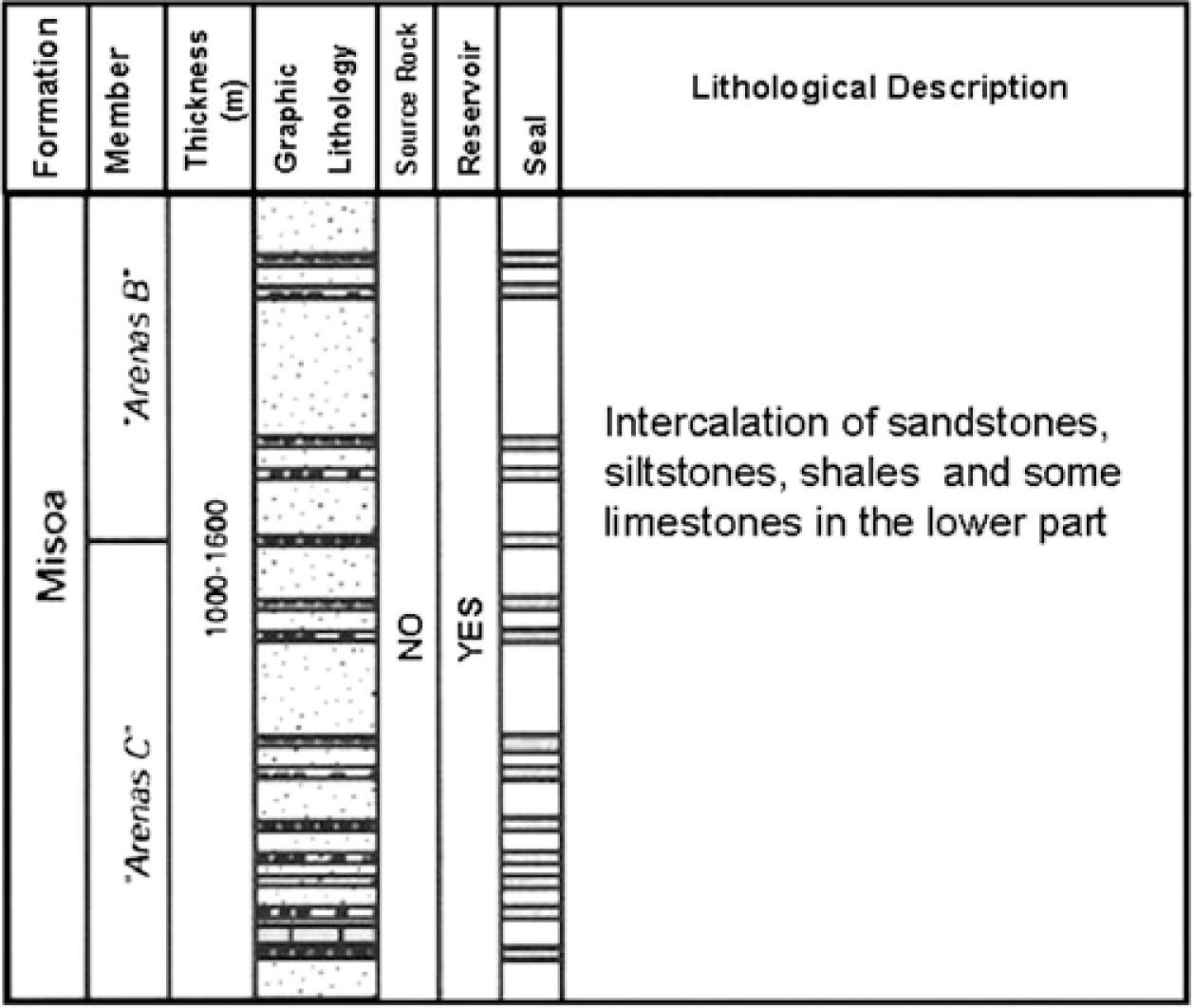
The reservoir of interest in this study corresponds to the C4 sands of the Lower Misoa Formation (Eocene). According to Talukdar and Marcano (1994) and Delgado (1993), the Lower Misoa strata were deposited in a tide-dominated delta setting with the sediment source located to the west or southwest. Ambrose and Ferrer (1997) describe the Lower Misoa Formation as structurally complex, heterogeneous, with estuarine-delta and tide dominated shelf reservoirs. The C4 sands of the Misoa Formation compresses thick layers of sandstones interbedded with thin shale and siltstone layers (Yoris and Ostos, 1997) (Figure 2).

Figure 2.

Lithological description of the Misoa Formation. (Modified from Yoris and Ostos, 1997)

Methodology

In order to define and characterize the litostratigraphic units used as input in the probabilistic and statistic algorithms, a stratigraphic correlation was carried out. This phase makes it possible to define the thickness in depth of the unit of interest. This unit was named as Unit 1 and compresses, mainly, the C4 sands of the Misoa Formation. These sandstones consist of deltaic interbedded sandstones, shales and siltstones, accumulated during the Eocene (Yoris and Ostos, 1997).

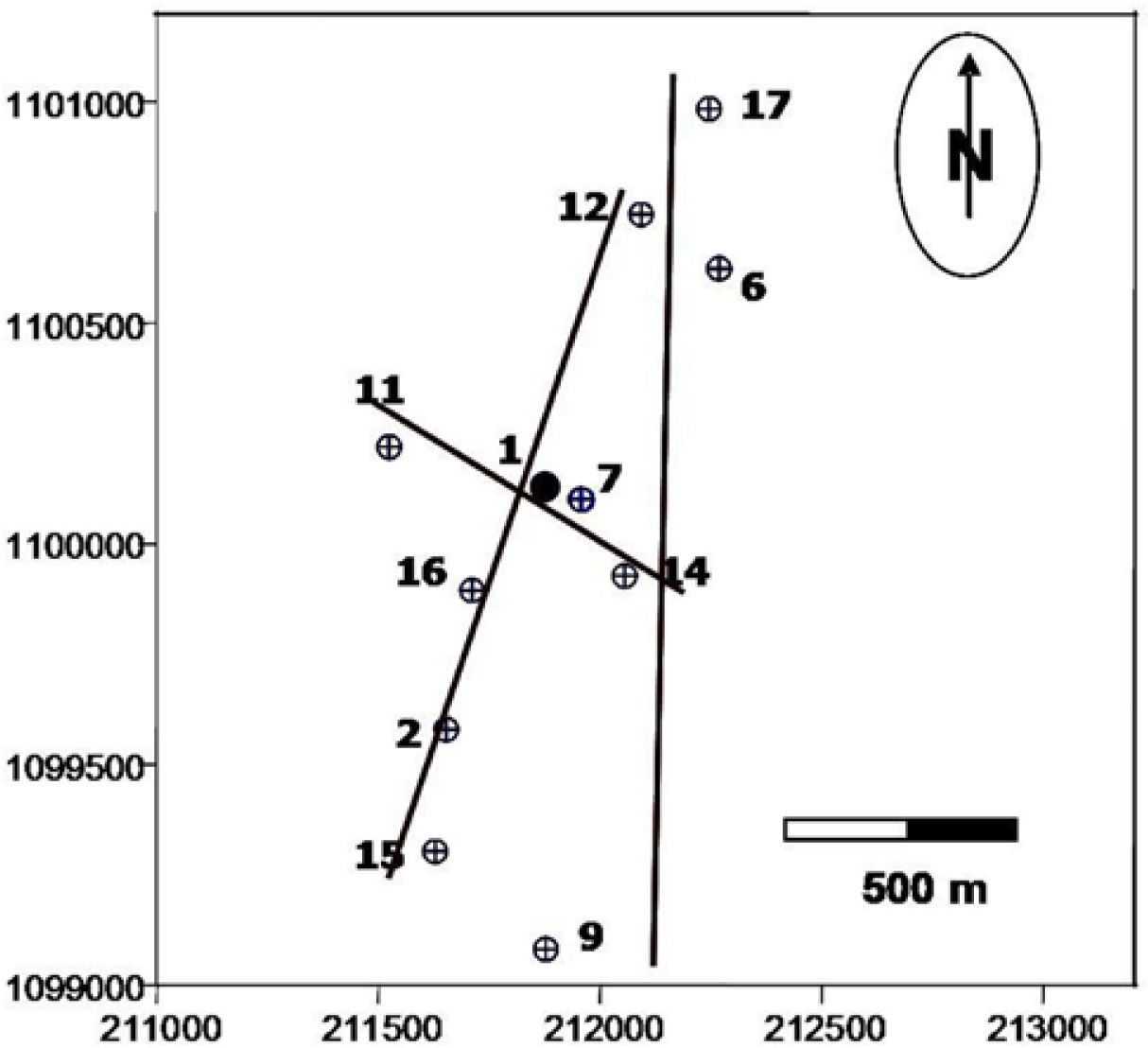
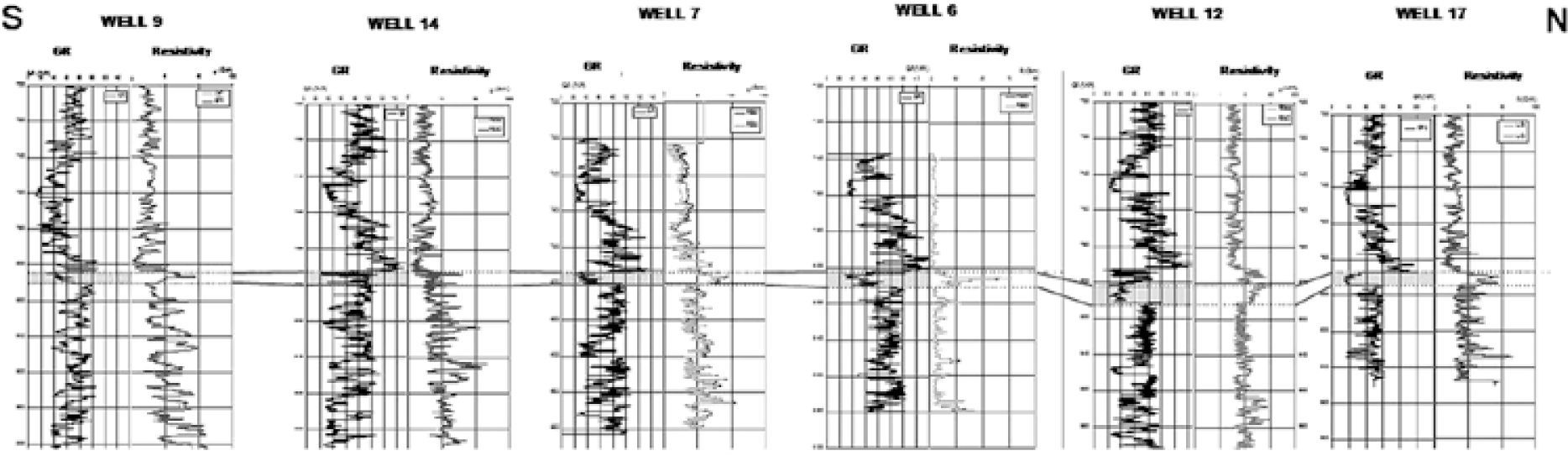
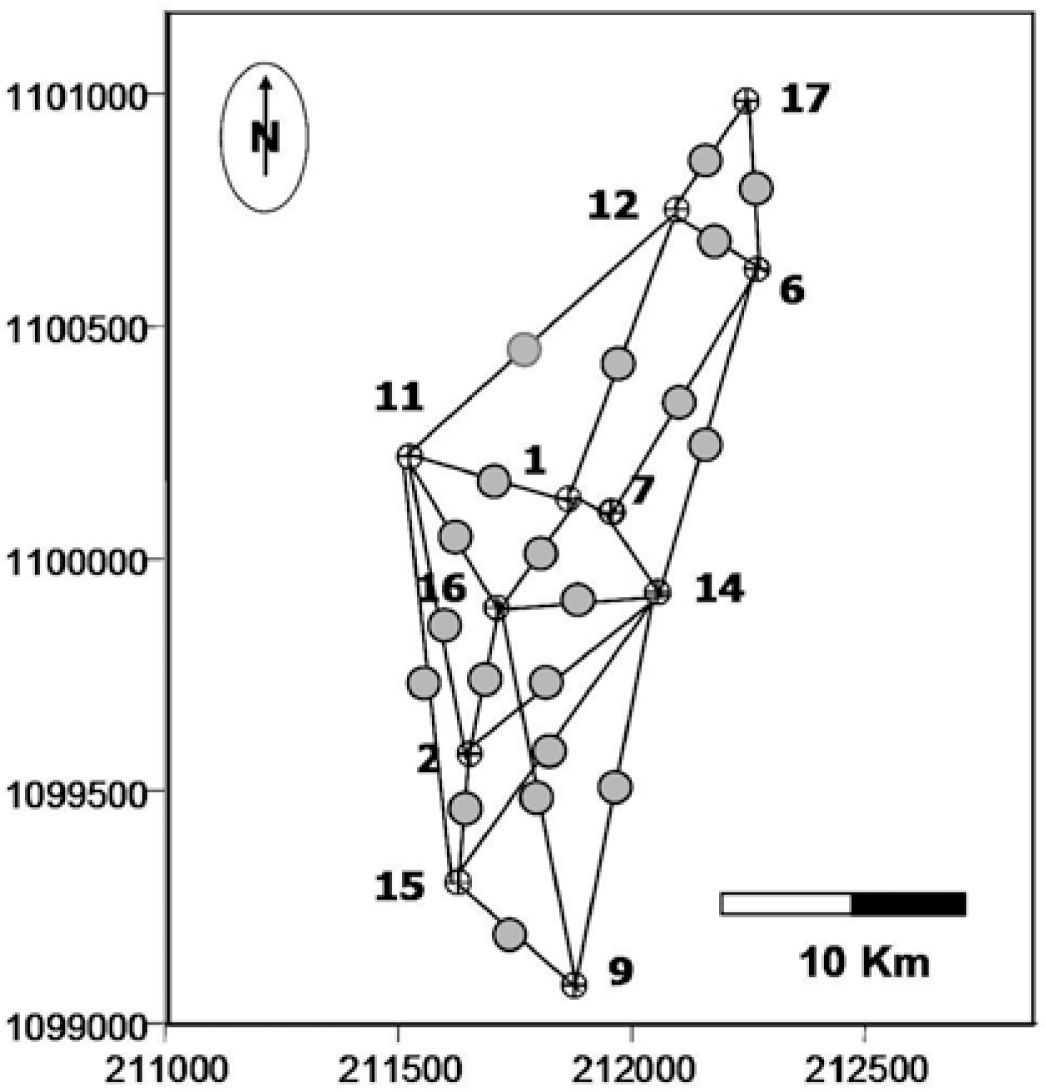
Three transects, that include the 11 wells available in the area, were used for the stratigraphic correlation. Figure 3 shows the wells, located to the southwest of the Lama Field, and the selected transects for the stratigraphic correlation sections. The first section has a southwest-northeast direction and includes wells 15, 2, 16, 1 and 12. Along this section, the unit thickness varies between 61 ft (≈19 m) and 168 ft (≈50 m). The major thicknesses are observed in well 12, and could be related to sand bars. The second correlation section has a northwest-southeast direction, including wells 11, 1, 7 and 14. In this case, the strata thicknesses vary gradually between 67 ft (≈20 m) and 91 ft (≈28 m). The last correlation is a north-south stratigraphic section, passing through wells 9, 14, 7, 6, 12 and 17 (Figure 4). In wells 12 and 17, the thickness increases to 106 ft. (≈32 m) and decreases to 52 ft. (≈16 m), respectively.

Figure 3.

Location of the wells at the study area. The lines represent the stratigraphic correlation sections.

Figure 4.

Stratigraphic correlation section (Nort-South direction) that comprises wells 9, 14, 7, 6, 12 and 17.

In this study, the Markovian analysis was used to estimate and quantify vertical and horizontal lithofacies variations. The algorithm developed here is based on previous studies by Sinvhal and Khattri (1983), Sinvhal and Sinvhal (1992), Doveton (1994), Suarez (1997) and Eidsvik et al. (2004a). The algorithm, implemented in MatLab, includes four main steps: (a) load and analysis of well logs, (b) counter matrix calculation, (c) probability matrix calculation and (d) pseudo-well estimation and generation.

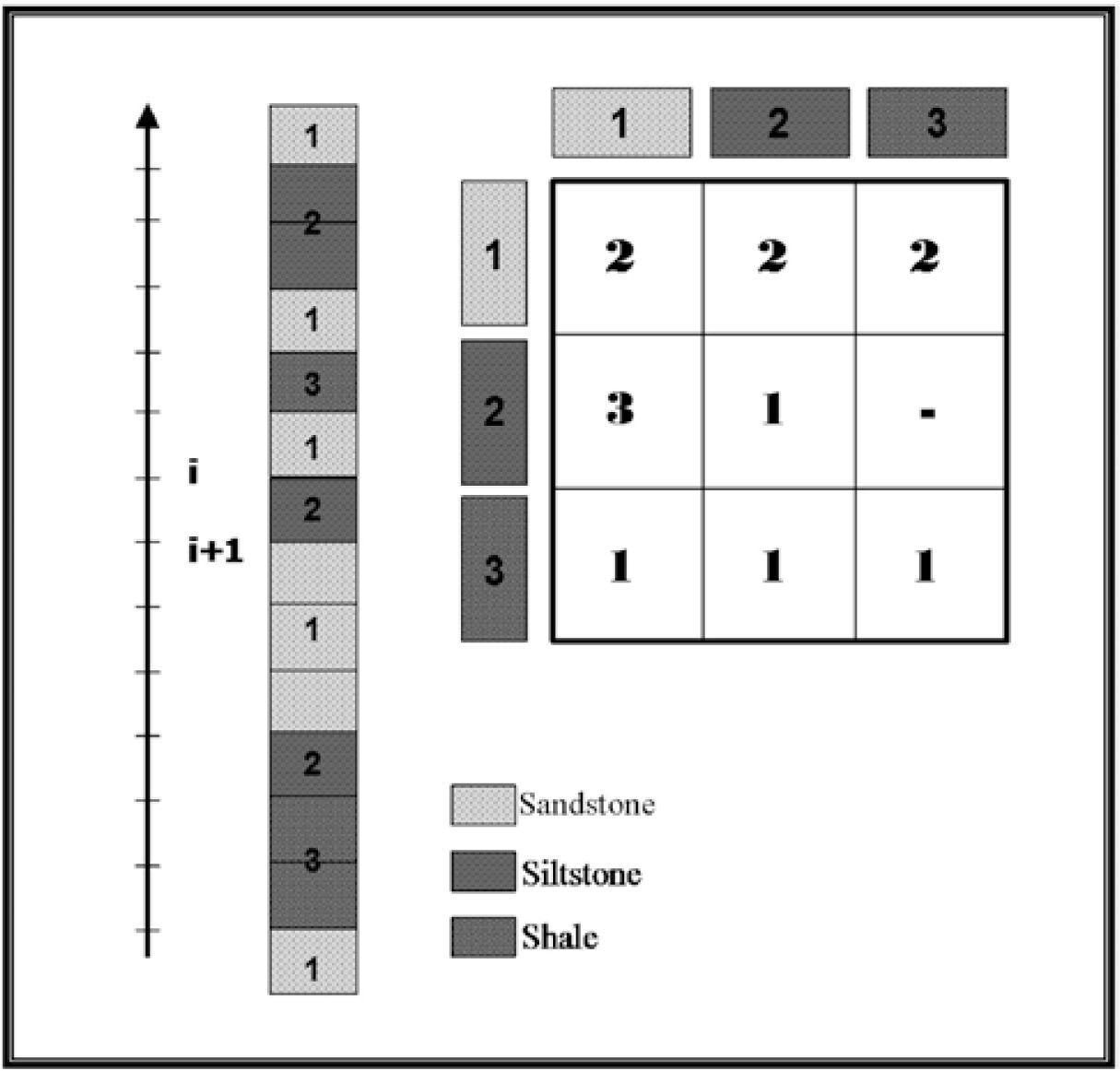
Gamma ray, Resistivity and/or Spontaneous Potential well logs were used to recognize the main facies and to perform the alternation probability analysis (i.e. the transition probability of overlying and underlying lithologies). To discriminate and select the facies along the wells, response intervals for the input logs were defined and assigned to the interpreted facies (i.e. sandstone, siltstone and shale) in order to automatically discriminate and select them in depth. The response of the different logs depends on the lithology. The gamma-ray log is used to identify different grain sizes. Two cutoff lines are chosen. Gamma-ray values below the lowest cutoff line correspond to bigger grain sizes, i.e., sandstones; between the cutoff lines, middle grain sizes are expected (silts); values above the highest cutoff line represent finer grain sizes, i.e. clays. In the case of the SP logs, clays (that are impermeable) will generate a voltage value and permeable sands in contact with them will generate an opposite one. On the other hand, in resistivity logs high values are observed usually at permeable intervals containing hydrocarbons. The three lithologies were discriminated combining all these responses (Bassiouni, 1994). For each rank, a numeric response was generated to distinguish one facies from another: (1) sandstone, (2) siltstone and (3) shale. Figure 5 shows a lithologic column where every sequence corresponds to a number (1, 2 or 3), i.e. the algorithm generates an alphanumeric response in depth which represents a lithofacies column from a geologic point of view.

Figure 5.

Ideal example of a succession of sandstone (1), siltstone (2) and shale (3), in depth and/or time, and the counter matrix associated to this column. (Modified from Doveton, 1994).

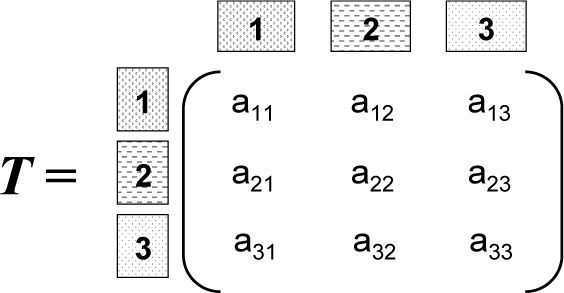
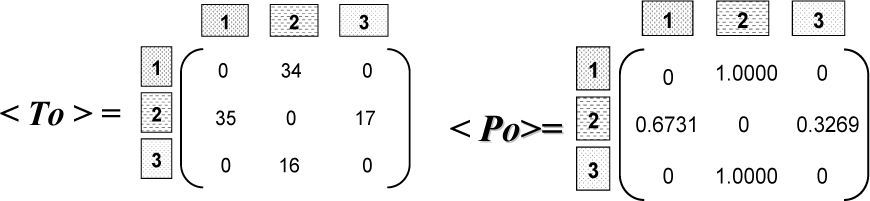
The relationship between adjacent geological events can be summarized with a transition counter matrix (T). In this matrix, every cell sums the number of times that a lithotype, identified by the matrix rows, is overlaid by another, identified by the matrix columns (see Figure 5). In this study, the matrix T was obtained for each well according to the lithology identified using the well logs available in the area (mainly Gamma Ray and Resistivity logs). Hence, the counter matrix T has the form:

where aij represents the number of times that the facies j overlies the facies i, i.e. the number of upward transitions from facies i to facies j (see Figure 5).

The transition probability matrix (P) is obtained from the T matrix according to:

In the relation above, sumi corresponds to the sum of the elements of the i row, i.e. the row of the element aij in the T matrix. The P matrix shows the probability that a facies overlays a given one, i.e. the probability of alternation of a given facies.

P and T matrices were calculated for each well. The cumulative probability matrix, Pcum, is obtained from the P matrix as the accumulated sum along each row. The last element of Pcum at a given row should be 1. The Pcum matrix is the starting point for the pseudo columns simulation.

Pseudo-stratigraphic Markov columns were generated at 20 new locations. The grid shown in Figure 6 was used to optimize the spatial sampling of the study area. The pseudo-wells were located equidistant to each pair of original wells. Therefore, only the contribution of the two closest colinear wells was taken into account. No weight dependency on the distance to the estimation point was used. Hence a simple average, that represents the same weight for each pair of wells in the segments, was applied. At each new location,

and matrices were generated using the counter transition information of the two equidistant wells. For each new location, 10 Markov realizations were performed with these matrices and a mean pseudo column was finally obtained. Although lithological lateral variability can exist between sequences (Eidsvik et al., 2004a; Eidsvik et al., 2004b), the analyzed lithological sequences correspond to the same stratigraphic parasequence (i.e the same time interval in a sedimentary setting) and hence, the simple average is enough to take this variation into account. The initial state was selected randomly in each realization, i.e. a random seed from a uniform distribution is generated to obtained the initial state; the next facies was obtained by sampling . In this fashion, to select the next facies along a sequence, the i column of the matrix (i is the number of the present state, i.e. 1, 2 or 3), was sampled to infer the immediate posterior state. A random number (Rn) between 0 and 1 was generated and compared with the ranges of values of the i row of the matrix. If 0_i1, the next facies should be 1. If a_i1i2, the next facies will be 2; if a_i2Sinvhal and Sinvhal, 1992). This process was iterated until the whole column was completed. The generation of each pseudo-column starts from base and goes to top, trying to simulate the sedimentation process. Pseudo-sequences were estimated at some selected well positions in order to test the reliability of the stochastic Markov Chain simulation and to estimate the prediction error.

Figure 6.

Locations of the pseudo-columns (grey dots). These new locations were placed equidistant to the 11 wells (black dots) available at the study area.

At each well and pseudo-well location, the percentage of each lithofacies was calculated and maps of facies distribution were obtained integrating the information given by the facies columns, obtained from the well logs, and the Markovian pseudo-columns.

For the cyclicity analysis, a total and an average occurrence probability matrix

were obtained for the study area using all the available wells. Hence, in this study we used more than one vertical sequence to define the genetic relations between lithofacies; in fact, 11 vertical sequences were used to determine a mean facies behavior in the study area. The nature of the cyclic processes observed was studied using the embedded Markov Chain method (Harbaugh and Bonham-Carter, 1970). To do so, transitions between the same facies are not allowed and, hence, the diagonal of the and

matrices should be set to zero. This gives rise to two new matrices, and . As stated by Miall (1973), this method highlights the actual change, focusing on the evolution of the depositional processes. A matrix that shows the probability that a given transition occurs randomly (an independent trials probability matrix, I) was obtained in the embedded Markov chain case according to (Miall, 1973):

were total is the total number of transitions in the matrix , and sumj and sumi are the sum of the elements in column j and in row i of this matrix, respectively. The difference matrix between and I was also calculated to analyze the cyclicity of the transitions. Positive entries in the matrix indicate which transition occurred with probability greater than a random frequency and, hence, underlies the Markov property (Miall, 1973). The highest values of and the positive entries of were analyzed to determine the cyclic processes at the studied Block of the Lama Field.

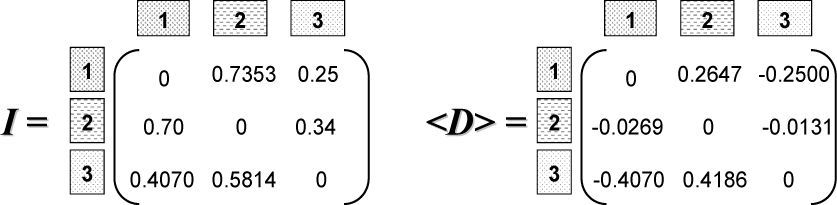
The Markov property of the matrix was tested using a chi-square (χ²) test according to (Harbaugh and Bonham-Carter, 1970):

where

Po_ij= the element in cell i,j of the mean transition probability matrix

Po_j=marginal probabilities for the jth column, i.e.

a_ij= transition frequency in cell i,j of the matrix

m= number of states

In the expression above, −2lnλ behaves asymptotically as χ² with (m-1)²-m degrees of freedom for the embedded Markov case (Harbaugh and Bonham-Carter, 1970).

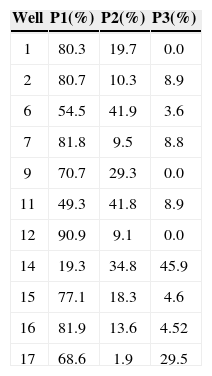
Results

To evaluate the change of state in terms of its relative occurrence probability, the lithology content at each well location, estimated from the well logs, was considered. Particularly, the sandstone content was analyzed in detail as it represents the reservoir rock in the study area. Table 1 shows the sandstone (P1), siltstone (P2) and shale (P3) content for each of the studied wells in the field. As can be observed, sandstone content predominates, varying from 90.9% to the north of the study area to 19.3% in the central part of it (see well location in Figure 4). In spite of the P1 values variation, its mean (68%) indicates high sandstone content in most of the area. These values were calculated for the Markovian pseudo sequences obtained at test well locations. Particularly, for well 2 the pseudo sequence was obtained using the information of the two equidistant wells 15 and 16 (see Figure 6); this pseudo well is designated as W15-16. Figure 7 shows the first three runs of the Markovian algorithm for this location. The final column is the mean after ten runs.

Table 1.

Sandstone (P1), siltstone (P2) and shale (P3) content at each well of the study area.

Well	P1(%)	P2(%)	P3(%)
1	80.3	19.7	0.0
2	80.7	10.3	8.9
6	54.5	41.9	3.6
7	81.8	9.5	8.8
9	70.7	29.3	0.0
11	49.3	41.8	8.9
12	90.9	9.1	0.0
14	19.3	34.8	45.9
15	77.1	18.3	4.6
16	81.9	13.6	4.52
17	68.6	1.9	29.5

Figure 7.

Pseudo-stratigraphic columns generated at the location of well 2, using the information of the equidistant wells 15 and 16. The first three runs are shown. The final column at this location is the mean after ten runs.

The mean P1, P2 and P3 values obtained are 78.7%, 13.6% and 7.7%, respectively. Although the vertical distribution of the shale and siltstone beds differs for the estimated pseudo well, there is a good agreement between the average content of each lithofacies obtained from the pseudo sequences and those calculated from the well logs (see Table 1).

Proportional (EPROP) and distributive (EDIST) errors were also estimated. The EPROP was estimated from the differences between the normalized lithology proportion (sandstone, siltstone and shale) along well 2 and along the pseudo well W15-16. The EDIST error measures the difference between the lithofacies distribution at both columns. The values obtained indicate that the Markovian technique, applied to this well, has a confidence of 82% regarding the lithology content and 67% related to the lithology distribution.

A net sand content map, combining the information of the original sequences at the well locations and the Markovian pseudo sequences at the 20 new locations, was generated in order to observe the variation of this parameter at Unit 1. The map of Figure 8 shows, towards the mid-west part of the study area, a high sand content, that varies between 60% and 80%. This content diminishes gradually to the southeast, where well 14 achieves the lowest sand value (19.3%). This map also shows a SW-NE sedimentary direction, in agreement with previous geological analyses in the area (Arminio et al., 1994; Cedillo et al., 2004); according to these studies, the thick Eocene fluvial-deltaic sediments prograded eastward and northeastward on the platform (Ambrose and Ferrer, 1997).

Figure 8.

Map of sand percentage obtained after integrating the well and the Markov pseudo-columns

The total and the

matrices for the study area are:

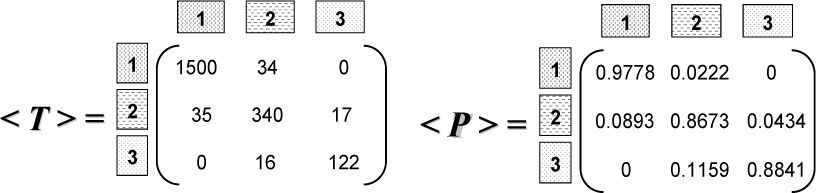
According to the

matrix, the major number of transitions occurs from sandstone to sandstone. This correlates well with the results of the net sand distribution in the study area. Transitions between shale to shale and from siltstone to siltstone have the next probability to occur. According to this matrix, transitions from sandstone to shale and viceversa are not expected to occur in the study area.

The , , I and matrices obtained for the cyclicity analysis are:

A chi-square value of 138.32 was obtained for the matrix. For a total number of states m=3, as in the case of this study, and hence one degree of freedom for the embedded Markov method, the 95% confidence level has a limit chi-square value of 7.81473. Therefore, the Markovian property is present in the studied sequence and the transitions are not independent (Harbaugh and Bonham-Carter, 1970).

The difference matrix indicates cyclic transitions just from sandstone to siltstone and from shale to siltstone (see Figure 9). The transitions not present in the diagram could be considered as random changes of the sedimentation processes or non cyclic transitions (Miall, 1973).

Figure 9.

Cyclic processes for the study sequence (Unit 1). The probability of occurrence is also indicated

The results obtained suggest that coarsening upward and fining upward processes dominate the study sequence. In a nearby block (Block V) Arzuman (2002) observed that the sandy layers of the C-4 interval show coarsening upward, blocky, and fining upward log patterns on the Gamma Ray trace of the studied well (VLE 196). Previous studies in the Lama Field indicate that the Lower Misoa formation was deposited in a tide-dominated delta setting (Talukdar and Marcano, 1994; Ambrose and Ferrer, 1997). The morphology of these tide-dominated deltaic systems could be the result of the tide action over the fluvial sedimentation. According to Galloway and Hobday (1996) these kinds of systems show few to many estuarine distributary channels, characterized by broad, funnel-shaped mouths, and narrow, sinuous upper reaches. The general upward-coarsening character of the distributary mouth bars tends to produce sandstone bodies that are usually upward-fining (Scheihing and Atkinson, 1992; Arzuman, 2002). It is important to point out that these channel deposits and distributary mouth bars usually involve the best reservoir quality bodies within a delta system (Arzuman, 2002).

Hence, the combination of the processes indicated above, i.e. the interaction/competition between the tides and the fluvial transport, could explain the Markovian transitions observed in the study area. Ideally, a matrix with sand to silt, silt to sand, silt to clay and clay to silt transitions could be expected for coarsening upward and fining upward processes in a deltaic environment. Nevertheless, it is important to point out that mean matrices for the whole area were used for this cyclicity analysis. Therefore, the matrix obtained here shows the mean or more significant transitions. In fact, according to Ambrose and Ferrer (1997), the Lower Eocene sandstone depositional axes in the Lama Field are narrow, linear, and commonly projected between the existing control wells at 80-acre spacing as a result of the depositional architecture. According to the lithological percentage observed at the studied well (see Table 1), most of these wells drilled the thick sandstones of the Eocene fluvial-deltaic sediments. If more wells outside the narrow channels are used, it should be possible to observe the siltstone to sandstone and siltstone to shale transitions probably hidden due to the mean analysis performed here.

Conclusions

The Markov analysis of the C4 sands of the Misoa Formation, at the Lama Field, allowed to properly model the vertical and horizontal heterogeneities of the reservoir, as was indicated by the map of sandstone content obtained integrating the columns derived directly from the well logs and the Markovian pseudo-columns. This map clearly depicts a NE-SW axis coincident with the sedimentation direction of the thick Eocene fluvial-deltaic sediments observed in the area. The Markovian embedded analysis of the mean transition probability of the study area indicates cyclic transitions from sandstone to siltstone and shale to siltstone, representative of fining-upward and coarsening-upward processes, expected for delta environments as the tide-dominated one studied here. These transitions were observed with the Markovian approach even though some bias is given by the well distribution, as these wells mainly drilled the thick sandstones of the area. These results emphasize the additional advantages of this kind of stochastic characterization compared with other statistical methods as crossplots or semivariograms analyses.