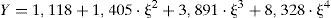La construcción del Puente de la Constitución de 1812 sobre la Bahía de Cádiz ha supuesto la suma de voluntades y esfuerzos de múltiples equipos de trabajo. Entre ellos, el Ministerio de Fomento encargó a APIA XXI realizar los trabajos de asistencia técnica para la supervisión estructural de las principales maniobras del proceso constructivo del tablero. En el presente artículo se relacionan los trabajos más significativos desarrollados en el ámbito de esta supervisión estructural. También se describe un caso concreto de estudio relacionado con el control de deformaciones del tablero bajo el proceso de atirantamiento mediante el método de la isotensión. Finalmente se presenta un análisis encaminado a valorar la sensibilidad a fractura de las barras de retenida del carro de izado de dovelas.
Construction of Constitución de 1812 cable-stayed Bridge over the Cadiz Bay has needed the combination of efforts and determinations of many working teams. Among them, APIA XXI was commissioned by the Ministry of Public Work to develop the Proof Check Consultancy for the more relevant phases of the erection procedure of the bridge. In this article the main tasks carried out inside this field are described. In addition, a specific case of study related to the geometric control of the bridge during the cable staying phases is explained. Finally, an analysis to evaluate the sensitivity to fracture of the retainer bars of the Lifting Frame is presented.
Profundidad de grieta.
Módulo elástico del acero de los cordones del tirante.
Fuerza aplicada en el tesado del cordón patrón.
Fuerza experimentada por los cordones del tirante tras el tesado del segundo cordón.
Fuerza experimentada por los cordones del tirante tras el tesado del tercer cordón.
Fuerza teórica en los cordones del tirante tras finalizar el proceso de tesado.
Fuerza real en los cordones del tirante tras finalizar el proceso de tesado.
Rigidez teórica del anclaje de un tirante.
Rigidez real del anclaje de un tirante.
Rigidez del cordón patrón.
Factor de intensidad de tensiones.
Tenacidad a fractura.
Longitud de un cordón del tirante.
Distancia entre anclajes de un tirante antes de comenzar el proceso de tesado.
Distancia entre anclajes de un tirante tras el tesado del cordón patrón.
Factor adimensional de corrección para el factor de intensidad de tensiones.
Correlación entre las rigideces teórica y real del anclaje de un tirante.
Correlación entre las fuerzas de tesado real y teórica de un tirante.
Pérdida de fuerza de tesado en el cordón patrón como consecuencia del tesado del segundo cordón.
Acercamiento entre anclajes de un tirante como consecuencia del tesado del cordón patrón.
Deformaciones teóricas de la estructura.
Deformaciones reales de la estructura.
Deformación experimentada por el anclaje y por el cordón patrón tras el tesado del segundo cordón del tirante.
Profundidad relativa de la grieta.
Tensión nominal de tracción de la barra, supuesta la ausencia de cualquier tipo de defecto o grieta.
Área de un cordón del tirante.
La construcción del Puente de la Constitución de 1812 sobre la Bahía de Cádiz ha supuesto la suma de voluntades y esfuerzos de múltiples equipos de trabajo [1]. Entre ellos, el Ministerio de Fomento encargó a APIA XXI realizar los trabajos de asistencia técnica para la supervisión estructural de las principales maniobras del proceso constructivo del tablero.
Este trabajo de supervisión estructural se ha concretado en las siguientes tareas:
- -
Supervisión de los cálculos realizados por el proyectista del puente.
- -
Supervisión de los cálculos realizados por los proyectistas de los medios auxiliares.
- -
Realización de un modelo de cálculo independiente del puente, para llevar a cabo un contraste paralelo de tensiones y deformaciones durante el proceso constructivo.
- -
Realización de modelos de contraste de los medios y estructuras auxiliares principales.
- -
Asesoramiento a pie de obra para la definición y control de las principales maniobras del proceso constructivo.
Para las tareas de seguimiento y contraste de la evolución tenso-deformacional del puente durante el proceso constructivo se ha elaborado un modelo de cálculo propio, evolutivo, tanto del tramo atirantado como del tramo de hormigón. De esta forma cada una de las fases críticas del proceso constructivo ha sido chequeada de forma independiente.
Algunas de las principales maniobras estudiadas (además de las propias relacionadas con el ciclo de izado, posicionamiento, soldadura, hormigonado y tesado de tirantes de cada dovela) han sido las siguientes [2]:
- -
Desbloqueo de empotramiento tablero-pila 12 y 13.
- -
Paso del tablero sobre la pila 11 y la pila 14.
- -
Llegada del tablero a la pila 10 y conexión con el viaducto desmontable.
- -
Llegada del tablero a la pila 15 y conexión con el viaducto contiguo de hormigón.
- -
Cierre del tablero en vano principal.
- -
Retirada y desmontaje de los medios auxiliares.
- -
Transporte e izado del tramo desmontable.
- -
Secuencia constructiva del tramo de hormigón.
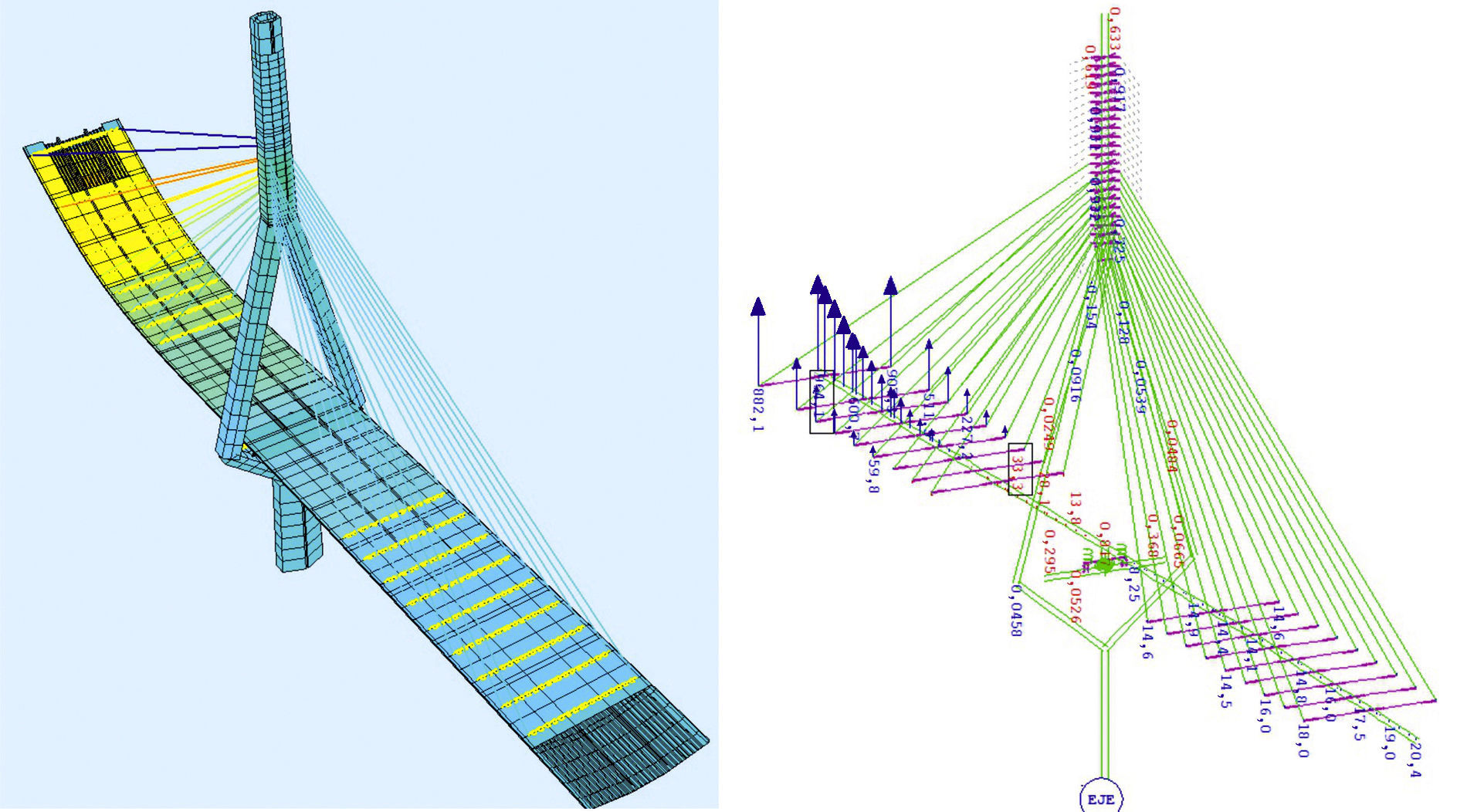
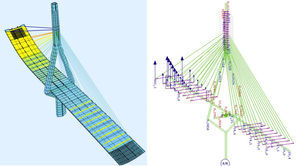
La figura 1 muestra una imagen del modelo de cálculo para una fase típica de tesado de una familia de tirantes.
2.2Revisión de medios y estructuras auxiliaresLas especiales características de este puente han conllevado a que la propia concepción, diseño e implantación de los medios auxiliares indispensables para su construcción suponga un reto de una magnitud considerable [3]. Ha sido un empeño particular de todos los agentes implicados en esta obra el hecho de que el tratamiento dado a los medios y estructuras auxiliares fuera comparable, en cuanto a los requisitos de diseño, revisión y control, al de los propios elementos definitivos del puente, para garantizar así la máxima eficacia y seguridad en cada una de las operaciones del proceso constructivo. En esta línea se ha realizado también una supervisión estructural crítica de los siguientes medios y estructurales auxiliares:
- -
Carro de izado y posicionamiento de dovelas.
- -
Carro de soldadura.
- -
Pórticos de izado del tramo desmontable.
- -
Pescantes para paso por pila.
- -
Elementos de fijación provisional para cierre en clave.
- -
Carro de alas para hormigonado de voladizos.
- -
Cimbra cuajada y porticada para el tramo de hormigón.
- -
Cestos de tirantes.
- -
Ascensor.
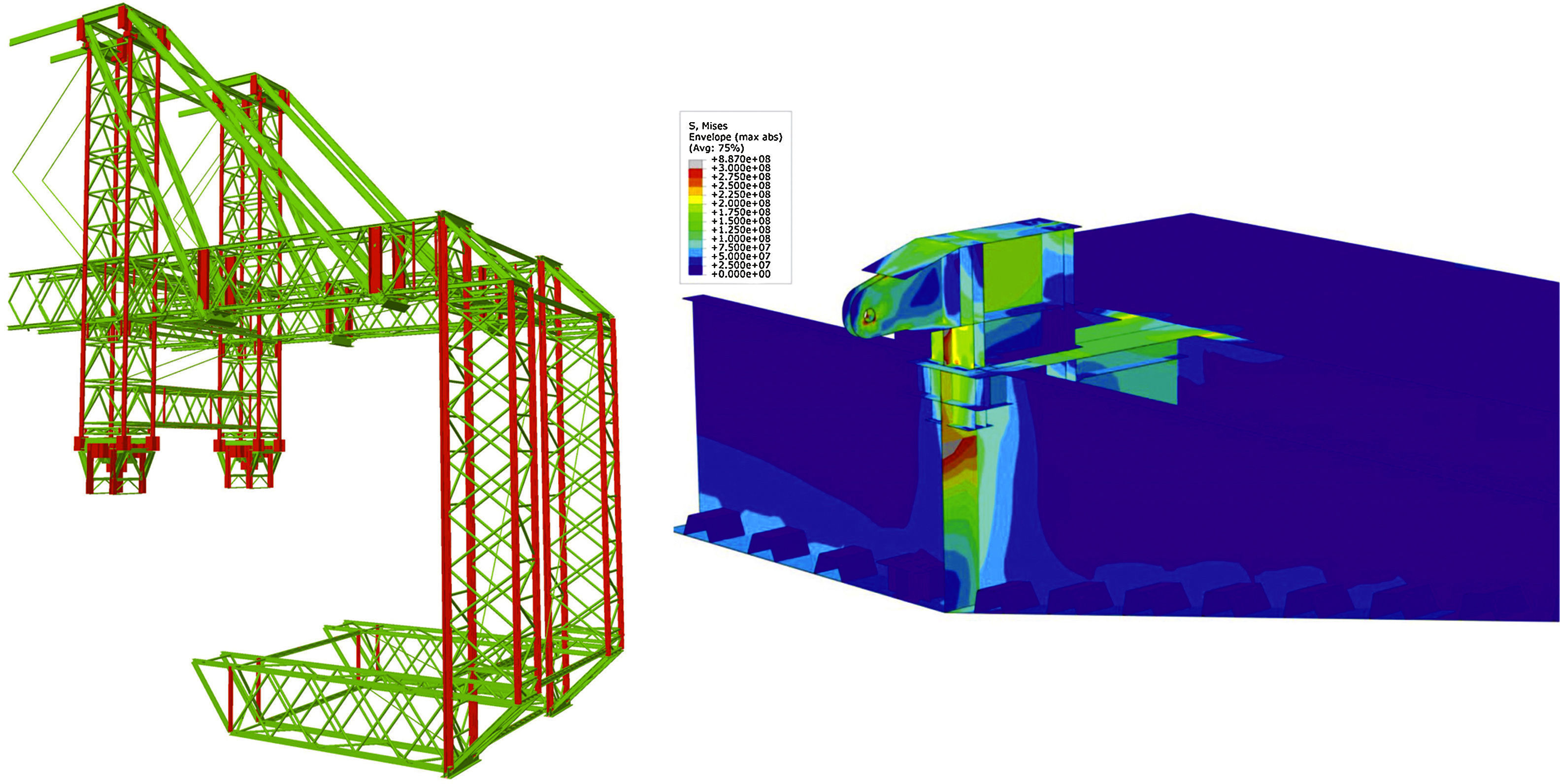
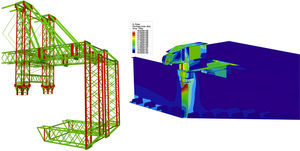
Esta revisión crítica de los principales medios y estructuras auxiliares ha exigido realizar modelos de cálculo de contraste de detalle, tal como muestra la figura 2.
2.3Seguimiento a pie de obraLa asistencia técnica para la supervisión estructural ha mantenido también un equipo a pie de obra, involucrado en las tareas de concepción, coordinación y supervisión de las principales maniobras del proceso constructivo del tablero.
Entendemos que, en su conjunto, esta metodología de trabajo, similar a la que se establece internacionalmente en puentes de parecida envergadura bajo la denominación de Third Party-Independent Design and Construction Check o Proof Checking Consultancy, ofrece una garantía adicional en el control de la construcción del puente.
3Caso concreto: análisis de sensibilidad de las fuerzas de tesado y deformaciones del tablero en relación con las variaciones de rigidez de la estructura3.1Planteamiento del caso de estudioLas labores de supervisión estructural llevadas a cabo no solo incluyen comprobaciones a tiempo real de la conducta prevista del viaducto y revisiones de los cálculos de los medios auxiliares específicos para los complejos procesos constructivos, sino que, yendo más allá, procuran también dar explicación de cuantos aspectos del comportamiento cotidiano de la obra parecen salirse de lo obvio y por lo tanto pudieran crear incertidumbres o perplejidad.
A manera de ejemplo de lo anterior, y como caso concreto, un hecho que llamaba la atención en la obra era que tras los tesados de los tirantes (por el procedimiento de isotensión), en ocasiones se obtenían cargas en los mismos que presentaban variaciones con respecto a las cargas teóricas finales, lo que aparentemente no se reflejaba en la deformada del tablero, que sí se asemejaba mucho a la teórica.
El procedimiento de isotensión de tirantes consiste en tesar los cordones individuales de cada tirante de manera sucesiva con gato unifilar, controlando que sean iguales la fuerza aplicada en cada uno de los cordones que se van tesando y la fuerza remanente en el primer cordón de los tesados, o cordón patrón. Ambas fuerzas se controlan mediante sendas células de carga instaladas en el cordón patrón y en el gato. Con este procedimiento se asegura que al terminar el tesado de un tirante todos los cordones posean la misma carga o tensión [4,5].
Ahora bien, durante el tesado sucesivo de los cordones de un tirante se produce un hecho que es intuitivo: los cordones del mismo tirante instalados anteriormente se van descargando. Esto implica necesariamente que el cordón patrón deba tesarse a una tensión superior que irá disminuyendo progresivamente hasta que se tese el último cordón. La carga final a la que quede el tirante constituye entonces una apuesta basada en el mejor conocimiento posible de la rigidez de la estructura, puesto que partimos de unas tensiones incrementadas teóricamente en el cordón patrón que únicamente al final del tesado coincidirán exactamente con nuestro objetivo de carga en el tirante si el comportamiento deformacional real de la estructura es idéntico al estimado en nuestros modelos [6].
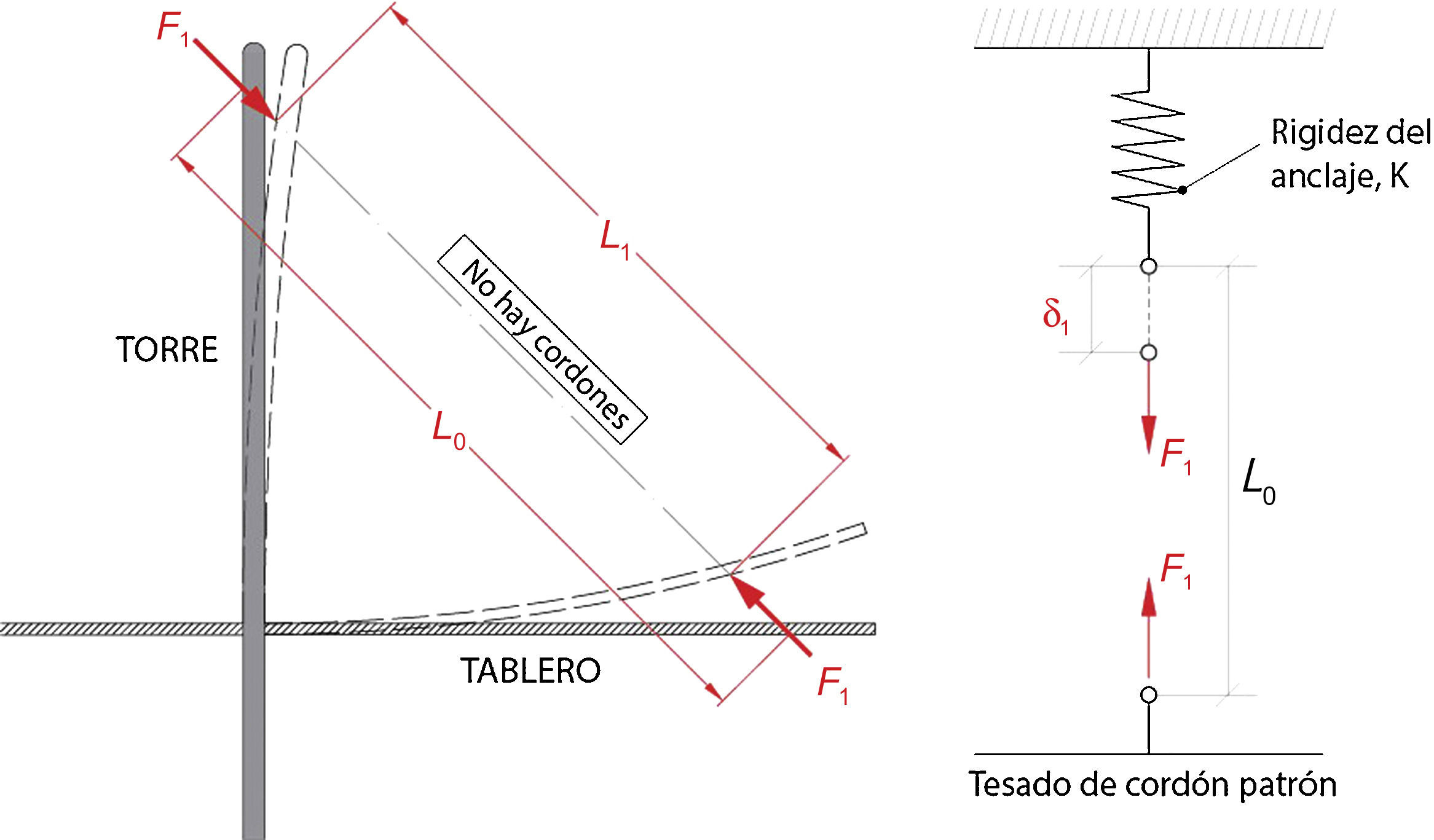
3.2Descripción del proceso de tesado llevado a cabo en los tirantesCuando se tesa el cordón patrón de la estructura, los anclajes del mismo se acercan entre sí una cierta distancia (ΔL):
Podemos llamar «rigidez del anclaje» (K) al cociente entre la fuerza aplicada en el cordón patrón (F1) y el acercamiento entre anclajes (ΔL), de modo que:
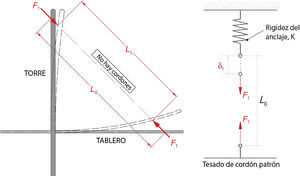
El valor de la rigidez del anclaje es teórico antes de proceder al tesado del tirante y se obtiene, por lo tanto, del modelo de cálculo de la estructura. El tesado del cordón patrón puede esquematizarse según la figura 3, donde el acercamiento entre placas de anclaje correspondiente tiene un valor de δ1.
Cuando se procede al tesado del segundo cordón del tirante, resulta que la rigidez del anclaje habrá incrementado levemente su valor, puesto que ahora se le sumaría la rigidez aportada por la presencia del cordón patrón, de valor K′:
siendo Ω el área de un cordón, E el módulo elástico del acero del cordón y L su longitud (y suponiendo, como puede comprobarse, un comportamiento perfectamente lineal).
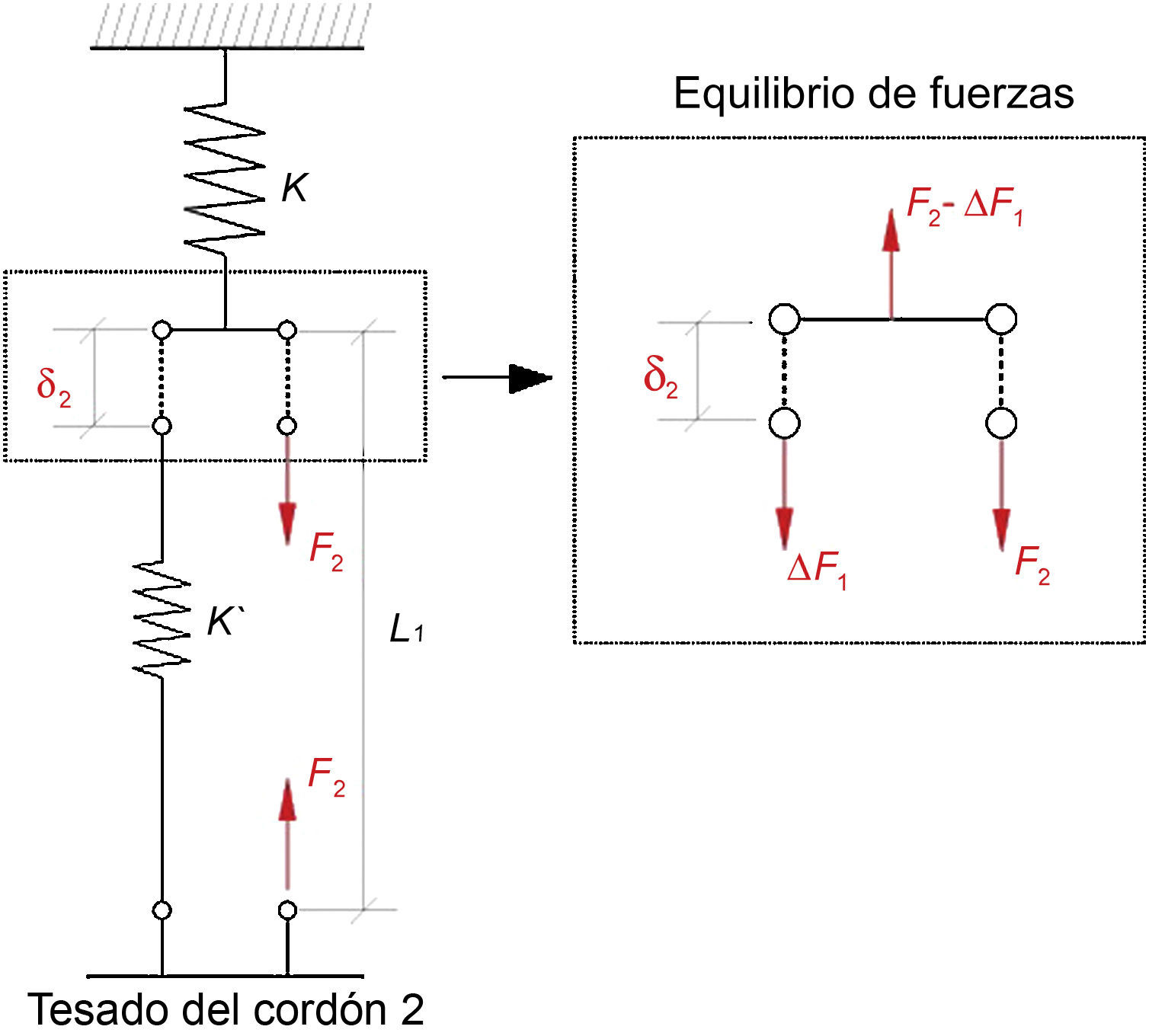
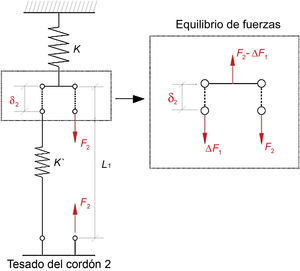
En el proceso de tesado del segundo cordón se genera el reparto de fuerzas mostrado en la figura 4. A partir de las deformaciones experimentadas por el anclaje y por el cordón patrón (δ2), se establece la siguiente condición de compatibilidad:
Al aplicar el proceso de isotensión en el tesado del segundo cordón (F2=F1-ΔF1), la carga de este y la del cordón patrón se habrán igualado hasta un valor de F2. El valor de esta carga se obtiene sustituyendo la condición de isotensión en la ecuación 4:
Tras el tesado del tercer cordón, operando de manera similar, las cargas de los 3 cordones tesados se habrán igualado hasta un valor de F3:
Generalizando a n cordones, una vez terminado de tesar el tirante, cada uno de ellos tendrá la misma carga, igual a Fn:
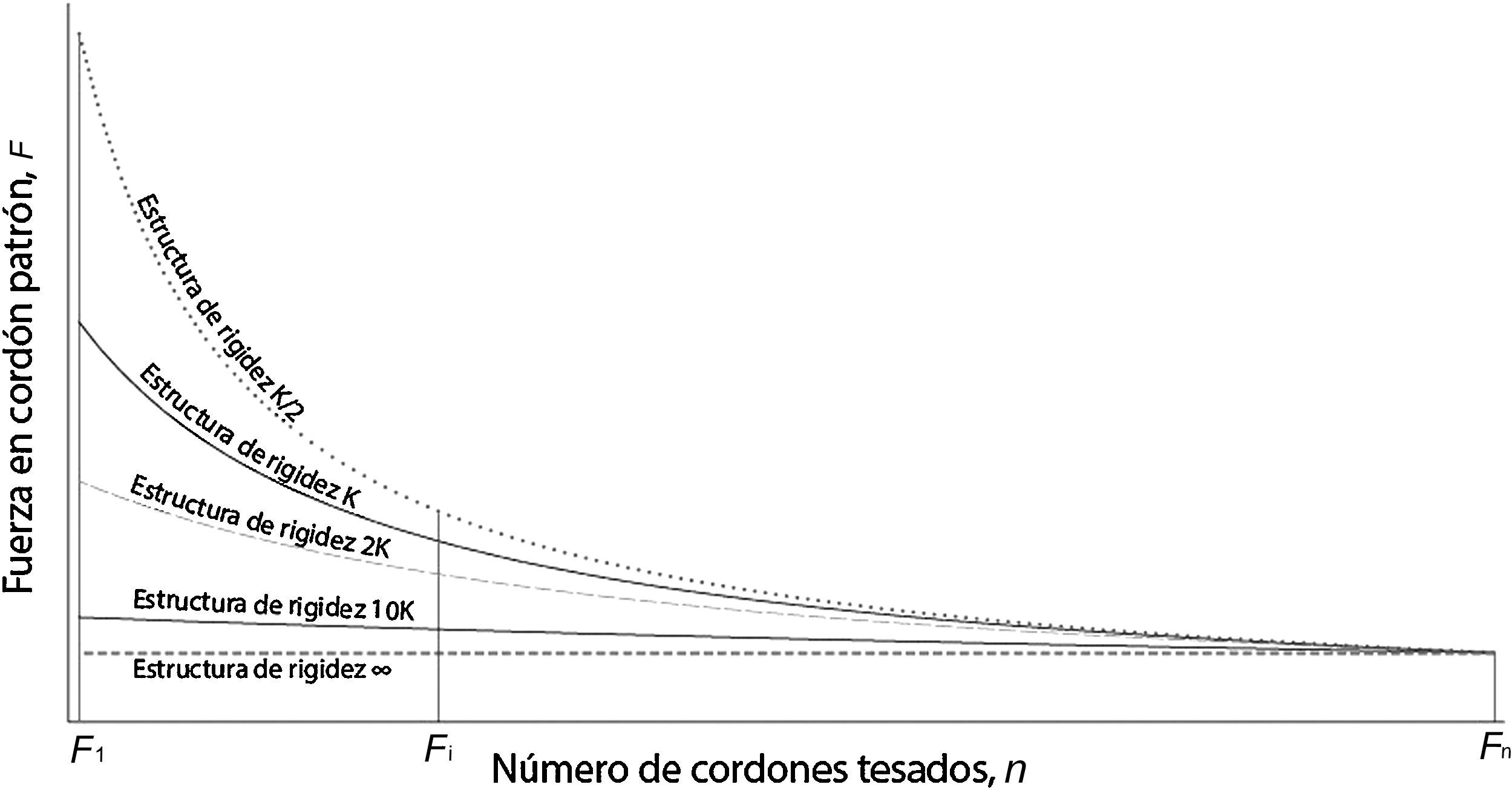
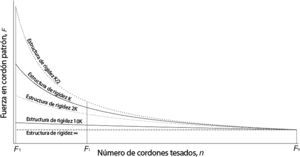
En la figura 5 se muestra la evolución de la fuerza en el cordón patrón a medida que se tesa el tirante (añadiendo cordones).
De acuerdo con la ecuación 7, si el tesado de cordones se realiza sobre una estructura muy flexible, entonces existirá mucha diferencia entre la fuerza del cordón patrón de inicio (F1) y el último cordón tesado del tirante (Fn). Si la estructura fuese muy rígida, la curvatura de la gráfica de evolución de la fuerza en el cordón patrón disminuiría, reduciéndose la diferencia entre F1 y Fn.
3.3Influencia de la variación de la rigidez de la estructura en la fuerza final del tiranteImaginemos que hemos obtenido teóricamente que la «rigidez del anclaje» es K. Entonces, a partir de la ecuación 7 habremos estimado una fuerza en el cordón patrón igual a F1.
Ahora bien, si la rigidez real es K*=αK, distinta de la teórica, nos encontraremos que la fuerza en cada cordón del tirante tras finalizar el tesado el mismo será:
y por lo tanto:
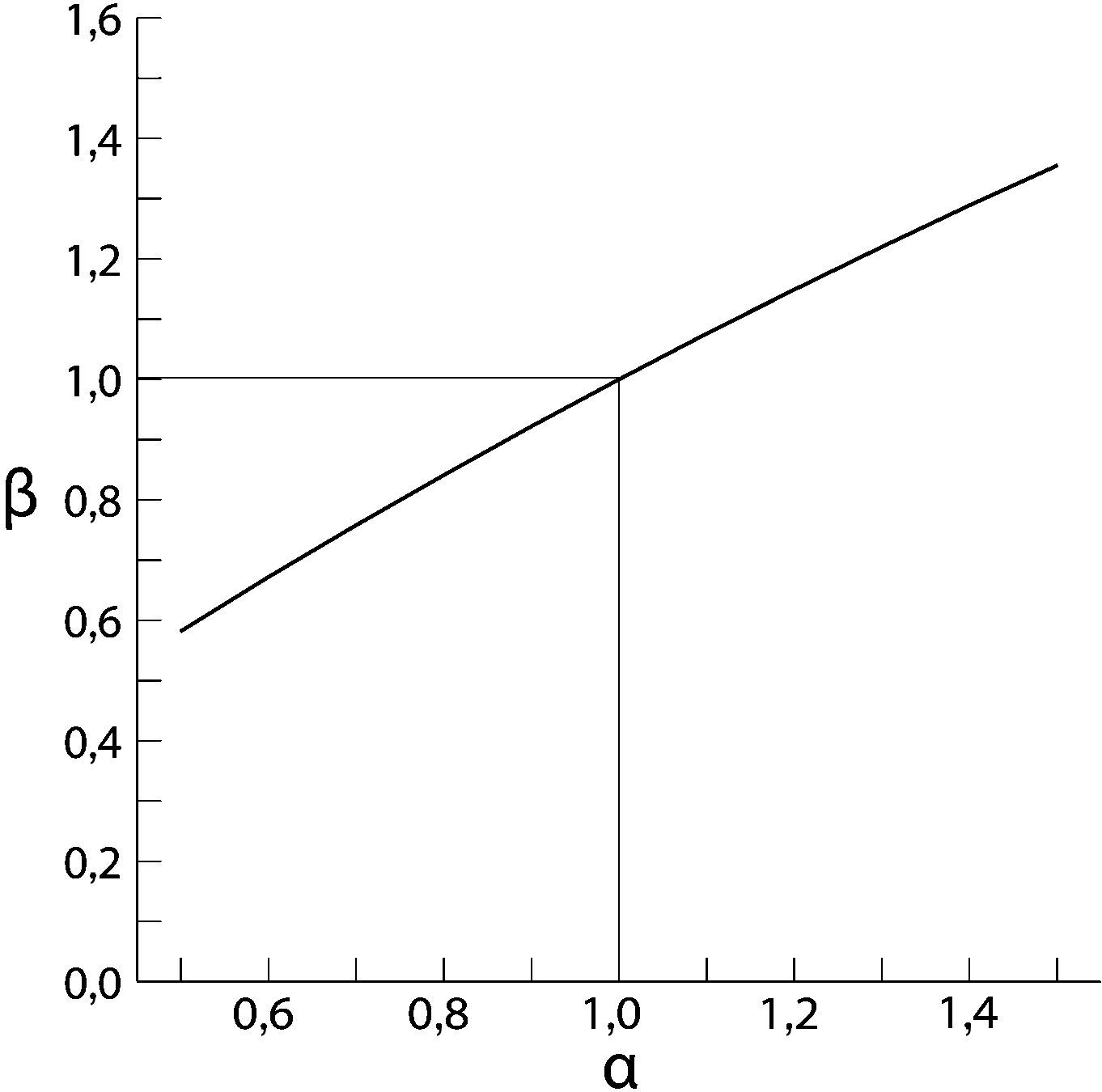
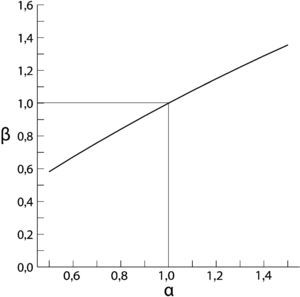
El coeficiente β expresa la ratio entre la fuerza real que toman los cordones y la fuerza teórica que se les pretendía aplicar, supuesta una rigidez real K*=αK distinta a la teórica estimada a priori de valor K. En la figura 6 se observa la relación existente entre α y β.
Según la relación establecida, se obtiene (como conclusión esperada) que si la estructura resulta en la realidad más rígida que el valor teórico estimado en el modelo de cálculo, entonces el tirante se cargará más al aplicar el procedimiento de isotensión, y viceversa. En estructuras tan flexibles como el Puente de la Constitución de 1812 sobre la Bahía de Cádiz, la desviación obtenida en la carga final del tirante es del orden de magnitud y similar a la variación inicialmente considerada en la estimación de la rigidez de la estructura.
3.4Influencia de la variación de la rigidez de la estructura en la deformada finalSegún lo visto anteriormente, para una estructura de rigidez real K*=αK, se obtendría una fuerza real en los cordones del tirante de valor Fn*=βF.
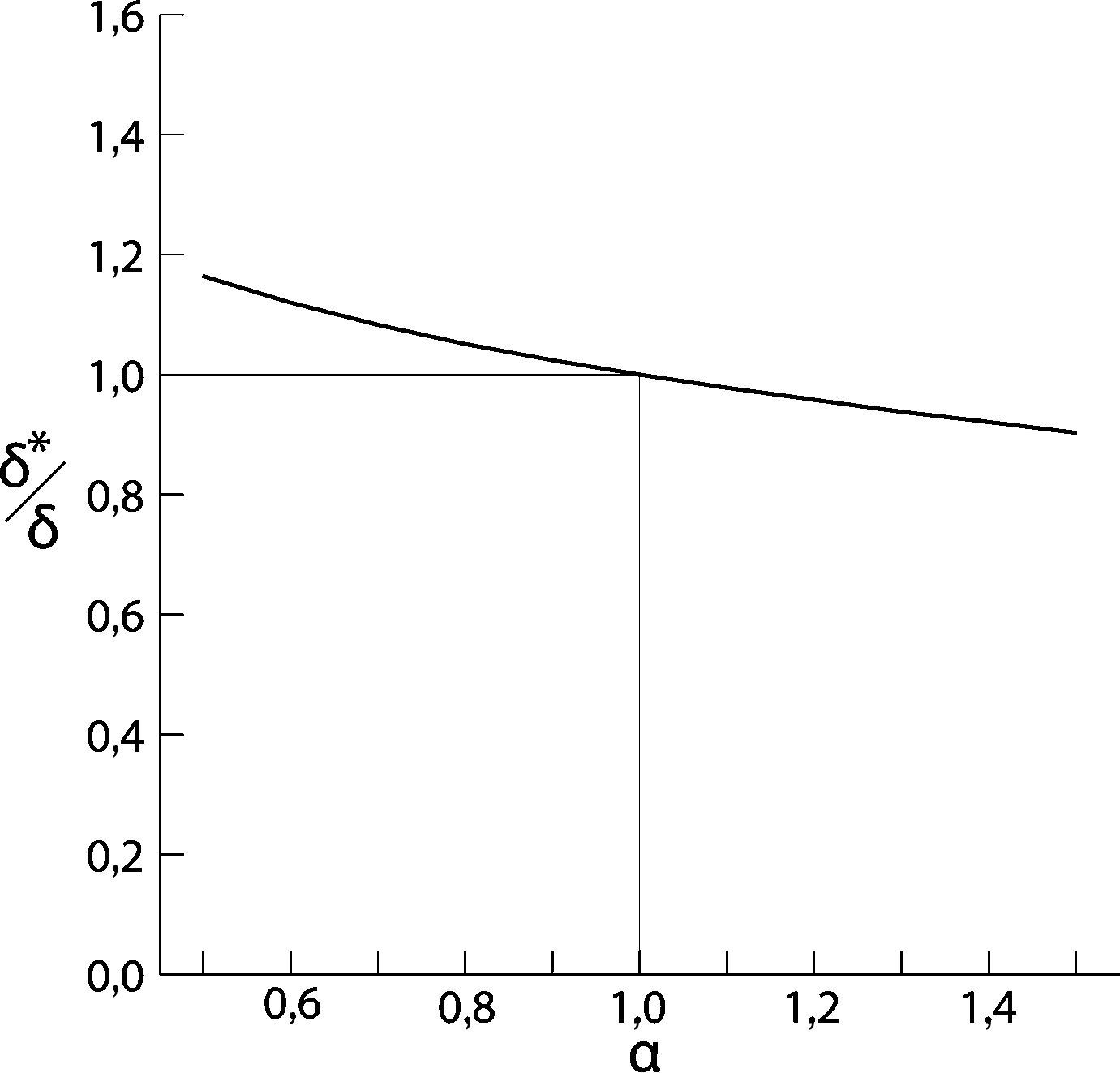
Estableciendo una ratio entre las deformaciones teóricas de la estructura (δ=F/K) y las deformadas reales obtenidas (δ*=F* / K*=(βF) /(αK)) obtenemos la siguiente expresión:
En la figura 7 se representa la ecuación 10 para los valores de α y β determinados en el apartado anterior, correspondiente a un caso concreto del Puente de la Constitución de 1812 sobre la Bahía de Cádiz.
En la figura 7 se observa cómo la relación existente entre el cociente de los valores de deformaciones reales y teóricas y el valor de α (representativo de la variación considerada en la obtención de la rigidez de la estructura) se asemeja a una recta cuasi horizontal. Se deduce que para variaciones del 20% en la estimación de la rigidez, por defecto o por exceso, la ratio obtenida entre las deformaciones reales y teóricas no supera el 5%.
A partir de estos resultados, eminentemente conceptuales, se puede concluir que variaciones relevantes en la estimación de la rigidez de la estructura tienen escasa influencia en la deformada obtenida tras el tesado de tirantes por el proceso de isotensión.
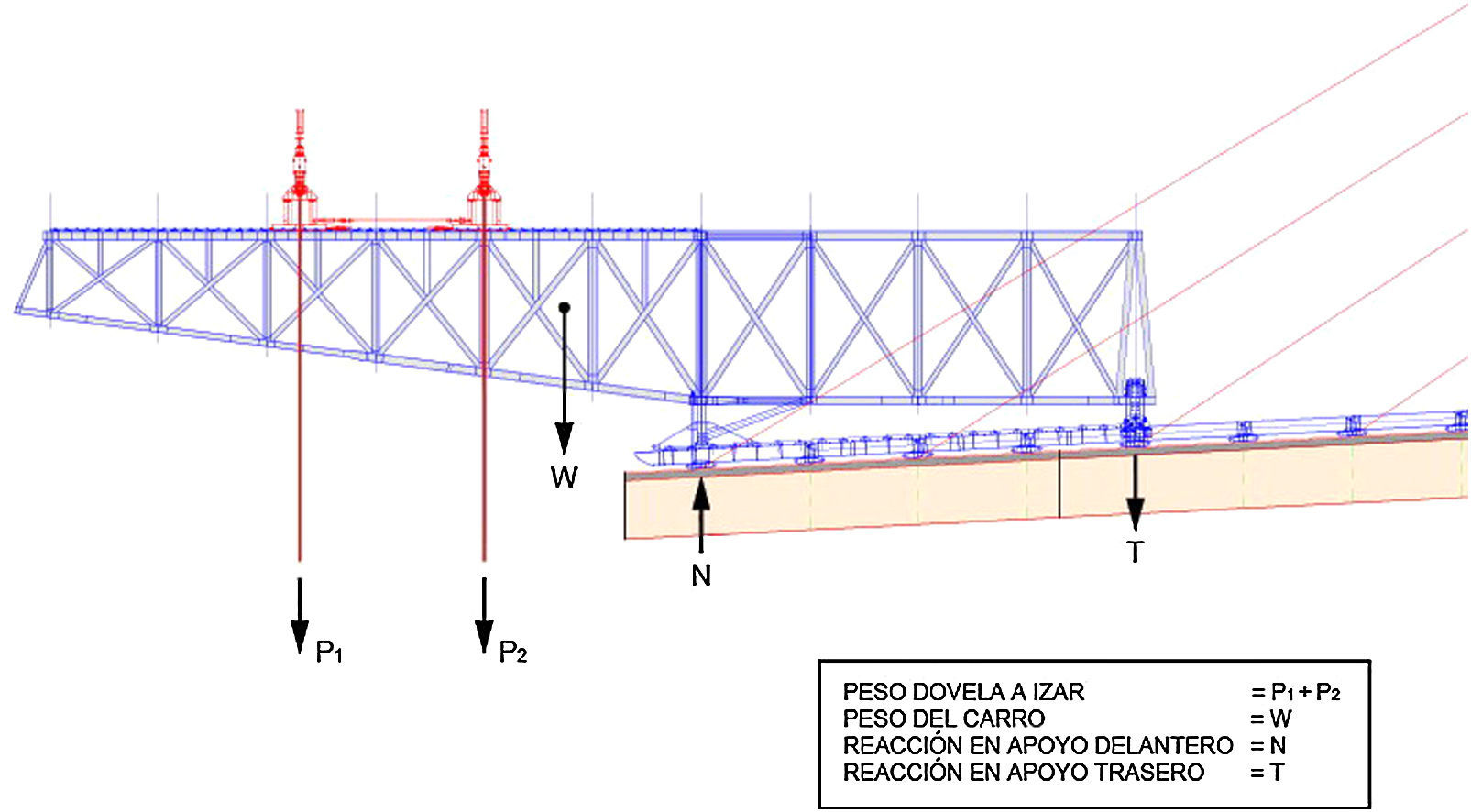
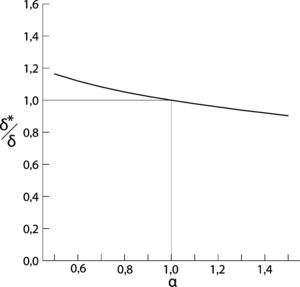
4Caso concreto: análisis de la sensibilidad a fractura de las barras de retenida de los medios auxiliares empleados para el izado de dovelas4.1Descripción de los medios auxiliares empleados para el izado de dovelasEl izado de las dovelas del tramo atirantado se realiza mediante los medios auxiliares específicos denominados «carros de izado». En esta obra se dispusieron 4 unidades simultáneamente, una por cada avance en voladizo. El esquema estático longitudinal de estos carros es el de 2 vigas en celosía paralelas de gran canto dispuestas cada una con un vano biapoyado y un voladizo en extensión, del que se cuelga la dovela a izar. Evidentemente el apoyo de la viga adyacente al voladizo (o apoyo delantero) se comprime fuertemente por efecto del peso de la dovela (reacción positiva), mientras que el apoyo trasero se tracciona (reacción negativa).
Los carros de izado constituyen, pues, una estructura externamente isostática, lo que presenta la ventaja del conocimiento perfectamente definido de las reacciones teóricas que sufren durante el izado, unívocamente definidas con las ecuaciones de la estática; pero presenta la desventaja de constituir un sistema en el que el fallo total de uno de sus apoyos pudiera provocar un quebranto global. Así, desde el punto de vista del equilibrio, la fiabilidad del sistema de izado reside en la propia seguridad individual de los apoyos delanteros y traseros. En las figuras 8 y 9 se muestra el diagrama de cuerpo libre del carro de izado donde se reflejan tanto las cargas exteriores (peso de la dovela y peso propio del carro), como las reacciones en apoyos delantero y trasero.
La necesidad de dotar de versatilidad geométrica al carro, además de la recomendación de eliminar cualquier mínima holgura en el apoyo trasero, motivaron que dicho anclaje a tracción fuera materializado mediante 2 grupos paralelos (uno por cada alineación de viga longitudinal paralela) de 4 barras pretensadas de acero de alto límite elástico. Las barras tienen un diámetro efectivo de 47mm, equivalente a una sección de cálculo de 1.735mm2, y son de calidad S-950/1050. Cada una de las 8 barras dispuestas en cada carro cuenta, por tanto, con una capacidad a tracción nominal de 1.648kN en el límite elástico (1.822kN en rotura).
4.2Diseño de las barras de anclaje traseras del carro de izadoDesde el inicio del diseño conceptual de los carros de izado se procuró que la seguridad estructural de los anclajes traseros residiese tanto en un abundante sobredimensionamiento como en cerciorarse de una conveniente ductilidad del sistema, minimizando la probabilidad de rotura frágil en las barras de alto límite elástico. Así, para la situación pésima de izado de dovelas, se calculó una tracción máxima teórica en cada conjunto de 4 barras de 1.889kN, lo que, supuesto un reparto uniforme de la carga entre ellas, equivale a 472kN nominales en cada una. Este valor se corresponde con una tensión nominal de servicio máxima en cada barra de 272Mpa; valor que equivale aproximadamente a un 30% de su capacidad en el límite elástico.
El valor anterior está tomado en servicio, y no recoge las inevitables desviaciones que se han de producir entre barras de un mismo grupo (por diferencias en su carga de pretensado y por el leve efecto hiperestático derivado de la no coincidencia en planta de sus 4 barras) o entre los 2 grupos de cada carro.
Una de las principales preocupaciones durante el desarrollo de la obra fue limitar el riesgo de rotura frágil de estas barras como consecuencia de hipotéticas concentraciones de tensiones por existencia de defectos (entallas o grietas) previos en el material (una vez descartados otros factores teóricamente influyentes como las bajas temperaturas o la velocidad de la carga). Para ello, además de adoptar medidas adecuadas de inspección y protección de las barras, se llevó a cabo un análisis del riesgo de rotura frágil de dichas barras, tal como se describe a continuación.
4.3Mecánica de la fractura. Evaluación de la integridad estructural de la barraEs sabido que el incremento de fuerzas axiles de tracción sobre una barra puede originar la formación y el crecimiento de una grieta de tamaño a en primera fase de forma estable, pues aquella crece en relación con el crecimiento de las fuerzas, y por último, de forma inestable o súbita. La causa del avance del defecto es el incremento de tensiones existente en el fondo de la grieta en relación con las tensiones nominales introducidas por una fuerza P[7].
La intensidad de la tensión en el extremo de la grieta, causa de su crecimiento, es función tanto de la tensión nominal σnom como de las dimensiones geométricas de la barra y grieta. Se define así un parámetro denominado factor de intensidad de tensiones, denominado KI, definido por la expresión 11:
donde:
KI=factor de intensidad de tensiones.
Y=factor adimensional de corrección, que depende de la geometría concreta del caso de estudio, de la forma de aplicación de las cargas y de las condiciones de contorno.
σnom=tensión nominal de tracción de la barra, supuesta la ausencia de cualquier tipo de defecto o grieta.
a=profundidad de grieta.
La rotura de la barra tiene lugar cuando KI alcanza un valor crítico Kic denominado tenacidad a fractura del acero. Aplicando la teoría elástica lineal de la mecánica de la fractura, la tensión nominal de rotura de una barra sometida a esfuerzo axil de tracción, con presencia de una grieta de profundidad a sería:
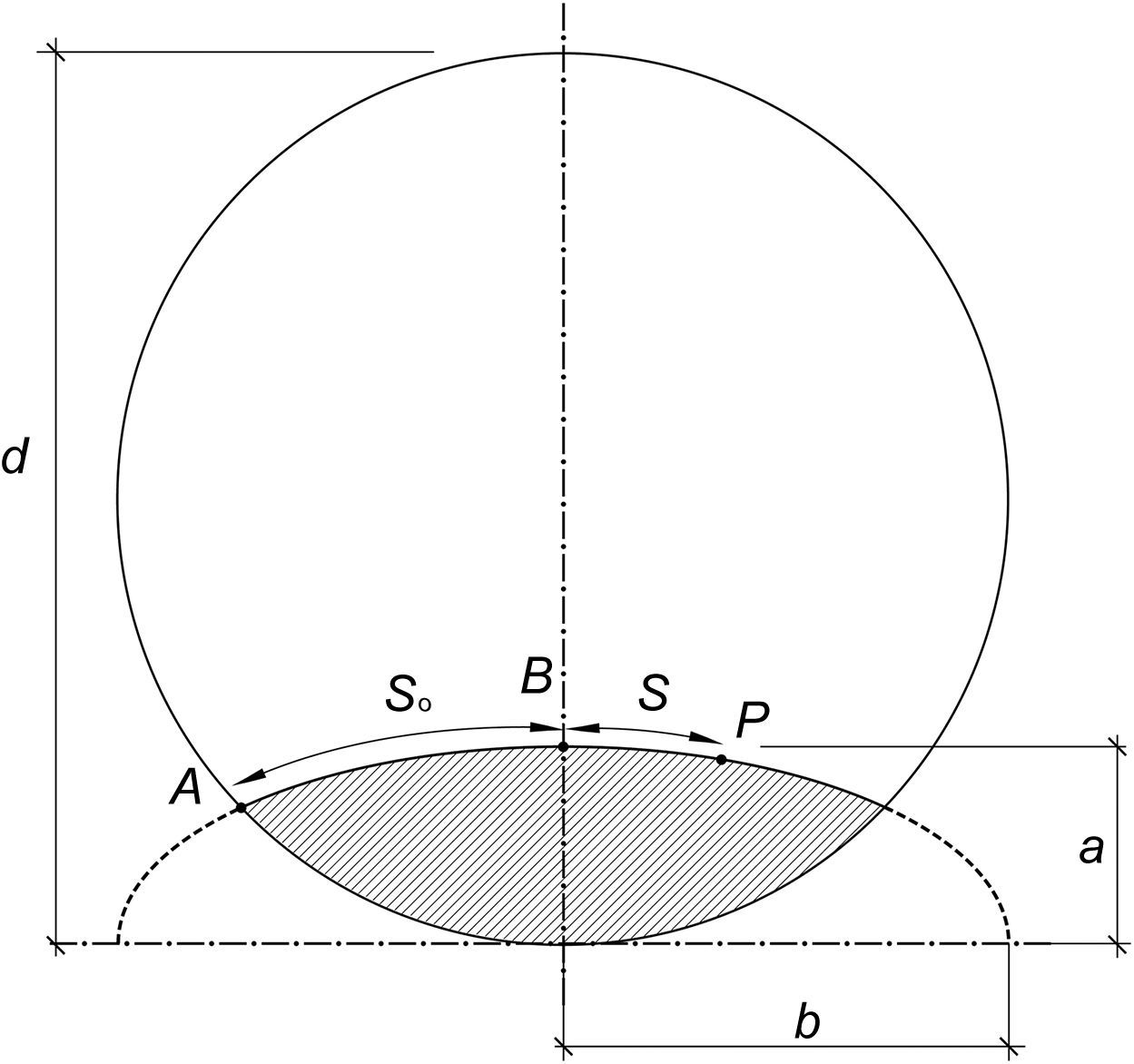
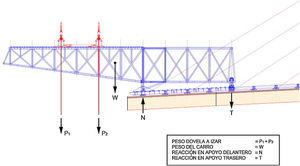
Modelizando las hipotéticas grietas como elípticas (semiejes a y b, ver figura 10), el factor Y puede obtenerse, según [8], mediante la siguiente expresión:
Grieta hipotética con forma semielíptica en plano perpendicular al eje de la barra [9].
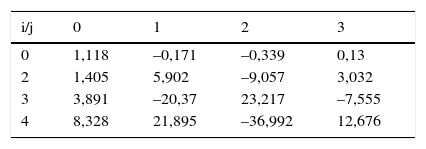
Donde los coeficientes Cij, denominados coeficientes de Astiz, se corresponden con los mostrados en la tabla 1.
Coeficientes de Astiz
| i/j | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| 0 | 1,118 | –0,171 | –0,339 | 0,13 |
| 2 | 1,405 | 5,902 | –9,057 | 3,032 |
| 3 | 3,891 | –20,37 | 23,217 | –7,555 |
| 4 | 8,328 | 21,895 | –36,992 | 12,676 |
Fuente: [9].
El valor más alto de la expresión (11) (valor más desfavorable) se obtiene siempre para b>a, convirtiéndose la expresión (13) en:
Donde ξ=a/D, profundidad relativa de la grieta.
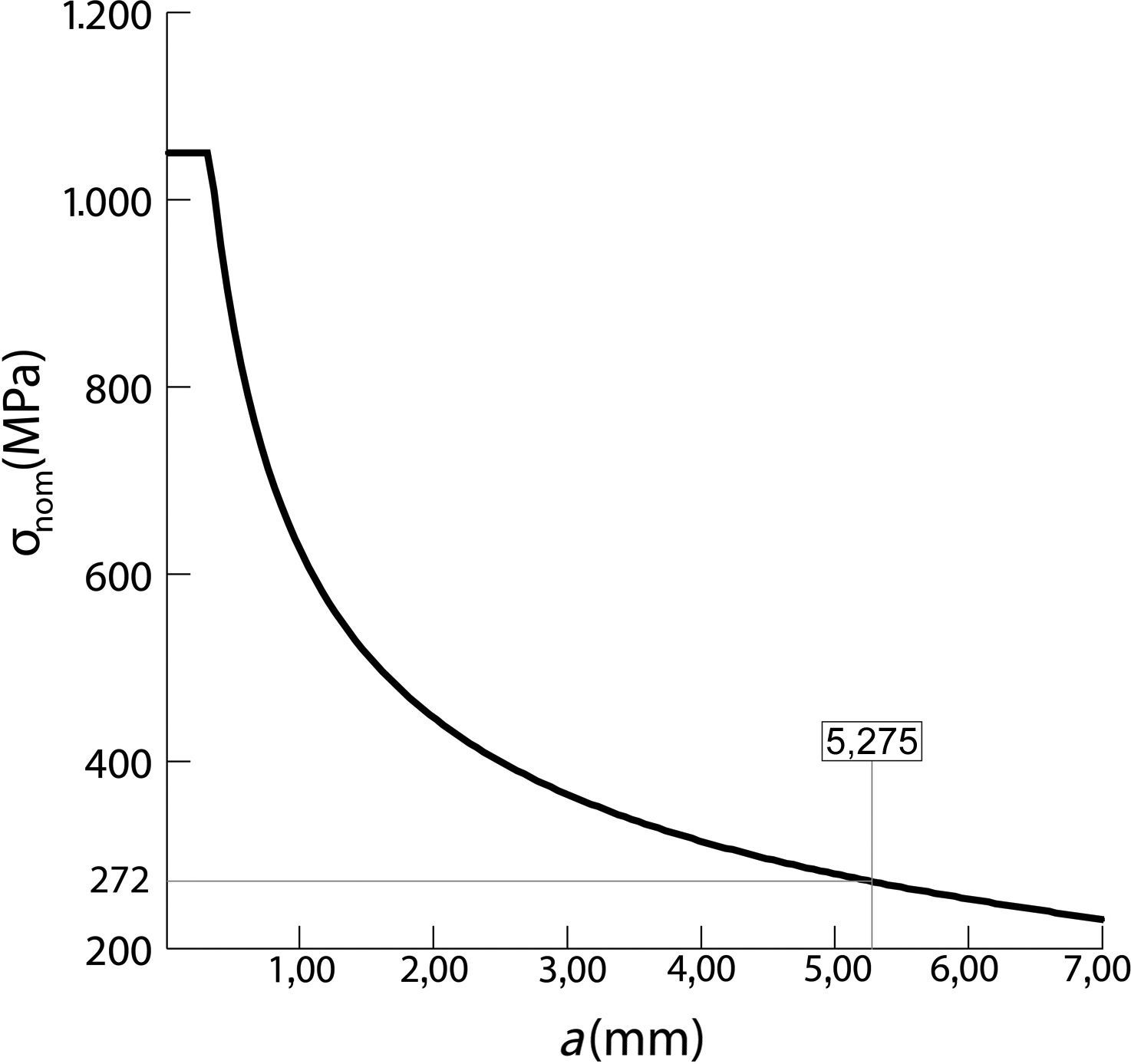
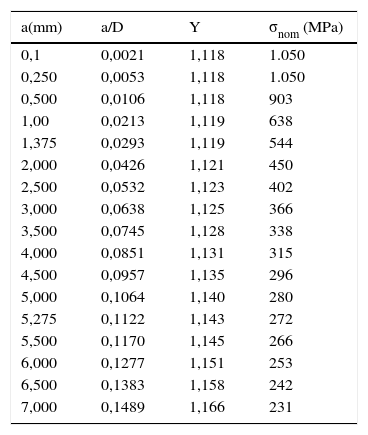
Particularizando la expresión (12) para un diámetro de barra de 47mm, y considerando una tenacidad a fractura convencional de valor Kic=40MPa m1/2 (el cual se ha confirmado con un ensayo específico), obtenemos los valores mostrados en la tabla 2 para la tensión nominal de rotura de la barra en función de la profundidad del defecto a y del factor Y determinado según la expresión (14).
Tensión nominal de rotura de la barra en función de la profundidad del defecto «a»
| a(mm) | a/D | Y | σnom (MPa) |
|---|---|---|---|
| 0,1 | 0,0021 | 1,118 | 1.050 |
| 0,250 | 0,0053 | 1,118 | 1.050 |
| 0,500 | 0,0106 | 1,118 | 903 |
| 1,00 | 0,0213 | 1,119 | 638 |
| 1,375 | 0,0293 | 1,119 | 544 |
| 2,000 | 0,0426 | 1,121 | 450 |
| 2,500 | 0,0532 | 1,123 | 402 |
| 3,000 | 0,0638 | 1,125 | 366 |
| 3,500 | 0,0745 | 1,128 | 338 |
| 4,000 | 0,0851 | 1,131 | 315 |
| 4,500 | 0,0957 | 1,135 | 296 |
| 5,000 | 0,1064 | 1,140 | 280 |
| 5,275 | 0,1122 | 1,143 | 272 |
| 5,500 | 0,1170 | 1,145 | 266 |
| 6,000 | 0,1277 | 1,151 | 253 |
| 6,500 | 0,1383 | 1,158 | 242 |
| 7,000 | 0,1489 | 1,166 | 231 |
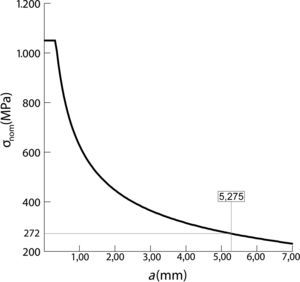
Como puede observarse en la figura 11, para la máxima carga esperada en una barra (tensión nominal de 272MPa), el tamaño máximo de grieta que se puede propagar previo a la rotura frágil de la barra es superior a 5mm. Es este un valor muy alto, indicativo de la alta fiabilidad existente frente a este tipo de fallo. Basta darse cuenta que el reflejo de una entalla así en la superficie de una barra presentaría una longitud de 31mm, y que, de acuerdo al documento NASA STD 5009 [10], se establece como factible la detección de indicaciones de 0,64mm de profundidad mediante líquidos penetrantes y de 0,97mm utilizando partículas magnéticas.
4.4Protocolo para inspección, mantenimiento y sustitución periódica de barrasUna vez establecida la vital influencia que en la estabilidad del carro de izado tienen las barras del apoyo trasero, y analizado el bajo riesgo de rotura frágil —debido precisamente a las bajas tensiones de trabajo—, se procedió a definir un protocolo para la inspección, mantenimiento y sustitución periódica de las citadas barras, con el fin de asegurar en el tiempo su estabilidad, dado el alto número de operaciones asociadas a cada carro. A continuación se resume dicho protocolo, que fue seguido estrictamente durante todo el desarrollo de la obra:
- •
Se implantó un sistema físico de protección de las barras de los anclajes traseros frente a golpes fortuitos, proyecciones, calentamientos, etc.
- •
Dentro del sistema de calidad, se estableció un reconocimiento visual de las barras combinado con una inspección mediante partículas magnéticas o líquidos penetrantes, con el fin de detectar cualquier grieta o daño mecánico superficial, no aceptándose ningún tipo de defecto independientemente de su tamaño.
- •
Todas y cada una de las barras fueron instrumentadas con el fin de conocer su estado tensional en todo momento, ya sea con bandas extensométricas o con células de carga.
- •
Anteriormente a cada ciclo de izado se realizó una prueba de carga de las barras consistente en un tesado de las mismas al 70% de su límite elástico. De este modo, cualquier defecto o grieta debería propagarse en la prueba produciendo la rotura durante el ensayo.
- •
Se previó una sustitución periódica de las barras, con una regularidad acorde a la duración del proceso constructivo, eliminando así del escenario la posibilidad de propagación no detectada y consiguiente rotura frágil.





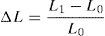
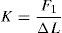
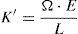
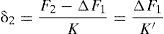
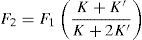
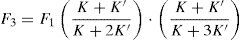
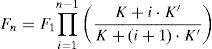
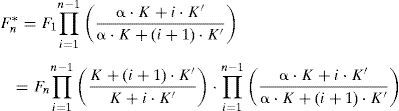
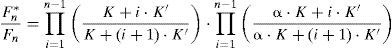
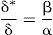

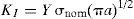
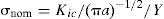
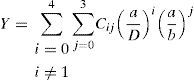
![Grieta hipotética con forma semielíptica en plano perpendicular al eje de la barra [9]. Grieta hipotética con forma semielíptica en plano perpendicular al eje de la barra [9].](https://static.elsevier.es/multimedia/04395689/0000006700278279/v4_201610150126/S0439568916000218/v4_201610150126/es/main.assets/thumbnail/gr10.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)