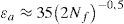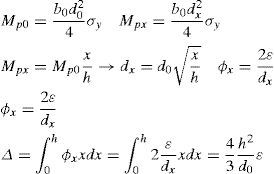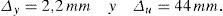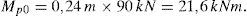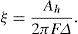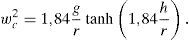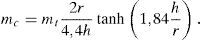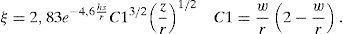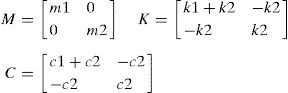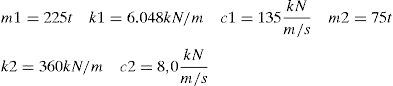El esquema propuesto para el depósito, basado en una curva de histéresis tipo «flag», y por consiguiente autocentrante, nos permite acotar con claridad el cortante y por lo tanto el momento máximo que la acción sísmica impone en la torre y su cimentación. Una clara optimización es pues posible con respecto a un esquema convencional. Los disipadores metálicos con geometría «hourglass» nos incrementan el amortiguamiento disponible, y serán los únicos elementos a sustituir tras un sismo significativo.
The structural system considered for the tank is based on a ‘flag’ hysteresis curve, and as a result is self-centering, allowing us to clearly limit the shear and also the bending moment that due to seismic action we have on the tower and its foundations. A clear optimization is so possible in relation to a more typical structural design. Steel dissipators with ‘hourglass’ geometry provide additional damping and would be the only elements to be changed after a significant quake.
FCC está actualmente ejecutando un nuevo hangar en el aeropuerto Juan Santamaría de Costa Rica. Dentro de estas obras se ha de realizar un depósito de agua potable de 35,0m de altura y 250m3 de capacidad.
En la ubicación de la obra la aceleración de diseño es de 0,375g. La acción sísmica es dominante y el depósito debe permanecer completamente operativo tras el sismo de diseño.
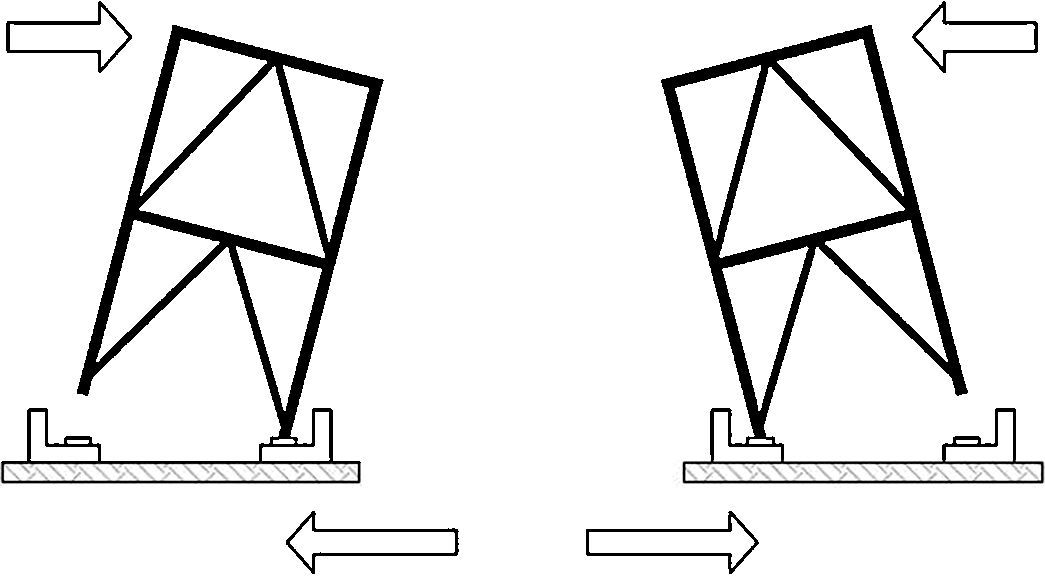
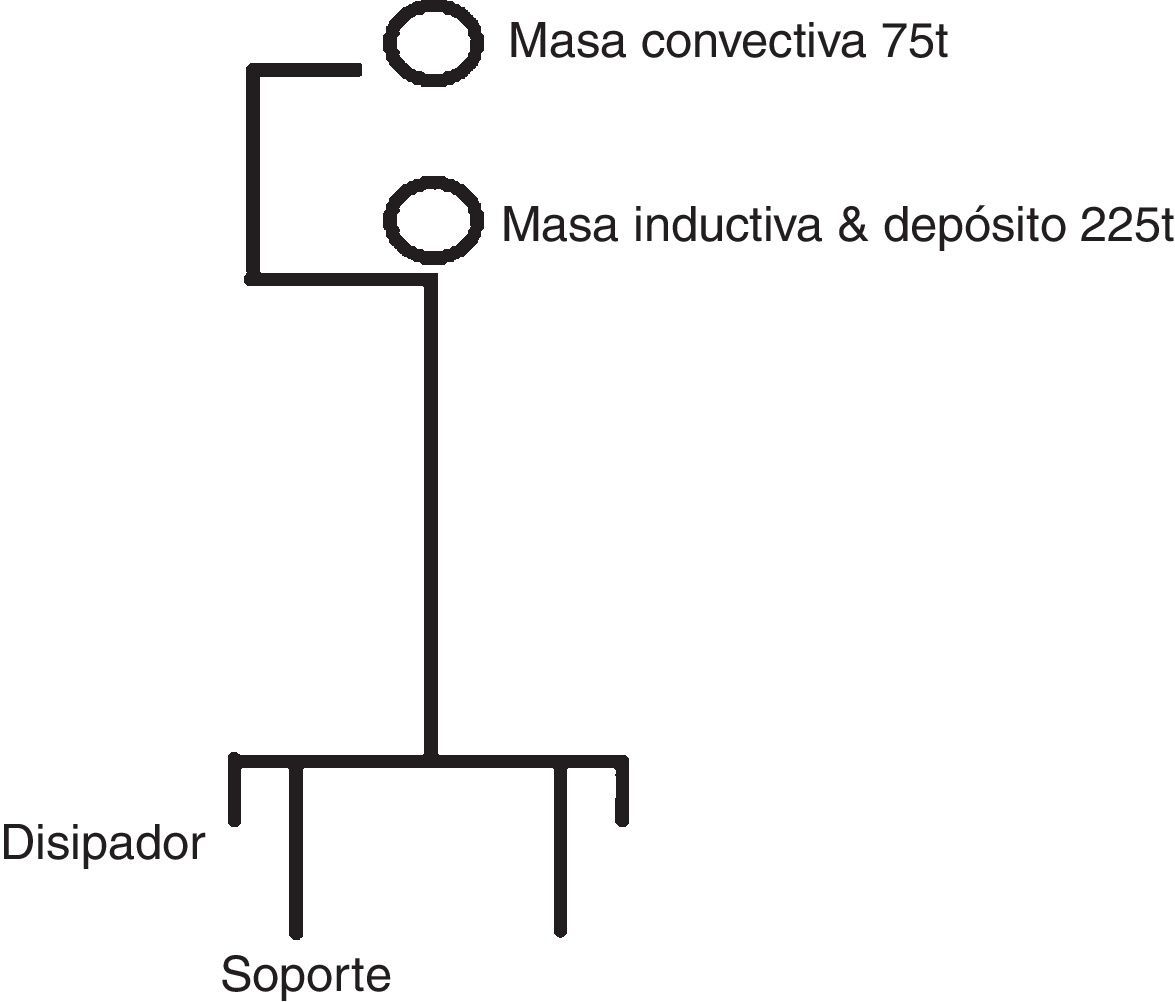
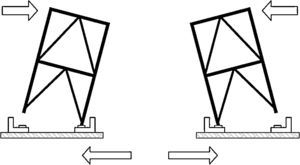
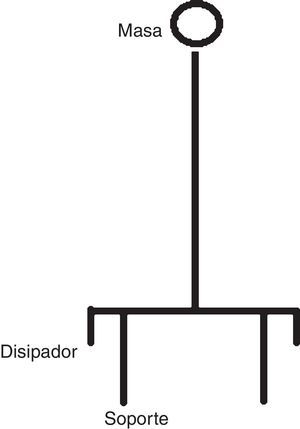
En el diseño sísmico de este tanque se ha buscado controlar la respuesta mediante el propio esquema estructural, para lo cual se ha recurrido a lo que podemos denominar un sistema de balanceo autocentrante como filosofía del diseño estructural del tanque (fig. 1).
En este artículo se explicará este concepto, su fundamento y aplicaciones, así como los instrumentos de cálculo que han permitido primero diseñar y luego analizar la respuesta sísmica del depósito en el que se ha implementado.
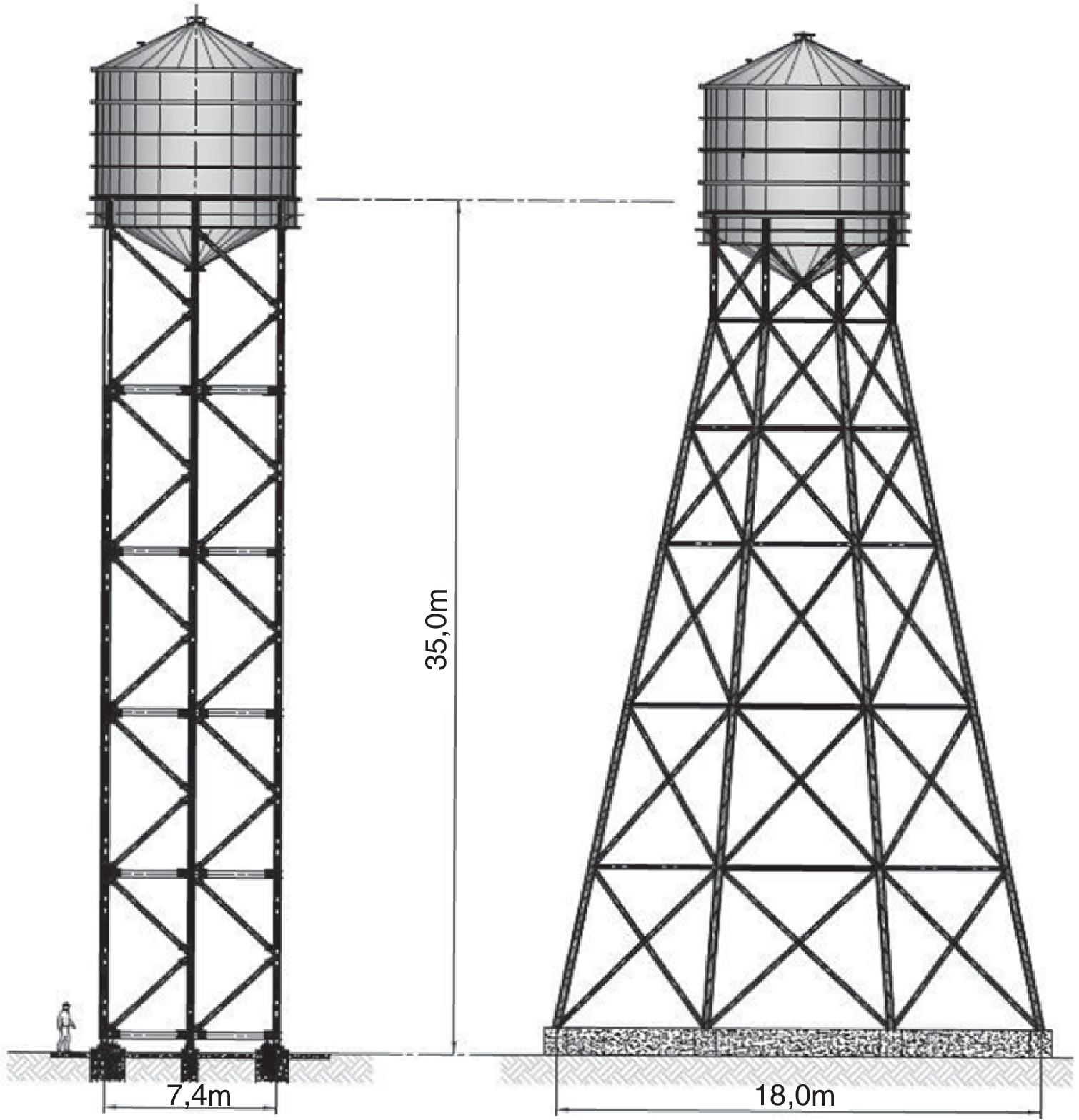
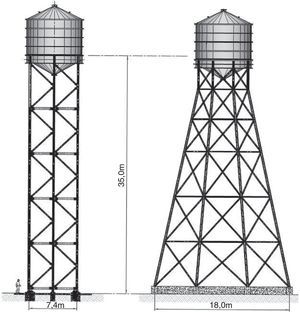
En el diseño previo, la torre de sustentación del depósito constaba de 8 pilares divergentes hacia la base con objeto de hacer frente al momento inducido por la acción sísmica actuando sobre el depósito; el diámetro a nivel de cimentación era de 18,0m. En la solución propuesta la torre consta de 6 pilares verticales dispuestos en un diámetro de 7,4m (fig. 2).
Aun con una «geometría regular» y unos detalles de «ductilidad local adecuada», utilizando nomenclatura del código sísmico de Costa Rica CSCR2010, una estructura en «péndulo invertido» no admite más de una ductilidad global de 1,50, y para el cálculo de las cimentaciones no debe emplearse ductilidad alguna y considerar una sobrerresistencia de 1,20.
Es evidente que aun la supuesta ductilidad de 1,50 requiere de la plastificación alternativa de las diagonales, y no se puede garantizar que tras la acción sísmica la torre permanezca vertical, pudiendo quedar desplomes remanentes, que condicionarían la funcionalidad del depósito.
Considerando, en primera aproximación y con objeto de centrar ideas, el depósito como un sistema de un grado de libertad, con una masa de 300t a 35,0m, se obtiene un periodo propio inferior a 1,00s con la solución previa, y del orden de 1,40s con la solución propuesta.
El cortante horizontal resultante con la solución previa está por encima de los 1.100kN, mientras que con la solución propuesta se demostrará que queda acotado a 350kN.
La diferencia es sin duda sustancial, tanto para las cimentaciones como para el cálculo de la propia torre. Además, con la solución propuesta no se producen deformaciones remanentes: la torre queda vertical tras el evento sísmico. Puede asimismo realizarse un cálculo elástico de todas las uniones tipo, que no requieren de ductilidad, lo cual siempre complica su diseño si debe lograrse de un modo efectivo.
Todas estas son las razones que nos han llevado a este diseño. En contra se tiene la necesidad de emplear métodos no convencionales de cálculo, pues el sistema planteado no puede analizarse por métodos basados en el uso típico de espectros de respuesta recogidos en la normativa de Costa Rica o en el propio Eurocódigo.
2Sistema autocentrante2.1Objetivos del sistema autocentranteLa filosofía actual de diseño frente a la acción sísmica implica que la mayoría de las estructuras se diseñan para responder en régimen anelástico frente al sismo de diseño. Es económicamente inviable un análisis puramente elástico, por lo que se aceptan mecanismos de respuesta dúctil que limitan los esfuerzos en el sistema estructural con respecto a los que implicaría un diseño elástico lineal. Es cierto también que cada vez es más habitual la consideración no solo de sismos de diseño sino también de sismos de servicio, en los que se controlan/limitan las deformaciones, que es un modo de acotar los daños en elementos no estructurales. En definitiva, cada vez es más frecuente, sobre todo en estructuras esenciales, el plantearse la situación de la estructura tras el evento sísmico. No son raros los casos de estructuras que sobreviven a la acción del sismo, pero que finalmente deben derruirse por ser su coste de puesta en operación superior al de una nueva estructura, y en otros casos el coste de puesta en operación es sumamente elevado.
Por consiguiente, se plantean, para determinados edificios, estructuras que han de ser completamente operativas tras el evento sísmico, para lo cual la limitación de las deformaciones remanentes pasa a ser un importante factor de diseño.
En un sistema elástico lineal, la respuesta medida a través del cortante es más elevada que la de un sistema dúctil, pero en cambio la deformación remanente es esencialmente nula, mientras que en el sistema dúctil no lo es. Sin fuerza, el sistema no queda con deformación nula.
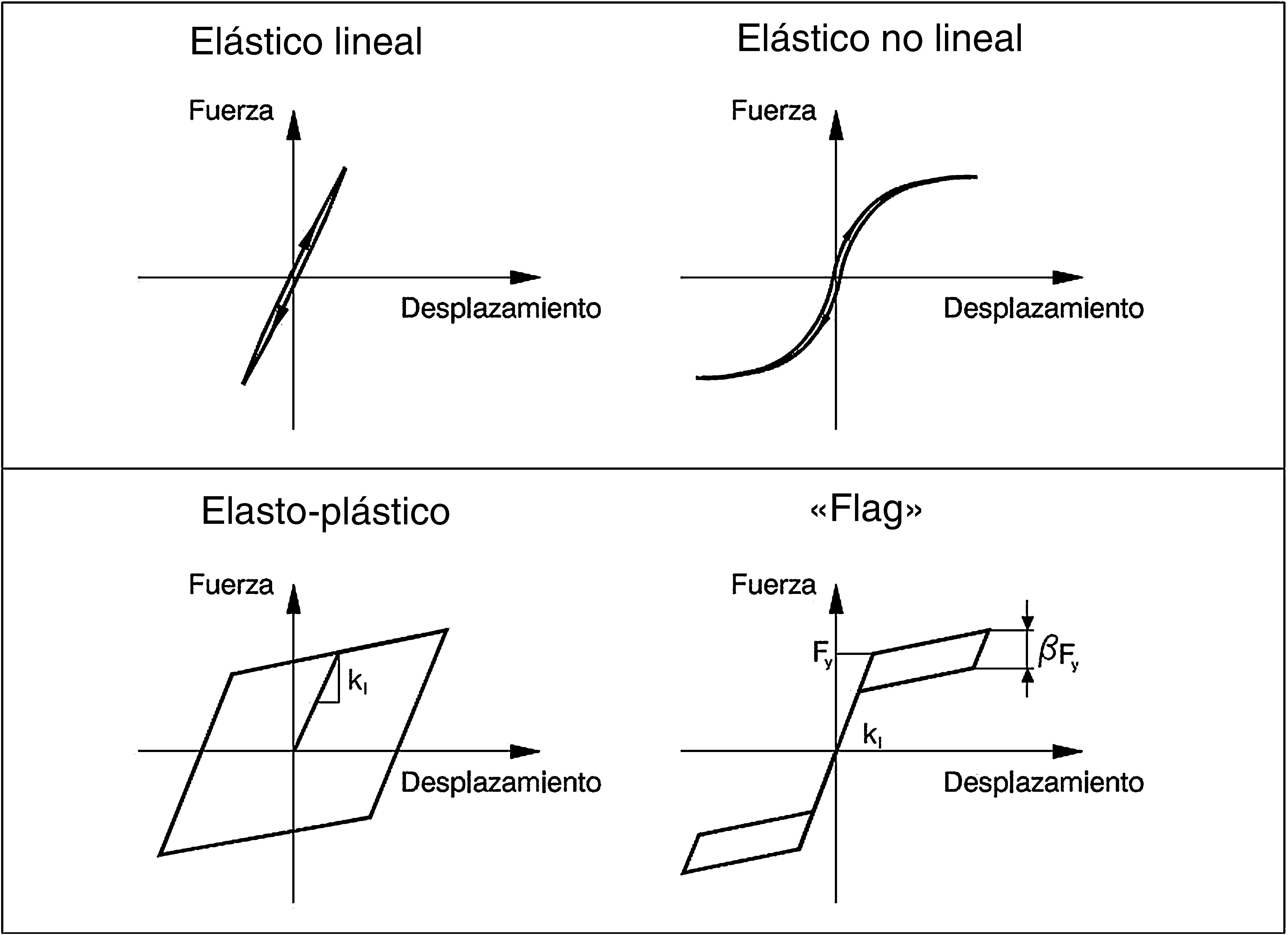
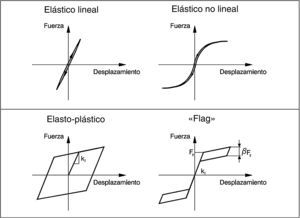
En un sistema dúctil, se valora esencialmente la capacidad de absorber energía en cada ciclo de deformación, lo que podemos cuantificar mediante el área de la curva de histéresis: cuanto mayor sea esta área, mejor. En un sistema elástico, lineal o no, esta área es evidentemente nula (fig. 3).
Lo mencionado parece indicar que no es viable conseguir las tres cosas al mismo tiempo: acotar la fuerza por debajo de la que implica un comportamiento elástico lineal, tener deformación remanente nula, e incluso conservar cierta capacidad de disipación por ciclo. La respuesta está en un diagrama tipo «flag».
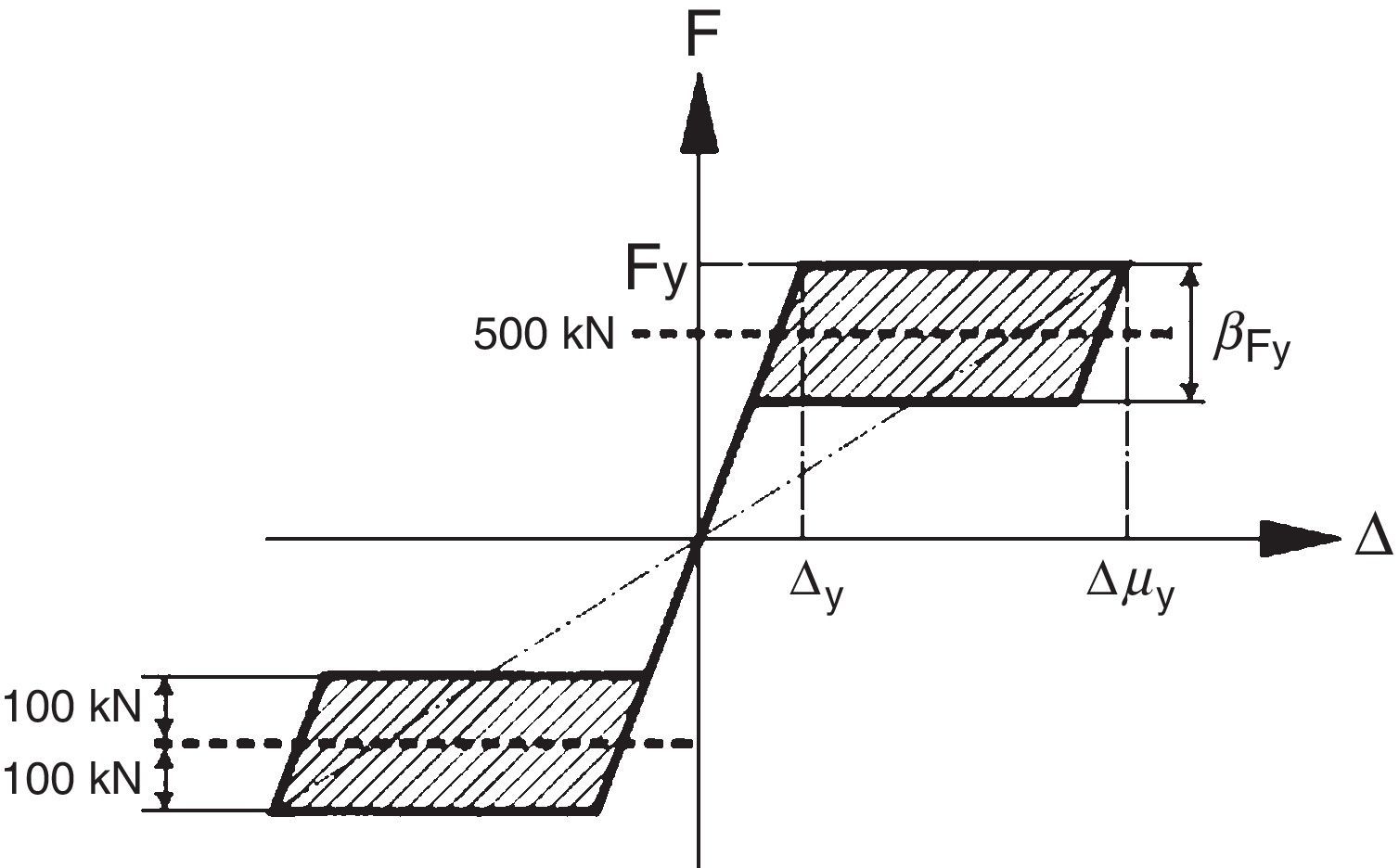
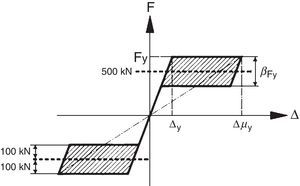
2.2Diagrama fuerza-desplazamiento tipo «flag» (bandera)El diagrama fuerza-desplazamiento es sin duda muy útil para caracterizar la respuesta de una estructura o un elemento estructural.
Un sistema con autocentrado se caracteriza por un diagrama fuerza-desplazamiento tipo bandera.
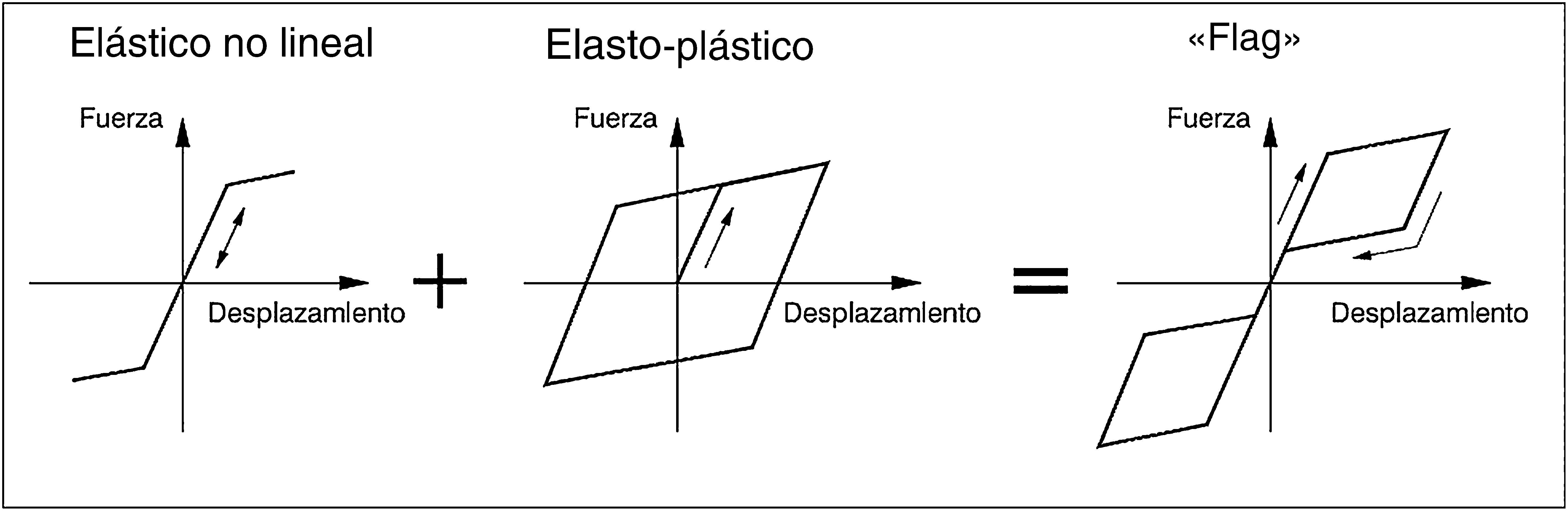
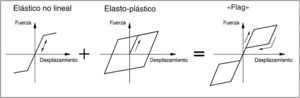
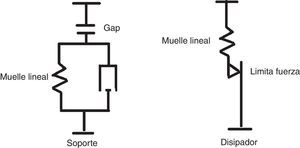
Un diagrama de este tipo siempre puede obtenerse mediante la combinación de un diagrama elástico no lineal, y un diagrama elasto-plástico debido a un elemento de disipación (fig. 4).
En nuestro caso, el diagrama no lineal se logra mediante una combinación del peso propio del depósito y el no anclaje de los pilares a la cimentación.
Cuando tiene lugar el sismo, la estructura responde de un modo elástico pero no lineal: inicialmente, mientras que la tracción inducida por el momento en la base de la torre no supere en ninguno de los soportes la compresión debida al peso propio de la estructura y del contenido, la estructura responde en régimen lineal, pero llegado el punto en que la resultante en un soporte se anula, este soporte se levanta de la losa de cimentación, pues no están anclados, y se pierde drásticamente rigidez. Cuando se levantan todos los soportes salvo uno, la rigidez incluso se hace negativa por efecto P-delta.
En otros casos, en vez del peso propio o complementando al mismo, se utiliza un pretensado, con el mismo efecto.
El mecanismo anteriormente expuesto sería completamente elástico, aunque no lineal, careciendo por consiguiente de capacidad de disipación. Para dotar al conjunto de la estructura de una capacidad de disipación que permita controlar el nivel de los desplazamientos máximos, se dispone en correspondencia con cada soporte de la torre de un disipador metálico. Este disipador proporciona el diagrama elasto-plástico complementario que buscamos.
Este disipador tipo «hourglass» proporciona, además de absorción de energía en cada ciclo, un muelle adicional complementario en cada soporte, lo que permite controlar la otra hipótesis dimensionante: depósito vacío y viento máximo.
Ante el sismo de diseño, el único daño se concentra en los disipadores de energía. El resto de la estructura de la torre permanece completamente elástica y por tanto sin ningún daño, como en cambio implicaría hacer uso de la ductilidad de la propia estructura. La accesibilidad de los disipadores y su tamaño permitirán su sencilla sustitución.
En resumen, la componente no lineal y el recentrado se consiguen con el balanceo y el peso propio, y la componente de disipación mediante disipadores metálicos tipo «hourglass».
Una solución completamente análoga, que se utiliza con pantallas de hormigón prefabricadas, emplea un pretensado vertical centrado no adherente como fuerza de recentrado, y la disipación la proporcionan unas armaduras pasivas laterales.
2.3Aplicaciones del sistema autocentranteEn los últimos 20 años se han desarrollado analítica y experimentalmente varios sistemas basados en conceptos análogos, tanto en acero como en hormigón prefabricado, con variantes en los elementos de disipación y en el elemento que proporciona el recentrado. Se han efectuado ensayos a escala real y en algunos casos se han redactado guías de diseño. Asimismo, se han ejecutado, tanto en edificación como en obra civil, estructuras pioneras que han respondido con fiabilidad ante sismos reales de gran intensidad.
Desde un punto de vista histórico, como señala Priestley [1], varios depósitos elevados aparentemente poco estables apenas sufrieron daños durante el sismo de Chile de 1960, mientras que otros más sólidos quedaron seriamente dañados. Asimismo, durante los terremotos de California de 1952, las torres de las industrias petroquímicas evitaron daños significativos cuando tras deformar los pernos de anclaje a la cimentación se levantaron y balancearon sobre la misma.
Ya en aplicaciones más modernas, cabe mencionar la chimenea de Christchurch (1983) de 36m de altura y las pilas del puente de ferrocarril de Rangitikei (1981) de 70m de altura (fig. 5), ambas en Nueva Zelanda.
Para facilitar la implementación de soluciones prefabricadas de hormigón en zona sísmica, se desarrolló el programa Precast Seismic Structural Systems (PRESSS) [2] entre Estados Unidos y Japón. Se desarrollaron y ensayaron extensamente en la década de los noventa soluciones que utilizan el diagrama tipo «flag» que caracteriza los sistemas de recentrado. En todas las soluciones se permite la separación entre componentes mediante un movimiento de rotación.
Esto se puede conseguir mediante diferentes configuraciones, vigas rotando con relación a los pilares, pilares o pantallas girando con respecto a la cimentación. Se produce una apertura y un cierre de la junta, mientras los elementos propiamente dichos permanecen elásticos. Estos «rocking systems» con la ayuda de elementos de pretensado no adherente tienden a su posición inicial en cada ciclo; son pues sistemas autocentrantes.
Se han elaborado guías de diseño de soluciones postesadas de hormigón, como la Seismic Design Guidelines for Special Hybrid Precast Concrete Shear Walls (2012) [5].
Tanto en la Universidad de Illinois a escala 1:2 como en las gigantescas instalaciones del E-defense a escala 1:1 se han ensayado pórticos arriostrados metálicos, con resultados completamente acordes con los análisis teóricos (fig. 6).
Una aplicación muy reciente, también en Nueva Zelanda, es la estructura metálica del Campus Universitario de Te Puny Village, que se completó antes del sismo de 6,5 de julio de 2013, al que respondió perfectamente (fig. 7).
3Prediseño de la soluciónA continuación vamos a describir sucintamente el proceso seguido para el prediseño de la torre propuesta.
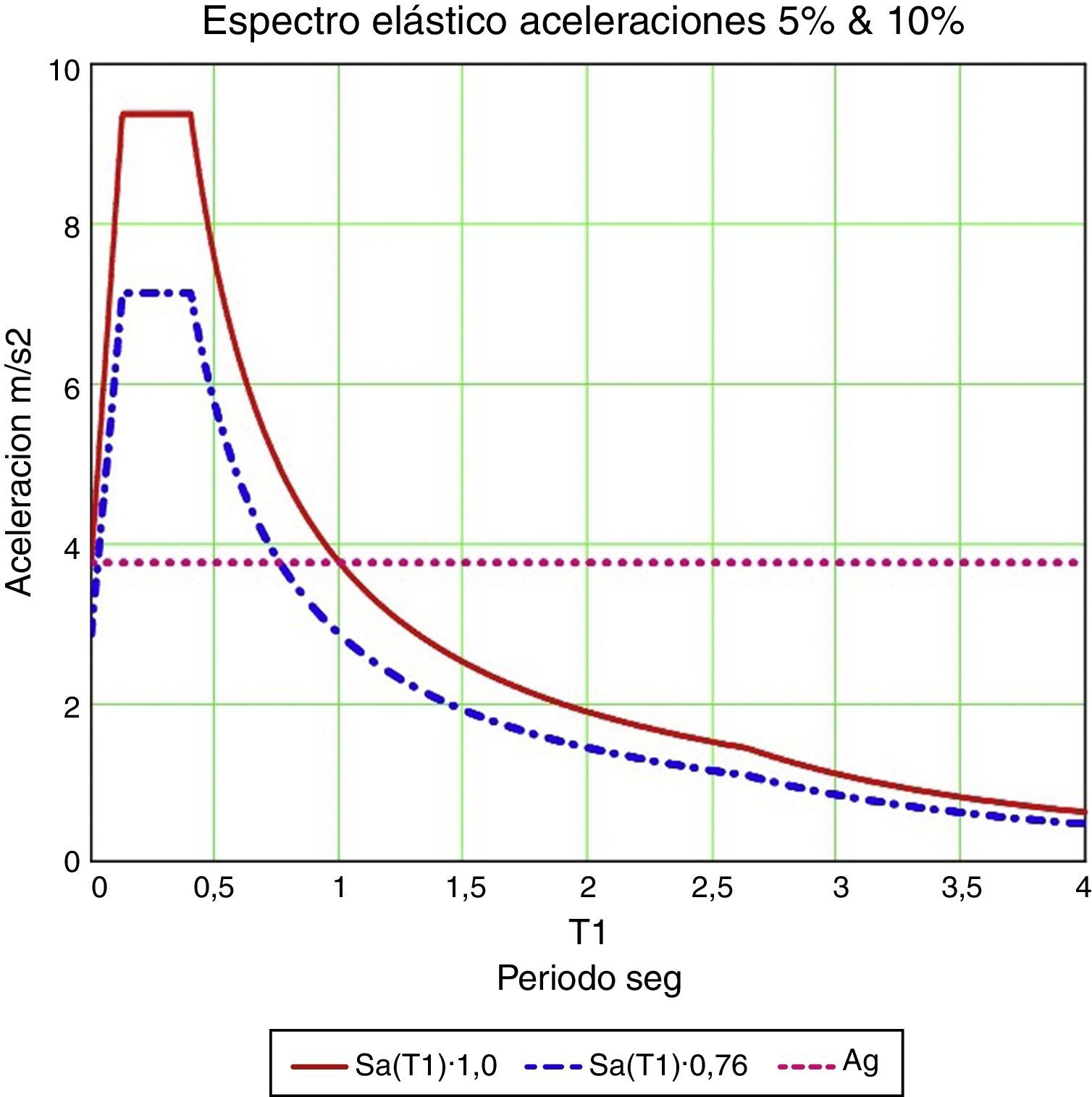
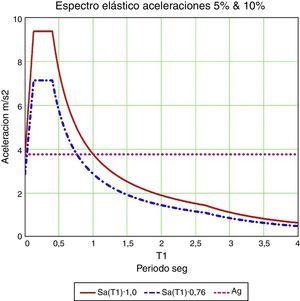
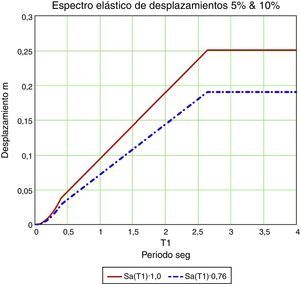
3.1Diagrama demanda-capacidadEl CSCR 2010 define la acción sísmica a considerar, como es habitual, a través del espectro elástico de aceleraciones asociado a una estructura con un amortiguamiento del 5%. También el Eurocódigo define la acción sísmica mediante el espectro de aceleraciones y hace asimismo referencia al espectro de desplazamientos, aunque es sin duda una norma basada en fuerzas y no en desplazamientos, en contra de la realidad física.
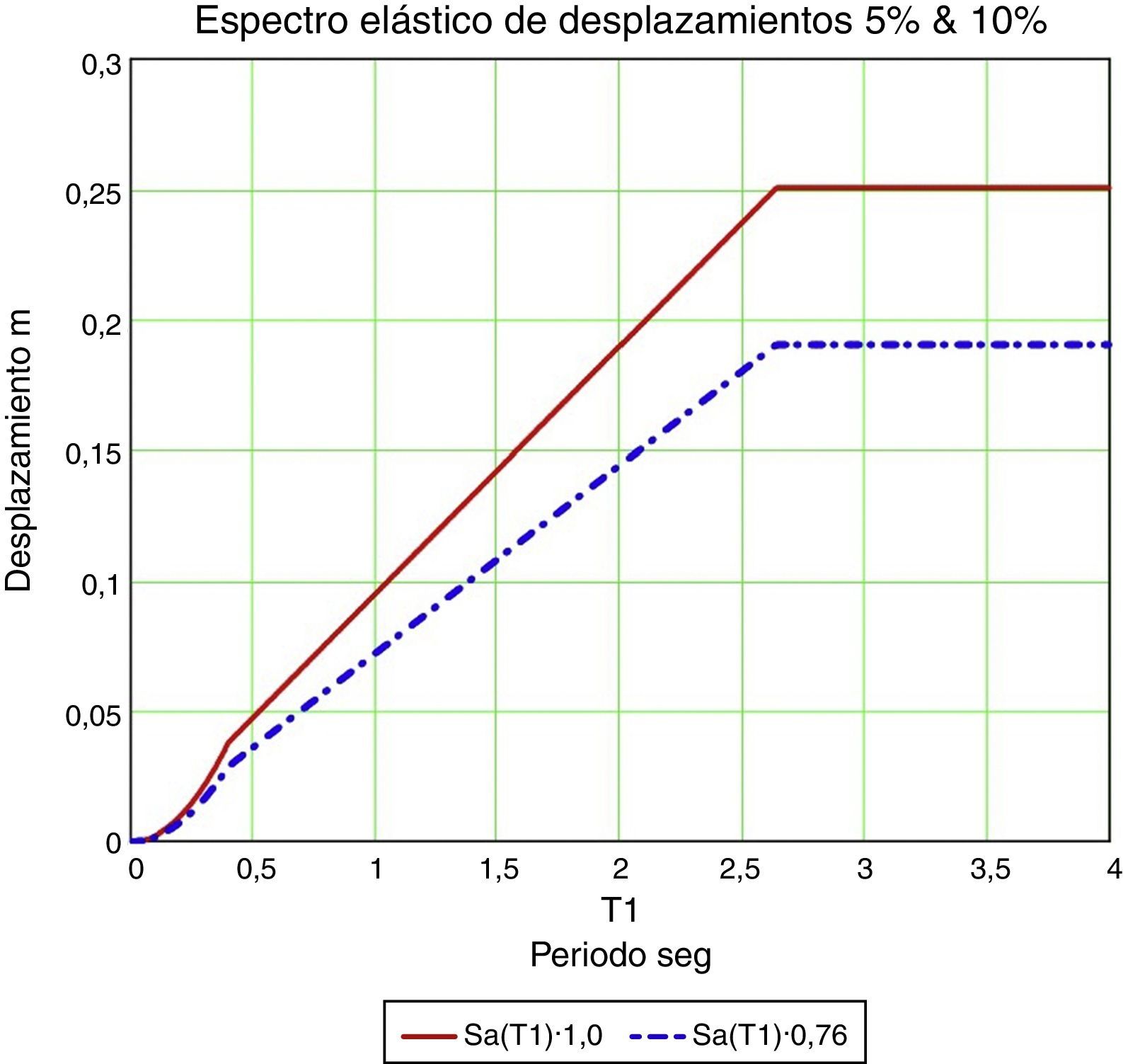
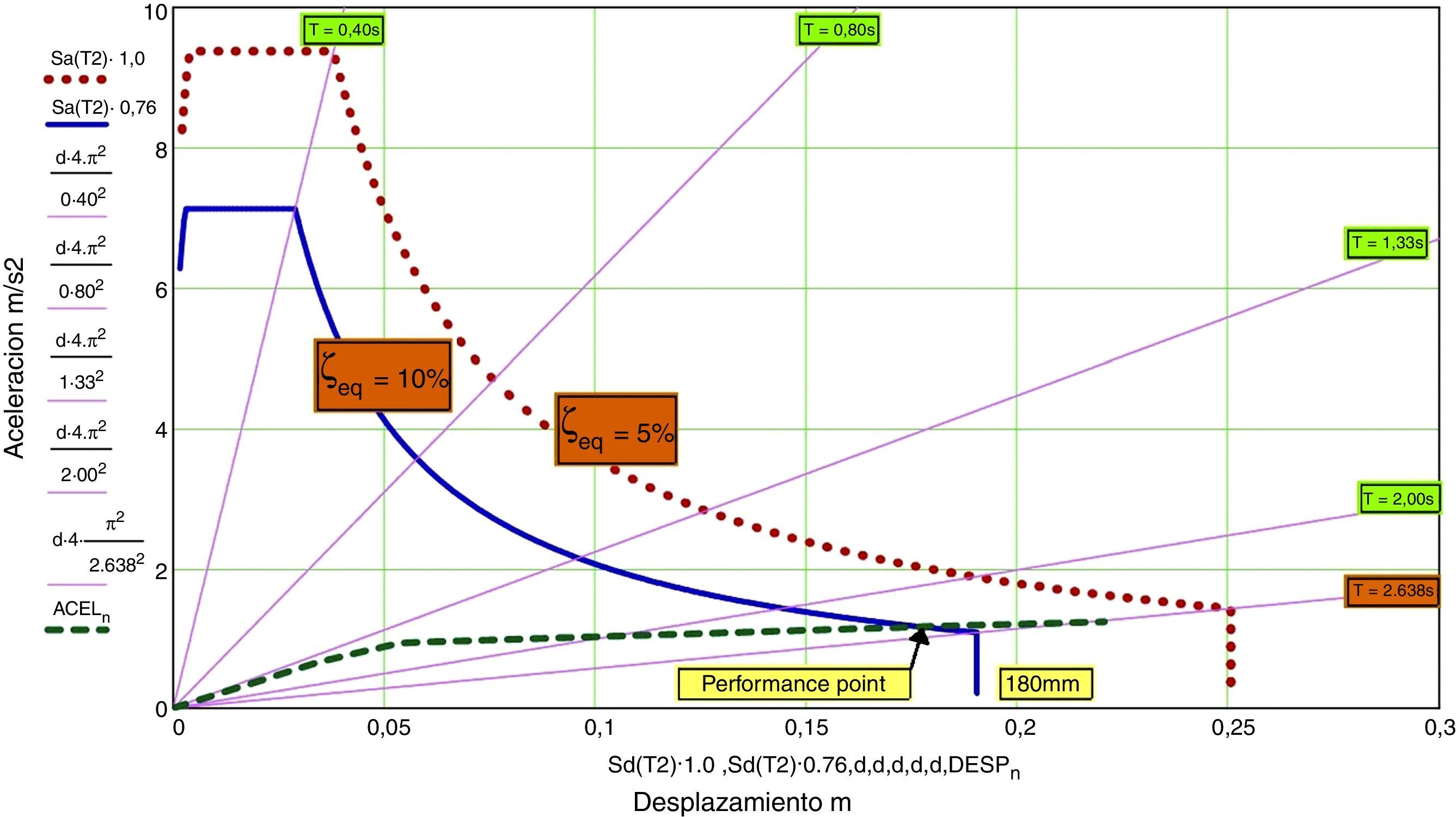
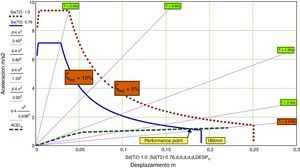
Las figuras 8 y 9 relacionan periodo con aceleración o desplazamiento. Un gráfico sumamente útil y que en cambio suele presentarse menos es el que relaciona aceleración y desplazamiento, que en nomenclatura americana sería el diagrama demanda-capacidad (fig. 10).
Este diagrama nos va a ser de gran utilidad pues permite combinarlo con el comportamiento de la estructura, descrito a través de su diagrama fuerza horizontal-desplazamiento (push-over) y es ampliamente utilizado en toda la metodología basada en análisis en desplazamientos. Es fácil interpretrar el diagrama fuerza-desplazamiento de un sistema de un grado de libertad como aceleración-desplazamiento, simplemente dividiendo por la masa (en sistemas de varios grados de libertad, la transformación es asimimo sencilla).
Por consiguiente, podremos disponer en un solo diagrama la demanda que impone el sismo y el comportamiento de la estructura. La intersección nos dará el punto de respuesta de la estructura.
Realmente habremos de actuar iterativamente, pues en el punto de respuesta, asociado a un desplazaniento (una ductilidad), la estructura en función de su tipo de curva de histéresis tendrá un amortiguamiento adicional determinado. La intersección habrá de ser con la curva de demanda asociada al amortiguamiento total disponible.
Las normas nos proporcionan formas de modificar el espectro de respuesta para amortiguamientos diferentes al 5%, y el amortiguamiento adicional de la estructura en función del desplazamiento y tipo de curva de histéresis también se puede estimar razonablemente, con formulaciones algo menos frecuentes.
Puede decirse que el prediseño de la solución se basa en este diagrama, y el resto de los cálculos son realmente verificaciones.
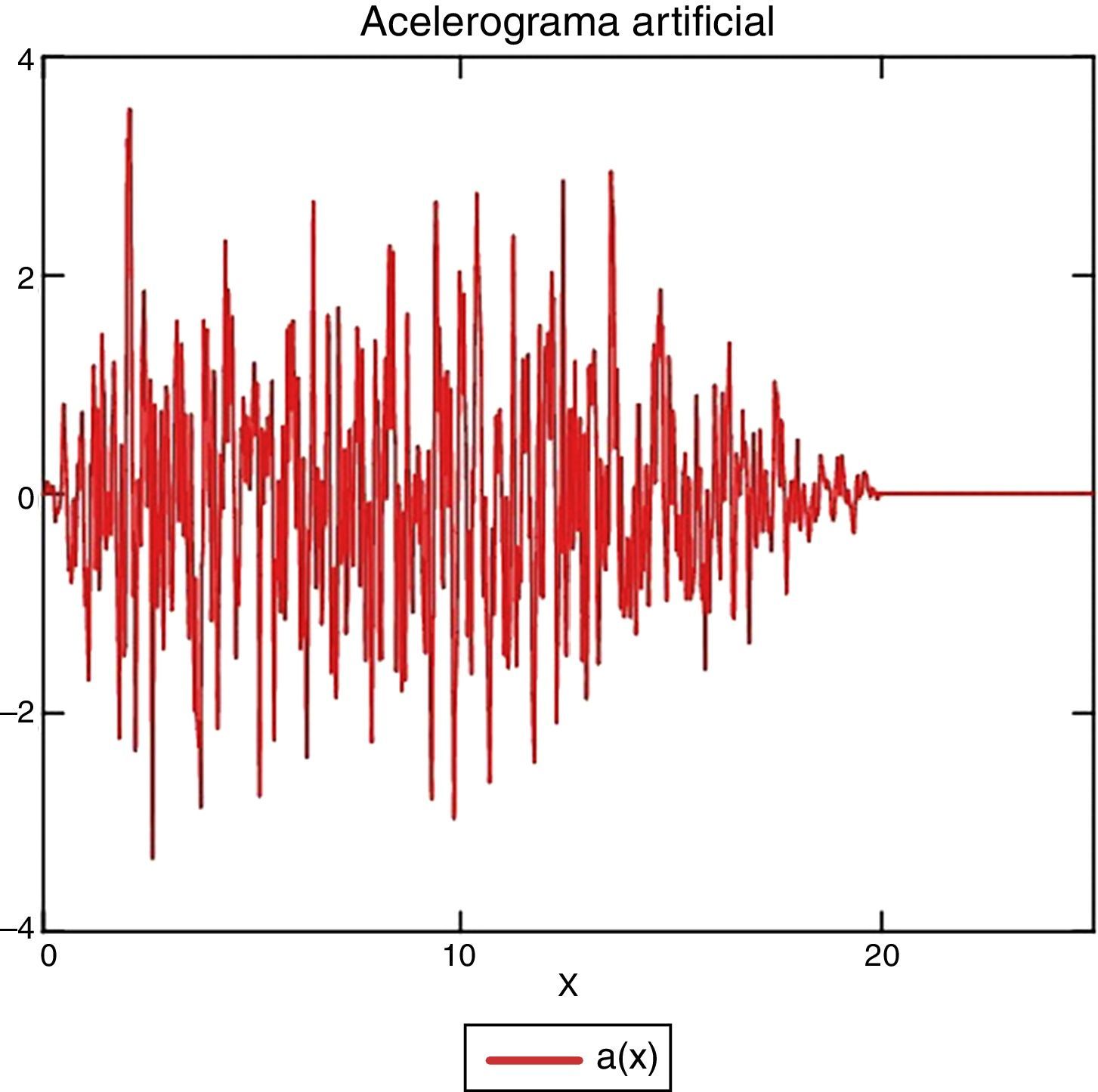
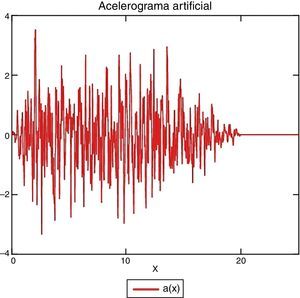
3.2Análisis en el dominio del tiempoPara verificar la idoneidad del diseño así planteado, efectuaremos un análisis con un acelerograma compatible con el espectro de diseño. Son numerosos los programas disponibles para la generación de estos acelerogramas artificiales, y hemos utilizado el SIMQKE del MIT (fig. 11).
En primer lugar, por sencillez, efectuamos un análisis sin elementos de disipación adicionales, por consiguiente lo que tenemos es, en lugar de un sistema elástico lineal de rigidez constante, un sistema elástico no lineal.
Lo estudiamos inicialmente con su ecuación diferencial resuelta con Mathcad, donde es muy sencillo introducir el muelle no lineal (tabla 1).
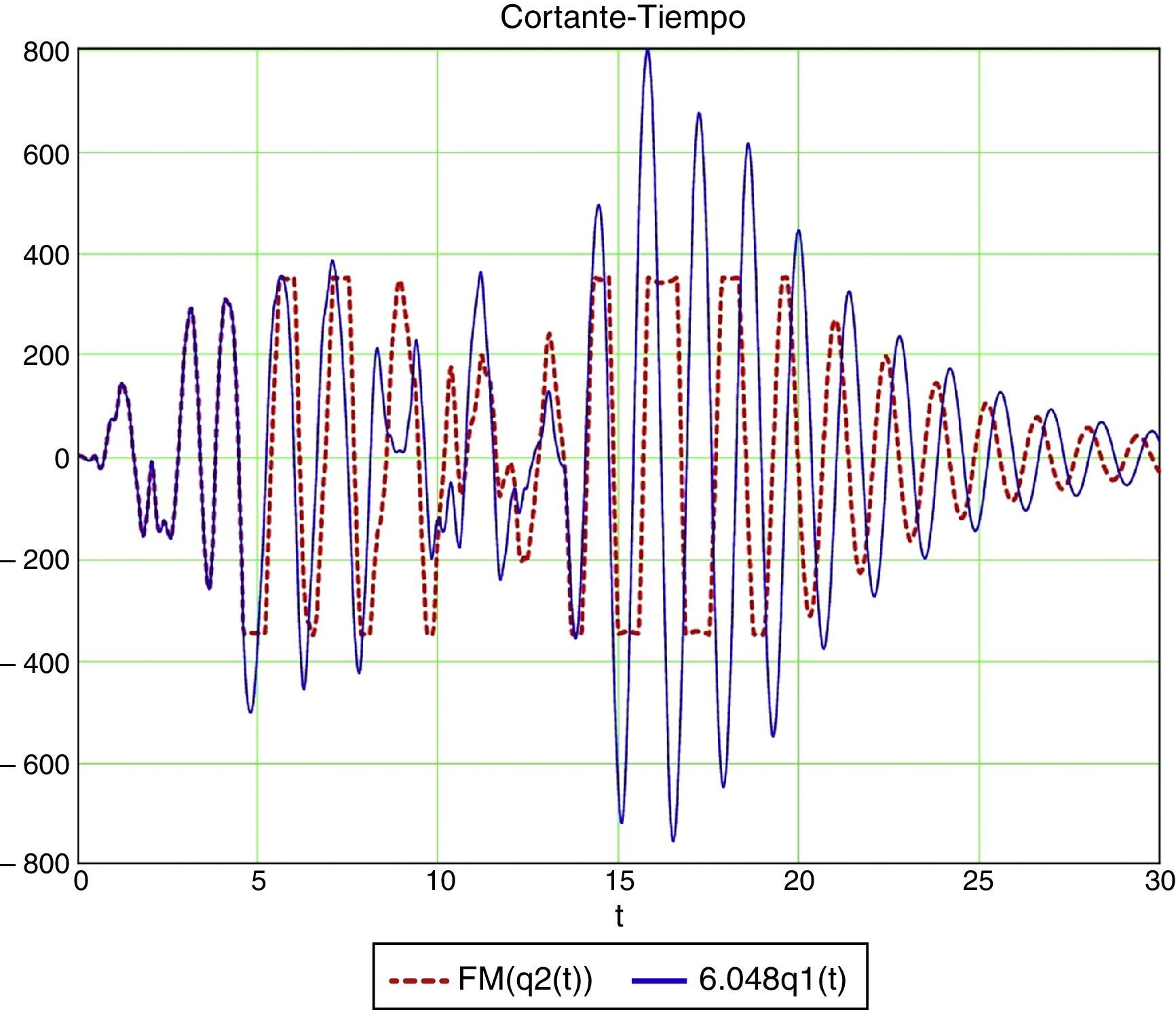
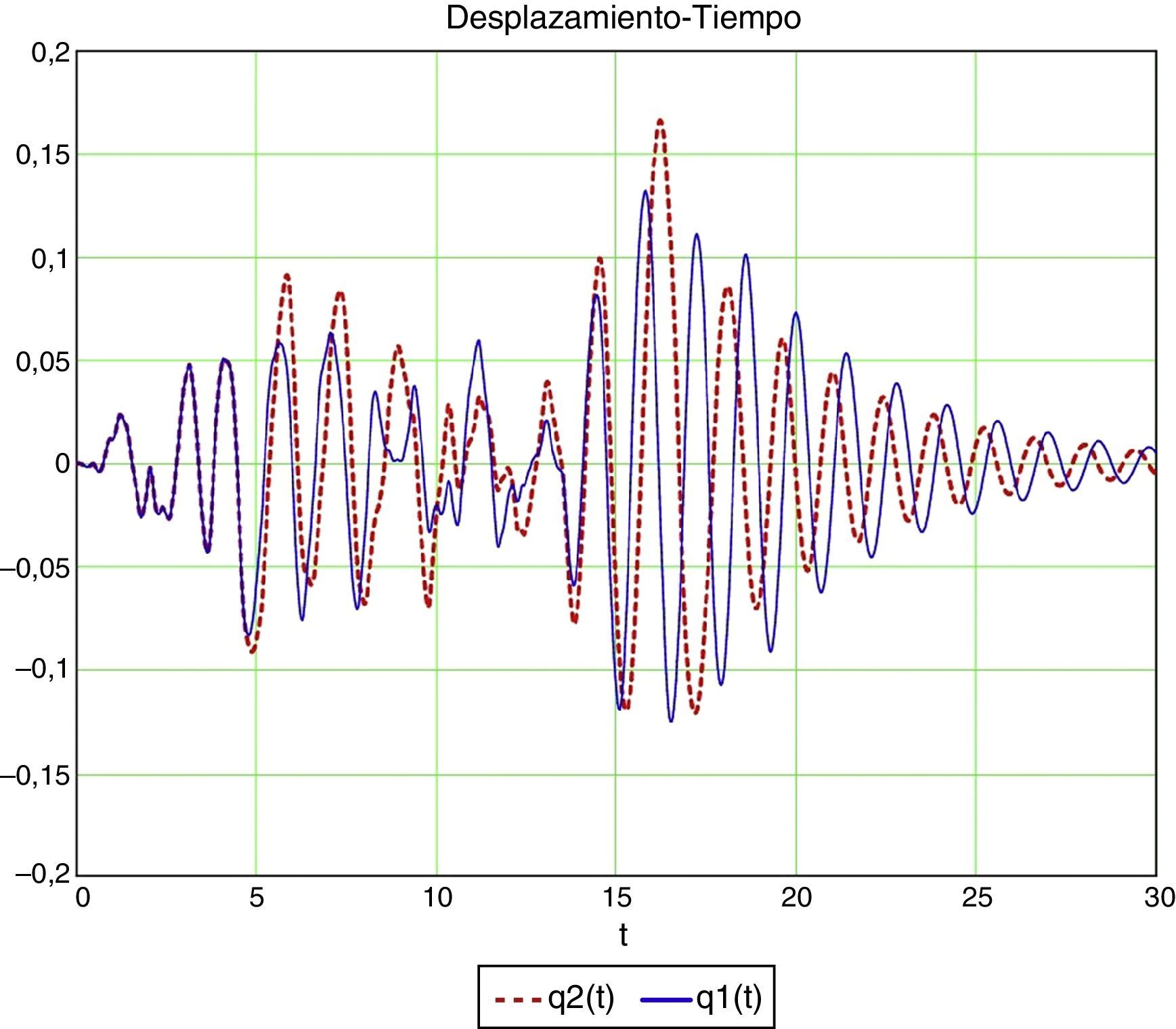
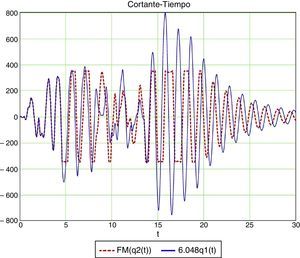
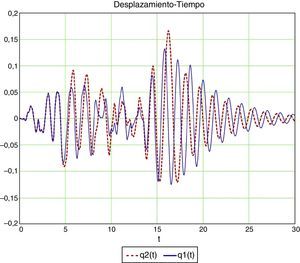
En las figuras 12 y 13 se muestra una comparativa en desplazamientos y en esfuerzos.
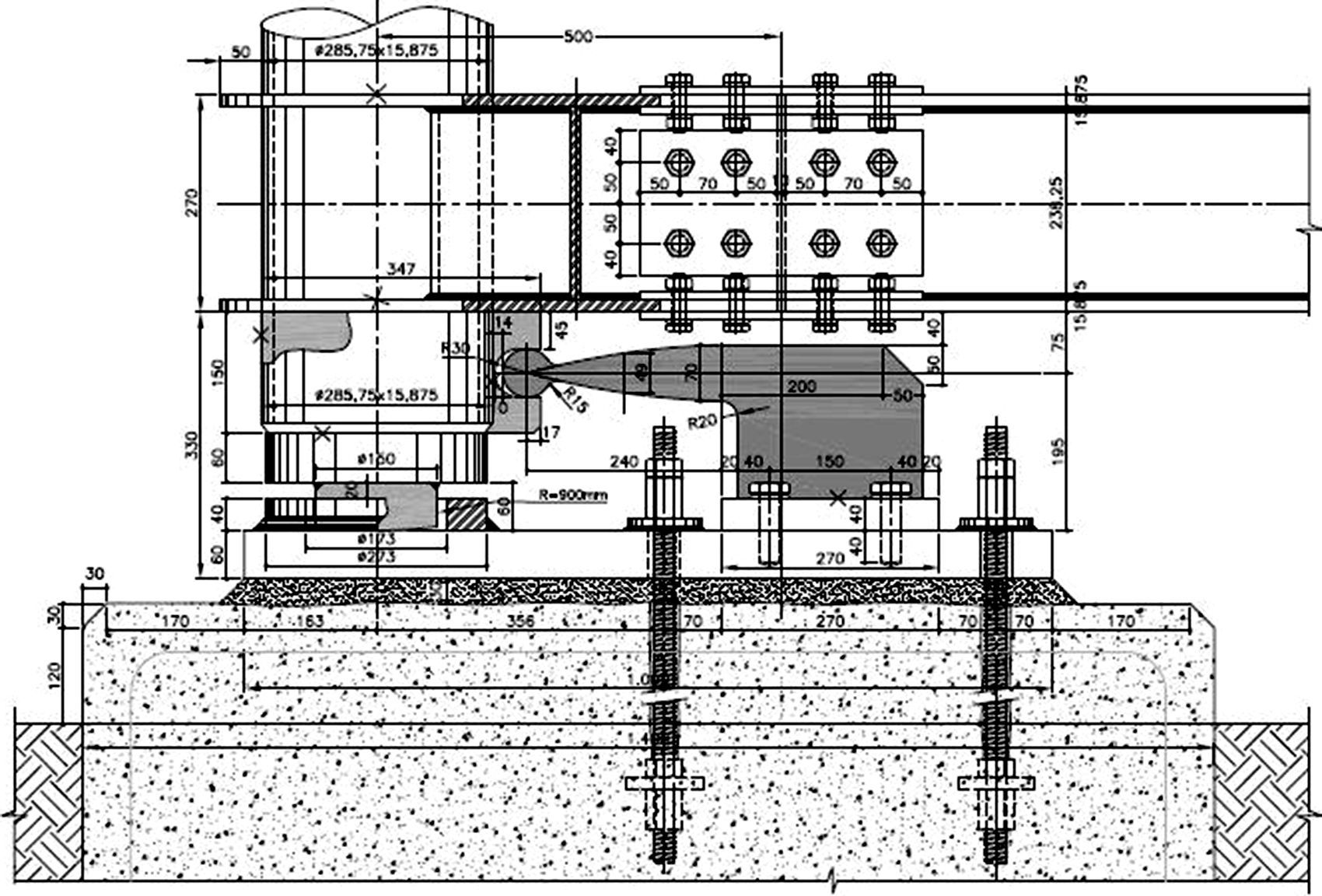
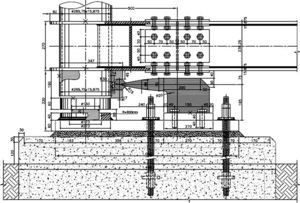
4Muelle/disipador «hourglass»Una vez que se ha determinado el desplazamiento horizontal necesario (aproximadamente 180mm), y por consiguiente lo que se ha de levantar el soporte con respecto a la cimentación (44mm), procedemos a diseñar el elemento complementario de disipación que se dispone en esta ubicación: entre soporte y cimentación (fig. 14).
4.1Geometría del disipadorEl disipador se ejecutará con acero estructural S355 K2, por lo que su deformación elástica será del orden de 0,2%; para establecer la deformación última admisible, hemos de tener en cuenta la fatiga de bajo número de ciclos.
La amplitud total de deformación podemos relacionarla con el número de ciclos en un acero estructural mediante la fórmula de Coffin-Manson con coeficientes 35 y –0,5 [4]:
Esto supone para una amplitud de deformación total εa=3, 5% 50 ciclos y para εa=7, 0% 12 ciclos.
Por consiguiente, adoptando una deformación del orden del 4%, es decir, 20 veces la deformación elástica, nos resiste unos 40 ciclos, suficiente para 2 sismos de 20s.
La geometría del disipador viene condicionada por buscar alcanzar la plastificación simultáneamente en las fibras extremas a lo largo de todo el dispositivo. Surge de este modo la geometría tipo «hourglass», donde el módulo resistente varía linealmente con la distancia.
Vemos que con h=0, 24m&d0=70mm obtenemos con εy=0, 002yεu=0, 04
La capacidad buscada para el disipador es 90kN, por lo que con h=0, 24m tenemos
Vemos que con b0=50mm S355K2 Mp=22, 0kNm.
Las características mecánicas de las chapas de las que se obtengan los disipadores se ensayarán, y se ajustará la geometría final en función de las mismas.
4.2Amortiguamiento adicional de los disipadoresPara el cálculo general lo que nos interesa determinar es el amortiguamiento adicional que nos proporcionan estos disipadores.
En primera aproximación (fig. 15):
Con un diagrama tipo «flag» tenemos Ah=2βFyμ−1Δy y se obtiene ξ=βμ−1πμ.
Estimando una ductilidad global del orden de μ=5, obtenemos, con β=0,33, un amortiguamiento de área del orden del 8%, que añadido al 5% supone un 13% de amortiguamiento total.
Sin embargo, el amortiguamiento así obtenido no es completamente correcto, y existen formulaciones que nos permiten obtener valores más ajustados.
Para β=0,33 ξ=0,05+0,186μ−1πμ (Priestley) [1] con lo que obtenemos aproximadamente ξ=10%, que es lo considerado en el diagrama demanda-capacidad.
5Análisis de la superficie líquidaNo se puede obviar la existencia de una superficie líquida. Lo habitual es descomponer la masa de agua en 2 partes: la masa impulsiva situada en la parte inferior del tanque, y que se mueve junto con las paredes del mismo, y la masa convectiva situada en la parte superior y que experimenta el fenómeno de superficie libre que conocemos como «sloshing».
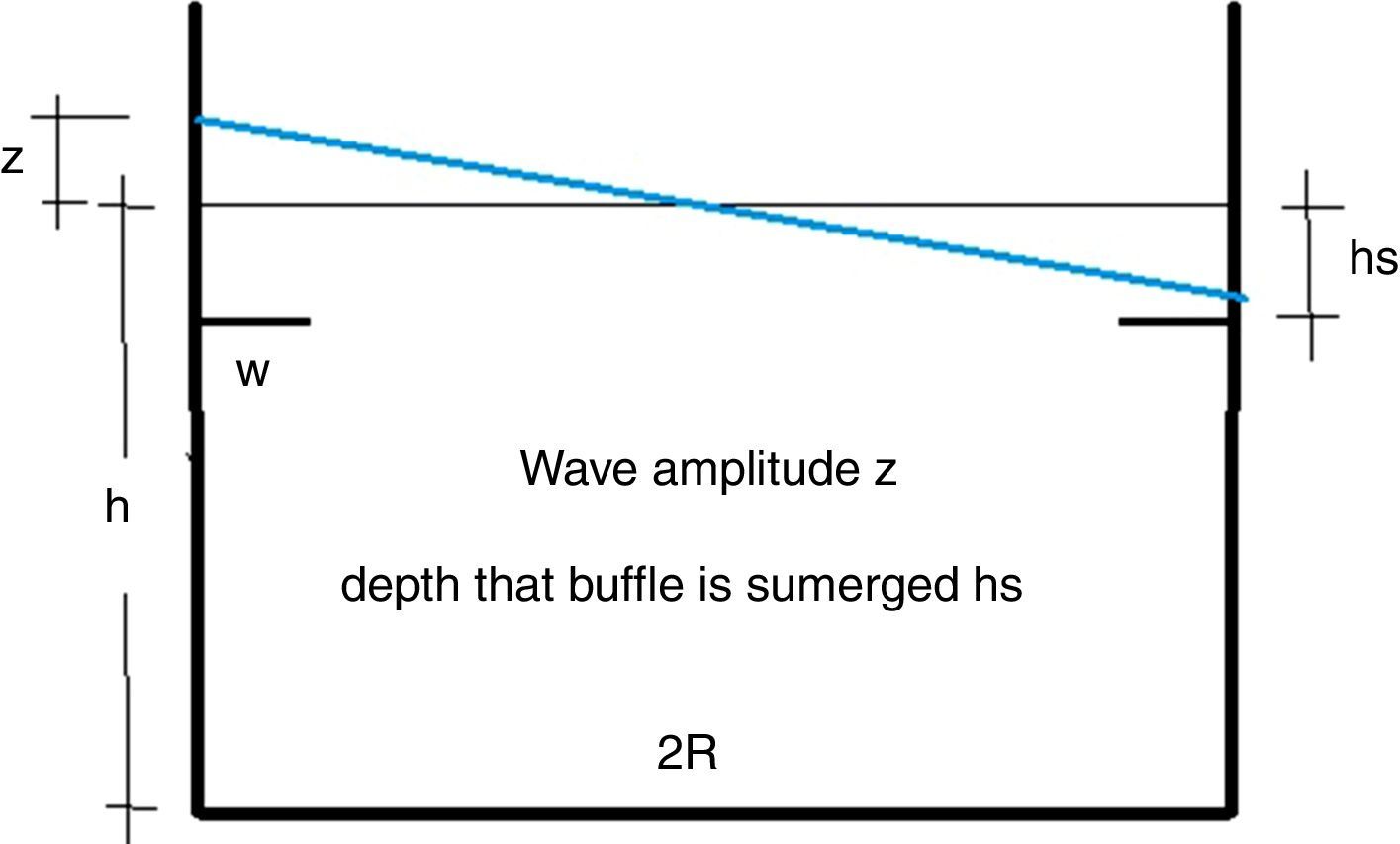
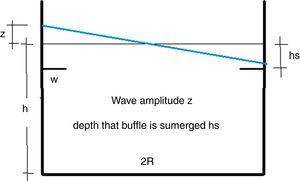
La masa impulsiva experimenta aceleraciones elevadas y por consiguiente es determinante para el cortante y momento en la base del depósito, mientras que la masa convectiva experimenta aceleraciones mucho más reducidas, por lo que contribuye poco al cortante. Sin embargo, la masa convectiva requiere de espacio, espacio de resguardo, para acomodar los desplazamientos verticales que el «sloshing» supone. Es conveniente disponer de altura de resguardo suficiente con objeto de impedir que la ola del «sloshing» impacte con el techo del depósito durante el evento sísmico (fig. 16).
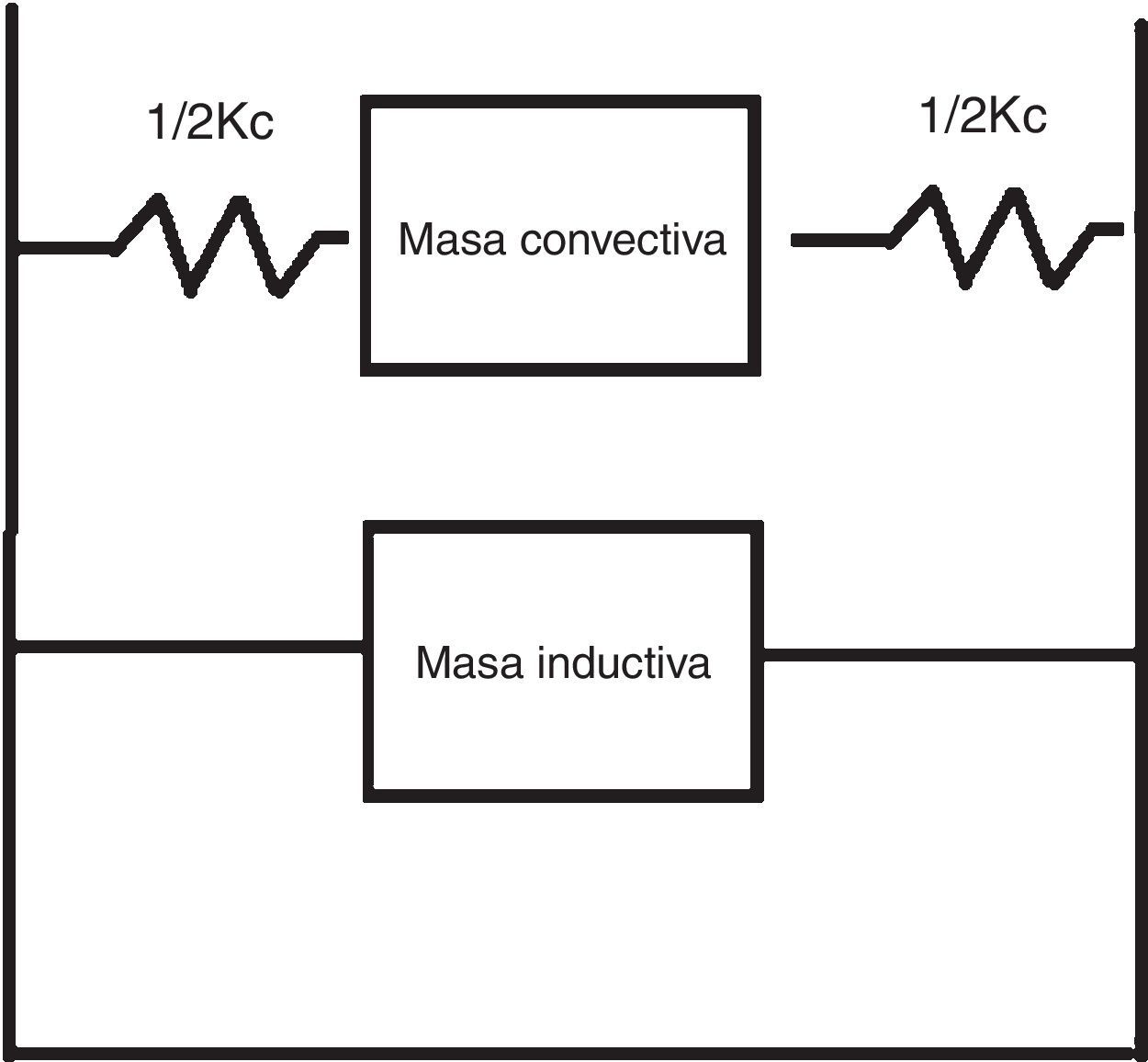
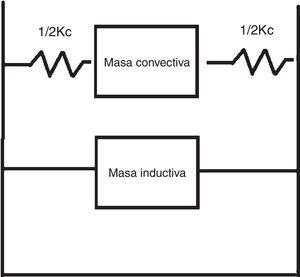
Como es habitual, la consideración de estas 2 masas la trataremos mediante un modelo mecánico con 2 grados de libertad.
5.1Masa convectivaSi bien en depósitos elevados y a efectos del cortante o momento está del lado de la seguridad considerar toda la masa como inductiva, esto no sucede en el caso de depósitos apoyados en el suelo, donde sí se requiere el análisis de la masa convectiva para determinar el resguardo necesario en el depósito.
La determinación de la masa convectiva y de su frecuencia la hacemos con las formulaciones habituales (primer modo):
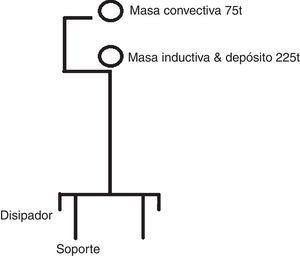
Con h/r=0,36m obtenemos mc=0, 31mt≈75t, y wc=2,20rads→Tc=2,85seg & Kc=360kN/m.
El amortiguamiento asociado al «sloshing» en una superficie lisa es muy bajo, en torno al 0,5%, o incluso inferior, por lo que el espectro de respuesta adecuado para la masa convectiva no es el asociado a un amortiguamiento del 5%, como empleamos en la estructura, sino más bien al 0,5%. El espectro de aceleraciones es del orden de un 67% superior.
Para pasar de espectro de 5% a espectro del 0,5% hemos utilizado la relación «antigua» del EN η=7/2+ξ0,5 que se ajusta mejor que la nueva.
Veamos, con datos de nuestro depósito, la influencia en el resguardo que el porcentaje de amortiguamiento supone.
Utilizando el espectro obtenemos con ξ=5% una aceleración de 0, 121g, lo que supone una inclinación de la superficie libre de 0,121 y, por consiguiente, una altura de ola debida al «sloshing» de δ=0, 121r=0, 44m, y con ξ=0, 5% obtenemos una inclinación de la superficie libre de 0,202 y, por consiguiente, una altura de ola de 0,75m.
5.2Incremento del amortiguamientoLa idea es incrementar el amortiguamiento de la masa convectiva, con objeto de reducir la dimensión del resguardo necesario. En distintas aplicaciones se han utilizado distintos dispositivos con este fin, pero sin duda el más eficaz es la disposición de rigidizadores anulares en la pared interior del tanque (fig. 17).
El amortiguamiento que se obtiene viene dado por la siguiente formulación [3]:
Lo primero que se observa es que el amortiguamiento depende de la propia altura de ola: z/r de modo no lineal.
Si adoptamos un rigidizador de 0,22m cada 0,3m, tendremos: wr=0,06→C1=0,116 y hsr=0,081.
Obtenemos un amortiguamiento relativo de: ξ=0,077zr1/2, el 3% para una altura de ola de 0,6m.
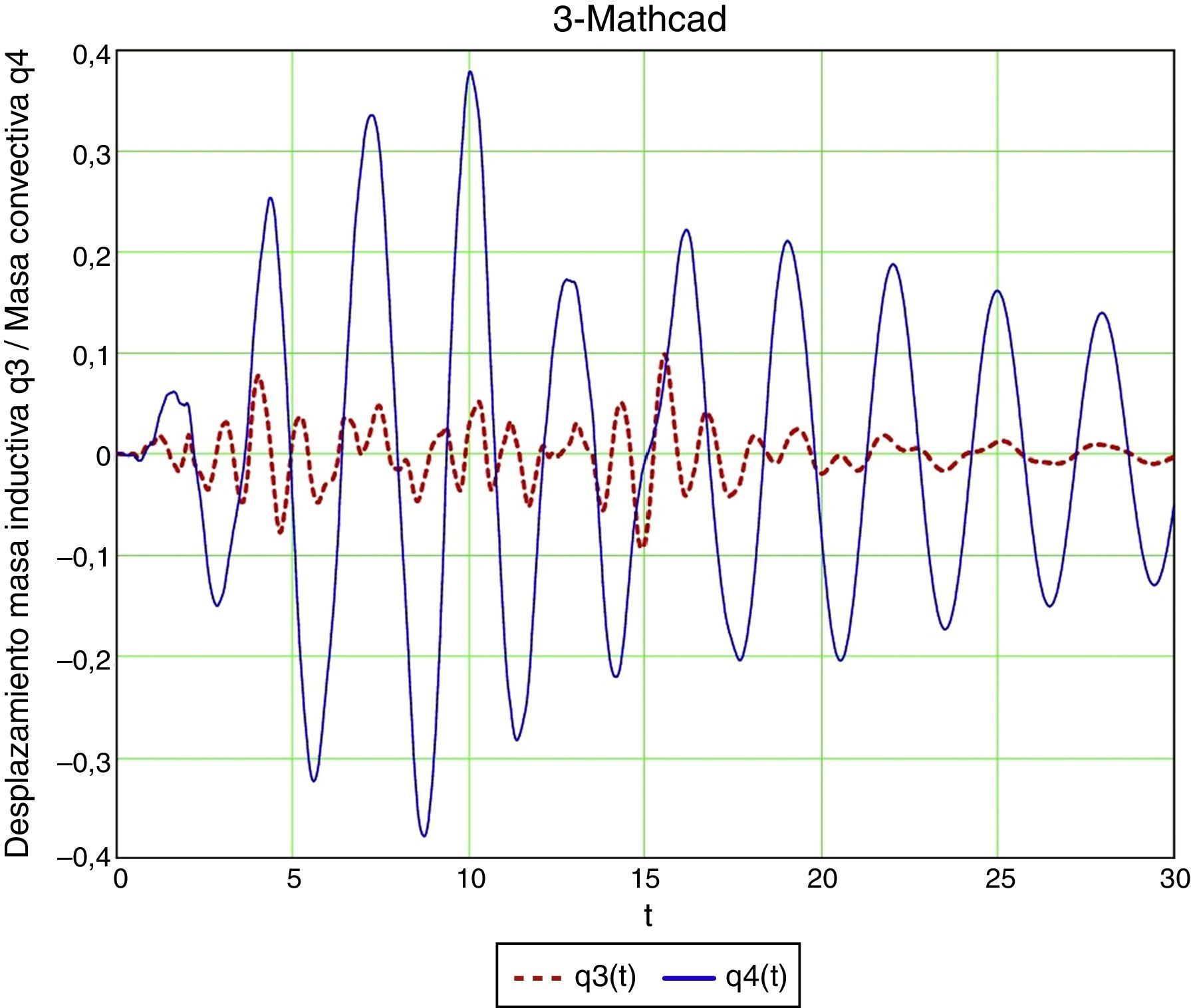
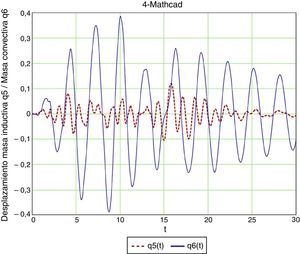
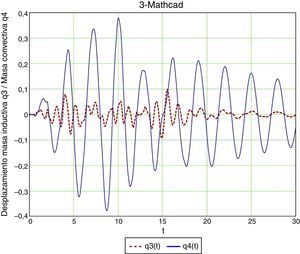
5.3Análisis en el dominio del tiempo mediante MathcadConsideremos ahora un sistema de dos grados de libertad, al que aplicaremos el acelerograma artificial y que resolvemos de nuevo con Mathcad (figs. 18 y 19).
Los resultados del modelo de dos grados de libertad con amortiguamientos del 5% y del 2,5% indican un desplazamiento horizontal de la masa convectiva del orden de 0,375m (tabla 2). El ángulo de inclinación de la superficie libre lo obtenemos dividiendo por IV=14775=1,96m, y obtenemos 0,191, con lo que la altura de ola es de 0,70m.
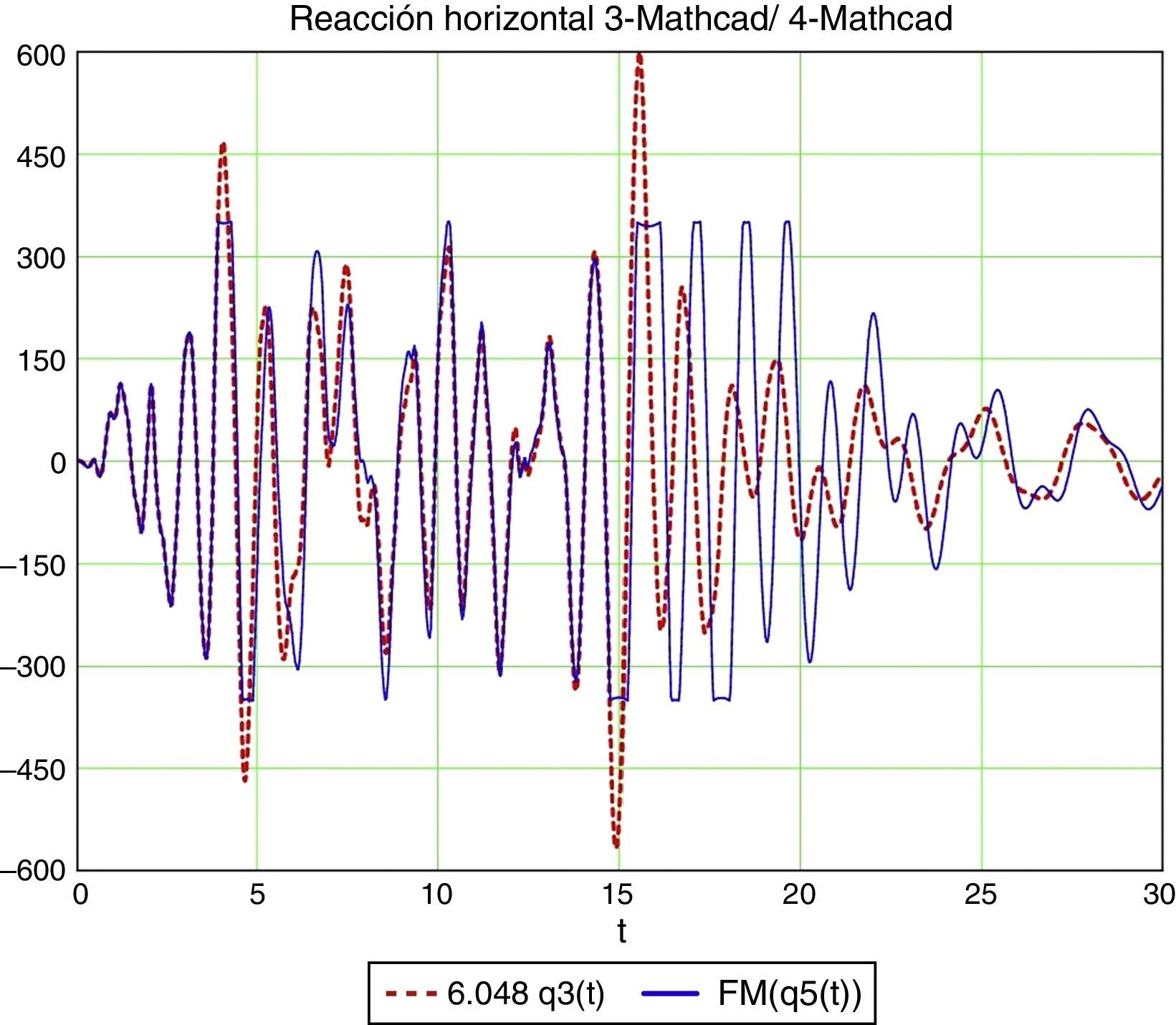
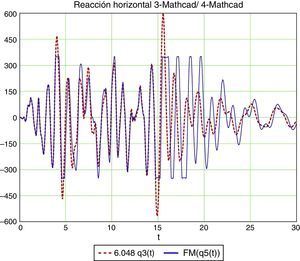
Vemos que la consideración de la masa convectiva reduce la reacción horizontal, aun con muelle lineal, de 803 a 590kN (figs. 20 y 21).
6Análisis global conjuntoPara verificar la influencia conjunta y no lineal de los distintos factores mencionados, incluyendo la masa convectiva y los disipadores, es preciso recurrir a un modelo algo más elaborado, que en nuestro caso hemos analizado con ANSYS.
Aun así hemos procurado mantener el modelo lo más sencillo posible, y lógicamente contrastarlo con los modelos ya mencionados, sometiéndolo al mismo acelerograma artificial empleado anteriormente para comparar la respuesta.
En el diseño final se sometió el depósito a un conjunto de 3 acelerogramas como establecen el Eurocódigo y el propio CSCR2010.
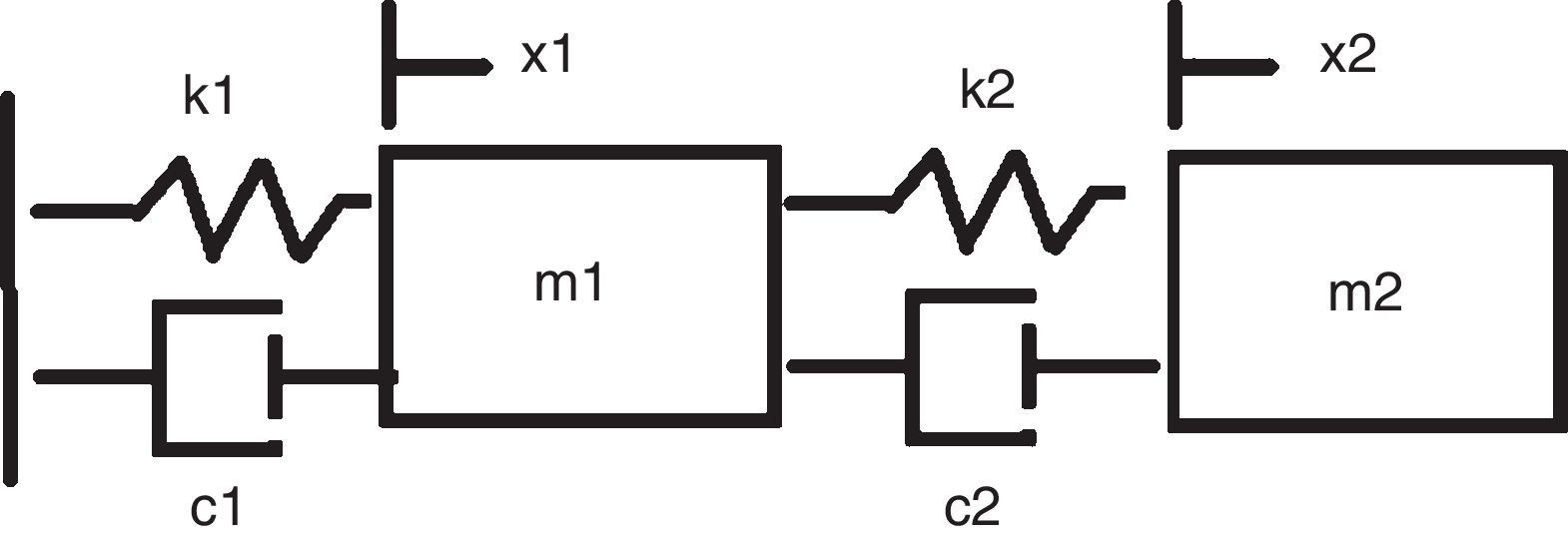
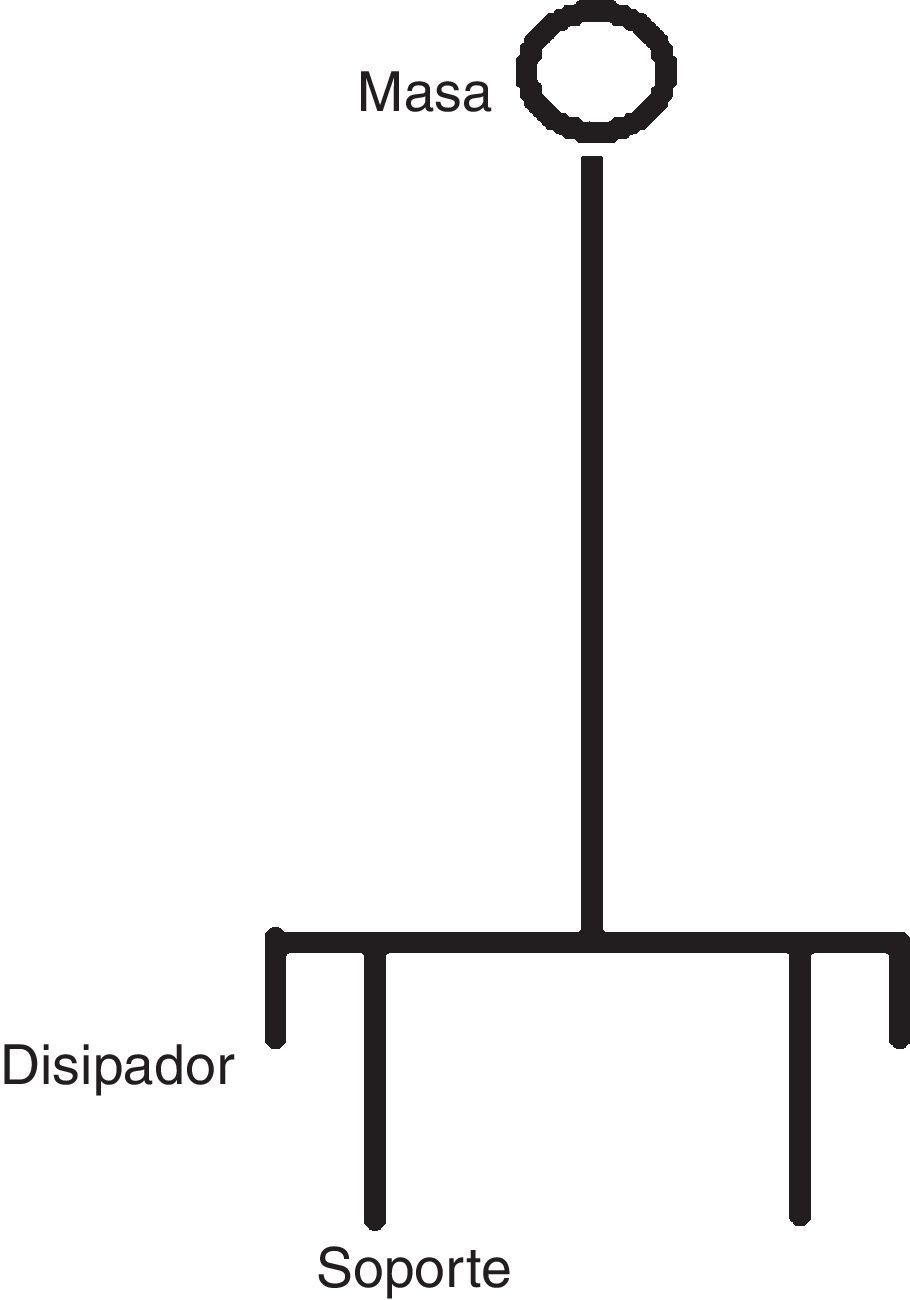
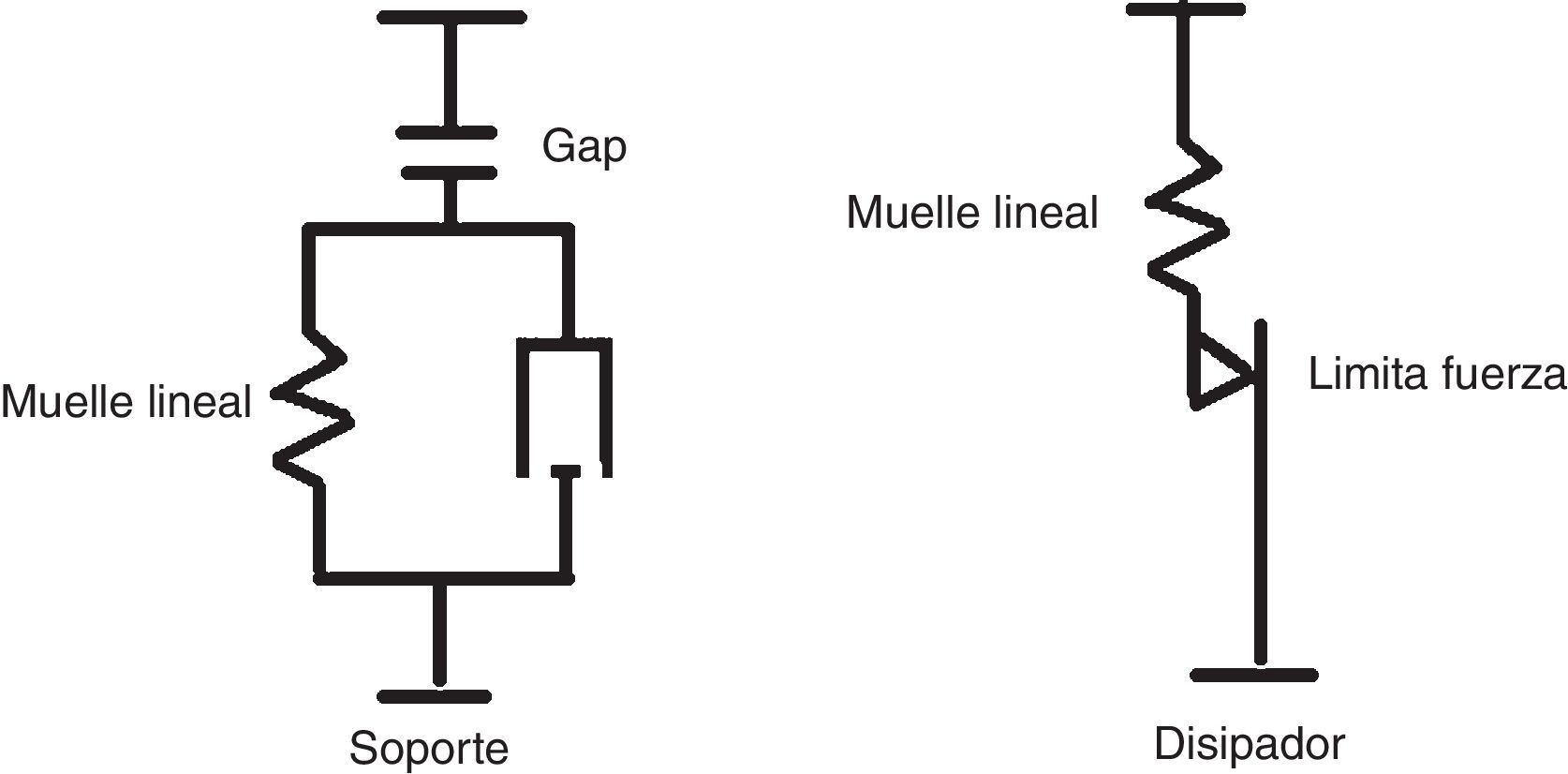
6.1Descripción del modelo de ANSYSSe trata de un modelo plano, en el que tanto la respuesta no lineal de los soportes como de los disipadores se modela mediante el elemento COMBIN40 (figs. 22 y 23).
En los soportes este elemento permite modelizar el despegue de la cimentación cuando la reacción se anula, y en el disipador permite modelizar el comportamiento elasto-plástico del mismo. En el soporte se introduce asimismo cierto amortiguamiento.
Cuando se distingue entre masa inductiva y masa convectiva es preciso considerar lógicamente dos masas (fig. 24).
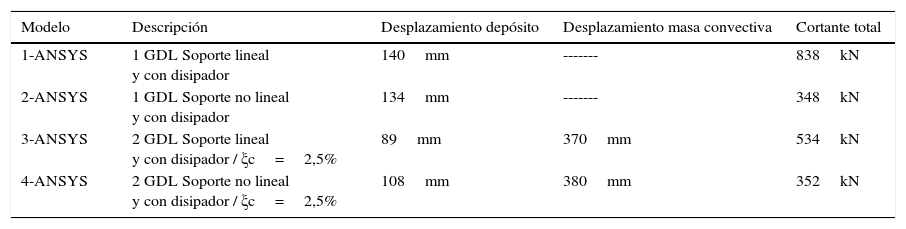
6.2ResultadosLa tabla 3 resume alguno de los datos más significativos.
Resultados del análisis de carga
| Modelo | Descripción | Desplazamiento depósito | Desplazamiento masa convectiva | Cortante total |
|---|---|---|---|---|
| 1-ANSYS | 1 GDL Soporte lineal y con disipador | 140mm | ------- | 838kN |
| 2-ANSYS | 1 GDL Soporte no lineal y con disipador | 134mm | ------- | 348kN |
| 3-ANSYS | 2 GDL Soporte lineal y con disipador / ξc=2,5% | 89mm | 370mm | 534kN |
| 4-ANSYS | 2 GDL Soporte no lineal y con disipador / ξc=2,5% | 108mm | 380mm | 352kN |
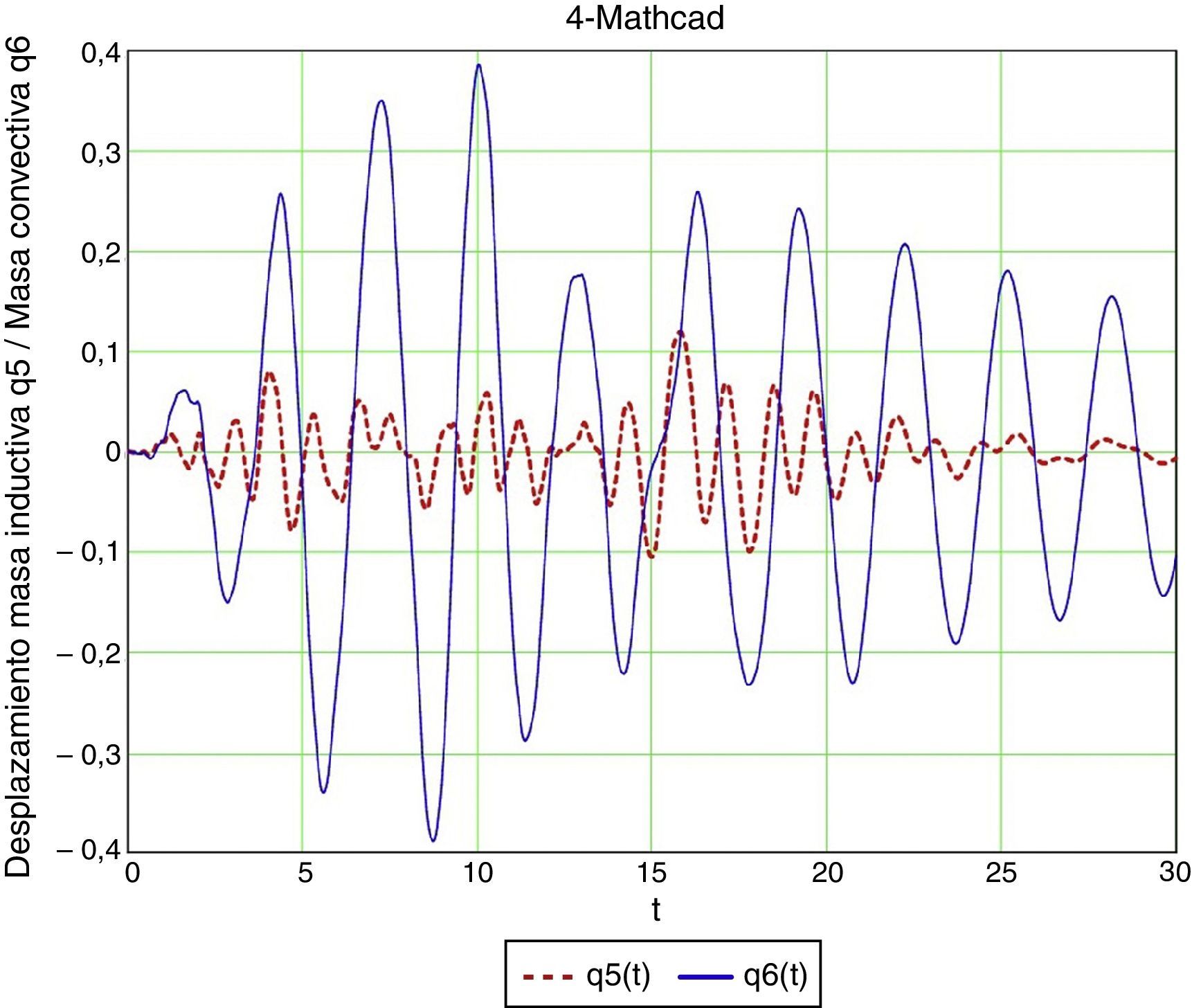
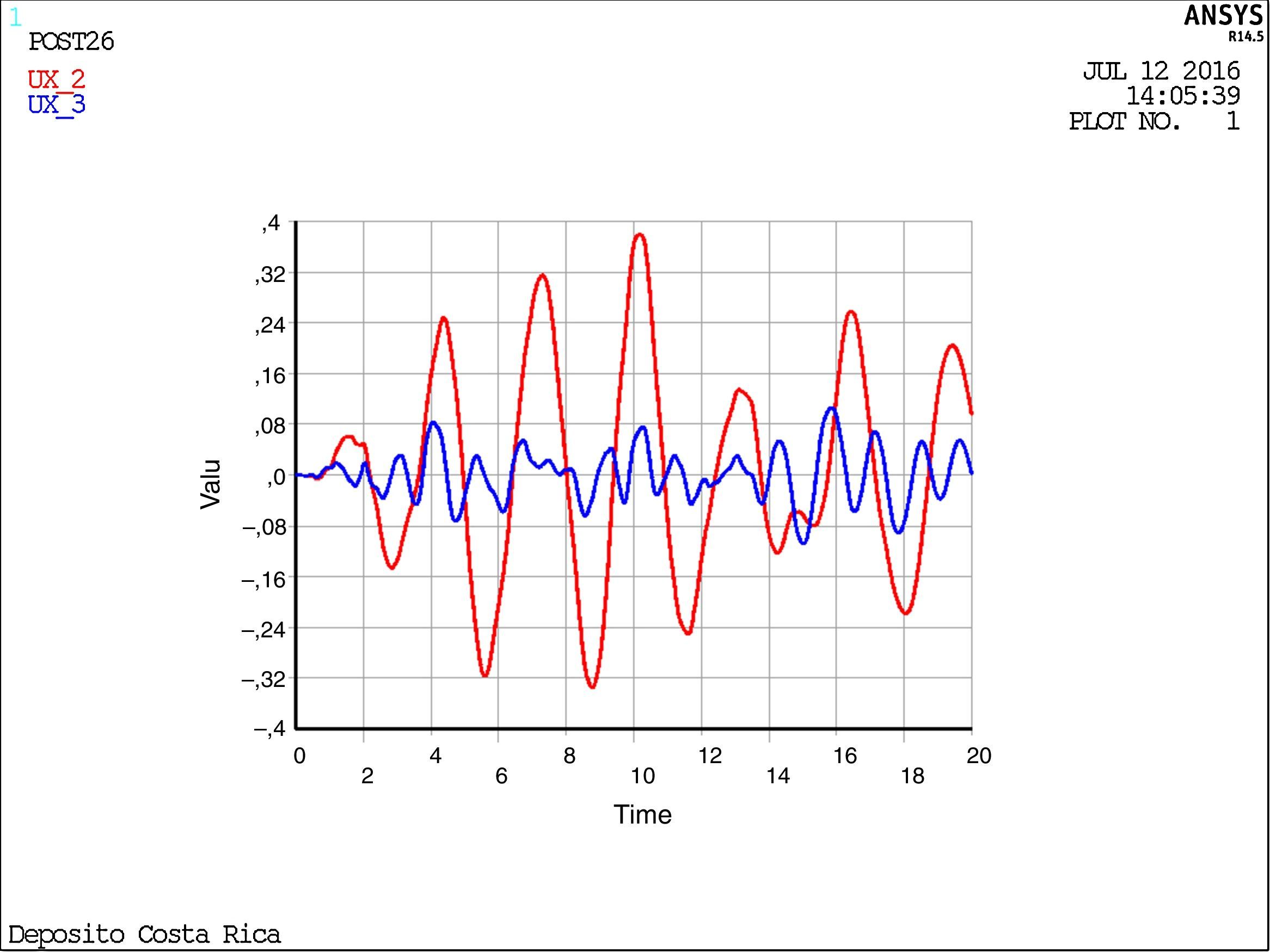
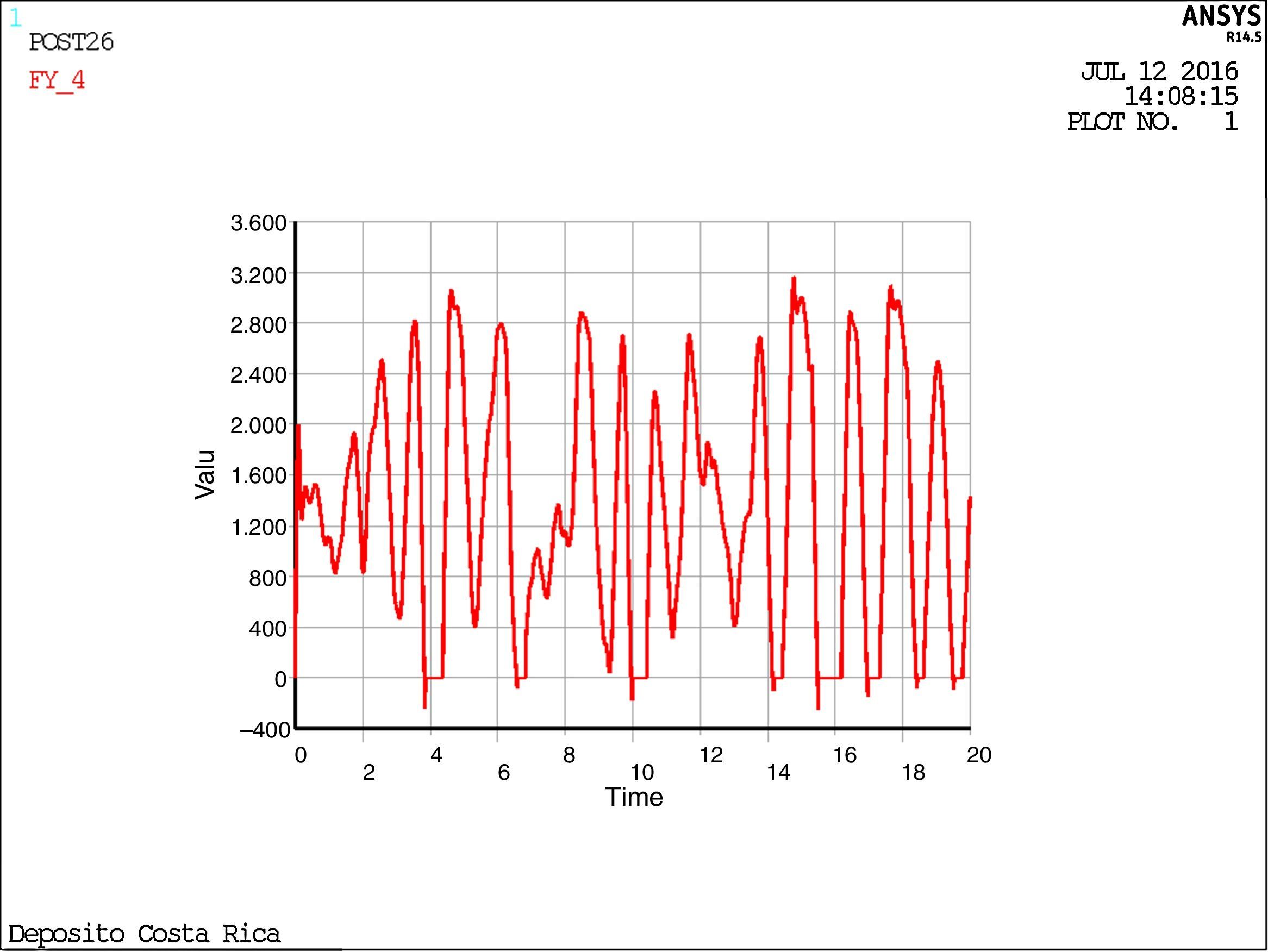
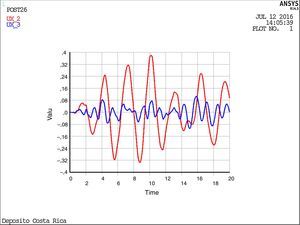
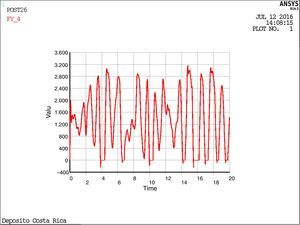
Utilizando el modelo 4-ANSYS, se obtienen los desplazamientos de la masa inductiva y de la masa convectiva mostrados en la figura 25, mientras que la figura 26 muestra la variación del axil en el soporte de la torre con el tiempo, observándose los periodos de despegue.
El esquema de balanceo autocentrante que se ha propuesto para el depósito, nos permite acotar con claridad el cortante y por consiguiente el momento máximo que la acción sísmica impone en la torre y su cimentación, tal y como nos proponíamos.
El instrumento básico para el prediseño es el diagrama demanda-capacidad. En el análisis ulterior se han utilizado modelos de uno o dos grados de libertad, según se considere o no explícitamente la masa convectiva del agua, y sometidos a un sismo artificial compatible con el espectro del CSCR, para visualizar mejor los distintos aspectos del comportamiento de la estructura.
Con Mathcad, la implementación del muelle no lineal es sencilla y permite resolver con gran agilidad distintas variantes, pero en cambio no nos permite considerar los disipadores. Con ANSYS es posible incorporar tanto las no linealidades debidas al despegue en los soportes como el comportamiento elasto-plástico de los disipadores, pero, y pese a la sencillez de los modelos, se requiere un tiempo de cálculo muy superior.