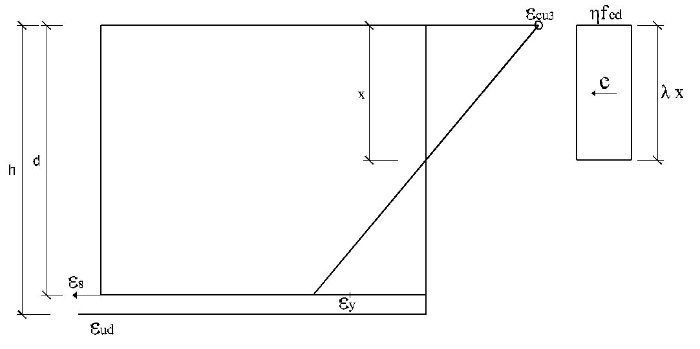
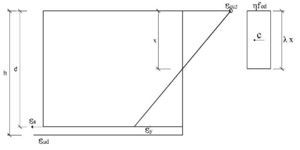
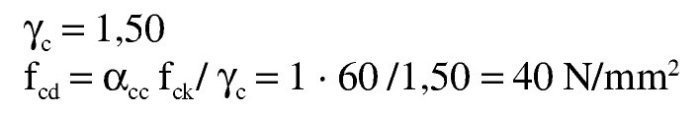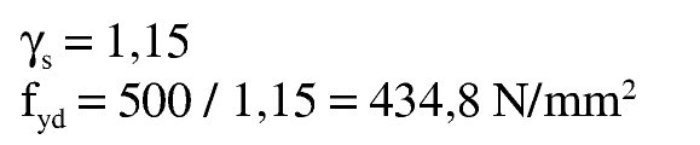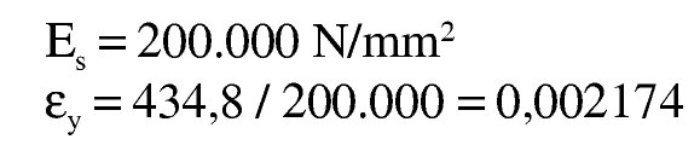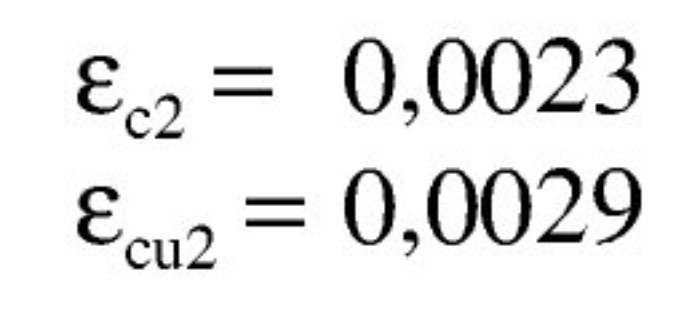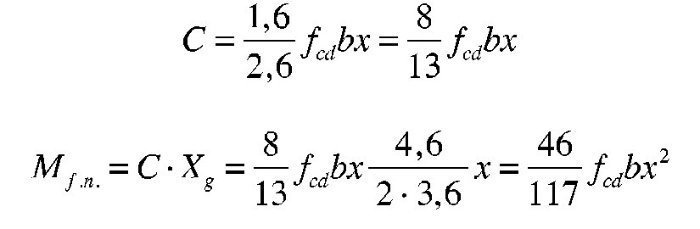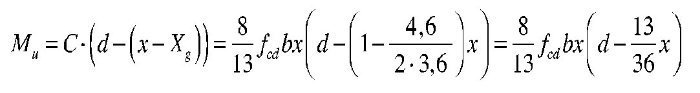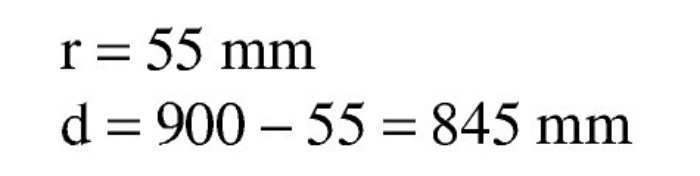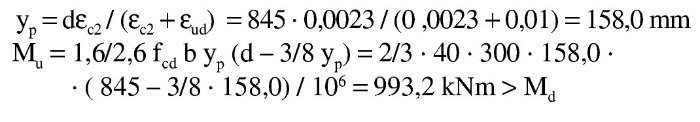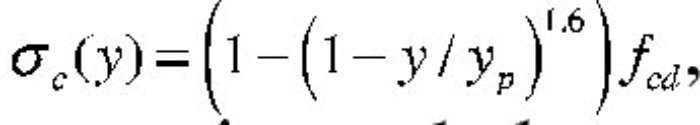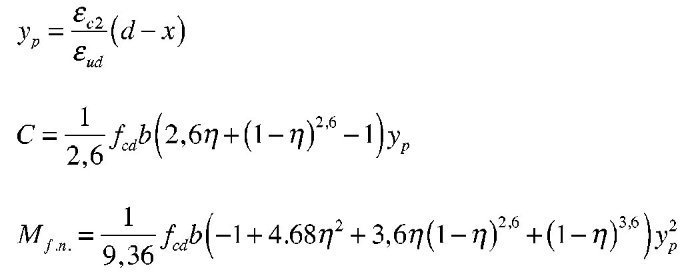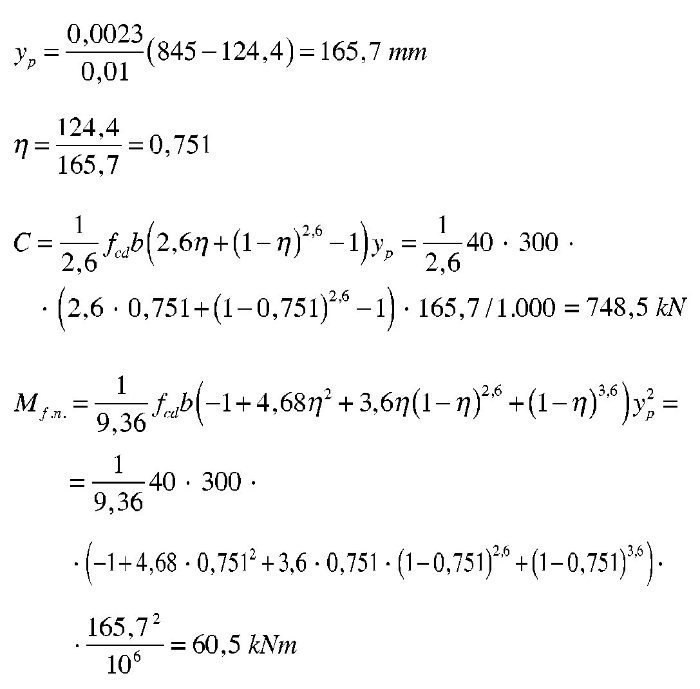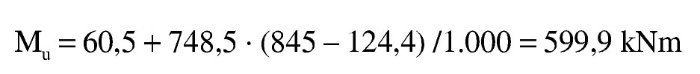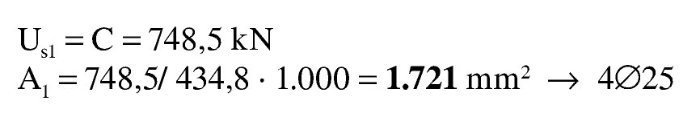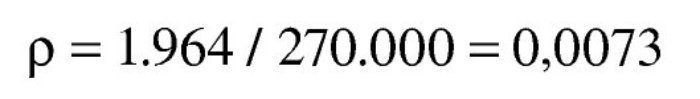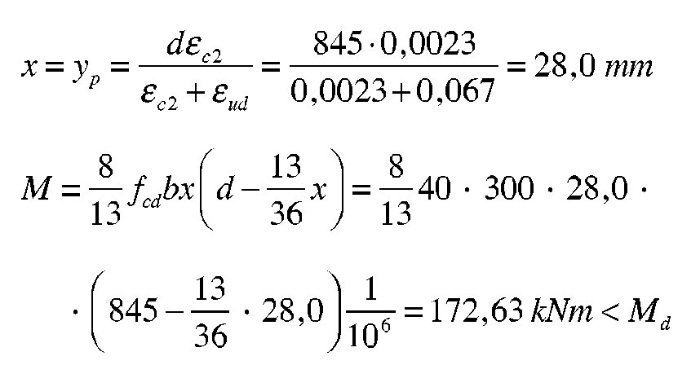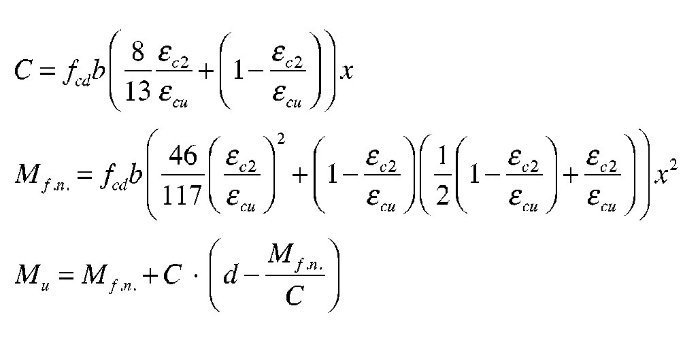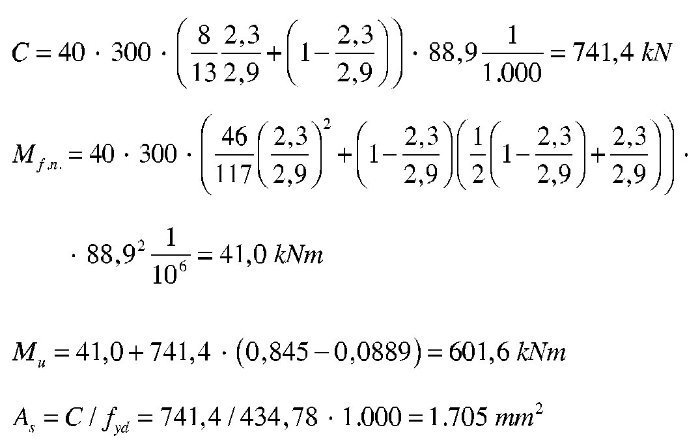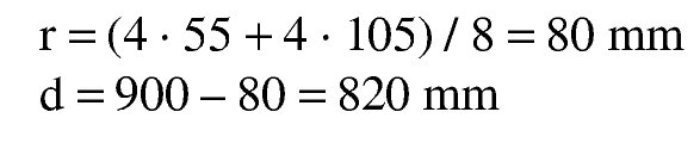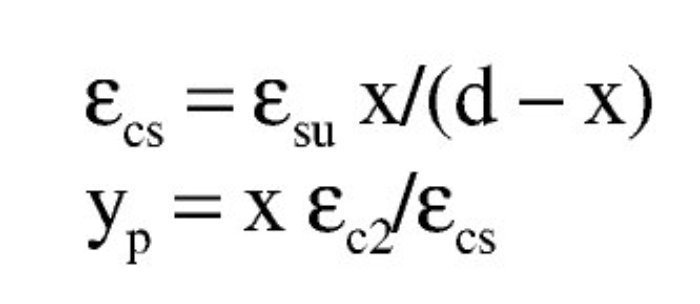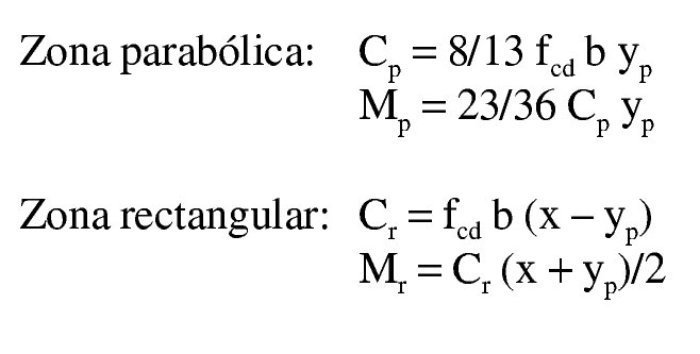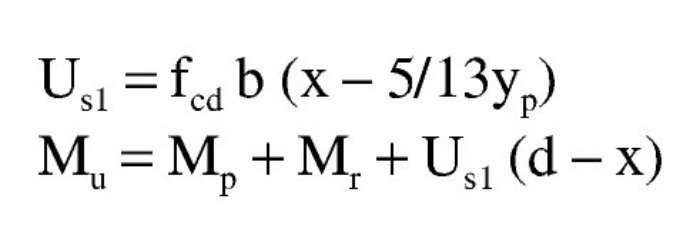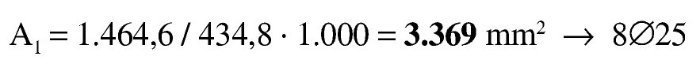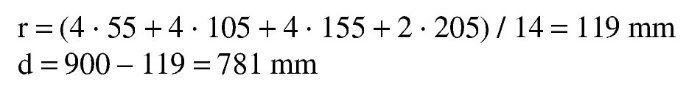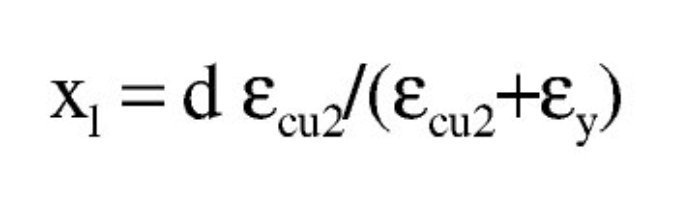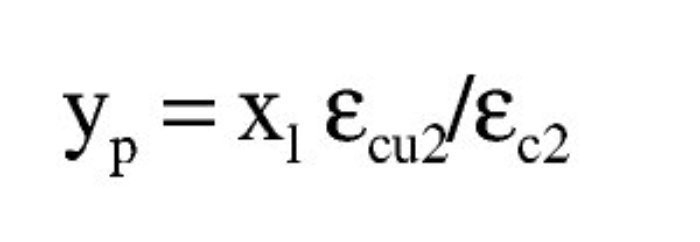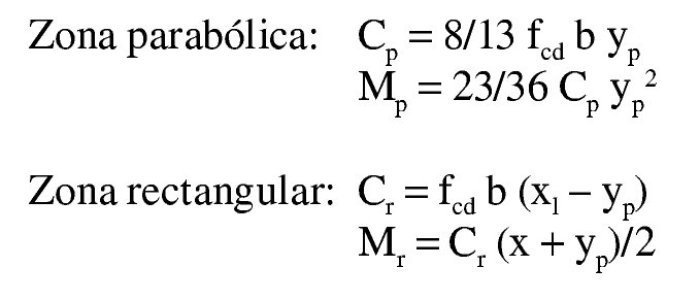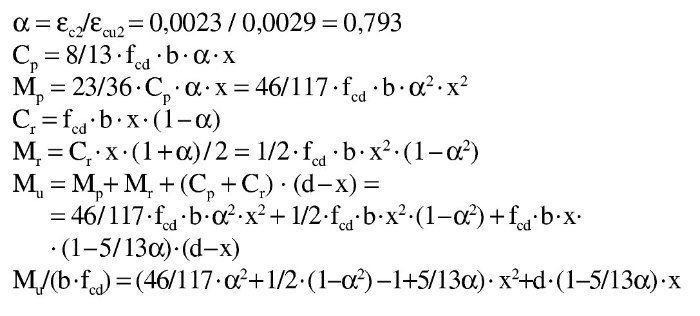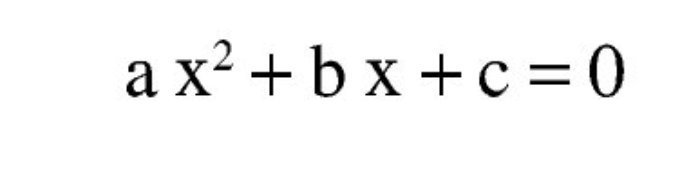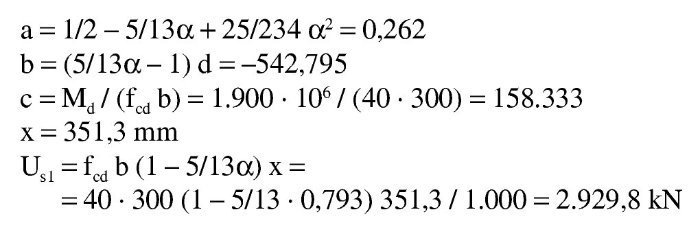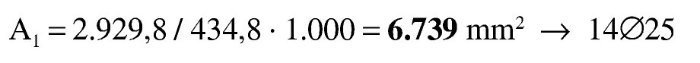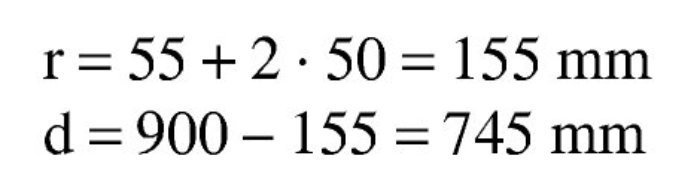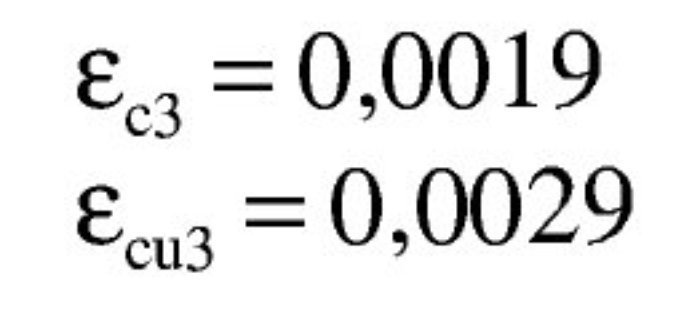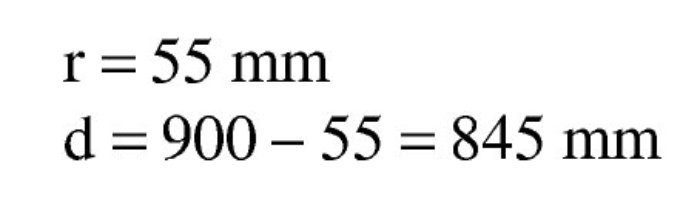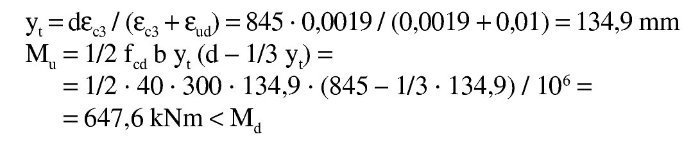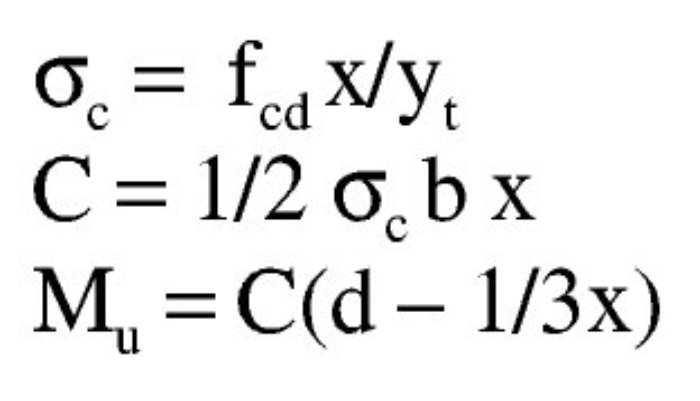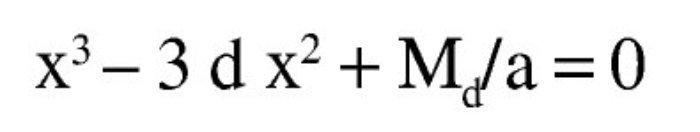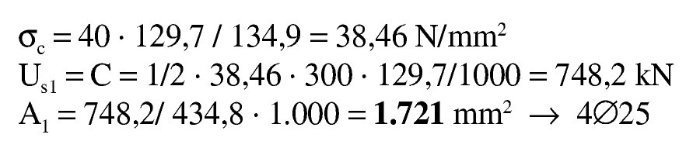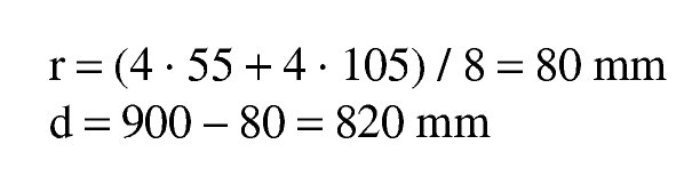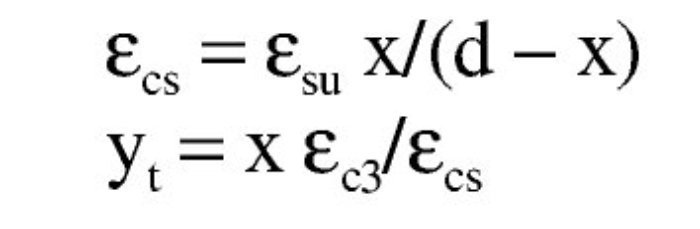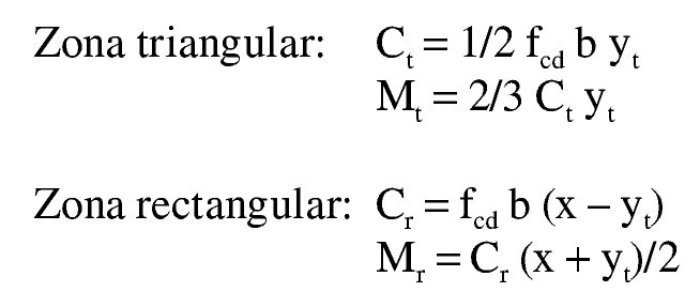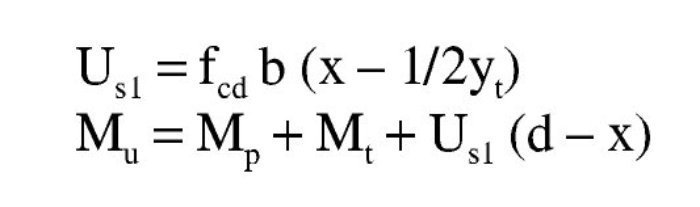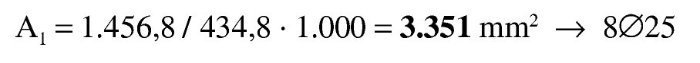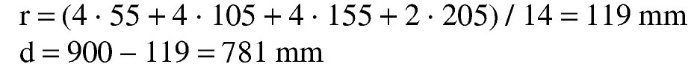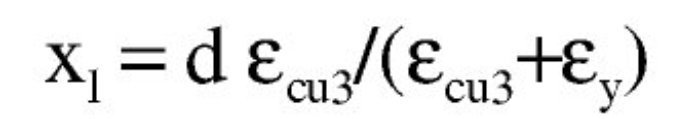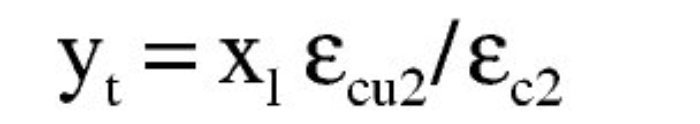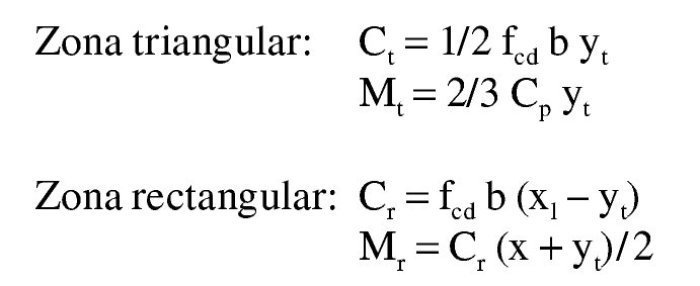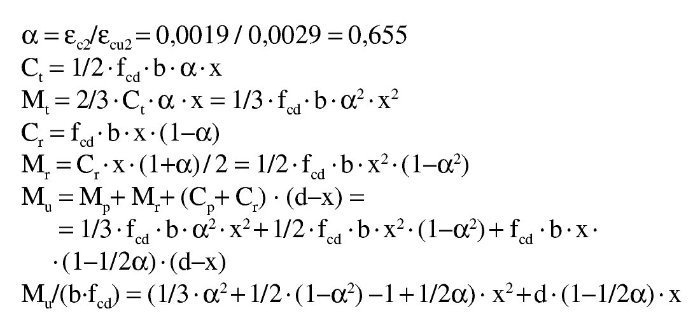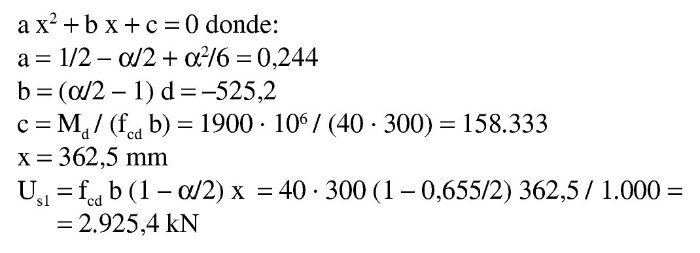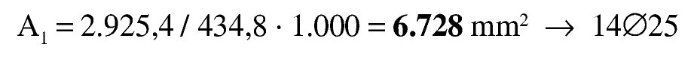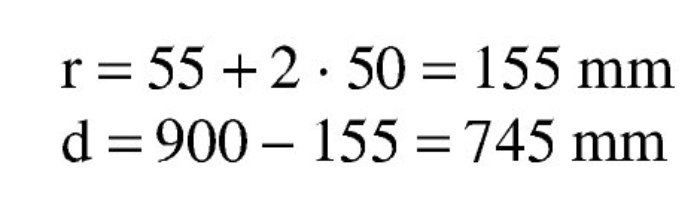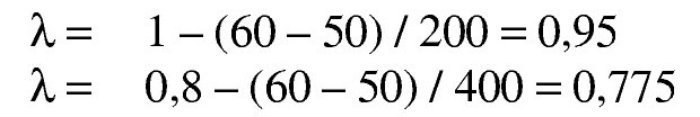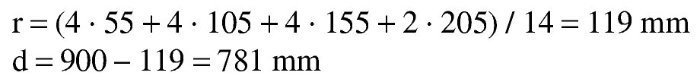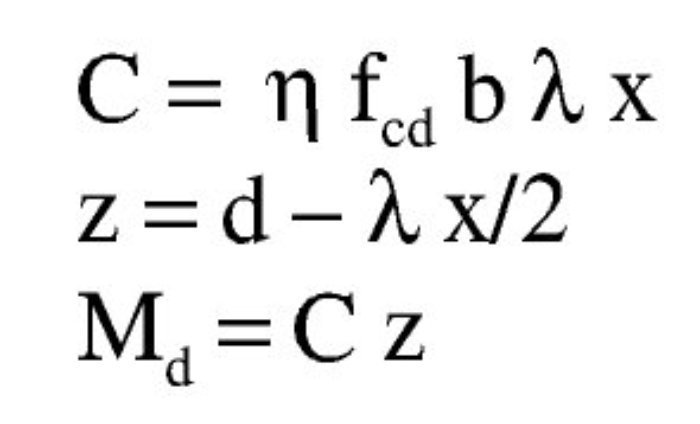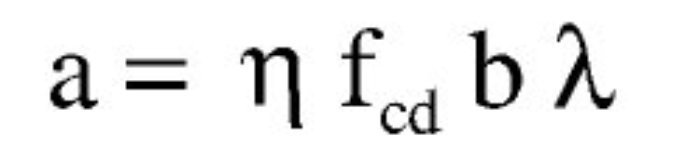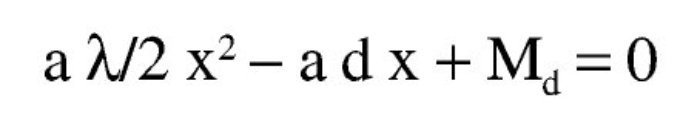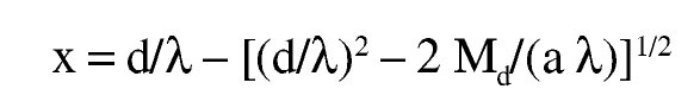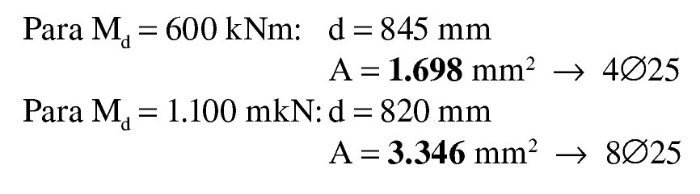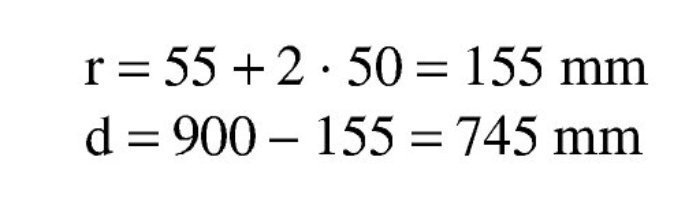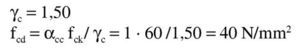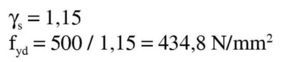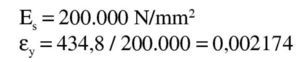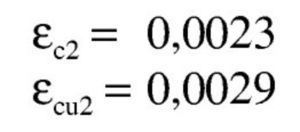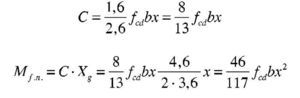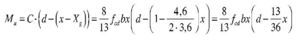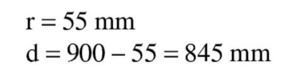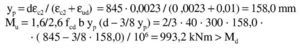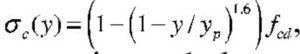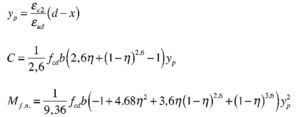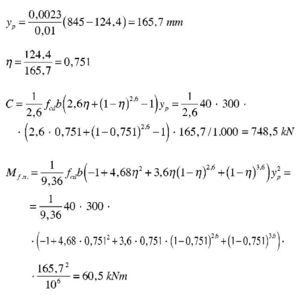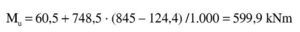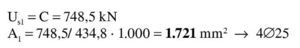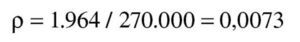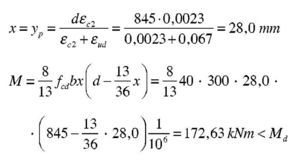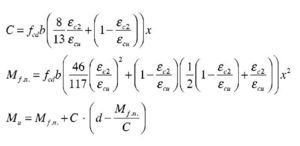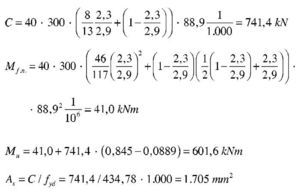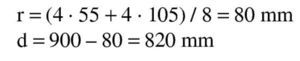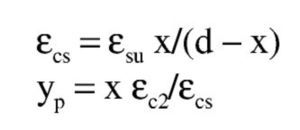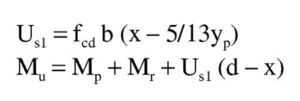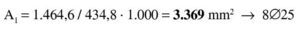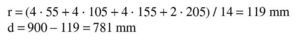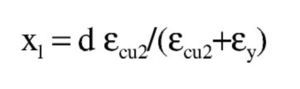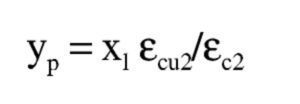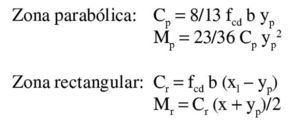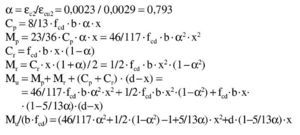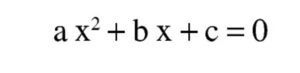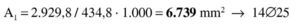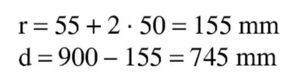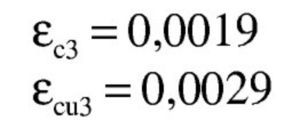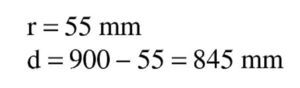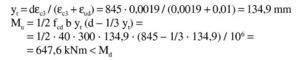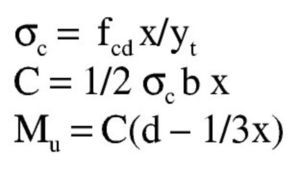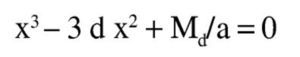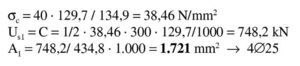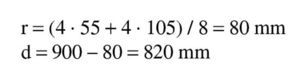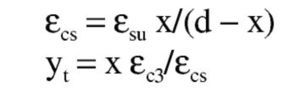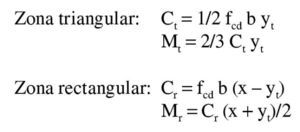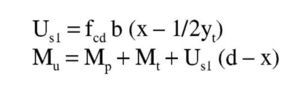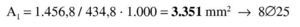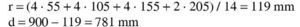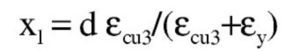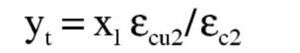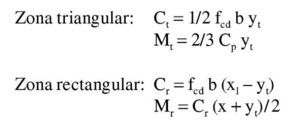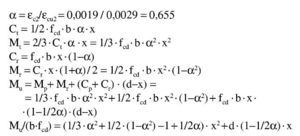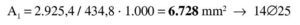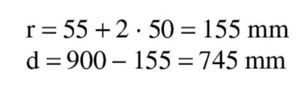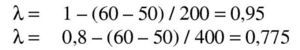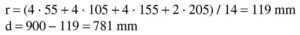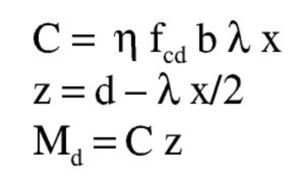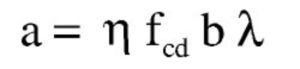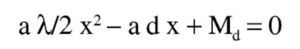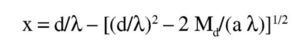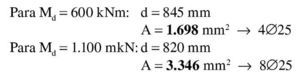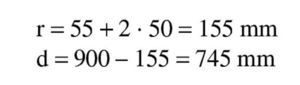Ejemplo 1: Flexión simple en sección rectangular según EN 1992-1-1:20041
Ejemplo planteado:
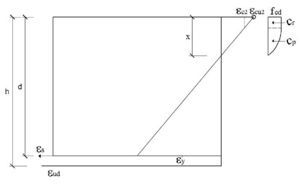
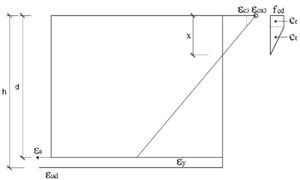
Se trata de dimensionar a flexión simple una sección rectangular de 0,30 m de ancho y 0,90 m de canto construida con hormigón C60/75 y acero B500S. Se utilizarán para el hormigón los diagramas parábola-rectángulo, bilineal y rectangular. El armado se hará con ∅25 dispuestos con un recubrimiento teórico mínimo de 55 mm. Los momentos con los que se efectuará el cálculo serán de 600, 1.100, 1.900 y 2.500 kNm. Se calcularán también los resultados para un brazo mecánico aproximado de 0,9d. No se incluye la comprobación de la abertura de fisura.
Resistencias de cálculo para la solución:
El coeficiente de cansancio para el hormigón es αcc (Art.3.15 de EN 1992-1-1). El valor recomendado en EN 1992-1-1 es de 1.
El Anejo Nacional dice que se puede adoptar un valor comprendido entre 0,85 y 1 si el porcentaje de la carga permanente supera el 70% de la total.De acuerdo con esto, tanto con los parámetros nacionales recomendados en EN 1992-1-1 como con el Anejo Nacional español, la tensión de cálculo del hormigón es:
Para el acero, EN 1992-1-1 no tipifica las resistencias, para las que se da un rango de límite elástico entre 400 y 600 MPa.
El Anejo Nacional limita el valor superior a 500 MPa.La tensión de cálculo del acero a tracción es:
Este valor es igual para el acero en compresión.
Los valores de las deformaciones correspondientes al límiteelástico y a la deformación última del acero, con cualquiera de los diagramas que se utilicen, son:
Estas diferencias demuestran que el límite del 10‰ utilizado tradicionalmente en España es un límite convencional que no refleja una rotura real de la pieza. Para los cálculos realizados con los parámetros recomendados de EN-1992-1-1, y con objeto de explorar las diferencias que surgen, se adoptará un acero de clase C con una deformación última de cálculo deεud = 0,9 × 75‰ = 0,067.
Soluciones con diagrama parábola-rectángulo:
Los valores de las deformaciones últimas del hormigón parael C60 (tabla 3.1 de EN 1992-1-1) son:
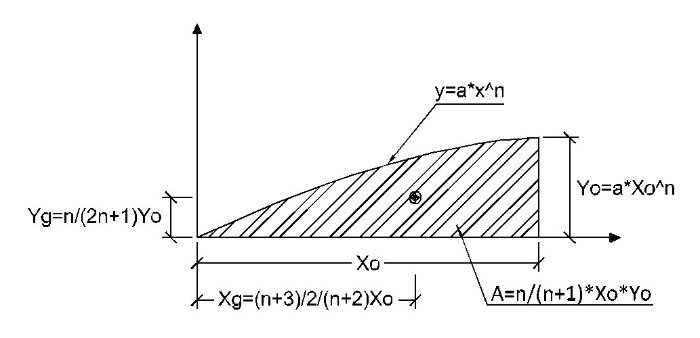
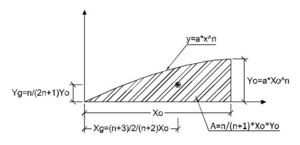
Por otra parte, para este hormigón, el exponente de la parábola es 1,6 en lugar del valor 2,0 tradicional para hormigones normales. En la figura siguiente se muestra la posición del centro de gravedad y el área de un tramo de parábola de grado n, que incluye el punto de tangente horizontal. Estas expresiones serán útiles para las verificaciones que se incluyen más adelante.
Para el caso concreto de una parábola de exponente 1,6, se obtienen los siguientes valores para la integral del área de la parábola completa y para el momento correspondiente respecto de la fibra neutra:
Si se toma el momento respecto al centro de gravedad de las armaduras, la expresión correspondiente será:
Md = 600 kNm:
Se estima que va a ser necesaria una armadura de 4∅25 (600 / 0,9 / 0,85 / 50 · 1,15 = 18 cm2 → 3,7Φ25), con lo que el recubrimiento teórico y el canto útil serán:
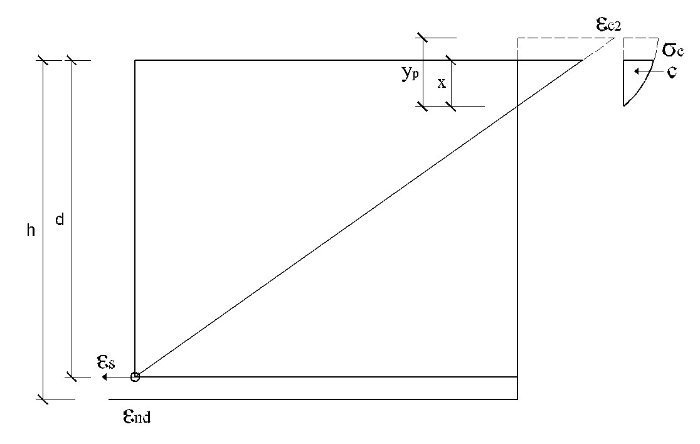
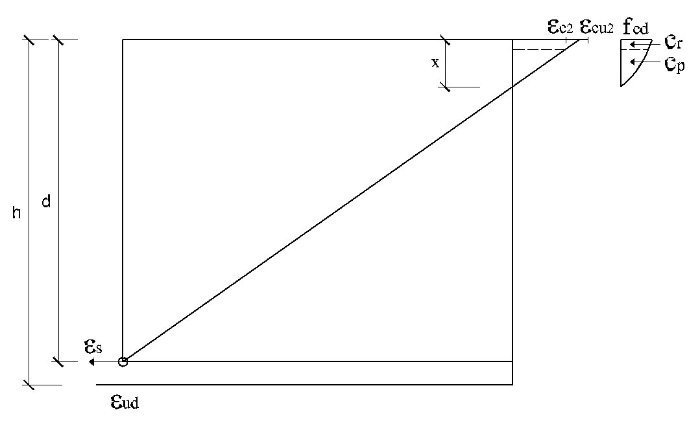
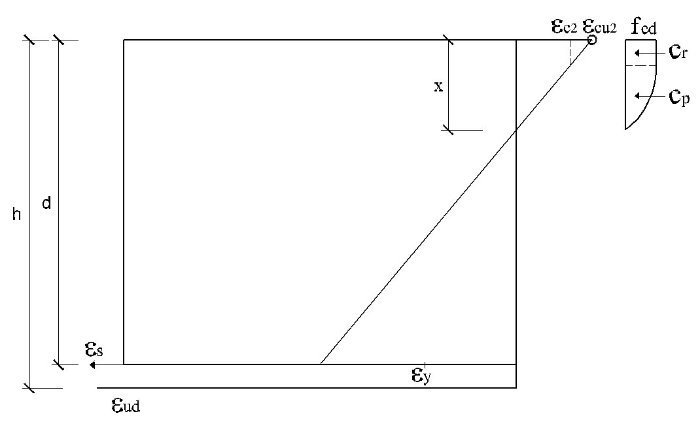
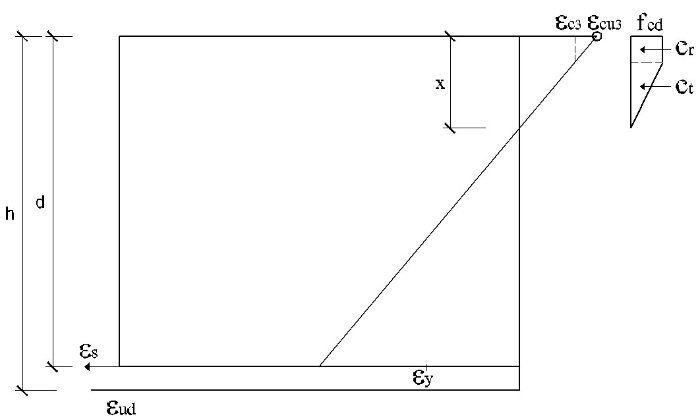
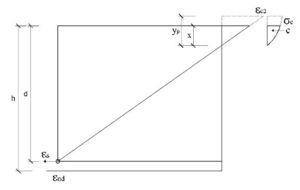
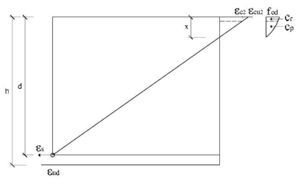
El subdominio en que comienza la flexión simple se tiene pivotando en el punto de εud en la armadura de tracción y con deformaciones del hormigón crecientes desde 0 a εc2. En este último punto se desarrolla por completo el bloque parabólico de tensiones. La profundidad de la fibra neutra correspondiente y el momento último alcanzado utilizando los parámetros del Anejo Nacional, son:
Así pues, con el valor de Md el bloque de compresiones en el hormigón se extiende parcialmente en la zona parabólica. Si se denomina η a la relación entre la altura comprimida e yp, que se acaba de obtener, teniendo en cuenta que la ley de tensiones, tomando como origen la fibra neutra, viene dada por la parábola
, las expresiones que dan el volumen de compresiones de la zona comprimida y el momento respecto a la fibra neutra (donde yp es la altura de la zona parabólica total) se obtienen integrando la ley de tensiones y son:
Se tantea una posición de la fibra neutra, dado que las expresiones analíticas a que dan lugar las fórmulas anteriores serían muy complicadas. Naturalmente, el valor de x que se tantee ha de ser inferior a yp. Para x = 124 mm se tiene:
El momento último respecto a la armadura de tracción es:
La aproximación es suficiente. La armadura de tracción es:
La cuantía geométrica resulta:
Las cuantías mínimas son, normalmente inferiores al 3‰, por lo que la cuantía dispuesta debería cumplir los valores mínimos. No obstante, a continuación se incluye esta verificación dado que permite exponer las formulaciones correspondientes.
La cuantía mínima según EN 1992-1-1, artículo 9.2.1.1 es:
As,min = W/z fctm,fl/fyd
z (brazo mecánico) = 0,8 h = 0,8 · 900 = 720 mm
W (momento resistente) = 300 · 9002 / 6 = 40.500.000 mm3
fctm,fl (Resistencia media a flexotracción – Art. 3.1.8 de EN 1992.1.1) = max{(1,6 – h/1.000) fctm ; fctm} = 4,4 N/ mm2
As,min = 40.500.000 / 720 · 4,4 / 434,8 = 569 mm2 → Cumple
Según los parámetros recomendados de EN 1992-1-1, en los que el pivote A corresponde a una deformación mucho mayor (6,7 veces más en el caso estudiado correspondiente a un acero de clase C), se tiene, para la fibra neutra que supone el fin de la zona parabólica del diagrama parábola-rectángulo (x = yp):
Se observa, que se obtiene un valor muy inferior al momento solicitante si sólo se considera la zona parabólica del diagrama parábola rectángulo. Este resultado indica que resulta difícil obtener una rotura por el Pivote A (rotura por alargamiento excesivo del acero) al aumentar la deformación admisible del acero y considerar el valor real del material en lugar de un valor convencional como se ha hecho tradicionalmente en la práctica española. No obstante, como se verá la diferencia en términos de armadura no es significativa.
Se debe, en este caso, modificar la estrategia y plantear larotura por el pivote B:
Lógicamente, al plastificar el hormigón debe reducirse la fibra neutra respecto del cálculo anterior, aumentando algo el brazo mecánico y obteniendo una cuantía ligeramente menor. Probando, igual que antes, con yp = 88,9 mm:
Se observa que se obtiene una cuantía ligeramente inferior al cálculo según el Anejo Nacional, lo cual resulta consistente con el ligero aumento del brazo mecánico.
Observada esta diferencia, en el resto de los ejemplos se mantendrá el cálculo únicamente con el criterio del Anejo Nacional.
Md = 1.100 kNm:
Se estima que va a ser necesaria una armadura de 8∅25 (1.100 / 0,9 / 0,80 / 50 · 1,15 = 35 cm2 → 7,2 Φ25), con lo que, suponiendo dos capas de armadura iguales, el recubrimiento teórico y el canto útil son:
El subdominio a que corresponde este caso es continuación del anterior y se tiene pivotando en el punto de εud en la armadura de tracción y con deformaciones del hormigón crecientes desde εc2 a εcu2. En este último punto se desarrolla por completo el bloque rectangular de tensiones. Por tanto, la zona parabólica se desarrolla por completo, pero la rectangular es parcial. La deformación superior del hormigón εcs y la altura yp de la zona parabólica para una profundidad x de la fibra neutra son:
La altura de la zona rectangular es x – yp. Los volúmenes de compresiones y sus momentos respecto a la fibra neutra son:
El volumen de compresiones total, igual a la capacidad mecánica de la armadura de tracción, y el momento respecto a ésta son:
Al final del subdominio, en el punto en que se alcanza εcu2, se tiene:
Para el valor de Md que se está considerando, se tantea una posición de la fibra neutra. Para x = 178,7 mm se tiene:
La aproximación es suficiente (Error 0,03%). La armadura de tracción es:
Md = 1.900 kNm:
Se estima que va a ser necesaria una armadura de 14∅25 (1.900 / 0,9 / 0,80 / 50 · 1,15 = 61 cm2 → 12,3 Φ25), con lo que el recubrimiento teórico y el canto útil son:
El dominio a que corresponde este caso es continuación del anterior y se tiene pivotando en el punto de εcu2 en el hormigón y con deformaciones decrecientes de la armadura traccionada desde εud a εy. En este dominio ya no influye el valor que se tome para la deformación máxima del acero y por tanto, los resultados serán los mismos tanto con los parámetros recomendados en EN 1992-1-1 como con los del Anejo Nacional. En todo el dominio se desarrollan por completo tanto el bloque rectangular de tensiones como la zona parabólica. Al final del dominio se tiene la profundidad límite xl de la fibra neutra, con una armadura de tracción y un momento como sigue:
La altura yp de la zona parabólica para la profundidad xl de la fibra neutra es:
La altura de la zona rectangular es x – yp. Los volúmenes de compresiones y sus momentos respecto a la fibra neutra son:
Al final del subdominio, en el punto en que se alcanza εy, se tiene en este caso:
Para Md = 1.900 kNm, se puede resolver directamente una ecuación de segundo grado en x:
Reordenando los términos, se obtiene una ecuación de segundo grado en x:
donde:
La armadura de tracción es:
Md = 2.500 kNm:
Se estima que va a ser necesaria una armadura de tracción de 20∅25 (2.500 / 0.75 / 0.80 / 50 · 1.15 = 95.8 cm2 → 19.5 Φ25) 2, con lo que el recubrimiento teórico y el canto útil son:
En este caso no se recorre un dominio de deformaciones, sino que se mantienen constantes las deformaciones εcu2 del hormigón y εy de la armadura traccionada. Para mantener este plano de rotura, se complementa la armadura de tracción con armadura de compresión con objeto de poder plastificar la armadura traccionada en rotura. En todo el dominio se desarrollan por completo tanto el bloque rectangular de tensiones como la zona parabólica. La profundidad límite xl de la fibra corresponde a la expresión expuesta en el caso anterior como punto final del subdominio. Dado el cambio de canto útil, resulta necesario calcularla de nuevo, así como la armadura de tracción y el momento correspondientes:
Al ser inferior este momento al de cálculo, aunque se podría aumentar la armadura de tracción y hacerla trabajar a deformaciones inferiores a εy, esto no sería económico, por lo que es preferible absorber la diferencia Md-Ml con una armadura de compresión, cuya capacidad mecánica se debe sumar también al Us1 anterior. Se tiene así, para una armadura de compresión con el recubrimiento teórico d′ = 55 mm:
Soluciones con diagrama bilineal
Los valores de las deformaciones últimas del hormigón para el C60 (tabla 3.1 de EN 1992-1-1) son:
Md = 600 kNm
Se estima que va a ser necesaria una armadura de 4∅25, igual que anteriormente, con lo que el recubrimiento teórico y el canto útil son:
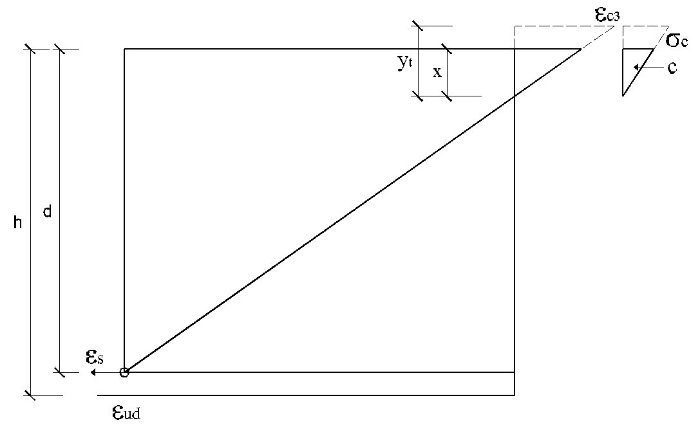
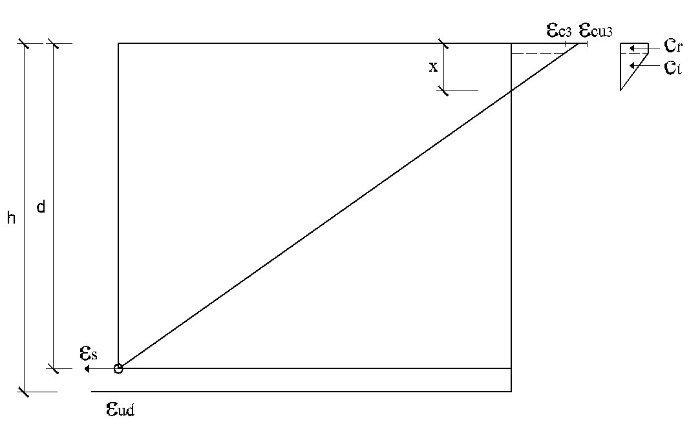
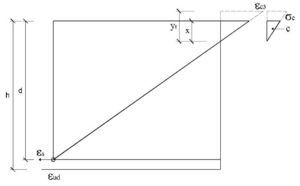
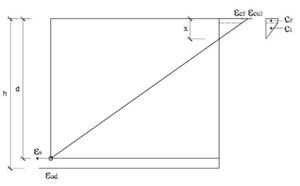
El subdominio en que comienza la flexión simple se obtiene pivotando en el punto de εud 3 en la armadura de tracción y con deformaciones del hormigón crecientes desde 0 a εc3. En este último punto se desarrolla por completo el bloque triangular de tensiones. La profundidad de la fibra neutra correspondiente y el momento último alcanzado son:
Así pues, con este momento el bloque de compresiones en el hormigón se extiende parcialmente en la zona triangular. Para una profundidad x de la fibra neutra, las expresiones que dan la tensión superior en el hormigón, el volumen de compresiones de la zona y el momento último respecto a la armadura traccionada son:
Sustituyendo y haciendo a = 1/6 fcd b/yt se tiene:
Esta ecuación se puede resolver directamente o por tanteos para hallar la posición de la fibra neutra. Naturalmente, el x que se tantee ha de ser inferior a yt. En este caso se tiene:
La solución es x = 129,71 mm, con la que:
Md = 1100 kNm:
Se estima, igual que antes, que va a ser necesaria una armadura de 8∅25, con lo que el recubrimiento teórico y el canto útil son:
El subdominio a que corresponde este caso es continuación del anterior y se tiene pivotando en el punto de εud en la armadura de tracción y con deformaciones del hormigón crecientes desde εc3 a εcu3. En este último punto se desarrolla por completo el bloque rectangular de tensiones. Por tanto, la zona triangular se desarrolla por completo, pero la rectangular es parcial. La deformación superior del hormigón εcs y la altura yt de la zona triangular para una profundidad x de la fibra neutra son:
La altura de la zona rectangular es x – yt. Los volúmenes de compresiones y sus momentos respecto a la fibra neutra son:
El volumen de compresiones total, igual a la capacidad mecánica de la armadura de tracción, y el momento respecto a ésta son:
Al final del subdominio, en el punto en que se alcanza εcu2, se tiene en este caso:
Para el valor de Md considerado, se tantea una posición de la fibra neutra. Para x = 182,1 mm se tiene:
La aproximación es suficiente (Error 0,12%). La armadura de tracción es:
Md = 1.900 kNm:
Se estima, igual que antes, que va a ser necesaria una armadura de 14∅25, con lo que el recubrimiento teórico y el canto útil son:
El dominio a que corresponde este caso es continuación del anterior y se tiene pivotando en el punto de εcu3 en el hormigón y con deformaciones decrecientes de la armadura traccionada desde εud a εy. En todo el dominio se desarrollan por completo tanto el bloque rectangular de tensiones como la zona parabólica. Al final del dominio se tiene la profundidad límite xl de la fibra neutra, con una armadura de tracción y un momento (momento límite) como sigue:
La altura yt de la zona parabólica para la profundidad xl de la fibra neutra es:
La altura de la zona rectangular es x – yp. Los volúmenes de compresiones y sus momentos respecto a la fibra neutra son:
Al final del subdominio, en el punto en que se alcanza εy, se tiene, en este caso:
Para Md = 1.900 kNm, se puede resolver directamente una ecuación de segundo grado en x:
Reordenando los términos, se obtiene una ecuación de segundo grado en x:
La armadura de tracción necesaria es:
Md = 2500 kNm:
Se estima, igual que antes, que va a ser necesaria una armadura de tracción de 20∅25, con lo que el recubrimiento teórico y el canto útil son:
En este caso no se recorre un dominio de deformaciones, sino que se mantienen constantes las deformaciones εcu3 del hormigón y εy de la armadura traccionada. En todo el dominio se desarrollan por completo tanto el bloque rectangular de tensiones como la zona triangular. La profundidad límite xl de la fibra neutra es la que ya se ha calculado en el caso anterior como límite del subdominio. Dado el cambio de canto útil, resulta necesario calcularla de nuevo, así como la armadura de tracción y el momento correspondientes:
Al ser inferior este momento al de cálculo, aunque se podríaaumentar la armadura de tracción y hacerla trabajar a deformaciones inferiores a εy, esto no sería económico, por lo que es preferible absorber la diferencia Md-Ml con una armadura de compresión, cuya capacidad mecánica se debe sumar también al Us1 anterior. Se tiene así, para una armadura de compresión con el recubrimiento teórico d′ = 55 mm:
Soluciones con diagrama rectangular
Los valores de las deformaciones últimas del hormigón para el C60 (tabla 3.1 de EN 1992-1-1) son:
Los parámetros aplicados al diagrama rectangular, al ser la resistencia del hormigón superior a 50 N/mm2, son:
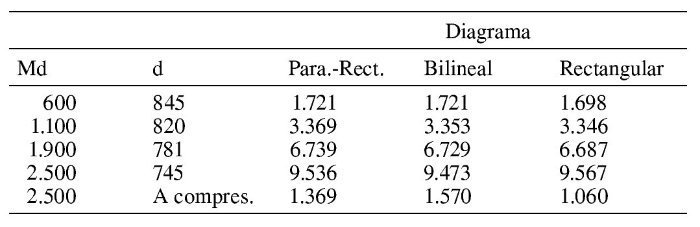
Con objeto de limitar la extensión del ejemplo y debido a que no existen para este diagrama diferencias conceptuales entre el dimensionamiento para 600 kNm, 1.100 kNm y 1.900 kNm, solo se expone este último caso, indicando para los primeros solamente los resultados.
Md = 1.900 kNm
Se estima, igual que antes, que va a ser necesaria una armadura de 14∅25, con lo que el recubrimiento teórico y el canto útil son:
Se tiene:
Con:
se tiene la ecuación de segundo grado:
cuya solución es:
En nuestro caso, transformando Md a Nmm:
El cálculo con los valores inferiores es idéntico:
Md = 2.500 kNm:
Se estima, igual que antes, que va a ser necesaria una armadura de tracción de 20∅25, con lo que el recubrimiento teórico y el canto útil son:
En este caso no se recorre un dominio de deformaciones, sino que se mantienen constantes las deformaciones εcu3 del hormigón y εy de la armadura traccionada. La profundidad límite xl de la fibra neutra y el momento correspondiente (momento límite) son:
Al ser inferior este momento al de cálculo, aunque se podría aumentar la armadura de tracción y hacerla trabajar a deformaciones inferiores a εy, esto no sería económico, por lo que es preferible absorber la diferencia Md-Ml con una armadura de compresión, cuya capacidad mecánica se debe sumar también al Us1 anterior. Se tiene así, para una armadura de compresión con el recubrimiento teórico d′ = 55 mm:
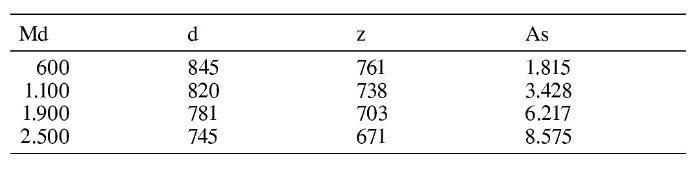
Soluciones con brazo mecánico 0,9d
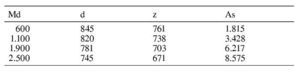
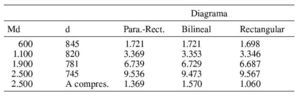
Resumen de resultados de armadura (mm2):
Se ve que la coincidencia entre las tres leyes de tensiones es muy buena, por lo que en un cálculo manual lo más recomendable es utilizar la ley rectangular.
Se observa, además, que en los dos últimos casos se subestima la armadura necesaria considerando z = 0,9d, para 1.900 kNm, porque se trata de un momento próximo al momento límite y para 2.500 kNm porque se trata de un momento superior al momento límite. En estos casos, se obtiene una mejor aproximación utilizando un brazo mecánico de 0,75d para el predimensionamiento.
1. Ejemplo elaborado por Rafael Chueca: rafa@rchueca.com
2. Se utiliza z~0.75d debido a que este momento es superior al momento límite (calculado en el paso anterior e igual a 2.388,6 kNm) para el cual resulta necesario disponer armadura de compresión para conseguir plastificar la armadura traccionada, como se verá más adelante.
3. Se adopta en este caso ε = 0,01 según el Anejo Nacional. No obstante, igual que en caso del diagra ma parábola-rectángulo, se podría adoptar, aplicando loe valores recomendados de EN 1992-1-1 un valor mucho mayor para este valor (hasta 0,067) con un resultado similar. No se efectúa el cálculo paralelo con objeto de limitar la extensión del ejemplo.