La entrada en vigor de los Eurocódigos, que son ya la única normativa vigente en la mayoría de los países euopeos, incluyendo Francia, Alemania y Reino Unido, y la idea, ya en fase de implementación a través del futuro Código Estructural, de que la parte de cálculo de las Instrucciones españolas de hormigón, acero y estructuras mixtas va a ser copia literal de los Eurocódigos, pone de manifiesto que la comunidad ingenieril española debe centrar sus esfuerzos en formarse para poder aplicar correctamente los eurocódigos y debe invertir energía en mejorar las futuras versiones de los eurocódigos. En este trabajo se señalan algunos problemas que se han detectado en la aplicación del Eurocódigo 2, para el proyecto de estructuras de hormigón, y se sugiere una serie de posibilidades de mejora que se han concretado en propuestas concretas transmitidas a través de AENOR al Subcomité 2 del Comité técnico TC-250 del CEN (Comité Europeo de Normalización), que es la empresa europea encargada, bajo mandato de la Comisión Europea, de la redacción de los Eurocódigos, para su consideración de cara a la nueva versión de los Eurocódigos cuya publicación está actualmente prevista para el año 2020.
The Eurocodes, which are now the only valid structural code now in force in the majority of European countries, including France, Germany and the UK, and the idea, already under implementation, that the part dealing with structural design of the future Spanish Structural Code will be a literal copy of the Eurocodes, makes it evident that the Spanish engineering community must make an effort to obtain adequate training in the application of the Eurocodes and direct its energy at improving future versions of the Eurocodes, not at producing new national standards. In this paper some problems that have been detected in professional practice when applying Eurocode 2 to structural projects are described, as well as proposing some improvements to the current text. These suggestions for improvement have been transmitted through AENOR to Sub-Committee 2 of Technical Committee TC-250 of CEN. CEN (European Committee for Standardisation), is the European company charged, under mandate by the European Commission, with the review of the Eurocodes aimed at producing a new, easier-to-use and broader generation for the year 2020.
A partir del año 2010 y con cierto retraso en función de los distintos países, por la necesidad de definir parámetros nacioanales de aplicación, se adoptaron, ya sea como normativa única (Alemania, Francia, Reino Unido, Austria), ya sea como noramativa alternativa a la normativa nacional (España, Italia) los Eurocódigos. En muchos de los países europeos se están deasarrollando los primeros proyectos utilizando exclusivamente los Eurocódigos y esto hace que la experiencia de uso de esta normativa sea aún limitada. Sin embargo, poco a poco esta exaperiencia va poniendo de manifiesto distintos problemas que surgen en la aplicación de los mismos y las diferencias que ello supone respecto de la práctica tradicional de los d ist intos países.
Actualmente se está llevando a cabo la revisión de los Eurocó-digos que se prevé terminar para el año 2020. Para ello, en el seno del CEN-TC250/SC2 (subcomité europeo, constituido por técniacos de todos los países, en el que se desarrolla el Euro código 2) se ha creado el grupo de trabajo WG1. A través del AN/CTN-140/SC2 (subcomité español espejo del CEN-TC250/SC2) se ha reaalizado una serie de propuestas encaminadas a hacer evolucionar los Eurocódigos en la dirección de mejorar aspectos concretos y contribuir al esfuerzo europeo para modernizar esta normativa. E n e st e a r t ícu lo se pla nt e a n a lg u nos de e stos a sp e ctos justificando por qué deben ser objeto de revisión e indicando una posible diarección en la que puede plantearse dicha revisión.
2Efecto de la distribución de la carga en la resistencia a cortante de elementos con armadura transversalEl modelo para el cálculo a cortante de elementos sin armaadura transversal incluido en EN 1992-1-1 (Parte 1-1 del Euro-código 2 Proyecto de estructuras de hormigón) se basa en un ajuste empírico seguro respecto de ensayos de laboratorio de elementos estructurales isostáticos sometidos a cargas punatuales. Debido a la gran influencia que tiene en la resistencia a cortante medida en este tipo de ensayos la relación entre la distancia de la carga al apoyo (a) y el canto útil (d), los ensayos utilizados para este ajuste cumplen la condición a/d >2,50. En la figura 1 se muestra, como ejemplo para ilustrar este aspecto, algunos de los ensayos llevados a cabo por Díaz de Cossío y Siess de vigas sometidas a carga puntual [1] con valores de a/d variables.
Ejemplo de la influencia de la relación a/d en la resistencia a cortante de elementos sin armadura transversal (Ensayos de Díaz de Cossío y Siess [1]).
Sin embargo, las cargas que solicitan a muchos de los eleamentos que se han proyectado tradicionalmente sin armadura de cortante no responden a este esquema, puesto que se encuenatran sometidos a cargas uniformes (losas en edificios) o trianagulares (muros sometidos a empujes de tierra). No es posible mantener el proyecto de muchos de estos elementos sin armaadura transversal, si se aplican para su proyecto estrictamente los criterios establecidos en EN 1992-1-1. Para un análisis más profundo de este aspecto ver la referencia [2].
Por otra parte, la experimentación demuestra que la resisatencia a cortante es más elevada cuando se ensayan elemenatos sometidos a carga distribuida e investigaciones recientes muestran que este aumento puede ser espectacular para caragas triangulares, lo cual tiene una aplicación muy clara para el proyecto de muros [3]. En el trabajo descrito en la referenacia [3] se ensayaron 8 vigas, idénticas dos a dos para detectar resultados anómalos, compuestas por un voladizo compensado por un tramo anclado de tal forma que se aplicaba la carga al voladizo provocando una reacción en el anclaje trasero (ver esaquema estructural en la figura 2). De esta forma el tramo de anclaje representa un voladizo sometido a carga puntual, mienatras que el voladizo frontal está sometido a una carga uniforme o triangular. Los ensayos se concibieron para que la relación M/(V·d), que, para el típico ensayo de viga bi-apoyada sometida a carga puntual, es igual a la relación a/d, fuera el mismo para el voladizo frontal que para el voladizo trasero. De esta forma se puede comparar en el mismo elemento con el mismo hormiagón, la resistencia frente a carga puntual y a carga distribuida o triangular, eliminando una variable muy importante como es la interacción Momento-Cortante. En estos ensayos la relación M/V se tomó igual a 1,65/0,55 = 3,0, un valor que es apropiado de cara a minimizar el efecto de la relación a/d en la resistencia.
Esquema estructural de ensayo de los elementos de la referencia [3]. Se ensayan a cada lado del apoyo central un voladizo sometido a carga puntual y otro sometido a carga uniforme o triangular manteniendo constante la relación M/V.
Las vigas se denominaron con las letras “C” o “V” en funación de si eran de canto constante o variable, seguidas de “R” o “T” en función de si el voladizo se cargaba con carga repartida o triangular y el número 1 o 2 debido a que se ensayaron dos vigas de cada tipo, como ya se ha indicado. Todas las probeatas se proyectaron con una armadura de flexión compuesta por 2 barras 026,5 de calidad 850/1050 no pretensadas. Se usaron barras de alta resistencia para poder representar elementos con cuantías geométricas bajas (0,79% en este caso), dado que los elementos que se proyectan sin armadura de cortante tienen cuantías bajas (losas), y evitar una rotura por flexión.
Los resultados obtenidos se detallan en la figura 3. Todos los ensayos rompieron a cortante primero por el vano anclado (carga puntual). Tras esta rotura se reparaba dicho vano mediante placas de acero colocadas en la cara superior e inferior de la viga y cosidas mediante 6 barras 012. Tras la reparación se procedía a un nuevo ciclo de carga hasta producir la rotura por el voladizo. Aquí también se produjo una rotura a cortante en todos los casos. Se observa claramente en la figura 3 que los elementos sometidos a carga distribuida resisten más que los soametidos a carga puntual. Esta diferencia es del orden de un 20% cuando la carga es distribuida, y se dispara hasta valores de más del 100% para carga triangular. Por otra parte, se observa que, para carga puntal, no existe contribución de la componente vertical de la flexión, debido a que la biela entra directamente al apoyo y este esquema es el mismo independientemente de si el canto es constante o variable. Por ello, la resistencia del vano sometido a carga puntual es la misma con canto constante o vaariable. Este es un aspecto que no está explícito en la normativa y que debería reflejarse dado que puede dar lugar a errores en proyecto.
Resultados brutos de los ensayos de la referencia [3].
En la tabla 1 se presenta un análisis más elaborado de los resultados en donde se resta a los elementos de canto variable la contribución de la componente de la flexión tomada fuera de la zona de entrada directa de la carga. Se observa que con esta corrección el incremento de resistencia en elementos soametidos a carga uniforme está entre el 20 y el 30% mientras que en elementos con carga triangular la sobre-resistencia es de más del doble, salvo para el elemento VT2 donde el valor es del 43%. No obstante, parte de esta diferencia se debe a que la resistencia de este elemento frente a carga puntual es relatiavamente elevada.
Resultados brutos de los ensayos de la referencia [3]. Se corrigen los ensayos de canto variable restando al cortante resistente la componente vertical de la flexión, solamente para carga distribuida
| Ensayo | Cortante último medido en ensayo | VR,di/VR,P | ||||
|---|---|---|---|---|---|---|
| Carga puntual VR,P [kN] (1) | Carga distribuida (DL) VR,di [kN] (2) | Componente vertical de la flexión Vcd [kN] | DL-Vcd (VR,di) [kN] (3) | Ensayo (2)/(1) | Ensayo corregido (3)/(1) | |
| CR1 | 132 | 174 | 0 | 174 | 1,32 | 1,32 |
| CR2 | 154 | 190 | 0 | 190 | 1,23 | 1,23 |
| VR1 | 148 | 236 | 45,3 | 191 | 1,59 | 1,29 |
| VR2 | 144 | 240 | 46,1 | 194 | 1,67 | 1,35 |
| CT1 | 114 | 241 | 0 | 241 | 2,11 | 2,11 |
| CT2 | 149 | 308 | 0 | 308 | 2,07 | 2,07 |
| VT1 | 118 | 300 | 57,6 | 242 | 2,54 | 2,05 |
| VT2 | 141 | 250 | 48,0 | 202 | 1,77 | 1,43 |
Si se aplica la fórmula de EN 1992-1-1 para la geometría de estos ensayos, con una resistencia del hormigón correspondienate a un valor medio de 35 MPa, la resistencia a cortante que se obtendría sería de:
Se observa que este valor está en línea con los valores más bajos obtenidos en estos ensayos (114 y 118 kN), lo cual confirama que la fórmula de EN 1992-1-1 es una buena aproximación para elementos sometidos a carga puntual alejada del apoyo.
Por otra parte, si se corrige el cortante resistente para tener en cuenta la parte de carga que entra directamente al apoyo (lo cual supone, según EN 1992-1-1, considerar el 25% del cortante situado entre el apoyo y el 0,5d y un valor variable de la carga entre el 25% y el 100% del cortante para la carga situada entre 0,5d y 2d) se puede obtener el cortante predicho para el ensayo por el modelo de EN-1992-1-1 a partir de la ecuación (1) para carga uniformemente repartida y a partir de la Ecuación (2) para carga triangular. En estas expresiones qu es la carga última uniforme y qumax el máximo valor de la carga última triangular que producirían el agotamiento de la pieza de acuerdo con EN 1992-1-1, d es el canto útil y L la luz del voladizo.
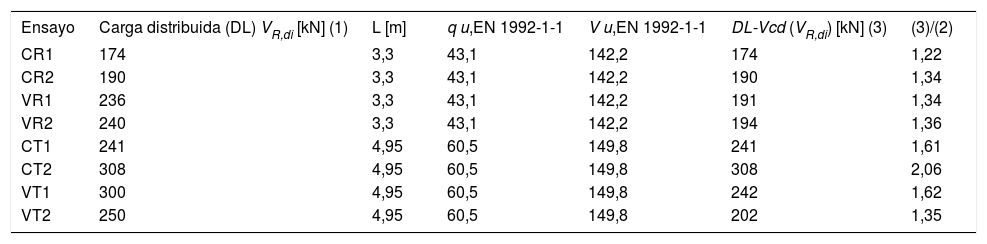
En la tabla 2 se aplica este criterio a los ensayos de la referenacia [3] y se comparan con los valores medidos. Se observa que EN 1992-1-1 queda siempre del lado de la seguridad.
Evaluación del modelo de EN 1992-1-1 teniendo en cuenta la corrección por la carga que entra directamente al apoyo
| Ensayo | Carga distribuida (DL) VR,di [kN] (1) | L [m] | q u,EN 1992-1-1 | V u,EN 1992-1-1 | DL-Vcd (VR,di) [kN] (3) | (3)/(2) |
|---|---|---|---|---|---|---|
| CR1 | 174 | 3,3 | 43,1 | 142,2 | 174 | 1,22 |
| CR2 | 190 | 3,3 | 43,1 | 142,2 | 190 | 1,34 |
| VR1 | 236 | 3,3 | 43,1 | 142,2 | 191 | 1,34 |
| VR2 | 240 | 3,3 | 43,1 | 142,2 | 194 | 1,36 |
| CT1 | 241 | 4,95 | 60,5 | 149,8 | 241 | 1,61 |
| CT2 | 308 | 4,95 | 60,5 | 149,8 | 308 | 2,06 |
| VT1 | 300 | 4,95 | 60,5 | 149,8 | 242 | 1,62 |
| VT2 | 250 | 4,95 | 60,5 | 149,8 | 202 | 1,35 |
Todos estos datos, junto con otras evidencias de más amplio espectro (ver, por ejemplo, el análisis recogido en [4]), hacen necesario el planteamiento de la inclusión del efecto de la inaf uencia de la carga en la resistencia a cortante de elementos sin armadura transversal en la futura versión de EN 1992-1-1. Para ello se está trabajando en el seno del CEN-TC250/SC2/WG1 en una propuesta concreta.
3Inclusión de una formulación para el anclaje de barras mediante placaEN 1992-1-1 no cubre el anclaje de barras mediante placa (figura 4), una tecnología que es fundamental en muchas aplicaaciones prácticas, en particular en zonas con gran congestión de armadura. Este tipo de solución está muy extendida en particualar en el proyecto de plataformas off-shore. Tradicionalmente, su cálculo se ha hecho considerando la propuesta de la norma ACI-318 [5]. Sin embargo esta propuesta presenta una serie de limitaciones debido a que su origen es empírico. Estas limitaaciones son:
1/3 del anclaje de la barra debe realizarse por adherencia
El acero debe tener un límite elástico inferior a 413 MPa
El hormigón debe tener una resistencia superior a 34 MPa
En muchos casos el recubrimiento lateral que exige el ACI-318 es excesivo
Debido a estas limitaciones, el modelo deja sin respuesta un sinfín de problemas prácticos. Con este trasfondo, FHECOR Ingenieros Consultores, junto con la UPM, colaboraron en el proyecto de investigación liderado por ARMATEK, “Investiagación y desarrollo de un nuevo método de anclaje de barras de acero corrugadas en hormigón y estudio de sus aplicaciones en la construcción”, parcialmente f nanciado por el CDTI con el código de proyecto IDI-20110631.
Como resultado de este proyecto se desarrolló un modelo teórico, basado en una idea física, que no tiene las limitaciones del modelo del ACI-318 y que además se ajusta sensiblemente mejor a los resultados experimentales disponibles.
Este modelo parte de la formulación clásica de una carga aplicada sobre un macizo de hormigón que se aplica de forma habitual para dimensionar la armadura necesaria para difundir la carga (figura 5 y figura 6). En el caso de una barra anclada con placa no se dispone una armadura para resistir las tracciones que se generan. Por ello el modelo se basa en estimar cuál es la resisatencia a tracción del hormigón sin armadura en términos de fuerza, suponiendo un modelo tipo splitting. El modelo se basa en estimar que la superf cie de hormigón que resiste la tracción es una superf cie vertical y rectangular que tiene un canto igual al ancho del bloque (a) (cuyas dimensiones vendrán delimitadas por el recubrimiento frontal -es decir, será igual a dos veces la distancia entre el eje de la barra y el borde del bloque más próximo a la barra) y cuyo ancho corresponde a un ancho eficaz definido de acuerdo con la ecuación (3), donde b es el ancho del bloque, cuya dimensión vendrá fijada por la separación entre barras o el recubrimiento lateral (en este caso b sería igual a dos veces la distancia entre el eje de la barra y el borde paralelo a la dimensión a más próximo) y b1 es el ancho de la placa, paralelo a la dimensión b. β es un parámetro de modelo que se toma igual a 1,00, lo cual supone una difusión de la fuerza igual en las dos direcciones (consistente con amod= 26,56°).
Con estos criterios, se plantea la ecuación (4). En esta ecuaación TSd es la tracción solicitante, derivada del modelo de bielas y tirantes clásico, y TRd es la tracción que resiste el hormigón. K es un factor de modelo que tiene en cuenta que la distribución de tracciones en la sección resistente no es uniforme y adopta un valor de 2/3 que correspondería a una distribución de tenasiones parabólica.
La ecuación (5) muestra cómo queda la expresión de la rotuara por tracción debida a la difusión con los valores numéricos de los parámetros de modelo adoptados.
Adicionalmente, es posible que la rotura se produzca por compresión excesiva. Esta compresión puede ser más o meanos uniaxial, cuando las dimensiones de la placa se asemejan a las dimensiones del bloque, o por compresión triaxial cuando las dimensiones del bloque son muy grandes respecto de las diamensiones de la placa. Esta segunda condición viene expresada por la ecuación (6) y corresponde a un planteamiento clásico.
El valor de kct adoptado normalmente por la normativa, inacluyendo EN 1992-1-1, es de 3,0, o, en algunos casos 3,3. No obstante, este valor es muy conservador y en la referencia [6] el propio Leonhardt, padre de esta expresión, indica que el factor de 3,0 lleva implícito un factor de seguridad de 3. Por ello, en las comparaciones con los datos experimentales se ha adoptado un valor de k igual a 9,0.
En la figura 7 se muestra la comparación del modelo proapuesto para los ensayos llevados a cabo por De Vries [7]. Estos ensayos consisten en ensayos de pull-out profundos donde las barras se encuentran ancladas en un bloque de hormigón a una profundidad suficiente para que el tipo de rotura sea de tipo blow-out. Se han considerado solamente ensayos en los que no hay adherencia entre la barra y el hormigón, algo que se consigue mediante un envainado de la barra hasta la posición de la placa de anclaje. Por otra parte, debido a que en [7] se especifica solamente la resistencia media del hormigón a compresión, para esta comparación, la resistencia a tracción se ha estimado a partir de la fórmula: fct, m = 0, 3fcm23. En la referencia [8] se demuestra que esta formulación mejora significativamente los modelos propuestos por el propio De Vries que forman la base de la propuesta del código americano ACI-318. Igualmente en dicha referencia se contrasta el modelo con 383 ensayos lleavados a cabo por Niyogi [9], también con excelentes resultados.
Contrastación experimental del modelo propuesto frente a los ensaayos de referencia (De Vries [8]).
Respecto de la seguridad del modelo, en la figura 8 se muesatra la comparativa utilizando los ensayos de De Vries introduaciendo la resistencia característica del hormigón (restándole a los valores medidos 8 MPa) y un coeficiente de minoración de la resistencia del hormigón de 1,50. Se observa que la formulaación propuesta es suficientemente segura.
Seguridad del modelo evaluada utilizando los ensayos de De Vries [8].
A la vista de lo expuesto anteriormente, se considera una necesidad que el Eurocódigo cubra en su próxima revisión el problema de las barras ancladas con placa. Por otra parte, el moadelo que se propone mejora los modelos implementados en otras normas y resulta suficientemente seguro.
4Relación entre durabilidad y abertura de fisura, en particular en presencia de recubrimientos importantesLos elementos en contacto con tierras deben necesariamente proyectarse con grandes recubrimientos (70 mm). La formulaación de fisuración de EN 1992-1-1 hace que estos elementos se vean penalizados al aumentar la separación entre fisuras con el recubrimiento, de tal forma que muchos de estos elementos y en particular los muros pantalla, vienen dimensionados por la necesidad de limitar la abertura de fisura. Esta circunstancia es relativamente paradójica puesto que se provee a estos elementos de un recubrimiento importante precisamente para mejorar sus condiciones de durabilidad.
Teniendo en cuenta este contexto, COMSA lideró el proyecto de investigación “Estudio de fisuración en muros pantalla” con la participación de FHECOR Ingenieros Consultores y el gruapo de Hormigón Estructural de la Universidad Politécnica de Madrid. Este proyecto fue parcialmente financiado por el CDTI bajo el código de proyecto IDI-20080937.
Como parte de los trabajos realizados en este contexto, se llevaron a cabo ensayos a escala real en vigas simplemente apoyadas con dos voladizos, con una amplia zona de flexión constante [10,11]. Estos ensayos se concibieron de tal forma que se pudiera poner claramente de manifiesto la influencia del reacubrimiento. En las figura 9figura 10 se muestra el esquema del ensayo y las secciones transversales de las vigas ensayadas, respectivamente.
Secciones transversales de los elementos ensayados. Se variaron los siguientes parámetros: relación 0/p, (utilizando 4012 o 4025 en la cara traccio-nada), el recubrimiento (20 o 70 mm) y la cuantía de armadura transversal con elementos sin cerco, con cercos a 10 cm y con cercos a 30 cm.
Los ensayos se identifican con un código de 3 números del tipo ω-c-s, siendo
- •
ω, el diámetro en mm
- •
c, el recubrimiento geométrico en mm
- •
s, la separación entre cercos en cm (este código vale 00 para los elementos que no lleven cercos en la zona central)
En la tabla 3 se muestran los valores de la abertura de fisura media y la abertura de fisura máxima medidas para una tensión de trabajo nor ma l en ser vicio de 250 M Pa. Igua lmente se recogen los valores correspondientes calculados con los modelos de las principales normas de hormigón estructural. Destaca que para el recubrimiento de 70 mm, las aberturas de fisuras son excesiavas, particularmente para los elementos con mayor armadura. El mejor comportamiento de las vigas menos armadas se atribuye a que el efecto de contribución entre fisuras es todavía muy imaportante para este nivel tensional. También se observa que los valores proporcionados por la normativa se quedan cortos.
Abertura de fisura (mm) medida (valor medio/valor máximo) y valores obtenidos por aplicación de las principales normas de hormigón estructural
| Ensayo | EN-1992 | MC-90 | EHE/EHE-08 | BS | ACI-318 | Ensayo |
|---|---|---|---|---|---|---|
| 12-20-00 | 0,09/0,16 | 0,10/0,16 | 0,11/0,18 | 0,06/0,11 | 0,11/0,15 | 0,15/0,31 |
| 12-20-10 | 0,19/0,33 | |||||
| 12-20-30 | 0,26/0,33 | |||||
| 12-70-00 | 0,19/0,24 | 0,16/0,24 | 0,20/0,34 | 0,15/0,25 | 0,25/0,34 | 0,28/0,42 |
| 12-70-10 | 0,32/0,35 | |||||
| 12-70-30 | 0,39/0,49 | |||||
| 25-20-00 | 0,09/0,15 | 0,08/0,11 | 0,13/0,22 | 0,09/0,15 | 0,12/0,16 | 0,20/0,34 |
| 25-20-10 | 0,16/0,29 | |||||
| 25-20-30 | 0,19/0,33 | |||||
| 25-70-00 | 0,20/0,35 | 0,09/0,14 | 0,25/0,42 | 0,24/0,40 | 0,30/0,40 | 0,35/0,61 |
| 25-70-10 | 0,27/0,63 | |||||
| 25-70-30 | 0,34/0,64 |
Se plantea por tanto la pregunta acerca de si esto es realmenate un problema desde el punto de vista de la durabilidad, dado que ciertamente lo será si el problema es de apariencia. La figuara 11 muestra una interpretación respecto de por qué crece tanto la abertura de fisura con el recubrimiento. La fisuración en torno a una barra de acero se puede descomponer en una fisuración principal que está formada por las fisuras pasantes que llegan a la superficie del hormigón y una serie de fisuras secundarias (fisuras de Goto [12]). De esta forma la abertura de fisura es muy pequeña en la proximidad de la barra porque la diferencia de deformación entre el hormigón y el acero se absorbe por la abertura de muchas fisuras. A medida que la abertura de la fisura pasante se evalúa más lejos de la cara de la barra su valor crece debido a que se van cerrando las fisuras secundarias (ver tamabién las referencias [13] y [14]). Por tanto, cuanto más importanate es el recubrimiento menor será el número de fisuras pasantes. En el ejemplo de la figura 11 la abertura de fisura superficial será el doble en el elemento superior, que tiene más recubrimiento, respecto de la del elemento inferior, que tiene menos recubriamiento. Sin embargo, en la barra no hay ninguna razón para pensar que ambas aberturas de fisura no serán iguales.
Separación entre fisuras superficiales en función del recubriamiento del elemento. En el elemento superior la abertura de fisura en superaficie será el doble de la que se medirá en el elemento inferior. Sin embargo, a nivel de la barra, ambos elementos tendrán, en principio, la misma aberatura de fisura.
Una forma de tener en cuenta este aspecto es exigir el cálculo de la abertura de fisura para un recubrimiento nominal (por ejemplo 25 mm, por ser éste una valor tradicional) a efectos de limitar su valor por razones de durabilidad, mientras que se haaría el cálculo con el recubrimiento real a efectos de apariencia o control de las aberturas de fisura reales en obra.
5Límites de esbeltez para vigas y losasLos límites de esbeltez planteados en EN 1992-1-1 para eviatar el cálculo de deformaciones llevan implícitos una serie de supuestos cuya variación influye de forma muy significativa en los valores de dichos límites [15]. En particular, la formulaación actual lleva implícita una relación entre carga permanente (Qperm) y carga total (Qtot) del 60% y considera la fisuración solamente debida a la carga cuasipermanente, y no tiene en cuenta que la posible aplicación de la sobrecarga característica daría lugar a un deterioro del efecto de la contribución de la resistencia a tracción del hormigón entre fisuras. Este último supuesto, adoptado en su día para no incrementar los valores de límites de esbeltez tradicionales manejados hasta esta fecha, no es consistente con métodos constructivos muy habituales en los que se cimbran en edificios dos o tres plantas sobre las losas ya construidas induciendo en las mismas cargas que se aproximan a sus valores característicos, y ha sido criticado por Vollum [16].
En la figura 12 se muestra la influencia de la relación Qperm/Qtot en el valor del límite de esbeltez para un hormigón C30/37. Se observa una diferencia importante. Para una cuantía geo-mé trica de la armadura traccionada ρ = As/ (bd) = 1,5%, se obtienen valores de la relación luz/flecha (L/f) de 15,5 para Qperm/Qtot = 50%, 14,1 para Qperm/ Qtot = 60% y 12,3 para Qperm/Qtot = 75%. Hay por tanto un amplio margen de maniobra y resulta deseable incorporar esta variable en el modelo.
De la misma forma, en la figura 13 se muestra la influencia de considerar la aplicación de la carga característica o solamenate la de la carga cuasipermanente a efectos de evaluar la contriabución del hormigón entre fisuras. El gráfico está obtenido para un hormigón C30/37 y una relación Qperm/ Qtot = 60%. Se obserava que la diferencia se concentra en la zona de cuantías bajas, debido a que, para cuantías altas, el efecto de la contribución del hormigón entre fisuras es mucho menos importante. Aunaque la diferencia es relativamente modesta (L/f = 20 si sólo se considera la carga cuasipermanente y L/f = 19 si se considera la carga característica), se podrían obtener valores mayores para otras resistencias y otras distribuciones de carga y se considera necesario corregir el modelo actual para adaptarlo a la considearación de unas condiciones de contribución del hormigón entre fisuras más desfavorables.
Finalmente, se hace hincapié en el carácter prestacional que debe tener la normativa moderna, de tal forma que debe ser el propietario de la estructura quien decida cuál es el límite admisible para las flechas de su estructura en función del uso que quiera darle a la misma. Queda claro que la formulación del límite de esbeltez variará de forma importante si se fija el límite de la flecha en L/300 o L/200 en lugar del valor adoptado actualmente de L/250.
Se propone por tanto modificar la formulación de los límites de esbeltez para tener en cuenta los siguientes parámetros, acatualmente implícitos o no considerados:
- •
Distribución de la carga (es decir, relación Qperm/Qtot).
- •
Aplicación de la sobrecarga característica simultáneamente con el peso propio de la estructura, con objeto de minimizar el efecto de la contribución del hormigón entre fisuras, obateniendo un modelo más conservador, dado que el modelo actual podría quedar del lado de la inseguridad.
- •
Generalización de la formulación para poder fijar el límite admisible de la flecha.
Como se deduce del cuerpo de este artículo, el Eurocódigo de hormigón estructural EN 1992, siendo un buen documento, requiere una serie de modificaciones y adiciones importantes de cara a su aplicación práctica. En este trabajo se han detallado y fundamentado algunas de ellas, todas las cuales tienen una clara aplicación al proyecto y además suponen un impacto ecoanómico sobre las estructuras que se proyectarán en el futuro:
- •
Debe mantenerse la posibilidad de seguir proyectando eleamentos sin armadura transversal con las mismas caracterísaticas de otras estructuras con gran tradición y que no han generado casos de patología. Para ello debe incorporarse a los modelos de cálculo la consideración de cómo está distriabuida la carga solicitante.
- •
Debe incorporarse un modelo para el proyecto de estructuaras con barras ancladas mediante placa. Dicho modelo debe tener una base física que permita analizar geometrías habiatuales con distintas calidades de los materiales y debe ajus-t a rse bien a la base empírica existente. Pa ra el lo ya existe una propuesta que se ha descrito brevemente en el apartado 3.
- •
Deben replantearse los límites a la abertura de fisura cuanado se disponen grandes recubrimientos y el límite máximo viene dado por condiciones de durabilidad. En estas circunsatancias no deben penalizarse los recubrimientos importantes porque en la proximidad de la barra la abertura de fisura en elementos con menor recubrimiento y con mayor recubriamiento serán, en principio iguales, aunque en superficie se observen grandes diferencias. La razón hay que buscarla en el cierre de las fisuras secundarias, no visibles, a medida que la abertura de fisura se mide más lejos de la barra.
- •
Resulta necesario adaptar la formulación del límite de esbelatez para incluir parámetros importantes que no contempla la formulación actual. Éstos son:
- –
La relación Carga permanente/Carga total
- –
La posibilidad de fisuración temprana por aplicación de la carga característica durante el proceso constructivo
- –
La posibilidad de que la propiedad exija otros límites a la fleacha (L/f = 200 o L/f = 300) en lugar del valor de L/250 que está implícito en la formulación actual, favoreciendo una fialosofía prestacional en el uso de la normativa
- –
Debe aprovecharse la revisión de los Eurocódigos para inacluir todos los aspectos anteriores de tal forma de hacer progreasar la normativa, incorporando el conocimiento acumulado en los últimos años y que no estaba disponible durante el proceso de redacción de la versión actual.



















![Ejemplo de la influencia de la relación a/d en la resistencia a cortante de elementos sin armadura transversal (Ensayos de Díaz de Cossío y Siess [1]). Ejemplo de la influencia de la relación a/d en la resistencia a cortante de elementos sin armadura transversal (Ensayos de Díaz de Cossío y Siess [1]).](https://static.elsevier.es/multimedia/04395689/0000006500000272/v2_201807260414/S0439568914700038/v2_201807260414/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Esquema estructural de ensayo de los elementos de la referencia [3]. Se ensayan a cada lado del apoyo central un voladizo sometido a carga puntual y otro sometido a carga uniforme o triangular manteniendo constante la relación M/V. Esquema estructural de ensayo de los elementos de la referencia [3]. Se ensayan a cada lado del apoyo central un voladizo sometido a carga puntual y otro sometido a carga uniforme o triangular manteniendo constante la relación M/V.](https://static.elsevier.es/multimedia/04395689/0000006500000272/v2_201807260414/S0439568914700038/v2_201807260414/es/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Resultados brutos de los ensayos de la referencia [3]. Resultados brutos de los ensayos de la referencia [3].](https://static.elsevier.es/multimedia/04395689/0000006500000272/v2_201807260414/S0439568914700038/v2_201807260414/es/main.assets/thumbnail/gr3.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
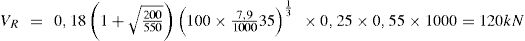









![Contrastación experimental del modelo propuesto frente a los ensaayos de referencia (De Vries [8]). Contrastación experimental del modelo propuesto frente a los ensaayos de referencia (De Vries [8]).](https://static.elsevier.es/multimedia/04395689/0000006500000272/v2_201807260414/S0439568914700038/v2_201807260414/es/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Seguridad del modelo evaluada utilizando los ensayos de De Vries [8]. Seguridad del modelo evaluada utilizando los ensayos de De Vries [8].](https://static.elsevier.es/multimedia/04395689/0000006500000272/v2_201807260414/S0439568914700038/v2_201807260414/es/main.assets/thumbnail/gr8.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)




