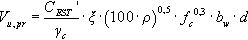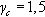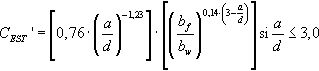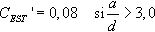El mecanismo de resistencia a esfuerzo cortante de las secciones de hormigón armado, es muy complejo, debido al gran número de factores influyentes que intervienen en la evaluación de esta resistencia. Dentro del marco de una investigación más extensa se realiza un análisis de las formulaciones que incorporan las normas ACI 318-11, CM 2010, EC-2 y EHE-08 a la luz de los resultados de ensayos existentes sobre rotura por cortante en elementos lineales sin armadura transversal. Aunque de los resultados del análisis se desprende la validez de los modelos simples de comprobación, se establecen conclusiones sobre la conveniencia de modificar las formulaciones actuales para mejorar su coherencia y su ajuste con los resultados experimentales.
© 2013, Asociación Científico-Técnica del Hormigón Estructural (ACHE). Publicado por Elsevier España, S.L. Todos los derechos reservados.
It can be demonstrated that the mechanism of resistance regarding shear is very complex because of the great number of factors involved in the evaluation of this resistance. Within the framework of a more extensive investigation, an evaluation of the equations of the Spanish, European and American codes has been made in light of existing tests with reinforced concrete beams without transverse reinforcement on shear failure. Even though the validity of these simple verification models can be gathered from results of the analysis, conclusions about the convenience of modifying the current formulations to improve the coherence and the adjustments between theory and investigation have been established.
© 2013, Asociación Científico-Técnica del Hormigón Estructural (ACHE). Published by Elsevier España, S.L. All rights reserved.
Actualmente no existe un modelo sin lagunas con el que se pueda predecir el fallo por esfuerzo cortante en elementos de hormigón armado sin armadura transversal. Sin embargo, en las últimas décadas, se han desarrollado modelos físicos o mecánicos basados en la mecánica de la fractura o de análisis no lineal con elementos finitos que permiten una buena aproximación del fenómeno, identificando parámetros y coeficientes a partir de una cierta experimentación [1–4].
No obstante lo anterior, debido al carácter prestacional de los marcos reglamentarios estructurales, la evaluación de la capacidad última a cortante de elementos de hormigón armado sin armadura transversal se simplifica en las normativas vigentes mediante la aplicación de una fórmula derivada de un ajuste experimental (en la que, en general, se identifican los parámetros más influyentes pero en la que no se cuantifica la interferencia de otros efectos relevantes), como alternativa a la aplicación de un modelo racional estructural de respuesta más complejo.
Las primeras investigaciones que se realizaron mediante modelos experimentales (Mörsch, E., 1909) se plantearon con el objetivo de determinar la relación entre la tensión media de cortante con la resistencia a tracción del hormigón. Actualmente, los modelos experimentales son la base de varios códigos vigentes para el cálculo del estado límite último a cortante, aunque existen notables diferencias entre las distintas fórmulas empíricas debido a varios factores:
- •
La falta de certeza en la influencia de los parámetros en la resistencia cortante, que se complementa con la complejidad de expresarlos en una fórmula del modo más simple posible.
- •
La representación de algunos parámetros influyentes es escasa en los ensayos considerados (sirva como ejemplo los pocos ensayos realizados de vigas con poca armadura longitudinal, de vigas realizadas con hormigones de alta resistencia o de vigas sometidas a solicitaciones de tracción).
- •
La resistencia a tracción del hormigón a menudo no es evaluada ni controlada.
Dentro del ámbito de una investigación más extensa, cuya parte experimental, realizada en el Laboratorio Central de INTEMAC, ha cubierto tanto el campo de los hormigones convencionales como de los hormigones de altas prestaciones, se realiza un análisis de las formulaciones que incorporan el Eurocódigo 2 [5] (EC-2), la Instrucción Española [6] (EHE-08), el Código Modelo 2010 [7] (CM 2010) y el Código ACI 318-11 [8]. El objetivo de este análisis es evaluar la coherencia y el ajuste de estas formulaciones con los resultados experimentales.
Para realizar dicho análisis, adicionalmente se consideran los datos de los ensayos incluidos en la base de datos recopilados en 2008 por Collins, Benz y Sherwood [9], correspondiente a 1848 ensayos que fueron publicados entre 1948 y 2006.
2Objeto del análisisLas formulaciones empleadas en la evaluación de la resistencia a cortante de los elementos lineales sin armadura transversal, que contemplan normas de aplicación común en diversos países, son muy diferentes.
Además, estas formulaciones presentan algunas faltas de coherencia tanto en sí mismas como con los resultados experimentales obtenidos en diferentes investigaciones realizadas al efecto. A modo de ejemplo, como se expone más adelante, la formulación general para estimar esta resistencia recogida en la EHE-08 y el EC-2 es coincidente, si bien el valor del cortante mínimo definido propuesto en la formulación de la Instrucción EHE-08 se incrementa de manera sustancial frente a los valores estimados de acuerdo a la formulación referente a dicho cortante mínimo del EC-2.
Por ello se realiza un análisis comparativo entre las formulaciones contempladas en las diferentes normas siendo el objeto de este artículo presentar sus resultados así como los del análisis de su contraste y coherencia con los resultados de ensayo que presentan determinadas bases de datos experimentales disponibles.
A partir de lo anterior, en este análisis se indican, en primer lugar, las formulaciones teóricas incorporadas en las normas EC-2, EHE-08, ACI 318-11 y el Código Modelo. Además, se expone la base de datos experimentales considerada para pasar a continuación a realizar el análisis de contraste de las formulaciones teóricas citadas.
En función de los resultados de este análisis se establecerán las conclusiones que se deriven y se formulará una propuesta de recomendaciones para mejorar en su caso tanto la metodología como el ajuste de la comprobación indicada.
3Formulaciones teóricas sobre el comportamiento a esfuerzo cortanteSe consideran como significativas, para el presente estudio, las formulaciones incorporadas en la vigente EHE-08, en el EC-2, en el CM 2010 y en el Código ACI 318-11, tanto por su relevancia actual en el ámbito de la práctica como por su notoriedad en el ámbito de la investigación sobre esfuerzo cortante. A continuación se resumen los aspectos más importantes que incorporan los procesos de dimensionamiento y comprobación de la capacidad última a esfuerzo cortante por tracción excesiva de alma de acuerdo con los modelos y formulaciones citadas.
3.1Formulación EC-2La resistencia de cálculo a cortante de la pieza sin armadura de cortante (VRd,c) ha de ser superior al valor de cálculo del esfuerzo cortante (VEd):
donde:
con un valor mínimo de:
donde:
fck Resistencia característica a compresión (MPa)
Asl Área de armadura longitudinal (mm2)
σ′cd Tensión axil media en el alma de la sección (tracción negativa)
Nd Fuerza axil en el alma de la sección (compresión positiva) (N)
Ac Área bruta de la sección de hormigón (mm2)
γc Coeficiente parcial de seguridad, igual a 1,5
d Canto útil (mm)
bw Anchura mínima de la sección a lo largo del canto útil (mm)
En la versión definitiva del Eurocódigo, se pone el acento en el análisis seccional propuesto, y la contribución al esfuerzo de cálculo a cortante VEd debe ser multiplicada por un término reductor β=av/(2·d) si la carga se encuentra a una distancia de 0,5·d<av<2,5·d del apoyo, aunque dicha reducción solo sea válida para cargas aplicadas en la parte superior del elemento y donde la armadura longitudinal esté completamente anclada al nudo. Para distancias de carga que cumplan av<0,5·d, el valor de b será constante e igual a 0,25, donde cabe indicar que el término av se refiere a la distancia entre el borde de la placa de apoyo y el borde de la placa de aplicación de la carga [5].
3.2Formulación EHE-08Para estimar la capacidad resistente a cortante de elementos lineales de hormigón armado sin armadura transversal (Vu) se sigue la Ecuación (5) de origen experimental referente a piezas de hormigón armado en regiones fisuradas a flexión, la cual, del mismo modo que se indica en el apartado anterior referente al EC-2, debe ser superior al valor de cálculo del esfuerzo cortante en la sección considerada (Vd):
con un valor mínimo Vu,min que se obtiene de la Ecuación (6):
donde:
ρl Cuantía geométrica de la armadura longitudinal traccionada anclada a una distancia igual o mayor que d a partir de la sección de estudio.
b0 Anchura neta mínima menor del elemento (mm). En secciones rectangulares será el ancho y en secciones T o П será el ancho mínimo del alma.
fcv Resistencia efectiva del hormigon a cortante en N/mm2 de valor fcv=fck con fcv no mayor que 15N/mm2 en el caso de control indirecto de la resistencia del hormigón, siendo fck la resistencia a compresion del hormigón. La EHE-08 solo permite su uso hasta fck=100MPa, adoptando para fcv un límite superior de 60MPa.
σ′cd Tensión axil media en el alma de la sección (tracción negativa) con un valor máximo indicado en Ecuación (7)
γc Coeficiente de seguridad parcial igual a 1,5 en situación persistente o transitoria. En la formulación de la EHE-98, ya derogada, el coeficiente 0,18/γc se expresaba como 0,12, el cual es igual al valor resultado de operar 0,18/1,5.
Como puede observarse, la ecuación general adoptada en la EHE-08 es semejante a la recogida en el EC-2, salvo en la estimación del valor del cortante mínimo que resiste la sección de estudio, sin que se haya encontrado en la bibliografía consultada justificación de este aspecto, y en la consideración de la influencia del efecto de la relación a/d.
3.3Formulación CM 2010Para determinar la resistencia a cortante VRd,c, el Código Modelo [7] permite varios niveles de aproximación, los cuales difieren en la complejidad de los métodos aplicados y en la precisión de los resultados.
En general, el nivel de aproximación I (Ecuación (8)) puede ser usado para el dimensionamiento de una nueva estructura:
donde:
kv Coeficiente cuya expresión es la siguiente:
z z≈0,9·d
fck Resistencia característica a compresión del hormigón a cortante en N/mm2 en el caso de que fck≤8MPa. En caso contrario, fck≤8MPa
El nivel de aproximación II es apropiado igualmente para el diseño de una nueva estructura así como para la valoración de una estructura existente pero no es aplicable a elementos sin armadura transversal.
En cuanto al nivel de aproximación III, es apropiado para el diseño de una estructura sometida a un estado de cargas complejo o para una valoración más elaborada de una estructura existente. Considera el diámetro máximo del árido y la deformación longitudinal en la fibra media de la sección.
La aplicación del nivel de aproximación IV requiere una cierta experiencia del proyectista para asegurar que los resultados obtenidos sean seguros y consistentes. La resistencia a esfuerzo cortante del elemento se determina mediante la comprobación de condiciones de equilibrio y compatibilidad de deformaciones usando diagramas de tensión-deformación apropiados para la armadura y el hormigón fisurado.
En todos los niveles de aproximación se considera el mismo término reductor β del esfuerzo de cálculo a cortante indicado en el EC-2.
3.4Formulación ACI 318-11La normativa americana [8] estima, de modo simplificado, la capacidad resistente a cortante de elementos lineales de hormigón armado sin armadura transversal no sometidos a solicitaciones axiles con la Ecuación (10):
donde:
fc′ Resistencia específica del hormigón a compresión (N/mm2) menor que 70MPa
bw Espesor mínimo del alma (mm)
Ø Coeficiente de comportamiento en cortante igual a 0,75
Cabe advertir que las formulaciones enunciadas no son directamente comparables, toda vez que la resistencia específica del hormigón (fc′) representa un fractil del 9% mientras que la resistencia característica del hormigón (fck) representa un fractil del 5%.
4Estudios previos y bases de datos experimentales disponiblesEl primero de los términos de la ecuación para calcular la capacidad resistente a cortante de las secciones recogida en la EHE-08 (Ecuación (5)) y el EC-2 (Ecuación (2)) fue deducido a partir de un estudio preliminar y análisis de regresión de los resultados experimentales de 201 ensayos en los cuales el efecto arco tenía poca influencia.
En 2008, Collins, Benz y Sherwood [9] elaboraron una base de datos de ensayos de elementos cuya rotura se había producido por cortante (ESDB). Son 1.848 ensayos que fueron publicados por la ACI y en Magazine of Concrete Research, en Engineering Structures, en Transactions of the Japan Concrete Institute y en varias tesis doctorales e informes de campañas experimentales. Dicha base de datos se realizó de modo que ningún ensayo fue intencionadamente ignorado y, por supuesto, incluye ensayos de las anteriores bases de datos de ensayos publicadas en 1962, 2002, 2003 y 2006 por la ACI. Las reglas generales de selección de ensayos para la realización de la base citada son las siguientes:
- •
Hormigón armado.
- •
Secciones rectangulares y con forma de T.
- •
Sin solicitaciones axiles (tracción o compresión).
- •
Sin armadura transversal.
- •
Sin restricciones en el límite elástico de la armadura longitudinal.
- •
Cargas puntuales y cargas uniformes.
- •
Vigas simplemente apoyadas y continuas.
- •
No aparecen ensayos con fallos de anclaje.
- •
Sin límites geométricos.
En el presente estudio, intencionadamente se eliminan aquellos ensayos que pueden inducir resultados con mayores desviaciones y, en consecuencia, menos precisos (tal es el caso de aquellos ensayos cuyo modo de fallo observado fue por flexión y ensayos realizados con cargas uniformes).
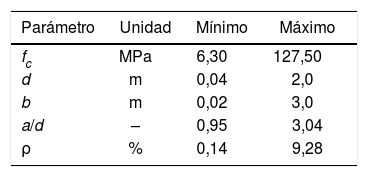
En la tabla 1 se muestran los intervalos de cada parámetro considerados en el análisis de regresión realizado que se expone en los siguientes apartados:
5Ajuste de la formulación de los modelos de la EHE-08, EC-2, CM 2010 y ACI 318-11Tal y como se indica anteriormente, el Estado Límite de Agotamiento por esfuerzo cortante en piezas sin armadura transversal se produce por tracción excesiva del alma. La expresión indicada por la EHE-08 y por el EC-2 es de origen experimental (Ecuación (2) y Ecuación (5)) y presenta dos términos sumatorios: el primer término depende tanto de la resistencia del hormigón fck como de la cuantía ρl de la armadura longitudinal de tracción existente y el segundo término refleja la influencia de las solicitaciones axiles, tanto de tracción como de compresión.
La estructura de la formulación del primer término fue obtenida por Zsutty a partir de un análisis de regresión [10]. Antes de realizar el análisis de regresión, Zsutty propuso un análisis dimensional para obtener el formato básico de la ecuación de predicción de capacidad cortante aplicando el teorema de П de Buckingham con el que llegaba a cuatro términos adimensionales a partir de las variables Vcr (capacidad a esfuerzo cortante), b (ancho), d (canto efectivo), As (área de armadura longitudinal traccionada) y a (distancia del apoyo al punto de aplicación de la carga puntual en elementos biapoyados sometidos a cargas puntuales), los cuales son los siguientes:
Zsutty rechazó tener en consideración el término adimensional b/d porque los valores b/d de los ensayos pertenecientes a la base de datos disponible eran semejantes y asumió que dicho cociente tenía muy poca influencia en la capacidad a cortante de elementos de proporciones normales. La ecuación adimensional para predecir la capacidad a cortante de un elemento estructural usada por Zsutty para el análisis de regresión fue:
En realidad, Zsutty decidió realizar dos análisis de regresión: uno para aquellos ensayos con relaciones a/d menores que 2,5, en los que se movilizaba el efecto arco, y otro para los ensayos con relaciones a/d mayores que 2,5.
El análisis de regresión realizado sobre los 151 elementos lineales con relaciones a/d mayores que 2,5, en los que actúan esfuerzos de flexión y cortante combinados, arrojaron los siguientes resultados, donde b1, b2 y b3 son las incógnitas a determinar de la Ecuación (15) mediante este procedimiento de análisis [11] (tabla 2).
Valores obtenidos por Zsutty mediante análisis de regresión de las incógnitas de la Ecuación (15) con 151 ensayos con relaciones a/d >2,5
| b1 | b2 | b3 | Coeficiente de variación del error |
|---|---|---|---|
| 0,31 | 0,37 | 0,27 | 9,8 % |
El bajo coeficiente de variación del error indicó que la ecuación propuesta era consistente y que era posible una predicción satisfactoria para la capacidad a cortante de elementos lineales con relaciones a/d mayores que 2,5. Sin embargo, en el caso del análisis realizado en las 60 vigas sometidas al efecto arco, Zsutty consideró que los resultados no aportaban una ecuación satisfactoria y que era necesaria una investigación más profunda para predecir la capacidad a cortante en estos casos en los que la influencia del tamaño, la posición de las cargas y las condiciones de apoyo inducían una pobre correlación con un coeficiente de variación del error superior a un 25%.
En el caso de realizar el análisis con los datos cuya relación a/d fuera mayor que 2, el coeficiente de variación se incrementaba a un 15%. Esta es la razón por la que Zsutty estableció este valor para distinguir aquellos ensayos gobernados por el efecto viga y aquellos gobernados por el efecto arco.
Una vez obtenidos estos datos, Zsutty atendió al hecho de que los valores b1, b2 y b3 eran muy próximos entre sí y decidió racionalizar el resultado de su análisis aproximándolos a un valor igual a 1/3 para relaciones a/d>2,5, sin afectar sensiblemente a las conclusiones ya expuestas.
El Código Modelo CEB-FIP, en 1990, sugiere [12] una fórmula empírica basada en la Ecuación (15), añadiendo un término adicional para tener en cuenta el efecto tamaño. König y Fischer [13] utilizaron esta fórmula experimental para realizar un análisis de regresión sobre 176 ensayos que avalaron una correcta deducción del término C de la estructura de esta formulación (C·k·(100·ρl·fc)1/3). La Instrucción española, en 1998, y el Eurocódigo, en 2004, adoptaron esta formulación en valores de diseño.
Consecuentemente, dado que en la ESDB se incluye una relación de un número importante de ensayos cuya relación a/d es menor que 3, para realizar el análisis de los resultados obtenidos de la base de datos y de la campaña experimental realizada se considera necesario [14] que la influencia de la relación a/d se incluya tanto en la formulación expuesta en la EHE-08 como en la de la ACI 318-11, tal y como dedujo Zsutty para valores de relación a/d menores de 2,5 en la expresión que postuló de origen experimental y según recomendaron Hedman y Losberg [15] con relaciones a/d menores de 3.
En este sentido, las formulaciones del EC-2 y CM 2010 incluyen la influencia de la relación a/d, tal y como se indica en los apartados 3.1 y 3.3, por lo que no ha sido necesario deducir ningún modelo adicional.
La expresión deducida de la formulación para estimar la capacidad a cortante de los ensayos que no están sometidos a esfuerzos axiles según la EHE-08, es la Ecuación (16) expresada en valores medios:
donde fc es la resistencia media a compresión del hormigón en la fecha del ensayo, y CEHE′ es el factor que representa la influencia adicional de la forma de la sección y de la relación a/d y que, por consiguiente, es necesario deducir a partir de un análisis de regresión.
La influencia de la forma de la sección sobre la capacidad a cortante fue originalmente intuida por los investigadores P.M. Ferguson y J.N. Thompson en 1953 [16]. Realizaron 24 ensayos en vigas biapoyadas de sección constante en T en varias series, en las cuales se variaba principalmente el ancho del alma, bien a lo largo de todo el canto de la sección o parcialmente a distintas alturas. Demostraron con esta campaña experimental que las ecuaciones usadas en la época podrían ser conservadoras cuando la dimensión del ancho del alma fuera mayor en la fibra neutra, a partir de lo cual convenía tener en cuenta una dimensión algo mayor del ancho mínimo del alma para el cálculo de la capacidad a cortante en vigas en T.
Por consiguiente, los modelos que predicen los valores de ensayo deberían incluir dicho efecto [17].
Se ha realizado un análisis de regresión simple mediante el método denominado «Stepwise» consistente en analizar únicamente la relación de la variable de respuesta Vc,EHE-08, la cual consta a su vez de varias variables cuya importancia en el modelo es significativa, con la variable predictora a/d. Dado que, a priori, no se puede deducir el tipo de modelo más razonable para explicar la relación de estos dos términos, se seleccionan varios subconjuntos de casos que tengan un valor particular para la variable predictora (0,50, 0,75, …, 3,00) y, consecuentemente, sirvan para estimar el modelo de regresión.
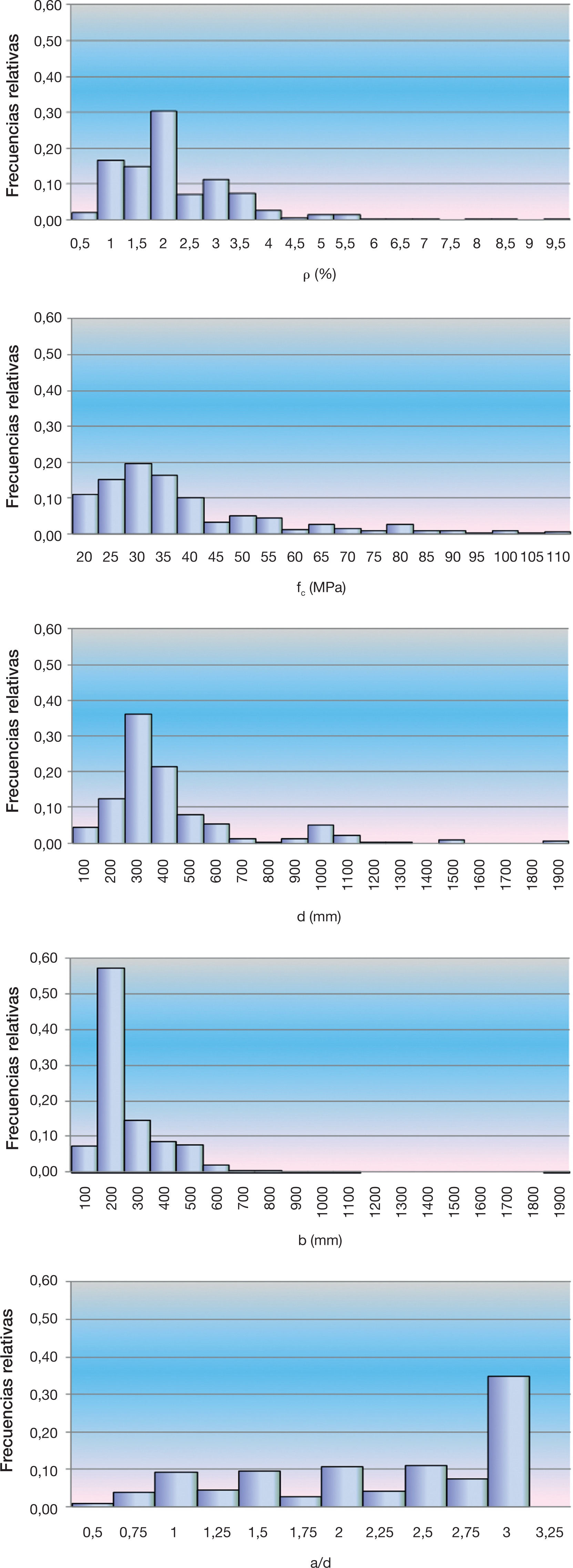
En total se seleccionan 935 ensayos de ESDB (los intervalos de cada parámetro han sido indicados en la tabla 1), cuyo número de datos es incluso mayor que el utilizado por los ya citados por Zsutty y König y Fischer para deducir el coeficiente CEHE′. En la figura 1 se muestran las frecuencias relativas de cada uno de los parámetros considerados.
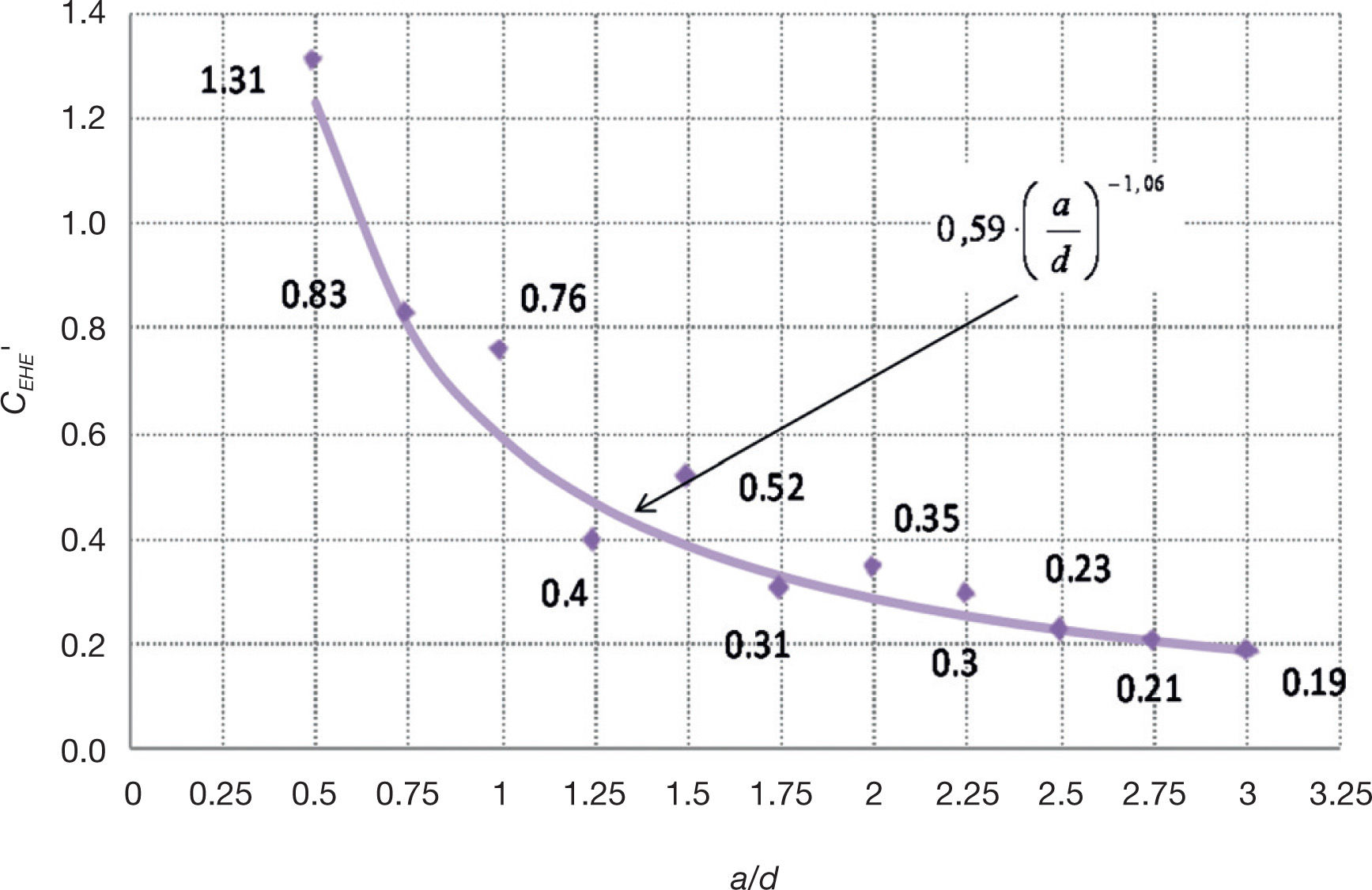
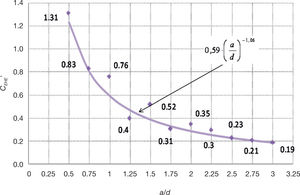
El siguiente paso es describir estadísticamente los datos observados para la variable de respuesta y la variable predictora mediante un tipo de tendencia potencial que, se considera, se ajusta con una mayor precisión a los valores discretos obtenidos por cada subconjunto seleccionado, con independencia de la forma de la sección transversal, tal y como se muestra en el gráfico de la figura 2.
Consecuentemente y como se indica anteriormente, se contemplan los ensayos con secciones transversales en forma de T en cada subconjunto de datos y se realizan nuevos análisis de regresión simple considerando únicamente los ensayos con forma de T en cada subconjunto de datos.
Los valores discretos de las variables predictoras en los modelos de regresión simple de la variable respuesta fueron menores para los subconjuntos de todos los ensayos considerados que para los subconjuntos de ensayos con secciones en T, siendo aproximadamente iguales con relaciones a/d superiores a 3,5. Por tanto, se deduce que la influencia de la forma de la sección considerada para predecir la capacidad a cortante debe ser tenida en cuenta, en especial con relaciones a/d bajas.
En este sentido, varios investigadores han considerado la influencia de este parámetro en sus fórmulas predictoras. Por ejemplo, Bairán, Marí, Romia y Ametller [18] presentaron un estudio paramétrico sobre el comportamiento resistente de secciones de hormigón armado sometidas a esfuerzo cortante y a solicitaciones axiles en el que incluían dicha influencia para relaciones a/d iguales a 1,5, 2 y 3. Del mismo modo, Haddadin, Hong y Mattock [19] incluyeron la influencia de la geometría de secciones en T junto con la influencia de la relación a/d al estimar la eficacia de la disposición de cercos en un elemento lineal sobre la capacidad a cortante.
Por tanto, adicionalmente se introduce la influencia de la forma de la sección del elemento lineal en el caso de que la relación a/d sea menor que 3 mediante la relación bf/bw, donde bf es el ancho del ala sometida a tensiones de compresión por el momento aplicado y bw es el ancho mínimo del alma de la sección (equivalente a la variable b0 indicada en la EHE-08 para secciones en T con ancho de alma constante). Para ello se realizó un nuevo análisis de regresión múltiple considerando todos los ensayos con secciones en forma de T de la base de datos de Collins, Benz y Sherwood cuya relación a/d fuera menor que 3 para realizar el ajuste del término que incluyera la variable predictora bf/bw.
En total se han considerado 65 ensayos para realizar el análisis de regresión múltiple que implemente la influencia de la forma de la sección. Sin embargo, dado el bajo número de ensayos que presentan valores de la variable bf/bw superiores a 3 (7 ensayos), no se implementa un valor superior a 3.
Por consiguiente, la variable CEHE′ incluye la influencia de la forma de la sección transversal y de la relación a/d y responde a la tendencia potencial siguiente:
Con la formulación del código ACI 318-11 se sigue el mismo procedimiento, obteniendo la variable CACI′, que se desprende de la Ecuación (19), de tendencia potencial, y que multiplica la expresión simplificada para la estimación de la capacidad a cortante de la normativa americana en valores medios, del siguiente modo:
6Análisis cualitativo de los modelos de cálculoEn este apartado se ponen de relieve varios aspectos que deben ser observados en el modelo de cálculo deducido de la EHE-08 para elementos de hormigón armado sin armadura transversal no solicitados a esfuerzos axiles, objeto del presente análisis:
- •
El modelo de la EHE-08 y el EC-2 establece recomendaciones de valores límite en las variables predictoras por escasez de evidencias experimentales. Sirva como ejemplo la limitación establecida para el valor de la variable ξ con la que se incluye la influencia del efecto tamaño (no mayor que 2,0), la limitación de la cuantía geométrica longitudinal (no mayor que 0,02) o la limitación de la resistencia efectiva del hormigón a cortante (no mayor que 60MPa). Dicho aspecto debería ser revisado con bases de datos experimentales actualizadas.
- •
Los modelos citados establecen un valor de cortante mínimo, si bien este límite inferior no es el mismo (ver Ecuación (3) y Ecuación (6)). Dicho límite fue establecido para evitar que la estimación de la capacidad a cortante fuera nula en elementos estructurales con una cuantía de armadura longitudinal nula [20]. Cabe indicar que en ambos casos, en la bibliografía consultada, no se incluye ninguna justificación o evidencia experimental sobre su aplicación. En concreto, debería ser analizada la investigación experimental realizada con elementos de hormigón armado con bajas cuantías (ρ<0,6 %) y grandes cantos (d>1000mm), tanto en hormigones convencionales como de altas prestaciones. Además, la necesidad del establecimiento de un valor mínimo a cortante debería ser objeto de estudio, toda vez que ambas normas contemplan la influencia de las solicitaciones axiles de compresión y el uso de hormigón en masa y definen una cuantía mecánica mínima para la comprobación y dimensionamiento de elementos de hormigón armado.
- •
La influencia de parámetros tales como la relación a/d o la forma de la sección [21] puede llegar a ser relevante en la evaluación de la capacidad resistente del elemento por lo que dicho aspecto debería, al menos, ser investigado y, en su caso, ser implementado en las expresiones de los modelos considerados en este estudio.
Se contempla la posibilidad de un nuevo ajuste de la expresión indicada por el EC-2 y la EHE-08 para calcular el esfuerzo cortante de agotamiento por tracción en el alma en elementos lineales sin armadura transversal que no están sometidos a solicitaciones axiles, extraída previamente la seguridad mediante análisis de regresión semejantes a los indicados anteriormente considerando los datos de la ESDB, ya citada.
Se reconsidera el procedimiento de análisis de regresión múltiple realizado por Zsutty sobre una expresión semejante a la Ecuación (15) para predecir la capacidad a cortante de un elemento estructural lineal sin armadura transversal y sin considerar la aplicación de solicitaciones axiles:
donde:
VEST Esfuerzo cortante de agotamiento en valores de ensayo sin considerar la influencia de las solicitaciones axiles de tracción (N)
bw Anchura neta mínima menor del elemento (mm). Es equivalente a la variable b0 considerada en la formulación de la EHE-08
Adicionalmente, se considera que la variable k responde a la Ecuación (21):
donde K es una constante por determinar en el análisis de regresión
En este sentido, es de destacar que no se incluye el término ξ, dependiente del canto efectivo, como variable predictora del análisis múltiple de regresión, dado que se conserva el factor de corrección por efecto tamaño incluido en la Instrucción EHE-08 en la expresión del ajuste. El hecho de considerar esta variable como predictora en el análisis supondría la modificación de la expresión del factor ξ.
Asimismo, la fórmula de ajuste no considera los límites superiores de las variables correspondientes a la cuantía geométrica de armadura longitudinal y a la resistencia a compresión del hormigón que se incluyen en la EHE-08 o el EC-2 así como las expresiones que establecen un valor mínimo de cortante (cuya justificación experimental no se ha encontrado en la bibliografía consultada), para no condicionar a priori los resultados estadísticos del modelo de regresión.
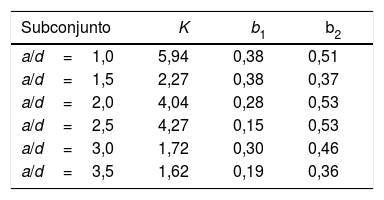
Al igual que antes, para realizar los análisis de regresión múltiple se consideran los subconjuntos de datos de la ESDB con relaciones a/d constantes e iguales a 1,0, 1,5, 2,0, 2,5, 3,0 y 3,5. Hay que recordar que por cada subconjunto considerado de datos que presenta relaciones a/d semejantes se realiza un análisis de regresión y, por consiguiente, no se puede evaluar su influencia como variable predictora en un análisis múltiple de regresión que incluya únicamente los datos del subconjunto establecido. Por consiguiente, en el análisis de regresión múltiple realizado en cada subconjunto de datos se han eliminado los términos referentes a a/d y b3 dado que se ha considerado insignificante su influencia en cada subconjunto.
Específicamente, las constantes K, b1 y b2 de la Ecuación (20) se obtienen finalmente del análisis múltiple de regresión de cada subconjunto de datos en la forma logarítmica de la Ecuación (22):
Los valores de las constantes resultantes del análisis de regresión realizado para cada subconjunto de datos se muestran en la tabla 3.
Al igual que Zsutty decidió aproximar los valores de las variables b1 y b2 a un valor igual a 1/3 para relaciones a/d>2,5, se decide racionalizar la expresión del ajuste con un valor de b1 igual a 0,3 y un valor de b2 igual a 0,5, los cuales representan el valor medio de los valores obtenidos de cada coeficiente por subconjunto de datos considerado.
En este sentido, se propone una expresión en la que la influencia de la cuantía geométrica de armadura longitudinal es mayor que en la Ecuación (16), la cual, expresada en valores medios, es la siguiente:
donde CEST′ es el factor que representa la influencia adicional de la forma de la sección y de la relación a/d y que es necesario deducir a partir de análisis simples adicionales de regresión mediante el método «Stepwise» indicados en el apartado anterior. Responde a la Ecuación (24) para relaciones a/d<3 [21]:
Cabe indicar que las predicciones expuestas para la propuesta preliminar de la capacidad a cortante en elementos de hormigón armado sin armadura transversal realizada por Cladera y Marí [22] concluyen en una influencia proporcional a ρ0,5 tanto para hormigones de altas prestaciones como para hormigones normales mediante la aplicación del desarrollo de Redes Neuronales Artificiales (ANN), del mismo modo que recogemos en la Ecuación (23).
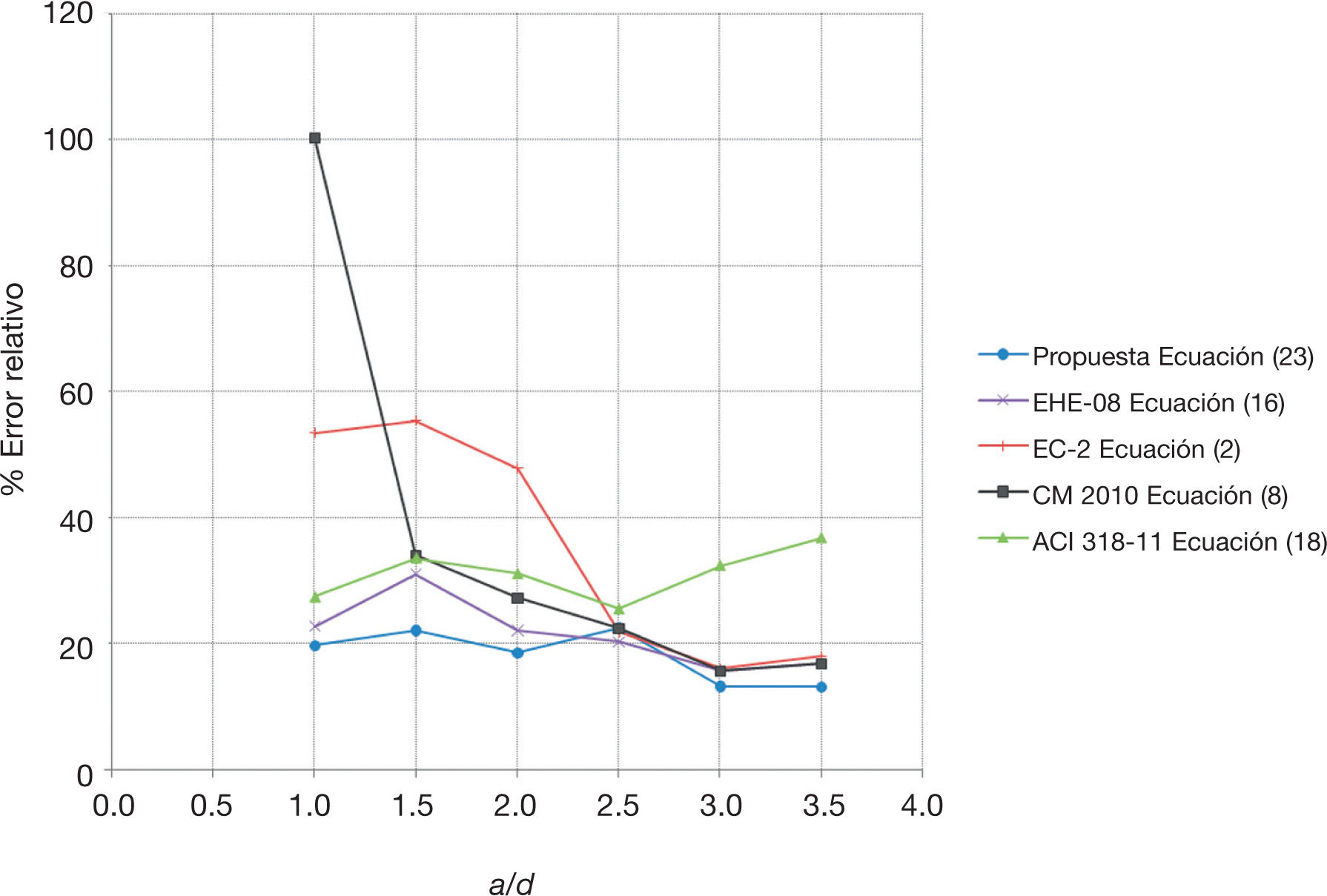
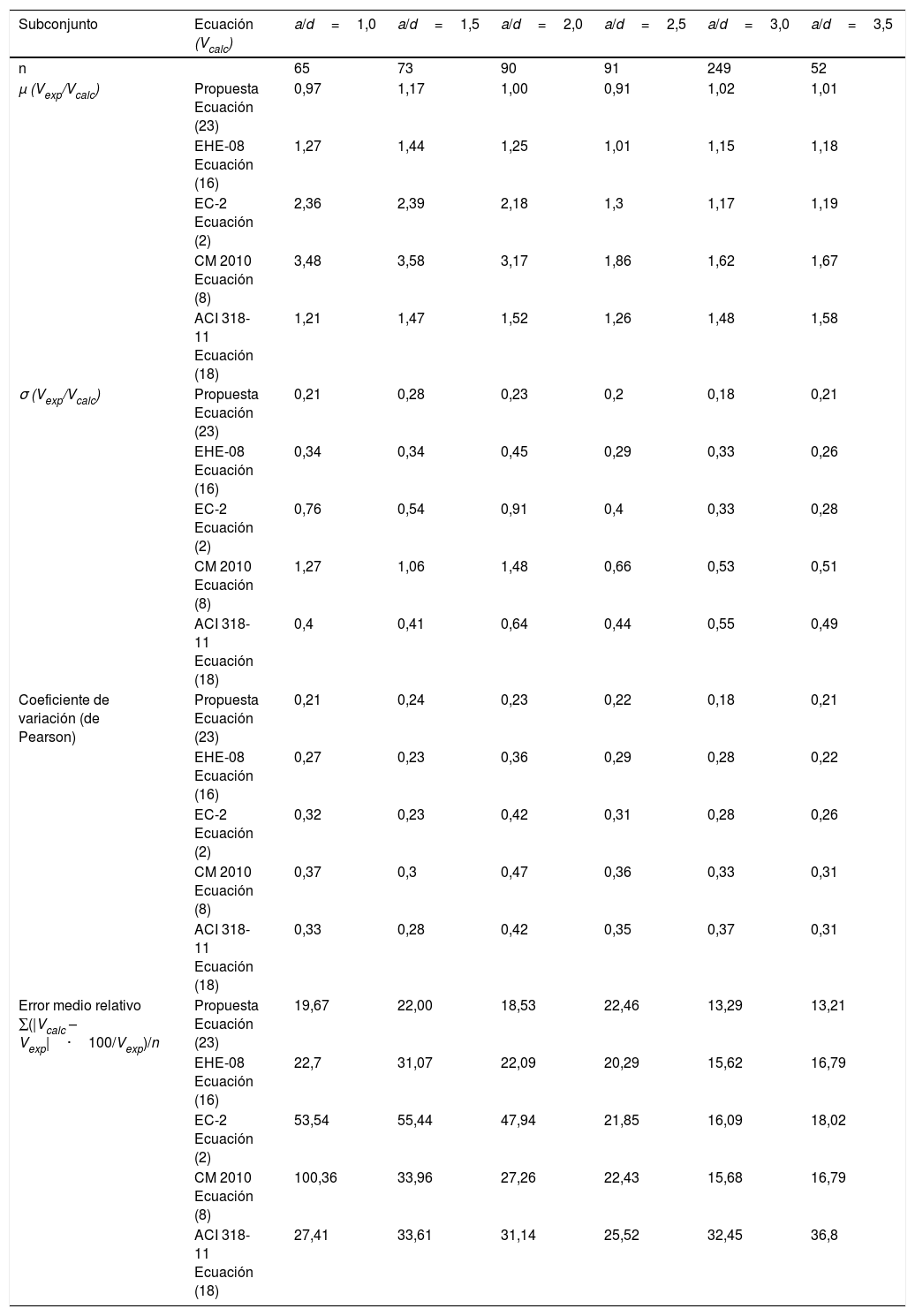
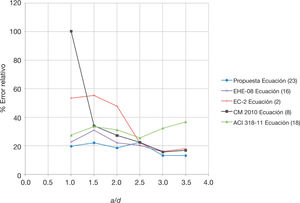
8Análisis y comparación de las diferentes propuestas de evaluación de la capacidad a cortante de elementos de hormigón armado sin armadura transversal sin considerar la influencia de solicitaciones axilesEn la tabla 3 se muestran los resultados estadísticos obtenidos al comparar los valores de esfuerzo cortante de agotamiento de los ensayos seleccionados (Vexp) con las estimaciones obtenidas (Vcalc) con la Ecuación (23), la Ecuación (16) del modelo deducido de la EHE-08, la Ecuación (2) del deducido del EC-2, la Ecuación (8) dada por el nivel de aproximación I del CM 2010 y la Ecuación (18) del modelo deducido de la ACI 318-11. Asimismo, en el gráfico de la figura 3 se comparan los errores relativos (según eje de ordenadas) indicados en la tabla 4 por cada subconjunto de datos (en función de la relación a/d, según eje de abscisas) para los modelos de regresión analizados.
Valores de las constantes resultantes de los análisis de regresión múltiple realizados por cada subconjunto de ESDB
| Subconjunto | Ecuación (Vcalc) | a/d=1,0 | a/d=1,5 | a/d=2,0 | a/d=2,5 | a/d=3,0 | a/d=3,5 |
|---|---|---|---|---|---|---|---|
| n | 65 | 73 | 90 | 91 | 249 | 52 | |
| μ (Vexp/Vcalc) | Propuesta Ecuación (23) | 0,97 | 1,17 | 1,00 | 0,91 | 1,02 | 1,01 |
| EHE-08 Ecuación (16) | 1,27 | 1,44 | 1,25 | 1,01 | 1,15 | 1,18 | |
| EC-2 Ecuación (2) | 2,36 | 2,39 | 2,18 | 1,3 | 1,17 | 1,19 | |
| CM 2010 Ecuación (8) | 3,48 | 3,58 | 3,17 | 1,86 | 1,62 | 1,67 | |
| ACI 318-11 Ecuación (18) | 1,21 | 1,47 | 1,52 | 1,26 | 1,48 | 1,58 | |
| σ (Vexp/Vcalc) | Propuesta Ecuación (23) | 0,21 | 0,28 | 0,23 | 0,2 | 0,18 | 0,21 |
| EHE-08 Ecuación (16) | 0,34 | 0,34 | 0,45 | 0,29 | 0,33 | 0,26 | |
| EC-2 Ecuación (2) | 0,76 | 0,54 | 0,91 | 0,4 | 0,33 | 0,28 | |
| CM 2010 Ecuación (8) | 1,27 | 1,06 | 1,48 | 0,66 | 0,53 | 0,51 | |
| ACI 318-11 Ecuación (18) | 0,4 | 0,41 | 0,64 | 0,44 | 0,55 | 0,49 | |
| Coeficiente de variación (de Pearson) | Propuesta Ecuación (23) | 0,21 | 0,24 | 0,23 | 0,22 | 0,18 | 0,21 |
| EHE-08 Ecuación (16) | 0,27 | 0,23 | 0,36 | 0,29 | 0,28 | 0,22 | |
| EC-2 Ecuación (2) | 0,32 | 0,23 | 0,42 | 0,31 | 0,28 | 0,26 | |
| CM 2010 Ecuación (8) | 0,37 | 0,3 | 0,47 | 0,36 | 0,33 | 0,31 | |
| ACI 318-11 Ecuación (18) | 0,33 | 0,28 | 0,42 | 0,35 | 0,37 | 0,31 | |
| Error medio relativo ∑(|Vcalc – Vexp|·100/Vexp)/n | Propuesta Ecuación (23) | 19,67 | 22,00 | 18,53 | 22,46 | 13,29 | 13,21 |
| EHE-08 Ecuación (16) | 22,7 | 31,07 | 22,09 | 20,29 | 15,62 | 16,79 | |
| EC-2 Ecuación (2) | 53,54 | 55,44 | 47,94 | 21,85 | 16,09 | 18,02 | |
| CM 2010 Ecuación (8) | 100,36 | 33,96 | 27,26 | 22,43 | 15,68 | 16,79 | |
| ACI 318-11 Ecuación (18) | 27,41 | 33,61 | 31,14 | 25,52 | 32,45 | 36,8 |
En todo caso, al igual que Zsutty, se obtienen coeficientes de variación, dispersiones y errores relativos menores evaluando el esfuerzo cortante de agotamiento mediante la expresión propuesta que mediante la expresión de los modelos del EC-2 y del CM 2010 (nivel de aproximación I) y de los deducidos de la expresiones de la EHE-08 o la ACI 318-11. Del mismo modo, considerando una clasificación por Puntos de Demérito [21], semejante a la clasificación realizada por Cladera y Marí para estudiar la bondad de los diferentes procedimientos de cálculo y, en especial, de su propuesta preliminar [22], anteriormente citada, el ajuste propuesto obtiene la mejor puntuación, por lo que se mejora el ajuste del modelo deducido del EC-2 en el que se considera la influencia de la relación a/d.
Con el modelo propuesto, el del EC-2 y el deducido de la EHE-08, se obtienen bajas dispersiones y correlaciones que se consideran aceptables para predecir la capacidad a cortante de elementos sin armadura transversal sin aplicar solicitaciones axiles. Si bien, cabe indicar que con la predicción realizada mediante el modelo propuesto se obtiene un ajuste más preciso y que los resultados de la evaluación realizada con el modelo propuesto arrojan menores dispersiones que los resultados obtenidos con el modelo deducido de la EHE-08 y con el del EC-2 para relaciones a/d superiores a 2,5.
En cuanto a los resultados obtenidos con relaciones a/d menores o iguales que 2,5, de nuevo se comprueba que las conclusiones de Zsutty son aplicables a los modelos analizados obteniendo pobres correlaciones para los subconjuntos de datos estudiados. No obstante lo anterior, con el modelo propuesto se obtienen errores máximos relativos ligeramente superiores a un 20%, los cuales además suponen una reducción de los errores relativos en un 27% respecto a los obtenidos con el modelo deducido de las expresiones de la Instrucción EHE-08.
En concreto, en el caso del modelo del EC-2 y de la formulación considerada del CM 2010, si bien se considera adecuado contemplar el efecto arco, y lo que es más importante, contemplar dicha influencia en la evaluación de los esfuerzos solicitantes y no en la evaluación de la capacidad, se pone de manifiesto que la influencia de la relación a/d es mayor que la considerada en el modelo vigente europeo por lo que es posible reconsiderar este aspecto con bases de datos actualizadas.
En el caso del modelo del CM 2010 y del modelo deducido de la ACI 318-11, ambos arrojan resultados demasiado conservadores (μmedio=2,56 y 1,42, respectivamente), imprecisos y altamente dispersos (Coeficiente de variación medio=0,36 y 0,37, respectivamente) en todos los subconjuntos de datos considerados frente al modelo propuesto (μmedio=1,01 y coeficiente de variación medio=0,21). Es interesante observar que dichos modelos parece que han sido propuestos con cierta «hiporresistencia» sobre la capacidad real del elemento ensayado, cuya evaluación no se ha encontrado en la bibliografía consultada.
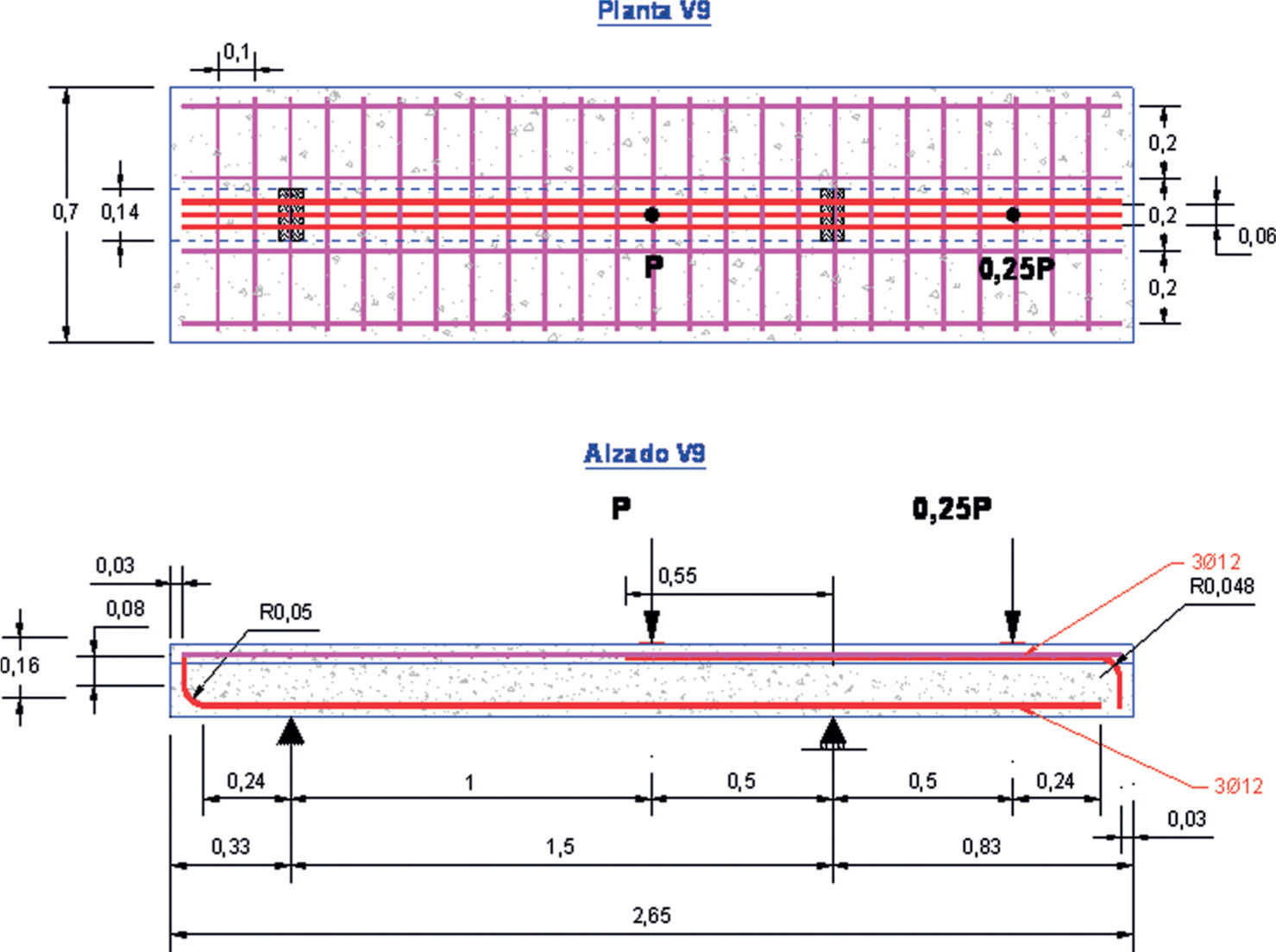
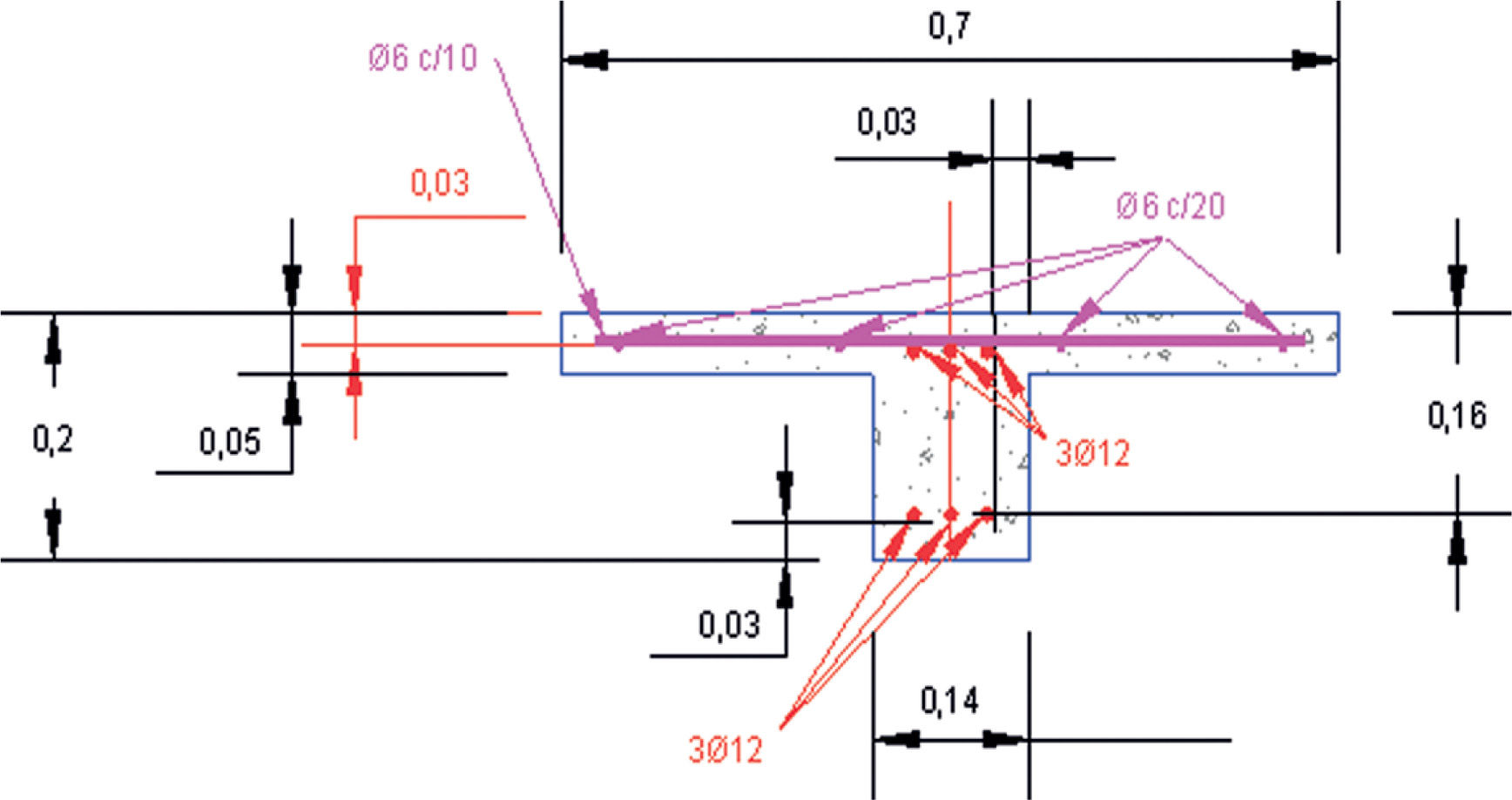
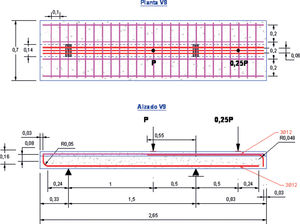
9Verificación experimentalEn el Laboratorio Central de INTEMAC se ha llevado a cabo una campaña experimental con hormigones convencionales y de altas prestaciones que se encuadró dentro de un programa de investigación (fig. 4) para [21], en el que se obtuvieron resultados para evaluar la influencia adicional de la forma de la sección y de las solicitaciones axiles de tracción en elementos sin armadura transversal. En todos los ensayos de dicha campaña se alcanzó la capacidad a esfuerzo cortante de los elementos estructurales. En la figura 5 se muestra un esquema de la disposición de ensayos (en concreto, de las vigas tipo V9 cuya cuantía de armadura longitudinal es aproximadamente igual a un 1,5%).
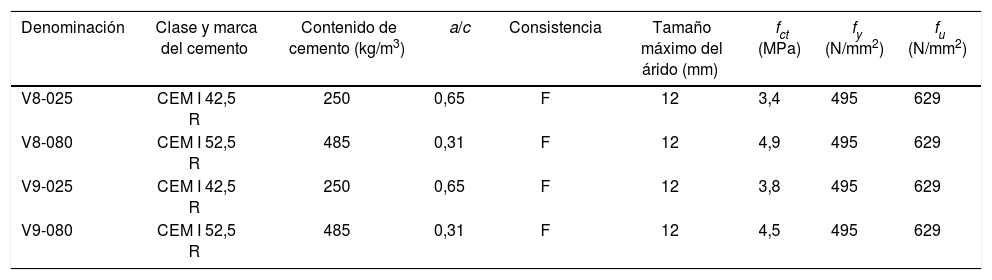
El acero previsto para la armadura pasiva de los elementos estructurales fue B500SD para barras longitudinales y B500T para la malla de la losa superior. Fueron ensayos con piezas fabricadas con hormigones convencionales, cuya resistencia característica a compresión fuera aproximadamente igual a 25MPa, y con hormigones de altas prestaciones, cuya resistencia a compresión fuera aproximadamente igual a 80MPa (ver valores adicionales de los materiales utilizados en la tabla 5).
Características de los materiales de la campaña experimental de [21]
| Denominación | Clase y marca del cemento | Contenido de cemento (kg/m3) | a/c | Consistencia | Tamaño máximo del árido (mm) | fct (MPa) | fy (N/mm2) | fu (N/mm2) |
|---|---|---|---|---|---|---|---|---|
| V8-025 | CEM I 42,5 R | 250 | 0,65 | F | 12 | 3,4 | 495 | 629 |
| V8-080 | CEM I 52,5 R | 485 | 0,31 | F | 12 | 4,9 | 495 | 629 |
| V9-025 | CEM I 42,5 R | 250 | 0,65 | F | 12 | 3,8 | 495 | 629 |
| V9-080 | CEM I 52,5 R | 485 | 0,31 | F | 12 | 4,5 | 495 | 629 |
En la campaña experimental se pudo observar que en todos los ensayos la fisuración diagonal por cortante es independiente del desarrollo de las fisuras por el momento flector existente, la cual comenzaba desde un punto interior en la viga cuando las tensiones principales de tracción superaban la resistencia a tracción del hormigón. Se iniciaba en la fibra neutra y se propagaba hacia el punto de carga en su parte superior y hacia los apoyos en su parte inferior. Estas fisuras cortaban las fisuras previas existentes por flexión. A partir de este momento, ocurrían dos tipos de fisuraciones: una debida al cortante en el alma y otra producida por la interacción flexión-cortante. El colapso ocurría poco después de que las fisuras diagonales hubieran llegado a tener muy poca pendiente (casi horizontales). En general, las fisuras que se formaban a lo largo de las barras longitudinales se desarrollaban gradualmente y eventualmente causaban un fallo por adherencia en toda la longitud hasta el apoyo. Con el desarrollo de estas fisuras el desplazamiento relativo entre las caras de la fisura se incrementaba rápidamente.
Cabe apuntar que el estado de los áridos en el plano de rotura fue distinto entre los ensayos realizados con hormigones convencionales y los de altas prestaciones. En general, las fisuras partían el árido en los ensayos realizados con hormigones de alta resistencia, aspecto que no sucedió tan claramente en el resto de ensayos realizados con hormigones convencionales.
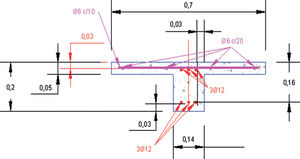
Se han considerado cuatro de estos ensayos, cuya sección transversal recta es constante y en forma de T (fig. 6), en los que no se aplicaban solicitaciones axiles para verificar que las estimaciones de la capacidad a cortante con los modelos incluidos en las normas vigentes tenidas en cuenta en este estudio no se corresponden adecuadamente con la resistencia real de ensayo.
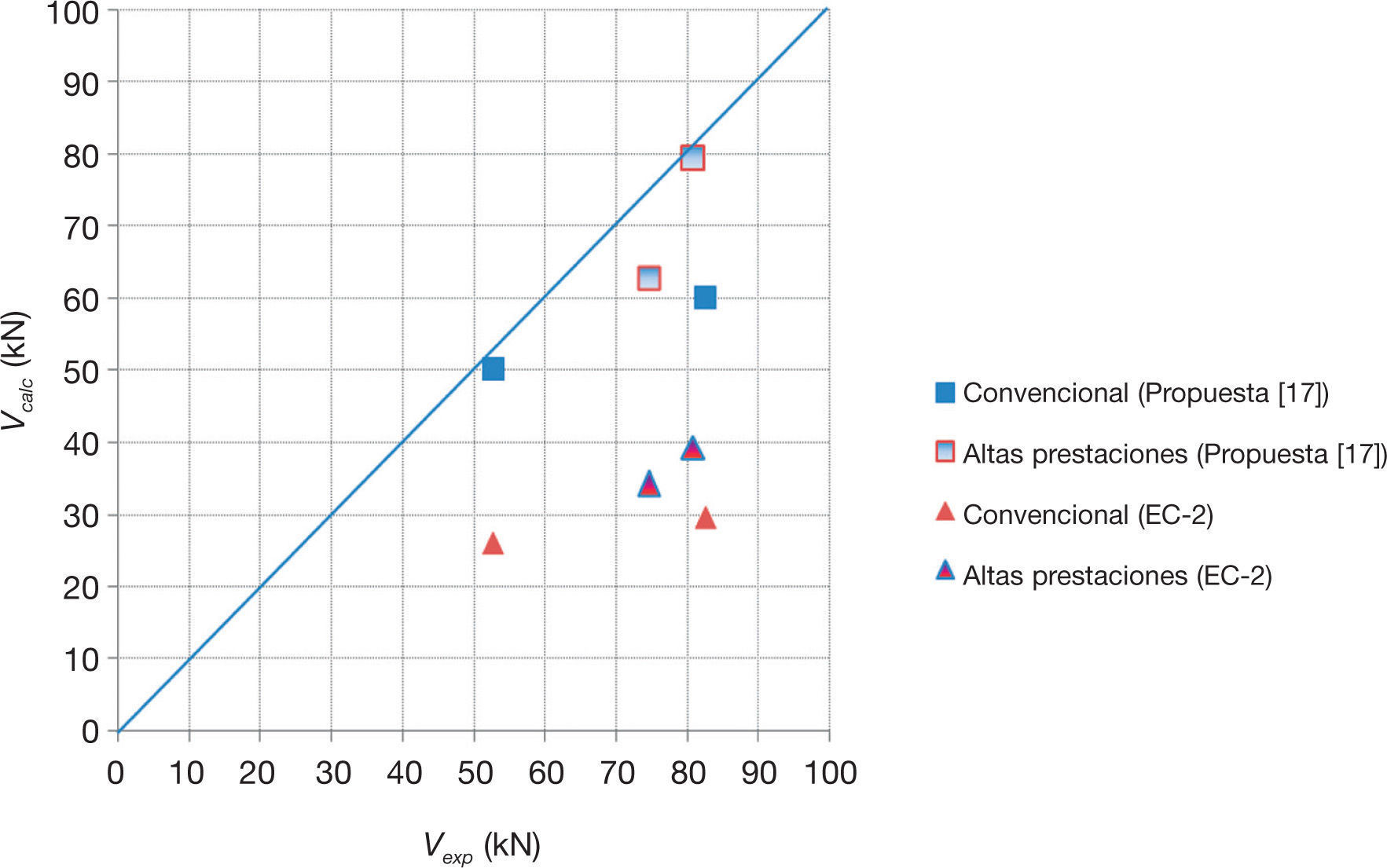
En la tabla 6 se incluyen algunos datos de dichos ensayos (ver información ampliada sobre el modelo de ensayo, características de materiales y procedimiento de realización en [21]), así como la evaluación de la capacidad a cortante con la expresión propuesta (Ecuación (23)) y con la Ecuación (2) del EC-2. En el gráfico de la figura 7, en el que se comparan las estimaciones citadas (Vcalc) y las capacidades reales (Vexp), se puede comprobar que el ajuste realizado en los ensayos de la campaña experimental es mejor que el del EC-2, el cual arroja resultados demasiado conservadores, tanto con hormigones convencionales como de altas prestaciones.
Ensayos de la campaña experimental de [21]
| Denominación | Fecha | bf (mm) | bw (mm) | d (mm) | ρ (%) | fc (MPa) | a/d | Vexp (kN) | Vcalc (kN) | Vcalc (kN) |
|---|---|---|---|---|---|---|---|---|---|---|
| Propuesta | EC-2 | |||||||||
| V8-025 | 2011 | 700 | 140 | 164 | 0,98 | 33,6 | 1,9 | 52,74 | 50,15 | 26,07 |
| V8-080 | 2011 | 700 | 140 | 164 | 0,98 | 75,0 | 1,9 | 74,65 | 62,83 | 34,38 |
| V9-025 | 2011 | 700 | 140 | 164 | 1,47 | 32,9 | 1,9 | 82,69 | 60,10 | 29,62 |
| V9-080 | 2011 | 700 | 140 | 164 | 1,47 | 76,6 | 1,9 | 80,89 | 77,44 | 39,63 |
Comparación entre valores de ensayo y valores medios estimados con las formulaciones del EC-2 y de la propuesta [21].
Una vez expuesto lo observado en el análisis de contraste entre las expresiones del modelo propuesto y aquellas deducidas de modelos experimentales, se puede aseverar que la expresión matemática propuesta para estimar la capacidad a cortante en elementos sin armadura transversal predice valores consistentes que presentan menor dispersión que los valores obtenidos con las distintas formulaciones de la normativa, a partir de los datos registrados en la campaña experimental realizada y los ensayos recopilados de la bibliografía consultada.
En consecuencia, una vez realizado el ajuste y tarado del modelo propuesto con los valores experimentales disponibles, se deducen los valores de cálculo de la formulación propuesta a partir de los principios de seguridad estructural indicados en la normativa vigente.
El método probabilístico que se emplea para establecer el criterio de diseño es el método de los coeficientes parciales descrito en el Anexo B de la norma ISO 2394. En ausencia de datos más precisos, se asume una distribución normal para las acciones y una distribución lognormal para los parámetros de resistencia.
Cabe indicar que el método de los coeficientes parciales de seguridad depende de la relación entre los efectos de las acciones variables y los efectos de las acciones permanentes. En este sentido, se realiza un cálculo de los coeficientes parciales para un valor de esta relación igual a 0,2 y otro para un valor igual a 2, tanto para hormigones convencionales como de altas prestaciones. El valor de los coeficientes de variación de las variables consideradas así como el valor de la relación entre los valores medios y característicos han sido extraídos de [23] considerando un modelo de cálculo de gran incertidumbre [21]. Se realiza el proceso iterativo indicado en [23] para obtener el coeficiente parcial de seguridad del modelo propuesto en el caso de que no exista influencia de las solicitaciones axiles y se considera suficiente un valor de γc igual a 1,5.
Por consiguiente, habiendo introducido la seguridad estructural en el modelo, se resume la formulación propuesta para la estimación del esfuerzo cortante de agotamiento por tracción en el alma de elementos de hormigón armado sin armadura transversal no sometidos a solicitaciones axiles en la Ecuación (25).
donde:
11Conclusiones y recomendacionesSe ha logrado un ajuste, que incluye explícitamente la consideración de la luz a cortante (a/d), más preciso del primer término de las expresiones indicadas por la EHE-08 y el EC-2 para calcular la capacidad a cortante de elementos de hormigón armado sin armadura transversal, sin establecer recomendaciones de valores límite en las variables predictoras, mediante análisis de regresión considerando los datos de los ensayos incluidos en la base de datos recopilados en 2008 por los investigadores Collins, Benz y Sherwood. En particular:
- 1.
Aunque la EHE-08, el EC-2, el CM 2010 y la ACI 318-11 reproducen y predicen adecuadamente en forma cualitativa el fenómeno de la resistencia última a cortante a partir de formulaciones distintas, sus resultados finales cuantitativos no son coincidentes según se desprende de la comparación realizada.
- 2.
El modelo propuesto no establece un valor de cortante mínimo, si bien se considera necesaria una mayor investigación experimental en elementos de hormigón armado con bajas cuantías y grandes cantos, tanto en hormigones convencionales como de altas prestaciones.
- 3.
Para relaciones a/d superiores a 2,5 se obtienen errores relativos mínimos, bajas dispersiones y correlaciones que se consideran aceptables con los modelos europeos considerados. Si bien, cabe indicar que la predicción realizada con el modelo propuesto obtiene un ajuste más preciso y que arroja menores dispersiones que con el modelo deducido de la Instrucción española y del Eurocódigo.
- 4.
En cuanto a los resultados obtenidos con relaciones a/d menores o iguales que 2,5, se comprueba que con el modelo propuesto se obtienen errores máximos relativos ligeramente superiores a un 20%, los cuales son admisibles y además suponen una reducción de los errores relativos en un 27% respecto a los obtenidos con el modelo deducido de la Instrucción EHE-08, el cual arroja pobres correlaciones y no se puede considerar consistente.
- 5.
Específicamente, la influencia de la relación a/d es mayor que la considerada en el modelo vigente europeo y, dada las bases de datos existentes revisadas y actualizadas, es posible reconsiderar la valoración de la influencia del efecto arco.
- 6.
En ocasiones, la escasez de ensayos no permite una correcta evaluación de la influencia determinante de algunos parámetros (forma de la sección, bajas cuantías, hormigones de altas prestaciones,…) sin establecer valores límite en las normas, lo que debería ser reconsiderado con bases de datos actualizadas o con investigación experimental adicional.
- 7.
El modelo propuesto por el CM 2010 y el modelo deducido de la ACI 318-11 arrojan resultados demasiado conservadores, imprecisos y altamente dispersos.
En resumen, se pone de manifiesto la bondad de un modelo cuyas expresiones propuestas para estimar el esfuerzo cortante se consideran adecuadas para el dimensionamiento y comprobación de elementos de hormigón armado sin armadura transversal. El establecimiento de la aplicación del modelo propuesto satisface las exigencias de resistencia establecidas en la normativa europea, al menos con el mismo nivel de garantía.
AgradecimientosA la Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos de Madrid y a INTEMAC, especialmente a todo el equipo que ha colaborado directamente en la realización de este trabajo, del que puede obtenerse información complementaria en [21].







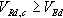
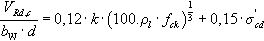
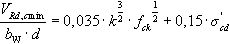
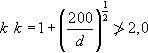
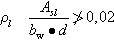
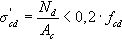
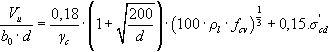
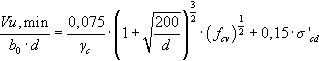
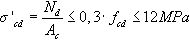
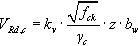
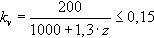
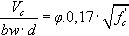
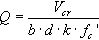
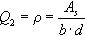
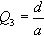
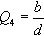
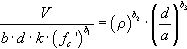
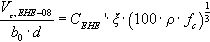
![Frecuencias relativas de parámetros en los 935 ensayos extraídos de [9] para obtener el valor de cálculo del coeficiente CEHE′ en la Ecuación (16). Frecuencias relativas de parámetros en los 935 ensayos extraídos de [9] para obtener el valor de cálculo del coeficiente CEHE′ en la Ecuación (16).](https://static.elsevier.es/multimedia/04395689/0000006500000271/v2_201808020449/S0439568914500083/v2_201808020449/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
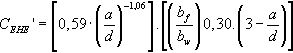
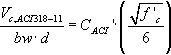
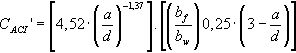
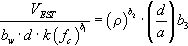
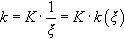
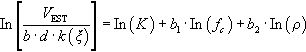
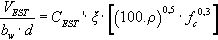
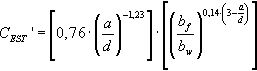

![Comparación entre valores de ensayo y valores medios estimados con las formulaciones del EC-2 y de la propuesta [21]. Comparación entre valores de ensayo y valores medios estimados con las formulaciones del EC-2 y de la propuesta [21].](https://static.elsevier.es/multimedia/04395689/0000006500000271/v2_201808020449/S0439568914500083/v2_201808020449/es/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)