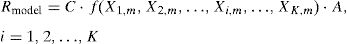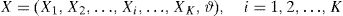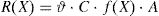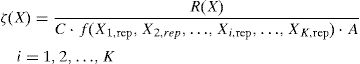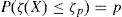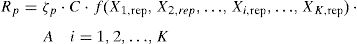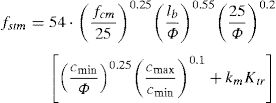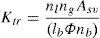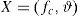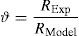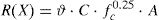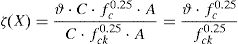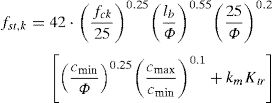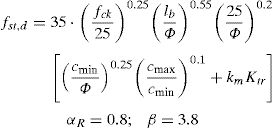From experiments to design: A probabilistic definition of design formulations from empirical and semi-empirical resistance models

Abstract

The definition of design equations from empirical or semi-empirical resistance models is a matter of relevance for structural engineering. In common practice, the limit states design approach predicts the direct application of partial safety factors to the resistance of the materials in order to obtain design formulations coherent with a prescribed level of reliability. As empirical or semi-empirical models are calibrated, adjusting empirical coefficients to fit a set of experimental data, the application of partial safety factors to material properties alone is not able to provide a correct estimation of structural reliability.

In the present paper, a methodology based on the Monte Carlo method for probabilistic calibration of empirical and semi-empirical resistance models is proposed. Its application related to the probabilistic calibration of the semi-empirical model proposed by fib Model Code 2010 for the estimation of laps and anchorages tensile strength in reinforced concrete structures is reported and discussed.

Resumen

La definición de las ecuaciones de proyecto a partir de modelos resistencia empírica o semiempírica es una cuestión de importancia para la ingeniería estructural. En la práctica común, el proyecto segun los estados límites prevee la aplicación directa de factores de seguridad parciales a la resistencia de los materiales, con el fin de obtener formulaciones de diseño coherentes con un nivel de fiabilidad prescrito. Como los modelos empíricos o semiempíricos se calibran ajustando los coeficientes empíricos para adaptarse a un conjunto de datos experimentales, la aplicación de factores de seguridad parciales a las propiedades de los materiales por sí sola no permite una estimación correcta de la fiabilidad estructural.

En el presente trabajo se propone una metodología basada en el método de Monte Carlo para la calibración probabilística de modelos de resistencia empírica y semiempírica. Su aplicación relacionada con la calibración probabilística del modelo semiempírico para la estimación de la resistencia a tracción de superposiciones y anclajes en estructuras de hormigón armado es reportada y comentada.

1

Introduction

Commonly, in structural engineering design formulations must always comply with a prescribed reliability level. To this end, physical or empirical and semi-empirical resisting models should be properly calibrated by the application of consistent safety formats.

The resisting models based both on physical laws (e.g. equilibrium of forces and kinematic compatibility) and on semi-empirical or empirical formulations (e.g. [1,2]) fitted on experimental results are really frequent in structural engineering.

In the limit states semi-probabilistic design approach [3], the safety requirements are fulfilled applying partial safety factors accounting for material properties and geometry statistical variability and model uncertainties. Concerning the resisting models based on physical assumptions, the direct application of partial factors to materials strength leads to design expressions consistent with a specific reliability level. This does not happen in the case of empirical or semi-empirical resisting models that are based on experimental test set. In such kind of models, all the empirical coefficients embedded in the formulation are calibrated as best fitting on the experimental results and assuming mean values of material properties (i.e. the actual values measured during the experiment execution). In this case, it implies that the direct application of partial safety factors to materials strength does not lead to a proper evaluation of reliability.

In the literature, several methodologies for probabilistic assessment of physical, empirical and semi-empirical models are proposed [4–6]. In order to apply these theoretical procedures consistently, an accurate assessment of model uncertainties is necessary as proposed in [7–11].

However, a general and ease-to-apply procedure able to calibrate empirical or semi-empirical formulation in relation to a specific level of reliability is still not available and defined.

In the present paper a methodology based on the Monte Carlo method [12] for calibration of empirical and semi-empirical resisting models is proposed. This procedure is able to account for both statistical variability of material and geometric properties and the influence of the resisting model uncertainties. After the detailed description of the methodology, its application to the calibration of the semi-empirical model for laps and anchorages tensile strength evaluation suggested by Model Code 2010 [13] is proposed and commented.

2

Methodology for the assessment of design expressions from empirical or semi-empirical resisting models

In this section the methodological approach for probabilistic calibration of empirical and semi-empirical models is described.

The proposed methodology grounds on four main points:

• -

  the individuation of the empirical or semi-empirical resisting model;

• -

  the definition of the probabilistic model;

• -

  the definition and characterization of the resistance random variable;

• -

  the estimation of the fractiles of the resistance random variable and determination of the design expressions.

2.1

Individuation of the empirical or semi-empirical resisting model

In general, an empirical or semi-empirical resting model is calibrated grounding on a set of experimental results and the estimated value of the resistance R_model can be expressed in the following form:

where C is best fitting empirical coefficient calibrated on the experimental database; X_i is a set of K random variables which plays a significant role in the resisting model (i = 1, 2, …, K); f(X_1,m, X_2,m, …, X_i,m, …, X_K,m) is a function of the abovementioned random variables assumed with their mean or experimental value; A is a function of all the parameters that can be assumed as deterministic (e.g. geometry).

The value of R_model estimated by means of Eq. (1) should be intended as a mean resistance as it is calculated assumed mean or experimental material properties and empirical coefficients fitted on experimental tests. Then, the direct application of Eq. (1) for design purposes it is not correct as it is deprives of any safety assumption.

2.2

Definition of the probabilistic model

Once all the parameters that can influence the resisting model with their statistical variability are selected, the following vector of random variables X can be defined:

The vector of random variables X includes also the model uncertainty random variable ϑ that should be calibrated base on the statistical assessment of the ratio between experimental results and model predictions according to [14]. The vector of random variables X can group both statistically independent and statistically dependent random variables.

All the random variables grouped in X have to be represented by their probabilistic distribution (i.e. PDFs and/or CDFs) which must be able to describe their statistical variability accurately.

Suggestions for the definition of the probabilistic model can be acknowledged by [14].

2.3

Definition of the resistance random variable

The resistance random variable can be evaluated in function of the vector X descending from Eq. (1) as follow:

The expression reported by Eq. (3) is able to represent the random variability of the resistance accounting for material statistical fluctuations and model uncertainties. However, in order to propose a not case dependent and general procedure, the following ratio has to be addressed:

where ζ(X) is the resistance ratio random variable and (X_1,rep, X_2,rep, …, X_i,rep, …, X_K,rep) are the representative values of the main random variables (e.g. 5% characteristic or nominal value).

The random variable ζ(X) can be assessed by means of the Monte Carlo method [11] sampling from the probabilistic distributions of the random variables involved by Eq. (4). When a significant number of samples of the population of ζ(X) is available, the most suitable probabilistic distribution able to describe ζ can be selected.

2.4

Estimation of fractiles of the resistance random variable

In order to define relationships for design purposes, it is convenient to assess particular fractiles from the resistance random variable.

This can be performed defining the following probability:

where ζ_p is the fractile related to a certain probability to not be exceeded of the random variable ζ(X); p represent the probability of not exceedance for the value of ζ_p.

In common engineering practice and according to international codes [15,13], the following fractiles of ζ(X) are estimated:

• -

  characteristic value ζ_k, setting p = 0.05;

• -

  design value ζ_d, setting p = Φ(−α_R·β);

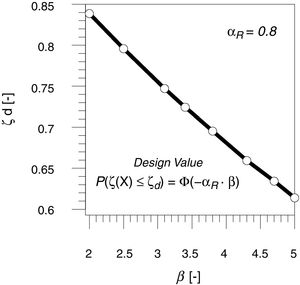
with β reliability index [16], α_R first order reliability method (FORM) correction factor (assumed equal to 0.8 for dominant resistance variables) [13] and Φ(·) cumulative standard normal distribution.

Once the probabilistic coefficient ζ_p has been estimated, the general formulation for the selected fractile of the resistance random variable R_p can be expressed as follow:

3

Application example: laps and anchorages tensile strength in fib Model Code 2010

In this section, an example of application of the procedure so far described is reported. Usually, in reinforced concrete structures, due to technical and construction reasons, it is required to interrupt the longitudinal tensile steel reinforcements. It is then necessary to provide an adequate length of overlapping or anchorage in order to allow continuity in the transferring of forces within the structure.

In [13,17] the evaluation of the maximum tensile strength of a lapped joint or anchorage can be assessed by means of a semi-empirical formulation. Subsequently, the proposed methodology will be applied for the calibration of the abovementioned resisting model.

3.1

Laps and anchorages tensile strength formulation in Model Code 2010

In the fib Model Code 2010 [13] the evaluation of laps and anchorages tensile strength f_stm is performed by means of the semi-empirical model proposed in [17], that is a modification of the approach suggested in [18] based on [19,20].

The best-fitting semi-empirical expression for laps and anchorages strength estimation, which is calibrated on a large set experimental results [21], is represented by Eq. (7):

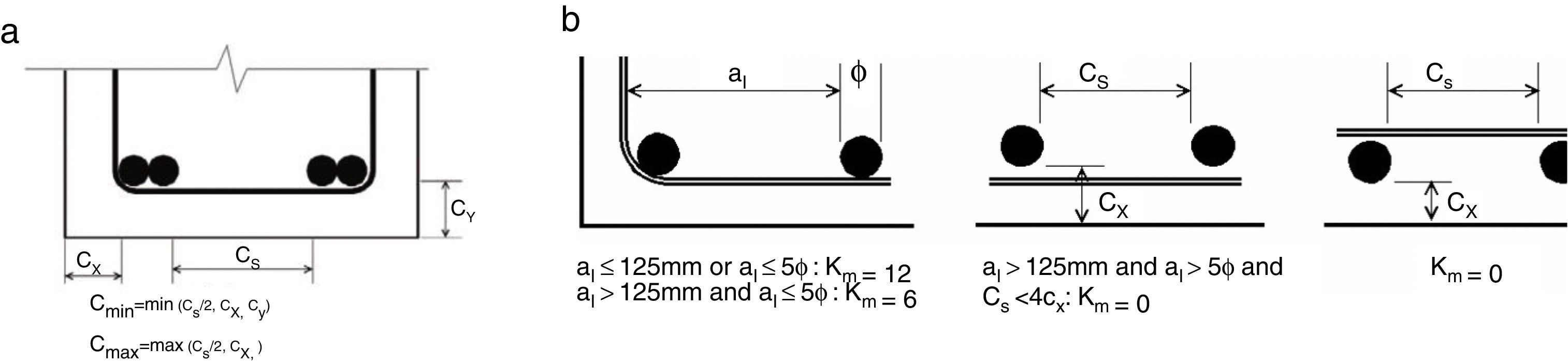
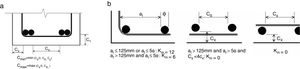
where f_cm is the mean concrete compressive strength; l_b is the lap/anchorage length; Φ is the bar diameter; concrete covers c_min, c_max and effectiveness coefficient k_m are evaluated according to Fig. 1(a and b).

Figure 1.

Determination of concrete cover c_min and c_max in Eq. (1) (a) and assessment of the effectiveness of shear links (b).

The coefficient K_tr accounts for the effect of confinement provided by shear links/stirrups situated along the lap or anchorage and can be calculated as follow:

where n_l is the number of legs of a link/stirrup; n_g is the number of groups of links/stirrups; A_sv is the transverse area of each leg of a link/stirrup; n_b is the number of individual anchored bars of pairs of lapped bars.

The assessment of Eq. (7) have been performed base on an experimental database counting more than 800 tests on laps and anchorages coming from American (ACI) and European investigations [21]. In the fib Bulletin No. 72 [17] are provided the following limits for Eq. (7) as they represent also the limits of the abovementioned database:

• -

  15 MPa ≤ f_cm ≤ 110 MPa;

• -

  K_tr ≤ 0.05;

• -

  0.5 ≤ c_min/Φ ≤ 3.5 and c_max/c_min ≤ 5;

• -

  l_b ≥ 10Φ;

• -

  25/Φ ≥ 2.

3.2

Probabilistic model

As reported in Section 2, a set of relevant random variables have to be defined. These random variables have to represent parameters that are explicitly considered into the resisting model.

In this case, may be reasonable consider as random variable only the concrete compressive strength, which strongly affect the resisting mechanism with its statistical variability. At the purpose of this example all the other parameters involved by Eq. (7) can be assumed as deterministic.

However, the resisting models shows an intrinsic uncertainty due to simplified assumptions in their definition and in disregarding parameters that can have some influence on the actual resisting mechanism. This involves that the resisting model uncertainties have to be accurately addressed and included into the probabilistic model.

Therefore, in the present application the following random variables will be considered in the vector X:

where:

• -

  f_c, is the cylinder compressive strength random variable. According to fib Model Code 2010 [13] the statistical variability of f_c can be described by means of a log-normal distribution with coefficient of variation V_c equal to 0.15 and mean value equal to f_cm depending by the concrete strength class (Table 1).

  Table 1.

  Statistical parameters and probabilistic distribution for the random variables affecting the resisting model.

  	Ref.	Mean value	C.o.V	Type of distribution
  Concrete compressive strength, fc [MPa]	[13]	fcm	0.15	Log-normal
  Model uncertainties, ϑ [–]	[22]	0.98	0.13	Log-normal
• -

  ϑ, is the resisting model uncertainty random variable. In compliance with JCSS Probabilistic Model Code [14] the statistical characterization of ϑ can be performed defining the following ratio:

where R_Exp is the actual resistance estimated from laboratory tests and R_Model is the resistance estimated by the model.

The model uncertainties related to Eq. (7) have been estimated base on the database of experimental results reported in [21]. The mean value μ_ϑ and the coefficient of variation V_ϑ are listed in Table 1 according to the statistical investigation proposed by [22] concerning the case of new structures. According both with [22,14]ϑ can be described by means of a log-normal distribution.

3.3

Resistance random variable

Defining the resistance random variable R as the lap or anchorage tensile strength f_st, according with Section 2, Eq. (7) can be rewritten as follow:

with:

and the empirical coefficient C set equal to 54.

Defining as the representative value for concrete compressive strength the characteristic one, the resistance ratio random variable ζ(X) can be determined as subsequently reported:

where f_ck is the 5% characteristic value for cylinder concrete compressive strength.

By means of Monte Carlo technique it is possible to generate a large sample of the population of the random variable ζ(X).

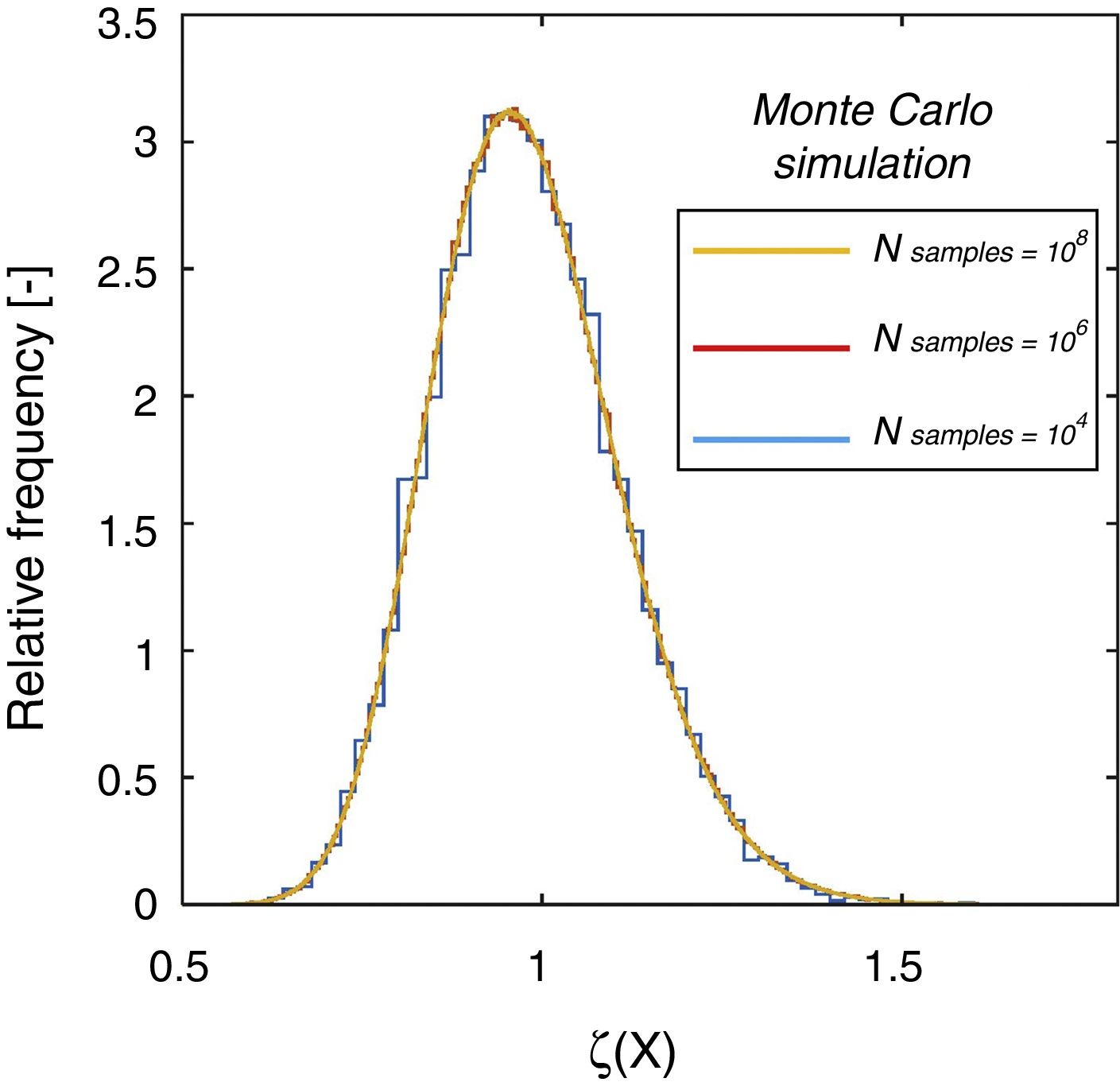
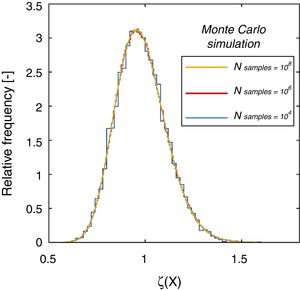
In the present example a number of samples N equal to 10⁴, 10⁶ and 10⁸ has been generated adopting the direct Monte Carlo sampling from the probabilistic distributions of the basic variables listed in Table 1. The associated relative frequency histogram is reported in Fig. 2.

Figure 2.

Relative frequency histogram for the Monte Carlo simulation of the random variable ζ(X) in the hypothesis of 10⁴, 10⁶ and 10⁸ samples.

As R(X) is a function of two log-normally distributed random variables (i.e. f_c and ϑ), it is expected that ζ(X) is log-normally distributed too [4].

A shown by Fig. 2, the results obtained adopting 10⁴, 10⁶ and 10⁸ samples give not appreciable difference in the estimation of the distribution parameters for the random variable ζ(X). Being the total number of samples required for the Monte Carlo simulation inversely proportional to the probability of failure to be estimated, a number of samples set N = 10⁶ can be considered sufficient for the present investigation (as, in Section 3.4, the minimum estimated probability is around 10⁻³, which corresponds to the fractile of the distribution of ζ(X) associated to the value of the product α_R·β with β = 3.8 and α_R = 0.8).

However, in the case of the estimation of smaller probability of failure, a larger number of samples is recommended in order to represent, inside the sample, also lower extreme values of the involved random variables.

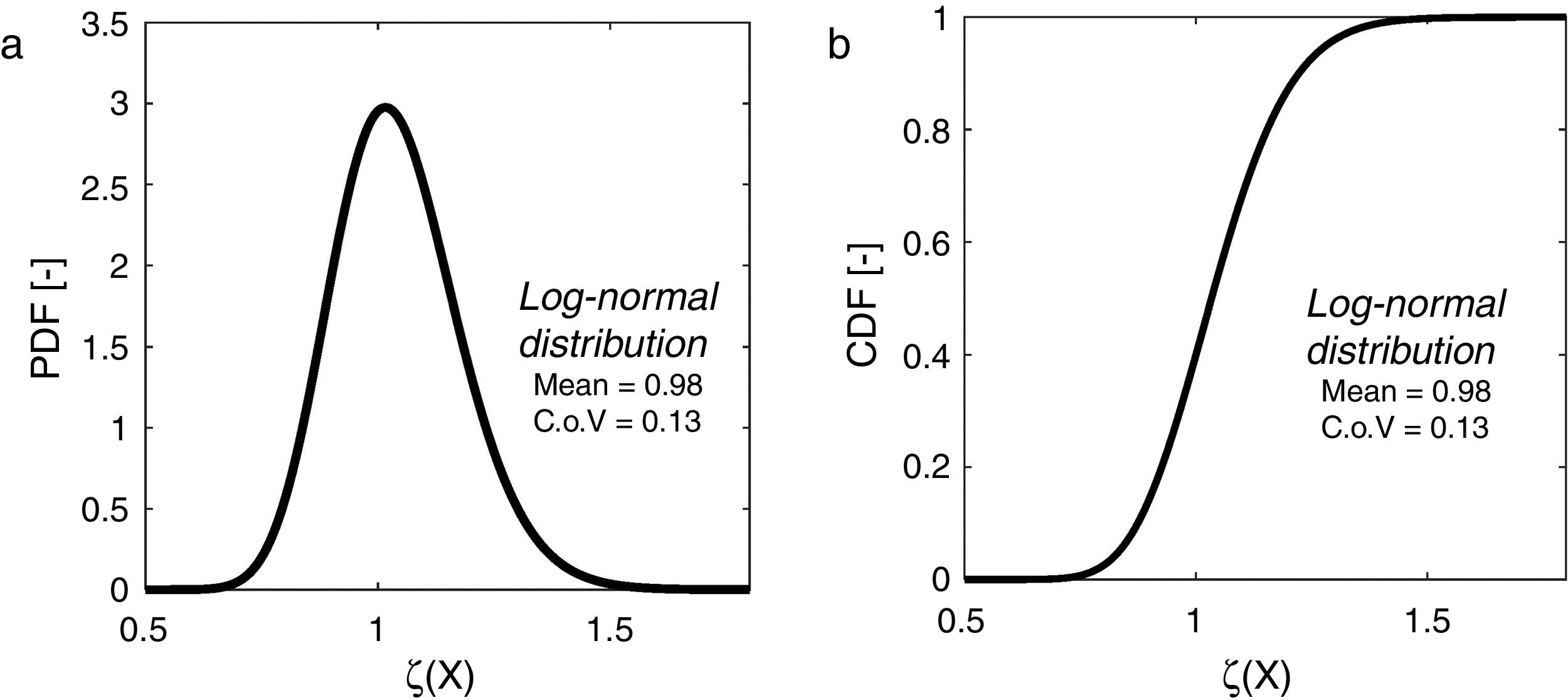
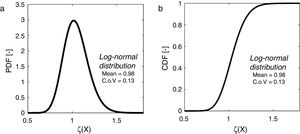
Finally, concerning the population with 10⁶ samples of the random variable ζ(X), the Chi-square goodness of fit test with 5% level of significance testing the hypothesis of normality of the sample of ln(ζ(X)) have been performed confirming the hypothesis of log-normality of the variable ζ(X). Hence, the resistance ratio random variable ζ(X) can be described by means of a lognormal distribution having mean value equal to 0.98 and coefficient of variation (C.o.V) equal to 0.13 (Fig. 3(a and b)).

Figure 3.

Log-normal distribution (PDF (a) and CDF (b)) for the random variable ζ(X).

3.4

Derivation of the characteristic and design expressions

Once the probabilistic distribution for the random variable ζ(X) has been determined and characterized, it is possible to calculate its fractiles as described by Eq. (5). In Table 2 are reported the 5% characteristic value ζ_k and design value ζ_d (assuming the reliability index β = 3.8 as in the case of ordinary structures with 50 years service life [13,15]. The abovementioned values have been compared in Table 2 with the results coming from the simplified analytical procedure proposed by Taerwe [4] (which was applied in [22] to Eq. (7)) valid in the case of log-normally distributed random variables.

Table 2.

Comparison between the proposed method based on Monte Carlo simulation with N = 10⁶ samples and the analytical method proposed by [4].

	Proposed	[4,22]
	N = 10^6
ζk [–]	0.78	0.83
ζd [–] (αR = 0.8; β = 3.8)	0.65	0.69

The simplified analytical method [4,22] leads to results close to the ones obtained with the simulation technique. However, the proposed methodology can be easily applied in case of probabilistic distributions for main random variables different from the log-normal one.

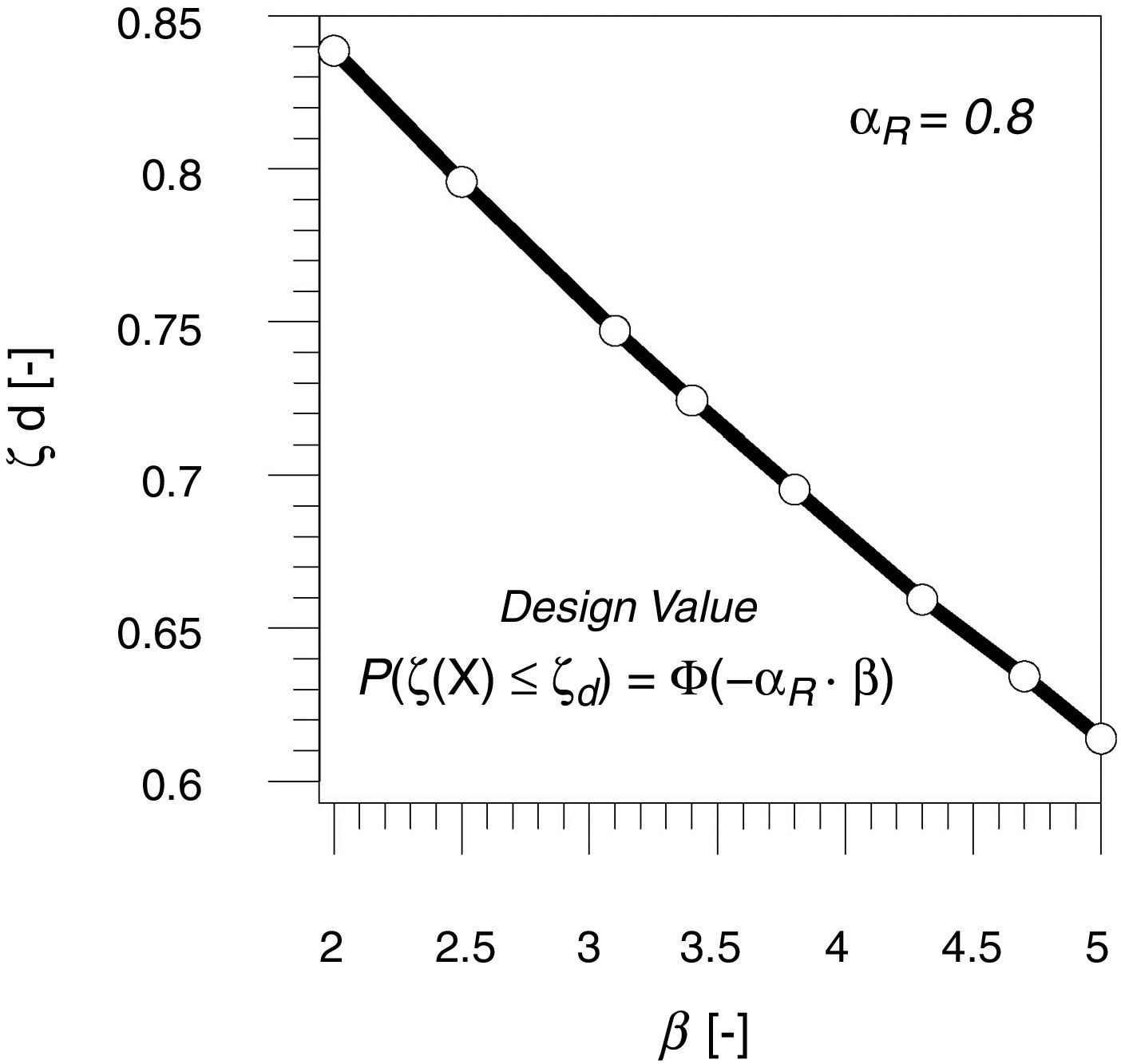
As international codes [3,13,23] suggests different levels of reliability distinguishing between new or existing structures in function of the service life of the structure, it is useful to define the trend of variation of the design probabilistic coefficient ζ_d versus the reliability index β. The variation of ζ_d in function of the reliability index β in proposed in Fig. 4. The calibration of the design expressions related to original semi-empirical model (Eq. (7)) can be performed specifically in function of the target reliability level.

Figure 4.

Variation of the design probabilistic coefficient ζ_d in the function of the reliability index β.

Finally, the 5% characteristic f_st,k and the reliability-based design f_st,d expressions for the semi-empirical model proposed by [17,13] for laps and anchorages tensile strength estimation can be evaluated as follow according to Eq. (6) and Table 2:

4

Conclusions

A probabilistic procedure based on the Monte Carlo method for the derivation of design formulas by empirical or semi-empirical resisting models has been proposed. The procedure allows the correct evaluation of the influence of material and resisting model uncertainties in the reliability-based calibration of the abovementioned kinds of resisting models.

This result can be obtained by means of the definition of multiplicative probabilistic coefficients ζ_p, which are related to a specific probability of not exceedance p. As the probability p is directly related to a certain value of the reliability index β, the final design equations can be derived in function of the level of reliability required by the codes.

The proposed procedure is very general as it is independent from the probabilistic model defined for the main random variables. Furtherly, it is suitable for the calibration of design formulations both in the case of serviceability and ultimate limit states.

Acknowledgements

This work is part of the collaborative activity developed by the authors within the framework of Task Group TG 3.1 of the Fédération Internationale du Béton (fib).