Importance of creep and ASR gel diffusion in predicting ASR induced expansion

Abstract

The paper reviews development of a diffusion-based and creep-based model for calculating the evolution of expansion and damage induced by alkali-silica reaction (ASR). First, the model of Bažant and Steffens (2000) is adopted to calculate the rate of production of the ASR gel within the aggregate. Next, a non-linear diffusion according to Rahimi-Aghdam and Bažant (2017) is presented to model the penetration of ASR gel into the micropores, nanopores and microcracks. The gel diffusion into pores of the aggregate causes expansion and damage to the surrounding concrete, and is found to be an important modeling aspect. The damage is assessed by microplane model M7, into which the creep is incorporated. The creep is found to have a significant influence on the long-term evolution of ASR-induced damage. The predictions are in good agreements with the laboratory experiments and the model appears to be ready to predict the ASR effects in real structures.

Resumen

El artículo analiza el desarrollo de un modelo basado en la difusión y en la deformación por fluencia lenta para calcular la evolución de la expansión y el daño provocado por la reacción de álcali-sílice (RAS). Primero, se adopta el modelo de Bažant y Steffens (2000) para calcular la tasa de producción de gel para la RAS dentro del conglomerado. A continuación, se presenta una difusión no lineal según Rahimi-Aghdam y Bažant (2017) para modelar la penetración del gel para la RAS en los microporos, nanoporos y microfisuras. La difusión del gel en los poros del conglomerado provoca expansión y daño al hormigón cercano, y se encuentra que es un aspecto importante de modelado. El daño se valora mediante el modelo de microplanos M7, al cual se incorpora la deformación por fluencia lenta. Se cree que esta tiene una influencia considerable sobre la evolución a largo plazo del daño provocado por la RAS. Las predicciones son coherentes con los ensayos de laboratorio y parece que el modelo está preparado para predecir los efectos de la RAS en estructuras reales.

1

Introduction

The alkali-silica reaction (ASR; aka alkali-aggregate reaction, AAR) attacks mineral aggregates in concrete when they contain imperfectly crystalline silica. The reaction produces a gel that can imbibe enormous amount of water and cause swelling. The induced swelling, progressing for many months, years or even decades, often causes significant strength degradation and damage in concrete structures. Because drying diminishes the rate of ASR, the worst damage usually occurs in massive structures such as large bridges and dams, and nuclear power plant structures in which the cross-section core remains undried for years, even decades. As a result, preventing the ASR-induced damage is one important goal of sustainable design.

The ASR-induced damage was first identified by Stanton in 1942 [1]. Since that time many researchers have worked on this problem and a vast body of literature has been gathered. A comprehensive literature review has recently been published by Saouma and Xi [2,3].

Although several models have been proposed to predict the ASR-induced damage, they consider a simplistic constitutive law for concrete. An exception is a recent model Alnaggar and Cusatis [4] which uses Cusatis’ lattice discrete particle model, and in the particle contacts an excellent material model for concrete. However, all these models do not consider the diffusion of ASR gel into pores and cracks, and all except Alnaggar and Cusatis’ neglect the effect of creep. Both phenomena significantly mitigate the ASR-induced damage.

The current models, except [4], assume that the only phenomenon that controls the rate of ASR-induced swelling is the production of ASR gel and its water imbibition. In modeling the diminishing rate and stoppage of ASR-induced swelling, which happen after a few months in accelerated tests, these models consider the ASR gel to reach the maximum capacity of water imbibition relatively fast and water imbibition to stop after that. This assumption contradicts the experimental results showing that the ASR gel can imbibe a vast amount of water, even 100-times its initial volume. The only reasonable justification for the diminishing and stoppage of ASR-induced swelling is the diffusion of ASR gel into the surrounding pores, and also into the microcracks produced by the diffusion in the aggregate pieces and surrounding cement mortar. After significant damage the diffusion rate exceeds the rate of water supply which causes the swelling to slow down and eventually to stop.

This study reviews the recent development of a comprehensive model for ASR [7,31] and provides some improved explanations and justifications of its main features, which include:

• 1.

  The delay in ASR due to production of ASR gel and its diffusion into the pores and expanding cracks.

• 2.

  Fracturing of the solid framework of concrete as a two-phase medium, caused by diffusion of the ASR into pores and cracks in the aggregates and surrounding mortar.

• 3.

  The differences in cracking patterns of the damage induced by the ASR under different confinement conditions, applied stress states and boundary conditions.

• 4.

  The effect of creep on mitigating the ASR damage.

• 5.

  The effect of alkali content on the ASR-induced damage and swelling.

• 6.

  The effect of temperature on ASR-induced damage and swelling.

Analysis of these effects must be coupled with a realistic model for ASR gel production within the reactive aggregate pieces. Such a model was developed by Bažant and Steffens [8] and was also used and improved by Alnaggar and Cusatis [4]. Here this model is coupled with the analysis of the aforementioned phenomena.

Analysis of the ASR gel diffusion is an essential aspect of prediction. A nonlinear diffusion model has been developed and calibrated for this purpose. To predict the ASR-induced damage in larger structures, a macroscopic continuum model, endowed with a localization limiter preventing spurious instability of softening damage, is necessary. The microplane constitutive damage model [5,6] is most realistic for this purpose. It can distinguish different damage patterns under various stress states. Its latest version, M7, is adopted. Since creep of the solid framework significantly mitigates the ASR damage, a concrete creep model is incorporated into M7.

2

Review of simplified model of kinetics of ASR gel production

First, we need to introduce a model for the kinetics of gel production in mineral aggregates. To this end, the simplified model of Bažant and Steffens [7], as improved by Bažant and Rahimi-Aghdam [8,9] and used, in improved form, by Alnaggar and Cusatis [4], is adopted.

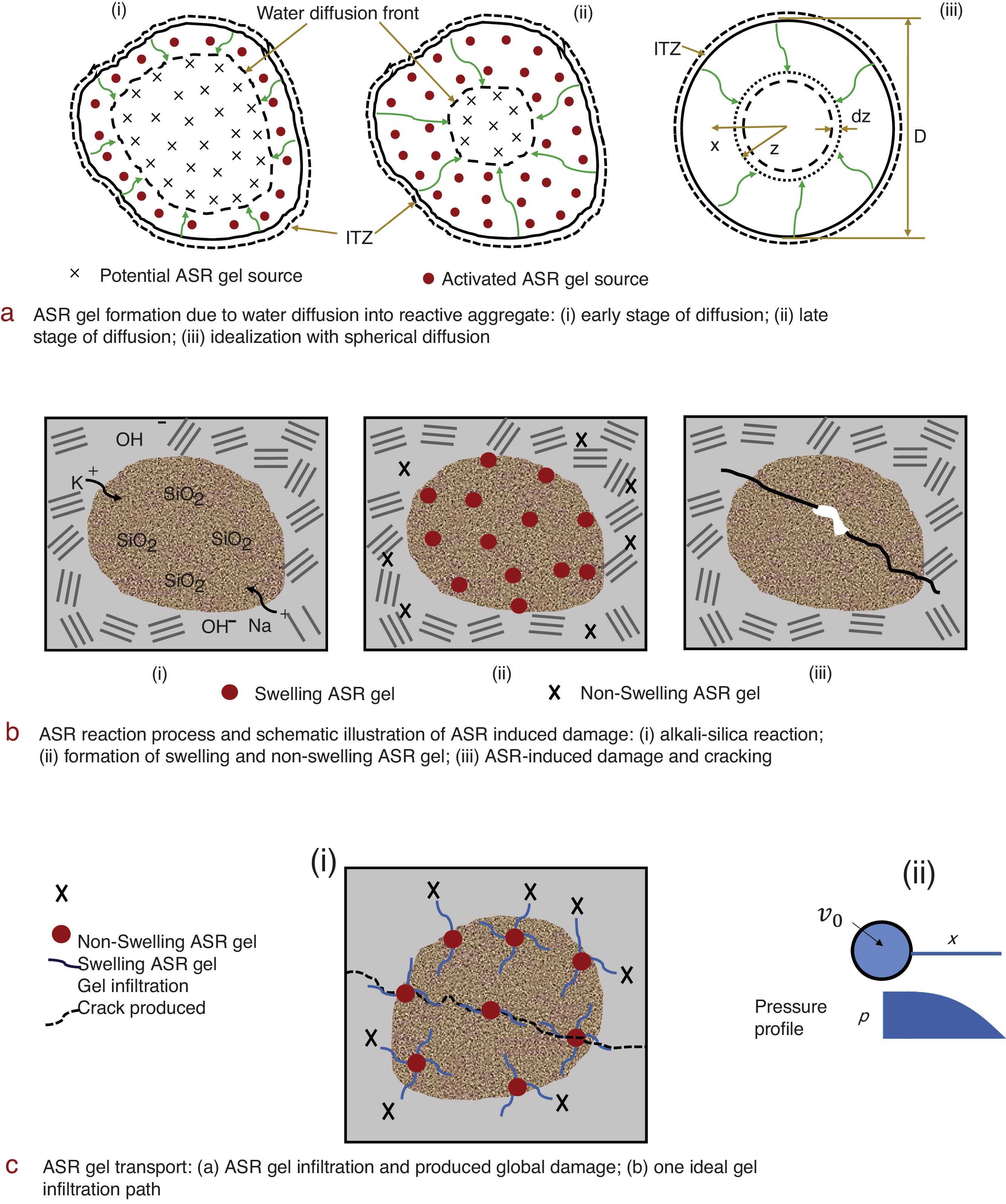
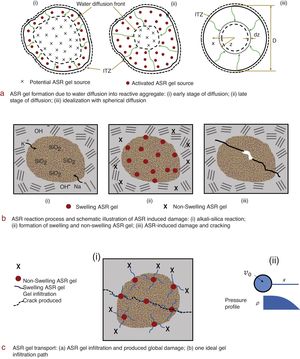
Since the shape of aggregate grains is not too important, spherical grains of diameter D are considered (Fig. 1a). The ASR reaction occurs at various randomly located discrete sources inside the grain. Those near the grain surface will be activated first and the time to activate the deeper sources will grow with the depth, z. Thus, as an average behavior of many aggregate grains, we introduce a smeared continuum model in which water diffuses radially into a spherical aggregate grain [8], with a spherical front of radius z at which the ASR reaction takes place. The ASR reaction is assumed to occur instantly at the front of water penetration (Fig. 1a). The reaction is slowed down by the diffusion of water through the aggregate piece, and particularly through the layer of ASR gel already formed.

Figure 1.

Formation of the ASR gel and its diffusion.

The coupling with the penetration of ASR gel into the pores of the mortar surrounding the aggregate piece is assumed to be one-way, i.e., the evolution of gel mass w(t) is considered to be independent of pressure p(t) developed in the pores surrounding the aggregate piece. This is, of course, a simplification, although probably not a major one since the pore pressures sustainable by concrete cannot be large enough to slow down the alkali-silica reaction appreciably.

In this study, the same set of equations as Bažant and Rahimi-Aghdam (2017) is used to calculate w(t) and the mass of imbibed water, w_i(t). It should be noted that we assume the ASR gel to imbibe water for years, and even decades. The main reason for the deceleration of the ASR-induced swelling is the diffusion of ASR gel into the cracks produced by ASR (and, often, diminishing of water supply). Several other studies assumed the ASR gel to imbibe only an assumed limited amount of water for only an assumed limited time, considering these phenomena to diminish and stop according to a chosen schedule. This simplification disagrees with the experimental results, which show ASR gel can imbibe an almost unlimited amount without any particular time limitation. These oversimplifications were necessary because the diffusion of ASR gel into the pores was not considered.

3

Diffusion of ASR Gel into surrounding pores

The penetration of gel from a gel source into adjacent pores and cracks is another mechanism which controls the rate of ASR and prolongs the process enormously (Fig. 1c). This process can be formulated as a diffusion process obeying the Darcy law. The flow velocity is z˙ = dD∇p where ∇ denotes the gradient and bD is the Darcy permeability (dimension m³s/kg). In detailed analysis, one could consider a differential equation for the diffusion in radial direction z, embedded in a continuum point. However, considering all the uncertainties and simplifications, it appears sufficient to replace the flow velocity, z˙, with the velocity of the diffusion front, dx/dt, and the pressure gradient with the average pressure gradient ∇p = p/x. Using these reasonable simplifications, we can write the simplified Darcy diffusion equation as given in Fig. 2a.

Figure 2.

Calculating the diffusion of ASR gel and Induced pressure inside pores.

The ASR gel first penetrates at near-zero pressure p into the empty and easily accessible pores of volume fraction vo. The easily accessible pores are of three kinds: (1) pores inside the aggregate, the distribution and size of which depends strongly on the type of aggregate; (2) the cement paste pores (since the hardened cement paste always contains empty pores, due to self-desiccation); and (3) the bigger pores in the interface transition zone (ITZ) surrounding the aggregate, more easily fillable due to a lower mass density and higher porosity in that zone.

Note that, in real structures, the filling of empty pores of volume fraction vo can take many years and decades. This is the reason for the great delay in the initiation of the ASR-induced expansion. Only after the empty pores get filled, further imbibition of water can produce a significant pressure in the gel, produce cracks and penetrate them (Fig. 1b and c).

We assume that one or several basic gel sources form in each reactive aggregate (when it contains reactive silica). From each gel source, the gel diffuses in multiple random directions (Fig. 1a and c) into nearby pores, microcracks and ITZ. Note that the gel that penetrates into cement paste (farther from the aggregate) will calcify and thus no longer imbibe water and swell, thus becoming harmless. The direction of ASR gel diffusion is random and the distances from the different gel sources to the fronts of diffusion paths also vary randomly (Fig. 1c). Therefore, on the continuum scale, it is reasonable to consider a volumetric average diffusion instead of a directional diffusion. The volumetric diffusion equation can be written as shown Fig. 2b, where p is the average gel pressure; b is an effective Darcy permeability (dimension m²/Ns or ms/kg), which is proportional to the actual Darcy permeability, bD; and vef is an effective volume fraction.

It is clear that permeability must increase due to cracking. If we denote the crack opening as δ and use the crack band model as a localization limiter [10,11], then we have δc ≈ lo∈'', where lo is a material characteristic length, and ∈ '' is the inelastic part of average tensile strain across the crack band.

Since the induced cracks can run randomly in any direction, expansion in all directions is expected, i.e., the inelastic strain must be volumetric, ∈v'' considered to be a function of the principal inelastic strains. Among them, the increase of permeability can be caused only by those tensile strains that exceed a certain empirical finite threshold, ∈0'' (which is here assumed to be 0.001%). Thus, the effect of inelastic strain (damage) on gel permeability may be introduced as seen Fig. 2c.

4

Evolution of ASR gel pressure at constant total gel mass

During the filling of empty, easily accessible, pores, of volume fraction vo, the pressure is approximately zero. After these pores get filled completely, the pressure in the pores starts to develop. For simplicity, we assume the radial pressure profiles to be similar as the penetration depth grows. The type of profile makes little difference for the results. We assume a uniform pressure p up to volume v₀. Beyond that, a parabolic pressure drop (as sketched in Fig. 2d) is most realistic.

Now that we have assumed the self-similar profile in the pores, we can use an explicit computational algorithm to calculate the pressure evolution. However, very short time steps would be needed to ensure numerical stability and convergence. This limitation becomes a serious problem in simulating long-term ASR. The same problem was faced in modeling long-term creep of concrete structures. The creep proceeds rapidly at first, which needs time steps in the order of seconds at the beginning. But to run calculations up to, e.g., 50 years, the time steps for creep integration need to be extended to months in duration. The same increase in the time step must possible here since, after several years, the pressure evolution becomes very slow.

Therefore, an analog of the unconditionally stable exponential algorithm for creep [12,13] has been developed for gel diffusion. Similar to piece-wise strain constancy in the unconditionally stable exponential algorithm for creep [12,13], we assume the mass of gel to be held constant during each time step Δt and allow the pressure to relax due to diffusion. At the end of each time step, the pressure and gel mass are corrected by an abrupt change. Fig. 2e describes the relaxation of pressure at the constant gel mass, with tp playing the role of characteristic time. It should be noted that the pressure relaxation equation is nonlinear since tp depends on variables such as volume fractions and permeability, which themselves depend on pressure. However, since these variables do not change significantly during the time step, tp may be considered as a constant during each time step and calculated using the values from previous time step. This allows the pressure relaxation equation to be integrated by separation of variables.

5

Constitutive law for the solid part of concrete and incorporation of creep

Generally in structures undergoing ASR, the concrete experiences complex multiaxial stress states. Thus, anisotropic damage should be expected. The anisotropic damage of concrete can be described effectively by the microplane constitutive model M7 [5,6]. The basic idea of microplane model is to formulate the constitutive law in terms of the vectors of stress and strain acting on a generic plane of any orientation in the material microstructure, called microplane. The use of vectors, instead of tensors, is similar to the Taylor models, used for plasticity of polycrystalline metals, but there are major differences; especially, the static constraint instead of a kinematic one is considered. In this study, the latest version of microplane model, M7, is used. Model M7 has been demonstrated to give rather good predictions of the behavior of quasibrittle materials over a broad range of loading conditions.

The ASR-induced damage in structures evolves over years, even many decades. Therefore, creep and shrinkage play a major role. Creep and shrinkage can even have a significant effect on relatively short laboratory experiments. To determine the creep and shrinkage in undamaged concrete, RILEM model B4 [14] is used in this study. However, the ASR damage in the presence of external loads causes fracturing. Thus, the creep and shrinkage cannot be calculated simply using a plain creep model, such as B4. It needs to be calculated using a combination of the creep model with the microplane model M7.

In undamaged material between the expanding pores and cracks, the creep is aging viscoelastic and linear in stress, while the fracturing damage leading to cracks depends on stress nonlinearly. As a result, the creep strain can be considered to be additive to fracturing strain. Since the ASR-induced pressure and damage evolve in time and influence the constitutive law, the rate-type creep model [15] must be used, rather than hereditary integral-type. The rate type creep model can be structured according to the Kelvin or Maxwell chain. The former is more convenient since model B4 specifies the compliance, rather than relaxation, function (Fig. 3a).

Figure 3.

Incorporation of creep and two-phase medium.

The spring and dashpots moduli of the Kelvin units in the chain can be obtained by discretizing the continuous retardation spectrum [16]. Due to aging, the spectrum is significantly different for every time step and every integration point. The retardation times are selected to make a geometric progression with quotient 10 and must cover the whole time range of interest (Fig. 3a). Time integration allowing an arbitrary increase of the time steps as creep slows down needs to use the exponential algorithm [12], which is unconditionally stable. On the tensorial level, the exponential algorithm leads to the incremental stress-strain relation as shown in Fig. 3b, in which, ∈ijcr is the creep strain increment tensor that is calculated from Bazant's exponential algorithm for Kelvin chain model; E¯ is the incremental modulus which is obtained from the exponential algorithm; εsh is the shrinkage strain increment, and αΔT is the thermal strain. To combine M7 with creep, all the stress predictions in the microplane model are written in a form analogous to the equation in Fig. 3b.

It should be mentioned that in this study, for simplicity, model B4, which gives average creep for cross section, is used. However, due to damage and non-uniformity of stress it is beneficial to use pointwise creep laws such as XMPS model [17].

6

Two-phase medium for loading of concrete by pressure in pores and cracks

It is standard to model saturated porous solids with fluid in their pores using Biot two-phase medium. For Biot medium, the volumetric equilibrium relation reads Sv = σv−αp, in which Sv is the volumetric stress in the solid phase (dry material).); σv is the total volumetric stress in the two-phase medium (solid and fluid), which is used in finite element analysis to determine the nodal forces; and α = Biot coefficient which it related to porosity, but is usually approximated such that 1−α would represent the ratio between the bulk moduli of solid with and without pore fluid [18]. However, concrete is not a standard porous solid and the formulation of Biot medium is not completely applicable for concrete. The main reasons for the inapplicability of Biot relations to concrete are: (1) Concrete in never fully saturated, due to self-desiccation and drying (and the existence of anticlastic capillary menisci), which is why its pores are filled with both vapor and liquid (and adsorbed water); (2) unlike normal saturated two-phase media such as soils, considerable amount of evaporable water is contained in the nanopores (only a few atoms wide). This water behaves partly as a load-bearing solid.

Therefore, the Biot medium relations need to be adapted for concrete. Bažant and Rahimi-Aghdam (2017) modified Biot relations by using effective porosity ϕ instead of Biot coefficient. The same modification is used here. Using effective porosity ϕ instead of Biot coefficient α, the incremental volumetric and tensorial two-phase equilibrium relations can be written as Fig. 3c.

7

Modeling ASR for various aggregate sizes

For simplicity, all the preceding equations in this study are formulated for one equivalent aggregate size. But in reality, the sizes of reactive aggregates are distributed statistically over a broad range.

The kinetics of reaction depends strongly on the aggregate size and small aggregates react much faster than big ones. Therefore, considering one effective aggregate size cannot capture the fast expansion occurring in the small aggregates, and the predicted expansion curves always show an initial delay. In detailed calculations, one should consider the real distribution of aggregate size, but this is computationally complicated and usually the exact distribution of aggregates sizes in not available. A simple way to avoid the unrealistic initial delay is to consider two different aggregate sizes, with different computational weights ws and wb for small and big aggregate sizes, Ds and Db. Thus, the total mass of imbibed water wi is calculated as shown in Fig. 3d.

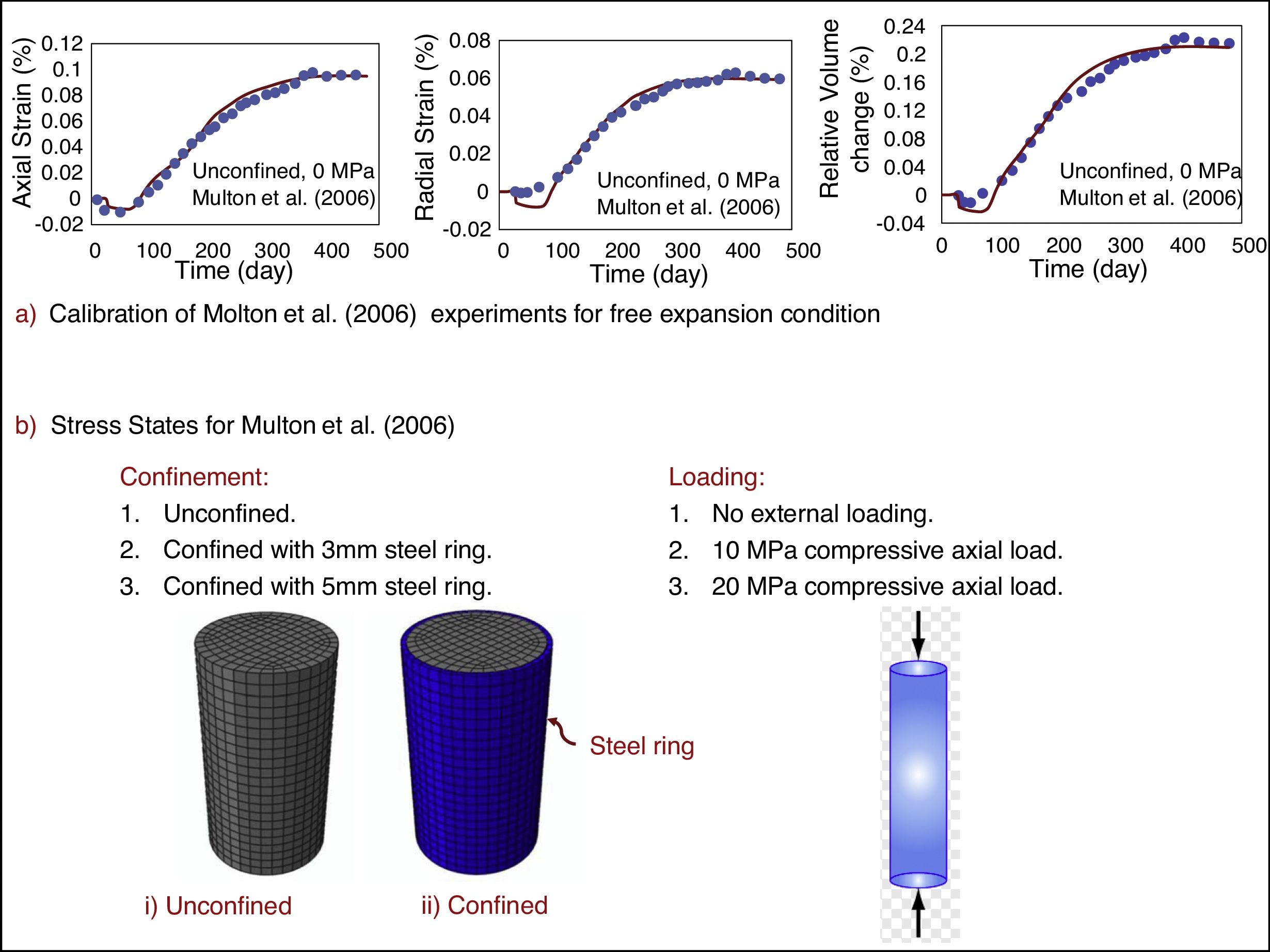
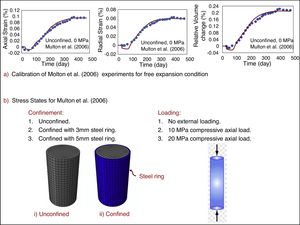
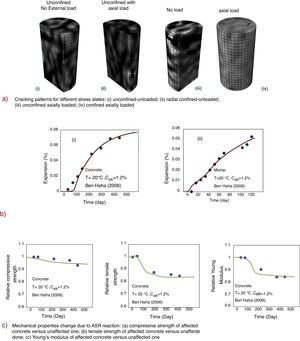
8

Effect of various stress states on ASR-induced expansion

Several numerical and experimental studies showed a significant effect of applied stress state and confinement on ASR-induced expansion and damage [4,19–22]. Particularly, experiments showed that the effect of loading on the ASR-induced volume expansion is minimal and usually the applied stress changes only the direction of expansion. For instance, large compressive stress in one direction transfers the expansion to other directions with smaller or no compression. To analyze the ability of the proposed model to predict the ASR-induced expansion and deterioration at different stress states, we consider some published experimental data. First we analyze the accelerated laboratory tests of Multon and Toutlemonde (2006). The duration of these tests was 450 days and the accelerated ASR-induced expansion was comparable to that obtained during 5 to 50 years in actual structures (in which the reaction is not accelerated). In these tests, concrete cylinders of diameter 130 mm and height of 120 mm, with the water-cement ratio of 0.45, was used. To accelerate the rate of ASR, potassium hydroxide was dissolved in the mixing water to increase Na₂O_eq to 1.25% of the mass of cement.

The model was first calibrated for the case of free expansion. Two aggregate sizes were considered: D = 9 mm for 85% of aggregates, and D = 4.2 mm for 15%. Fig. 4a shows the calibrated results for the free expansion case. As the figure shows, considering two aggregate size is enough, and the predicted initial expansion has no delay.

Figure 4.

Calibration of Multon et al. experiment and stress states.

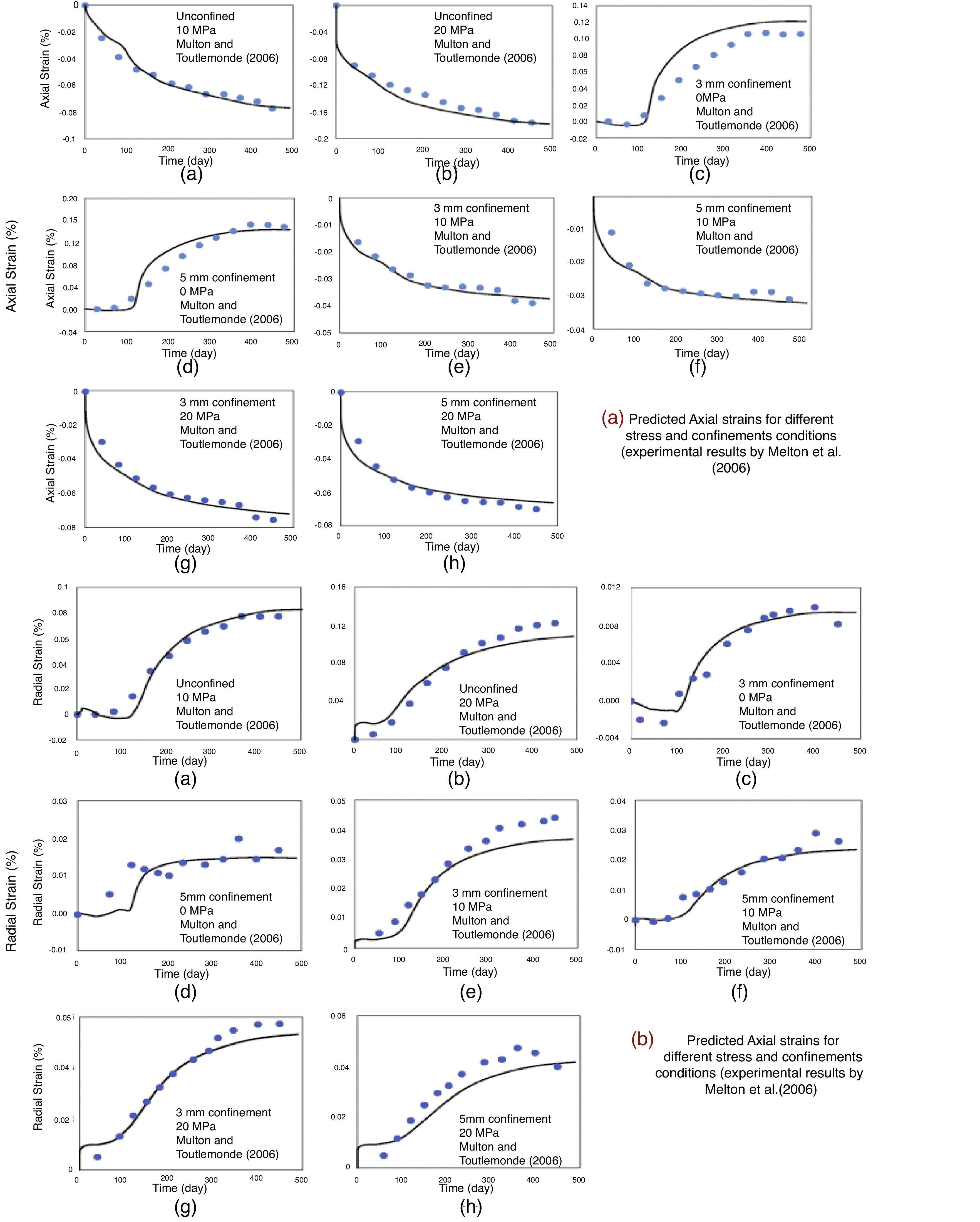
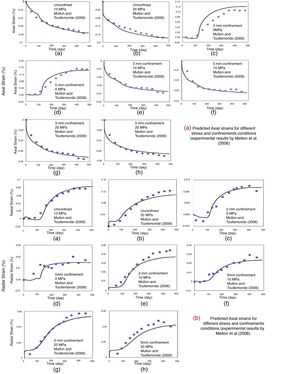
Multon and Toutlemonde (2006) analyzed the effect of various stress states on the ASR-induced expansion. Fig. 4b shows the confinement used and the loading conditions. In total, they tested specimens at nine different stress states. Here we use one of them (the free expansion) to calibrate our model and then analyze the calibrated model ability to predict ASR-induced swelling in other stress states. Fig. 5a shows the plot of predicted vs. experimental results for the axial deformations and Fig. 5b shows the same for the radial deformations. These figures demonstrate that the model is able to predict the ASR-induced expansion in good agreement with the experimental results. In particular, they confirm that the present model can predict the so-called ‘expansion transfer’, i.e., the load-induced transfer of ASR expansion to another direction.

Figure 5.

Predicted vs. experimnetal results for Multon et al. (2006) experiments.

It should be noted that in the cylinders confined by tubular steel envelopes, the concrete was considered to slide against the steel. For sure this slide was not frictionless and the friction could be significant. However, the friction coefficient was not reported. In simulations, it was assumed to be 0.15.

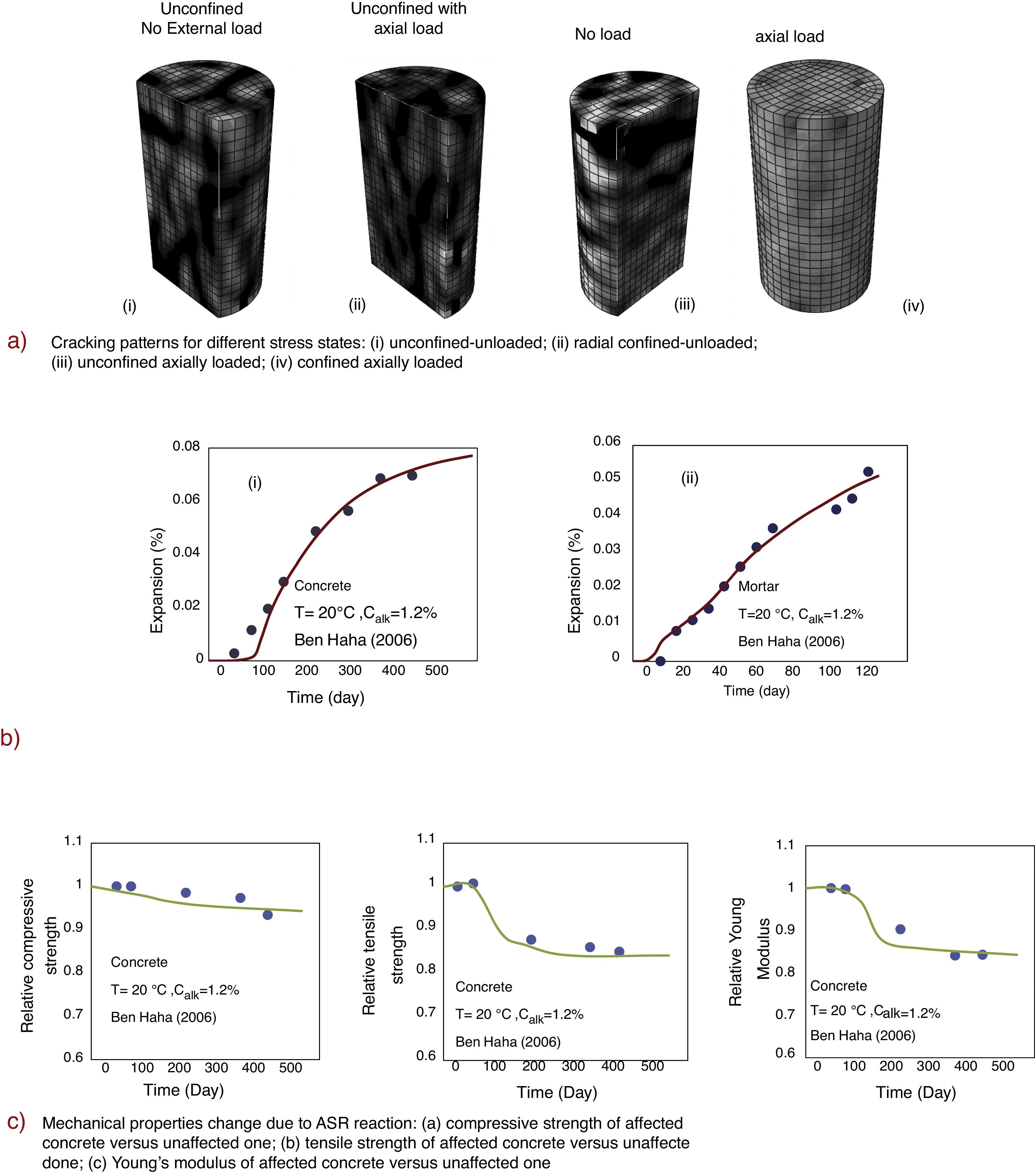
As a consequence of the loading and confinement conditions, the damage and cracking pattern are also different for various stress states. Fig. 6a shows the predicted cracking pattern for Multon and Toutlemonde (2006) experiments. For the unconfined load-free case, the cracks can propagate randomly in all directions, but as it can be seen, for radial confinement the cracks are mostly radial. Adding a sufficient axial compressive load will prevent the damage bands, or macrocracks, in the loading direction.

Figure 6.

Cracking pattern for ASR-induced damage at different stress states and the degradation of mechanical properties due to ASR-induced damage.

9

The effect of ASR on mechanical properties

As many studies showed, the ASR-induced expansion generates microcracks and cracks that weaken the concrete [23–32]. Here we analyze the influence of ASR on: (1) the compressive strength; (2) the tensile strength; and (3) Young's modulus.

The model predictions are compared with the experimental data of Ben Haha [25,26]. His experiments include accelerated tests of concrete prisms of dimensions 70 × 70 × 280 mm, submerged in water. Since no measurements are reported for autogenous shrinkage and swelling, their effects are neglected, although they might have had considerable effects on the deformations.

First, we calibrate the model to fit Ben Haha's measured ASR-induced expansion. We consider 85% of aggregates to have the size of D = 10 mm, and 15% D = 4.3 mm. Fig. 6b compares the experimental and calculated ASR induced expansions. Now that the model is calibrated to predict the measured expansion, we can test its power in predicting the effect of ASR on the mechanical properties. In this study, we analyze the effects of an axial load, tensile or compressive, at different stages of the ASR.

Let us begin with the compressive strength. To determine the ASR effect on the compressive strength, a compressive axial force, increased to reach the strength limit, is applied to the specimen at different reaction times. Although it seems rational that the compressive strength declines due to ASR, because it generates micro- and macro-cracking, there is a disagreement among various experimenters. For instance, Clark and Ono [27,29] found that ASR can decrease the compressive strength significantly (up to 40%), while Monette [28] did not see any significant change. However, in this regard it should be noted that the ASR and the aging due to cement hydration have opposite effects, the former decreasing the strength and the latter increasing it. Another source of increase in compressive strength may be the extra C–S–H that is produced outside the aggregate when the ASR gel gets calcified. These competing effects must be the main reason for this discrepancy.

To isolate the effect of ASR, we consider the relative compressive strengths of specimens with and without the reactive aggregates. For calculating the aging due to hydration, the model by Rahimi-Aghdam et al. [33] is used. Fig. 6c shows the compressive strength ratio for concretes affected or unaffected by ASR, at various reaction times, and shows that the compressive strength decreases by about 5% due to ASR, which is in agreement with the experimental results.

The same procedure is used to determine the effect of ASR on the tensile strength and Young's modulus. As Fig. 6c shows that the effects of ASR on the tensile strength and on Young's modulus are more pronounced. The model is able to predict these effects well. The ASR expansion is here found to decrease the tensile strength and Young's modulus by nearly 15%.

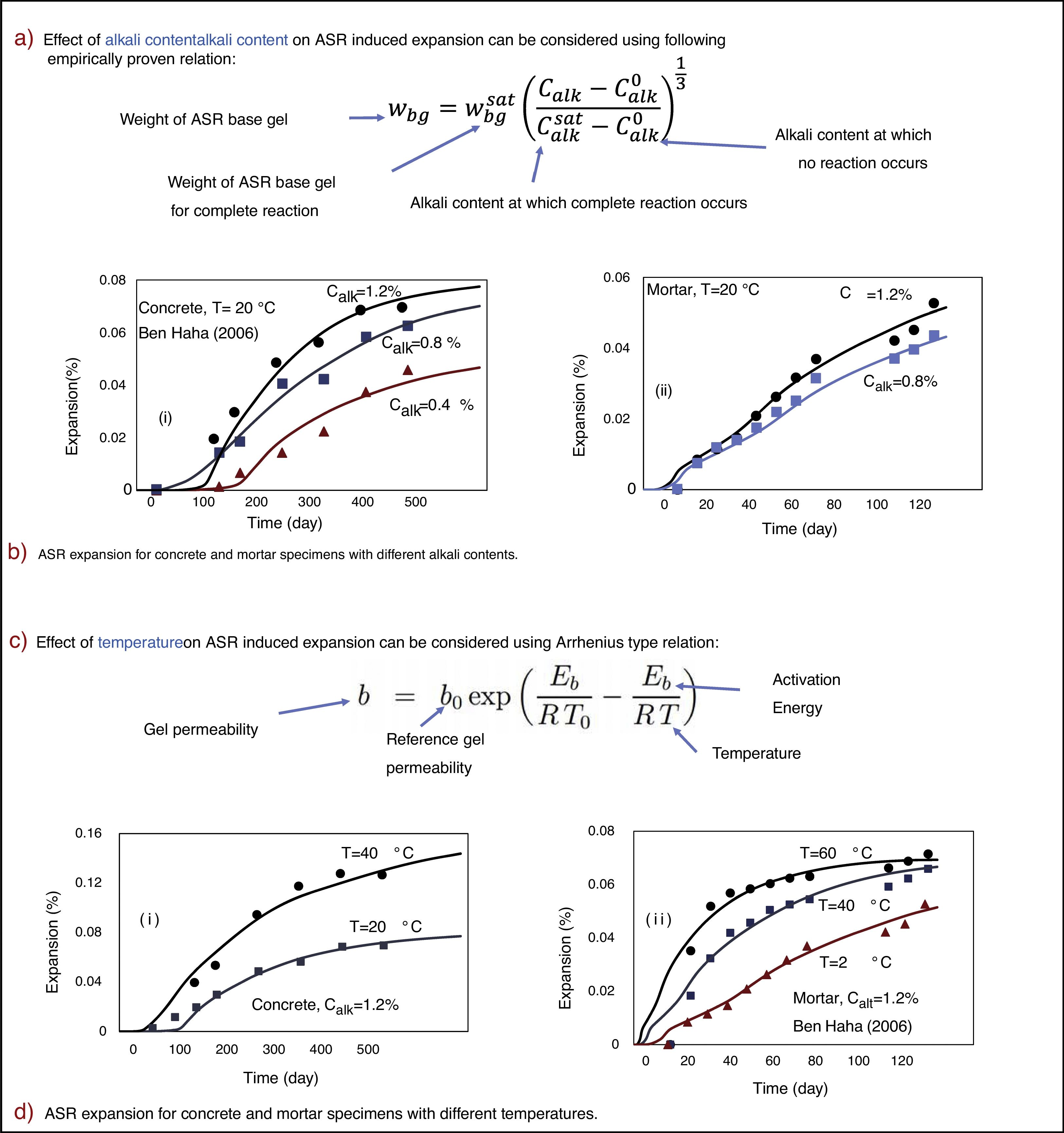
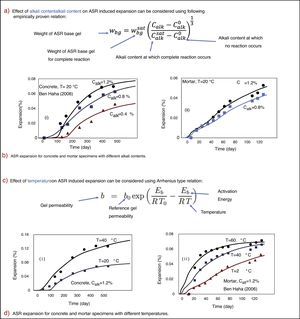
10

Effect of alkali content on ASR induced-expansion

The alkali content can have a considerable influence on the ASR reaction [34,35]. The availability of alkali ions and hydroxyl ions is what controls the ASR kinetics. Often, we should assess the ASR for the concrete in which reactive silica content is insufficient to complete the ASR reaction. To model this, we must relate the amount of the ASR gel produced to the alkali content. Fig. 7a shows the empirical relation that is considered in this study, in which Calk is the alkali content (ratio of the mass of alkali to cement mass), Calk0 is the alkali content at which ASR stops or does not begin, and Calk* is the alkali content at which alkali ions are adequate for complete reaction. In this study, we assume Calk* = 0.1%, and Calk* is set equal to 1.25% for concrete and 1% for mortar. The value of Calk* is smaller for mortar since c/a is higher in a mortar and we calculate the alkali content as a function of cement (c/a = cement-to-aggregate ratio, by mass). It would be better to find an empirical equation for Calk* as a function of c/a, but there are not enough experimental data to verify that equation.

Figure 7.

Effect of alkali content and temperature on ASR-induced expansion.

We consider two sets of experiments to assess the effect of alkali content. The first is the same as that already considered in analyzing the effect of ASR on the degradation of mechanical properties. The second is Ben Haha's (2006, 2007) set of tests of saturated mortar prisms of size 40 × 40 × 160 mm. The experimental and predicted results for different alkali contents are compared in Fig. 7a. The predictions are in good agreement with the experimental results.

11

Effect of temperature on ASR-induced expansion

Like in all chemical reactions, the temperature change alters the ASR kinetics [31,36–41], and this causes changes in the ASR-induced expansion and damage. The temperature effect is considered to follow the Arrhenius equation (Fig. 7b) for permeability of water through the ASR gel, for initial diffusivity of cement mortar around the aggregate, and for permeability of the ASR gel; here T = current absolute temperature, R = universal gas constant.

For the experimental comparisons and calibration, Ben Haha's tests [25,26] were used again to assess the ability of the model in predicting the effect of temperature. Fig. 7b shows the experimental vs. predicted results for concrete and mortar prisms. The fits are seen to be quite close.

12

Conclusion

The mechanical analysis as well as the attainment of a good agreement of numerical predictions with the experimental observations confirm that both the long-term creep and the long-term diffusion, which causes the ASR gel to penetrate into pores and new cracks in the mineral aggregates and cement mortar near aggregate pieces, are important mechanisms in ASR damage to structures. They mitigate the damage substantially.

Acknowledgment

Partial financial supports from the NEUP Program of the U.S Department of Energy under grant DE-AC07-05/D14517, and from the U.S. National Science Foundation under grant CMMI-1153494, both to Northwestern University, are gratefully acknowledged