La obtención de resultados precisos en un análisis estático no lineal requiere una adecuada modelización de las rótulas plásticas generadas en la estructura, para lo que conviene emplear expresiones empíricas capaces de modelizar la relación fuerza-deformación de la rótula. El objetivo principal de esta contribución es estudiar la influencia de diferentes modelos de rótula plástica en el comportamiento no lineal de estructuras aporticadas de hormigón armado. Se realizan análisis no lineales considerando diversos modelos de rótula, como el incluido en el código FEMA-356 y dos modelos desarrollados a partir de expresiones empíricas calibradas con diferentes bases de ensayos experimentales. Los resultados obtenidos muestran que el modelo propuesto por los autores refleja con mayor precisión el comportamiento de edificios convencionales de hormigón armado situados en zonas sísmicas. Además, el modelo puede emplearse para contrastar los resultados ofrecidos por otros modelos incluidos en la diversa normativa de diseño sísmico de edificación.
An adequate modelling of the plastic hinges generated during the pushover analysis is crucial in order to obtain accurate results. Thus, empirical expressions must be used appropriately in order to model the generalised force-deformation relationship of plastic hinges. The main aim of this article is to study the influence of different plastic hinge models on the non-linear structural behaviour of reinforced concrete structures. To that end, several non-linear analyses have been performed using the following plastic hinge models: the model included in the code FEMA-356 and two additional models developed by some researchers by using empirical expressions calibrated with different experimental data. The results obtained show that plastic hinges modelled with empirical expressions can be used to more precisely model the behaviour of structural elements in ordinary buildings located in seismic areas, and to compare with the results offered by the models included in seismic building design codes.
La predicción y simulación del comportamiento sísmico de estructuras empleando modelos numéricos es un campo de interés creciente en los últimos años, debido a la importancia de conocer de forma precisa los efectos y las consecuencias provocadas por la acción sísmica sobre las estructuras.
El análisis sísmico se puede realizar siguiendo diferentes procedimientos en función del nivel de precisión que se quiera alcanzar en los resultados. El análisis estático no lineal mediante empuje incremental o pushover es uno de los métodos más frecuentemente empleado en ingeniería estructural, debido a su relativa simplicidad y a las prescripciones incluidas en las principales normas de diseño sísmico de edificación para su implementación. Este tipo de análisis ofrece información relevante desde el punto de vista sísmico, como es el caso de la resistencia y capacidad de deformación de la estructura. El análisis pushover puede implementarse siguiendo diferentes estrategias, como el pushover modal [1], el pushover consecutivo modal [2], el upper bound pushover[3], el mass proportional pushover[4] y el pushover adaptativo [5]. Sin embargo, la mayor precisión de estos métodos se consigue renunciando a la característica más atractiva del análisis pushover convencional, esto es, su simplicidad [6,7], motivo por el cual ha sido este último el tipo de análisis empleado en esta contribución.
Se necesita conocer el comportamiento seccional de los elementos estructurales en los estados de plastificación y de rotura para poder definir adecuadamente las propiedades de las rótulas plásticas generadas durante el análisis no lineal, en particular el momento de plastificación My, el giro de plastificación θy y el giro último θu de la sección.
Es recomendable utilizar expresiones empíricas que reproduzcan los estados de plastificación y de rotura de la sección del elemento estructural en el análisis sísmico [8–10]. Debido a su relativa simplicidad y a que están calibradas con ensayos experimentales, estas expresiones son suficientemente precisas y eficientes desde un punto de vista computacional.
El objetivo principal de esta contribución es evaluar la influencia del tipo de rótula plástica considerado en el comportamiento no lineal de estructuras. Para ello se realizan varios análisis pushover sobre dos ejemplos de estructuras de hormigón armado, considerando los siguientes tipos de rótulas plásticas:
Rótulas plásticas modelizadas según el código de la FEMA-356 [11], incluidas por defecto en el software SAP2000®[12].
Rótulas plásticas definidas mediante las expresiones empíricas disponibles en [9,10].
Rótulas plásticas modelizadas con las expresiones desarrolladas por los autores de este trabajo en investigaciones previas [13,14].
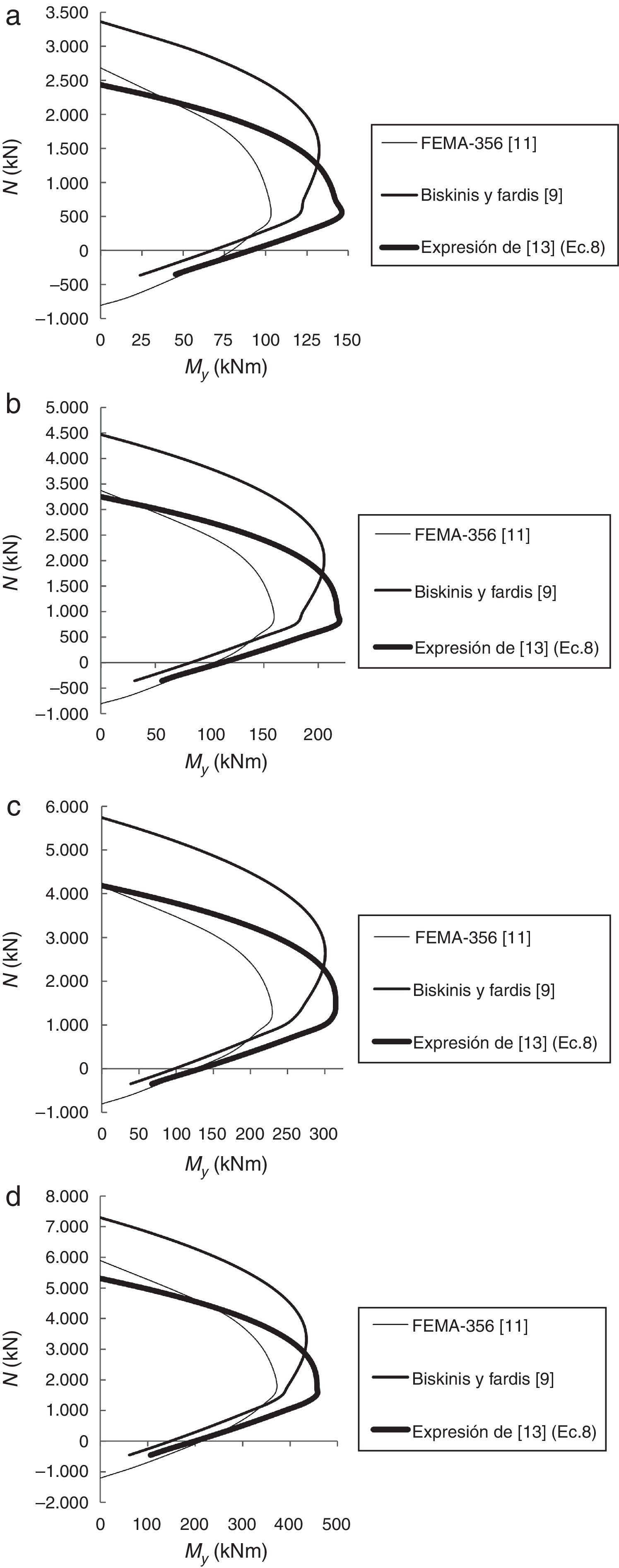
Para definir las propiedades de las rótulas plásticas consideradas se obtienen las relaciones momento-giro de la sección con los métodos anteriormente citados. Con objeto de considerar la influencia del esfuerzo axil N en el valor del momento de plastificación My, se definen ciertas curvas N-My para los pilares de las estructuras.
En el análisis pushover es conveniente estudiar los denominados puntos de plastificación global y de colapso de la estructura, que proporcionan información acerca de la ductilidad, obteniendo para dichos puntos los correspondientes parámetros de desplazamiento de control δ, cortante basal Fb y aceleración espectral Sa, así como las curvas de capacidad Fb - δ de la estructura.
Finalmente, se ha implementado el método N2 [15] propuesto en el EC-8 para las dos estructuras consideradas, escogiendo ciertos valores de la aceleración del suelo ag para estudiar la influencia de este parámetro en las diferencias obtenidas con los distintos tipos de rótulas plásticas.
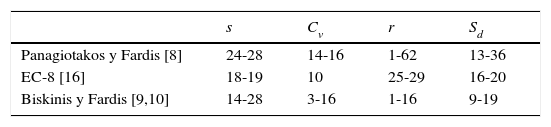
2Modelos de rótula plástica y metodología de análisis2.1Ecuaciones de comportamiento seccionalExisten diversas expresiones capaces de reproducir el comportamiento de plastificación y de rotura de secciones de hormigón armado a partir de su geometría, de su configuración de armaduras y de las propiedades mecánicas de los materiales. Panagiotakos y Fardis [8] propusieron expresiones para obtener el momento de plastificación My, el giro de plastificación θy el giro de rotura θu, las cuales se calibraron con una base de datos de más de 1.000 ensayos experimentales realizados sobre vigas, pilares y muros de cortante. Posteriormente, Biskinis y Fardis [9,10] modificaron estas expresiones calibrándolas con una base de datos que incluía elementos rehabilitados, resultando las ecuaciones 1 a 3. Mencionar que también el EC-8 [16] incluye algunas ecuaciones que proporcionan el giro de plastificación y de rotura de la sección.
Los autores de esta contribución han propuesto otras expresiones para obtener My, θy y θu[13,14], para lo cual calibraron las expresiones de Biskinis y Fardis [9,10] utilizando un conjunto de ensayos seleccionados de la base de más de 1.000 ensayos incluida en [8], selección compuesta por vigas y pilares de hormigón armado con sección rectangular que cumplan con las prescripciones constructivas y sísmicas incluidas en las principales normas de diseño de edificación, concretamente en EC-2 [17], EC-8 [18] y ACI-318 [19].
Dado que las variables de los elementos estructurales incluidos en la base de datos original [8] presentan un amplio rango de valores, se escogieron 5 grupos de parámetros para cumplir las especificaciones impuestas en las normas de edificación consideradas: las dimensiones de la sección transversal, las propiedades mecánicas de los materiales, el diámetro de las armaduras, el área de las armaduras y el espaciamiento de la armadura de cortante. Algunos de estos parámetros (dimensiones de la sección transversal, área de las armaduras y espaciamiento de la armadura de cortante) están directamente relacionados con el nivel de ductilidad considerado, por lo que se escogió el rango de variación más amplio posible de forma que se satisfagan los requerimientos sísmicos de los códigos y se consideren solo elementos reales (diseñados y construidos bajo un determinado código sísmico).
Se propusieron nuevos coeficientes (C1 a C15) para calibrar las expresiones de Biskinis y Fardis [9,10] con los resultados experimentales de la selección de ensayos. Estos coeficientes Ci se propusieron tras realizar un análisis de sensibilidad de los diferentes términos de las expresiones propuestas en [9,10], no alterando los coeficientes con base teórica sino modificando solo los coeficientes empíricos. Las expresiones modificadas mediante los nuevos coeficientes vienen dadas por las ecuaciones (4) a (6):
Para conseguir la mejor calibración posible de las expresiones con la selección de ensayos se implementó un procedimiento de optimización basado en algoritmos genéticos (GA), siendo las variables del problema de optimización los coeficientes C1 a C15. La función objetivo que se utilizó fue el coeficiente de variación Cv de una variable x, definida como el cociente entre el valor experimental xexp y el valor predicho xpred (obtenido mediante las expresiones afectadas por los coeficientes C1 a C15) para cada ensayo de la selección. Se obtuvieron diversos parámetros estadísticos de la variable x=xexp/xpred, como el coeficiente de variación Cv, la media muestral x¯, la desviación típica muestral s y el coeficiente de correlación lineal muestral r entre los valores experimentales y predichos.
Además, se empleó el sumatorio Sd de los valores absolutos de las diferencias entre los valores experimentales y predichos para proporcionar una estimación de la calidad de los resultados (a menor valor del sumatorio, más precisa es la calibración):
Las expresiones obtenidas tras la aplicación del procedimiento basado en GA vienen dadas por las ecuaciones (8) a (10).
Conviene destacar que los efectos del esfuerzo cortante influyen en el valor obtenido para θy. Dichos efectos se consideran mediante el parámetro av en la ecuación (9). Así, av adopta el valor 1 si la plastificación por flexión se produce tras la fisuración diagonal de la sección, y 0 en caso contrario. Además, el segundo término de la ecuación (9) se corresponde con la deformación por esfuerzo cortante a lo largo del vano de cortante Ls.
La tabla 1 muestra un resumen de los rangos de mejoras conseguidas en ciertos parámetros estadísticos al aplicar las expresiones propuestas por los autores [13] respecto a otras expresiones, pues se reduce la dispersión (menores valores de s, CV y Sd) y mejora la correlación lineal entre los valores experimentales y predichos, obteniéndose valores más altos del coeficiente de correlación lineal r.
La principal aportación de estas expresiones no es tanto la mejora conseguida respecto a otras ecuaciones previamente propuestas sino que, al estar calibradas con la selección de ensayos, son aplicables a elementos estructurales de edificios habituales de hormigón armado situados en zonas sísmicas. Para más información acerca de las ecuaciones (8) a (10) se pueden consultar las referencias [13,14].
2.2Análisis pushover. Consideraciones específicas.En este trabajo se han realizado varios análisis pushover de tipo convencional, considerando un patrón invariante de cargas laterales. De acuerdo con EC-8, se consideran 2 distribuciones verticales de carga lateral: a)un patrón uniforme, basado en fuerzas laterales proporcionales a la masa sin considerar su altura; y b)un patrón modal, proporcional a los desplazamientos de las masas en el modo fundamental de vibración. Las dos distribuciones verticales se obtienen aplicando las ecuaciones (11) y (12), respectivamente.
Si la influencia de otros modos de vibración resulta relevante para estimar la respuesta sísmica de la estructura, Mortezaei y Ronagh [20] aplicaron el patrón modal dado por la ecuación (13), incluido en FEMA-356 [11].
Las cargas gravitatorias están uniformemente distribuidas en las vigas, de acuerdo con la ecuación (14), incluida en EC-8 [18].
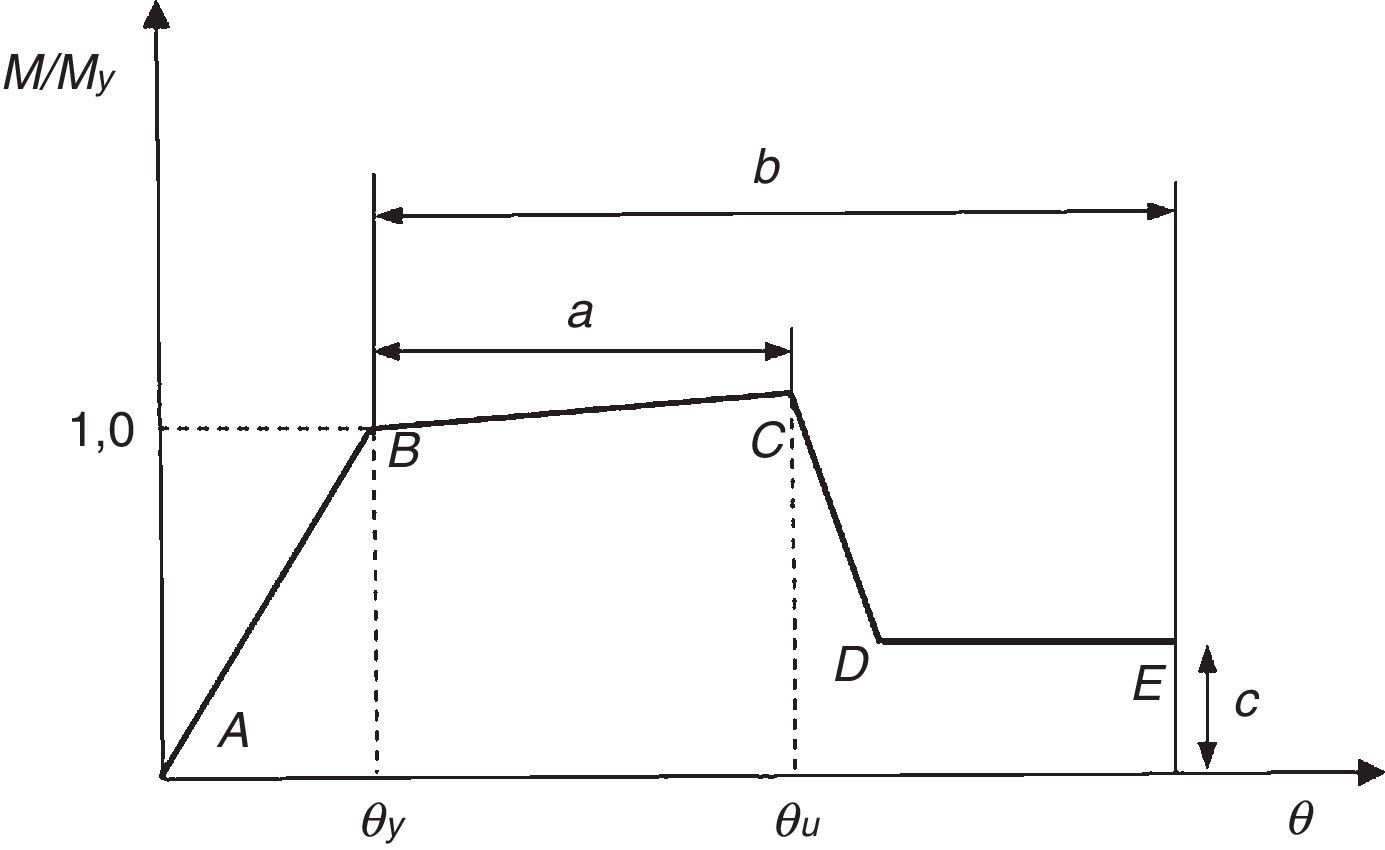
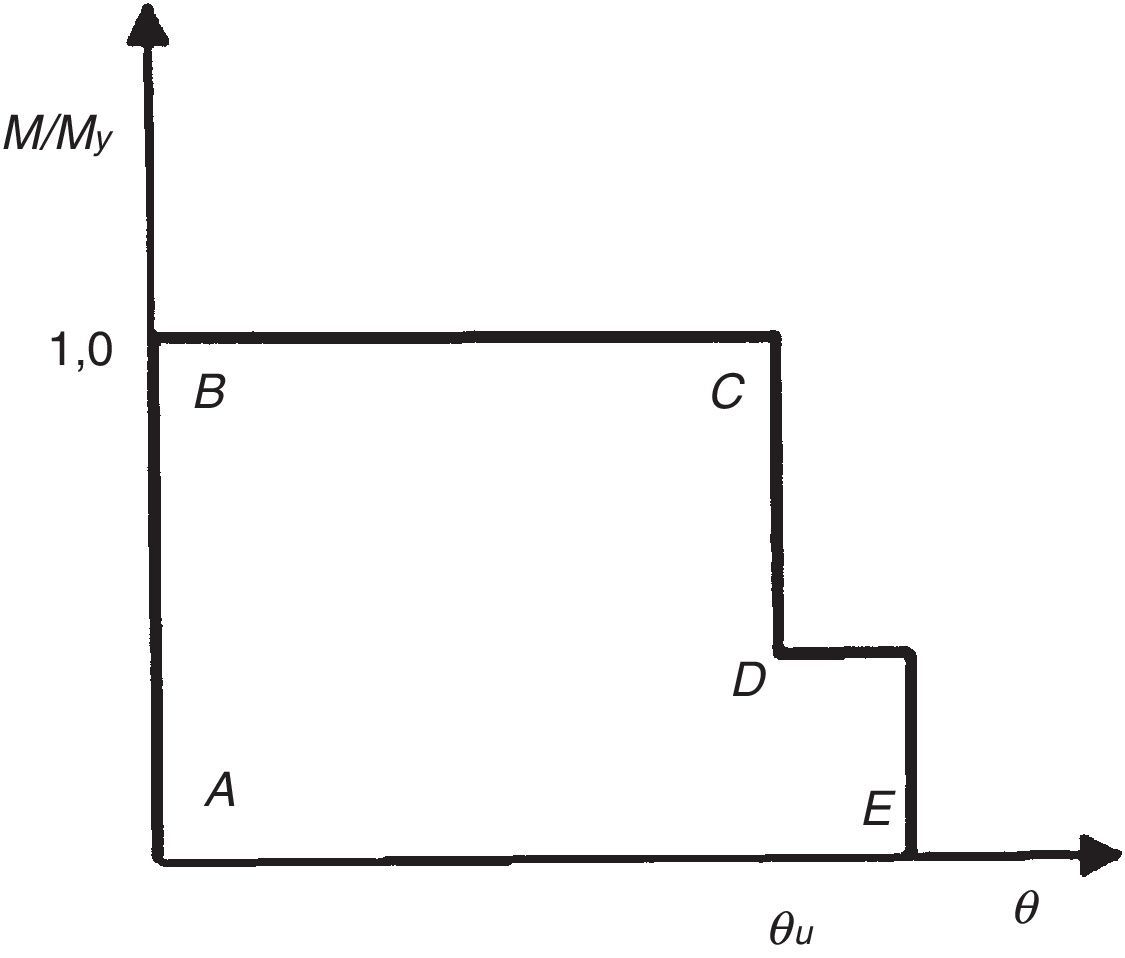
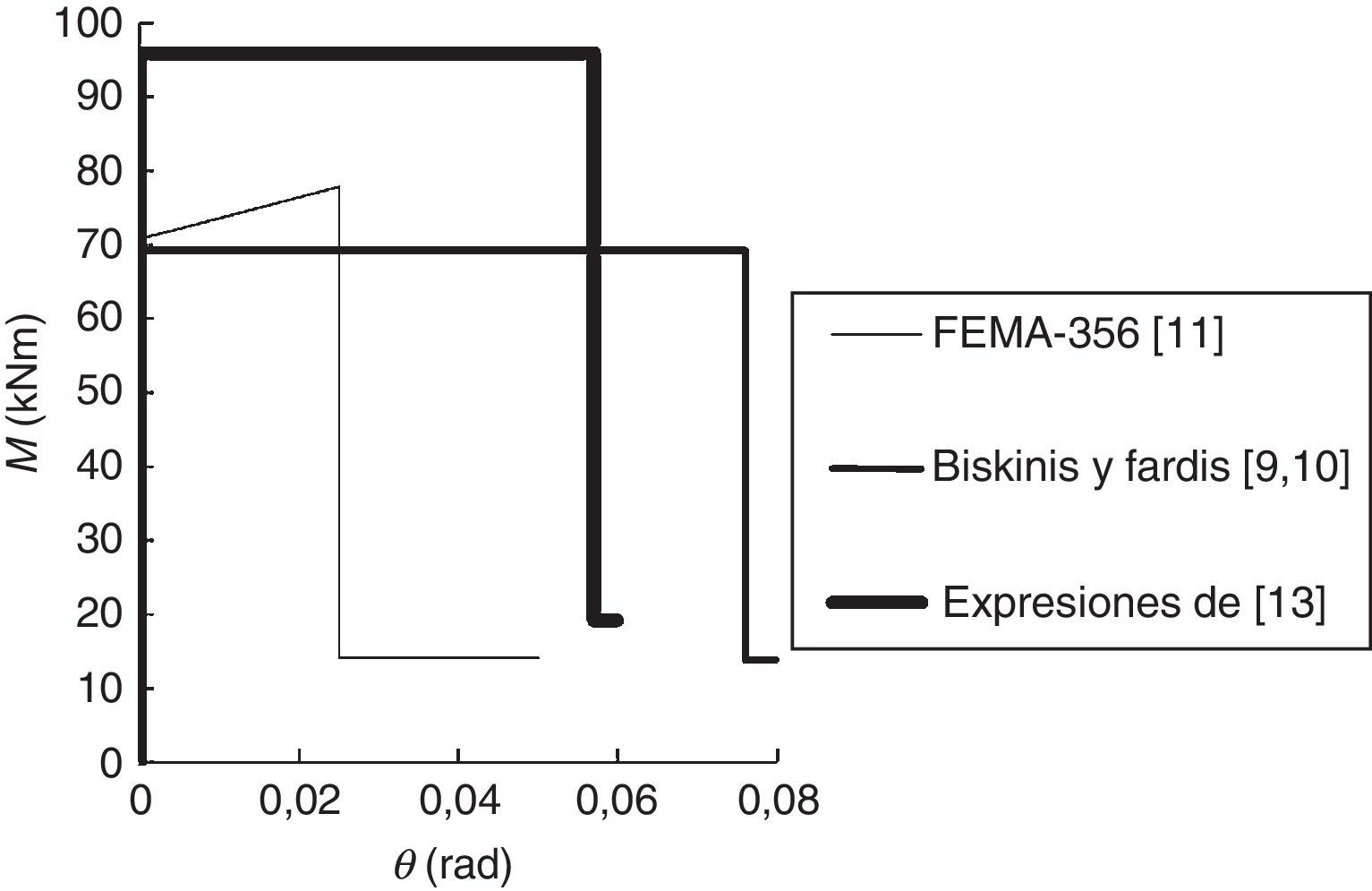
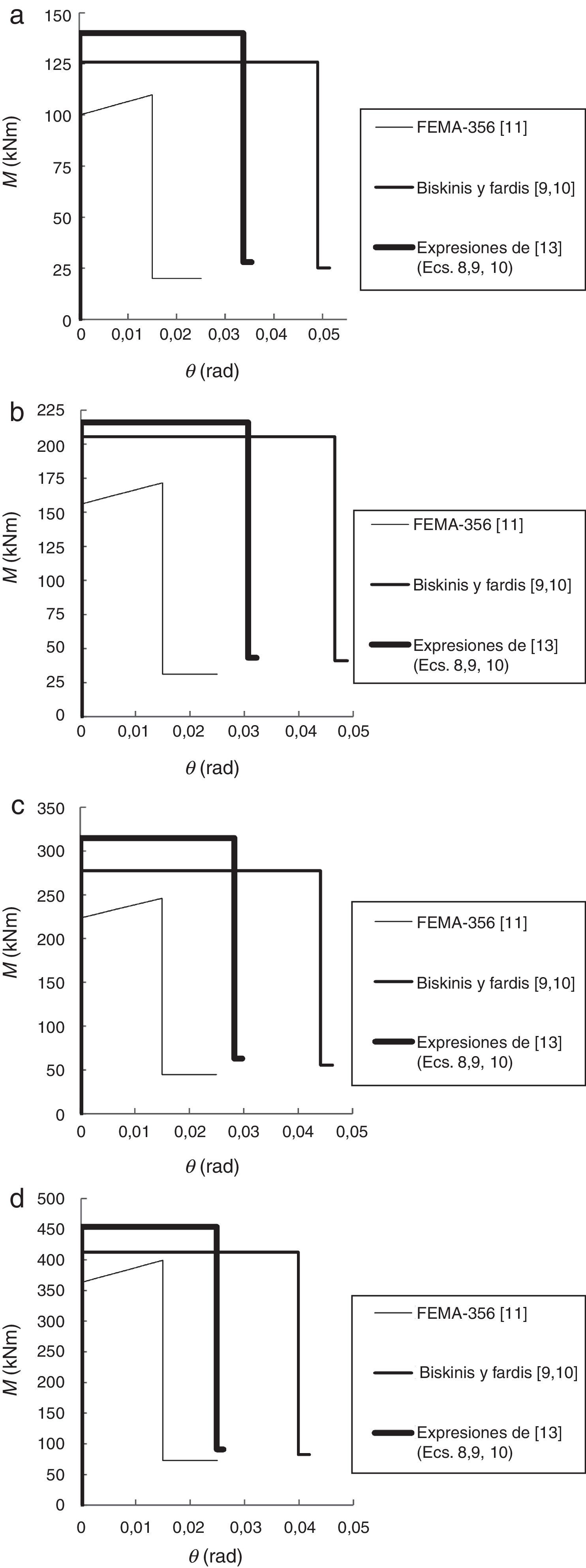
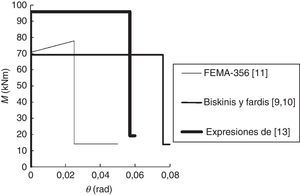
Los análisis se ejecutan empleando el software SAP2000®[12], considerando rótulas plásticas de longitud nula, cuya localización ha de ser definida por el usuario. En este trabajo, las rótulas plásticas generadas se localizan únicamente en los extremos de las vigas y los pilares, y se han modelizado mediante relaciones momento-giro definidas por control de deformación. Dichas relaciones dependen del tipo de rótula plástica considerada en el análisis. Así, las rótulas plásticas incluidas por defecto en SAP2000® presentan la relación mostrada en la figura 1, definida en FEMA-356 [11], mientras que las rótulas plásticas definidas mediante las expresiones incluidas en [9,10,13] se modelizan mediante las relaciones momento-giro incluidas en la figura 2.
Relación momento-giro para las rótulas plásticas [11].
Relación momento-giro para las rótulas plásticas [9,10,13].
Los efectos P-Delta se han considerado en los análisis pushover conforme a EC-8 [18]. Además, con objeto de considerar el efecto de la fisuración, la rigidez a la flexión y cortante de los elementos estructurales se ha reducido a la mitad respecto a los elementos sin fisurar.
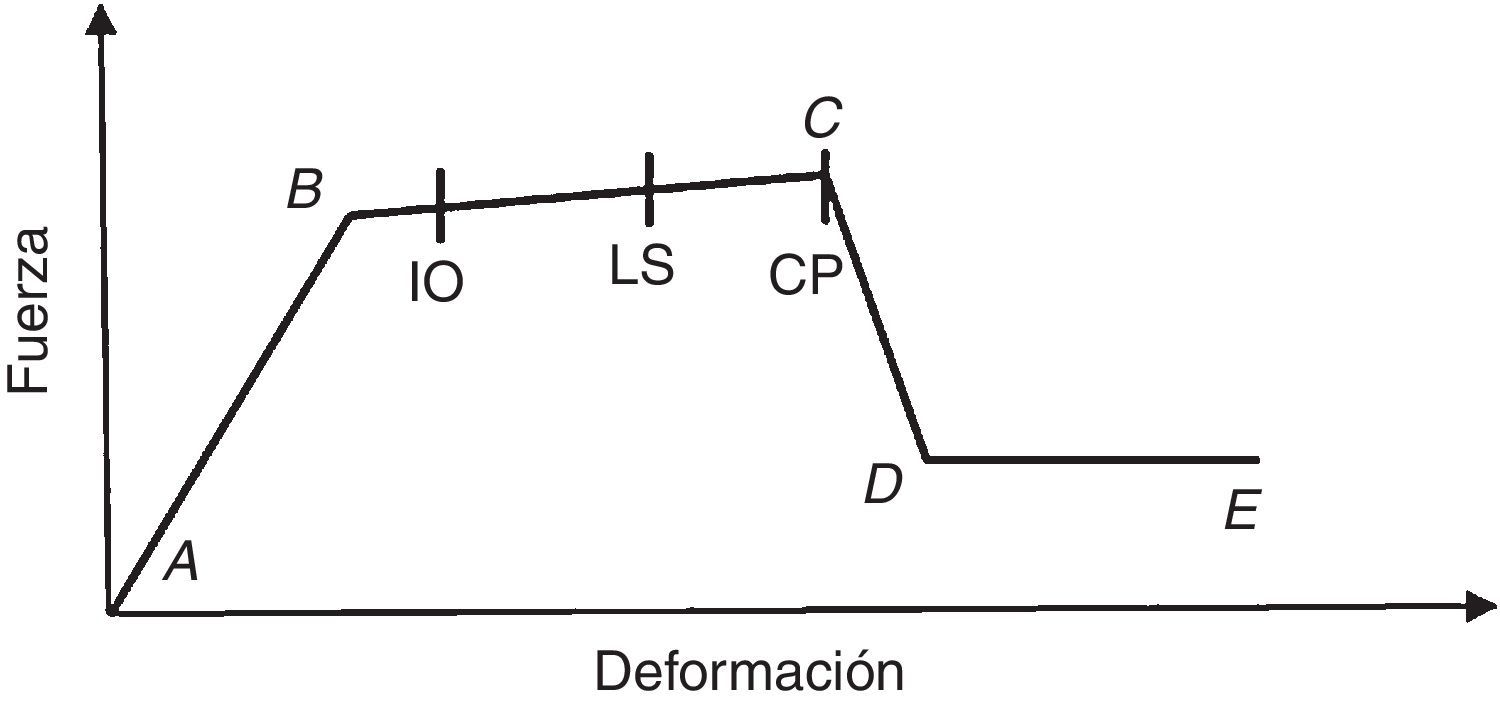
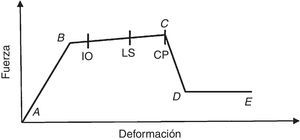
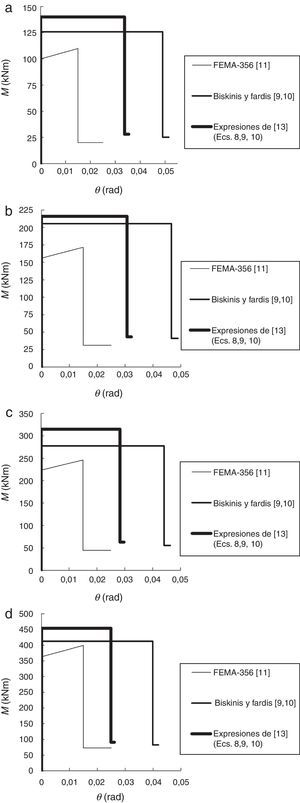
El código de la FEMA-356 [11] define 3 niveles de comportamiento estructural o niveles de desempeño, denominados Immediate Occupancy (IO), Life Safety (LS) y Collapse Prevention (CP). En este trabajo, dichos niveles corresponden al 40, 80 y 100% del giro de rotura θu para las vigas, y el 25, 75 y 100% para los pilares. Estos valores son similares a los considerados por otros autores, como Inel y Ozmen [21]. La figura 3 muestra los niveles de desempeño en la relación esfuerzo-deformación de una rótula plástica.
2.3Influencia de la aceleración del suelo agLa respuesta sísmica de una estructura depende en gran medida del valor considerado para la aceleración del suelo ag. Se ha analizado la influencia de este parámetro mediante la implementación del método N2, propuesto por Fajfar y Gaspersic [15] e incluido en el EC-8 [18], considerando las estructuras descritas en el apartado 3.1. Estas estructuras se cimentan sobre un terreno tipoC y en una zona en la que se aplica el espectro tipo2 [18]. Respecto a la aceleración del suelo ag, se han empleado 3 valores: 0,1g, 0,2g y 0,3g, siendo este último un valor suficientemente alto para el espectro tipo2. Para estos valores se ha obtenido el esfuerzo cortante en la base Fb, la aceleración espectral Sa y la distribución de rótulas plásticas en la estructura.
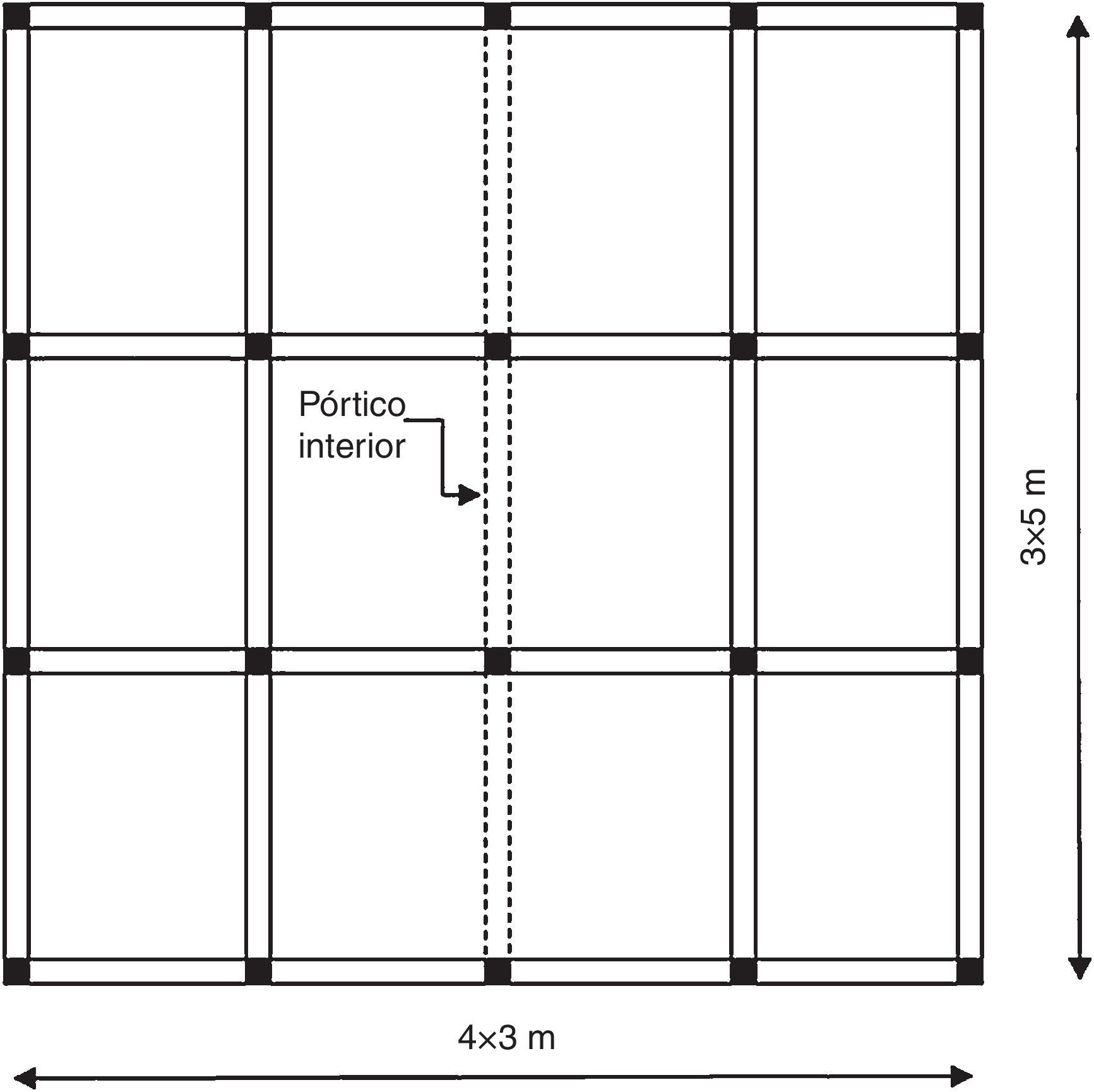
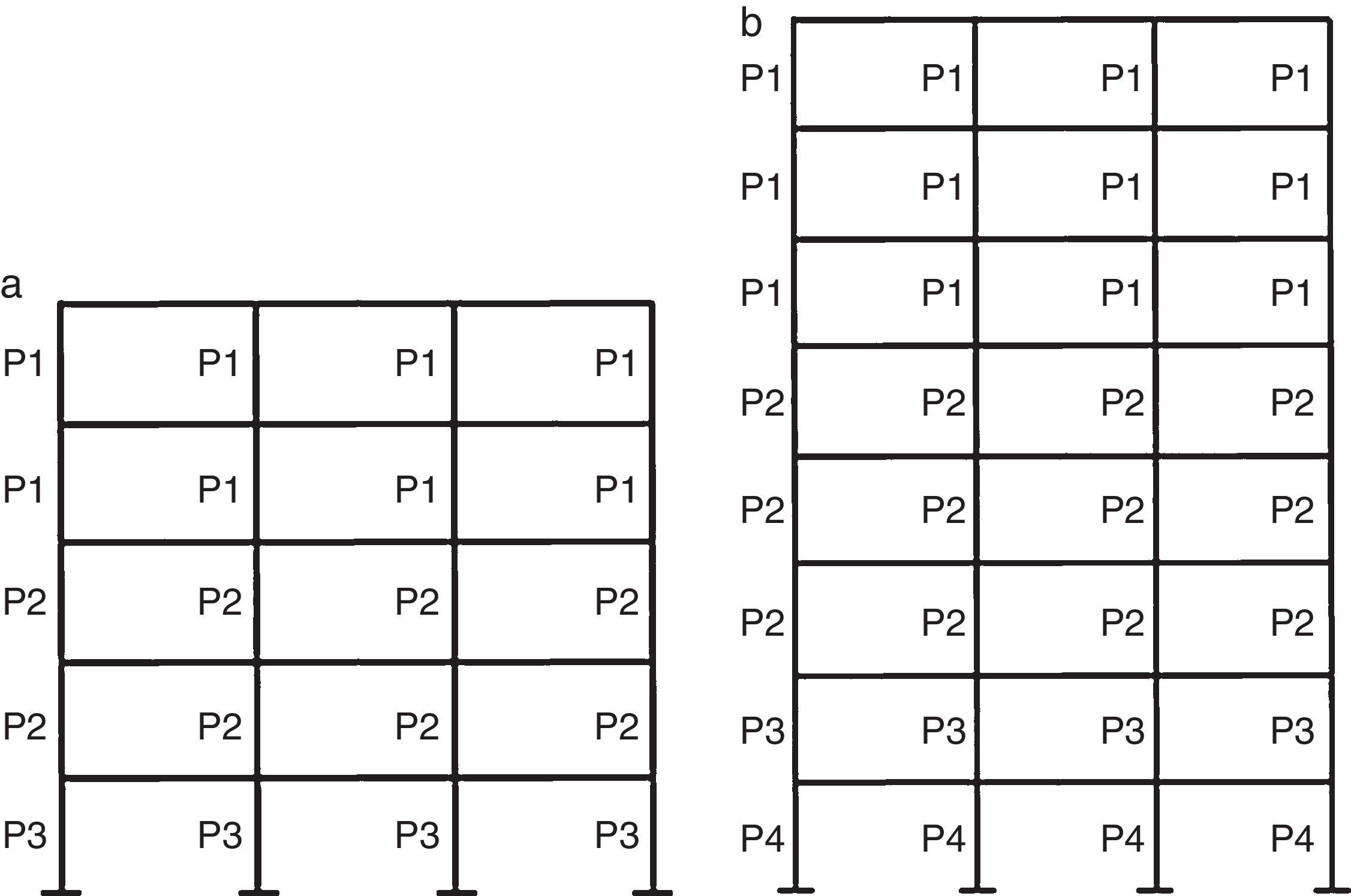
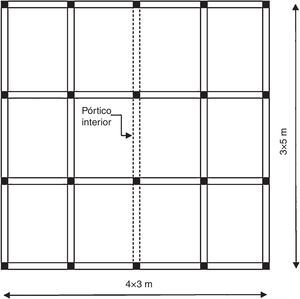
3Comportamiento de las secciones de hormigón armado en las estructuras consideradas3.1Descripción de las estructurasSe han analizado las estructuras de 2 edificios de hormigón armado de 5 y 8 plantas, compartiendo ambos la misma configuración en planta (fig. 4).
Esta tipología es habitual, según Carvalho, Coelho y Fardis [22], en los edificios residenciales de pequeña y mediana altura diseñados con el EC-8. El alzado del pórtico interior de cada estructura se muestra en la figura 5, con una altura entre plantas de 3m y una longitud de vano de 5m para ambas estructuras.
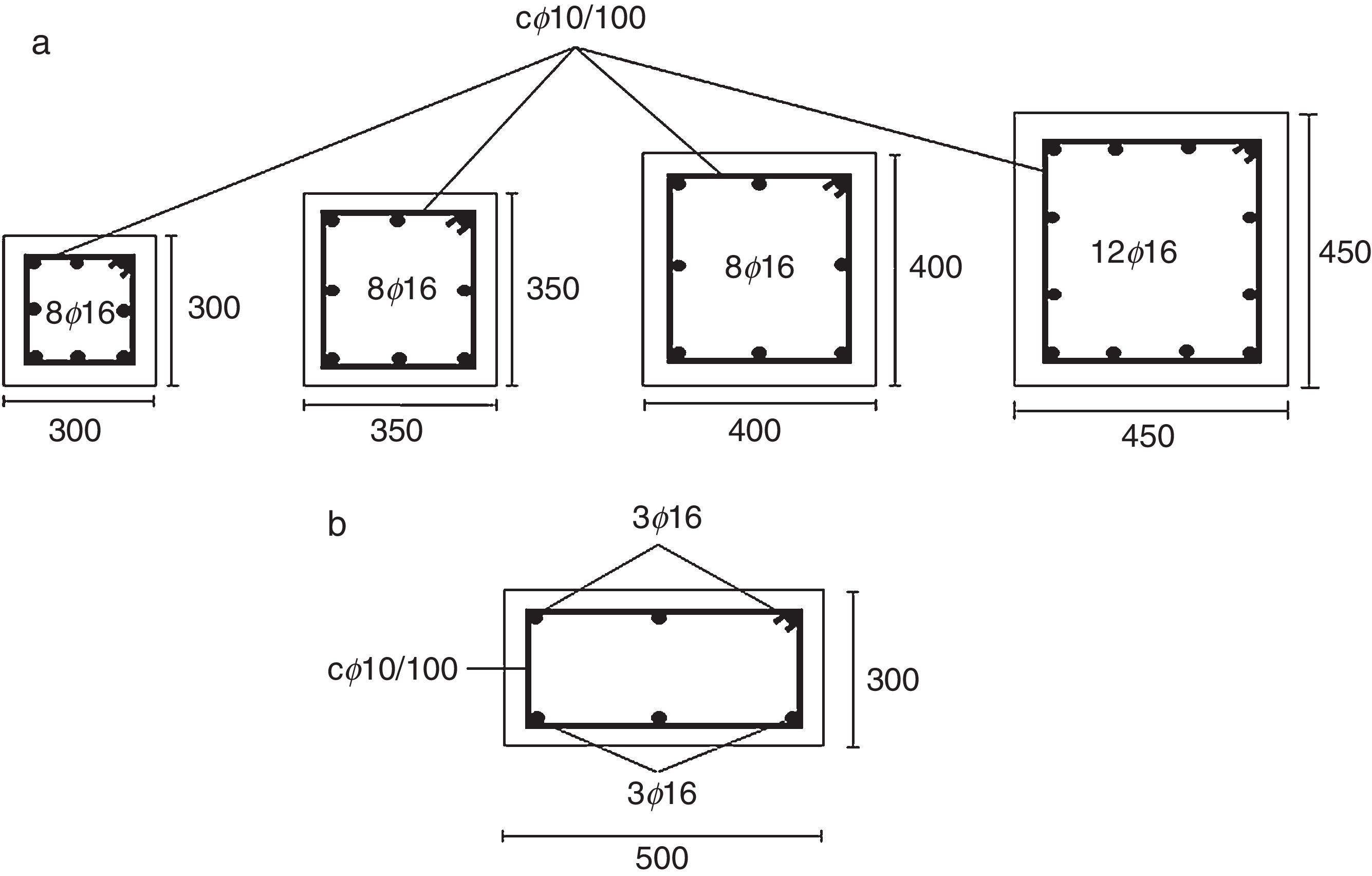
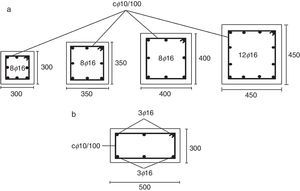
En la figura 6 se muestra la geometría y el armado de las secciones transversales de los elementos de los pórticos, constituidos por vigas planas y pilares de sección cuadrada. El hormigón es de 25MPa de resistencia a compresión simple, con un módulo elástico de 27.200MPa y un coeficiente de Poisson de 0,2. El acero de la armadura es de 500MPa de límite elástico y se ha empleado un espaciamiento de 100mm para la armadura de cortante en aquellas zonas donde pueden generarse rótulas plásticas. Conviene destacar que no se han considerado rótulas plásticas de cortante en los análisis pues, conforme al trabajo de Inel y Ozmen [21], la resistencia del hormigón y el espaciamiento de la armadura de cortante considerados resultan suficientes para impedir el fallo por esfuerzo cortante.
Conviene aclarar que, con objeto de simplificar la interpretación de los resultados, se han utilizado estructuras de geometría regular, presentando todas las vigas las mismas dimensiones y con armadura constante a lo largo de toda la viga. Se han empleado vigas planas, pues a pesar de su inadecuado comportamiento sísmico se utilizan habitualmente en países del área mediterránea con sismicidad moderada, como España, Italia y Portugal [23].
Respecto a las acciones gravitatorias, se ha empleado una carga permanente de 5kN/m2 y una sobrecarga de uso de 3kN/m2, correspondientes al uso de edificio residencial [17], distribuidas uniformemente sobre las vigas. El periodo fundamental T obtenido, considerando las masas concentradas en las plantas del edificio, ha sido de 1,24s para el pórtico de 5 plantas y de 1,9s para el pórtico de 8 plantas.
3.2Relaciones momento-giro y curvas de plastificaciónLas relaciones momento-giro consideradas según diferentes métodos para las rótulas plásticas que se generen en vigas y pilares se muestran en las figuras 7 y 8, respectivamente. En todos los casos, las expresiones propuestas por los autores [13] ofrecen valores de My superiores y de la capacidad de deformación intermedios respecto a los obtenidos aplicando las expresiones de Biskinis y Fardis [9] y del código de la FEMA-356 [11].
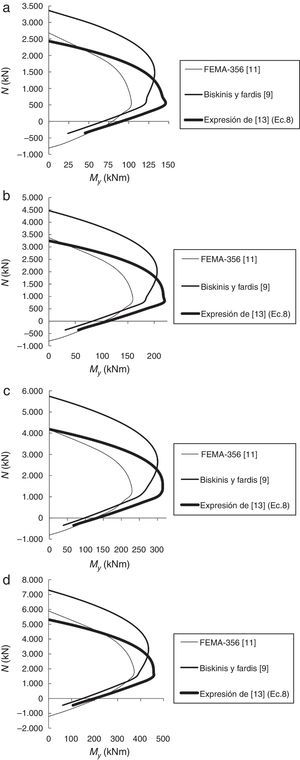
A diferencia de otros estudios, como el de Inel y Ozmen [21], en este trabajo se definen curvas de plastificación N-My para considerar, en el análisis no lineal, la influencia del esfuerzo axil N en el momento de plastificación My (fig. 9). Puede destacarse que las curvas obtenidas aplicando las expresiones empíricas desarrolladas por Biskinis y Fardis [9] y por los autores [13] muestran valores de My superiores a los obtenidos con el código de la FEMA-356 [11], correspondiendo los valores máximos de My a las expresiones propuestas por los autores [13].
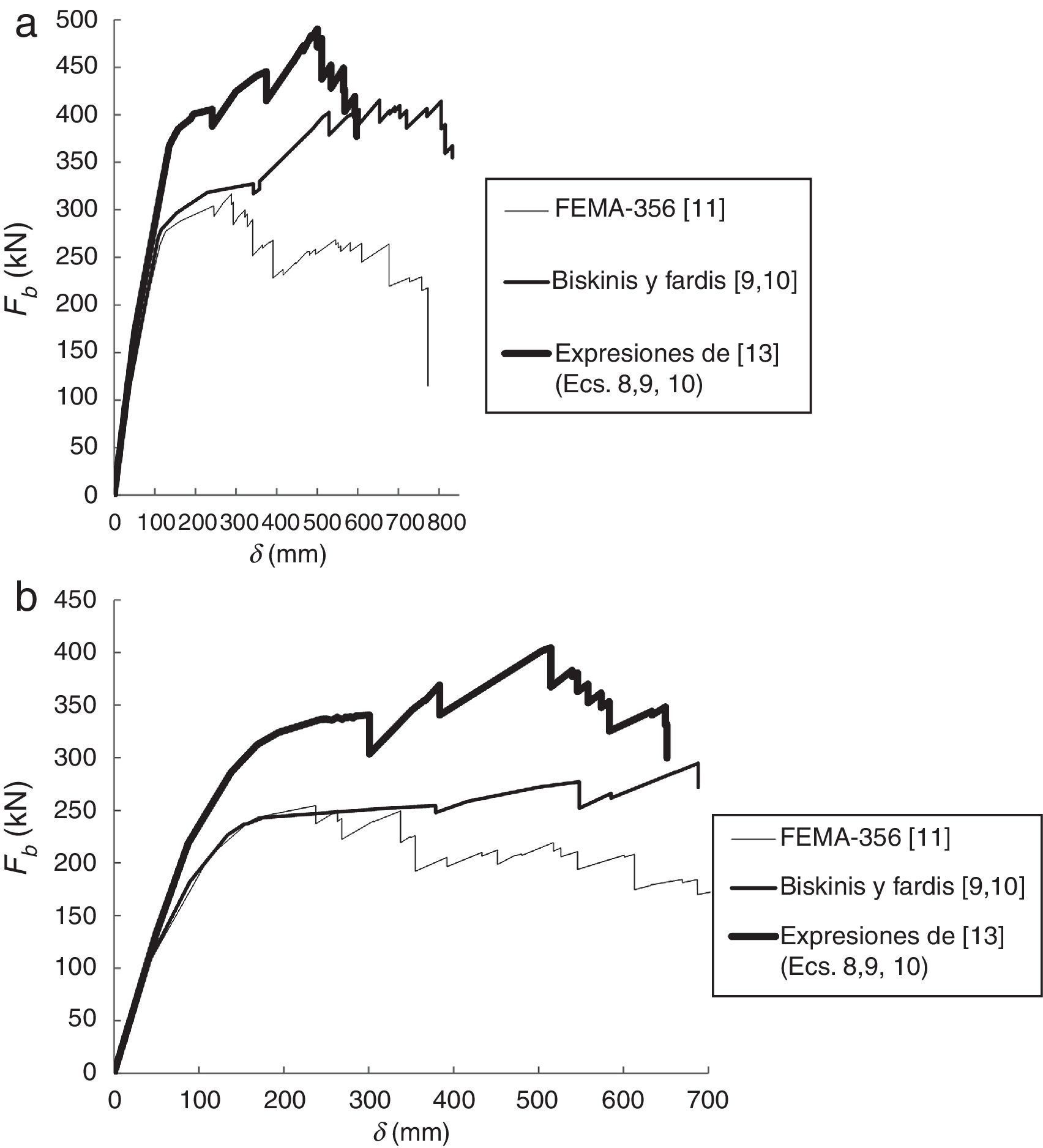
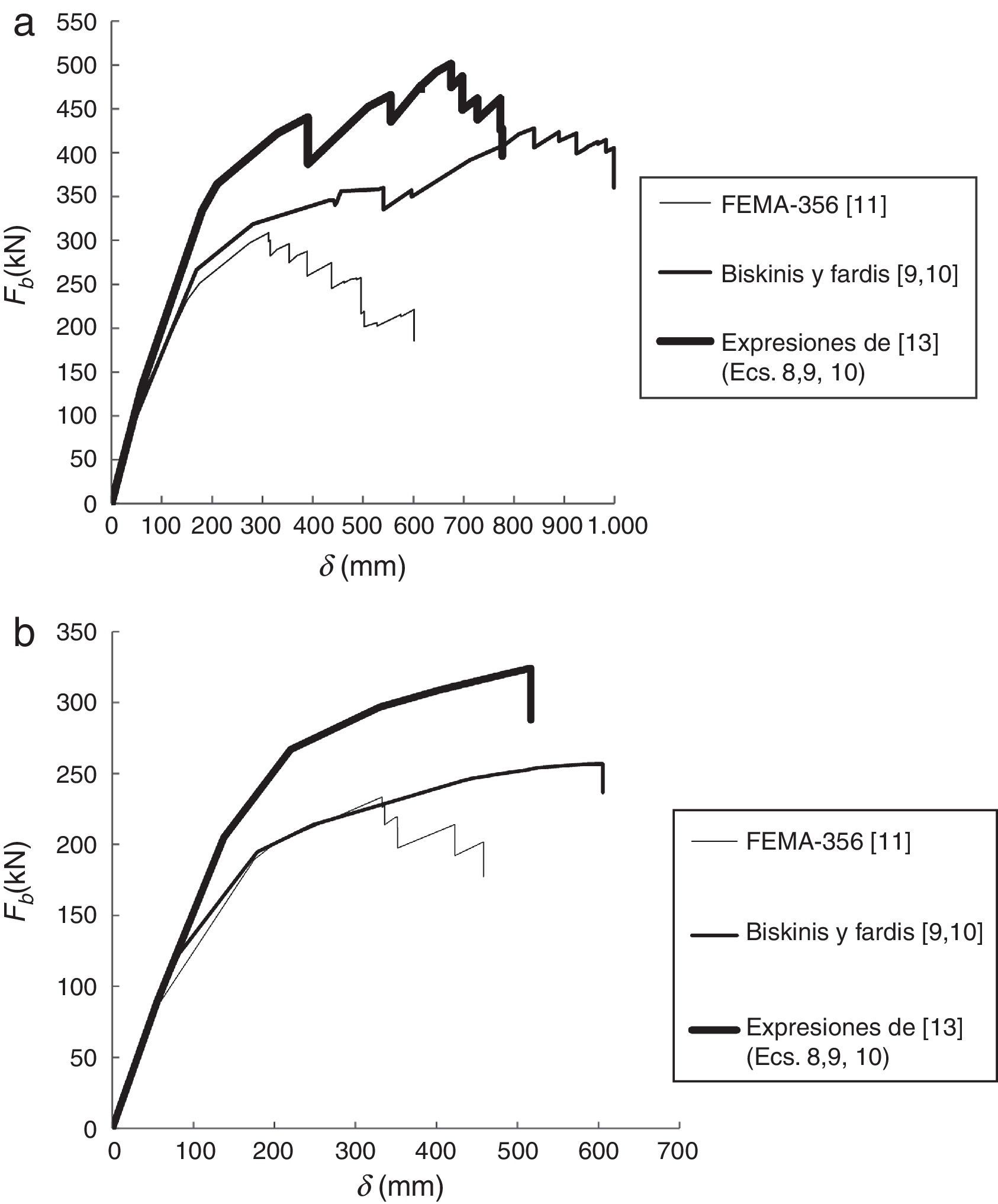
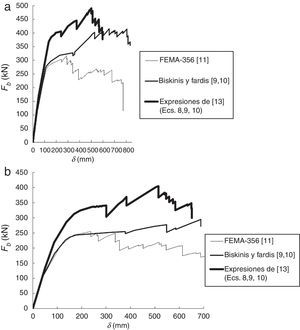
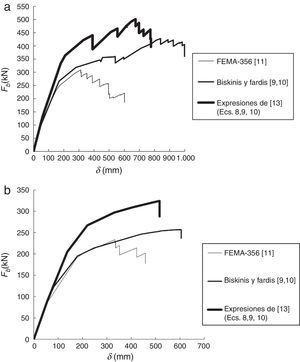
4Resultados y discusiónLas curvas de capacidad Fb-δ obtenidas para las estructuras consideradas, empleando rótulas plásticas definidas con diferentes métodos, y con los patrones de carga uniforme y modal, se muestran en las figuras 10 y 11 para los pórticos de 5 y 8 plantas, respectivamente. Además, se ha empleado el patrón de carga lateral modal de la ecuación (13) en el pórtico de 8 plantas para considerar el efecto de los modos de vibración superiores al fundamental.
Puede destacarse que las rótulas plásticas modelizadas con las expresiones propuestas por Biskinis y Fardis [9,10] y por los autores [13] ofrecen valores del esfuerzo cortante basal Fb superiores a los obtenidos con las modelizadas en el código de la FEMA-350 [11], aunque si el desplazamiento de control δ se encuentra en el intervalo (0, 250)mm, el valor resultante de Fb es similar tanto para las expresiones de Biskinis y Fardis [9,10] como para las de la FEMA-356 [11].
Puede comprobarse la relación existente entre el cortante basal Fb y el momento de plastificación My de las rótulas plásticas, por la cual a mayor valor de My mayor valor de Fb. Esta relación justifica que los máximos valores de Fb se obtienen al considerar rótulas plásticas modelizadas con las expresiones propuestas por los autores [13], pues dichas expresiones son las que ofrecen los máximos valores de My.
Otro aspecto a destacar es que las curvas de capacidad obtenidas aplicando las expresiones propuestas por los autores [13] y las propuestas por Biskinis y Fardis [9,10] se cruzan para un cierto valor de δ, pues de acuerdo con la figura 9, estas expresiones pueden ofrecer el mismo valor de My y, en consecuencia, de Fb.
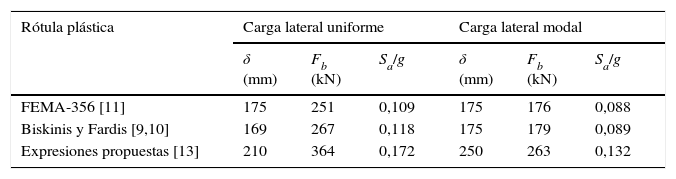
El punto de plastificación global de la estructura puede definirse como el punto de la curva de capacidad en el que finaliza el comportamiento elástico lineal [21]. Para este punto, en las tablas 2 y 3 se muestran los valores del desplazamiento de control δ, el cortante basal Fb y la aceleración espectral Sa. Esta aceleración Sa se ha obtenido transformando la curva de capacidad Fb-δ en el espectro de capacidad con el formato aceleración-desplazamiento Sa-Sd, aplicando la ecuación propuesta en el documento ATC-40 [24].
Puede destacarse que las rótulas plásticas modelizadas con las expresiones propuestas por los autores [13] ofrecen los valores máximos de Fb, δ y Sa para todos los casos analizados, debido a que proporcionan los máximos valores de My. Las diferencias obtenidas respecto a otros métodos se sitúan entre el 7 y el 42% para δ, entre el 33 y el 49% para Fb, y se obtiene una diferencia máxima del 58% para Sa. Estas diferencias se incrementan con la altura de la estructura al considerar el patrón de carga lateral modal.
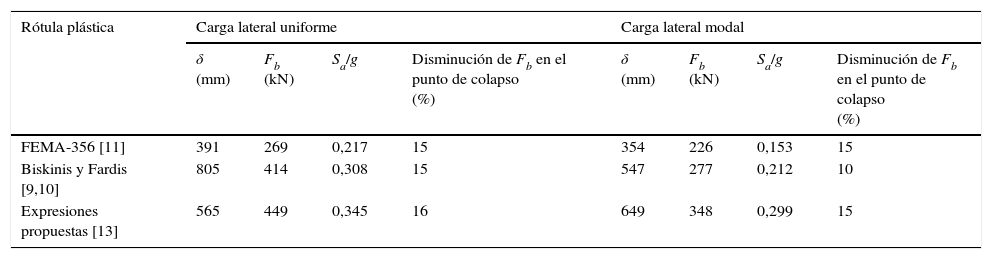
También se ha estudiado el punto de colapso de la estructura, que depende del nivel de seguridad considerado. Este punto puede definirse en términos del porcentaje de descenso de Fb en la curva de capacidad, el 20% por ejemplo [21], o en términos del fallo a nivel seccional, en base al porcentaje de descenso de la carga lateral aplicada al ensayar un determinado elemento, el 15% por ejemplo [8]. En este estudio se ha considerado que el colapso de la estructura se produce al disminuir Fb un 15% en la curva de capacidad. Los resultados para este punto se muestran en las tablas 4 y 5.
Resultados para el punto de colapso del pórtico de 5 plantas
| Rótula plástica | Carga lateral uniforme | Carga lateral modal | ||||||
|---|---|---|---|---|---|---|---|---|
| δ (mm) | Fb (kN) | Sa/g | Disminución de Fb en el punto de colapso (%) | δ (mm) | Fb (kN) | Sa/g | Disminución de Fb en el punto de colapso (%) | |
| FEMA-356 [11] | 391 | 269 | 0,217 | 15 | 354 | 226 | 0,153 | 15 |
| Biskinis y Fardis [9,10] | 805 | 414 | 0,308 | 15 | 547 | 277 | 0,212 | 10 |
| Expresiones propuestas [13] | 565 | 449 | 0,345 | 16 | 649 | 348 | 0,299 | 15 |
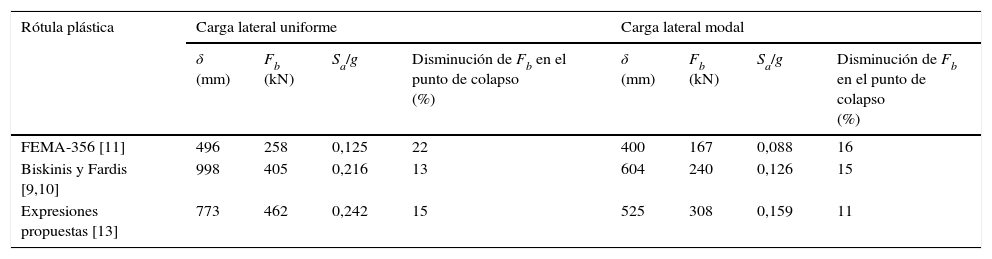
Resultados para el punto de colapso del pórtico de 8 plantas
| Rótula plástica | Carga lateral uniforme | Carga lateral modal | ||||||
|---|---|---|---|---|---|---|---|---|
| δ (mm) | Fb (kN) | Sa/g | Disminución de Fb en el punto de colapso (%) | δ (mm) | Fb (kN) | Sa/g | Disminución de Fb en el punto de colapso (%) | |
| FEMA-356 [11] | 496 | 258 | 0,125 | 22 | 400 | 167 | 0,088 | 16 |
| Biskinis y Fardis [9,10] | 998 | 405 | 0,216 | 13 | 604 | 240 | 0,126 | 15 |
| Expresiones propuestas [13] | 773 | 462 | 0,242 | 15 | 525 | 308 | 0,159 | 11 |
Puede comprobarse que en la estructura de mayor flexibilidad, la del pórtico de 8 plantas, aparecen valores superiores de δ y valores inferiores de Fb y Sa/g. Las expresiones de Biskinis y Fardis [9,10] proporcionan generalmente los máximos valores de δ, ya que dichas expresiones ofrecen la mayor capacidad de deformación entre los métodos considerados (figs. 7 y 8). Además, estas expresiones proporcionan los menores porcentajes de disminución de Fb en el punto de colapso, habiéndose considerado disminuciones inferiores al 15% como excepción. Las expresiones propuestas por los autores [13] proporcionan los máximos valores de Fb, obteniéndose diferencias máximas del 84% respecto a otros métodos. En el caso de Sa, estas expresiones ofrecen valores superiores a los obtenidos con otros métodos, obteniéndose una diferencia máxima del 95%.
Los resultados obtenidos para los diferentes valores considerados de la aceleración del suelo ag se muestran en las tablas 6 y 7. El desplazamiento objetivo dt de una estructura puede definirse como la demanda sísmica deducida a partir del espectro de respuesta elástica, en términos de desplazamiento de un sistema equivalente de un grado de libertad [18]. Al estar el desplazamiento objetivo relacionado con el comportamiento de un sistema de un grado de libertad, en esta contribución solo se han considerado las curvas de capacidad obtenidas con el patrón modal de carga lateral. Aunque el desplazamiento objetivo obtenido es el mismo para los diferentes tipos de rótulas plásticas, las diferentes curvas de capacidad (figs. 10 y 11) proporcionan diferentes valores de Fb y Sa para un valor considerado de aceleración del suelo.
Resulta de interés mencionar que las diferencias entre métodos se obtienen para valores de la aceleración del suelo ag superiores a 0,1g. Estas diferencias se incrementan con el valor de la aceleración del suelo, mientras que la altura de la estructura no presenta una influencia significativa en los resultados. Se obtienen valores superiores de Fb y Sa al aplicar las expresiones propuestas por los autores [13], estando las diferencias comprendidas entre el 14 y el 30% para Fb y entre el 5 y el 31% para Sa respecto al modelo incluido en el código de la FEMA-356 [11].
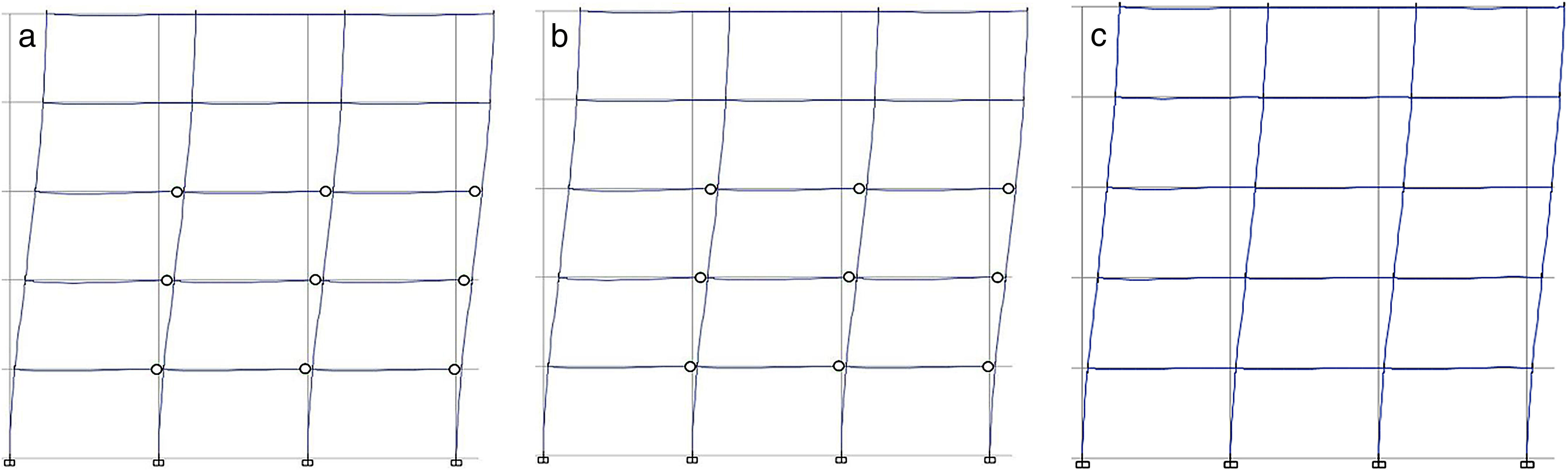
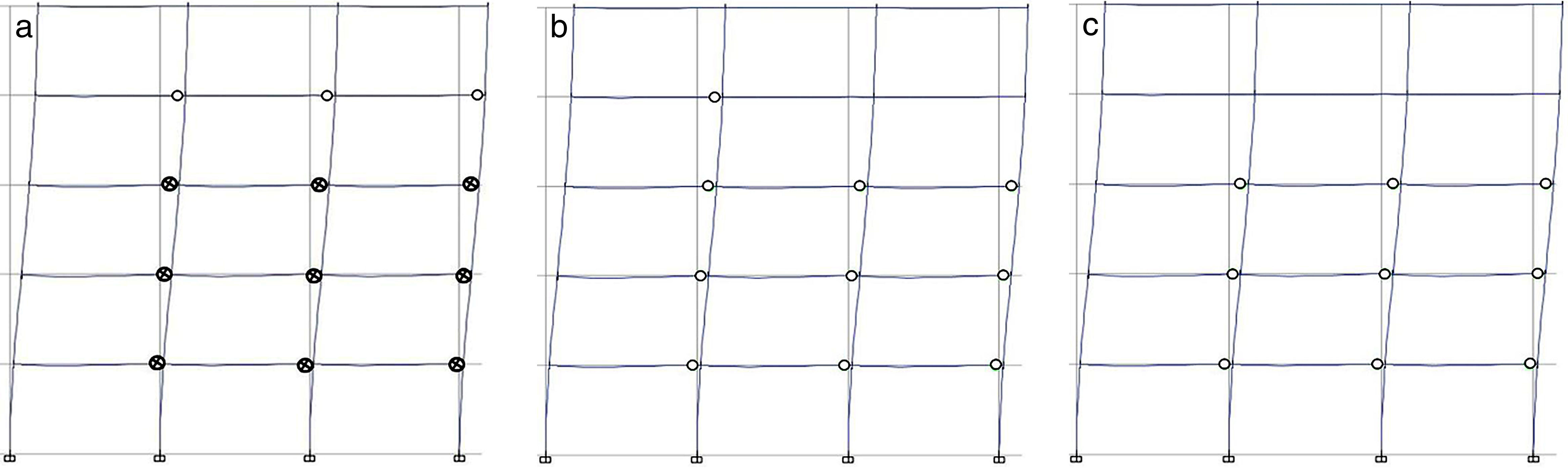
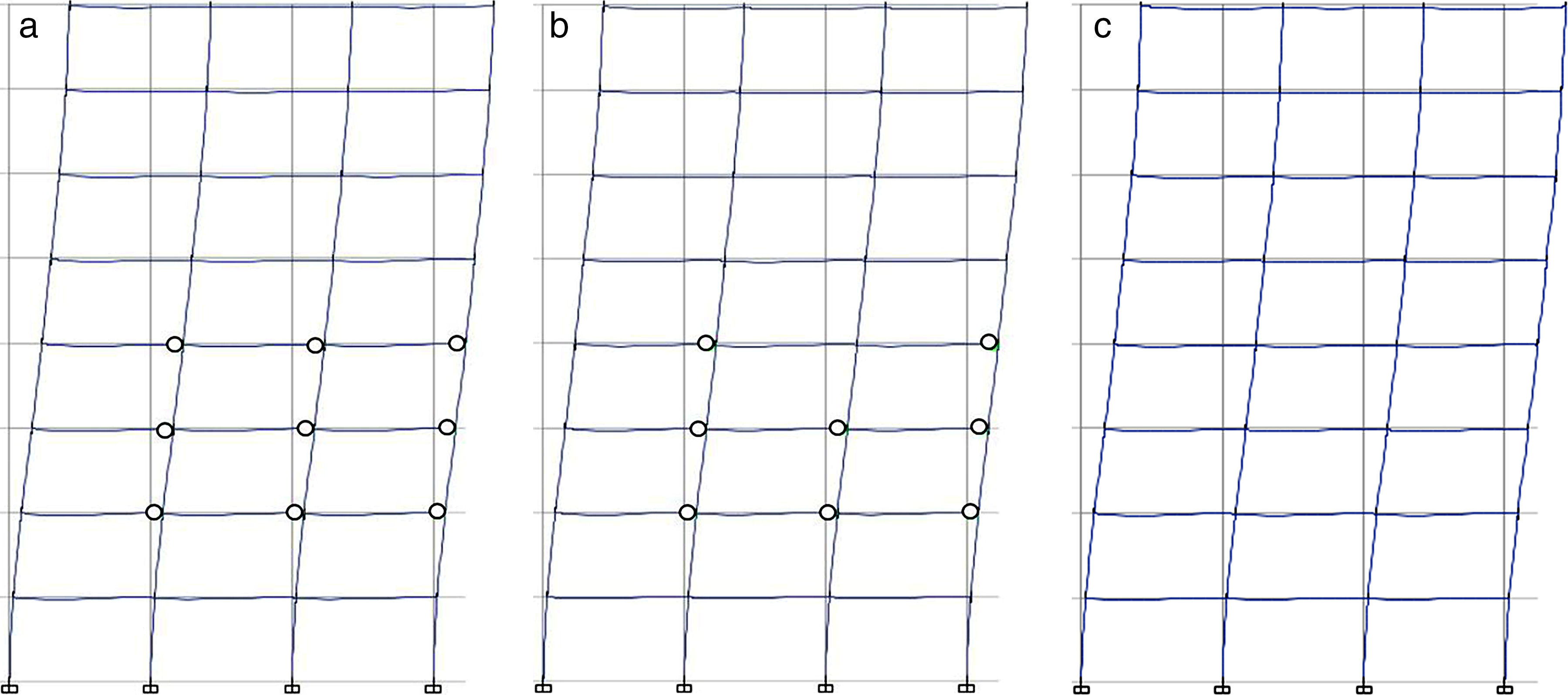
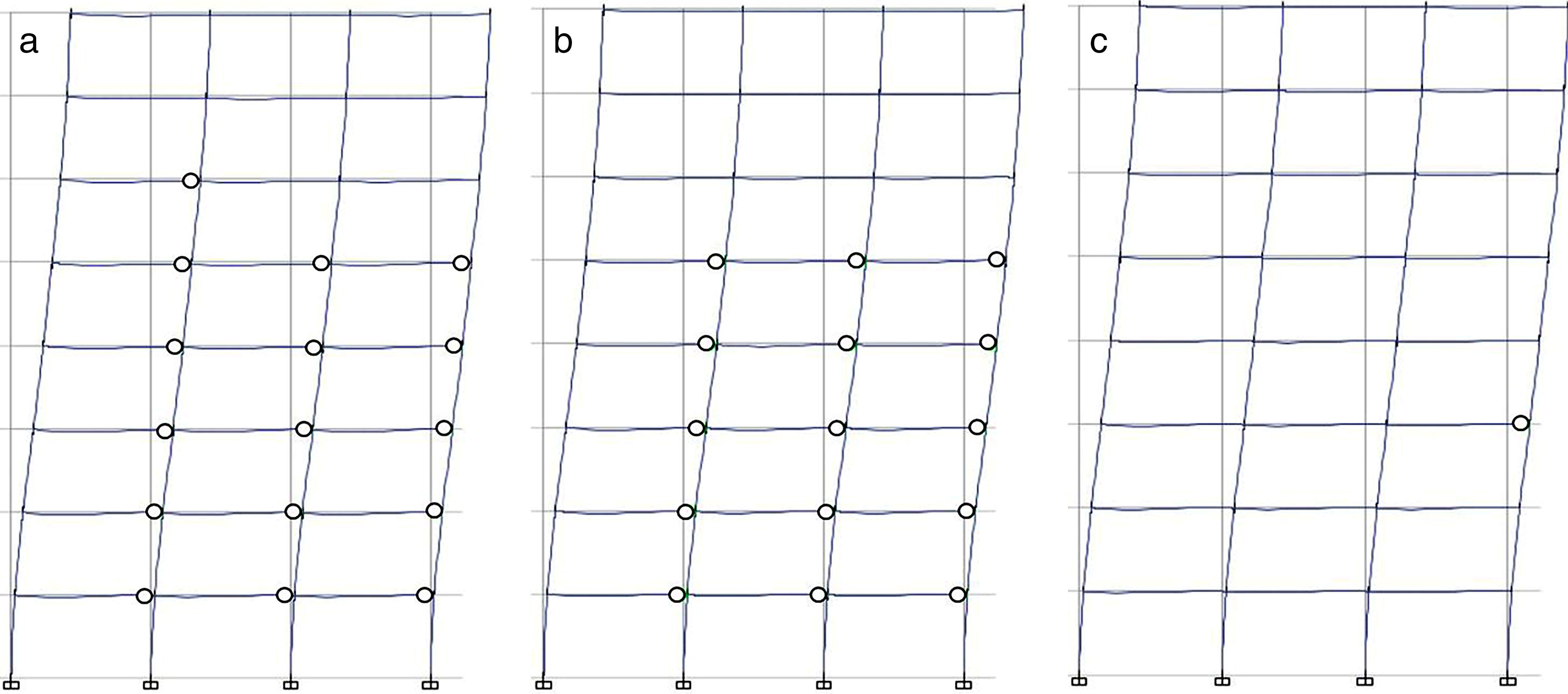
En las figuras 12 a 15 se muestra la distribución de rótulas plásticas generadas en la estructura para valores de la aceleración del suelo ag de 0,2g y 0,3g, pues para 0,1g no se obtienen diferencias apreciables, según puede desprenderse de las tablas 6 y 7
En cualquier caso, el estado de las rótulas plásticas generadas se sitúa entre los puntosB yC de las figuras 1 y 2, no produciéndose por tanto colapso de ninguna rótula plástica para los valores de aceleración considerados. El desplazamiento objetivo obtenido considerando el espectro tipo2 y valores bajos de aceleración generan reducidos niveles de daño en la estructura; de hecho, en los pórticos de 5 plantas solo se alcanza el nivel de comportamiento Immediate Occupancy (IO) empleando el modelo de rótulas incluido en el código de la FEMA-356 [11] y para ag=0,3g. Como puede suponerse, el número generado de rótulas plásticas se incrementa con el valor de la aceleración del suelo. Puesto que las expresiones propuestas por los autores [13] ofrecen valores superiores del momento de plastificación My (figs. 7 y 8), el número de rótulas plásticas generadas en este caso es inferior. De hecho, para el valor más bajo de la aceleración del suelo (ag=0,2g) la estructura permanecería en estado elástico.
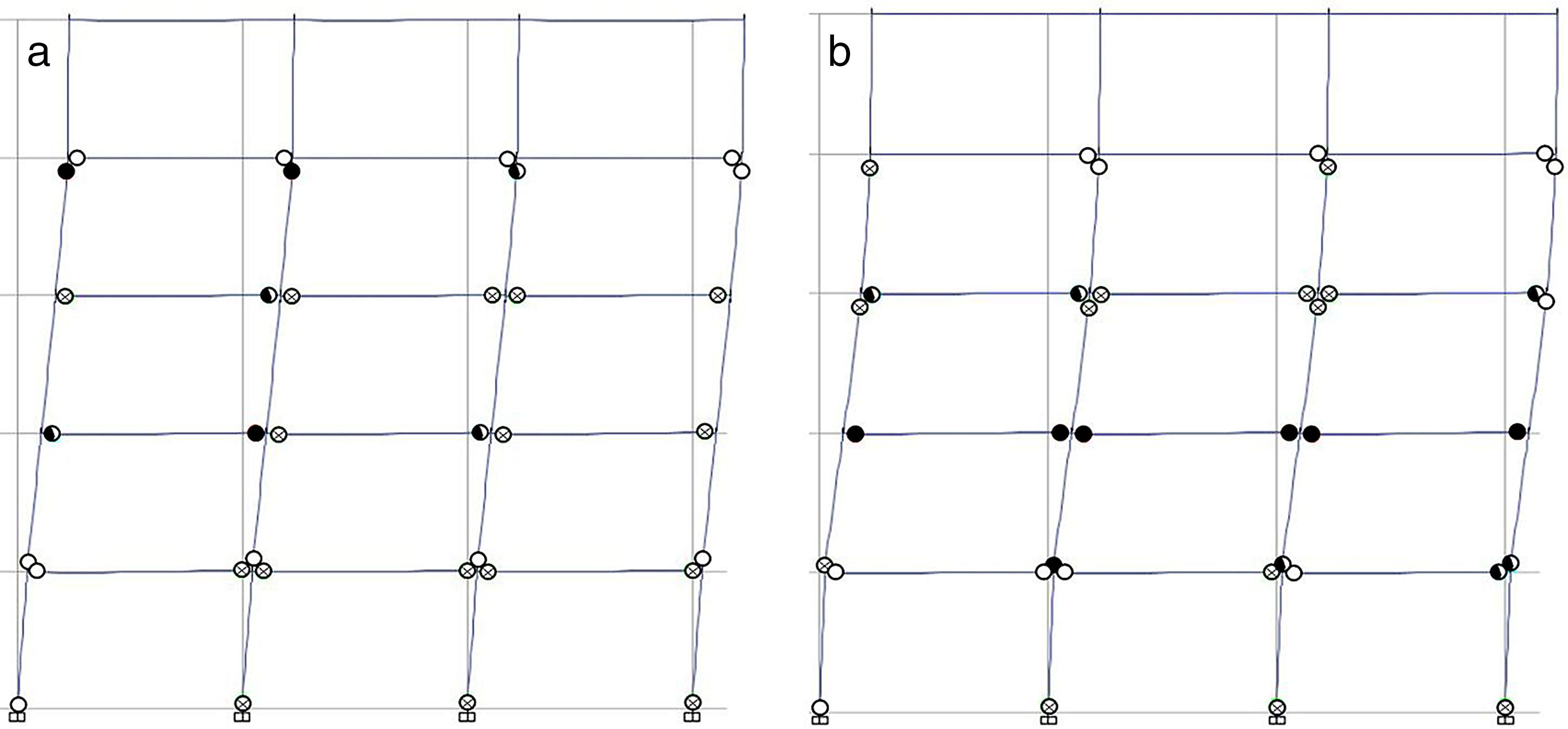
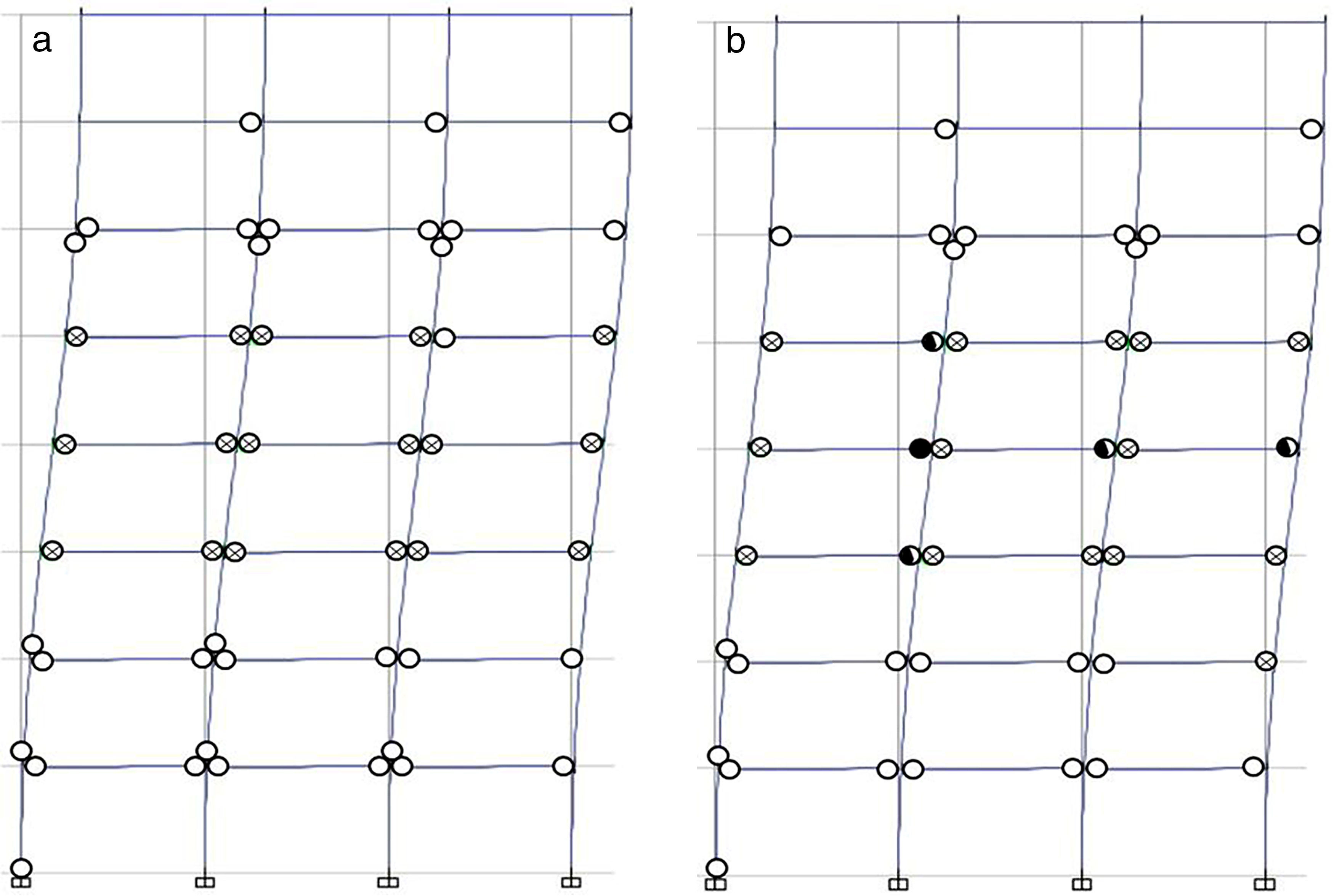
Con objeto de inducir la aparición de rótulas plásticas en los pilares y mostrar la capacidad de los diferentes métodos para detectarlas, se ha obtenido la distribución de rótulas en las estructuras estudiadas para el desplazamiento del punto de colapso (figs. 16 y 17), obtenido este con las expresiones propuestas por los autores [13] y por Biskinis y Fardis [9,10]. No se ha empleado el modelo de rótula incluido en el código de la FEMA-350 [11] porque el desplazamiento impuesto es mayor que la capacidad de desplazamiento obtenida con este modelo. Se han considerado los patrones de carga lateral uniforme y modal para los pórticos de 5 y 8 plantas, respectivamente.
Puede apreciarse que no hay diferencias significativas entre ambos métodos, tanto en la distribución general de rótulas plásticas como en su localización en los pilares, aunque aparece un mayor nivel de daño, sobre todo en las plantas intermedias, para el caso de las expresiones propuestas por los autores [13]
5ConclusionesEn esta contribución se ha evaluado la influencia que tiene el modelo de rótula plástica en el comportamiento no lineal de estructuras aporticadas de hormigón armado. Se han realizado diversos análisis no lineales empleando diferentes modelos de rótulas, incluyendo expresiones empíricas de comportamiento seccional capaces de reproducir los estados de plastificación y de rotura de la sección. Con objeto de simplificar la interpretación de resultados, se han utilizado como ejemplo estructuras de geometría regular, teniendo todas las vigas las mismas dimensiones y con la armadura constante en toda su longitud.
La mayor resistencia y capacidad de deformación de la sección ofrecida al emplear el modelo de las expresiones propuestas por los autores [13] justifica que se obtengan valores superiores en el esfuerzo cortante basal Fb y en el desplazamiento de control δ, lo que implica una mayor resistencia y capacidad de deformación de la estructura. Además, con estas expresiones se obtiene una distribución más favorable de rótulas plásticas en la estructura, aunque es cierto que los valores resultantes para la aceleración espectral Sa son superiores, lo que conlleva mayores esfuerzos en la estructura al actuar la acción sísmica.
El modelo de rótula plástica propuesto permite servir de contraste respecto a los modelos incluidos en la normativa de diseño, que suelen ofrecer resultados más conservadores. Este contraste es más pronunciado cuanto mayor sea la altura de la estructura y el valor de la aceleración del suelo, así como al considerar el patrón de carga lateral modal en el análisis.
Puesto que las expresiones propuestas por los autores [13] están calibradas con una selección de ensayos que cumple los requerimientos sísmico-constructivos de la normativa de diseño en edificación más relevante a nivel internacional, las rótulas plásticas así modelizadas resultan adecuadas para una mayor variedad de casos que los modelos incluidos por defecto en una determinada norma o código estructural, pues estos modelos normalmente se han desarrollado a partir de elementos constructivos de hormigón armado que siguen una práctica de diseño y constructiva circunscrita al correspondiente ámbito geográfico de aplicación del código.
Por otro lado, el hecho de estar calibradas las expresiones propuestas con una base más homogénea de ensayos experimentales reduce la dispersión ofrecida respecto a otras expresiones, o que las hace adecuadas para modelizar el comportamiento seccional de las rótulas plásticas generadas durante el análisis no lineal de estructuras de hormigón armado.







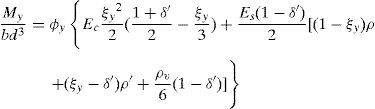
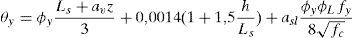
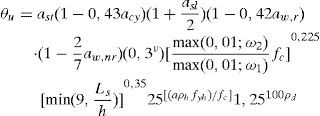
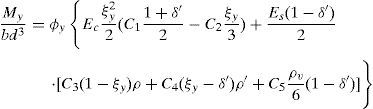
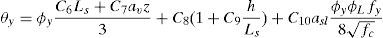
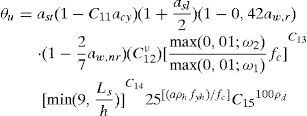
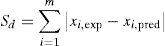
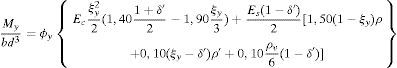
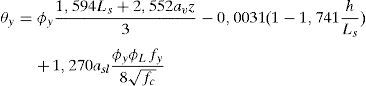
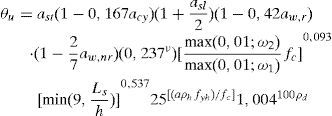
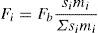
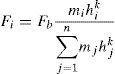
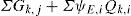
![Relación momento-giro para las rótulas plásticas [11]. Relación momento-giro para las rótulas plásticas [11].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Relación momento-giro para las rótulas plásticas [9,10,13]. Relación momento-giro para las rótulas plásticas [9,10,13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr2.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Distribución de rótulas plásticas para el pórtico de 5 plantas y ag=0,2g. (a) FEMA-356 [11]. (b) Biskinis y Fardis [9,10]. (c) Expresiones propuestas [13]. Distribución de rótulas plásticas para el pórtico de 5 plantas y ag=0,2g. (a) FEMA-356 [11]. (b) Biskinis y Fardis [9,10]. (c) Expresiones propuestas [13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr12.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Distribución de rótulas plásticas para el pórtico de 5 plantas y ag=0,3g. a)FEMA-356 [11]. b)Biskinis y Fardis [9,10]. c)Expresiones propuestas [13]. Distribución de rótulas plásticas para el pórtico de 5 plantas y ag=0,3g. a)FEMA-356 [11]. b)Biskinis y Fardis [9,10]. c)Expresiones propuestas [13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr13.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Distribución de rótulas plásticas para el pórtico de 8 plantas y ag=0,2g. a)FEMA-356 [11]. b)Biskinis y Fardis [9,10]. c)Expresiones propuestas [13]. Distribución de rótulas plásticas para el pórtico de 8 plantas y ag=0,2g. a)FEMA-356 [11]. b)Biskinis y Fardis [9,10]. c)Expresiones propuestas [13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr14.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Distribución de rótulas plásticas para el pórtico de 8 plantas y ag=0,3g. a)FEMA-356 [11]. b)Biskinis y Fardis [9,10]. c)Expresiones propuestas [13]. Distribución de rótulas plásticas para el pórtico de 8 plantas y ag=0,3g. a)FEMA-356 [11]. b)Biskinis y Fardis [9,10]. c)Expresiones propuestas [13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr15.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Distribución de rótulas plásticas para el pórtico de 5 plantas en el punto de colapso. a)Biskinis y Fardis [9,10]. b)Expresiones propuestas [13]. Distribución de rótulas plásticas para el pórtico de 5 plantas en el punto de colapso. a)Biskinis y Fardis [9,10]. b)Expresiones propuestas [13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr16.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Distribución de rótulas plásticas para el pórtico de 8 plantas en el punto de colapso. a)Biskinis y Fardis [9,10]. b)Expresiones propuestas [13]. Distribución de rótulas plásticas para el pórtico de 8 plantas en el punto de colapso. a)Biskinis y Fardis [9,10]. b)Expresiones propuestas [13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300189/v1_201710110055/es/main.assets/thumbnail/gr17.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)