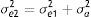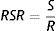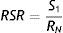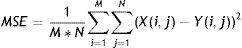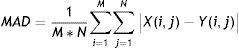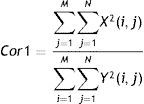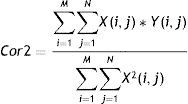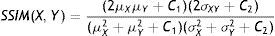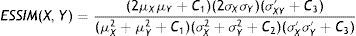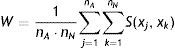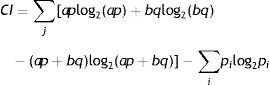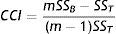Análisis del efecto de la reducción de dosis en la detectabilidad y la localización de lesiones

Resumen

Objetivo

Este trabajo tiene como propósito describir una estrategia para evaluar la detección y la localización de lesiones, con el fin de determinar el valor de dosis o los valores a partir de los cuales la calidad de la imagen se degrada significativamente haciéndola insuficiente para el diagnóstico.

Material y métodos

Para complementar y tener una estimación de la calidad de las imágenes se estableció un conjunto de medidas de tipo objetivo, al igual que se evaluó la calidad diagnóstica de las imágenes a través de un conjunto de observadores utilizando el análisis ROC y LROC.

Resultados

Para los análisis ROC y LROC se obtuvo el comportamiento del área bajo la curva en relación con los 4 niveles de dosis propuestos. Para niveles de dosis altos, la detección fue buena. Los valores de área bajo la curva disminuyeron a medida que el índice de dosis disminuyó, cayendo hasta valores que indican una baja exactitud en el diagnóstico. Este resultado indica que el área bajo la curva decrece junto al índice de dosis. La correlación entre estos parámetros fue de 0,98.

Conclusiones

Se concluyó que las medidas de calidad objetivas seleccionadas son representativas de los cambios que ocurren en la imagen y aportaron como resultado información sobre los cambios ocurridos en las imágenes que afectan la percepción de los observadores. Los experimentos ROC y LROC permitieron determinar el intervalo de valores de dosis a partir del cual la degradación de las imágenes hace que exista una baja exactitud en el diagnóstico.

Abstract

Objetive

This paper aims to describe a strategy to evaluate the detection and location of lesions, in order to determine the dose or doses required from which the image quality is significantly degraded making it unsuitable for the diagnosis.

Methods and materials

A group of objective measurements were established to complement and make an estimate of the diagnostic quality of the images which were also evaluated by a group of observers using ROC and LROC analyses.

Results

For ROC and LROC analyses, the behaviour of the area under the curve in relation to the four proposed dose levels was obtained. For high dose levels, detection was good. The values of area under the curve decreased as the dose rate decreased, falling to values indicating low accuracy in diagnosis. These results indicate that the area under the curve decreases by the dose rate. The correlation between these parameters was 0.98.

Conclusions

We conclude that the objective quality measurements selected are representative of the changes that occur in the resulting image, and provided information on changes in the perception of observers. The ROC and LROC experiments allowed the range of dose values to be determined, from which the image degradation leads to a low accuracy in the diagnosis.

Introducción

La tomografía computarizada (TC) por rayos X constituye una de las principales herramientas para diagnosticar múltiples patologías. Sin embargo, la principal limitación de la TC es el uso de radiación ionizante, que conlleva un potencial riesgo de inducir algún tipo de afección en pacientes que son expuestos a ella^1,2.

Informes procedentes de Estados Unidos señalan que la radiación per cápita se ha duplicado en los últimos 30 años, y la razón principal es el uso de modalidades de imágenes médicas como la TC, la radiografía, la fluoroscopia y la medicina nuclear³.

El riesgo del uso de radiación ionizante durante la adquisición de imágenes, para un paciente, es muy bajo, y en la mayoría de los casos el beneficio de un correcto diagnóstico a tiempo justifica su uso. A pesar de esto, es de interés disminuir las dosis de radiación particularmente en pacientes pediátricos, que, de ser expuestos a estas radiaciones múltiples veces durante su vida, podrían acumular una dosis significativa de radiación ionizante, aumentando el riesgo de cáncer radioinducido⁴.

En la TC existe un compromiso entre la calidad de la imagen y la dosis de radiación ionizante⁵. Una disminución en la dosis de radiación provoca un aumento del ruido en las imágenes. Esto se debe a que los detectores del tomógrafo reciben una cantidad menor de fotones, lo que disminuye la relación señal a ruido. Como consecuencia, el ruido puede ocultar detalles anatómicos y disminuir la detectabilidad de lesiones con bajo contraste⁶. A dosis muy bajas, también pueden aumentar efectos indeseados en las imágenes, tales como artefactos. De este modo, para conservar un balance adecuado, el principio por el cual se rige la TC es el de usar las menores dosis de radiación que conservan razonablemente la calidad en la imagen⁵.

Un área actual de intensa investigación consiste en buscar métodos para reducir la dosis al paciente, manteniendo una calidad de la imagen suficiente para el propósito diagnóstico⁵.

En este trabajo proponemos una estrategia para evaluar la calidad de las imágenes partiendo del diagnóstico por imagen de un conjunto de observadores. El objetivo consistió en determinar los valores de dosis que degradan la calidad de imagen significativamente, haciéndola insuficiente para el diagnóstico. El conocimiento obtenido podrá utilizarse para determinar las restricciones de diferentes métodos de reducción de dosis. Para determinar la calidad de las imágenes se estableció un conjunto de medidas de tipo objetivo y subjetivo.

Material y métodos

Imágenes utilizadas

Se utilizaron 100 imágenes axiales del sistema nervioso central de pacientes adultos. Las imágenes fueron previamente clasificadas por 3 radiólogos expertos con más de 5 años de experiencia, los cuales suministraron información sobre la localización y las características de las lesiones.

Las imágenes utilizadas se obtuvieron de un equipo modelo Sensation Cardiac 64 de la firma Siemens; la dimensión de las imágenes fue de 512 × 512 píxeles.

Simulación del ruido en las imágenes

La técnica de simulación utilizada en este trabajo se basa en un modelo que añade ruido gaussiano a las imágenes originales para simular una reducción de la corriente del tubo. La cantidad de ruido añadido a las imágenes simula el aumento del ruido que se produciría en las imágenes realmente obtenidas con menores niveles de corriente del tubo.

La metodología utilizada parte de determinar la cantidad de ruido que hay que añadir en la imagen a simular, partiendo del conocimiento del ruido en la imagen a simular (σ_e1) y en una imagen obtenida a un nivel de exposición más bajo (σ_e2), que sería el nivel de ruido que se quiere simular. A través de la siguiente ecuación se puede calcular el ruido a agregar:

Donde σa2 es el ruido a añadir en la imagen. Esta técnica ha sido descrita en detalle por Britten et al.⁷.

Para la obtención de los diferentes valores de corriente del tubo se modificó, a través de la consola del equipo, la carga del tubo en miliampere × segundo (mAs).

Los valores de mAs obtenidos para la simulación fueron de 380, 336, 272, 209 y 145. Los valores de índice de dosis volumétrico (CTDI_VOL) se tomaron de los reportados por el sistema en la consola del operador. En este trabajo se asume una incertidumbre expandida del 6% para el CTDI_VOL al igual que en Miller-Clemente et al.⁸. Los valores de CTDI_VOL, correspondientes a los niveles de mAs, fueron: 59,66 ± 3,58; 52,82 ± 3,17; 42,65 ± 2,56; 32,88 ± 1,97 y 22,90 ± 1,37 mGy respectivamente.

Las imágenes originales obtenidas a los niveles de referencia fueron procesadas a través del software Image J 1.43u. Este software modifica las imágenes ya adquiridas agregando el ruido a partir de la desviación estándar para generar las imágenes simuladas a diferentes valores de mAs.

Medidas objetivas

Para evaluar la calidad de las imágenes se seleccionó un conjunto de medidas objetivas; estas fueron seleccionadas bajo la condición de que devuelvan una estimación cuantitativa del nivel de calidad a partir de la información en los píxeles de las imágenes analizadas.

Entre las medidas utilizadas se encuentran las medidas de distancia, y entre ellas la relación señal-ruido (RSR), que puede definirse como:

donde S es el valor medio de la intensidad de la señal en la imagen o en una región de interés (ROI, region of interest) y R el ruido de la misma imagen o ROI⁹.

Una de las formas más utilizadas es la propuesta por la National Electric Manufacturers Association (NEMA)¹⁰, la cual en muchos casos es aceptada como regla de oro, por lo general, para calcular este descriptor. Esta consiste en la obtención de este parámetro empleando 2 imágenes obtenidas consecutivamente. Para ello se determina (S) en una ROI de la imagen original y luego se calcula píxel a píxel la imagen diferencia (Imagen3 = Imagen1 – Imagen2), siendo el ruido (R_N) la desviación estándar en la ROI de la imagen3. La RSR según NEMA es calculada como:

Este método es considerado muy exacto y se hace más o menos preciso en todos los sistemas que no sean invariantes temporales.

Medidas objetivas bivariadas

Las medidas de tipo bivariadas comparan la imagen original con la que ha sido procesada para ofrecer una estimación de cuánta distorsión ha sufrido la imagen por la acción del procesamiento realizado.

Algunas de estas medidas objetivas de calidad son:

• El error cuadrático medio (MSE)¹¹:

donde X (i,j) es el valor del píxel ubicado en la coordenada i,j de la imagen original, Y(i,j) es el equivalente en la imagen procesada, M es el número de filas y N es el número de columnas de estas imágenes.

• La distancia media absoluta (MAD)¹¹ descrita por la expresión:

• Medidas de correlación (Cor1,Cor2)¹¹ descritas por las expresiones:

• El índice de similitud estructural (SSIM, structural simmilarity)¹² descrito por la expresión:

donde μ_X y μ_Y son los valores de luminancia de la imagen original y la procesada, σ_X y σ_Y son los valores de contraste de estas imágenes, σ_xy es el coeficiente de correlación entre X (i,j) y Y(i,j). C₁ y C₂ son constantes empleadas para evitar la inestabilidad de las expresiones y están relacionadas con el rango dinámico L de los píxeles (255 para imágenes en escala de grises [8-bit]) de la siguiente forma: C_i = (KL)² con K<<1.

• El índice de similitud estructural basado en el borde (ESSIM, edge-based structural similarity) está dado por¹³:

donde σ ' _x, σ ' _y y σ ' _xy son los valores de contrastes y el coeficiente de correlación de las imágenes después de la aplicación del operador de borde. C₃ cumple la misma función que C₁ y C₂.

Con el fin de obtener la medida general de estos parámetros sobre toda la imagen se calcula sus valores medios:

y

donde x_i e y_i son los contenidos en la imagen dentro de la ventana local i-ésima y W es el número de ventanas locales consideradas.

Análisis ROC y LROC

Con el objetivo de estimar la calidad diagnóstica de las imágenes para los valores de CTDI_VOL simulados, se llevó a cabo el análisis de curvas ROC y LROC teniendo en cuenta el área bajo estas curvas (ABC). A través de este parámetro se puede evaluar el rendimiento diagnóstico de los observadores que evaluaron las imágenes.

La detectabilidad y la localización de las lesiones en las imágenes fueron estimadas a través de 10 experimentos utilizando 5 observadores: 3 radiólogos y 2 especialistas en imagenología. Ninguno de ellos participó en el diseño de los experimentos.

Las 56 imágenes de pacientes con alguna anormalidad y 44 de pacientes sanos fueron distribuidas para 4 niveles de mAs, cada uno con 25 imágenes: 14 patológicas y 11 negativas o no patológicas.

Cada observador evaluó las 25 imágenes sin tener conocimiento del índice de dosis al que fueron obtenidas. La evaluación se llevó a cabo teniendo en cuenta los siguientes niveles de certeza: seguramente anormal, probablemente anormal, probablemente normal y seguramente normal para las curvas ROC, y seguro, probable, posible y dudoso para las curvas LROC.

Para determinar el tipo de localización (correcta e incorrecta) se concretó una zona de aceptación a través del promedio de varias localizaciones realizadas por 3 especialistas con más de 5 años de experiencia (se determinó el valor medio ± desviación estándar). Se determinó un radio de aceptación dentro del cual estarían las localizaciones correctas. La metodología utilizada ha sido propuesta por algunos autores para la construcción de curvas ROC de localización^14,15.

Los experimentos se realizaron de forma independiente, con un tiempo de 10 min/experimento y con una o 2 semanas de diferencia para repetir cada experimento.

El cálculo del área bajo la curva (ABC) se realizó por el método trapezoidal y por el estadístico W de Wilcoxon¹⁶, descritos por las expresiones:

donde f(x) representa la ecuación que describe la curva, n_A y n_N representan el número de imágenes anormales y normales y S(x_j,x_k) es el puntaje dado al par compuesto por el j-ésimo paciente con la enfermedad y el k-ésimo paciente sin la enfermedad. S(x_j, x_k) es 1 si x_j > x_k, 1/2 si x_j = x_k y 0 si x_j < x_k.

Teoría de la información

Para tener una estimación de la pérdida de información, a la hora de evaluar cada sistema de imágenes se calculó el contenido de información (CI). El análisis de este parámetro parte de la siguiente ecuación^17-19:

donde a es la tasa de verdaderos positivos, b es la tasa de falsos positivos, p es la prevalencia de la enfermedad o probabilidad pretest y q es la prevalencia de que no exista la enfermedad (1 – p)^17-19.

El resultado obtenido al aplicar la ecuación se hallaría entre 0 y 1 bit. Si la prueba diagnóstica provee toda la información necesaria para hacer el diagnóstico (certeza completa), entonces el contenido de información de la prueba será de 1 bit. En caso de que solo dé información parcial, por ejemplo 0,5 bit, esto indicará que la prueba provee solo la mitad de la información necesaria para establecer o excluir un diagnóstico¹⁸.

Variación interobservador e intraobservador

Para calcular los grados de acuerdo interobservador e intraobservador se utilizó el coeficiente correlación intraclase propuesto por Bland y Altman²⁰, descrito por la expresión:

donde SS_B y SS_T son la suma de cuadrados entre sujetos y la suma total de cuadrados, respectivamente, obtenidas de un modelo de análisis de varianza (ANOVA), y m el número de mediciones.

Resultados y discusión

Las medidas objetivas seleccionadas y presentadas anteriormente fueron calculadas entre la imagen a los niveles de CTDI_VOL de referencia (59,66 mGy) y las simuladas a valores de 52,82, 42,85, 32,88 y 22,90 mGy.

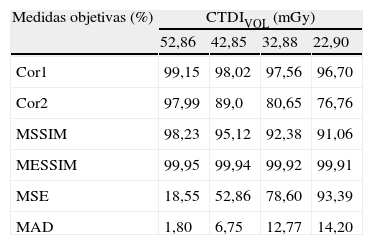
Las medidas objetivas se normalizaron para estudiar su comportamiento. En la tabla 1 se muestran algunas de estas medidas, y su comportamiento individual.

Tabla 1.

Variación de las medidas objetivas en los 4 valores de CTDI_VOL

Medidas objetivas (%)	CTDIVOL (mGy)
	52,86	42,85	32,88	22,90
Cor1	99,15	98,02	97,56	96,70
Cor2	97,99	89,0	80,65	76,76
MSSIM	98,23	95,12	92,38	91,06
MESSIM	99,95	99,94	99,92	99,91
MSE	18,55	52,86	78,60	93,39
MAD	1,80	6,75	12,77	14,20

Cor1: correlación de contenidos estructurales; Cor2: correlación cruzada; MAD: diferencia media absoluta; MESSIM: similitud estructural basada en el borde; MSE: error cuadrático medio; MSSIM: similitud estructural.

Medidas como la similitud estructural promedio (MSSIM) son de particular interés al tener en cuenta la información sobre las intensidades, el contraste y la estructura de las imágenes que compara. En estas medidas reviste gran importancia su comportamiento cuantitativo. Como puede observarse, los valores de algunas de estas medidas decrecen junto con el índice de dosis (Cor1, Cor2, MSSIM MESSIM).

Las variaciones están dadas por las alteraciones que produce el ruido en los valores de intensidad de los píxeles. Estas medidas realizan una comparación píxel a píxel entre ambas imágenes.

En la tabla puede observarse otro conjunto de medidas que, a diferencia de las anteriores, crecen mientras decrece el índice de dosis. Medidas como MSE o la distancia media absoluta (MAD) son representativas de las diferencias existentes entre las imágenes cuando disminuye el índice de dosis. Su comportamiento se relaciona también con las variaciones que produce el aumento del ruido en los valores de intensidad de las imágenes.

En la tabla también se refleja el comportamiento de una medida objetiva relacionada con los bordes: MESSIM. El MESSIM muestra una ligera variación en su comportamiento, lo que está relacionado con el aumento del ruido, ya que con un incremento de este se originan falsos bordes, que son interpretados como zonas de cambio de intensidad al igual que los bordes. A esta medida se aplica un operador de borde que binariza la imagen realzando los bordes, y es la información de estos la que es comparada.

Esta medida posee gran importancia, pues el ojo humano es muy susceptible a la información que brindan los bordes y contornos, lo que es vital a la hora de determinar las estructuras anatómicas en una imagen.

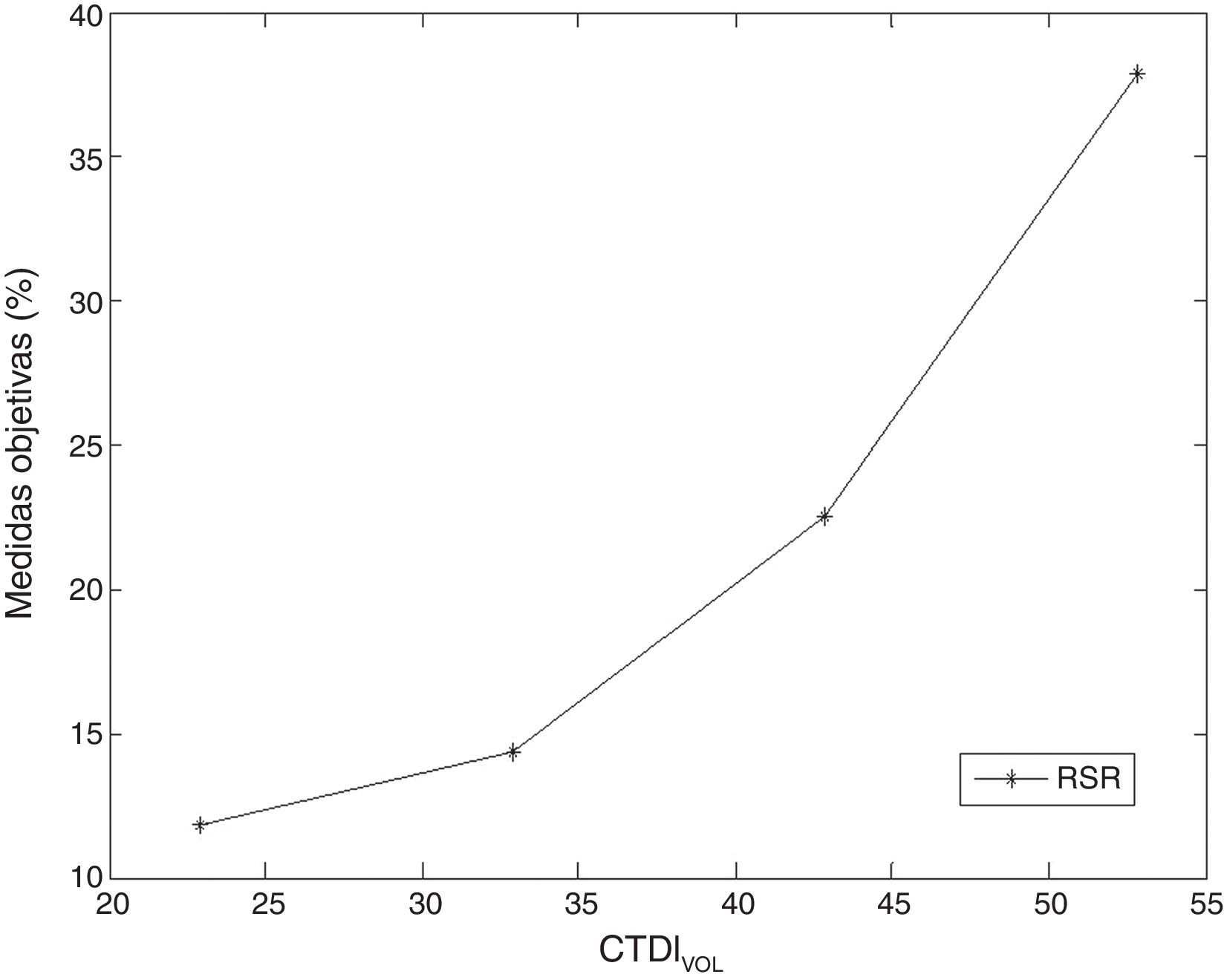
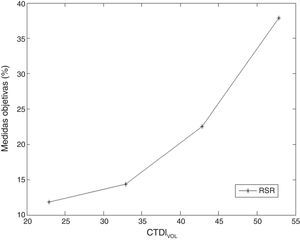
La RSR experimenta una disminución en sus valores, ya que percibe el deterioro en la calidad debido a la relación existente entre la dosis y el ruido (fig. 1). Una disminución de la dosis trae consigo aumento del ruido presente en las imágenes.

Figura 1.

Comportamiento de la relación señal-ruido en el intervalo de valores de CTDI_VOL propuestos.

Para entender este comportamiento hay que tener en cuenta algunas relaciones existentes entre ambos parámetros. Cabe recordar que la dosis de radiación es proporcional al número total de fotones (N) y el ruido es proporcional a 1 entre la raíz de N e inversamente proporcional a la RSR⁵. Una disminución en N trae consigo un aumento del ruido en las imágenes, y por ende una disminución de la RSR.

El conjunto de las medidas objetivas empleadas, aunque representativo de la distorsión que provoca el ruido en las imágenes, solo aporta información de los cambios que ocurren en la calidad de la imagen.

Con el fin de evaluar hasta qué punto el deterioro de la calidad en las imágenes podría hacerlas inservibles para tareas de diagnóstico, se emplearon experimentos ROC y LROC con observadores expertos.

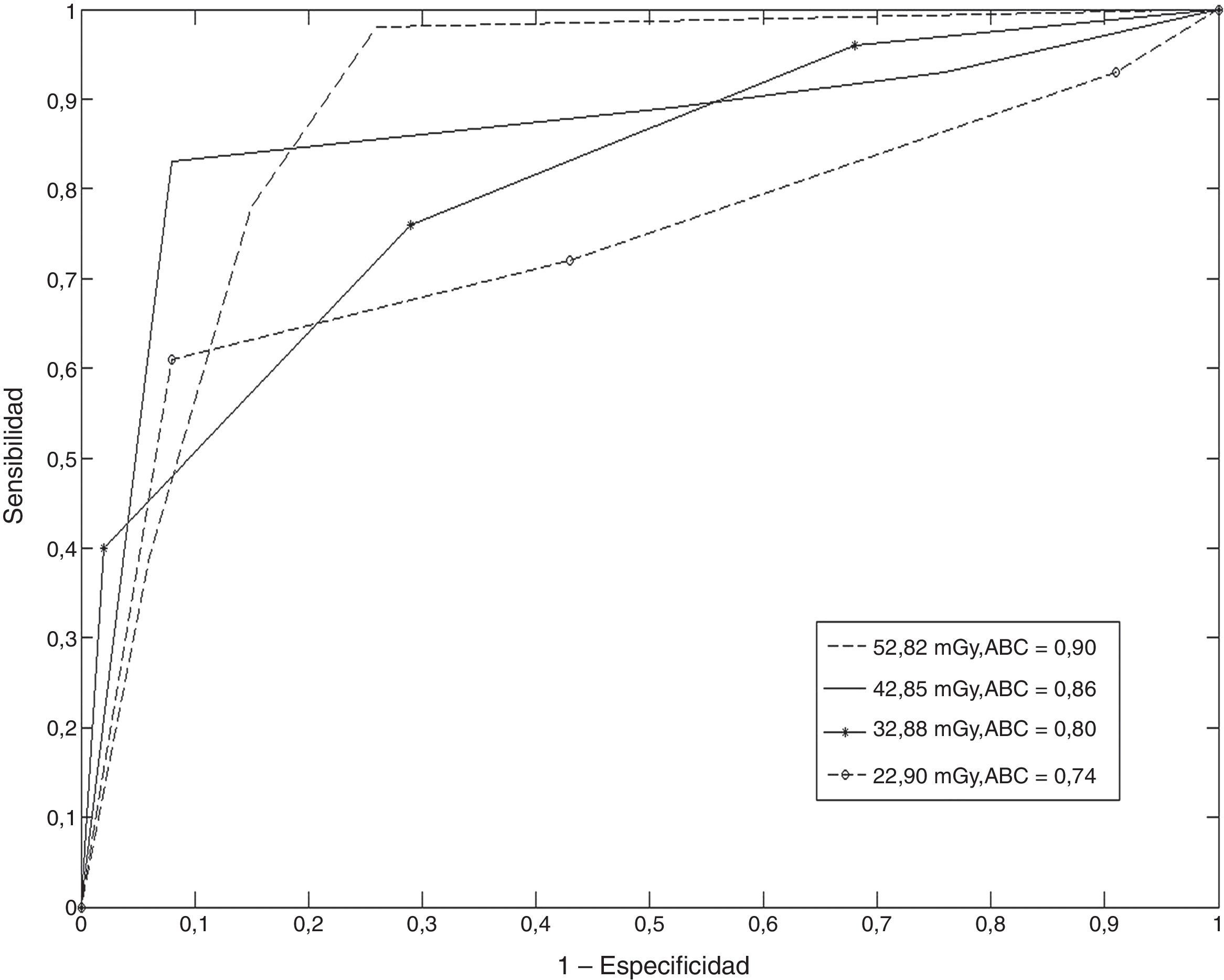
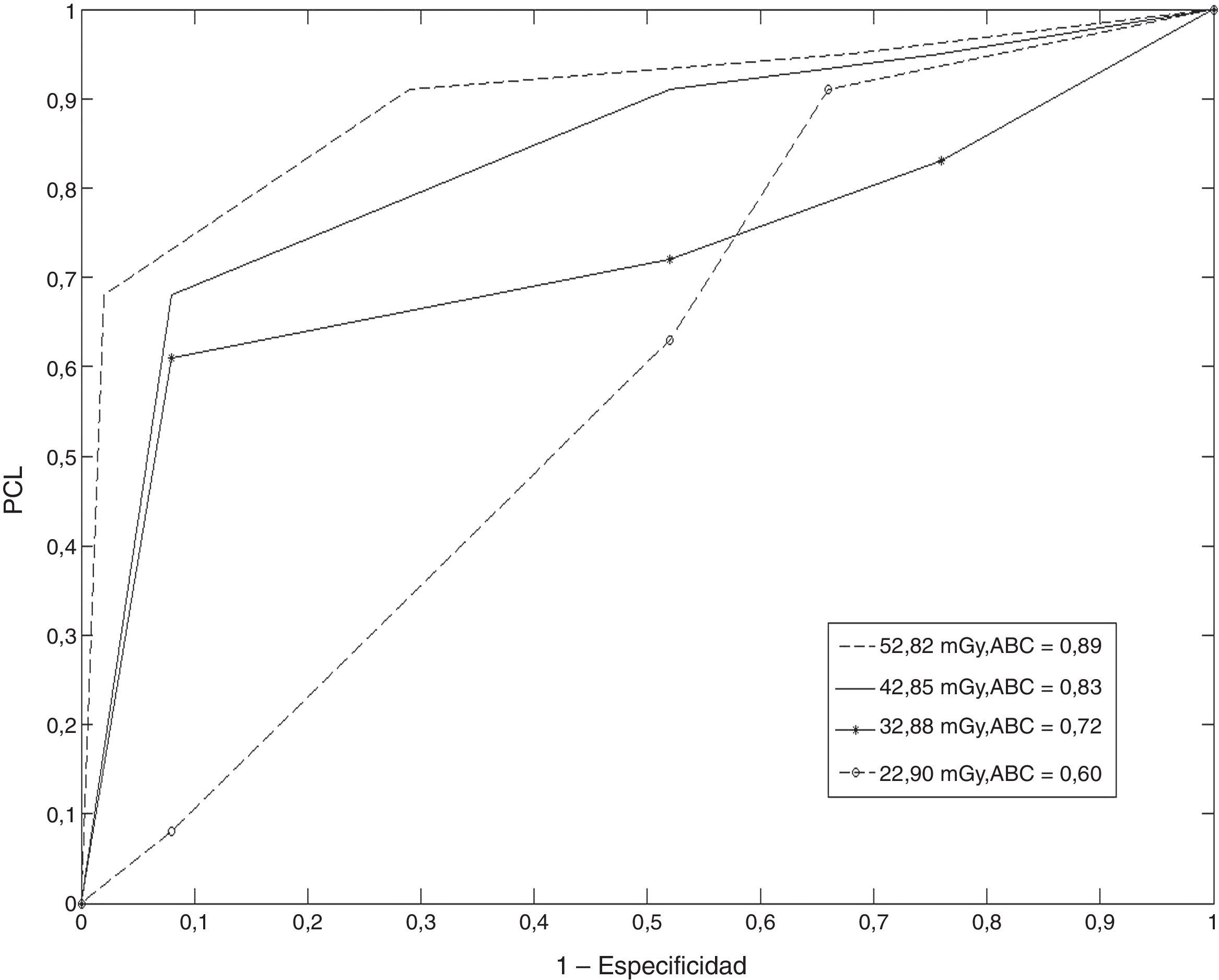
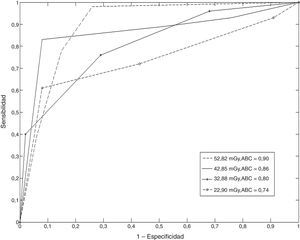
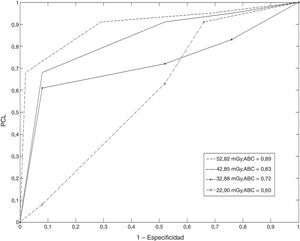
Resultados de la aplicación de los experimentos ROC y LROC

Para complementar los resultados obtenidos, se realizaron los experimentos ROC y LROC. Las figuras 2 y 3 muestran 4 curvas ROC y LROC obtenidas por uno de los observadores.

Figura 2.

Curvas ROC obtenidas de las observaciones realizadas por los observadores a 4 niveles de CTDI_VOL.

Figura 3.

Curvas LROC obtenidas de las observaciones realizadas por los observadores a 4 niveles de CTDI_VOL.

El grado de acuerdo intraobservador e interobservador para el caso del análisis ROC fue de 95,97 ± 0,8% y 94,48 ± 1,7%, respectivamente, y en el caso del análisis LROC, de 96,49 ± 1,5% y 95,38 ± 1,8%.

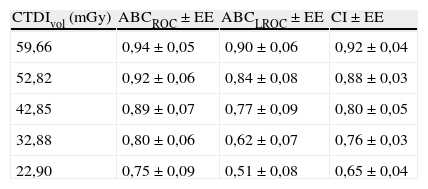
Los experimentos ROC y LROC empleando observadores dieron como resultado los valores representados en la tabla 2.

Tabla 2.

Área bajo la curva ROC, LROC y contenido de información para los valores de CTDI_VOL simulados

CTDIvol (mGy)	ABCROC ± EE	ABCLROC ± EE	CI ± EE
59,66	0,94 ± 0,05	0,90 ± 0,06	0,92 ± 0,04
52,82	0,92 ± 0,06	0,84 ± 0,08	0,88 ± 0,03
42,85	0,89 ± 0,07	0,77 ± 0,09	0,80 ± 0,05
32,88	0,80 ± 0,06	0,62 ± 0,07	0,76 ± 0,03
22,90	0,75 ± 0,09	0,51 ± 0,08	0,65 ± 0,04

ABC_LROC: área bajo la curva LROC; ABC_ROC: área bajo la curva ROC; CI: contenido de información; CTDI_VOL: índice de dosis volumétrico; EE: error estándar.

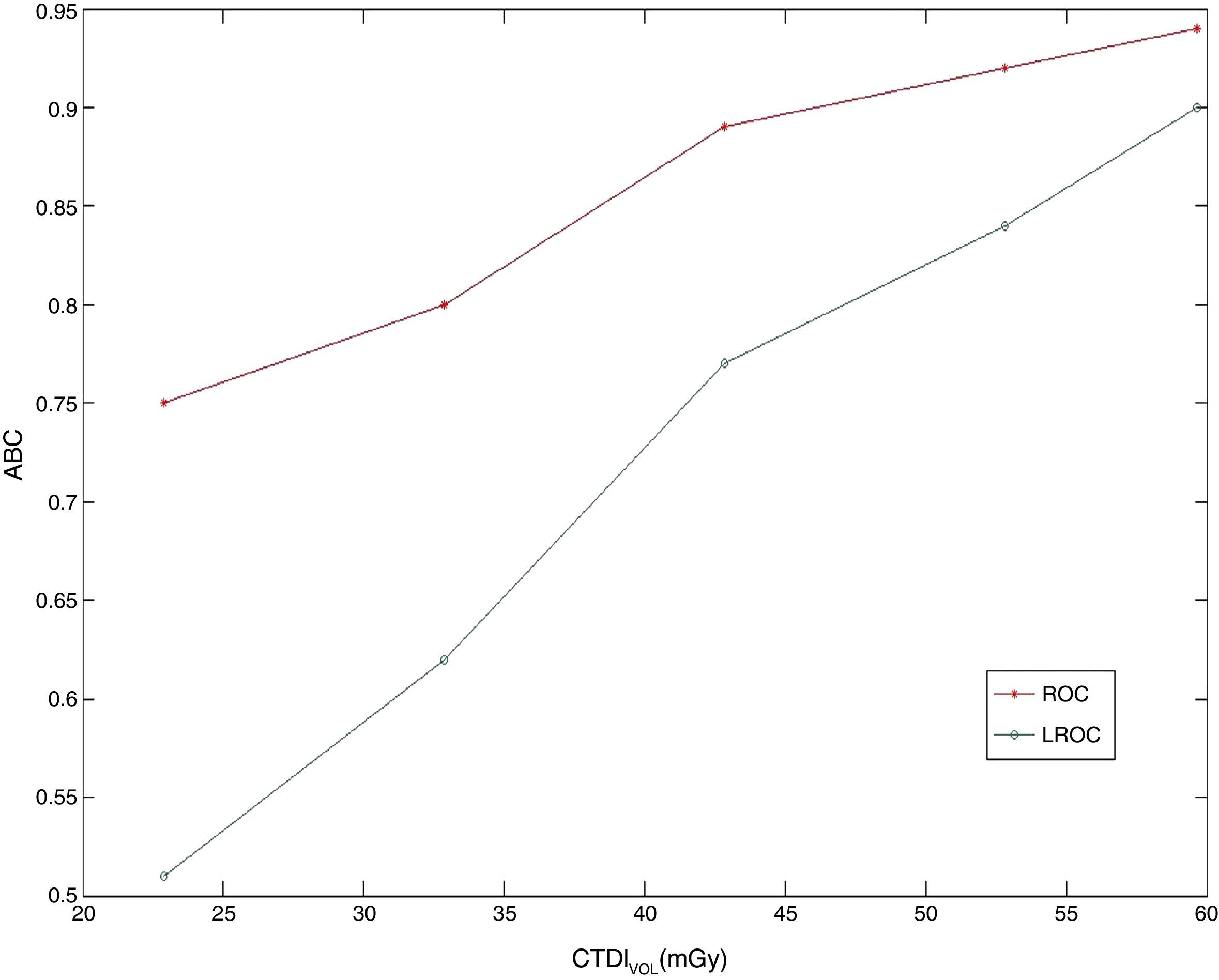
Puede observarse que la capacidad de detección y de localización de los observadores disminuye a medida que disminuye el valor de CTDI_VOL, hecho que está relacionado con la pérdida de calidad en la imagen.

La diferencia en estos mismos valores para el ABC_ROC entre los 2 primeros valores de CTDI_VOL es de 0,02 unidades de área aproximadamente, lo cual significa que la capacidad de clasificar correctamente una lesión disminuye en un 2% entre estos 2 valores. La diferencia en estos mismos valores para el ABC_LROC es de 0,06 unidades de área (disminuye en un 6%).

Puede observarse que a partir del valor de CTDI_VOL de 42,85 mGy, en el análisis ROC, la capacidad de detectar correctamente una lesión disminuye en un 5%, y en el caso del análisis LROC, en un 13%. También se observa que la capacidad de localización por debajo de este valor es del 62%, lo cual indica una baja exactitud en el diagnóstico.

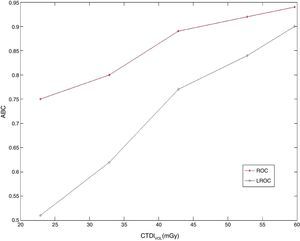
La figura 4 muestra la relación entre los promedios de las áreas bajo la curva de los observadores y los 4 niveles de dosis propuestos. Para niveles de dosis altos, la detección fue buena. Los valores de ABC disminuyeron a medida que el CTDI_VOL disminuyó, cayendo hasta valores que indican una baja exactitud en el diagnóstico. Este resultado indica que el área bajo la curva decrece junto al CTDI_VOL. La correlación entre estos parámetros fue de 0,98, lo que indica una correlación positiva. Este tipo de correlación ha sido reportado en la literatura²¹. Los valores de ABC_LROC son inferiores a los del ABC_ROC, lo cual se debe a que el proceso de localización tiene un mayor grado de complejidad con respecto a la detección. Una de las limitaciones de la curva ROC convencional es que no toma en cuenta la información de la localización de las lesiones, que es considerada en el análisis LROC.

Figura 4.

Relación entre los promedios de las áreas bajo la curva de los observadores y los 4 niveles de dosis propuestos.

El contenido de información necesario para establecer el diagnóstico también se ve afectado. Puede observarse cómo va disminuyendo el CI y cómo existe una pérdida de información al disminuir los valores de CTDI_VOL. Esto afecta la detección y la localización de las lesiones, ya que esta es la información que perciben por los observadores al realizar el diagnóstico.

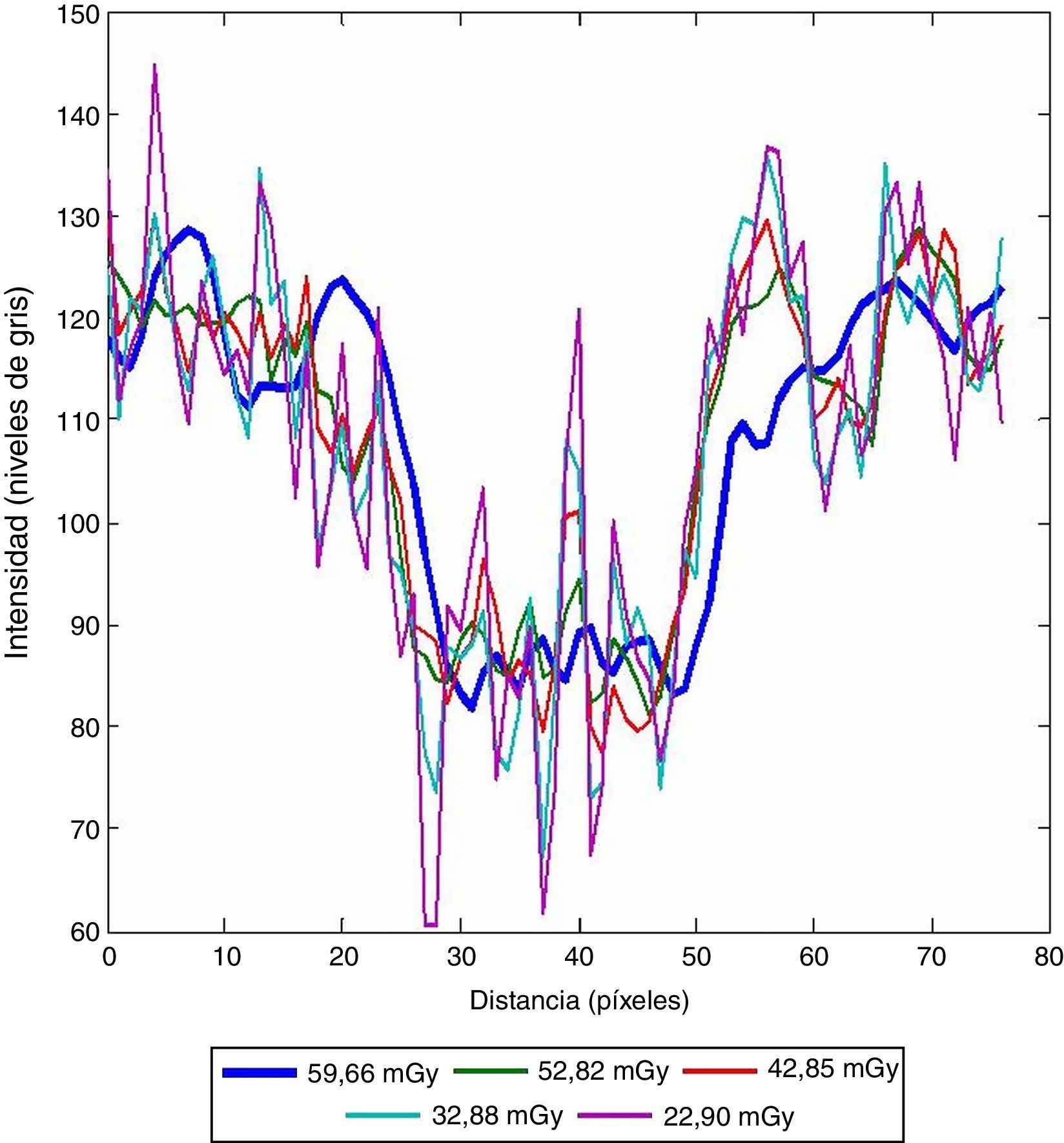
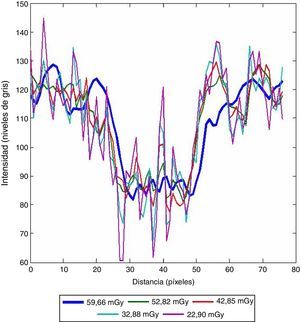
En la figura 5 observamos el perfil de intensidad a través de una lesión. Al comparar el perfil de intensidad del índice de dosis al nivel de referencia (59,66 mGy) con el perfil del índice de dosis más bajo (22,90 mGy) se observa la variación en los niveles de intensidad. Este comportamiento es debido a la presencia del ruido y es el responsable de la baja exactitud en el diagnóstico en los índices de dosis más bajos.

Figura 5.

Perfiles de intensidad para cada uno de los valores de CTDI_VOL.

Otro aspecto a destacar en estos perfiles son las alteraciones en los valores de intensidad en los bordes de las lesiones. Estas variaciones influyen en la exactitud de la localización de las estructuras anatómicas. Estos comportamientos también explican los cambios en las medidas objetivas utilizadas anteriormente.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.