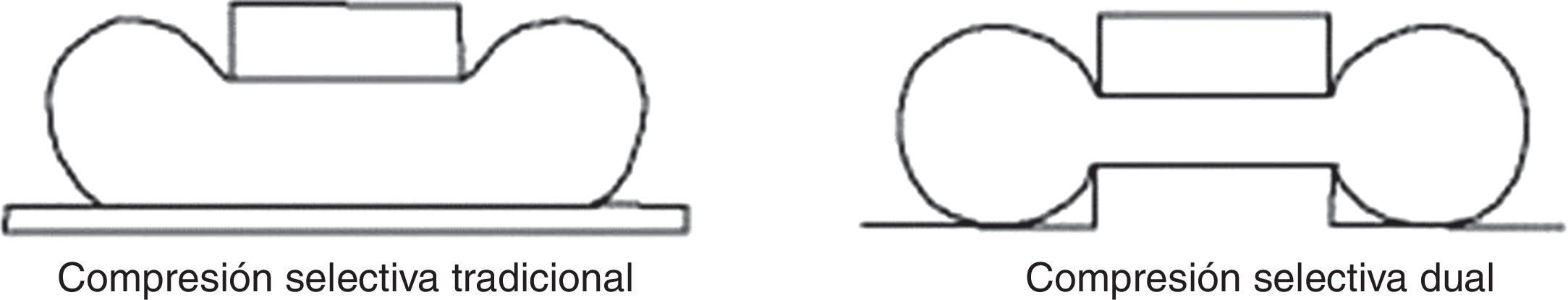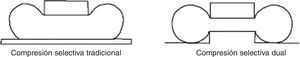Aplicaciones de técnicas de segmentación avanzada en mamografía: hipótesis para un método básico de evaluación elastográfica

Resumen

La elastosonografía es una modalidad diagnóstica de ultrasonido que añade información estructural, evalúa la consistencia o dureza de los tejidos y permite alcanzar mejores resultados de especificidad, pues está demostrado que las lesiones malignas muestran dureza superior a las lesiones benignas.

En este estudio se propone un método de evaluación elastográfica mediante la aplicación de técnicas de segmentación avanzada a imágenes mamográficas.

El método, si es validado por ensayos clínicos, podría ser una herramienta válida y de bajo coste para la caracterización preliminar de lesiones sospechosas y para la reducción de falsos positivos.

Abstract

Elastosonography is an ultrasound diagnostic method that adds information to the morphological structure by evaluating the consistency or hardness of tissues, as well allowing better results to be achieved in specificity, since malignant lesions show more hardness than benign ones.

This study attempts to propose an elastographic evaluation method by applying advanced segmentation techniques to mammographic images.

Proposed method, if validated by clinical trials, could be a valid and low-cost tool for preliminary characterization of suspicious lesions and a reduction in false positives.

Introducción

La elasticidad es la propiedad mecánica de algunos materiales de sufrir deformaciones reversibles cuando se encuentran sujetos a la acción de fuerzas exteriores y de recuperar su aspecto original cuando esas fuerzas cesan. A nivel microscópico, se explica en las fuerzas de interacción que actúan entre las partículas que componen un cuerpo, cuya variación, consecuencia de la tensión externa, provoca un cambio en la distancia mutua entre las partículas mismas, resultando en la deformación macroscópica del cuerpo.

En los tejidos mamarios, una lesión sólida tiene tendencia a tener compresibilidad diferente al tejido glandular normal en función de su propia naturaleza y composición¹. En 1998, Krouskop estableció las bases de la aplicabilidad clínica de la técnica y clasificó la dureza de los tejidos mamarios según la siguiente escala creciente: tejido adiposo, tejido glandular normal, tejido fibroso, CDIS, CDI^2,3. En la tabla 1 se muestra el comportamiento de los carcinomas infiltrantes en función de la tensión (strain) y en comparación con el contexto tisular. Estas diferencias se atribuyen a la reacción desmoplásica que rodea a esas tipologías de tumores⁴.

Tabla 1.

Comportamiento del carcinoma infiltrante de mama como resultado de la compresión externa

Carcinomas infiltrantesA 1% strain A 15% strain
>10x más duro que la grasa	>70x más duro que la grasa
>2,5x más duro que el tejido normal	±5x más duro que el tejido normal

Estas definiciones son la base de la elastosonografía, técnica de ultrasonido ya ampliamente en uso que, sin embargo, requiere medidas adicionales de imagen biomédica y gastos adicionales, además de tener una eficacia limitada por la profundidad de las lesiones (de hecho se recomienda que las lesiones a estudiar estén situadas a no más de unos 2,5-3,5 cm de la piel)⁵.

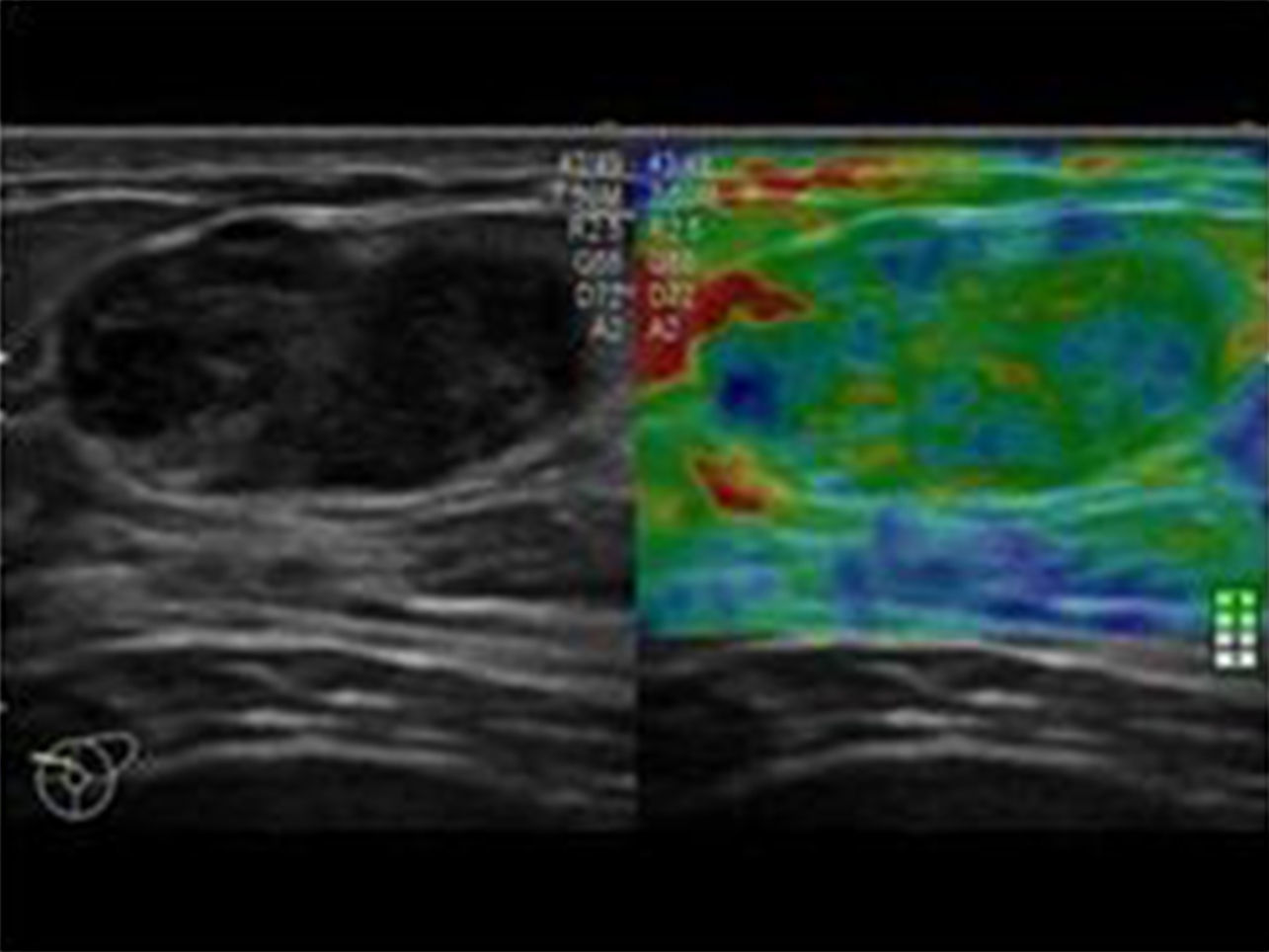
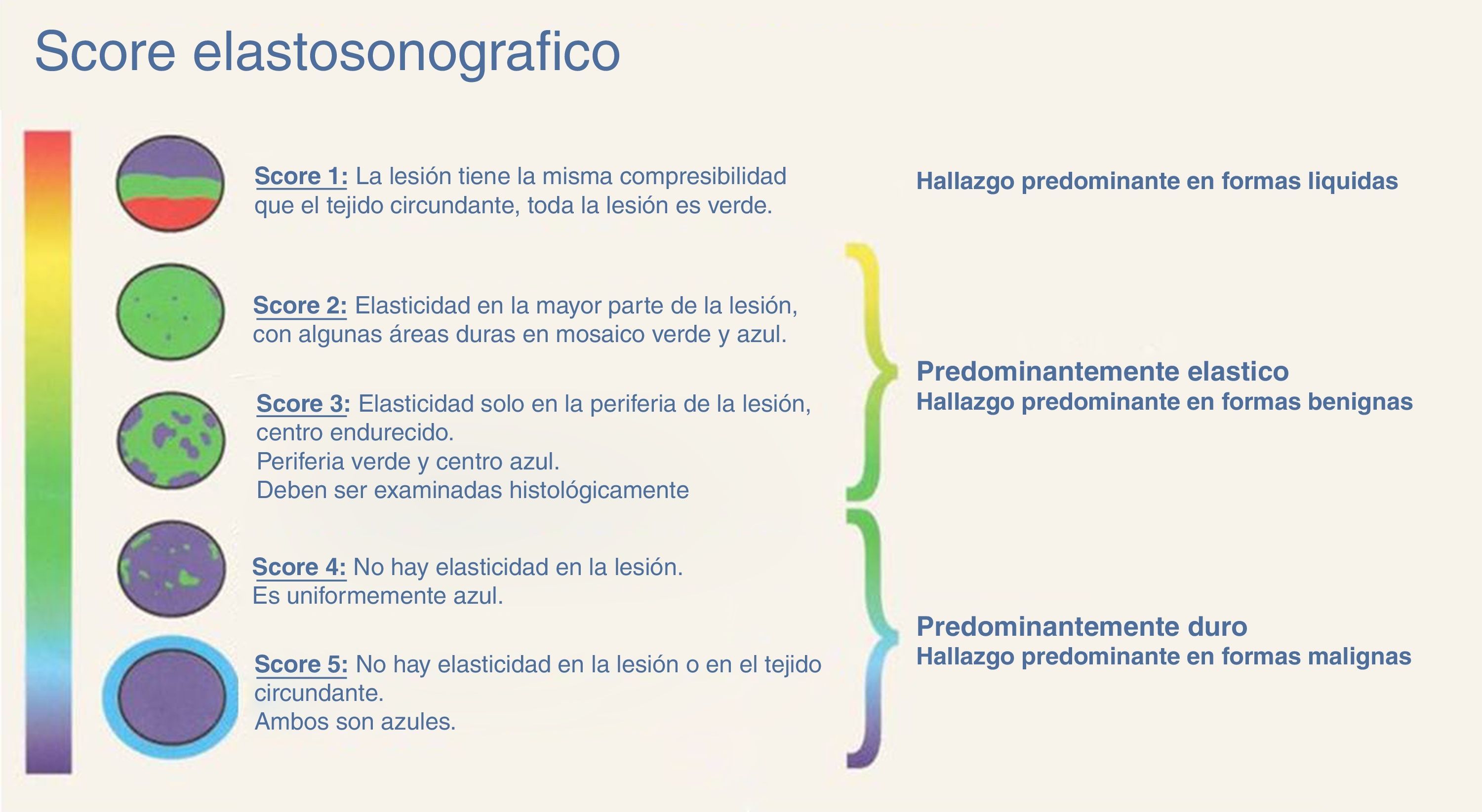
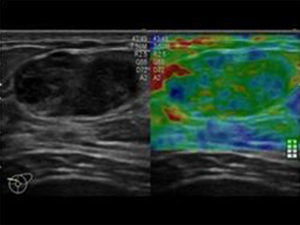
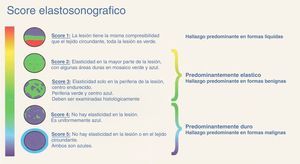
Con el método elastosonográfico, la información que se obtiene es el desplazamiento relativo del tejido tras la compresión, que nos indica su dureza; como el desplazamiento se verifica a lo largo de la dirección del haz ultrasónico, el cálculo se efectúa en la dirección axial, o z⁶. El análisis, de tipo semicuantitativo, se efectúa mediante la correlación computarizada de los mapas anatómicos de elasticidad antes y después de ejercer una compresión externa sobre el tejido, resultando en una escala de colores que se proyectan sobre la imagen en modo B⁵ (fig. 1). Los cambios en la elasticidad se evalúan en tiempo real mediante una anotación elastosonográfica (fig. 2) basada en la escala de Ueno⁷, la más frecuentemente utilizada en la literatura internacional.

Figura 1.

Representación de la imagen elastográfica en la pantalla del ecógrafo.

Figura 2.

Score elastosonográfico.

En la práctica mamográfica se suelen documentar densificaciones sospechosas o distorsiones arquitecturales con una compresión focalizada. Esta solución técnica, que se fundamenta en el desplazamiento de las estructuras supra- y subyacentes, proporciona una mejor visualización y análisis del área de interés, cuya modificación en su aspecto morfológico representa un elemento de diagnóstico diferencial. Analizando con técnicas de segmentación básicas cientos de mamogramas con características de sospecha y las compresiones focalizadas posteriormente realizadas, se ha observado una constante de fijeza dimensional en los hallazgos altamente sospechosos de malignidad, de acuerdo con los resultados del estudio de Wellman et al.¹, lo que ha sugerido una investigación sobre el potencial diagnóstico de un análisis elastomamográfico, llevada con método semiempírico.

Puesto que, en mamografía, cuanta más compresión se aplica a la mama, mayor es la distribución de tejidos en las direcciones x e y, lo primero ha sido observar que el desplazamiento relativo del tejido, que como en la elastosonografía está determinado por la compresión a lo largo de la dirección del haz (eje z), se produce en dirección lateral. Se deduce que:

• a)

  aplicando 2 niveles distintos de compresión, según la naturaleza de la lesión, se obtendrán 2 diferentes valores de desplazamiento x e y;

• b)

  mediante la aplicación de técnicas de segmentación como los contornos activos sería posible medir el diferencial de desplazamiento de la lesión y obtener informaciones sobre la dureza de la lesión analizada.

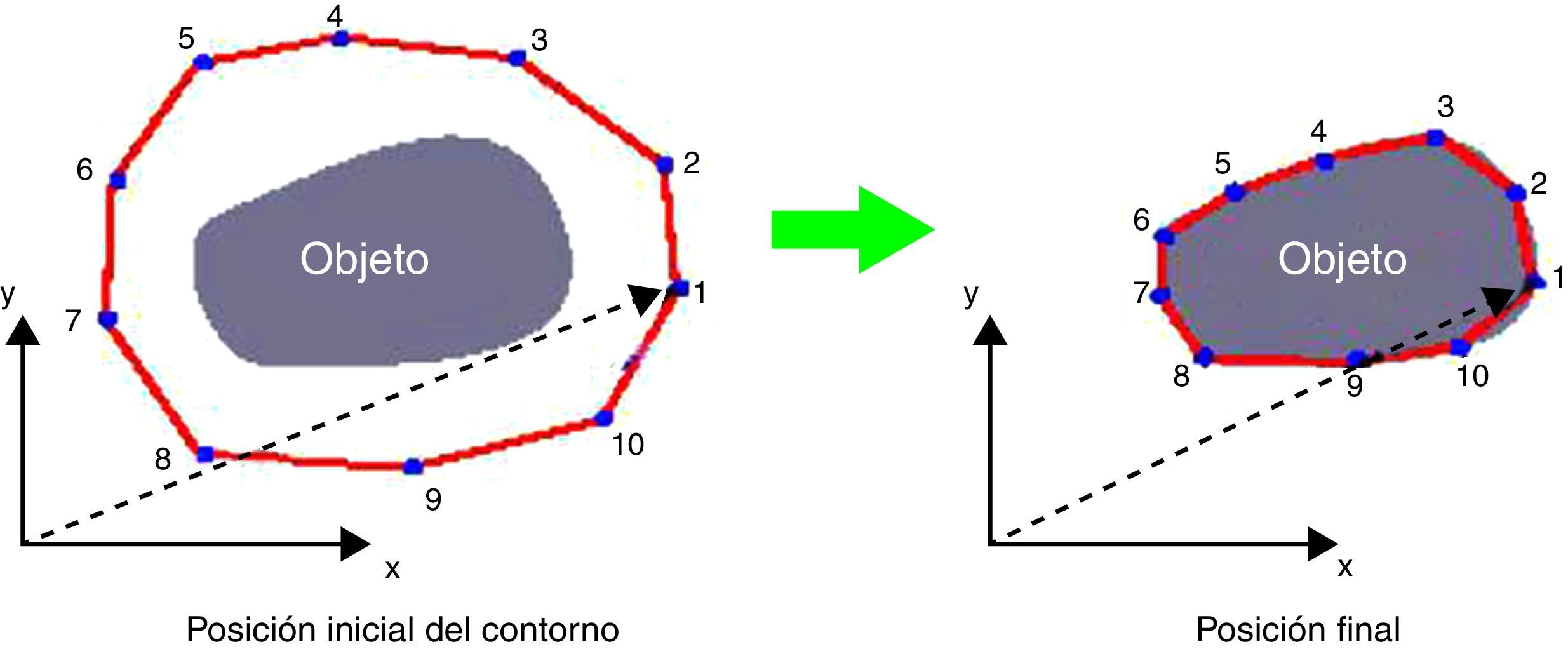
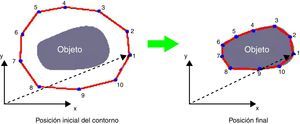
Los contornos activos, o «serpientes» (active contour snakes), fueron propuestos en 1988⁸ y desde entonces han sido muy utilizados en el procesamiento de imágenes médicas^9–14 y en una gran variedad de aplicaciones, entre ellas los sistemas de detección asistida por ordenador (CAD). De forma genérica, consisten básicamente en una curva (o superficie) elástica que puede variar dinámicamente para adaptarse a las formas de los objetos como respuesta a fuerzas internas (fuerzas elásticas) y fuerzas externas (fuerzas de la imagen y restricciones añadidas) (fig. 3).

Figura 3.

Comportamiento de una serpiente de contornos activos.

Fuente: Guindy y Farag (1999).

Serpientes clásicas

En concreto una serpiente clásica (classic contour snake) es una curva elástica que se mueve a través del dominio espacial de una imagen para minimizar su energía funcional^15–17 y se asocia con una energía constituida por la suma de 2 términos fundamentales (E snake = E interna + E externa). La energía interna, que es la energía intrínseca de la curva, también está formada por 2 términos (E interna = E elástica + E curvatura) y actúa como obstáculo para suavizar la serpiente. La energía elástica es directamente proporcional a la elasticidad (o tensión) y a la primera derivada de la curva, y representa la tendencia de la serpiente a mantener su forma oponiéndose a la tracción.

Pues la energía elástica se relaciona con la distancia entre los puntos que constituyen la serpiente: al aumentar la distancia entre 2 puntos aumenta la energía elástica y, reduciendo al mínimo la energía elástica, se reduce al mínimo la longitud total de la serpiente. La energía de curvatura, en cambio, es directamente proporcional a la rigidez y a la segunda derivada de la curva, y representa la tendencia de la serpiente a oponerse al cambio de su curvatura: al aumentar la rigidez, se maximizan los ángulos interiores de la serpiente y se eliminan los bordes afilados. La variación de los parámetros de elasticidad y rigidezafectará el aspecto de la serpiente resultante. Con respecto a la energía externa (o la energía de la imagen), esta representa las características de la imagen adonde tenderá la serpiente, cambiando en función de las diversas aplicaciones, desde la simple luminancia (para acercar la serpiente a las áreas más o menos brillantes en la imagen) al gradiente de la imagen (para acercar la serpiente a los contornos) al flujo de vector gradiente (GVF).

El mayor inconveniente en la utilización de contornos activos clásicos reside en el hecho de que es un método paramétrico en el que los parámetros suelen ajustarse de modo manual por el usuario, dependiendo de la imagen sobre la que se aplique. Por ejemplo, la inicialización del contorno inicial debe elegirse cercana a la solución deseada para obtener buenos resultados, ya que una selección inadecuada de los puntos iniciales de la serpiente dará lugar a un imperfecto ajuste al objeto. Por ello, la aproximación inicial se suele hacer manualmente, a ojo, así como otros parámetros, como la elasticidad y rigidez de la curva, se suelen definir manualmente para controlar la evolución de la serpiente y su punto final. El proceso deja de ser automático, puede resultar afectado por los demás contornos de la imagen y por la presencia de diferentes regiones y texturas en la imagen misma¹⁸.

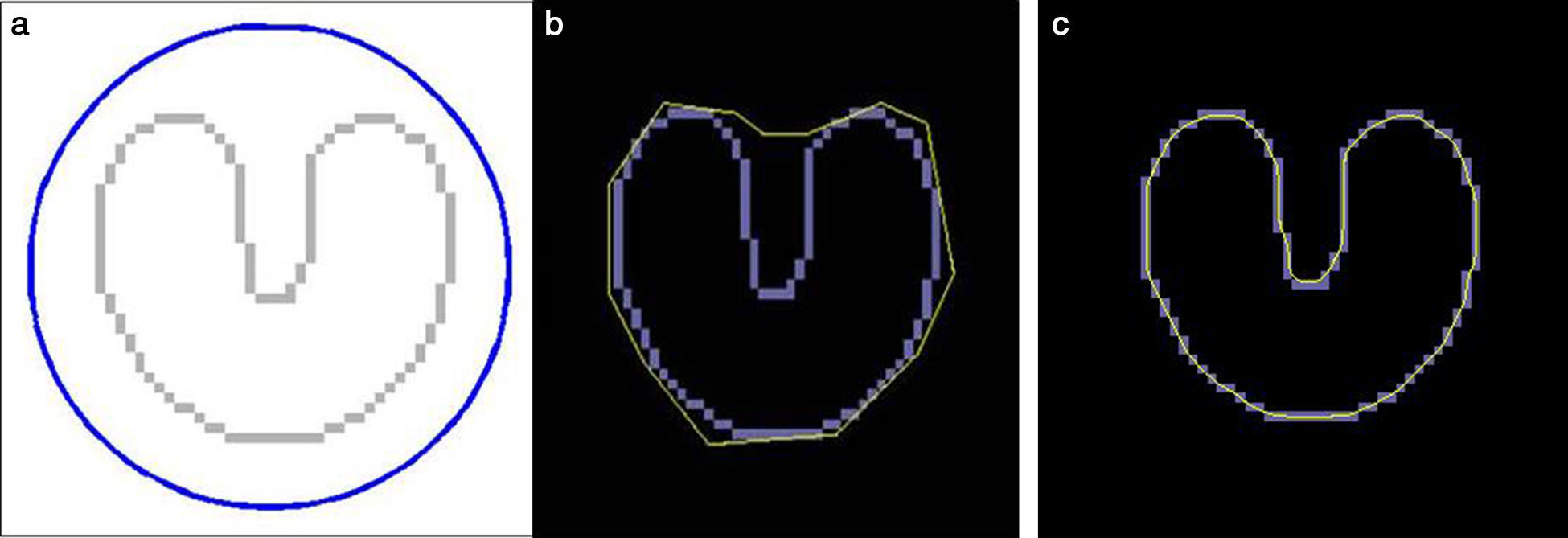
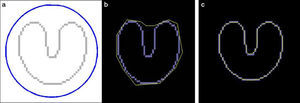
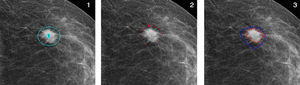
Flujo de vector gradiente (gradient vector flow)

El GVF se calcula como la difusión de los vectores gradiente de un mapa de contornos (binario o en escala de grises) derivado de la imagen. Sus ventajas se traducen en un rango muy amplio de captura, en el que los contornos activos están forzados a adaptarse hasta en regiones cóncavas (fig. 4), características que nos permiten medir con más precisión los contornos de la lesión a partir de una región de interés más amplia^15,16, con tiempos de cálculo mucho más rápidos en comparación con las serpientes clásicas¹⁹.

Figura 4.

a: Inicialización del contorno inicial con GVF. b: Las curvas se acercan al objeto. c: Las curvas penetran en las regiones cóncavas del objeto. La implementación de GVF permite una mejor definición del perfil a partir de una selección más gruesa del área de interés.

Por estas razones, se utiliza en implementaciones más refinadas y por las mismas razones ha sido elegido como herramienta de cálculo para esta investigación.

Material y métodos

El estudio se ha conducido mediante la aplicación de leyes y procedimientos teóricos y prácticos, utilizando hipótesis y parametrizaciones elegidas a partir de datos experimentales.

Se ha utilizado un mamógrafo GE Senographe DMR+, un soporte para compresión selectiva MammoSpot™ 1B, un CR mamográfico FUJI Profect dual reading con estación de elaboración posproceso, un software grafico/matemático Image J 1.45 instalado en un ordenador portátil con sistema operativo Windows 7.

Las pruebas prácticas se han llevado a cabo únicamente utilizando las imágenes que rutinariamente se adquieren en caso de densidades sospechosas con finalidad de diagnóstico, es decir estándar (CC o OML) + compresión focalizada.

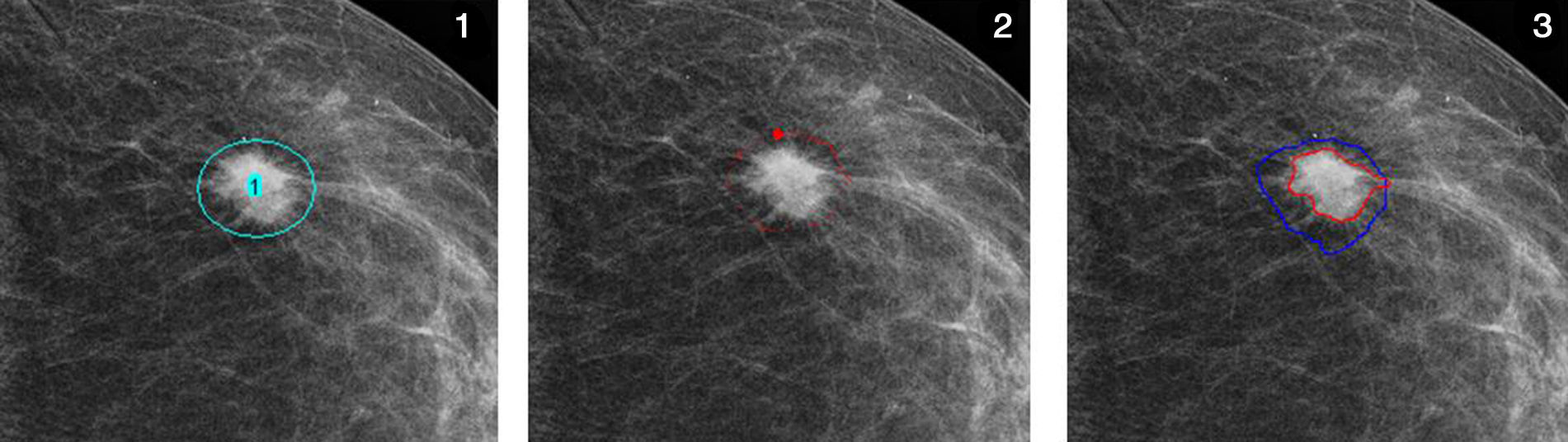
Una vez importado el archivo imagen en Image J y elegida la herramienta GVF, hay que posicionar unos nudos (knots) alrededor de la lesión, seleccionar el umbral y el número de pasos para visualizar los resultados intermedios; a partir de este momento comienza el proceso de inicialización de contorno. A diferencia de las serpientes tradicionales, donde hay que interrumpir la iteración cuando la energía total en 2 etapas sucesivas resulta ser igual, el proceso del GVF se interrumpe automáticamente cuando se minimiza la energía total. En esta fase de estudio se ha aplicado el proceso a la imagen presente en la proyección estándar y en la misma proyección con compresión focalizada, calculando en ambas el área de la densidad y el valor diferencial.

Para un estudio de validez, el proceso entero debería ser aplicado a 2 imágenes adquiridas en condiciones lo más análogas posible. Por lo tanto, se opta por la adquisición consecutiva con compresión en acto y con diferentes niveles de compresión para minimizar el margen de error de cómputo. Para realizar estas condiciones se ha utilizado un soporte para compresión selectiva MammoSpot™ 1B (fig. 5) juntamente con un compresor selectivo tradicional (fig. 6) para obtener una doble compresión selectiva (fig. 7). Se documenta la lesión sospechosa (previamente detectada en los mamogramas estándares) mediante 2 adquisiciones con diferentes cargas de compresión (ratio: 1.^a compresión = nkgf; 2.^a compresión = n·1,5 kgf). A continuación, se aplica a las 2 imágenes el proceso de segmentación con la modalidad descrita anteriormente, analizando en ambas el área de interés y su valor diferencial, interpretando el resultado como indicativo de la posible naturaleza de la lesión, en función de su compresibilidad. En la figura 8 se puede observar el resultado gráfico del proceso automático de aplicación de las curvas de restricción.

Figura 5.

MammoSpot™ 1B.

Figura 6.

Dispositivo de compresión selectiva dual.

Figura 7.

La doble compresión selectiva proporciona una mejor compresión de la región de interés y la casi total eliminación de las estructuras en superposición.

Figura 8.

Aplicación del GVF a una lesión. 1. Selección de la región de interés; 2. Tras unas 500 iteraciones; 3. Al final del proceso, tras 10.000 iteraciones, se define con precisión el contorno de la lesión (en rojo). El inicio del proceso (antes de la aplicación de las curvas de restricción) está marcado en azul.

Aspectos dosimétricos

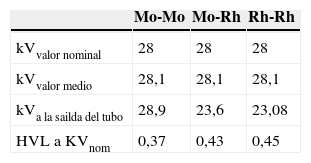
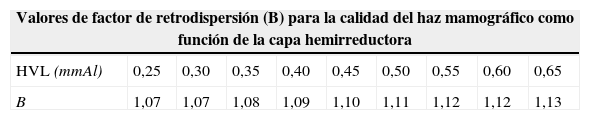
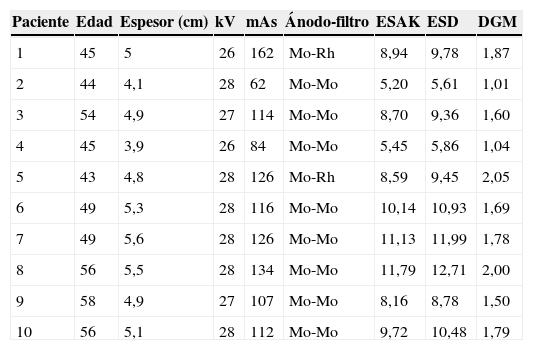
En una muestra de 10 mujeres tratadas mediante compresión selectiva como proyección adicional de diagnóstico, tras anotar la edad y los datos de espesor de mama, parámetros de exposición y combinación ánodo-filtro, se ha calculado el kerma en aire a la superficie de entrada (ESAK) tras haber determinado el rendimiento del tubo y el espesor de la capa hemirreductora (HVL) a un valor nominal de 28 kV para cada combinación ánodo-filtración, aplicando el método paramétrico de Robson²⁰ (tabla 2), la dosis a la superficie de ingreso (ESD), multiplicando ESAK por el factor de retrodispersión B, HVL-dependiente^21,22 (tabla 3) y la dosis glandular media (DGM).

Tabla 2.

Determinación del espesor de la capa hemirreductora (HVL) para diferentes combinaciones ánodo-filtro

	Mo-Mo	Mo-Rh	Rh-Rh
kVvalor nominal	28	28	28
kVvalor medio	28,1	28,1	28,1
kVa la sailda del tubo	28,9	23,6	23,08
HVL a KVnom	0,37	0,43	0,45

Tabla 3.

Relación HVL/factor de retrodispersión

Valores de factor de retrodispersión (B) para la calidad del haz mamográfico como función de la capa hemirreductora
HVL (mmAl)	0,25	0,30	0,35	0,40	0,45	0,50	0,55	0,60	0,65
B	1,07	1,07	1,08	1,09	1,10	1,11	1,12	1,12	1,13

Fuente: IAEA TRS 457.

Para la elaboración de los datos se ha utilizado la hoja de cálculo del ACR.

Los resultados en vivo (tabla 4) han mostrado valores promedios de 27,4 kV, 114,3 mAs, 5,4 cm de espesor de mama, 8,8 mGy (ESAK), 9,5 mGy (ESD), 1,6 mGy (DGM) y medianas de 28 kV, 115 mAs, 8,82mGy (ESAK), 9,61 (ESD), 1,69 (DGM).

Tabla 4.

Resultados dosimétricos en vivo

Paciente	Edad	Espesor (cm)	kV	mAs	Ánodo-filtro	ESAK	ESD	DGM
1	45	5	26	162	Mo-Rh	8,94	9,78	1,87
2	44	4,1	28	62	Mo-Mo	5,20	5,61	1,01
3	54	4,9	27	114	Mo-Mo	8,70	9,36	1,60
4	45	3,9	26	84	Mo-Mo	5,45	5,86	1,04
5	43	4,8	28	126	Mo-Rh	8,59	9,45	2,05
6	49	5,3	28	116	Mo-Mo	10,14	10,93	1,69
7	49	5,6	28	126	Mo-Mo	11,13	11,99	1,78
8	56	5,5	28	134	Mo-Mo	11,79	12,71	2,00
9	58	4,9	27	107	Mo-Mo	8,16	8,78	1,50
10	56	5,1	28	112	Mo-Mo	9,72	10,48	1,79

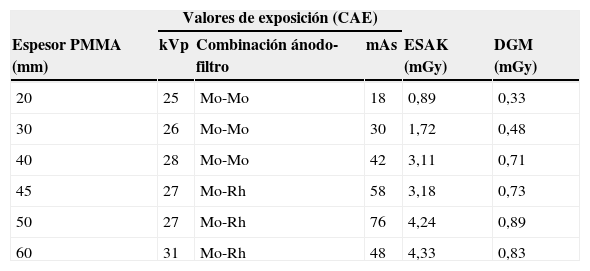
Cabe señalar que, como la limitación del área de exposición (9 × 9 cm) implicaría el conocimiento del factor correctivo g referente a la porción de glándula efectivamente expuesta, además, variable en función de la proyección adoptada (CC u OBL), la aplicación de los factores correctivos de porcentaje de tejido glandular y de su variación en relación con la edad no es confiable para el cálculo de la DGM efectiva. Por lo tanto, se procedió a la estimación de la DGM mediante la exposición de maniquís de PMMA de espesor creciente (de 20 a 60 mm) con CAE en modalidad estándar y en posición torácica, aplicando la fórmula DGM = ESAK g c s, donde ESAK es el kerma en aire a la superficie de entrada (sin retrodispersión) calculado en la superficie superior del maniquí, y g, c, s los factores correctivos propuestos por Dance^23,24.

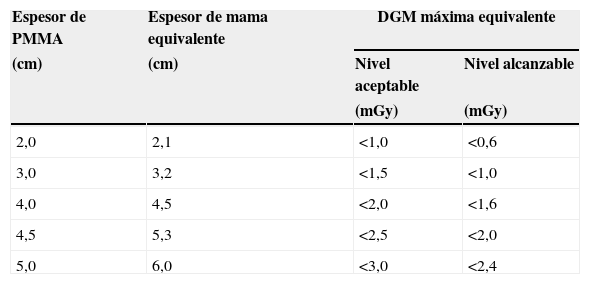
Los resultados en maniquí (tabla 5) han mostrado un ESAK mínimo de 0,89 mGy y máximo de 4,33 mGy (promedio 2,91 mGy; mediana 3,14 mGy) y una DGM mínima de 0,33 mGy y máxima de 0,89 mGy (promedio 0,61 mGy; mediana 0,72 mGy). Si bien se debe tener en cuenta que para espesores >50 mm el ESAK al maniquí es siempre mayor que el ESAK a la mama y menor para espesores <50 mm²⁵, en ningún caso, tanto en vivo como en maniquí, la DGM resultó exceder los valores máximos permitidos²⁶ (tabla 6), demostrando que la dosis global para un estudio estándar con 2 proyecciones adicionales no alcanza el valor de 10 mGy puesto como nivel de referencia para diagnóstico aceptable. A pesar de este resultado, se ha observado que, configurando el CAE a −1/−2 para las 2 compresiones selectivas, se logra una importante reducción del ESAK y de la DGM (respectivamente 2,3 y 0,52 medianas con CAE= −1; 1,8 y 0,41 medianas con CAE= −2), aunque a costa de la densidad óptica (DO 1,2; 1,0). Sin embargo, siendo en este caso la finalidad de las adquisiciones adicionales la segmentación de la imagen, el detrimento del SNR consecuente a la reducción del ESAK (SNR = 69,52 para ESAK, con mediana con CAE = 0; SNR = 54 con CAE= −1; SNR = 43 con CAE= −2) y a la elaboración necesaria para la optimización de la imagen^27–29 es despreciable. Por otro lado, la técnica de doble compresión selectiva permite una reducción de espesor adicional (±1 cm) y un mayor desplazamiento de los tejidos adyacentes, proporcionando menor difusión, mejor contraste y mejor definición de los contornos con un incremento relativo del SNR³⁰.

Tabla 5.

Resultados dosimétricos en maniquí

	Valores de exposición (CAE)
Espesor PMMA (mm)	kVp	Combinación ánodo-filtro	mAs	ESAK (mGy)	DGM (mGy)
20	25	Mo-Mo	18	0,89	0,33
30	26	Mo-Mo	30	1,72	0,48
40	28	Mo-Mo	42	3,11	0,71
45	27	Mo-Rh	58	3,18	0,73
50	27	Mo-Rh	76	4,24	0,89
60	31	Mo-Rh	48	4,33	0,83

Tabla 6.

Dosis máximas admisibles para espesores de PMMA y equivalente de mama

Espesor de PMMA	Espesor de mama equivalente	DGM máxima equivalente
(cm)	(cm)	Nivel aceptable	Nivel alcanzable
		(mGy)	(mGy)
2,0	2,1	<1,0	<0,6
3,0	3,2	<1,5	<1,0
4,0	4,5	<2,0	<1,6
4,5	5,3	<2,5	<2,0
5,0	6,0	<3,0	<2,4

Resultados

Puesto que el método propuesto necesita ensayos clínicos y una comparación cruzada con resultados citohistológicos para confirmar su eficacia, los resultados obtenidos demuestran claramente que es posible medir las variaciones dimensionales de algunas lesiones mamarias detectadas con mamografía mediante la aplicación de técnicas de segmentación avanzada.

Además, a diferencia del análisis elastosonográfico, basado en el diagnóstico por imagen de la tensión (strain imaging), en el que se mide el desplazamiento de la lesión independientemente de la presión aplicada (es un mapa de desplazamiento relativo al desplazamiento de las estructuras adyacentes), con este método se aplica el diagnóstico por imagen del módulo (modulus imaging), teóricamente más exacto, ya que tiene en cuenta la presión aplicada para obtener un desplazamiento concreto³¹.

Conclusiones

Las serpientes GVF dan buenos resultados en su aplicación en el método básico de elastomamografía propuesto que, una vez refinado y codificado, podría ser una herramienta válida para la caracterización preliminar de lesiones sospechosas y la reducción de falsos positivos.

La rápida curva de aprendizaje para la adquisición de imágenes, la reproducibilidad y la posibilidad de análisis diferida hacen que su aplicación sea competencia del técnico.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.