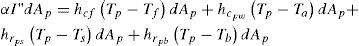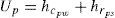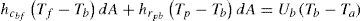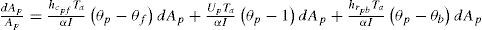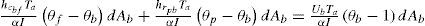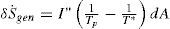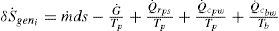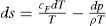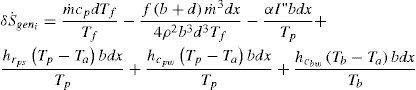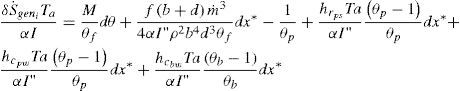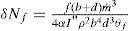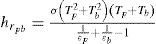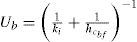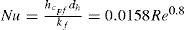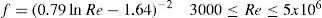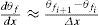Análisis de las irreversibilidades en colectores solares de placas planas no isotérmicos para calentamiento de aire utilizando un modelo adimensional

Resumen

En el presente trabajo, el modelo adimensional desarrollado y validado por Baritto y Bracamonte (2012) para describir el comportamiento térmico de colectores solares de placas planas sin cubierta transparente, se complementa con la ecuación adimensional de balance de entropía para un elemento diferencial de colector solar. El modelo se resuelve para un amplio rango de valores de relaciones de aspecto y número de flujo de masa. A partir de los resultados del modelo se desarrolla un análisis detallado de la influencia de estos parámetros sobre la distribución de irreversibilidades internas a lo largo del colector. Adicionalmente se estudia la influencia de estos parámetros sobre los números de generación de entropía por fricción viscosa, por transferencia de calor y total. Se encuentra que existen combinaciones de los parámetros antes mencionados, para los cuales, la operación del colector es termodinámicamente óptima para números de flujo de masa elevados.

Abstract

The dimensionless model developed and validated by Baritto and Bracamonte (2012) for the thermal behavior of flat plate solar collector without glass cover is improved by adding the entropy balance equation in a dimensionless form. The model is solved for a wide range of aspect ratios and mass flow numbers. A parametric study is developed and the distribution of internal irreversibilities along the collector is analyzed. The influence of the design parameters on the entropy generation by fluid friction and heat transfer is analyzed and it is found that for certain combinations of these parameters optimal thermodynamic operation can be achieved.

Introducción

Los colectores solares de placas planas pueden definirse como intercambiadores de calor que aprovechan la radiación solar global (directa y difusa) para calentar un fluido usualmente a bajas temperaturas (<373 K) (Altfeld et al., 1988a). Sus principales aplicaciones son el calentamiento de agua, acondicionamiento de aire y procesos de secado en aplicaciones agrícolas e industriales (Pangavhane, 2002; Chemkhi et al., 2004; Koyuncu, 2006; Forson et al., 2007).

Entre los calentadores solares de aire, los colectores de placas planas representan una de las configuraciones más económicas, de fácil instalación y mantenimiento (Kalogirou, 2004). Sin embargo, debido a la baja densidad y calor específico del aire, en muchas aplicaciones prácticas se requiere de altos flujos volumétricos que pueden provocar pérdidas por fricción considerables (Gupta y Kaushik, 2008). En el caso de calentadores solares de aire por convección forzada, un incremento en las pérdidas por fricción se traduce en un incremento del consumo de potencia del elemento motor que impulsa el flujo, lo que pudiera en ciertas condiciones hacer que el uso de estos colectores deje de ser ventajoso.

Los procesos de diseño y dimensionamiento de colectores solares deben, por lo tanto, atender la necesidad de incrementar las tasas de flujo de calor sin que esto signifique un incremento desproporcionado de las pérdidas por fricción. En este sentido, los análisis termodinámicos que involucran la segunda ley permiten cuantificar tanto las irreversibilidades asociadas a las pérdidas por fricción como aquellas asociadas a la transferencia de calor (Wu et al., 2007). Estos análisis podrían utilizarse incluso en la obtención de la configuración para la cual las irreversibilidades se minimicen, lo que equivale a determinar la configuración en la que la generación de entropía sea mínima (Bejan, 1996).

El método de minimización de generación de entropía consiste en utilizar las relaciones constitutivas de la transferencia de calor y la mecánica de fluidos para expresar la generación de entropía como una función de las características geométricas y parámetros de operación del sistema estudiado. La relación encontrada se somete entonces a un proceso de minimización y el resultado es la configuración termodinámicamente óptima del sistema (Bejan, 1996). En este sentido resulta importante estudiar la influencia que tienen los parámetros controlados por el diseñador de colectores solares sobre las irreversibilidades de estos dispositivos.

Antecedentes

La optimización termodinámica de colectores solares ha sido objeto de estudio de múltiples autores a partir de la década de los ochentas. Bejan et al. (1981) establecieron las bases analíticas para la optimización termodinámica de colectores solares. En este trabajo los autores utilizan modelos adimensionales simplificados que ignoran las pérdidas por fricción para estudiar colectores isotérmicos y no isotérmicos. En el caso de colectores isotérmicos obtienen la temperatura óptima de operación como una función de la temperatura ambiente y la temperatura de estancamiento. Para el caso de colectores no isotérmicos los autores suponen que el flujo se encuentra en equilibrio térmico con la superficie del colector, y obtienen el flujo de masa óptimo como una función de la temperatura ambiente, la temperatura de estancamiento y la temperatura de salida del colector. Altfeld et al. (1988a, b) utilizó un análisis de exergía, en el cual determina las irreversibilidades en varios modelos de colectores solares y estudia el efecto de la adición de superficies extendidas en las irreversibilidades del sistema y en el desempeño de este tipo de colectores. Torres et al. (2001a) utilizaron el modelo no isotérmico planteado por Bejan et al. (1981) y establecieron una metodología para determinar los parámetros óptimos de operación para colectores solares de placas planas a partir de las condiciones meteorológicas y el área del colector. En un trabajo posterior (Torres et al. 2001b) extendieron el análisis para incluir un estudio termoeconómico de este tipo de colectores. Luminosu y Fara (2005) llevaron a cabo un estudio exergético basado en simulación numérica con la que obtuvieron una expresión para la eficiencia de colectores solares de placas planas como función del área del colector y el flujo de aire; este estudio se limita a colectores solares con áreas entre 0 y 10 m² y para flujos de masa entre 0 y 0,0076 kg/s. Gupta y Kaushik (2008) utilizan el análisis exergético para determinar la relación de aspecto longitudinal y profundidad del colector que maximizan la exergía del flujo de aire caliente como función de las variables meteorológicas. Sus resultados son presentados para un amplio rango de flujos de masa, irradiación y temperaturas ambiente. Vale la pena destacar que en este trabajo se consideran flujos en régimen laminar y turbulento.

Baritto y Bracamonte (2012) desarrollaron y validaron un modelo adimensional para describir el comportamiento térmico de un colector solar de placas planas no isotérmico sin cubierta transparente. Este modelo considera la diferencia de temperatura entre cada uno de los elementos del colector y fue resuelto para un amplio rango de valores típicos de operación utilizando el método de diferencias finitas. Como resultado, Baritto y Bracamonte presentan una ecuación de fácil uso que permite el cálculo de la temperatura de descarga del aire como función del número de flujo de masa y las relaciones de aspecto longitudinal y transversal del colector.

En el presente trabajo se amplía el modelo propuesto por Baritto y Bracamonte (2012) para incluir la ecuación de balance de entropía en su forma adimensional. El modelo se resuelve para un amplio rango de condiciones de operación bajo régimen de flujo turbulento y se lleva a cabo un estudio de parámetros para determinar la influencia de las relaciones de aspecto y el número de flujo de masa en las irreversibilidades del sistema.

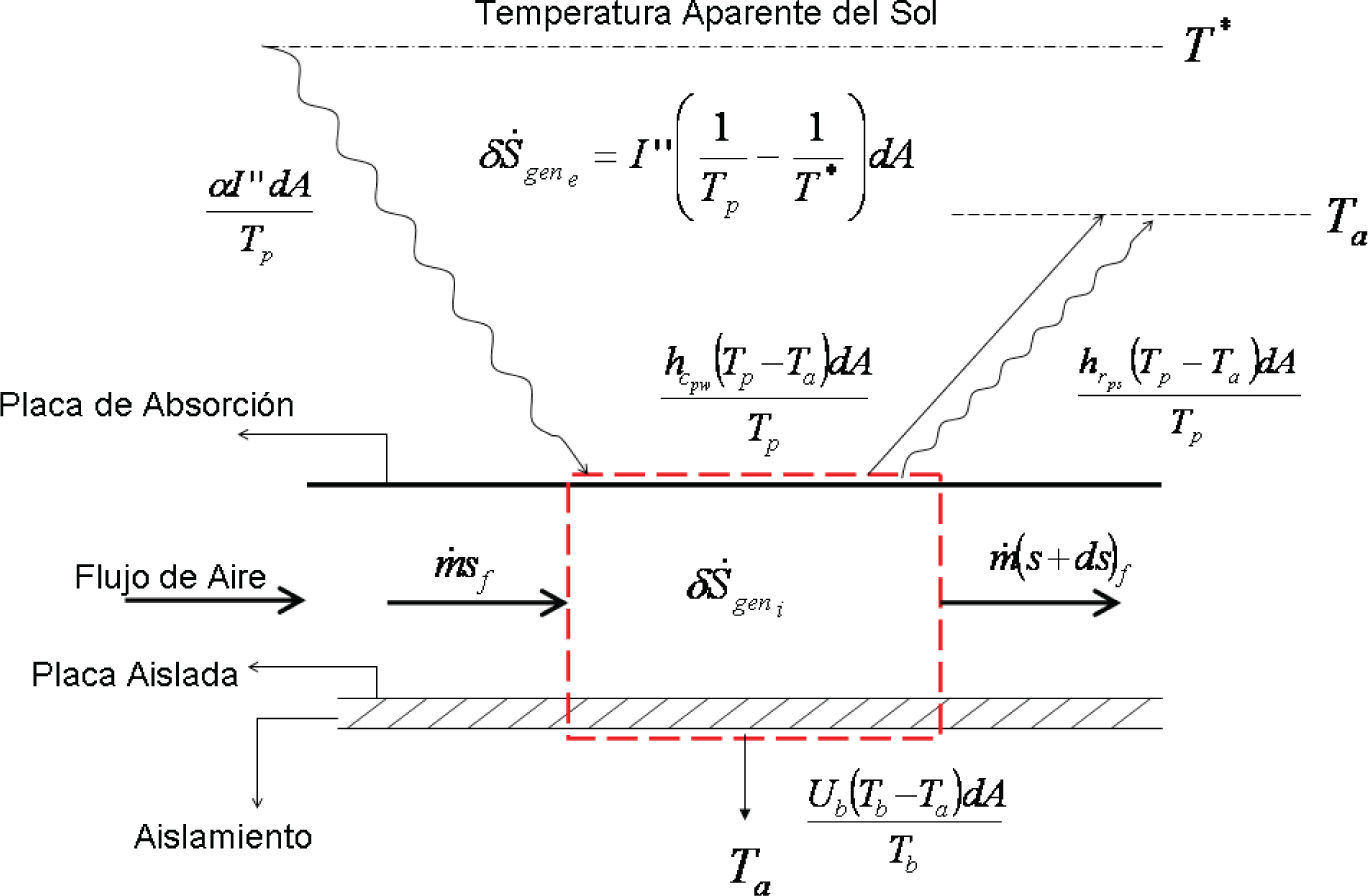
Modelo matemático

Baritto (2010) presenta un modelo para la predicción de la distribución de temperatura longitudinal en el flujo de aire, la placa de absorción y la placa de fondo, en un colector solar plano, de un paso, sin cubierta transparente. Un esquema del colector estudiado por Baritto se muestra en la figura 1 y básicamente consiste en un canal de sección rectangular. La placa superior, o de absorción, recibe la radiación solar difusa y directa, absorbiendo gran parte de la misma. Parte del calor absorbido por la placa es transferido por convección desde la misma hacia el aire que es forzado a fluir dentro del canal. La placa del fondo se encuentra térmicamente aislada, mientras que los lados laterales del canal se consideran adiabáticos. Con la finalidad de encontrar la distribución de temperatura en todos los componentes del colector se planteó una ecuación de balance de flujo de energía en ambas placas, y en el volumen de control de longitud diferencia!, indicado con líneas punteadas en la figura 1. El modelo se desarrolló bajo las siguientes consideraciones:

• 1.

  El colector solar opera en condiciones estacionarias.

• 2.

  Sólo se consideran gradientes de temperaturas en la dirección del flujo.

• 3.

  La conducción de calor despreciable a través de las placas.

• 4.

  Tanto las placas como el aire se consideran no isotérmicos.

• 5.

  El aire dentro del colector se considera un gas ideal y transparente a la radiación de cualquier longitud de onda.

Figura 1.

Esquema del balance de energía

Ecuaciones de balance de flujo de energía

Tomando en cuenta las anteriores consideraciones, a continuación se presentan las ecuaciones de balance de energía.

Para la placa de absorción:

Donde se ha considerado que la temperatura efectiva del cielo es igual a la temperatura ambiente (Duffie y Beckman, 1980), por lo que el coeficiente global de pérdida asociado a la placa de absorción es

Para el flujo de aire

Para la placa de fondo

Baritto y Bracamonte (2012) llevaron el modelo de Baritto (2010) a una forma adimensional, usando la temperatura ambiente como escala para las temperaturas y la radiación solar absorbida por la placa de absorción como escala para los flujos de energía. Las consideraciones hechas para seleccionar estas escalas responden a cuáles parámetros pueden ser modificados por el diseñador y cuáles están impuestos por las condiciones atmosféricas para cierta aplicación. Los detalles pueden encontrase en el trabajo de Baritto y Bracamonte (2012).

Las ecuaciones adimensionales de balance de flujo de energía son:

Para la placa de absorción

Para el flujo de aire

Para la placa de fondo

El grupo adimensional m˙cpTaαI" se identifica como el número de flujo de masa (M) y representa la relación entre la capacidad calorífica del flujo de aire y la energía absorbida por el colector.

Una condición ambiental que se encuentra fuera de control del diseñador es la rapidez del viento, de la cual dependen las pérdidas de calor. De hecho, la principal pérdida de calor se debe a la convección desde la placa de absorción hacia el viento en la parte externa del colector (Duffie y Beckman, 1980). Por esa razón, en este trabajo las pérdidas de calor se caracterizan por un coeficiente de pérdidas que toma en cuenta sólo las pérdidas desde la placa de absorción.

Ecuación de balance de entropía

El proceso de captar radiación térmica de una fuente de alta temperatura en un cuerpo a baja temperatura es intrínsecamente irreversible. La generación de entropía asociada a este proceso para un diferencial de área del colector está dada por la siguiente expresión

Dado que la temperatura aparente del Sol es mucho mayor que la temperatura de la superficie de absorción, la magnitud de este término es mucho mayor a la entropía generada por las irreversibilidades internas del colector (Bejan, 1981). Adicionalmente puede asegurarse que la magnitud de esta generación de entropía variará muy poco para las diferentes temperaturas que puedan alcanzar la superficie de absorción en los rangos de operación regulares.

Tomando esto en cuenta, resulta conveniente escoger un volumen de control en el que se consideren sólo las irreversibilidades internas, aquellas que podrán ser afectadas significativamente por modificaciones en el diseño del colector. En la figura 2 se muestra un dibujo esquemático del volumen de control escogido para el análisis de segunda ley de un elemento diferencial del colector solar. El balance de entropía para este elemento será

Recordando que para un gas ideal se cumple que

Figura 2.

Esquema de balance de entropía en un elemento diferencial del colector solar

Implementando la ecuación 11 en la ecuación 10 junto a las ecuaciones constitutivas de la transferencia de calor y la ecuación de Darcy-Weisbach para estimar la caída de presión en el elemento diferencial del ducto se obtiene

Al igual que para las ecuaciones de balance de flujo energía, se decide adimensionalizar la expresión anterior a fin de que sea válida para distintas condiciones ambientales.

Empleándose las escalas usadas para adimensionalizar las ecuaciones de balance de flujo de energía, se tiene

En donde el grupo adimensional δS˙genTaαI se define como el número de generación de entropía local (δN_s), y de acuerdo al teorema de Guy-Stodolla (Bejan, 1996), representa la relación entre las irreversibilidades internas del colector y la energía radiante absorbida por el mismo. Adicionalmente por conveniencia se establecerán las siguientes definiciones:

En donde δN_F representa el número de generación de entropía local por fricción viscosa y δN_T representa el número de generación de entropía por transferencia de calor en el colector.

Estimación de coeficientes de transferencia de calor y coeficiente de fricción

El coeficiente de transferencia de calor por radiación entre la placa de absorción y la placa de fondo, considerando ambas como grises a la radiación de longitud de onda larga, viene dado por

Considerando el cielo como un cuerpo negro para radiación de longitud de onda larga, el coeficiente de transferencia de calor por radiación desde la placa de absorción al cielo se define como

El coeficiente global de pérdida asociado a la placa de fondo está dado por

Debido a la baja viscosidad del aire es común encontrar flujo turbulento en estos equipos, y debido a que longitudes de entrada cortas son características del flujo turbulento (Kays y Crawford, 1993), aquí se considera flujo totalmente desarrollado.

Para flujo entre placas paralelas, turbulento, totalmente desarrollado, con un lado calentado y el otro aislado, el Número de Nusselt se puede determinar a partir de una correlación de los datos de Kays (Yeh y Lin, 1996)

La longitud característica en esta correlación es el diámetro hidráulico de la sección transversal del colector, y las propiedades del aire son evaluadas al promedio entre la temperatura de la placa de absorción y la temperatura de la placa de fondo. El coeficiente convectivo entre el flujo de aire y la placa de fondo es considerado igual al asociado a la placa de absorción.

El coeficiente convectivo entre la placa de absorción y el viento en el exterior del colector se determina a partir de una correlación propuesta por McAdams (1954)

Donde V es la rapidez del viento en m/s.

Para estimar el factor de fricción de Darcy-Weisbach se utilizó la correlación de Petukhov para flujo turbulento en ductos lisos (Incropera y DeWitt, 1999)

Método de solución

Se desarrolló un código computational de diferencias finitas para resolver el sistema de ecuaciones conformado por los balances de flujo de energía.

El colector se considera formado por secciones de igual ancho y longitud a través de las cuales las propiedades del fluido y las temperaturas de las placas se consideran constantes. La variación de la temperatura adimensional es considerada lineal para cada sección de la siguiente forma

Una vez obtenida la distribución de temperaturas puede calcularse el número de generación de entropía local para cada sección mediante la ecuación 12, y a través de un proceso de integración numérica pueden obtenerse los números de generación de entropía por fricción viscosa (N_f) por transferencia de calor (N_T) y total (N_s) para el colector solar.

Resultados y discusión

El modelo adimensional fue resuelto para el siguiente rango de parámetros de diseño:

Mientras que el número de pérdidas de calor P se fijó en un valor típico de 2.9.

El rango estudiado abarca, según el criterio de los autores, un amplio espectro de las posibles dimensiones prácticas que pudiera adoptar un colector solar. Para fines referenciales puede verificarse que si se fija el valor de la temperatura ambiente en 300 K y la intensidad de radiación solar en 900 W/m² (valores representativos en regiones tropicales), el rango de flujo de masa estudiado estaría acotado entre 0,002 y 0,03 kg/s. Mientras que la velocidad de viento asociado al factor de pérdidas de calor estaría entre 0,5 y 0,7 m/s, valores que se registran comúnmente en espacios abiertos.

Con respecto a las relaciones de aspecto resulta claro que si se estudia un colector solar con un ancho de 1 m, el rango de estudio abarca colectores con longitudes entre 1 y 20 m, con separación entre placas de 0,05 y 1 m.

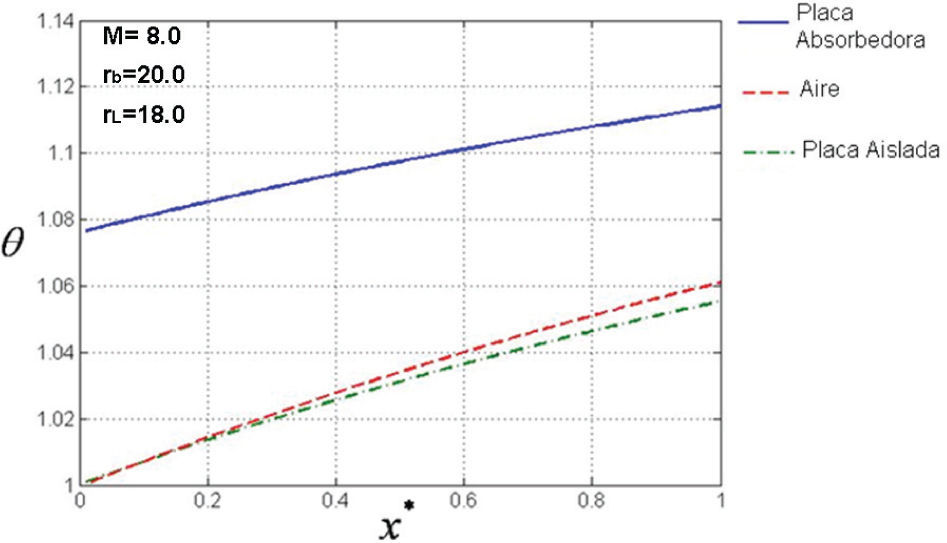
Distribución de temperaturas a lo largo del colector

En la figura 3 se muestra una distribución de temperatura adimensional en un colector solar plano para valores fijos de M, r_b y r_L. Se observa que a lo largo del colector la diferencia de temperatura entre la placa de absorción y el flujo tiende a disminuir, mientras que la diferencia de temperatura entre la placa de fondo y el flujo tiende a aumentar, pero en mucha menor proporción. Este comportamiento se repite en todos los casos estudiados, observándose que, en general, a medida que M aumenta, la diferencia de temperatura entre la placa de absorción y el flujo se hace más pequeña, aún cuando el calentamiento experimentado por ambos es menor. Lo contrario ocurre para valores menores de M, en donde se mantiene una diferencia de temperatura apreciable a la salida del colector y un mayor calentamiento tanto de la placa de absorción como del flujo de aire.

Figura 3.

Distribución de temperaturas adimensionales a lo largo del colector

Al mantener el valor de M fijo y variar las relaciones de aspecto se observa que para un área irradiada dada, los colectores más largos producen mayores temperaturas del aire a la salida, así también en colectores delgados, esto es un alto valor de r_b, la transferencia de calor desde la placa de absorción al flujo de aire se ve favorecida, obteniéndose también mayores temperaturas de aire a la salida. Detalles sobre estos comportamientos se encuentran en los trabajos de Baritto (2010) y Baritto y Bracamonte (2012).

Distribución de las irreversibilidades a lo largo del colector

La figura 4 muestra la distribución de números de generación de entropía local a lo largo del colector para un valor específico de M, r_b y r_L y. Se encontró que el comportamiento de las curvas es cualitativamente similar en todos los casos estudiados, resaltando como cambio significativo la magnitud relativa de N_f con respecto a N_T, lo cual será discutido en el siguiente apartado.

Figura 4.

Distribución de número de generación de entropía local a lo largo del colector.

Con respecto a la distribución de δN_f se encontró que el mismo aumenta levemente a medida que el flujo de aire avanza por el colector. Considerando que en el análisis numérico las secciones del colector se supusieron como ductos lisos de igual longitud y que la caída de presión en cada sección se consideró lineal se concluye que éste incremento se debe exclusivamente a la variación de las propiedades del aire a medida que éste se calienta.

La distribución de δN_T en cambio, demostró ser descendente para todos los casos estudiados. El motivo de esto puede explicarse atendiendo a la distribución de temperaturas a lo largo del colector (figura 3). A medida que el flujo se calienta se reduce la diferencia de temperaturas entre el fluido y la placa de absorción, disminuyéndose de ésta forma la irreversibilidad local por transferencia de calor en cada sección.

Tomando en cuenta que δN_T disminuye a lo largo del colector, y δN_f resultó ser prácticamente constante, el número de generación de entropía local es también descendente (figura 4), concluyéndose que las máximas irreversibilidades en un colector solar ocurren en la sección de entrada del mismo, en donde la diferencia de temperaturas entre el aire y la placa de absorción es máxima.

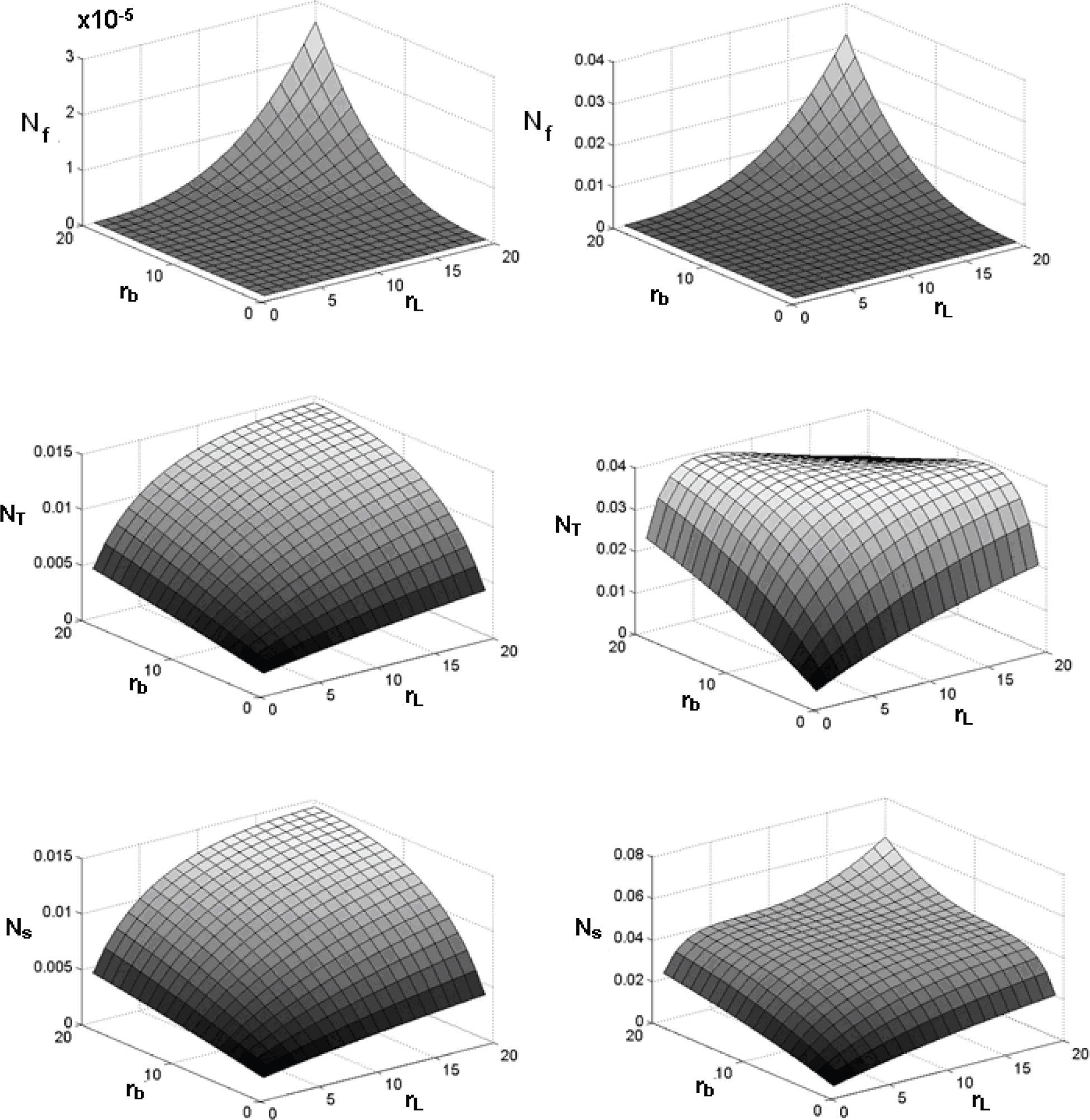
Influencia de los parámetros de diseño en el número de generación de entropía

La generación de entropía por fricción viscosa presentó, para todos los valores de M estudiados, el mismo comportamiento ante las variaciones de r_b y r_L (figura 5) tomando en cuenta que el incremento de cada uno representa respectivamente el decremento del diámetro hidráulico y el incremento de la longitud del colector, ambos provocan el aumento de las pérdidas de presión y por lo tanto de las irreversibilidades por fricción viscosa. En la figura 5 puede observarse que el efecto de los cambios de r_b y r_L sobre N_f son más significativos cuando ambas relaciones de aspecto alcanzan valores elevados. Adicionalmente se encontró que para valores de M por debajo de 4 la magnitud de N_f es despreciable frente a la magnitud de N_T para todas las relaciones de aspecto estudiadas. Esto se debe a que para bajos valores de M la velocidad del flujo es tan baja que los efectos de la fricción viscosa son poco significativos, incrementándose notablemente con los aumentos de M.

Figura 5.

Influencia de las relaciones de aspecto sobre las irreversibilidades. Columna izquierda M = 1, columna derecha M = 14

Con respecto a las irreversibilidades por transferencia de calor, se encontró que para todos los valores de M estudiados y para valores bajos de las relaciones de aspecto, N_T aumenta con el incremento de r_b y r_L. El motivo de esto es que para valores bajos de r_b y r_L el incremento de los mismos produce un incremento de la transferencia de calor, sin embargo, no lo suficiente como para reducir de manera significativa la diferencia de temperaturas entre la placa absorbedora y el flujo de aire, como consecuencia la irreversibilidad por transferencia de calor aumenta.

Para valores de M iguales o mayores a 5 se verificó que N_T decrece con el incremento de r_b y r_L cuando las relaciones de aspecto son elevadas (figura 5). De acuerdo a lo que se discutió acerca de la distribución de temperaturas a lo largo del colector, el incremento de M, r_b y r_L producen un incremento de la transferencia de calor, por lo que para valores elevados de estos parámetros la diferencia de temperaturas entre la placa absorbedora y el flujo de aire se reduce de manera drástica, que se traduce en un decremento de N_T, tal como se verifica en la figura 5, columna derecha.

Para valores de M por debajo de 5, el número de generación de entropía total es prácticamente igual a N_T debido a la poca influencia de las irreversibilidades por fricción viscosa. A partir de M igual a 5, el efecto de decremento de N_T y de incremento de N_f para valores elevados de r_b y r_L se contraponen, esto se manifiesta en la figura 5 columna derecha como una meseta en la gráfica de N_s.

Las configuraciones contenidas en esta meseta representan aquellas para las que se logra un calentamiento apreciable del flujo de aire sin incrementar en exceso las irreversibilidades por fricción viscosa. El análisis de la relación de N_s como función de M, r_b y r_L pueden conducir entonces a una metodología para la selección de las configuraciones de colectores solares termodinámicamente óptimas.

Conclusiones

El modelo adimensional propuesto por Baritto y Bracamonte (2012) para la distribución de temperatura en un colector solar plano para calentamiento de aire, fue complementado con la ecuación de balance de entropía, considerando las irreversibilidades internas al colector solar. Se presentaron sendas ecuaciones para el cálculo del número de generación de entropía local debida a la fricción viscosa, por la transferencia de calor y total. Al resolver el modelo para un amplio rango de números de flujo de masa y relaciones de aspecto, se pudo determinar la influencia de estos parámetros sobre las distintas fuentes de irreversibilidad.

Se encontró que para valores de M, r_b y r_L suficientemente grandes, el modelo predice la existencia de combinaciones de las relaciones de aspectos en donde la generación de entropía por fricción viscosa y por transferencia de calor se equilibran, lo que sugiere la existencia de configuraciones óptimas de diseño. La obtención de los parámetros de diseño óptimos como función de las condiciones ambientales disponibles en determinada aplicación será presentada en trabajos posteriores.

Nomenclatura

a

Área [m²]

b

ancho del colector [m]

c_p

calor específico isobárico [J/kgK]

d

Separación entre placas [m]

d_h

Diámetro hidráulico [m]

f

Factor de fricción

h_c

Coeficiente de transferencia de calor por convección [W/m²K]

h_r

Coeficiente de transferencia de calor por radiación [W/m²K]

I

Irradiación solar total [W]

I”

Intensidad de irradiación [W/m²]

k

Conductividad térmica [W/mK]

k_i

Conductividad térmica del aislante [W/mK]

L

Longitud del colector [m]

l

espesor del aislamiento [m]

M

Número de flujo de masa

ṁ

Flujo de masa [kg/s]

P

Número de pérdidas de calor

N_f

Número de generación de entropía por fricción viscosa

N_T

Número de generación de entropía por transferencia de calor

N_s

Número de generación de entropía total

Nu

Número de Nusselt

Re

Número de Reynolds

r_L

Relación de aspecto longitudinal = L/b

r_b

Relación de aspecto transversal = b/d

S_gen

 

T

Temperatura Absoluta [K]

T*

Temperatura aparente del sol [K]

U

Coeficientes de global de transferencia de calor [W/m²K]

V

Velocidad del viento [m/s]

x

Coordenada medida desde la sección de entrada del colector [m]

x*

Coordenada adimensional = x/L

Símbolos Griegos

α

Absortividad

δ

Diferencial inexacta

ε

Emisividad

θ

Temperatura adimensional = T/Ta

υ

Viscosidad cinemática [m²/s]

ϱ

Densidad [kg/m³]

σ

Constante de Stefan-Boltzmann [W/m²K⁴]

Subíndices

a

Ambiente

b

placa aislada

f

Air fluyendo a través del colector

i

Interno

e

Externo

p

placa de absorción

s

cielo