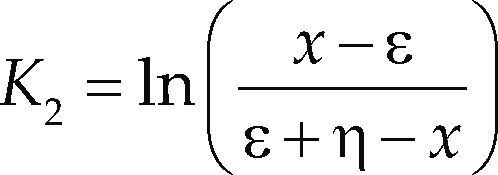Aplicación de la distribución de probabilidades no acotada del Sistema Johnson para estimación de crecientes

Resumen

Las crecientes de diseño son una estimación fundamental en el dimensionamiento de las nuevas obras hidráulicas, así como en la revisión de su seguridad hidrológica en las ya existentes. El método más confiable para su obtención consiste en ajustar un modelo probabilístico al registro disponible de gastos máximos anuales, para estimar sus magnitudes asociadas a ciertos periodos de retorno. Como tal modelo no es conocido, se prueban varios y se selecciona el más adecuado según un índice estadístico, comúnmente el error estándar de ajuste. Varias distribuciones de probabilidad han demostrado versatilidad y consistencia de resultados al procesar registros de crecientes y por ello, su aplicación se ha establecido como norma o precepto. El Sistema Johnson tiene tres familias de distribuciones, una de ellas es el modelo Log–Normal de tres parámetros de ajuste, que además es la frontera entre las distribuciones acotadas y aquéllas sin límite superior. Estas familias de distribuciones tienen cuatro parámetros de ajuste y convergen a la distribución Normal estándar, de manera que sus predicciones se obtienen con tal modelo. Habiéndose contrastado las tres distribuciones de probabilidad establecidas bajo precepto, en 31 registros históricos de eventos hidrológicos, se aplica ahora el Sistema Johnson a tales datos. Se comparan los resultados de la distribución no acotada del Sistema Johnson (SJU), con los óptimos procedentes de las tres distribuciones. Se encontró que las predicciones de la distribución SJU son similares a las obtenidas con los otros modelos, en los periodos de retorno bajos (< 50 años) y en general resultan del mismo orden de magnitud en los intervalos de recurrencia elevados (> 1000 años). Debido a su respaldo teórico, el modelo SJU se recomienda en la estimación de crecientes.

Abstract

Floods designs constitute a key to estimate the sizing of new water works and to review the hydrological security of existing ones. The most reliable method for estimating their magnitudes associated with certain return periods is to fit a probabilistic model to available records of maximum annual flows. Since such model is at first unknown, several models need to be tested in order to select the most appropriate one according to an arbitrary statistical index, commonly the standard error of fit. Several probability distributions have shown versatility and consistency of results when processing floods records and therefore, its application has been established as a norm or precept. The Johnson System has three families of distributions, one of which is the Log–Normal model with three parameters of fit, which is also the border between the bounded distributions and those with no upper limit. These families of distributions have four adjustment parameters and converge to the standard normal distribution, so that their predictions are obtained with such a model. Having contrasted the three probability distributions established by precept in 31 historical records of hydrological events, the Johnson system is applied to such data. The results of the unbounded distribution of the Johnson system (SJU) are compared to the optimal results from the three distributions. It was found that the predictions of the SJU distribution are similar to those obtained with the other models in the low return periods (< 50 years) and in general are of the same order of magnitude in higher recurrence intervals (> 1000 years). Because of its theoretical support, the SJU model is recommended in flood estimation.

Introducción

El cambio climático y sus consecuencias

El cambio climático (CC) inminente está generando condiciones meteorológicas más extremas: tormentas severas, periodos lluviosos con mayor duración y contra- riamente, sequías más prolongadas. Tales condiciones producirán, por una parte, crecientes o gastos máximos más grandes y repentinos y por la otra, mayor erosión de los suelos, debido al poder erosivo de la lluvia y a la menor densidad de cobertura vegetal (Martínez y Aguilar, 2008; Madsen et al., 2013).

Debido a que las crecientes o gastos de diseño son la estimación fundamental de todo estudio hidrológico tendiente a dimensionar la infraestructura hidráulica o a revisar su seguridad, para que no se encuentre en peligro ante los eventos extremos de la naturaleza, surge entonces esta pregunta básica: ¿Cómo mejorar la estimación del gasto de diseño de una obra hidráulica frente al CC?

Acciones necesarias ante cambio climático

En términos generales, ante el CC deben realizarse las siguientes tres acciones:

Primera: por ningún motivo suspender las mediciones hidrométricas y climatológicas, pues si estas eran importantes en el pasado para contar con registros cada vez mayores y con ello incrementar la confiabilidad de los resultados de su procesamiento estadístico, ahora resulta vital incorporar en estos los valores extremos recientes, de manera que las actualizaciones de los estudios hidrológicos reflejen realmente las nuevas condiciones o tendencias climáticas.

Segunda: debido a que las condiciones meteorológicas están cambiando y por consecuencia las climáticas, actualmente es más imperativo ampliar los puntos de medición para disponer de valores de apoyo reales en el transporte de información de sitios con registros amplios a estas nuevas localidades con escasez de datos, así como para poder realizar en el futuro análisis regionales más confiables.

Las dos acciones anteriores conciernen a la disponibilidad de datos y esta tercera está asociada con su manejo o procesamiento, integrando tres vertientes principales:

• 1)

  Con la idea de contrarrestar los efectos del CC, se sugiere aumentar el grado de confiabilidad de las estimaciones hidrológicas, con base en el incremento del intervalo promedio de recurrencia de los eventos, denominado periodo de retorno en años.

• 2)

  Estimar con mayor precisión los eventos de diseño, a través de diversos modelos probabilísticos, por ejemplo, los establecidos bajo precepto y otros nuevos que tienen bases teóricas sólidas.

• 3)

  Análisis probabilísticos avanzados (El-Adlouni et al., 2007), que consideran que los datos no constituyen un proceso estocástico estacionario, debido a los efectos del CC.

Estimación probabilística de crecientes

Actualmente, el método más confiable para estimar los gastos de diseño en una determinada localidad de un río, consiste en procesar el registro disponible de gastos máximos anuales ajustándole un modelo probabilístico o distribución de probabilidades y con base en esta obtener estimaciones o predicciones asociadas a ciertas probabilidades de excedencia.

Una ventaja importante de la serie anual de máximos al estar integrada por eventos extremos anuales, se presenta al aplicar el concepto básico de probabilidad del evento A, definida como el cociente entre el número de casos favorables (ncf) a un evento y el número de casos posibles (ncp), por lo tanto, es un número en el intervalo de cero a uno; o bien, entre cero y 100 cuando se expresa en porcentaje. Entonces, si un evento hidrológico, igual o mayor que un cierto límite, ocurre una vez en promedio en un lapso de Tr años, el cociente 1/Tr corresponderá a su probabilidad de excedencia, ya que es el cociente entre el ncf y el ncp. Lo anterior define el concepto de período de retorno (Tr) o intervalo promedio de recurrencia en años, como el inverso de la probabilidad de excedencia.

El periodo de retorno (Tr) es una forma de expresar la probabilidad de excedencia, por ello se dice: el gasto de diseño de Tr = 20 años o de Tr = 1,000 años, en lugar de decir, los eventos cuyas probabilidades de excedencia son 5% y 0.1% en cada año. El periodo de retorno no significa que un evento de Tr años ocurrirá exactamente cada Tr años, sino que existe una probabilidad de 1/Tr para que tal evento ocurra por año.

Incertidumbre en el análisis probabilístico de crecientes

Este análisis es una estimación basada en información limitada. Por lo anterior, siempre existe incertidumbre en el gasto máximo calculado o en el periodo de retorno estimado. Las causas son la amplitud reducida de los registros de gasto máximo anual, lo cual origina errores de muestreo y los errores propios de su medición. Además, este análisis acepta que los datos siguen un determinado modelo probabilístico y si este no captura plenamente el comportamiento real de los datos, entonces un error de modelo también es fuente de incertidumbre (Kjeldsen et al., 2014).

Evolución del análisis probabilístico de datos hidrológicos

El análisis probabilístico de gastos máximos, lluvias extremas, niveles y vientos máximos comenzó a mediados del siglo pasado, utilizando distribuciones de probabilidad de dos y tres parámetros de ajuste. Al final de la década de los años setenta, ya existían tres modelos probabilísticos que se debían aplicar por norma: la distribución Log–Pearson tipo III (LP3) en USA, la distribución General de Valores Extremos (GVE) en Inglaterra y la distribución Pearson tipo III (P3) en China. A comienzos de este siglo, Inglaterra cambió su distribución establecida bajo precepto y ahora es la Logística Generalizada (LOG).

Es importante destacar que los modelos P3 y LP3 provienen del sistema más antiguo que incluye 12 familias de distribuciones de probabilidad, el cual fue creado por Karl Pearson a finales del siglo XIX (Kottegoda, 1980; Bobée y Ashkar, 1991). Shapiro (1998) indica que el sistema de la Lambda Generalizada es el más reciente que se ha propuesto (Ramberg et al., 1979) y aún está en desarrollo. Intermedios entre estos dos existen el sistema de Halphen generado a inicio de los años cuarenta (Perreault et al., 1999) y el sistema de Johnson creado por Johnson (1949), el cual se describe y contrasta en este trabajo.

Objetivo del trabajo

Habiéndose realizado contrastes de las distribuciones GVE, LP3 y LOG en un grupo de 31 registros históricos, se propone ahora describir con detalle el sistema Johnson (SJ) de tres familias de distribuciones de probabilidad y aplicarlas al mismo grupo de registros, para seleccionar la más adecuada a cada uno y comparar sus resultados con los mejores obtenidos con estos tres modelos probabilísticos, cuya aplicación se realiza bajo precepto. Este grupo de muestras de eventos máximos anuales de tipo hidrológico, la mayoría crecientes, tomados de textos y otros trabajos relevantes al análisis probabilístico en esta disciplina, tienen amplitudes que varían de 16 a 113 años; sus datos generales, parámetros estadísticos, momentos L y referencias se pueden obtener en Campos (2013).

Métodos aplicados

Conceptos teóricos del Sistema Johnson

El sistema tiene tres familias de distribuciones de probabilidad, las cuales se generan a través de una transformación específica a la variable normal estándar (z). Las familias se llamarán SJU, SJB y SJL; la última es la distribución Log-Normal de tres parámetros de ajuste, la cual ocupa un lugar central en el sistema Johnson y cuya variable (x) está definida en el intervalo de ¿ a ∞, siendo ¿ un parámetro de ubicación. Las otras dos distribuciones tienen cuatro parámetros de ajuste, la familia SJU no tiene intervalo o frontera, por ello su designación, la cual viene de unbounded range; en cambio, la familia SJB se define en el intervalo de ¿ a ¿+η, siendo η un parámetro de escala y su designación deriva de bounded range. El sistema Johnson se genera con la ecuación general siguiente (Kottegoda, 1980; Slifker y Shapiro, 1980; Shapiro y Gross, 1981; Shapiro, 1998):

en donde, las funciones K_i se escogen para abarcar un gran número de formas posibles, las definidas por Johnson son las siguientes; para la familia SJU

para la familia SJB

y para la familia SJL

En la población de la variable original X, los parámetros ¿ y η rigen el extremo izquierdo y la escala, mientras que la forma de la distribución está gobernada por los parámetros δ y τ.

Selección de la familia Johnson a utilizar

El proceso de selección de la distribución de probabilidades que mejor se adapta o ajusta a los datos involucra la estimación de los percentiles correspondientes a 3z, z, –z y –3z, los cuales se designan como: X_3z, X_z, X_–z y X_–3z. Después se evalúan los siguientes tres parámetros y el de selección PS (Slifker y Shapiro, 1980; Shapiro y Gross, 1981; Shapiro, 1998):

Si PS > 1 se escoge la distribución SJU, si PS < 1 se adopta la distribución SJB y si PS 1 se selecciona la distribución SJL.

La estimación de los percentiles requiere la selección de un valor de z, la transformación de ±z y de ±3z a probabilidades Normales y de ahí a una estimación de la posición empírica (i) en la variable original X. En muestras de tamaño moderado, se utiliza comúnmente un valor de z menor de uno. Por ejemplo, adoptando un valor de z = 0.5483, se tiene que ±3z = ±1.645, valores que definen los percentiles de 95% y 5% de probabilidad de no excedencia [F(·)] en la distribución Normal y las otras probabilidades relativas a ±z son 70.8% y 29.2%. Ahora, resolviendo la siguiente ecuación empírica se obtienen las posiciones buscadas (Shapiro, 1998)

en donde, nd es el tamaño de la muestra, con los datos ordenados de menor a mayor e i es el valor buscado del percentil X_3z, X_z, X_–z y X_–3z. Lógicamente, habrá que interpolar entre la pareja de posiciones reales menor que i y mayor que esta. Usando z = 1.0 en muestras grandes (n > 1000), las probabilidades F(·) son 99.86%, 84.13%, 15.87% y 0.14% (Slifker y Shapiro, 1980). En muestras de tamaño moderado también se utilizó z = 0.524, generando las probabilidades siguientes: 94.2%, 70%, 30% y 5.8% (Shapiro y Gross, 1981).

Cálculo de los parámetros de ajuste de la distribución SJU

En la distribución GVE cuando su parámetro de forma (k) resulta positivo se define como distribución de probabilidades más conveniente el modelo Weibull con límite superior y concavidad hacia abajo en el papel de probabilidad Gumbel-Powell. Lo anterior ocurrió únicamente en los registros números 16, 20, 24 y 29. Cuando k es positivo, pero cercano a cero, indica que el modelo más adecuado es la distribución Gumbel, que es una línea recta en el papel Gumbel-Powell.

Por otra parte, las distribuciones LP3 y LOG no resultan acotadas en registros de crecientes con datos dispersos (outliers) y por ello no es procedente utilizar en esta comparación del sistema Johnson, la familia SJB, que presenta un límite superior en ¿+η. Tampoco se contrasta la familia SJL, pues la distribución Log-Normal se aplica de manera rutinaria en los análisis probabilísticos de crecientes (Kite, 1977; Stedinger et al., 1993; Rao y Hamed, 2000). Por lo anterior, únicamente se exponen las expresiones de cálculo de los cuatro parámetros de ajuste de la familia SJU (Slifker y Shapiro, 1980; Shapiro, 1998)

Las expresiones del arco coseno hiperbólico, del arco seno hiperbólico y del seno hiperbólico que será utilizada en la expresión de la solución inversa de la ecuación 1, son (Campos, 2003):

Cálculo del error estándar de ajuste

Este indicador de la calidad de ajuste que logra, con los datos del registro o muestra, la distribución que se prueba, se ha generalizado desde mediados de los años setenta y su expresión es la siguiente (Kite, 1977):

en donde, nd es el número de datos de la muestra, x_i son los datos ordenados de menor a mayor, son los valores estimados con el modelo probabilístico que se prueba, para una probabilidad de no excedencia P(X < x) estimada con la fórmula de Weibull (Benson, 1962)

en la cual, m es el número de orden del dato, con 1 para el menor y nd para el mayor. Por último, np es el número de parámetros de ajuste, con tres para las distribuciones GVE, LP3 y LOG, y cuatro para la distribución SJU. La solución inversa de la ecuación 1 para la distribución SJU es la siguiente (Slifker y Shapiro, 1980)

La probabilidad (P) estimada con la ecuación 18 se toma en cuenta para el cálculo de la variable normal estándar (z), en cuya estimación se utilizó el algoritmo siguiente (Zelen y Severo, 1972)

donde

c₀ = 2.515517 c₁ = 0.802853 c₂ = 0.010328

d₁ = 1.432788 d₂ = 0.189269 d₃ = 0.001308

La ecuación 20 se aplica cuando P varía de cero a 0.50 y entonces z será negativa, cuando P excede a 0.50 se emplea P = 1 – P.

Ajuste de la distribución SJU mediante optimización numérica

Durante los contrastes de las distribuciones GVE, LP3 y LOG con el grupo de 31 registros históricos hidrológicos, tales modelos se ajustaron mediante optimización numérica para minimizar el error cuadrático medio. Por lo anterior, también ahora se realizó el ajuste de la distribución SJU mediante optimización numérica utilizando como función objetivo (FO) el EEA (ecuación 17).

Nuevamente, este proceso se realizó con base en el algoritmo de múltiples variables no restringidas de Rosenbrock (Kuester y Mize, 1973; Campos 2003), considerando como variables a optimizar sus cuatro parámetros de ajuste (¿, η, δ, τ), cuyos valores iniciales se obtuvieron con las ecuaciones 10 a 13. El algoritmo citado, únicamente falló en los registros 1, 4, 11 y 19, excediendo el número máximo de evaluaciones de la FO de mil; o bien, no llegando a converger en el número máximo de etapas permitido, que fue de cincuenta. Ambos problemas se corrigieron limitando el número de etapas permitido a la última en que se tenían resultados consistentes.

Análisis de resultados

Registros que aceptan la distribución SJU

En la tabla 1 se concentraron los resultados de las ecuaciones 5 a 9, utilizando z = 0.5483, encontrado que únicamente en 13 registros de los 31 analizados, se aplica la familia de distribuciones SJU. Se observa que el procedimiento de selección trabaja correctamente, ya que detecta a la familia SJB como la más conveniente en los cuatro registros (16, 20, 24 y 29), que siguieron la distribución Weibull o modelo GVE con frontera superior.

Tabla 1.

Resultados de la selección de la familia de distribuciones Johnson

Núm. Reg.	nd	Parámetros de selección				Familia adoptada
		m	n	p	PS
1	16	1331.880	498.880	736.240	1.226	SJU
2	21	31.227	11.843	28.210	0.465	SJB
3	26	386.841	50.439	183.480	0.580	SJB
4	28	223.408	59.708	70.184	2.708	SJU
5	31	892.359	200.664	429.713	0.970	SJB o SJL
6	31	106.179	85.121	85.560	1.235	SJU
7	31	151.335	53.742	76.184	1.401	SJU
8	35	99.951	23.409	68.030	0.506	SJB
9	36	1039.868	209.912	590.520	0.626	SJB
10	39	364.200	31.863	123.341	0.763	SJB
11	40	1343.040	257.220	515.240	1.301	SJU
12	44	845.517	180.956	595.004	0.432	SJB
13	45	1257.480	499.240	835.280	0.900	SJB
14	47	53.172	10.058	26.622	0.755	SJB
15	50	2610.500	609.400	1179.100	1.144	SJU
16	53	76.770	55.683	74.387	0.773	SJB
17	53	8132.578	660.622	1619.448	2.049	SJU
18	55	499.395	348.637	530.997	0.617	SJB
19	55	1527.700	38.360	241.440	1.005	SJU o SJL
20	57	49.826	54.588	73.136	0.508	SJB
21	57	1173.640	278.880	598.480	0.914	SJB
22	58	220.726	77.969	95.928	1.870	SJU
23	59	233.568	104.645	124.112	1.587	SJU
24	66	603.475	561.726	752.978	0.598	SJB
25	67	2638.782	258.443	785.233	1.106	SJU
26	69	58.236	43.546	42.168	1.426	SJU
27	85	168.070	69.210	131.720	0.670	SJB
28	113	174.796	84.092	123.512	0.964	SJB o SJL
29	21	1.588	3.319	2.898	0.628	SJB
30	70	19.940	9.940	12.120	1.349	SJU
31	72	13.900	5.948	11.952	0.579	SJB

Resultados óptimos de los contrastes previos

En la tabla 2, para cada registro procesado se exponen ocho renglones de resultados, los dos primeros corresponden a los parámetros de ajuste (u, α, k), EEA y predicciones con periodos de retorno 10, 25, 50, 100, 500, 1 000 y 10 000 años, obtenidas con la distribución GVE. El primer renglón tiene los resultados de uno de los cuatro métodos de ajuste, el que condujo al EEA mínimo; el segundo renglón los resultados del ajuste mediante optimización numérica; por ello se indica en la columna 7 de la tabla 2, el número de etapas y evaluaciones de la función objetivo (EEA) realizadas.

Tabla 2.

Resultados del mejor método de ajuste (

NR	Parámetros o variables de ajuste				EEA	(etapas)	Periodos de retorno en años
	u (Ym) ¿	α (Sy) η	k (gc) δ	τ		Núm. eval.	10	25	50	100	500	1 000	10 000
1	1354.333	651.656	–0.01045	–	152.8	–	2838	3474	3950	4425	5538	6022	7654
1	1314.343	710.061	–0.04934	–	118.7	(6) 77	3004	3775	4370	4981	6477	7158	9593
1	7.33750	0.47700	–0.16191	–	164.1	–	2805	3448	3927	4406	5532	6026	7715
1	7.33095	0.54632	–0.05204	–	115.8	(5) 59	3063	3934	4620	5333	7116	7943	10979
1	1573.953	432.840	–0.17662	–	187.1	–	2736	3419	3996	4641	6466	7423	11590
1	1585.836	495.145	–0.22334	–	127.0	(9) 96	2990	3877	4656	5556	8248	9737	16711
1	719.122	678.821	1.60280	–1.6186	208.2	–	2737	3456	4041	4669	6312	7109	10192
1	682.916	682.736	1.44950	–1.5351	136.8	(5) 114	3018	3942	4715	5561	7839	8971	13482
4	304.603	65.360	–0.12830	–	21.2	–	475	563	636	714	926	1031	1456
4	302.703	70.727	–0.18816	–	15.1	(3) 36	501	613	710	820	1137	1306	2053
4	5.82925	0.25088	0.98022	–	21.1	–	471	535	582	628	737	784	946
4	5.83748	0.28246	0.16921	–	15.1	(3) 38	495	571	628	685	820	880	1089
4	330.268	46.375	–0.25466	–	23.1	–	467	557	639	735	1034	1205	2049
4	329.236	51.012	–0.33106	–	14.7	(2) 25	494	616	734	881	1380	1692	3426
4	296.257	36.719	0.82660	–0.6639	18.4	–	488	636	788	980	1630	2020	3984
4	299.694	47.526	0.86880	–0.5356	16.5	(4) 97	489	628	767	940	1509	1843	3483
6	193.794	77.343	0.09530	–	19.9	–	350	407	446	482	556	585	668
6	194.915	80.472	0.05088	–	18.2	(6) 82	366	432	480	525	623	663	786
6	5.36830	0.40380	0.03810	–	18.6	–	360	435	492	550	689	751	969
6	5.37352	0.41913	–0.03141	–	18.0	(7) 97	368	447	507	567	710	774	998
6	225.069	49.643	–0.08024	–	19.7	–	344	405	452	501	625	683	902
6	222.698	53.671	–0.15198	–	16.0	(4) 60	363	442	508	580	777	878	1301
6	184.379	170.753	2.27990	–0.5732	23.5	–	339	390	428	465	554	593	732
6	134.630	125.515	1.76910	–1.1231	17.0	(8) 155	363	441	502	567	731	808	1100
7	72.670	60.935	–0.14309	–	20.9	–	234	320	391	469	683	791	1238
7	69.492	61.054	–0.27199	–	11.6	(17) 142	259	381	494	629	1062	1314	2593
7	4.40899	0.93576	–0.75429	–	21.2	–	269	406	527	665	1056	1257	2088
7	4.51265	0.80294	0.01951	–	12.9	(15) 157	255	374	479	598	939	1117	1872
7	96.701	43.595	–0.26479	–	22.3	–	227	314	394	488	785	957	1819
7	93.038	45.880	–0.39338	–	10.1	(29) 254	253	384	516	687	1320	1742	4345
7	31.058	64.405	1.35460	–1.2045	23.3	–	228	313	385	465	686	797	1250
7	26.099	65.681	1.21440	–1.1184	13.3	(11) 157	259	372	471	585	908	1076	1789
11	653.307	326.064	–0.53163	–	435.4	–	2069	3399	4922	7116	16724	24165	82090
11	647.115	217.322	–0.86285	–	239.4	(24) 197	2151	4374	7696	13730	54049	98018	712207
11	6.77948	0.64206	1.12598	–	464.7	–	2069	3315	4662	6498	13755	18888	53440
11	6.83418	0.69789	0.42785	–	245.6	(17) 176	2328	3471	4551	5859	10031	12452	24405
11	800.681	288.286	–0.49667	–	527.8	–	1949	3034	4231	5908	12921	18150	56505
11	770.339	204.980	–0.88059	–	241.6	(15) 155	2149	4360	7704	13851	55856	102475	775362
11	383.398	226.361	1.08750	–1.5303	642.4	–	1877	2691	3436	4307	6903	8308	14509
11	568.382	216.943	0.65960	–0.6111	328.1	(22) 299	2474	4460	6733	9890	22085	30241	77514
15	2003.078	831.726	–0.21273	–	267.4	–	4404	5814	7060	8496	12756	15087	25828
15	2026.598	935.595	–0.17413	–	232.5	(6) 68	4604	6031	7253	8624	12507	14542	23365
15	7.79066	0.46651	0.30729	–	254.4	–	4451	5736	6798	7953	11059	12607	18866
15	7.79009	0.50601	0.03126	–	223.4	(7) 126	4626	5892	6892	7939	10581	11820	16438
15	2357.902	619.836	–0.30074	–	303.7	–	4288	5657	6940	8505	13648	16748	33184
15	2433.709	702.022	–0.27764	–	258.1	(5) 68	4559	6016	7355	8961	14095	17110	32518
15	1082.855	563.483	1.32000	–2.0376	244.0	–	4543	6038	7324	8761	12754	14790	23155
15	1053.838	611.719	1.34830	–2.0345	237.2	(9) 207	4606	6104	7386	8811	12743	14736	22869
17	1628.807	996.848	–0.57129	–	836.9	–	6195	10732	16097	24045	60616	90152	336240
17	1616.945	1421.410	–0.44506	–	675.4	(20) 276	7118	11683	16557	23166	49158	67510	190924
17	7.73260	0.76133	0.85203	–	815.7	–	6290	10492	15061	21301	45851	63053	175998
17	7.68163	0.95060	0.02212	–	611.7	(10) 150	7337	11533	15458	20126	34382	42580	78020
17	2106.257	909.645	–0.50858	–	1085.8	–	5786	9322	13263	18830	42460	60302	193860
17	2195.905	1188.785	–0.50726	–	706.0	(15) 153	6996	11601	16727	23962	54619	77735	250383
17	1115.911	354.767	0.66220	–1.0272	898.9	–	6909	12893	19733	29217	65771	90171	231217
17	1239.906	351.772	0.74800	–1.3118	704.6	(20) 316	6872	11795	17071	24033	48901	64520	147869
19	85.404	126.713	–0.59493	–	218.2	–	685	1301	2043	3160	8458	12845	50915
19	78.052	197.718	–0.52828	–	152.5	(30) 257	933	1732	2644	3956	9676	14089	48253
19	4.78295	1.48007	0.10623	–	160.8	–	807	1681	2718	4203	10282	14564	41466
19	4.92462	1.59587	–0.06368	–	132.6	(5) 46	1050	2171	3458	5242	12065	16576	42118
19	145.161	116.174	–0.58924	–	235.1	–	668	1231	1901	2904	7615	11490	44792
19	159.423	126.657	–0.70133	–	169.5	(3) 21	822	1656	2746	4511	14071	22909	115314
19	5.094	2.691	0.59440	–2.6384	227.6	–	990	2174	3618	5720	14465	20662	59483
19	7.760	2.786	0.71670	–3.3711	145.0	(8) 126	927	1776	2707	3957	8535	11470	27558
22	188.371	82.858	–0.09563	–	13.9	–	396	498	580	667	891	999	1412
22	186.696	90.853	–0.09092	–	11.5	(5) 30	414	524	612	706	946	1060	1496
22	5.39146	0.46596	0.11666	–	12.7	–	399	498	575	654	850	940	1268
22	5.39286	0.48836	0.00813	–	11.0	(9) 97	411	518	601	687	902	1001	1365
22	220.547	57.723	–0.23256	–	16.7	–	386	492	586	695	1025	1209	2086
22	220.547	63.495	–0.23256	–	13.5	(1) 9	403	519	623	742	1105	1308	2273
22	159.932	71.061	1.08400	–0.7922	17.0	–	395	528	648	789	1209	1436	2440
22	126.858	101.282	1.41970	–1.1866	12.0	(25) 348	406	522	618	724	1011	1155	1729
23	342.811	107.694	–0.05301	–	25.0	–	600	718	810	904	1135	1241	1621
23	329.147	117.360	–0.10033	–	21.6	(6) 91	625	772	890	1015	1341	1498	2106
23	5.95790	0.33555	0.34764	–	23.8	–	596	701	779	857	1041	1123	1406
23	5.96422	0.34782	0.10830	–	18.4	(9) 113	610	725	812	899	1110	1205	1542
23	383.728	73.255	–0.20427	–	23.7	–	587	712	819	942	1301	1495	2378
23	381.324	76.095	–0.27097	–	14.5	(6) 75	610	765	907	1076	1613	1925	3507
23	307.251	120.638	1.32490	–0.8408	22.8	–	595	725	837	961	1303	1477	2190
23	290.851	105.453	1.20180	–0.9116	15.5	(10) 188	609	768	908	1038	1524	1762	2776
25	425.699	403.393	–0.67640	–	286.2	–	2562	5019	8180	13221	39714	63594	302482
25	501.829	501.411	–0.55541	–	206.3	(7) 92	2749	4934	7484	11219	28068	41450	149948
25	6.43847	1.10027	0.08350	–	304.9	–	2562	4315	6046	8191	15158	19208	38805
25	6.38270	1.22503	0.00709	–	165.5	(5) 45	2841	5066	7362	10307	20369	26467	57562
25	653.192	398.602	–0.51895	–	453.1	–	2287	3882	5673	8223	19187	27557	91326
25	720.342	460.704	–0.57561	–	212.5	(10) 84	2755	4906	7439	11192	28519	42565	160487
25	70.196	126.890	0.89710	–2.0117	363.8	–	2562	4276	5967	8061	14850	18791	37792
25	15.936	121.364	0.80630	–1.8257	167.4	(11) 248	2878	5140	7478	10481	20761	27000	58857
26	169.825	39.034	0.03898	–	7.9	–	254	287	311	334	385	406	472
26	172.115	40.304	0.02645	–	7.7	(12) 131	260	296	322	347	403	427	502
26	5.22410	0.24629	0.13407	–	7.6	–	255	286	309	331	380	401	470
26	5.22655	0.25159	0.05087	–	7.2	(11) 114	257	290	314	338	390	413	488
26	185.141	25.224	–0.14524	–	7.2	–	250	287	317	350	440	485	673
26	185.141	27.746	–0.14524	–	6.5	(1) 9	257	297	330	367	465	515	722
26	168.627	63.343	1.73350	–0.4572	10.4	–	243	273	296	320	381	410	518
26	165.821	69.474	1.68090	–0.5281	7.2	(18) 251	256	292	320	349	425	461	598
30	41.793	11.095	0.07426	–	1.5	–	65	73	79	85	97	102	116
30	41.445	11.363	0.03287	–	1.3	(10) 98	66	76	83	90	105	112	132
30	3.82453	0.27009	0.14311	–	1.4	–	65	74	80	86	101	107	127
30	3.82584	0.27985	0.02164	–	1.3	(5) 67	66	75	82	88	104	110	132
30	46.034	7.031	–0.12331	–	1.4	–	64	73	81	89	112	123	167
30	45.908	7.343	–0.15104	–	1.0	(6) 62	65	76	85	95	122	135	193
30	35.255	14.569	1.63770	–1.0662	1.4	–	64	75	83	92	116	127	170
30	34.388	15.677	1.65590	–1.0868	1.1	(5) 101	65	77	86	95	120	131	177

Simbología:

NR = número del registro. u, α, k = parámetros de ubicación, escala y forma de la distribución GVE. Ym, Sy, g_c = media, desviación estándar y coeficiente de asimetría de los logaritmos, en la distribución LP3. ¿, η, δ, τ = parámetros de ubicación, escala y primero y segundo de forma de la distribución SJU. EEA = error estándar de ajuste (m³/s o mm).

De manera similar, en los renglones 3 y 4 de cada registro se presentan idénticos resultados para la distribución LP3, pero utilizando alguno de sus seis métodos de ajuste y el de optimización numérica. En los renglones 5 y 6 de cada registro están los resultados de la distribución LOG, en este caso se ajusta solo con el método de momentos L y mediante optimización numérica. Los resultados de los seis renglones descritos proceden de Campos (2013).

Resultados de los ajustes de la distribución SJU

Finalmente, en los renglones 7 y 8 de cada registro de la tabla 2 se exponen los resultados del ajuste de la distribución SJU, con base en las ecuaciones 10 a 13 para estimar sus parámetros de ajuste y 17 a 21 para calcular su EEA. La estimación de las predicciones asociadas a los siete periodos de retorno contrastados, utiliza las ecuaciones 19 a 21, en las cuales P es la probabilidad de no excedencia relativa a cada intervalo de recurrencia. En la figura 1 se muestra uno de tales ajustes.

Figura 1.

Ajuste de la distribución SJU a los datos del registro 15.

Apreciaciones generales en el contraste de la distribución SJU

Los cuatro modelos probabilísticos contrastados (GVE, LP3, LOG y SJU) conducen a predicciones casi idénticas en los periodos de retorno bajos (< de 50 años) e incluso en algunos registros hasta el de 100 años. Se observa una concordancia excelente en todas las predicciones de los seis registros con números: 1, 4, 6, 7, 15 y 23; ya que aún en los periodos de retorno de 1 000 y 10 000 años sus predicciones son del mismo orden de magnitud.

Las predicciones de la distribución SJU son menores en los periodos de retorno de 1 000 y 10 000 años en los registros 11, 17, 25 y 30. En el registro 25, reproduce los resultados del modelo LP3. Por el contrario, la distribución SJU aporta predicciones mayores en los periodos de retorno altos en los registros 19, 22 y 26.

Un aspecto muy importante asociado con la utilidad de la distribución SJU en los análisis probabilísticos de crecientes, es el hecho de resultar aplicable en registros que pueden catalogarse como “difíciles o complicados” de procesar por incluir valores dispersos o eventos extremos que se apartan del conjunto que integra la muestra. Tal es el caso de los registros con números 11, 17, 19 y 25, los cuales corresponden respectivamente a las hidrométricas de Jaina y Huites en la Región Hidrológica Núm. 10 (Sinaloa), Cerca del Moral en la Región Hidrológica Núm. 24-2 (Amistad-Falcón) y El Cuchillo de la Región Hidrológica Núm. 24-3 (Bajo Río Bravo).

Conclusiones

La aplicación de las cuatro distribuciones de probabilidad contrastadas (General de Valores Extremos, Log-Pearson tipo III, Logística Generalizada y Johnson con PS > 1) se recomienda en los análisis probabilísticos de crecientes y de otros datos hidrológicos extremos, debido a la consistencia o similitud numérica que presentan todas sus predicciones en los periodos de retorno reducidos (< 50 años), sin importar el método de ajuste.

El proceso de selección de la distribución de probabilidades del sistema Johnson que mejor se adapta o ajusta a los datos, se considera acertado, dada la similitud que mostraron las predicciones de los cuatro modelos contrastados (GVE, LP3, LOG y SJU) en los registros 1, 4, 6, 7, 15 y 23. En resumen, el modelo probabilístico descrito (SJU) es tan aproximado como los actualmente establecidos bajo precepto.

Además tal proceso define la aplicabilidad del modelo Johnson que no está acotado (PS > 1) hacia registros que presentan valores dispersos. Lo anterior convierte a la distribución SJU en un modelo que siempre será conveniente probar al estimar crecientes, debido a sus bases teóricas que la respaldan y a la con- sistencia general observada en sus predicciones en el contraste realizado, en los 13 registros en que resultó aplicable.

Agradecimientos

Se agradecen las correcciones sugeridas y las observaciones realizadas por los dos árbitros anónimos, las cuales permitieron eliminar errores de redacción y destacar los alcances del trabajo.