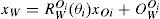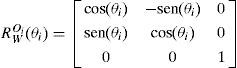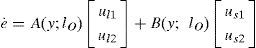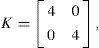El presente trabajo describe una propuesta de control visual para la formación de robots móviles tipo uniciclo bajo el esquema líder-seguidor. Se considera una sola cámara fija observando el espacio de trabajo de los robots que, en términos de la información procesada, puede ser compartida tanto por el robot líder como por el robot seguidor. Lo anterior permitiría que la realización de esta propuesta pueda llevarse a cabo por estrategias de control centralizadas o descentralizadas. Para efectos de simplificar el análisis, también se considera que el plano de imagen es paralelo al plano de movimiento de los robots. El objetivo de formación se establece directamente en coordenadas de imagen y el controlador visual propuesto no depende explícitamente de los parámetros (extrínsecos o intrínsecos) del sistema de visión; lo que en conjunto corresponde a la contribución principal de este artículo. Por último, también como parte importante de este trabajo, para validar la teoría propuesta se detallan experimentos satisfactorios utilizando un sistema de visión de tiempo real y alta velocidad.
This paper describes a visual control proposal for the formation of unicycle-like mobile robots under the leader-follower scheme. It is considered a single fixed camera observing the robots workspace that, in terms of the processed information, can be shared by both the leader robot and the follower robot. This would enable the implementation of this proposal to be performed by centralized or decentralized control strategies. For the purpose of simplifying the analysis, it is also considered that the image plane is parallel to the robots motion plane. The formation objective is established directly in image space and the proposed visual controller does not depend explicitly on the vision system parameters (extrinsic or intrinsic); which together represents the main contribution of this paper. Finally, also as an important part of this work, to validate the proposed theory satisfactory experiments using a real-time and high-speed vision system are detailed.
El problema de formación de robots consiste en establecer el movimiento de un grupo de robots para que, de una manera coordinada o colaborativa, lleven a cabo una tarea específica (Das et al., 2002). Recientemente este problema ha atraído significativamente la atención de la comunidad científica, ya sea por el reto de sus espacios de trabajo no estructurados o por las aplicaciones complejas que se pueden resolver. Existen ciertas tareas que son difíciles de lograr por un solo robot o que son más eficientes si se llevan a cabo mediante la coordinación de un grupo de robots. Entre los ejemplos de esas tareas tenemos: vigilancia, búsqueda de objetos, exploración, rescate y transportación de objetos; las cuales pueden realizarse en ambientes diversos utilizando robots móviles terrestres, aéreos, espaciales, marinos o submarinos.
En la literatura se mencionan diversos métodos para resolver el problema de formación de robots; destacándose los “basados en comportamiento” (Balch y Arkin, 1998; Lawton et al., 2003; Antonelli et al., 2006) en donde, precisamente, diferentes comportamientos, como mantener una formación o seguir un objetivo, se imponen a cada robot (en este método el control de formación exacto es difícil de garantizar); los de “estructura virtual” (Tan y Lewis, 1997; Belta y Kumar, 2002) que consideran al grupo de robots como una sola estructura rígida virtual (aquí es necesaria una comunicación interrobots muy amplia); y los de “líder-seguidor” (Desai et al., 2001; Monteiro et al., 2004; Shao et al., 2005; Consolini et al., 2006) en donde uno o varios robots se designan como los líderes de la formación y el resto como los seguidores, a los cuales se les especifica la postura (posición y orientación) deseada relativa al o los líderes. Este último método es de particular interés debido a su simplicidad y modularidad (Consolini et al., 2006).
Ahora bien, debido a que el espacio de trabajo en este problema de formación de robots es difícil de estructurar se hace necesaria la incorporación de sensores exteroceptivos (además de los propioceptivos o internos de cada robot) que midan de alguna manera tanto el entorno de interacción como las posturas de los demás robots en la formación. Esta situación se ha resuelto utilizando sistemas de posicionamiento global (GPSs), sistemas RADAR (mediante ondas de radio electromagnéticas), sistemas LIDAR (a través de detección láser) o mediante sistemas de visión (Benhimane et al., 2005; Mehta et al., 2006). Sin embargo, dados los recientes avances tecnológicos, los sistemas de visión están siendo cada vez más utilizados.
El uso de un sistema de visión para determinar el movimiento de un sistema robótico se denomina control visual o servo-visual (visual servoing) desde la propuesta original de Hill y Park (1979). Básicamente, existen dos alternativas para el control visual: la “basada en posición”, en donde la sucesión de imágenes se emplea para reconstruir el espacio tridimensional de trabajo; y la “basada en imagen”, en la cual el objetivo de control se da directamente en el espacio de imagen; de manera que en esta última alternativa se incrementa la posibilidad de no depender explícitamente de los parámetros extrínsecos (los que tienen que ver con la postura de la o las cámaras) o intrínsecos (los que tiene que ver con la estructura interna de la o las cámaras) del sistema de visión (Hutchinson et al., 1996).
En el presente trabajo se describe la propuesta de un controlador visual basado en imagen para la formación de dos robots móviles bajo el esquema líderseguidor. Los robots considerados corresponden a los robots móviles terrestres tipo uniciclo, los cuales se caracterizan por tener dos ruedas convencionales con actuadores independientes y una tercera rueda sin actuador para mantener su equilibrio horizontal. Esto los convierte en sistemas no-holonómicos que presentan ciertas propiedades interesantes; por ejemplo, el sistema linealizado es no-controlable, por lo que los métodos lineales de análisis y diseño no pueden aplicarse; tampoco existe una ley de control continua que incluya solo retroalimentación de estados capaz de estabilizar el sistema a un estado de equilibrio (Brockett, 1983). Trabajos relacionados con el objetivo de control de postura de un robot móvil mediante el control visual los podemos ver en Hashimoto y Noritsugu (1997), Conticelli et al. (1999), Mariottini et al. (2004), Fang et al. (2005) y López-Nicolás et al. (2006).
En particular, sobre el control visual con el objetivo de formación de robots móviles bajo el esquema líderseguidor, se pueden mencionar las propuestas de Renaud et al. (2004), Benhimane et al. (2005), Soria et al. (2006) y Min et al. (2009); las cuales emplean la alternativa basada en posición con cámara montada y con la necesidad del conocimiento total o parcial de los parámetros del sistema de visión. En Das et al. (2002) y Roberti et al. (2011) se proponen controladores con las mismas condiciones anteriores, pero utilizando sistemas de visión catadióptricos, básicamente para ampliar el campo de visión. En Dani et al. (2009) se describe un trabajo también basado en posición y con cámara montada, pero eliminando totalmente la necesidad del conocimiento de los parámetros del sistema de visión.
A diferencia de los trabajos recién citados, la disposición del sistema robótico en este documento considera una cámara fija observando todo el espacio de trabajo de los robots (figura 1) con la alternativa de control visual basada en imagen. Lo anterior va encaminado a la eliminación de los problemas de oclusión y la facilidad de establecer las variables de formación deseadas, sin necesidad de realizar medición tridimensional (en coordenadas de mundo ΣW) alguna. Dependiendo de la aplicación, dicha cámara puede estar instalada (o fija) en un globo aerostático, en un edificio o en alguna parte alta del entorno. Ahora bien, uno de los propósitos es que el sistema de visión sea compartido tanto por el robot líder como por el robot seguidor, de tal suerte que la implementación de la presente propuesta se pueda lograr por esquemas de control, tanto centralizados como descentralizados. Para efectos de simplificar el análisis, también se considera que el plano de imagen es paralelo al plano horizontal de movimiento de los robots. De esta manera, explícitamente el objetivo de formación se establece de manera directa en coordenadas de imagen y se logra que el controlador visual propuesto no dependa explícitamente de los parámetros (extrínsecos o intrínsecos) del sistema de visión; lo que en conjunto corresponde a la contribución principal de este artículo. Por último, también como parte importante de este trabajo, para validar la teoría propuesta se detallan experimentos satisfactorios utilizando un sistema de visión de tiempo real y alta velocidad.
FormulaciónEn este apartado se describe la formulación de la propuesta del controlador visual para la formación de robots uniciclos en el esquema líder-seguidor.
Modelo de imagenConsidere la vista de planta del sistema robótico mostrada en la figura 21. Observe que se han colocado diversos marcos coordenados (compare las figuras 1 y 2): ΣC el marco de la cámara con origen en el centro de la lente, ΣW el marco de mundo fijo en algún lugar del espacio de trabajo a una altura conveniente, ΣOl el marco del líder y ΣOs el marco del seguidor (estos dos últimos marcos con origen en el centro del eje que une sus dos ruedas a una altura convenientemente nula). Note que los ejes “3” de cada marco son paralelos (debido a la postura de la cámara utilizada), por lo que los planos W1−W2, C1−C2, Ol1−Ol2 y Os1−Os2 también son paralelos (tanto Ol1 como Os1 apuntan en la dirección de movimiento de cada uniciclo respectivo); sin embargo, puede existir rotación entre cada uno de estos planos.
Con base en la estrategia de control visual o servo-visual utilizada, considere como objetos de interés (Hutchinson et al., 1996) dos discos (de radios arbitrarios, pero con la condición de que sus centroides puedan ser procesados por el sistema de visión) localizados sobre los robots móviles (figura 2): el disco al del líder con centro xOla=[lO 0]T [m], el disco bl del líder con centro en xOlb=[0 0]T [m] (los subíndices Ol denotan que son vectores de posición respecto al marco ΣOl) y los discos as y bs del seguidor puestos de manera similar, es decir, con xOsa=[lO 0]T [m] y xOsb=[0 0]T [m] (los subíndices Os denotan que son vectores de posición respecto al marco ΣOs); donde la distancia lO>0 es una constante.
Ahora bien, el modelo de imagen considerado para el mapeo hacia el plano de imagen y1−y2 es el que corresponde al obtenido mediante trasformaciones y proyección de perspectiva con lente delgada, dado por (Kelly y Reyes, 2000):
donde xC=xC1xC2xC3T es el punto correspondiente con coordenadas tridimensionales respecto al marco ΣC de la cámara, αC es el factor de conversión de metros a píxeles (considerándose el mismo factor de conversión tanto para y1 como para y2), λC es la distancia focal de la lente y [uC vC]T es el vector que incluye el centro de la imagen y las posibles desalineaciones entre el eje óptico de la cámara y su arreglo de sensores fotosensibles. Observe que y1 siempre es paralelo y apunta en la misma dirección que C1 (lo mismo sucede con y2 y C2; consulte la figura 2).La transformación de coordenadas entre el marco del mundo y el marco de la cámara se puede realizar mediante
donde xW=xW1xW2xW3T es el punto tridimensional correspondiente respecto a ΣW, OWC es el vector de posición del origen de ΣC respecto a ΣWWX y
es la matriz de rotación de ΣC respecto a ΣW (π [rad] alrededor de W1 y φ [rad] alrededor de W3, por la probable rotación “desconocida” pero constante entre los planos W1−W2 y C1−C2).Modelo de los uniciclosEl robot líder y el robot seguidor considerados corresponden a los que se componen de dos ruedas convencionales con actuadores independientes y una tercer rueda sin actuador para mantener su equilibrio horizontal y que poseen el siguiente modelo cinemático (Canudas de Wit et al., 1996; Dixon et al., 2001):
donde l y s son subíndices para denotar correspondencia con el robot líder o con el robot seguidor, respectivamente. El vector xWi=xWi1xWi20T denota la posición del robot uniciclo i (el punto medio del eje que une las dos ruedas a una altura convenientemente nula, ver figuras 1 y 2, θi la orientación del uniciclo i, ambos respecto a ΣW. Las componentes del vector de entrada ui=[ui1ui2]T son la magnitud de la velocidad lineal (a lo largo de Oi1) y angular (alrededor de Oi3) del robot i, respectivamente.
Variables de formaciónLas variables de formación serán las referencias mediante las que se establecerá formalmente el objetivo de formación de los robots uniciclo, estas variables de formación estarán dadas directamente en coordenadas de imagen. Para esto, considere como variables de formación a ρ y α, donde (figura 2)
es la distancia en píxeles entre las proyecciones en el plano de imagen de los centroides de los discos a de los robots líder y seguidor, y α la orientación de la formación. Obsérvese en la figura 2 que donde γ es un ángulo auxiliar, ψl=θl−φ es la orientación del uniciclo líder en el plano de imagen y es el ángulo formado entre el eje y1 y la línea formada por yal y yas (para la cálculo de las variables α, β y ψl se recomienda utilizar la función atan2, ver por ejemplo Spong et al. (2006) y tener especial cuidado para que α, β, Ψl∈ℜ de manera que no se les limite a±π [rad]).ControladorEn esta sección se detallan el modelo a controlar y el diseño del controlador visual para la formación de uniciclos además de su prueba de estabilidad.
Modelo a controlarEl modelo a controlar corresponderá a la dinámica desarrollada por dos señales de error relacionadas con las variables de formación (4) y (5). En esta búsqueda, definimos el siguiente vector de error
donde ρd y αd son la distancia (en píxeles) y la orientación deseadas (y constantes) de la formación, respectivamente. De manera que la derivada respecto al tiempo de (7) resultapor lo que es necesario derivar respecto al tiempo (4) y (5). Antes de encontrar las derivadas temporales, primero observe que un punto xOi respecto al marco ΣOi (con i={l, s}) puede transformarse hacia el marco ΣW mediante
donde el vector OWOi denota el vector de posición del origen de ΣOi respecto a ΣW y representa la matriz de rotación (en función de θi) del marco ΣOi respecto a ΣW. De esta manera, utilizando (2), (3) y (9) se encuentra que la derivada temporal de (1) es (ecuación 10) donde ψi=θi−φ es la orientación del robot i en el plano de imagen.Ahora, siguiendo la metodología propuesta en Bugarin y Kelly (2008), para simplificar (10) definimos y¯i=yai-ybi, de modo que utilizando (1), (2) y (9) se puede llegar a lo siguiente
puesto que xCai3=xCbi3. En consecuencia, despejando sen(ψi) y cos(ψi) de (11) se puede simplificar (10) para la variación respecto al tiempo de yai, llegando al siguiente resultado
es decir, con las condiciones especificadas, la variación respecto al tiempo de yai no depende de los parámetros (intrínsecos o extrínsecos) de la cámara. Finalmente, después de derivar respecto al tiempo (4) y (5) utilizando (12), el modelo a controlar (8) se simplifica a
donde
con y¯ls=yal-yas. Cabe destacar que el determinante de B(y; lO) es igual a ‖ys‖lOρ, en donde tanto ‖y¯S‖ (la distancia en píxeles entre los centroides de los discos as y bs del robot seguidor) como lO son constantes, por lo que si ρ≠0 entonces existe la inversa de B(y; lO).Objetivo del control de formación y diseño del controladorEl objetivo del control de formación queda formalmente establecido en relación a (7) mediante
es decir, se desea que las variables de formación, especificadas directamente en coordenadas de imagen, lleguen asintóticamente a un valor constante deseado.
Por hipótesis supóngase que existe la inversa de B(y; lO), entonces para resolver el objetivo de control (14) recién descrito, el presente trabajo propone el siguiente controlador visual para el robot seguidor
donde K=KT>0 es una matriz de ganancia. Note que este controlador no depende de los parámetros (intrínsecos o extrínsecos) del sistema de visión y que puede ponerse en marcha completamente solo con mediciones directas en el plano de imagen. Asimismo, debe comentarse que se necesita la transmisión de las velocidades del líder al seguidor (trabajos recientes, como el de Dani et al., (2009), van en la dirección de estimar dichas velocidades para eliminar la necesidad de su transmisión; en el presente artículo esto se considera como un trabajo futuro) y del parámetro lO (el cual es un parámetro determinado por el propio usuario).
Para la prueba de estabilidad, se supone válida la existencia de la inversa de B(y; lO), luego se sustituye la ley de control (15) en el modelo (13) para encontrar la ecuación de lazo cerrado del sistema robótico, la cual queda expresada por
De esta manera, puede observarse que la ecuación del sistema en lazo cerrado corresponde a un sistema lineal e invariante en el tiempo (o autónomo) y debido a que por diseño K=KT>0 el origen es su único punto de equilibrio con la propiedad de ser exponencialmente estable de manera global (vea por ejemplo Khalil (2001)); de esta manera se demuestra que el objetivo de control (14) es satisfecho. Con esto también se demuestra que al tender los errores exponencialmente a cero, ρ tiende exponencialmente a ρd, de manera que si la condición inicial para ρ(0)≠0 y ρd>0 entonces ρ(t)≠0 ∀t>0; lo que implica que la suposición inicial de que la inversa de B(y; lO) existe es válida.
Cabe mencionar que en todo el análisis realizado se ha considerado el sistema robótico como un sistema continuo y determinista, por lo que la velocidad del robot líder ul especificada en (15) debe ser continuamente diferenciable. Por otro lado y para cuestiones prácticas, puede considerarse que el valor de ρ siempre tendrá una magnitud aceptable que no afectaría el cálculo de las matrices A(y; lO) y B(y; lO), puesto que de inicio debe existir una distancia mínima suficiente entre los robots para que estos físicamente no estén uno sobre el otro.
Validación experimentalPara validar la teoría propuesta, en este apartado se exponen experimentos desarrollados con dos robots uniciclo modelo YSR-A de la empresa Yujin. Dichos robots reciben las consignas de velocidad a través de un transmisor RF que se conecta a una computadora personal vía puerto serie. A esta misma computadora se le conecta (vía Camera Link), mediante una tarjeta video-procesadora Leonardo de la empresa Arvoo, una cámara de video digital de alta velocidad modelo UF-1000CL de la empresa UNIQ. Sobre el sistema operativo RTLinux se desarrolla un sistema de control de tiempo real para el procesamiento de las imágenes y la ley de control, obteniéndose un periodo de muestreo estricto de 0.005 [s]. Cabe mencionar que el procesamiento de las imágenes se lleva a cabo mediante segmentación binaria y seguimiento de la característica de imagen (el centroide de los discos).
A continuación se detallan dos escenarios que corresponden a las siguientes variables de formación deseadas:
ρd=70 [píxeles] y αd=90°,
con la ganancia en el controlador
y con la distancia entre los centros de los discos objetivo lO=0.0375 [m]. Estos 4 valores son los únicos necesarios para la experimentación.
Ahora bien, solamente para efectos de comparación, se realizaron simulaciones correspondientes con los siguientes parámetros del sistema de visión: αC=72000 [píxeles/m], λC=0.0075 [m], uC=160 [píxeles], vC=120 [píxeles], OWC = [001.5]T [m] y φ = 0 [rad]..
Escenario 1Este escenario 1 se experimentó con velocidades del líder nulas, es decir, con ul=0 y con las siguientes condiciones iniciales
xWl(0)=[0.0758m − 0.0086m 43.31°]T,
xWs(0)=[0.0837m 0.2750m 177.92°]T.
Estas condiciones iniciales corresponden a (en píxeles) yal(0)=[197.3 113.8]T, ybl(0)=[187.4 123.1]T, yas(0)=[176.7 20.0]T, ybs(0)=[190.3 20.5]T, ρ(0)=96.0 y α(0)=59.05°.
La figura 3 muestra las gráficas comparativas entre lo simulado y lo experimentado para el escenario 1. La figura 3a presenta, en el plano de imagen, yal mediante un círculo, ybl a través de un punto (ambas correspondientes al robot líder que no se mueve con una orientación de 43.31°, figura 2) y la traza del movimiento de yas, de manera que puede apreciarse (en el experimento) que conforme avanza el robot seguidor yas se mueve de yas(0)=[176.7 20.0]T [píxeles] hasta yas(3)=[149.6 62.1]T [píxeles]. Esto corresponde a una ρ(3)≈70.3 [píxeles] y a una α(3)≈89.4°, valores muy cercanos a los deseados (en la simulación los errores son prácticamente nulos). Las figuras 3b, 3c y 3d ilustran la evolución contra el tiempo de las señales de control del robot seguidor, de la señal de error eρ y de la señal de error eα, respectivamente. Como puede notarse, el desempeño es muy satisfactorio y las gráficas comparativas entre lo simulado y lo experimentado son muy similares.
Gráficas de la simulación (trazo discontinuo) y del experimento (trazo continuo) para el escenario 1
En el experimento del escenario 2 se pide el siguiente vector de velocidades al robot líder: ul=[0.05m/s 0rad/s]T, partiendo de las condiciones iniciales expresadas a continuación:
xWl(0)=[−0.1835m −0.1203m 34.67°]T,
xWs(0)=[−0.3392m 0.1976m −20.22°]T.
Estas condiciones iniciales corresponden a (en píxeles) yal(0)=[105.1 156.6]T, ybl(0)=[93.9 163.3]T, yas(0)=[51.1 56.4]T, ybs(0)=[39.4 49.6]T, ρ(0)=112.9 y α(0)=83.89°.
La figura 4a describe la traza, del experimento y de lo simulado, en el plano de imagen de la evolución tanto de yas como de yal; en el experimento yas parte de yas(0)=[51.1 56.4]T [píxeles] y termina en yas(7)=[169.5 24.0]T [píxeles] en tanto que yal inicia en yal(0)=[105.1 155.6]T [píxeles] y termina en yal(7)=[210.5 81.0]T. Esto corresponde a una ρ(7)≈70.1 [píxeles] y a una α(7)≈90.5°, los cuales son valores bastante aproximados a los deseados (nuevamente, en la simulación los errores son prácticamente nulos). Cabe destacar que el desempeño experimental es bastante satisfactorio y muy similar a lo simulado. Sin embargo, nótese que existen pequeñas diferencias entre lo simulado y lo experimentado en las trazas de yal (que corresponden al robot líder); lo anterior se debe a que el robot líder se mueve en lazo abierto y no se compensan las posibles perturbaciones presentes (derrapes, deslizamientos o desperfectos en el camino no modelados). También hay diferencias, al inicio del experimento respecto a lo simulado, en la traza de yas, las cuales también se deben a los posibles derrapes, deslizamientos y desperfectos en el camino, pero que ahora sí están compensadas por el controlador. Lo anterior se puede ver en la figura 4b que gráfica la evolución respecto al tiempo de las señales de control y en donde se observa un sobreimpulso en la señal de control us2 para solventar dichas situaciones. Las figuras 4c y 4d ilustran la evolución contra el tiempo de los errores de formación. En forma general se puede decir que el desempeño del sistema robótico con el controlador visual propuesto es muy satisfactorio, resaltándose que las gráficas en comparación (experimentos con simulaciones) son muy similares.
Gráficas de la simulación (trazo discontinuo) y del experimento (trazo continuo) para el escenario 2
Se describió la propuesta de un control visual para la formación de robots móviles tipo uniciclo bajo el esquema líder-seguidor que no depende de los parámetros (intrínsecos o extrínsecos) del sistema de visión. Para este efecto, se consideró una sola cámara fija observando el espacio de trabajo de los robots que, en términos de la información procesada, se puede compartir tanto por el robot líder como por el robot seguidor. Lo anterior permite que la implementación de esta propuesta pueda llevarse a cabo por estrategias de control centralizadas o descentralizadas. Ahora bien, el objetivo de control de formación se establece directamente en coordenadas de imagen. Cabe hacer notar que el controlador (además de mediciones en el espacio de imagen) solamente requiere el conocimiento de las velocidades del robot líder y de un parámetro establecido por el propio usuario; ambos requerimientos pudieran estimarse (ver por ejemplo, Dani et al., (2009)) o solventarse por alguna ley de adaptación (lo que se considera como un trabajo futuro, para efectos de este documento). Finalmente, también como parte importante de este trabajo, se detallan experimentos satisfactorios utilizando un sistema de visión de tiempo real y alta velocidad para validar la teoría propuesta con un periodo de muestreo estricto de 0.005 [s].
Se agradece el apoyo de CONACYT México (Proyecto 166654), PROMEP, DGEST y al Instituto Tecnológico de Ensenada.
Eusebio Bugarin-Carlos. Recibió el título de ingeniería en el Instituto Tecnológico de Tijuana (ITT) en 1995. Luego, en 1998, obtuvo el título de maestría en ciencias en ingeniería eléctrica por el Instituto Tecnológico de La Laguna (ITL) y, posteriormente, en 2009 el grado de doctor en ciencias en electrónica y telecomunicaciones por el Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE). Actualmente es profesor-investigador en el Instituto Tecnológico de Ensenada y sus áreas de interés incluyen control de robots, formación de robots y visión artificial.
Ana Yaveni Aguilar-Bustos. En 1995 obtuvo el título de ingeniería por el Instituto Tecnológico de Tijuana (ITT). Después, recibió tanto el título de maestría en ciencias en electrónica y telecomunicaciones (en 1998) como el grado de doctor en ciencias en electrónica y telecomunicaciones (en 2006) en el Centro de Investigación Científica y de Educación Superior de Ensenada (CICESE). Actualmente es profesor-investigador en el Instituto Tecnológico de Ensenada y sus principales áreas de interés son sistemas no-lineales, sistemas complejos y caos.